How to determine the consensus threshold in group decision making: a method based on efficiency benchmark using benefit and cost insight

Abstract

In the past 10 years, a large number of consensus-reaching approaches for group decision making (GDM) have been proposed. While these methods either focus on the cost of the consensus reaching or the convergency of the consensus process, the consensus efficiency has long been ignored. Meanwhile, the measurements of consensus threshold are often determined by some subjective and intuitive judgements, such as management experience and estimations for the degree of satisfaction, which lack a theoretical foundation. In management applications, how to measure consensus and how to evaluate a consensus reaching method are also ambiguous. To tackle these questions, we introduce efficiency measures into the consensus reaching process of GDM and achieve a comprehensive evaluation of current consensus methods through an efficiency analysis of consensus costs and consensus improvement. From the perspective of efficiency, we propose a benchmark in consensus reaching by data envelopment analysis without explicit input benchmark models, and then present an objective method for consensus threshold determination in GDM. Finally, we use numerical examples to illustrate the usability of our method.

1 Introduction

Consensus in group decision making (GDM) can improve the satisfaction of the decision makers (DMs) because their opinions are taken into consideration in order to achieve an acceptable level of consensus (Shi et al. 1996; Shi and Li 2007; Woolley et al. 2010; Dong et al. 2018; Zhang et al. 2019b; Ding et al. 2019). Many consensus deepening mechanisms, also called the consensus reaching process (CRP), have been developed to improve the consent state in GDM over the past 20 years (Herrera et al. 2001; Herrera-Viedma et al. 2002; Dong et al. 2015; Xu et al. 2015; Li et al. 2018, 2019; Liu et al. 2019; Lin et al. 2020, and so on). These studies on the process of reaching consensus can be divided into the following two categories:

• (1) Consensus reaching mechanism. This process focuses on how to effectively improve the consensus degree through the individual preference adjustment of DMs (Herrera-Viedma et al. 2002; Dong et al. 2015) or identification of influencing factors, such as non-cooperative and opinion dynamics (Palomares et al. 2014; Xu et al. 2015; Dong et al. 2016a, b), so as to reach a satisfactory consensus threshold.

• (2) Minimum consensus costs. The total consensus cost is to optimize minimum deviation from individual preferences to the collective opinion under a constraint of consensus degree (Dong et al. 2016a, b). In consideration of this consensus cost, it is generally believed that consensus reaching is to encourage DMs to change individual preferences through some compensation (Zhang et al. 2019a, c; Gong et al. 2015b; ; Xu et al. 2020).

To evaluate the CRP, Zhang et al. (2019b) proposed the following five metrics: the number of adjusted decision-makers (AE), the number of adjusted alternatives (AA), the number of adjusted preference values (AP), the distance between the original and the adjusted preference information (AD), and the number of negotiation rounds required to reach consensus (Z). In addition, many other metrics have been developed to deal with the consensus degree, such as total deviation among individual preference relations and a weighted deviation from each preference relation to the collective opinion (Chiclana et al. 2013; González-Arteaga et al. 2016; Herrera-Viedma et al. 2014; Zhang et al. 2018). Labella et al. (2018) compared the performance of the existing methods and summarized the challenges of CRP, such as the effectiveness and the time cost. Zhang et al. (2019b) studied consensus efficiency by performing a comprehensive analysis of various CRPs based on several established minimum cost criteria. Zhang et al. (2019c) studied a minimum consensus cost model under a soft consensus degree.

Although the methods to CRP have been investigated intensively and are very useful in GDM, there still exist gaps that must be filled for the following reasons:

• (1) These methods ignore consensus efficiency. They pursue higher consensus degree or minimum cost payment separately, regardless of the efficiency in CRP, that is, the equilibrium between consensus cost and consensus improvement. For instance, in an urban resettlement project, the real estate developer often hopes to obtain a consensus among households on the demolition alternative plans through the minimum compensation cost, but the unreasonable cost often results in lower consensus efficiency (a lower consensus degree among residents), and the consensus reaching process takes a long time and negotiations are difficult. It even caused nail households whose compensation cost are expensive for a higher consensus degree (Liu et al. 2020) or residents to breach their contracts due to the unsatisfied compensation (Wu et al. 2018). The cost reduction and the consensus improvement need to be balanced.

• (2) The consensus threshold cannot be determined using objective methods. Some subjective and intuitive judgements, such as management experience (majority principle) and estimates for the degree of satisfaction, are typically used in GDM (Shi and Yu 1989; Liu et al. 2019; Ding et al. 2019; Zhang et al. 2019b). The famous 80/20 Rule (Pareto principle) rule is a common approach. There are also some simplified methods, for example, it can be set to 2/3 according to the “minority obeying majority” principle in a democratic decision (Liu et al. 2019; Xu et al. 2015; Chao et al. 2021). The consensus level setting does not take into account the satisfaction degree of participants and the non-cooperative behaviors it causes, and the cost of consensus is not considered.

In order to overcome these shortcomings, this study aims to establish a method for evaluating consensus efficiency as well as a benchmark measurement using insights about costs and benefits in GDM. Based on this benchmark, we propose an objective method for determining the threshold of consensus degree by some data envelopment analysis (DEA) methods, which have been developed in recent years. DEA is a classic data-driven tool used to evaluate the efficiency of each production unit under minimum cost and maximum benefit (Charnes et al. 1978). It is generalized to include no explicit inputs (DEA-WEI) (Liu et al. 2011), so that the DEA can be used to arbitrary performance evaluation or score ranking without limitation of a production process with clear inputs and outputs. DEA benchmark models are developed to establish a target for each decision-making unit (DMU) to reach their reference with a DEA efficiency (Cook et al. 2014, 2017, 2019; Ruiz et al. 2015; Ruiz and Sirvent 2016). The implementation process includes the following:

We differentiate between cost and benefit metrics in the evaluation of CRP, and construct measures for this evaluation. We use a DEA-WEI model to assess CRP efficiency and then compare DEA efficiency with other exiting methods for evaluation. We then comprehensively analyze the efficiency performance of different CRP methods. For the second part of the implementation process, we establish an objective consensus threshold in CRP based on efficiency benchmarks from different CRP methods. Using the DEA-WEI benchmarking model, we can determine the efficiency target for each CRP method. It can be used to construct a consensus benchmark, which can be further used for determining the efficiency threshold. Finally, we give two application examples to show the process for establishing a consensus threshold for different CRP methods, justifying the feasibility and usability of the proposed approach.

The contributions of the paper are that the efficiency (cost and benefit insight) is introduced in group decision-making, and the objective determination method of group consensus degree is first proposed for CRP in group decision-making based on the efficiency benchmark.

The remainder of this study is organized as follows: Sect. 2 illustrates general CRP methods in GDM. Then, in Sect. 3, we introduce a new efficiency insight in the CRP, which is different from the concept in existing researches. The efficiency evaluation and comparison of different CRP methods are implemented using a DEA-WEI model. The results show the difference between the proposed efficiency and traditional research. Based on the previous DEA efficiency measurement, we use an efficiency benchmark in DEA to determine consensus threshold in GDM. Section 4 demonstrates the consensus threshold establishing process using the DEA-WEI benchmark model. In Sect. 5, we use two examples to illustrate the construction process for the consensus threshold. Finally, this study ends with some concluding remarks in Sect. 6.

Summary of the abbreviations and symbols used in this study.

Abbreviations	Meaning
GDM	Group decision making
MAGDM	GDM with multi-attribute preference matrix
PRGDM	GDM with preference relations
CRP	Consensus reaching process
DM	Decision maker
DEA	Data envelopment analysis
DEA-WEI	Data envelopment analysis without explicit inputs
DMU	Decision-making unit
E	The set of extreme efficient DMUs
AE	The number of adjusted decision-makers
AA	The number of adjusted alternatives
AP	The number of adjusted preference values
AD	The distance between the original and the adjusted preference information
Z	The number of negotiation rounds required to reach consensus.
CD	Consensus degree
DR	Direction rule
IR.	Preset threshold
AS	The smallest closed convex and free-disposal attainable set
PPS	A bounded production possibility set
PBOC	The people’s bank of China
P2P	Peer to peer online lending
Symbols
$e_{i}$	The ith DM.
$x_{i}$	The ith alternative
$a_{i}$	The ith attribute
$V^{(k)} = \left( {v_{ij}^{(k)} } \right)_{n \times l}$	The multiple attribute decision matrix
$\bar{V}^{(k)} = (\bar{v}_{ij}^{(k)} )_{n \times l}$	The adjusted multiple attribute decision matrix
$V^{(c)} = (v_{ij}^{(c)} )_{n \times l}$	The collective multiple attribute decision matrix
$\lambda = (\lambda_{1} ,\lambda_{2} , \ldots ,\lambda_{m} )^{T}$	A weighting vector for the DMs
$w = (w_{1} ,w_{2} , \ldots ,w_{l} )^{T}$	a weighting vector for the attributes
$P = (p_{ij}^{{}} )_{n \times n}$	A preference matrix
$\bar{P} = (\bar{p}_{ij}^{{}} )_{n \times n}$	The modified preference matrix
$P^{(c)} = (p_{ij}^{(c)} )_{n \times n}$	The collective preference matrix
$y_{1j} ,y_{2j} , \ldots ,y_{sj}$	The s consensus measure at period t-1.
$y_{1j}^{g} ,y_{2j}^{g} , \ldots ,y_{sj}^{g}$	The preset goal of the s consensus measure
$y_{1j}^{DEA} ,y_{2j}^{DEA} , \ldots ,y_{sj}^{DEA}$	The target of the DMUs at s consensus measure

2 Consensus reaching process

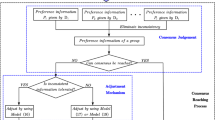
CRP aims to find the best collective alternative solution, in which DMs achieve a consent state for a collective opinion consolidated and aggregated preferences (or opinions) regarding a set of alternatives. The general CRP includes three steps (Fig. 1) to accomplish a GDM. (1) All of the individual preferences should be integrated as a collective opinion, which represents an evaluation or ranking of alternatives. (2) To judge whether the consensus degree for the collective opinion among DMs, the CRP go to next selection stage if the consensus degree can be accepted. (3) Consensus deepening is implemented by negotiation and through the modification of individual preferences.

Fig. 1

General consensus reaching process

Generally, the GDM can be divided into two different categories: GDM with multi-attribute preference matrix (MAGDM) and GDM with preference relations (PRGDM) based on the decision information provided by DMs. We assume that a finite set $DM = \{ e_{1} ,e_{2} , \ldots ,e_{m} \} (m \ge 2)$ is $m$ DMs, a finite set $X = \{ x_{1} ,x_{2} , \ldots ,x_{n} \} (n \ge 2)$ is $n$ alternatives, and $X = \{ a_{1} ,a_{2} , \ldots ,a_{l} \} (l \ge 2)$ is a finite set of attributes. For MAGDM, each DM provides their multiple attribute decision matrix $V^{(k)} = \left( {v_{ij}^{(k)} } \right)_{n \times l} ,k \in 1,2, \ldots ,m$, where $v_{ij}^{(k)}$ represents his or her preference value for the alternative $x_{i}$ with respect to the attribute $a_{j}$. Let $\lambda = (\lambda_{1} ,\lambda_{2} , \ldots ,\lambda_{m} )^{T}$ and $w = (w_{1} ,w_{2} , \ldots ,w_{l} )^{T}$ be a weighting vector for the DMs and the attributes. In PRGDM, each DM provides their preference relation $V^{(k)} = \left( {p_{ij}^{(k)} } \right)_{n \times n} ,k \in 1,2, \ldots ,m$ using a pairwise comparison matrix. In either MAGDM or PRGDM, the collective opinion is a ranking of the alternatives from the $V^{(k)}$. The related works and detailed steps are shown as follows:

Many rules for CRP are applied to improve reaching consensus, such as who should modify their preferences, whose preference value and alternatives deviate considerably from the group’s opinion. The different CRP methods are introduced in this subsection:

• (i) MAGDM

The main CRP methods in MAGDM are briefly described as follows (Zhang et al. 2019b):

MACRP1 (who should modify their preference): a preset threshold is denoted as IR.E. In each consensus round of MACRP1, according to IR.E, the DM with $CD(e_{k} )$ less than IR.E, i.e. $k \in \{ i\left| {CD(e_{i} ) \le IR.E,i = 1,2, \ldots ,m\} } \right.$ are regarded as contributing less to consensus. Thus, decision-maker $e_{k}$ should modify his or her preference according to direction rule (DR), while the other decision-makers’ preferences may remain unchanged.

We assume that $\bar{V}^{(k)} = (\bar{v}_{ij}^{(k)} )_{n \times l}$ is the adjusted multiple attribute decision matrix associated with $V^{(k)} = (v_{ij}^{(k)} )_{n \times l}$. The DR is $\bar{v}_{ij}^{(k)} \in \left[ {\hbox{min} \left( {v_{ij}^{(k)} ,v_{ij}^{(c)} } \right),\hbox{max} \left( {v_{ij}^{(k)} ,v_{ij}^{(c)} } \right)} \right]$ if $k \in \{ i\left| {CD(e_{i} ) \le IR.E,i = 1,2, \ldots ,m\} } \right.$. It is $\bar{v}_{ij}^{(k)} = v_{ij}^{(k)}$ if $k \notin \{ i\left| {CD(e_{i} ) \le IR.E,i = 1,2, \ldots ,m\} } \right.$. Particularly, in each round, the DR can select one DM with a minimum degree of consensus to modify their preference, i.e. $k \in \{ i\left| {CD(e_{i} ) = \hbox{min} CD(e_{k} ),k = 1,2, \ldots ,m\} } \right.$.

MACRP2 (which alternatives should be modified): for a given threshold IR.A. In each consensus round of MACRP2, according to IR.A, the alternatives with $CD(x_{h} )$ less than IR.A, i.e. $h \in \{ i\left| {CD(x_{i} ) \le IR.A,i = 1,2, \ldots ,n\} } \right.$ are regarded as contributing less to consensus. Thus, the alternative $x_{k}$ should be modified according to the DR.

The DR is such that $\bar{v}_{hj}^{(k)} \in \left[ {\hbox{min} \left( {v_{hj}^{(k)} ,v_{ij}^{(c)} } \right),\hbox{max} \left( {v_{hj}^{(k)} ,v_{ij}^{(c)} } \right)} \right]$, if $h \in \{ i\left| {CD(x_{i} ) \le IR.A,i = 1,2, \ldots ,n\} } \right.$.$\bar{v}_{hj}^{(k)} = v_{ij}^{(k)}$ and if $h \notin \{ i\left| {CD(x_{i} ) \le IR.A,i = 1,2, \ldots ,n\} } \right.$. Particularly, in each round, it can select one DM with minimum consensus degree to modify their preference, that is, $h \in \{ i\left| {CD(x_{i} ) = \hbox{min} CD(x_{i} ),i = 1,2, \ldots ,n\} } \right.$.

MACRP3 (which preferences should be modified): for a preset threshold IR.P in GDM. It can be used to determine the preference that should be adjusted in each consensus round of MACRP3. The preference $CD(p_{ij} )$, with consensus degree less than IR.P, that is, $(i,j) \in \{ (s,t)\left| {CD(p_{s,t} ) \le IR.P,s = 1,2, \ldots ,m;t = 1,2, \ldots ,n\} } \right.$ are regarded as contributing less to consensus. Thus, preference $p_{ij}$ should be modified according to the DR.

The DR is that $\bar{v}_{i,j}^{(k)} \in \left[ {\hbox{min} \left( {v_{ij}^{(k)} ,v_{ij}^{(c)} } \right),\hbox{max} \left( {v_{ij}^{(k)} ,v_{ij}^{(c)} } \right)} \right]$ if $(i,j) \in \{ (s,t)\left| {CD(p_{s,t} ) \le IR.P,s = 1,2, \ldots ,m;t = 1,2, \ldots ,n\} } \right.$. $\bar{v}_{ij}^{(k)} = v_{ij}^{(k)}$ if $(i,j) \notin \{ (s,t)\left| {CD(p_{s,t} ) \le IR.P,s = 1,2, \ldots ,m;t = 1,2, \ldots ,n\} } \right.$. Particularly, in each round, decision moderator can select one DM with a minimum consensus degree to modify their preference, that is, $(i,j) \in \{ (s,t)\left| {CD(p_{s,t} ) = \hbox{min} CD(p_{g,h} ),g = 1,2, \ldots m;h = 1,2, \ldots ,n\} } \right.$.

MACRP4 (preference modification in terms of DR): in MACRP4, the DR is feedback information from the collective opinion, which is used to help DMs make a judgment about their preferences. For an adjusted matrix $\bar{V}^{(k)} = (\bar{v}_{ij}^{(k)} )_{n \times l} ,\bar{v}_{ij}^{(k)} \in \left[ {\hbox{min} \left( {v_{ij}^{(k)} ,v_{ij}^{(c)} } \right),\hbox{max} \left( {v_{ij}^{(k)} ,v_{ij}^{(c)} } \right)} \right]$, for $i = 1,2, \ldots ,m;j = 1,2, \ldots ,l$.

MACRP5 (minimum number of adjusted DMs): it is a CRP with minimum number of adjusted DMs in each consensus round. That is:

$$ \begin{array}{*{20}l} {Min} & {\sum\limits_{k = 1}^{m} {z^{(k)} } } \\ \end{array} $$

(1)

where $z^{(k)} = \left\{ \begin{array}{ll} 0,&if\; {v_{ij}^{(k)} = \bar{v}_{ij}^{(k)} } \; {\forall i,j} \\ 1,&\,\,{\text{otherwise}} \hfill \\ \end{array} \right.$

MACRP6 (minimum number of adjusted alternatives): the number of adjusted alternatives should be as small as possible in the CRPs. MACRP6 means the number of adjusted alternatives in CRP:

$$ \begin{array}{*{20}c} {Min} & {\sum\limits_{k = 1}^{m} {\sum\limits_{i = 1}^{n} {y_{i}^{(k)} } } } \\ \end{array} $$

(2)

where $y_{i}^{(k)} = \left\{ \begin{array}{ll} 0,&\,\,if\; {v_{ij}^{(k)} = \bar{v}_{ij}^{(k)} } \; {\forall j} \\ 1,&\,\,{\text{otherwise}} \hfill \\ \end{array} \right.$

MACRP7 (minimum number of adjusted preferences): in CRPs, we hope the number of adjusted preference values are as small as possible. To do this, the CRP with the minimum adjusted preference values is as follows:

$$ \begin{array}{*{20}c} {Min} & {\sum\limits_{k = 1}^{m} {\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{l} {x_{ij}^{(k)} } } } } \\ \end{array} $$

(3)

where $x_{ij}^{(k)} = \left\{ \begin{array}{ll} 0,&if\,v_{ij}^{(k)} = \bar{v}_{ij}^{(k)} \hfill \\ 1,{\text{otherwise}} \hfill \\ \end{array} \right.$

MACRP8 (minimum distance between original preference and adjusted decision matrices): in CRP, the adjusted preference values should be as small as possible, such that the following target is given:

$$ \begin{array}{*{20}c} {Min} & {\sum\limits_{k = 1}^{m} {d(V^{(k)} ,\bar{V}^{(k)} )} } \\ \end{array} $$

(4)

where $d(V^{(k)} ,\bar{V}^{(k)} ) = \sum\limits_{k = 1}^{m} {\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{l} {\left| {v_{ij}^{(k)} - \bar{v}_{ij}^{(k)} } \right|} } }$.

From the above MACRP steps 1–7, the GDM aim to achieve a minimum consensus

$$ CD\{ e_{1} ,e_{2} , \ldots ,e_{m} \} = 1 - \frac{1}{mn(n - 1)}\sum\limits_{k = 1}^{m} {\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1,j \ne i}^{l} {\left| {v_{ij}^{(k)} - v_{ij}^{(c)} } \right|} } } . $$

(5)

• (ii) PRGDM

A GDM based on preference relations is another important type of decision question (Kou et al. 2014, 2016, 2021; Zhang et al. 2021). Compared with the multi-attribute preference matrix, preference relations in PRGDM is a pairwise comparison matrix, for which the entry is of relative importance for the two alternatives. The main CRP methods in PRGDM are briefly described as follows (Zhang et al. 2019b):

PRCRP1:

In each round of PRCRP 1, the DM with the lowest consensus degree is identified, as well as the direction of change in which the identified DM is expected to modify his or her preference

PRCRP2:

In each consensus round of PRCRP 2, the alternative with the lowest consensus degree is identified, and DMs are assisted in modifying their preferences with respect to the identified alternative

PRCRP3:

In each consensus round of PRCRP 3, the preference value with the lowest consensus degree is identified, and DMs are assisted in modifying their preferences with respect to the identified preference values

PRCRP4:

In each consensus round of PRCRP 4, DMs identify the direction to change their preference relations

PRCRP5:

In each consensus round of PRCRP 5, the optimization-based consensus rule is adopted to obtain the optimal adjusted preference relations by minimizing the adjusted DMs

PRCRP6:

In each consensus round of PRCRP 6, the optimization-based consensus rule is utilized to yield the optimal adjusted preference relations by minimizing the adjusted alternatives

PRCRP7:

In each consensus round of PRCRP 7, the optimization-based consensus rule is used to yield the optimal adjusted preference relations by minimizing the number of adjusted preference values

PRCRP 8:

In each consensus round of PRCRP 8, the optimization-based consensus rule is adopted to generate the optimal adjusted preference relations by minimizing the distance between individual original and adjusted preference relations

Based on the above two types of CRP processes, we decided to perform the efficiency analysis and efficiency benchmark in following sections and then establish a consensus threshold in CRP. The logical framework of this study is described below in Fig. 2.

Fig. 2

Logical flow of this study

In the Sect. 3, we will introduce the efficiency (cost and benefit) of the consensus-reaching process, and compare our efficiency with the previous literatures through numerical analysis, which is the basis for establishing the consensus threshold of the efficiency perspective. Then, in Sect. 4, we use an efficiency benchmark model to determine the threshold of the consensus degree based on the efficiency in the Sect. 3. This section uses numerical examples to illustrate the meaning of benchmarks, and then establishes a consensus threshold determination method. Finally, examples are used to show the process of the entire method.

3 Efficiency evaluation and comparison

Efficiency is the ability to allocate effort towards producing a specific outcome while reducing expenditures and unnecessary effort. In a large number of group decision-making cases, efficiency is the key factor affecting the successful implementation of the decision making (Labella et al. 2018). For example, in an urban resettlement project (Gong et al. 2015a; b), real estate developers wanted to obtain project approval from the majority of households (higher consensus degree) with minimal compensation costs. Another case considered emergency decision making (Xu et al. 2015), in which organizers needed experts to develop a consistent rescue plan in a short period of time. These cases reflect a need or desire for efficiency in decision making. A natural problem arising from the existing research, which considers many methods for consensus reaching in GDM, but for many of which efficiency is unclear, making it difficult to apply different methods in different real-world environments.

In GDM, the cost or expense is preference modification deviation or preference changing means cost of MAGDM or PRGDM, the outcome is consensus improvement. Zhang et al. (2019b) first proposed consensus efficiency and designed the comparison criteria for its measurement. These criteria include: the number of adjusted DMs, the number of adjusted alternatives, the number of adjusted preference values, the distance between the original and the adjusted preference information and the number of negotiation rounds required to reach consensus. In addition, many other consensus measurements were used in evaluate consensus degree, such as ordinal consensus degree (Herrera-Viedma et al. 2002; Dong et al. 2015) and cardinal consensus degree (Dong et al. 2015).

We can divide these most used measurements into the consensus benefit and cost as follows:

3.1 Evaluation indexes

The consensus measure can be divided and combined into the following cost and benefit measures: We took PRGDM as an example and assumed that $X = (x_{i} )_{n} ,i \in N$ represents alternatives and $DM = (e_{k} )_{m} ,k \in M$ is a DM. Let $P^{(k)} = (p_{ij}^{(k)} )_{n \times n} ,k \in M$ be an additive preference relation provided from DMs $e_{k} ,k \in M$, where $M$ is the total number of DMs and $n$ is the number of alternatives.

Benefit: A “soft” consensus is proposed to measure the consensus degree, which is essentially a total deviation from the individual preference or priority vector to the collective opinion (Cabrerizo et al. 2010; Chiclana et al. 2013).

The consensus degree (CD): Let $P^{(c)} = (p_{ij}^{(c)} )_{n \times n}$ be collective preference from individual decision makers:

$$ p_{ij}^{(c)} = \sum\limits_{k = 1}^{m} {\lambda_{k} \cdot p_{ij}^{(k)} } . $$

(6)

The CD is defined with the following levels:

$$ CD(e_{k} ) = 1 - \frac{1}{n(n - 1)}\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1,j \ne i}^{n} {\left| {p_{ij}^{(k)} - p_{ij}^{(c)} } \right|} } $$

(7)

$$ CD(x_{i} ) = 1 - \frac{1}{m(n - 1)}\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1,j \ne i}^{n} {\left| {p_{ij}^{(k)} - p_{ij}^{(c)} } \right|} } $$

(8)

$$ CD(p_{ij} ) = 1 - \frac{1}{m}\sum\limits_{k = 1}^{m} {\left| {p_{ij}^{(k)} - p_{ij}^{(c)} } \right|} $$

(9)

$$ CD\{ e_{1} ,e_{2} , \ldots ,e_{m} \} = 1 - \frac{1}{mn(n - 1)}\sum\limits_{k = 1}^{m} {\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1,j \ne i}^{n} {\left| {p_{ij}^{(k)} - p_{ij}^{(c)} } \right|} } } $$

(10)

The above consensus degrees, 2 through 5, are denoted as DMs, alternative and preference value, and total CD, respectively. The consensus degree of MAGDM can be denoted as follows in same way. For example:

$$ CD(e_{k} ) = 1 - \frac{1}{n(n - 1)}\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1,j \ne i}^{n} {\left| {v_{ij}^{(k)} - v_{ij}^{(c)} } \right|} } $$

(11)

$$ CD(x_{i} ) = 1 - \frac{1}{m(n - 1)}\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1,j \ne i}^{l} {\left| {v_{ij}^{(k)} - v_{ij}^{(c)} } \right|} } $$

(12)

$$ CD(p_{ij} ) = 1 - \frac{1}{m}\sum\limits_{k = 1}^{m} {\left| {v_{ij}^{(k)} - v_{ij}^{(c)} } \right|} $$

(13)

$$ CD\{ e_{1} ,e_{2} , \ldots ,e_{m} \} = 1 - \frac{1}{mn(n - 1)}\sum\limits_{k = 1}^{m} {\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1,j \ne i}^{l} {\left| {v_{ij}^{(k)} - v_{ij}^{(c)} } \right|} } } . $$

(14)

Cost: (Zhang et al. 2019a, b, c)

• (1) The cost comprises the actual number of adjusted DMs, the number of adjusted alternatives, the number of adjusted preference values and the distance between the original and the adjusted preference information that contains the same characters and, naturally, represent the total deviation after two rounds of preference modification.

Let $\bar{P}^{(k)} = (\bar{p}_{ij}^{(k)} )_{n \times n} ,k \in M$ be the modified preference information associated with $P^{(k)} = (p_{ij}^{(k)} )_{n \times n} ,k \in M$. Also let $P = \{ P^{(1)} ,P^{(2)} , \ldots , P^{(m)} \}$ and $\bar{P} = \{ \bar{P}^{(1)} , \bar{P}^{(2)} , \ldots ,\bar{P}^{(m)} \}$.

The number of adjusted decision-makers (AE) is as follows:

$$ AE = \sum\limits_{k = 1}^{m} {z^{(k)} } , $$

(12)

where $z^{(k)} = \left\{ {\begin{array}{*{20}l} {0,\, p_{ij}^{(k)} = \bar{p}_{ij}^{(k)} \forall i,j} \\ {1,\, {\text{otherwise}}} \\ \end{array} } \right.$.

The number of adjusted alternatives (AA) is as follows:

$$ AA = \sum\limits_{k = 1}^{m} {\sum\limits_{i = 1}^{n} {h_{i}^{(k)} } } , $$

(13)

where $h_{i}^{(k)} = \left\{ {\begin{array}{*{20}l} {0, \, p_{ij}^{(k)} = \bar{p}_{ij}^{(k)} \forall j} \\ {1, \,{\text{otherwise}}} \\ \end{array} } \right.$.

The number of adjusted preference values (AP) is as follows:

$$ AP = \sum\limits_{k = 1}^{m} {\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {l_{ij}^{(k)} } } } , $$

(14)

where $l_{ij}^{(k)} = \left\{ {\begin{array}{*{20}c} {0, \, p_{ij}^{(k)} = \bar{p}_{ij}^{(k)} } \\ {1,\, {\text{otherwise}}} \\ \end{array} } \right.$.

The distance between the original and the adjusted preference information (AD) is as follows:

$$ d(P,\bar{P}) = \sum\limits_{k = 1}^{m} {\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {\left| {p_{ij}^{(k)} - \bar{p}_{ij}^{(k)} } \right|} } } . $$

(15)

The $d(P,\bar{P}) = 0$ means the decision makers’ preference information does not change.

• (2) The number of negotiation rounds required to reach consensus (Z) is a maximum round to reach the preset threshold of the CD after individual preference modification is conducted with feedback information.

3.2 Efficiency evaluation methods

Many methods for evaluating efficiency have been developed over the past few decades, such as data envelope analysis (Charnes et al. 1978), which is used to evaluate the efficiency of each production unit, assuming minimum cost and maximum benefit. Let $\left\{ {Y_{j} \left| {j = 1,2, \ldots ,n} \right.} \right\}$ be a group of data in $\Re_{ + }^{s}$. The smallest closed convex and free-disposal attainable set (AS) that contains the observations is as follows (Liu et al. 2011):

$$ AS = \left\{ {Y\left| {Y \le \sum\limits_{j = 1}^{n} {\lambda_{j} Y_{j} } ,\sum\limits_{j = 1}^{n} {\lambda_{j} } = 1,\lambda_{j} \ge 0} \right.} \right\} $$

(16)

Let $P = \{ (X,Y)\}$ be a bounded production possibility set (PPS), which is a free-disposal and closed convex technology set. Then its projection of all outputs is as follows:

ASI = {$Y$: There is an $X$ such that $(X,Y) \in P$}, which defines a bounded, closed convex and free-disposal attainable set.

Let $\{ (X_{i} ,Y_{i} )\left| {i = 1,2, \ldots ,n} \right.\}$ be a group of input and output data. Then, it can define a bounded closed convex and free-disposal attainable set ASII as follows:

$$ ASII \, = \left\{ {F \le \sum\limits_{j = 1}^{n} {\lambda_{j} \frac{{Y_{j} }}{{X_{j} }}} ,\sum\limits_{j = 1}^{n} {\lambda_{j} } = 1,\lambda_{j} \ge 0} \right\} $$

(17)

where ${Y \mathord{\left/ {\vphantom {Y X}} \right. \kern-0pt} X}$ is the divided data, $\left\{ {\frac{Y}{X} = \left( {\frac{{Y_{1} }}{{X_{1} }},\frac{{Y_{2} }}{{X_{1} }}, \ldots ,\frac{{Y_{s} }}{{X_{1} }},\frac{{Y_{1} }}{{X_{2} }},\frac{{Y_{2} }}{{X_{2} }}, \ldots ,\frac{{Y_{s} }}{{X_{2} }}, \ldots ,\frac{{Y_{1} }}{{X_{m} }},\frac{{Y_{2} }}{{X_{m} }}, \ldots ,\frac{{Y_{s} }}{{X_{m} }}} \right)} \right\}$ are $s \times m$ dimension vectors with $X = \left( {x_{1} ,x_{2} , \ldots ,x_{m} } \right)$, and $Y = \left( {y_{y} ,y_{2} , \ldots ,y_{s} } \right)$ are input and output variables. Thus, the variables in DEA-WEI (Liu et al. 2011) constitute a ratio, rather than raw data:

$$ \begin{aligned} \theta^{*} = \begin{array}{*{20}c} {Max} & \theta \\ \end{array} \hfill \\ S.t.\,\,\,\,\,\sum\limits_{j = 1}^{n} {\lambda_{j} } Y_{rj} \ge \theta Y_{r0} ;\quad r \in E, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\sum\limits_{j = 1}^{n} {\lambda_{j} } = 1,\lambda_{j} \ge 0; \hfill \\ \,\,\,\,\,\,\,\,\,\,\,j = 1,2, \ldots ,n. \hfill \\ \end{aligned} $$

(18)

where $Y_{rj} = \frac{{Y_{j} }}{{X_{r} }}$ is the feasible ratio.

From the above analysis, the efficiency is estimated as the maximum benefit under the condition of limited resources (costs). Actually, the costs AE, AA and AP are necessary conditions of the AD, which means it is composed of changes to the three conditions. Because AD is actually a linear function of CD, we thus construct following metrics:

$y_{1} = \frac{CD}{AE}$, which means return consensus improvement on unit adjusted decision-makers;

$y_{2} = \frac{CD}{AA}$, which means return consensus improvement on unit adjusted alternatives;

$y_{3} = \frac{CD}{AP}$, which means return consensus improvement on unit adjusted preference values;

$y_{4} = \frac{CD}{Z}$, which means return consensus improvement at each iteration.

Therefore, the consensus efficiency needs to be measured using the model (18), a data-driven composite index for efficiency evaluation, which aims to judge whether the consensus steps (as a decision-making unit) can sustain a satisfactory level of efficiency.

3.3 Efficiency evaluation and comparison

In this subsection, we evaluate the relative efficiency of different consensus reaching methods in MACRPs and PRCRPs. In addition, we include the multi-stage optimization-based CRPs proposed in Zhang et al. (2019) in tracking the analysis of efficiency. The data used in these examples comprise the simulation results from that study.

3.3.1 Efficiency evaluation

Our examples aim to answer the following key questions:

• 1. How effective are the different consensus reaching methods in MACRPs and PRCRPs? Efficiency is facilitated by gaining the largest possible consensus improvement with the lowest possible cost.

• 2. How can one evaluate the consensus reaching mechanism comprehensively and objectively? That is, how do we integrate multiple consensus metrics?

To answer the above questions, we implemented a numerical simulation experiments to establish some general laws in a simulated environment. The simulation experiment was performed 1000 times and the average value of each index was taken. We then calculated a different value for each measure $\{ y_{1} ,y_{2} ,y_{3} ,y_{4} \}$ and used model (19) to analyze the efficiency of the different consensus processes. The simulation for the MACRP and PRCRP processes is listed in Tables 1 and 2.

Table 1 Simulation method for measuring the efficiency of MACRPs

Table 2 Simulation method for measuring the efficiency of PRCRPs

The difference for PRCRPs is that the decision matrix is a preference relationship, for which Table 2 illustrates the basic procedures.

In addition to the basic consensus method, a multiple-stage optimization method proposed in Zhang, et al. (2019b) was included in the scope of comparison, simplified as MACRP9. For MACRPs and PRCRPs, the parameter settings were $m = 3;n = 4;l = 4$ and $m = 4,n = 5,l = 4$, and $m = 4,n = 4$ and $m = 5,n = 5$, respectively.

The results of the efficiency analysis are shown in Tables 3 and  4. We observe that MACRP5 and MACRP6 were efficient for all cases of both MACRPs and PRCRPs. In addition, PRCRP4, PRCRP5, PRCRP6 and PRCRP7 were found to be efficient for PRCRPs.

Table 3 Consensus efficiency of different MACRPs

Table 4 Consensus efficiency of different PRCRPs

Furthermore, MACRP1, MACRP2 and MACRP3 were inefficient for MACRPs. Similarity, PRCRP1, PRCRP 2 and PRCRP3 were also not efficient enough for PRCRPs. MACRP8 and PRCRP8 had the lowest average efficiency.

Through the analysis of the efficiency of these different consensus methods, we obtained the following conclusions:

• (1) There is no direct correlation relation between efficiency and degree of consensus. In fact, the efficiency of consensus reaching clearly did not decrease with the increase of the consensus degree. In some cases, the efficiency of consensus was better under the condition of a high degree of consensus. For example, for MACRP2 in $m = 3;\;n = 4;\;l = 4$, its efficiency was 0.856 (with an $\alpha \; = \;0.88$), higher than 0.82 when the consensus degree was $\alpha \; = \;0.84$.

• (2) We identified that the fewest adjusted alternatives (MACRP5) and the fewest decision makers to adjust individual preference (MACRP6) are the most robust strategies for CRP in GDM. Theoretically, in the decision-making consensus mechanism, the fewest number of DMs that need to adjust preferences or modify their preferences on the least alternatives represent the basis for the most effective methods.

• (3) Determined alternatives that need to be adjusted (MACRP2) and optimized the total distance between original preferences and adjusted preferences (MACRP8) have a lower efficiency. In decision-making, it is often inefficient to determine the alternatives that need to be modified, or to plan the optimal decision-making adjustment matrix in negotiation. There is no objective standard for determining those alternatives, which can easily influence the efficiency of decision-making.

• (4) Multi-stage optimization (MACRP9) was found not to be the best solution for optimizing efficiency. Through simulation experiments, we observed that this consensus reaching process did not achieve the most effective results in some decision-making environments.

  • Additionally, for different evaluation indicators, our method was to fuse these indicators to obtain a comprehensive efficiency index. We suggest that the different CRP methods need to allow for adjustments to decision preferences—to varying degrees—while improving the consensus degree. For this study, we distinguished between the consensus improvement (outputs or benefits) of the decision consensus process and the preference adjustment (inputs or costs) made for it and, therefore, we obtained the following conclusions for the consensus measures.

• (5) In CRP, the best method should be selected to achieve a maximum degree of consensus improvement while requiring the smallest level of needed preference adjustment.

3.3.2 Comparison analysis

Zhang et al. (2019b) proposed a comprehensive efficiency based on the idea of averaging, that is, efficiency could be calculated by finding the mean value of all measures. We compare the two methods in Figs. 3 and 4. The MACRP3 and MACRP 4 have a comprehensive efficiency by their averaging index. Our method is MACRP 5 and MACRP 6 with the most stable efficiency.

Fig. 3

Consensus comparisons of MACRPs

Fig. 4

Consensus efficiency of PRCRPs

PRCRP3 and PRCRP4 are CRP methods with lower rank using Zhang et al. (2019b). From the perspective of DEA efficiency, PRCRP4, PRCRP5, PRCRP6 and PRCRP7 are the best choice for PRCRPs (Fig. 4). PRCRP9 had a higher efficiency in PRGDM, although it did not have the highest comprehensive score in Zhang et al. (2019b).

Using a comparative analysis, a difference can be found between the DEA efficiency of the cost–benefit perspective and average score of the consensus cost (Zhang et al. 2019b). The reason is that the two methods share different perspectives on the consensus process. We examined the balance of the consensus improvement and the consensus cost. The latter method is to minimize the consensus cost in CRP. The efficiency studied in this article is the concept of “relative”, not absolutely the lowest consensus cost or the highest degree of consensus degree. It argues that the efficiency of decision-making activities should take into account the consensus cost and the consensus degree, that is, to achieve a relatively higher degree of consensus through the smaller consensus cost. From the results of this efficiency analysis, we can conclude that the efficiency of consensus methods is different. Therefore, in CRP, different rules need different consensus costs to reach a given consensus threshold. We need, however, to further use the DEA benchmark model to establish the efficiency target of the consensus method, and to determine the consensus threshold based on the efficiency benchmark.

In this section, we have established the efficiency of the cost and benefit perspective in GDM. On this basis, we establish an objective method for determining the consensus threshold at the following Sect. 4.

4 Efficiency-based consensus threshold

In GDM, traditional consensus means a full and unanimous agreement in a group, but such type of consensus is virtually impossible in real-world settings (Kacprzyk and Fedrizzi 1986). Thus, consensus typically means to reach a consent and not necessarily the agreement of all group participants (Herrera-Viedma et al. 2014). This kind of GDM, as in this case, is usually defined by researchers as a soft consensus. A large number of measurement methods for soft consensus have been proposed and studied extensively. Overall, they can be divided into two ideas: the total distance among the DMs’ preferences and the total distance between individual preferences and the group’s opinion. Thus, the measure of the consensus degree is a value in the interval [0, 1] to indicate the consensus degree. Then, each CRP method is used to raise this value to a certain threshold, which is preset by the decision organizer or moderator.

However, it is of some importance to determine what threshold the consensus value reaches so that the consensus process ends, as well as the (probably different) threshold when we can think that the soft consensus has been reached. This generally proves to be a very difficult problem, both in application problems and theoretical research. The existing literature presently verifies the convergence of a consensus method, but the method for determining the consensus threshold is rarely involved. At present, there is no accepted standard for the selection of consensus threshold in the soft consensus, because of lack of theoretical basis. Subjective or empirical determination of consensus degree is often too high or too low, and there are shortcomings. A too lower consensus level leads to conflicting opinions and non-cooperative behavior, such as low consensus on policies poses a challenge to social stability, e.g. France’s Yellow Vests (Grossman 2019) and non-cooperative decision-making of emergency management plan after the Xuanwei earthquake in Yunnan, China (Xu et al. 2015). A higher consensus level may cause a waste of resources, because the choice of the final solution will not change with the consensus level. This is demonstrated in Liu et al. (2019) using an example of residential resettlement in the construction of a hydropower station in a river basin in China. Thus, an objective consensus determination method needs to be established. In this section, we try to provide a solution from the perspective of efficiency.

Using the DEA efficiency model, we built a consensus threshold based on the measure of consensus. The general idea was to determine the efficiency frontier boundaries of the consensus method, such as MACRP1-MACRP 8 (or PRCRP 8-PRCRP8) for the selected metrics, to determine their efficiency improvement targets for different methods, and then finally to obtain the consensus threshold based on these targets.

4.1 Model formulation

We assumed the goals of the consensus threshold for $s$ metrics of DMU set $G$, CRP methods at period t-1 were $y_{1j}^{g} ,y_{2j}^{g} , \ldots ,y_{sj}^{g} ,j \in M$ and the consensus measure was $y_{1j}^{{}} ,y_{2j}^{{}} , \ldots ,y_{sj} ,j \in M$ at period t-1. Then, we determined a target $y_{1j}^{DEA} ,y_{2j}^{DEA} , \ldots ,y_{sj}^{DEA}$, located at the efficiency frontier boundary to achieve the stated goal, so as to modify the goal in terms of the target with a higher level of efficiency. It should be emphasized that such a consensus degree should be made in terms of targets that are attainable and that also represent best practices with satisfactory level of efficiency. The DEA-WEI benchmark model (Cook et al. 2019) proposed adjusting the benchmark to the goals so that targets lie on the best practice frontier of the DEA technology associated with the actual performances of period t, that is $y_{rj}^{DEA} = y_{rj} + s_{rj}^{{}} ,r = 1,2, \ldots ,s;j \in M$, where the $s_{rj}$ is an incentive space for the improvement of the consensus according to the target using DEA. The consensus goal $y_{1j}^{g} ,y_{2j}^{g} , \ldots ,y_{sj}^{g}$ was adjusted in terms of $y_{rj}^{g} = y_{rj} + s_{rj}^{g}$, where $s_{rj}^{g}$ was the adjustment distance between the set goal and the actual consensus level. Thus, the consensus threshold is the optimal value $s_{rj}^{*}$ closest to $y_{rj}^{DEA}$, i.e.$y_{rj}^{DEA} = y_{rj}^{{}} + s_{rj}^{*}$. The optimized $s_{rj}^{*}$ is a solution for following optimization (19):

$$ \begin{aligned} Min\;\;\;\sum\limits_{j \in M} {\sum\limits_{r = 1}^{s} {\left| {s_{rj}^{g} - s_{rj} } \right|} } \\ & S.t.\,\,\,\,\,\,y_{rj}^{DEA} = y_{rj} + s_{rj} ,r = 1,2, \ldots ,s;j \in G;\,s_{rj} \,\,free,\forall r,j \\ \end{aligned} $$

(19)

Following this equation, we used an example to illustrate the detailed procedure on our proposed consensus threshold building method.

Example 1

(data in MACRPs): Let $\left\{ {e_{1} ,e_{2} , \ldots ,e_{m} } \right\}$ be $m$ number of decision makers for the given evaluation metrics $CD(e_{1} ,e_{2} , \ldots ,e_{m} )$ and AD as outputs in Eq. (10), which means the total consensus improvement and the total individual preference modifications. The performances in two periods of the eight methods on two indicators are listed below in Table 5.

Table 5 Data of numerical examples

From Table 6 below, we observe that the values of both indicators improved to varying degrees, but the levels of efficiency were different. For the benchmarks of the different measures, we hoped that this benchmark would be as close as possible to the corresponding point on its efficiency boundary. Table 6 also gives the goal of the CD measurement, the actual value and the corresponding efficiency target. The consensus benchmark, we have determined, was actually the corresponding target of each method on the frontier boundary of efficiency. If the goal value is smaller than the target on the efficiency boundary, it is clear that the decision-making needs to continue because the consensus can be improved in this consensus metric, for example, in MACRP1. If the consensus goal is equal to the corresponding target value on the efficiency boundary, it means that the consensus measure has reached the efficiency benchmark, such as MACRP 3.

Table 6 Results of numerical examples

This consensus benchmarking process is described in Fig. 5. MACRP7, MACRP5, MACRP3 and MACRP4 together constitute the frontier boundary of efficiency. Their consensus degree represents DEA efficiency. MACRP1, MACRP2 and MACRP6 fall out of the efficiency boundaries. Their efficiency benchmark on the corresponding efficiency boundary curve can be obtained by optimizing $s_{rj}^{*}$, by which $y_{rj}^{DEA}$ can be calculated and is served as the efficiency benchmark of these methods. The comparison of this value $y_{rj}^{DEA}$ with the goal $y_{rj}^{g}$ can determine whether the consensus process continues or terminates.

Fig. 5

The efficient boundary of the example 1

Using this example, we can show the process of establishing the efficiency threshold, which is actually the efficiency benchmark (target) corresponding to the DEA efficiency frontier in each evaluation index system. Relative to the subjectively determined threshold, we establish the efficiency frontier of different methods under different measures systems, and then compare the distance between the goal value ($y_{rj}^{g}$) and the efficiency benchmark value ($y_{rj}^{DEA}$), and adjust the consensus threshold appropriately. This process is an objective method for establishing consensus in GDM.

4.2 Benchmarking building

Next, we needed to determine the corresponding points $y_{rj}^{DEA}$ of each measure $y_{rj}$ on the efficiency frontier; they were closest to the target $s_{ij}^{*}$. Letting $\bar{p}_{ij}^{(k,B)}$ be an adjusted benchmark for comparison preference for alternative $i$ to alternative $j$ of decision maker $e^{(k)}$, the benchmark ideally belongs on the efficiency frontier. The characterization of a technically efficient boundary $\partial (AS)$ was used in the formulation of the benchmarking models as follows (Ruiz et al. 2015).

$$ \partial (AS) = \left\{ {(X,Y) \in \Re_{ + }^{m + s} \left| \begin{aligned} X = \sum\limits_{i \in E} {\lambda_{i} X_{i} } ,Y = \sum\limits_{j \in E} {\lambda_{j} Y_{j} } ,\sum\limits_{j \in E} {\lambda_{j} } = 1,\lambda_{j} \ge 0; \hfill \\ - vX + uY + u_{0} + d_{j} = 0;j \in E; \hfill \\ v_{r} \ge 1;r = 1,2, \ldots ,m; \hfill \\ u_{r} \ge 1;r = 1,2, \ldots ,n; \hfill \\ d_{j} \le Mb_{j} ;j \in E; \hfill \\ \lambda_{j} \le M(1 - b_{j} );j \in E; \hfill \\ d_{j} ,\lambda_{j} \ge 0;b_{j} \in [0,1];j \in E;u_{0} \in \Re ; \hfill \\ M\begin{array}{*{20}c} {\text{is}} & {\text{bigpositive}} \\ \end{array} \hfill \\ \end{aligned} \right.} \right\} . $$

(20)

where $E$ is the set of extreme efficient DMUs (Charnes et al. 1991). Following Charnes et al. (1991), the DMUs in E and E^’ are Pareto-efficient. E consists of the extreme efficient units, whereas those in E^’ are Pareto-efficient units that can be expressed as a combination of DMUs in E.

In GDM, the different consensus methods are collected as Table 3 in Zhang et al. (2019b). The input $X = \{ x_{ri} \} = \{ AE,AA,AP,d(P,\bar{P}),Z\left| {r \in E} \right.\}$ is the cost which is function of individual preference modification deviation, and the output $Y = \{ y_{rj} \} = \{ CD\{ e_{1} ,e_{2} , \ldots ,e_{m} \} \left| {r \in E\} } \right.$ is consensus improvement. The subjective set parameter $\alpha$(in Zhang et al. 2019b) is exogenous variable in efficiency model, which means the returns to scale. Based on the technically efficient bound $\partial (AS)$, the benchmark is constructed as follows:

$$ \begin{aligned} Min\,\,\,\,\,CD\{ e_{1} , \ldots ,e_{m} \}_{r} - CD\{ e_{1} , \ldots ,e_{m} \}_{r}^{*} \hfill \\ S.t.\,\,\,\,\,\,(X,Y) \in \partial (AS) \hfill \\ \end{aligned} . $$

(21)

In model (13), the unknown variable that needs to be optimized is a function of deviations in individual preferences. The detailed model is model (22):

$$ \begin{aligned} & Min\,\,\,CD\{ e_{1} , \ldots ,e_{m} \}_{r} - CD\{ e_{1} , \ldots ,e_{m} \}_{r}^{*} \\ & S.t.\,\,\,\sum\limits_{j \in E} {\lambda_{j} y_{rj} = y_{rj} + t_{j} ;\,\,\,r = 1,2, \ldots ,s} \,\,\,(22 - 1) \\ & \sum\limits_{j \in E} {\lambda_{i} x_{si} = y = x_{si} + h_{i} ;\,\,\,s = 1,2, \ldots ,n\,\,\,(22 - 2)} \\ & \sum\limits_{j \in E} {\lambda_{j} = 1,\lambda_{j} \ge 0;\,\,\,(22 - 3)} \\ & - vX + uY + u_{0} + d_{j} = 0;j \in E;\,\,\,(22 - 4) \\ & v_{i} \ge 1;\,\,\,i = 1,2, \ldots ,n\,\,\,(22 - 5) \\ & u_{i} \ge 1;\,\,\,i = 1,2, \ldots ,n\,\,\,(22 - 6) \\ & d_{j} \le Mb_{j} ;j \in E;\,\,\,(22 - 7) \\ & \lambda_{j} \le M(1 - b_{j} );j \in E;\,\,\,(22 - 8) \\ & d_{j} ,\lambda_{j} \ge 0;b_{j} \in [0,1];E;u_{0} \in \Re ;\,\,\,(22 - 9) \\ & M\,is\,big positive \\ \end{aligned} $$

(22)

where $CD\{ e_{1} , \ldots ,e_{m} \}^{*} = 1 - \frac{1}{m \times n \times (n - 1)}\sum\nolimits_{k = 1}^{m} {\sum\nolimits_{i = 1}^{n} {\sum\limits_{j = 1,j \ne i}^{n} {\left| {\bar{p}_{ij}^{(k)} - p_{ij}^{(c)} } \right|} } }$, $p_{ij}^{(c)} = \sum\limits_{M} {\sigma_{k} \bar{p}_{ij}^{(k)} }$. In GDM, the tth state of preference modification is usually taken as a test state to measure whether the consensus degree of the (t +1)th preference modification reaches an objective efficiency benchmark. That is, $CD\{ e_{1} , \ldots ,e_{m} \}_{r}^{*}$ is a known consensus degree at the (t +1)th preference modification, and the optimization is to seek the target of the efficiency boundary corresponding to the $CD\{ e_{1} , \ldots ,e_{m} \}_{r}^{*}$. If $CD\{ e_{1} , \ldots ,e_{m} \}_{r}^{*}$ is within the target efficiency boundary curve, further preference adjustments are needed to reach the efficiency boundary. Otherwise, the decision will have reached the efficiency benchmark and the CRP is brought to a stop.

In model (22), condition (22-1), (22-2) and (22-3) are to hold the optimization belonging to AS. The supporting hyper-planes contain facets of the Pareto frontier of AS (noting that their coefficients are restricted to be strictly positive) by virtue of conditions (22-4) and (22-5).

To covert the model (22) into a linear programming, we introduced two new parameters to the objective function $\left| {p_{ij}^{(k)} - p_{ij}^{(c)} } \right|$. There must exist $u_{ij}^{(r)} \ge 0,v_{ij}^{(r)} \ge 0\,{\text{and }}u_{ij}^{(r)} *v_{ij}^{(r)} = 0,$ such that $\left| {p_{ij}^{(k)} - p_{ij}^{(c)} } \right| = u_{ij}^{(r)} + v_{ij}^{(r)}$ and $p_{ij}^{(k)} - p_{ij}^{(c)} = u_{ij}^{(r)} - v_{ij}^{(r)}$. If product ∗ was defined, we set $u_{ij}^{(r)} = {{\left[ {\left| {p_{ij}^{(k)} - p_{ij}^{(c)} } \right| + \left( {u_{ij}^{(r)} - v_{ij}^{(r)} } \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {\left| {p_{ij}^{(k)} - p_{ij}^{(c)} } \right| + \left( {u_{ij}^{(r)} - v_{ij}^{(r)} } \right)} \right]} 2}} \right. \kern-0pt} 2},$$v_{ij}^{(r)} = {{\left[ {\left| {p_{ij}^{(k)} - p_{ij}^{(c)} } \right| - \left( {u_{ij}^{(r)} - v_{ij}^{(r)} } \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {\left| {p_{ij}^{(k)} - p_{ij}^{(c)} } \right| - \left( {u_{ij}^{(r)} - v_{ij}^{(r)} } \right)} \right]} 2}} \right. \kern-0pt} 2}$, letting the above conditions hold (Zhang et al. 2019c). The linear programming format is as follows:

$$ \begin{aligned} & \begin{array}{*{20}c} {Min} & {1 - \frac{1}{m \times n \times (n - 1)}\sum\limits_{k = 1}^{m} {\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1,j \ne i}^{n} {\left( {u_{ij}^{(r)} + v_{ij}^{(r)} } \right)} } } } \\ \end{array} - CD\{ e_{1} , \ldots ,e_{m} \}_{r}^{*} \\ & S.t.\,\sum\limits_{M} {\sigma_{k} \bar{p}_{ij}^{(k)} } = \bar{p}_{ij}^{(r)} + u_{ij}^{(r)} - v_{ij}^{(r)} ; \\ & \,\,\,\,\sum\limits_{j \in E} {\lambda_{j} y_{rj} = y_{rj} + t_{j} ;\,\,\,r = 1,2, \ldots ,s} \\ & \,\,\,\sum\limits_{i \in E} {\lambda_{i} x_{si} = x_{si} + h_{i} ;\,\,\,s = 1,2, \ldots ,n} \\ & \,\,\,\sum\limits_{j \in E} {\lambda_{j} = 1,\lambda_{j} \ge 0;} \\ & \,\,\, - vX + uY + u_{0} + d_{j} = 0;j \in E; \\ & \,\,\,v_{i} \ge 1;i = 1,2, \ldots ,n \\ & \,\,\,u_{i} \ge 1;\,\,\,i = 1,2, \ldots ,n \\ & \,\,\,d_{j} \le Mb_{j} ;j \in E; \\ & \,\,\,\lambda_{j} \le M(1 - b_{j} );j \in E; \\ & \,\,\,d_{j} ,\lambda_{j} \ge 0;b_{j} \in [0,1];E;u_{0} \in \Re ; \\ & \,\,\,M\,{\text{is}}\,{\text{big positive}} \\ \end{aligned} $$

(23)

If the inputs in DEA were unclear in the DEA benchmark model, the model (15) would convert into a DEA-WEI benchmark model, which was developed by Cook et al. (2019). Then, the obtained set of the efficiency boundary follows as Eq. (24):

$$ \partial (AS) = \left\{ {(X,Y) \in \Re_{ + }^{m + s} \left| \begin{aligned} Y = \sum\limits_{j \in E}^{{}} {\lambda_{j} Y_{j} } ,\sum\limits_{j \in E}^{{}} {\lambda_{j} } = 1,\lambda_{j} \ge 0; \hfill \\ uY + u_{0} + d_{j} = 0;j \in E; \hfill \\ u_{r} y_{rj} \ge 1;r = 1,2, \ldots ,s; \hfill \\ d_{j} \le Mb_{j} ;j \in E; \hfill \\ \lambda_{j} \le M(1 - b_{j} );j \in E; \hfill \\ d_{j} ,\lambda_{j} \ge 0;b_{j} \in [0,1];j \in E;u_{0} \in \Re ; \hfill \\ M\,is\,big \hfill \\ \end{aligned} \right.} \right\} . $$

(24)

Additionally, model (23) can be transformed into the following DEA-WEI benchmark model (25):

$$ \begin{aligned} & \begin{array}{*{20}c} {Min} & {1 - \frac{1}{m \times n \times (n - 1)}\sum\limits_{k = 1}^{m} {\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1,j \ne i}^{n} {\left( {u_{ij}^{(r)} + v_{ij}^{(r)} } \right)} } } } \\ \end{array} - CD\{ e_{1} , \ldots ,e_{m} \}_{r}^{*} \\ & S.t.\,\sum\limits_{G} {\sigma_{k} \bar{p}_{ij}^{(k)} } = \bar{p}_{ij}^{(r)} + u_{ij}^{(r)} - v_{ij}^{(r)} ; \\ & \,\,\,\sum {\lambda_{j} p_{rj} = p_{rj} + x_{rj} ;j \in E;\quad r = 1,2, \ldots ,s;} \\ & \,\,\,\sum\limits_{j \in E} {\lambda_{j} = 1;j \in E;} \\ & \,\,\,uY_{j} + u_{0} + d_{j} = 0;j \in E; \\ & \,\,\,u_{r} y_{rj} \ge 1;j \in E; \quad r = 1,2, \ldots ,s;; \\ & \,\,\,d_{j} \le Mb_{j} ;\quad j \in E; \\ & \,\,\,\lambda_{j} \le M(1 - b_{j} );j \in E; \\ & \,\,\,b_{j} \in [0,1];p_{rj}^{g} \in [0,1] \\ & \,\,\,h_{rj} ,l_{rj} ,d_{j} \ge 0;j = 1,2, \ldots ,s;\lambda_{r} \ge 0,j \in E;\quad u_{0} ,x_{rj} \in \Re ; \\ & \,\,\,M\,is\,big\,positive. \\ \end{aligned} $$

(25)

The above programming is a linear optimization. the benchmark for each DM can be given as a solution to models (23) or (25). The detailed procedure follows in Table 7.

Table 7 The consensus threshold building process

5 Applications

In this section, we use two practical examples to illustrate the specific process of consensus threshold establishment.

Example 2

(Targeted poverty reduction) “Targeted poverty reduction” is a concentrated project aimed at significantly reducing poverty in China (Bai et al. 2014; Couzin et al. 2011). As part of this effort, a large number of special funds and assistance projects have been invested in poor areas. However, this special funding has been launched from local, rural credit unions and has been supported by the Chinese government. The selection process has focused on projects targeting poor households that have regional incentives, project implementability and good credit because these funds cannot cover the country’s entire poor population for all poverty alleviation. This example is to evaluate several beneficiaries for one project in the Qinghai-Tibet Plateau. The funds are intended to be distributed as interest-free micro-credit (small loans) and are provided to people with a better repayment ability in this region, and whose annual income is lower than 212 US dollars. These data are accessible and were reported by Chao (2017) and Chao et al. (2018, 2021).

The alternatives in this project are listed as follows:

Alternative 1:

The potential beneficiary is a 55-year-old man with three laborers in his family. The purpose of the loan is to build a field free-range chicken farm

Alternative 2:

The potential beneficiary is a 51-year-old single man. The purpose of the loan is to get a life support when he is out-migration for work

Alternative 3:

The potential beneficiary is a 42-year-old man with two laborers in his family. The purpose of the loan is to get circulating capital for his family business, which is in the agricultural products trade

Alternative 4:

The potential beneficiary is a 45-year-old man. His family has four laborers and he owns eight cows and 24 sheep. The purpose of the loan is to buy a tractor to improve agricultural production

Alternative 5:

The potential beneficiary is a 42-year-old divorced man. He needs to take care of his father at home and has a daughter attending high school. The purpose of the loan is to rebuild his house, which collapsed during a heavy rain

Five major parties (52 decision makers) are involved in this GDM: officers from the People’s Bank of China (PBOC, the central bank of China), rural credit cooperatives, local government representatives, village committees, and delegates for low-income people.

Based on four collected different preference relations, such as preference ordering, utility value, multiplicative preference relation and additive preference relation, we simulated seven methods and determined the consensus benchmark for each method. The consensus reaching framework used in our example is a feedback adjustment mechanism articulated in Herrera-Viedma ret al. (2002). We set the maximum round of iterative individual preference modification to three. The evaluation measures are $CD$ and AD as outputs in the DEA-WEI benchmark model and there are no inputs. The difference between the seven methods is the use of different assembly methods in the preference aggregation process, as follows:

M1:

Algebraic average in Forman and Peniwati (1998);

M2:

Geometric mean in Forman and Peniwati (1998);

M3:

OWA operator in Yager (1988);

M4:

Chi Square Optimization in Wang et al. (2007);

M5:

Quadratic optimization in Xu et al. (2011);

M6:

Geometry optimization in Chao et al. (2017);

M7:

Quadratic optimization in Ma et al. (2006), Fan et al. (2006).

The experiment was implemented using the following three stages:

First, the calculation $p_{ij}^{(c)}$ of $CD\{ e_{1} , \ldots ,e_{m} \}^{*} = 1 - \frac{1}{m \times n \times (n - 1)}\sum\limits_{k = 1}^{m} {\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1,j \ne i}^{n} {\left| {\bar{p}_{ij}^{(k)} - p_{ij}^{(c)} } \right|} } }$ was obtained using the different methods M1 to M7.

The following three methods were used first to transform different preference relations into a uniform multiplicative preference relation.

$$ M1:p_{ij}^{(c)} = \sum\limits_{M} {\sigma_{k} \bar{p}_{ij}^{(k)} } ;, $$

(26)

$$ M2:p_{ij}^{(c)} = \prod\limits_{k = 1}^{K} {(\bar{p}_{ij}^{k} )^{{\lambda_{k} }} } , $$

(27)

$$ M3:p_{ij}^{(c)} = \phi_{Q} (\bar{p}_{ij}^{1} ,\bar{p}_{ij}^{2} , \ldots ,\bar{p}_{ij}^{n} ) = \sum\limits_{h = 1}^{n} {v_{h} d_{ij}^{h} \,} i = 1,2, \ldots ,n;j = 1,2, \ldots ,n. $$

(28)

where $v_{h} = Q\left( {\frac{h}{n}} \right) - Q\left( {\frac{h - 1}{n}} \right),h = 1,2, \ldots ,n.$

$$ Q\left( r \right) = \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {0,} & {r < \gamma } \\ \end{array} } \\ {\begin{array}{*{20}c} {\frac{r - \gamma }{\mu - \gamma },} & {\gamma \le r \le \mu } \\ \end{array} } \\ {\begin{array}{*{20}c} {1,} & {\mu < r} \\ \end{array} } \\ \end{array} } \right.. $$

The following four methods were used first to compute the collective opinion $w = (w_{1} ,w_{2} , \ldots ,w_{n} )^{T}$ and then to compute the corresponding multiplicative preference relation $p_{ij}^{(c)} = \frac{{w_{i} }}{{w_{j} }}$:

M4: the $w = (w_{1} ,w_{2} , \ldots ,w_{n} )^{T}$ was computed as follows:

$$ \begin{aligned} & Max\,\,\sum\limits_{k = 1}^{{k_{m} }} {\sum\limits_{j = 1}^{n} {\sum\limits_{i = 1}^{n} {\sigma_{k} \left[ {\frac{{(a_{ij}^{(k)} - w_{i} /w_{j} )^{2} }}{{w_{i} /w_{j} }}} \right]} } } + \sum\limits_{{k = k_{m + 1} }}^{K} {\sum\limits_{j = 1}^{n} {\sum\limits_{i = 1}^{n} {\sigma_{k} \left[ {\frac{{\left( {p_{ij}^{(k)} - w_{i} /(w_{i} + w_{j} )} \right)^{2} }}{{w_{i} /(w_{i} + w_{j} )}}} \right]} } } \\ & S.t.\,\left\{ {\begin{array}{*{20}c} {\sum\limits_{i = 1}^{n} {w_{i} = 1,} } \\ {w_{i} > 0,i = 1,2, \ldots n} \\ \end{array} } \right. \\ \end{aligned} $$

(29)

M5: the $w = (w_{1} ,w_{2} , \ldots ,w_{n} )^{T}$ was computed as follows:

$$ \begin{aligned} & \begin{array}{*{20}l} {\text{Min}} & {\left( \begin{aligned} \sum\limits_{k = 1}^{{m_{1} }} {\sum\limits_{j = 1}^{n} {\sum\limits_{i = 1}^{n} {\left| {w_{i} - {{u_{i}^{(k)} } \mathord{\left/ {\vphantom {{u_{i}^{(k)} } {\sum\limits_{j = 1}^{n} {u_{j}^{(k)} } }}} \right. \kern-0pt} {\sum\limits_{j = 1}^{n} {u_{j}^{(k)} } }}} \right|^{p} + \sum\limits_{{k = m_{1} + 1}}^{{m_{2} }} {\sum\limits_{j = 1}^{n} {\sum\limits_{i = 1}^{n} {\left| {w_{i} - {{\frac{{n - o_{i}^{(k)} }}{n - 1}} \mathord{\left/ {\vphantom {{\frac{{n - o_{i}^{(k)} }}{n - 1}} {\sum\limits_{j = 1}^{n} {\frac{{n - o_{j}^{(k)} }}{n - 1}} }}} \right. \kern-0pt} {\sum\limits_{j = 1}^{n} {\frac{{n - o_{j}^{(k)} }}{n - 1}} }}} \right|^{p} } } } } } } \hfill \\ + \sum\limits_{{k = m_{2} + 1}}^{{m_{3} }} {\sum\limits_{j = 1}^{n} {\sum\limits_{i = 1}^{n} {\left| {a_{ij}^{(k)} - \frac{{w_{i} }}{{w_{j} }}} \right|^{p} + \sum\limits_{{k = m_{3} + 1}}^{{m_{4} }} {\sum\limits_{j = 1}^{n} {\sum\limits_{i = 1}^{n} {\left| {p_{ij}^{(k)} - \frac{{w_{i} }}{{w_{i} + w_{j} }}} \right|^{p} } } } } } } \hfill \\ \end{aligned} \right)} \\ \end{array}^{1/p} \\ & {\text{S}} . {\text{t}} .\,\left\{ {\begin{array}{*{20}c} {\sum\limits_{i = 1}^{n} {w_{i} = 1,} } \\ {w_{i} > 0,i = 1,2, \ldots ,n} \\ \end{array} } \right. \\ \end{aligned} . $$

(30)

M6: the $w = (w_{1} ,w_{2} , \ldots ,w_{n} )^{T}$ was computed as follows:

$$ \begin{aligned} & {\text{Max}}\,\,\sum\limits_{{k \in \varOmega_{U} }} {\sum\limits_{j = 1}^{n} {\left\langle {\vec{u}^{(k)}_{ij} ,w} \right\rangle } } \\ & {\text{Max}}\,\,\sum\limits_{{k \in \varOmega_{O} }} {\sum\limits_{j = 1}^{n} {\left\langle {\vec{o}^{(k)}_{ij} ,w} \right\rangle } } \\ & {\text{Max}}\,\,\sum\limits_{{k \in \varOmega_{A} }} {\sum\limits_{j = 1}^{n} {\left\langle {\vec{a}_{ij}^{(k)} ,w} \right\rangle } } \\ & {\text{Max}}\,\,\sum\limits_{{k \in \varOmega_{B} }} {\sum\limits_{j = 1}^{n} {\left\langle {\vec{p}_{ij}^{(k)} ,w} \right\rangle } } , \\ \end{aligned} $$

(31)

$$ S.t.\,\left\{ {\begin{array}{*{20}c} {\sum\limits_{i = 1}^{n} {w_{i} = 1;} } \\ {0 \le w_{i} \le 1.} \\ \end{array} } \right. $$

M7: the $w = (w_{1} ,w_{2} , \ldots ,w_{n} )^{T}$ was computed as follows:

$$ \begin{aligned} & \begin{array}{*{20}c} {\text{Min}} & {\sum\limits_{k = 1}^{{m_{1} }} {\sum\limits_{j = 1}^{n} {\sum\limits_{i = 1}^{n} {\left( {w_{i} u_{j}^{(k)} - w_{j} u_{i}^{(k)} } \right)^{2} + \sum\limits_{{k = m_{1} + 1}}^{{m_{2} }} {\sum\limits_{j = 1}^{n} {\sum\limits_{i = 1}^{n} {\left( {w_{i} (n - o_{j}^{(k)} ) - w_{j} (n - o_{i}^{(k)} )} \right)^{2} } } } } } } } \\ \end{array} \\ & + \sum\limits_{{k = m_{2} + 1}}^{{m_{3} }} {\sum\limits_{j = 1}^{n} {\sum\limits_{i = 1}^{n} {\left( {w_{i} - w_{j} a_{ij}^{(k)} } \right)^{2} + } } } \sum\limits_{{k = m_{3} + 1}}^{{m_{4} }} {\sum\limits_{j = 1}^{n} {\sum\limits_{i = 1}^{n} {\left( {w_{i} - (w_{i} + w_{j} )p_{ij}^{(k)} } \right)^{2} } } } \\ & {\text{S}} .\begin{array}{*{20}c} {{\text{t}}.} & {\left\{ {\begin{array}{*{20}c} {\sum\limits_{i = 1}^{n} {w_{i} = 1,} } \\ {w_{i} > 0,i = 1,2, \ldots ,n} \\ \end{array} } \right.} \\ \end{array} \\ \end{aligned} . $$

(32)

Second, we computed the efficiency frontier boundary at period 2 and, based on this boundary, compared the consensus degree at period 3 (targets) and computed the target located at the frontier boundary, which was a target for the consensus benchmark for each method. Then, we computed a consensus threshold using this target (efficiency benchmark).

Third, we calculated the targets of all methods and converted the results into a consensus threshold.

Table 8 shows the consensus threshold results from the above seven methods. Among them, the mean, OWA operator and geometric optimization form the frontier boundary of DEA efficiency. For the method that did not reach the DEA efficiency, through Eq. (25), we obtained its corresponding efficiency target at boundary and used it as the method’s efficiency benchmark to determine whether further consensus negotiation would be needed.

Table 8 Results of consensus benchmark

In interactive group decision-making, the moderator needs to negotiate with the DMs and require the DMs to reconsider individual preferences. Then, the negotiation process facilitates an increase of the consensus degree. The red circle in Fig. 6 represents the state of each method during the second preference adjustment, and the blue dots are the consensus degree corresponding to the different methods during the third opinion adjustment. Figure 6 shows the consensus benchmark trend. The M1, M3 and M6 constitute the boundary and the targets of M1, M3 and M6 have reached compared to the consensus threshold (because they located in efficiency curve), For example, the M3 method in the second round of decision-making negotiations, the efficiency benchmark has been reached (on the efficiency curve). The remaining methods need to demand individual preferences to be adjusted again in order to improve their threshold with an DEA efficiency. The points of the two rounds of negotiations are on the outside of the curve, and it is necessary to negotiate again to improve consensus efficiency, such as M2, M7 and M5. For points distributed on both sides of the efficiency curve, in fact, the consensus degree of the third round of negotiations exceeds the consensus benchmark. It is also inefficient. This means that more resources are consumed (increasing the time cost of negotiation) but the increase in consensus degree does not match.

Fig. 6

Efficient boundary of the example 2

After examining the results from Example 2, we can conclude that, in the same group decision, different methods are needed to reach different consensus thresholds. M4 (Chi square optimization in Wang et al. 2007), M5 (quadratic optimization in Xu et al. 2011) and M7 (quadratic optimization in Ma et al. 2006) exhibit lower consensus thresholds, and the consensus threshold of the other methods is relatively high. This result is related to the aggregation method of individual preference relations. When nonlinear optimization was selected, we found that the change of deviation between the collective opinion and individual preferences was relatively slow, compared with the change of individual preferences. Thus,

Remark 1

We conclude that the consensus threshold established based on efficiency targets as a benchmark has the following characteristics: First, it establishes different consensus benchmarks for different efficiency performances in a set of methods. Different methods have their principles and calculation methods, which leads to different levels of consensus efficiency. Second, efficiency is a relative concept. This method establishes a benchmark by comparing the relative efficiency of different methods and, therefore, it does not target a particular method. This is the same as the actual application scenario. For a certain problem, it is necessary to select the applicable method from the existing methods.

Remark 2

The shortcomings of our proposed method are as follows: first, the method proposed in this article is a data-driven consensus benchmarking process, not a supervisory method, using parameters such as degrees of satisfaction or DM support levels. Second, the method of this study aims at a certain round of efficiency analysis. The test rounds of negotiation need to be determined according to specific issues under decision resources and costs in actual decision-making.

Example 3

(Online P2P lending) P2P online lending platform is an internet finance service website that combines peer to peer online lending. Online lending refers to the process of borrowing, where materials, funds, contracts, and procedures are all realized through the Internet. It is a new financial model developed by the development of the Internet and the rise of private lending. A P2P network lending platform that collects a small amount of funds to provide loans to those in need. Lenders and borrowers use P2P platforms for interest rate consensus, and platform operators always negotiate interest rates with lenders to compensate for interest rate adjustments and promote interest rate consensus between borrowers and lenders (Zhang et al. 2019c).

The pricing of loans on online platforms is a very complex problem, and it is also one of the most important commercial issues for lending platforms. There are two main pricing models: Direct mode (platform matching pricing) and indirect mode (platform independent pricing). The direct mode means that investors and borrowers determine the final loan interest rate through a bidding auction process, and the P2P platform is only used as a platform for matching transactions. The indirect mode means that the P2P platform determines the final loan interest rate based on the borrower’s credit information, and attracts investors for financing by promising fixed income returns. Under this mode, the P2P platform itself sets interest rates according to predetermined standards and algorithms, and undertakes the functions of information collection and integration, as well as risk assessment and pricing.

We take non-indirect mode as an example, and compare the efficiency of the consensus reaching of different methods using the example of the Chinese P2P platform PPDai.com (Zhang et al. 2019a, b, c). Suppose the lender registers on the platform to lend out M = 10,000 yuan. The plan selects four borrowers with different credit ratings (AA, A, B, and C) to obtain this loan. The expected interest rates of these four borrowers are $o_{1} = 11,o_{2} = 16,o_{3} = 22,o_{4} = 28$ (unit: \%; interest rate data comes from PPDai.com). Assume that the platform’s compensation strategy for four different credit ratings is that when the borrower’s interest rate is reduced by 1\%, the platform will provide compensation $c_{1} = 1.5,c_{2} = 1.0,c_{3} = 2.5,c_{4} = 2.0$ (unit: RMB 10). In order to avoid the risk of default, the lender adopted a basket of borrowers’ strategy. The funds allocated by the lender to the four lenders are 4000, 3000, 2000, and 1000 (unit: RMB), indicating that the weights of the four lenders are 0.4, 0.3, 0.2, and 0.1, respectively.

Consensus degree is the first issue that a p2p lending platform needs to consider as a primary task. It is necessary to establish a basic interest rate consensus between the borrower and the lender to retain customers. If the borrower and lender cannot establish a consensus on the pricing of interest rates, the loan cannot be completed on this platform. The cost of consensus compensation is the second issue. The platform needs to incentivizes borrower and lender to facilitate the adjustment of the expected interest rate through the payment cost to obtain a higher consensus degree. The consensus improvement and the optimization of cost are a pair of efficiency concepts. A high degree of consensus needs to be achieved through high compensation cost, but the cost is not unlimited. Therefore, it is necessary to determine the efficiency benchmark of interest rates through an objective method. For those whose efficiency is lower than the benchmark, increase the cost input to increase the degree of consensus. For those whose efficiency is higher than the benchmark, the compensation needs to be adjusted and reduced to obtain higher consensus efficiency.

The results of the total cost and consensus degree in this example are summarized in following Table 9 (using a method in Zhang et al. 2019c).

Table 9 The cost and consensus degree of the example 3

Table 10 shows the efficiency target of consensus degree and compensation cost. The I4, I5, I7 and I8 constitute (located) an efficiency curve. We use this curve as the efficiency benchmark and determine the point that is closest to the curve as the efficiency target of the point outside of the curve. I1, I2, I3 and I6 need to improve consensus degree by increasing costs and I9 needs to decrease cost to improve consensus efficiency.

Table 10 Results of consensus benchmark

Figure 7 describes the target setting of the efficiency. The green curve is the constructed efficiency curve, and the horizontal axis and vertical axis are the consensus degree and compensation cost, respectively. The curve constitutes an efficiency benchmark, that is, the cost and consensus efficiency on the curve are DEA effective. Those points outside the curve are inefficient, and we need to determine the DEA effective point for those outside points, which is the efficiency improvement target. The blue dots in the figure represents the targets.

Fig. 7

Efficient boundary of the example 3

The following enlightenment can be obtained from the example: (i) As a P2P network lending platform, it is inefficient to pursue the absolute consensus of both borrowers and lenders (such as I9). In actual management, the interest rate they expect can be determined within a threshold range, and the consensus that can be achieved is Effective. (ii) Lower consensus degree is inefficiency (such as I1, I2 and I3). Even if a certain degree of efficiency is met through additional costs payment, the degree of consensus is not significantly improved.

6 Conclusions

Decision efficiency means that in the group decision-making process, a higher degree of consensus can be obtained with as little consensus cost as possible. The assessment of consensus efficiency and the consensus threshold benchmark in GDM have become a hot topic in recent research. However, there are still many unknown problems not considered by this body of research. For example, the definition of input and output in group decision consensus efficiency, analysis methods and efficiency benchmarks, and so on. This study deconstructs CRP from a cost and benefit perspective towards achieving efficiency in GDM. For the MACRP and PRCRP methods, we proposed a method for evaluating the consensus efficiency of CRP based on the DEA-WEI benchmark model. Based on this, we established a DEA benchmark method for determining a consensus threshold. In CRP, the best method should aim to achieve the maximum degree of consensus improvement through the smallest necessary adjustment of preference.

From our empirical studies, we conclude that there is no direct correlation relation between consensus efficiency and the consensus threshold. We identified that the fewest adjusted alternatives and the fewest decision makers to adjust individual preference comprise the most robust strategies for CRP in GDM. Theoretically, in the decision consensus mechanism, the (relatively) most effective methods require the smallest number of decision makers to adjust their preferences, or for them to modify the preferences of the smallest number of alternatives. We determined the alternatives that needed to be adjusted, and that optimizing the total distance between the original and the adjusted preferences is a less efficient method for CRP. In addition, we illustrated the process for establishing a consensus benchmark. The consensus threshold we established is an efficiency target on the efficiency boundary, composed of a set of methods under different consensus metrics. Through numerical examples, we demonstrated the usability of this process.

Regarding the efficiency of GDM, a few directions that future research could take include the necessity of studying the correlation between consensus efficiency thresholds and level of satisfaction degree of DMs in GDM. Also, DEA involving large numbers of DMUs may increase the computational load to beyond what is practical with traditional DEA methods (Zhu et al. 2018). Thus, the study of consensus efficiency in a large-scale GDM environment is also very valuable, including large scale social network GDM. In addition, novel algorithms for DEA benchmark which can speed up the calculation process in the big data environment need to be developed.