Multi-sided assignment games on m-partite graphs

Abstract

We consider a multi-sided assignment game with the following characteristics: (a) the agents are organized in m sectors that are connected by a graph that induces a weighted m-partite graph on the set of agents, (b) a basic coalition is formed by agents from different connected sectors, and (c) the worth of a basic coalition is the addition of the weights of all its pairs that belong to connected sectors. We provide a sufficient condition on the weights to guarantee balancedness of the related multi-sided assignment game. Moreover, when the graph on the sectors is cycle-free, we prove the game is strongly balanced and the core is fully described by means of the cores of the underlying two-sided assignment games associated with the edges of this graph. As a consequence, the complexity of the computation of an optimal matching is reduced and existence of optimal core allocations for each sector of the market is guaranteed.

1 Introduction

Two-sided assignment games (Shapley and Shubik 1972) have been generalized to the multi-sided case. In this case, agents are distributed in m disjoint sectors. Usually it is assumed that these agents are linked by a hypergraph defined by the (basic) coalitions formed by exactly one agent from each sector (see for instance Kaneko and Wooders 1982; Quint 1991). A matching for a coalition S is a partition of the set of agents of S in basic coalitions and, since each basic coalition has a value attached, the worth of an arbitrary coalition of agents is obtained by maximizing, over all possible matchings, the addition of values of basic coalitions in a matching. When there are at least three sectors, the problem of finding an optimal matching in this multi-sided assignment market is known to be NP-hard. See for instance Burkhard et al. (2009) for a survey on some special cases, together with its applications, algorithms, and asymptotic behavior.

If we do not require that each basic coalition has exactly one agent of each side but allow for coalitions of smaller size, as long as they do not contain two agents from the same sector, we obtain a larger class of games, see Atay et al. (2016) for the three-sided case. But in both cases, the classical multi-sided assignment market and this enlarged model, the core of the corresponding coalitional game may be empty, and this is the main difference with the two-sided assignment game of Shapley and Shubik (1972), where the core is always non-empty.

A two-sided assignment game can also be looked at in another way. There is an underlying bi-partite (weighted) graph, where the set of nodes corresponds to the set of agents and the weight of an edge is the value of the basic coalition formed by its adjacent nodes. From this point of view, the generalization to a market with $m>2$ sectors can be defined by a weighted m-partite graph G. In an m-partite graph the set of nodes N is partitioned in m sets $N_1,N_2,\ldots ,N_m$ in such a way that two nodes in a same set of the partition are never connected by an edge. Each node in G corresponds to an agent of our market and each set $N_i$, for $i\in \{1,2,\ldots ,m\}$, to a different sector. We do not assume that the graph is complete but we do assume that the subgraph determined by any two sectors $N_i$ and $N_j$, with $i\ne j$, is either empty or complete. Because of that, the graph G determines a quotient graph $\overline{G}$, the nodes of which are the sectors and two sectors are connected in $\overline{G}$ whenever their corresponding subgraph in G is non-empty.

For each pair of sectors $N_r$ and $N_s$, $r\ne s$, that are connected in $\overline{G}$, we have a bilateral assignment market with valuation matrix $A^{\{r,s\}}$. For each $i\in N_r$ and $j\in N_s$, entry $a^{\{r,s\}}_{ij}$ is the weight in G of the edge $\{i,j\}$, and represents the value created by the cooperation of i and j.

Given the m-partite graph G, a coalition of agents in N is basic if it does not contain two agents from the same sector and its members are connected in G. Then, the worth of a basic coalition is the addition of the weights of the edges in G that are determined by nodes in the coalition. An optimal matching in this market is a partition of N in basic coalitions such that the sum of values is maximum among all possible such partitions.

We show that if there exists an optimal matching for the multi-sided m-partite market that induces an optimal matching in each bilateral market determined by the connected sectors, then the core of the multi-sided market is non-empty. Moreover, some core elements can be obtained by merging of one core element from each of the underlying bilateral markets associated with the connected sectors.

Secondly, if the quotient graph $\overline{G}$ is cycle-free, then the above sufficient condition for a non-empty core always holds and, moreover, the core of the multi-sided assignment game is fully described by “merging” or “composition” of the cores of the underlying bilateral games. A first consequence is that when $\overline{G}$ is cycle-free, an optimal matching can be found in polynomial time. Secondly, for each sector there exists a core allocation where all agents in the sector simultaneously get their maximum core payoff. This means that, although agents in a same sector compete for the best partners in the other sectors, there is still some coincidence of interests among them.

This model of multi-sided assignment market on an m-partite graph G where the quotient graph $\overline{G}$ is cycle-free can be related to the locally-additive multi-sided assignment games of Stuart (1997), where the sectors are organized on a chain and the worth of a basic coalition is also the addition of the worths of pairs of consecutive sectors. However, in Stuart’s model all coalitions of size smaller than m have null worth. It can also be related with a model in Quint (1991) in which a value is attached to each pair of agents of different sectors and then the worth of an m-tuple is the addition of the values of its pairs. Again, the difference with our model is that in Quint (1991) the worth of smaller coalitions is zero. In particular, the worth of a two-player coalition is taken to be zero instead of the value of this pair. Notice that in these models the cooperation of one agent from each side is needed to generate some profit. Compared to that, in our model, any set of connected agents from different sectors yields some worth that can be shared.

The assumption that one agent from each sector is needed to make any profit makes sense for instance in a supply chain network where some agents supply basic inputs for the industry, other agents purchase the final outputs and the rest are intermediaries who get their inputs from some agents in the industry, convert them into outputs at a cost and sell the outputs to some other agents (Ostrovsky 2008). In this setting, agents in excess in the large sectors of the market may not be able to find partners to complete a connected coalition between the suppliers of basic inputs and the final consumers, and hence get no reward in this market (see an example in Sect. 6). But there are other network situations in which the activity an agent carries out with one neighbour is independent of the activity this agent implements with other neighbours. Take as an example the network of European countries for road merchandise transport. A transport company can make a profit by its own by carrying goods to a neighbour country, but if it makes an agreement with a similar company in this second country, they both can reduce costs and hence make a larger profit, even if they are not part of a larger coalition that covers all the continent.

For arbitrary coalitional games, cooperation restricted by communication graphs was introduced by Myerson (1977) and some examples of more recent studies are Granot and Granot (1992), van Velzen et al. (2008), Grabisch and Skoda (2012), Grabisch (2013), and Khmelnitskaya and Talman (2014). The difference with our work is that in the multi-sided assignment game on an m-partite graph there exist well-structured subgames, the two-sided markets between connected sectors, that provide valuable information about the multi-sided market. This fact allows to find simple conditions for non-emptiness of the core, compared to other games defined on graphs (see for instance Deng et al. 1999).

Section 2 introduces the model. In Sect. 3, for an arbitrary m-partite graph, we provide a sufficient condition for the non-emptiness of the core. Section 4 focuses on the case in which the quotient graph is cycle-free. In that case, we completely characterize the non-empty core in terms of the cores of the two-sided markets between connected sectors. From that fact, additional consequences on some particular core elements are derived in Sect. 5. Finally, Sect. 6 concludes with some remarks.

2 The multi-sided assignment problem on an m-partite graph and its related coalitional game

Let N be the finite set of agents in a market situation. The set N is partitioned in m sets $N_1, N_2, \ldots , N_m$, each sector maybe representing a set of agents with a specific role in the market. There is a graph $\overline{G}$ with set of nodes $\{N_1,N_2,\ldots ,N_m\}$, that we simply denote $\{1,2,\ldots ,m\}$ when no confusion arises, and we will identify the graph with its set of edges.¹ The graph $\overline{G}$ induces another graph G on the set of agents N such that $\{i,j\}\in G$ if and only if there exist $r,s\in \{1,2,\ldots ,m\}$ such that $r\ne s$, $i\in N_r$, $j\in N_s$ and $\{r,s\}\in \overline{G}$. Notice that the graph G is an m-partite graph, that meaning that two agents on the same sector are not connected in G. We say that graph $\overline{G}$ is the quotient graph of G.²

For any pair of connected sectors $\{r,s\}\in \overline{G}$, there is a non-negative valuation matrix $A^{\{r,s\}}$ and for all $i\in N_r$ and $j\in N_s$, $v(\{i,j\})=a_{ij}^{\{r,s\}}$ represents the value obtained by the cooperation of agents i and j. Notice that these valuation matrices, $A=\{A^{\{r,s\}}\}_{\{r,s\}\in \overline{G}}$, determine a system of weights on the graph G, and for each pair of connected sectors $\{r,s\}\in \overline{G}$, $(N_r, N_s, A^{\{r,s\}})$ defines a bilateral assignment market. Sometimes, to simplify notation, we will write $A^{rs}$, with $r<s$, instead of $A^{\{r,s\}}$.

Then, $\gamma =(N_1,N_2,\ldots ,N_m; G; \{A^{\{r,s\}}\}_{\{r,s\}\in \overline{G}})$ is a multi-sided assignment market on an m-partite graph. When necessary, we will write $G^A$ to denote the weighted graph with the nodes and edges of G and the weights defined by the matrices $\{A^{\{r,s\}}\}_{\{r,s\}\in \overline{G}}$. Given any such market $\gamma$, a coalition $S\subseteq N$ defines a submarket $\gamma _{|S}=(S\cap N_1,\ldots , S\cap N_m; G_{|S}; A_{|S})$ where $G_{|S}$ is the subgraph of G defined by the nodes in S and $A_{|S}$ consists of the values of A that correspond to edges $\{i,j\}$ in the subgraph $G_{|S}$.

We now introduce a coalitional game related to the above market situation. To this end, we first define the worth of some coalitions that we name basic coalitions and then the worth of arbitrary coalitions will be obtained by just imposing superadditivity. A basic coalition E is a subset of agents belonging to sectors that are connected in the quotient graph $\overline{G}$ and with no two agents of the same sector. That is, $E=\{i_1,i_2,\ldots ,i_k\}\subseteq N$ is a basic coalition if $(i_1,i_2,\ldots ,i_k)\in N_{l_1}\times N_{l_2}\times \cdots \times N_{l_k}$ and the sectors $\{l_1,l_2,\ldots ,l_k\}$ are all different and connected in $\overline{G}$. Sometimes we will identify the basic coalition $E=\{i_1,i_2,\ldots ,i_k\}$ with the k-tuple $(i_1,i_2,\ldots ,i_k)$. To simplify notation, we denote by $\mathcal {B}^N$ the set of basic coalitions of market $\gamma$, though we should write $\mathcal {B}^{N_1,\ldots ,N_m}$, since which coalitions are basic depends heavily on the partition in sectors of the set of agents. Notice that all edges of G belong to $\mathcal {B}^N$. Moreover, if $S\subseteq N$, we denote by $\mathcal {B}^S$ the set of basic coalitions that have all their agents in S: $\mathcal {B}^S=\{E\in \mathcal {B}^N\mid E\subseteq S\}$.

The valuation function, until now defined on the edges of G, is extended to all basic coalitions by additivity: the value of a basic coalition $E\in \mathcal {B}^N$ is the addition of the weights of all edges in G with adjacent nodes in E. For all $E\in \mathcal {B}^N$,

$$\begin{aligned} v(E)=\sum _{\{i,j\}\in G_{|E}} v(\{i,j\})=\sum _{\begin{array}{c} i\in E\cap N_r,j\in E\cap N_s\\ {\{r,s\}\in \overline{G}} \end{array}}a^{\{r,s\}}_{ij}. \end{aligned}$$

(1)

A matching$\mu$ for the market $\gamma$ is a partition of $N=N_1\cup N_2\cup \cdots \cup N_m$ in basic coalitions in $\mathcal {B}^N$. We denote by $\mathcal {M}(N_1,N_2,\ldots ,N_m)$ the set of all matchings. Similarly, a matching for a submarket $\gamma _{|S}$ with $S\subseteq N$ is a partition of S in basic coalitions in $\mathcal {B}^S$.

A matching $\mu \in \mathcal {M}(N_1,N_2,\ldots ,N_m)$ is an optimal matching for the market $\gamma =(N_1,N_2,\ldots ,N_m; G; \{A^{\{r,s\}}\}_{\{r,s\}\in \overline{G}})$ if it holds $\sum _{T\in \mu }v(T)\ge \sum _{T\in \mu '}v(T)$ for all other matching $\mu '\in \mathcal {M}(N_1,N_2,\ldots , N_m)$. We denote by $\mathcal {M}_{\gamma }(N_1,N_2,\ldots ,N_m)$ the set of optimal matchings for market $\gamma$.

Then, the multi-sided assignment game associated with the market $\gamma$ is the pair $(N, w_{\gamma })$, where the worth of an arbitrary coalition $S\subseteq N$ is the addition of the values of the basic coalitions in an optimal matching for this coalition S:

$$\begin{aligned} w_{\gamma }(S)=\max _{\mu \in \mathcal {M}(S\cap N_1,\ldots ,S\cap N_m)}\sum _{T\in \mu }v(T), \end{aligned}$$

(2)

with $w_{\gamma }(\emptyset )=0$. Notice that if $S\subseteq N$ is a basic coalition, $w_{\gamma }(S)=v(S)$, since no partition of S in smaller basic coalitions can yield a higher value, because of its definition (1) and the non-negativity of weights.³ Trivially, the game $(N,w_{\gamma })$ is superadditive since it is a special type of partitioning game as introduced by Kaneko and Wooders (1982).

Multi-sided assignment games on m-partite graphs combine the idea of cooperation structures based on graphs (Myerson 1977) and also the notion of (multi-sided) matching that only allows for at most one agent of each sector in a basic coalition. It is clear that for $m=2$, multi-sided assignment games on bi-partite graphs coincide with the classical Shapley and Shubik (1972) assignment games. Notice also that for $m=3$, multi-sided assignment games on 3-partite graphs are a particular case of the generalized three-sided assignment games in Atay et al. (2016), with the constraint that the value of a three-person coalition is the addition of the values of all its pairs.

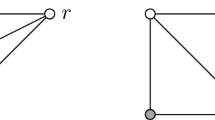
As for the related quotient graphs, for $m=2$ the quotient graph $\overline{G}$ consists of only one edge while, for $m=3$, $\overline{G}$ can be either a complete graph⁴ or a chain. Figure 1 illustrates both the graph G and its quotient graph $\overline{G}$ for the cases $m=2$ and $m=3$.

Fig. 1

2-partite and 3-partite graphs, and their quotient representation

As in any coalitional game, the aim is to allocate the worth of the grand coalition in such a way that it preserves the cooperation among the agents. Given a multi-sided assignment market on an m-partite graph $\gamma =(N_1,N_2,\ldots ,N_m; G; \{A^{\{r,s\}}\}_{\{r,s\}\in \overline{G}})$, a vector $x\in \mathbb {R}^N$, where $N=N_1\cup N_2\cup \cdots \cup N_m$, is a payoff vector. An imputation is a payoff vector $x\in \mathbb {R}^N$ that is efficient, $\sum _{i\in N}x_i=w_{\gamma }(N)$, and individually rational, $x_i\ge w_{\gamma }(\{i\})=0$ for all $i\in N$. Then, the core$C(w_{\gamma })$ is the set of imputations that no coalition can object to, that is $\sum _{i\in S}x_i\ge w_{\gamma }(S)$ for all $S\subseteq N$. Because of the definition of the characteristic function $w_{\gamma }$ in (2), given any optimal matching $\mu \in \mathcal {M}_{\gamma }(N_1,\ldots ,N_m)$, the core is described by

$$\begin{aligned} C(w_{\gamma })=\left\{ x\in \mathbb {R}^N\left| \sum _{i\in E}x_i=v(E) \text{ for } \text{ all } E\in \mu , \sum _{i\in E}x_i\ge v(E), \text{ for } \text{ all } E\in \mathcal {B}^N\right. \right\} . \end{aligned}$$

A multi-sided assignment game on an m-partite graph is balanced if it has a non-empty core. Moreover, and following Le Breton et al. (1992), we will say an m-partite graph $(N_1,N_2,\ldots , N_m; G)$ is strongly balanced if for any set of non-negative weights $\{A^{\{r,s\}}\}_{\{r,s\}\in \overline{G}}$ the resulting multi-sided assignment game is balanced. Recall from Shapley and Shubik (1972) that bi-partite graphs are strongly balanced. Our aim is to study whether this property extends to m-partite graphs or whether balancedness depends on properties of the weights or the structure of the graph.

3 Balancedness conditions

The first question above is easily answered. For $m\ge 3$, m-partite graphs are not strongly balanced. Take for instance a market with three agents on each sector. Sectors are connected by a complete graph: $N_1=\{1,2,3\}$, $N_2=\{1',2',3'\}$, $N_3=\{1'',2'',3''\}$, and $\overline{G}=\{(N_1,N_2), (N_1,N_3), (N_2,N_3)\}$. From Le Breton et al. (1992) we know that a graph is strongly balanced if any balanced collection⁵ formed by basic coalitions contains a partition. In our example, the collection

$$\begin{aligned} \mathcal {C}=\{\{1,1'\},\{1, 2''\}, \{2',1''\}, \{2,3'\}, \{3, 2''\}, \{3', 1''\}, \{3, 3''\}, \{2, 1'\}, \{2', 3''\}\} \end{aligned}$$

is balanced (notice each agent belongs to exactly two coalitions in $\mathcal {C}$) but we cannot extract any partition. To better understand what causes the core to be empty we complete the above 3-partite graph with a system of weights and analyse some core constraints.

Example 1

Let us consider the following valuations on the complete 3-partite graph with three agents in each sector:

In boldface we show the optimal matching for each two-sided assignment market. Now, applying (1), the reader can obtain the worth of all three-player basic coalitions and check that the optimal matching of the three-sided market is

$$\begin{aligned} \mu =\{(2, 1', 1''), (1, 3', 2''), (3, 2', 3'')\}. \end{aligned}$$

Notice that $v(\{2,1',1''\})=9+0+0=9$, $v(\{1,3',2''\})=0+5+0=5$ and $v(\{3,2',3''\})=0+4+6=10$.

Take $x=(u,v,w)\in \mathbb {R}^{N_1}\times \mathbb {R}^{N_2}\times \mathbb {R}^{N_3}$. If $x=(u,v,w)\in C(w_{\gamma })$, from core constraints $u_2+v_1+w_1=9$ and $u_2+v_1\ge 9$ we obtain $w_1=0$. Then, from $v_3+w_1\ge 2$ we deduce $v_3\ge 2$. Hence, $u_1+v_3+w_2=5$ implies $u_1+w_2\le 3$, which contradicts the core constraint $u_1+w_2\ge 5$. Therefore, $C(w_{\gamma })=\emptyset$.

We observe that the optimal matching $\mu$ in the above example induces a matching $\mu ^{23}=\{(1', 1''), (3', 2''), (2', 3'')\}$ for the market $(N_{2}, N_{3}, A^{\{2,3\}})$ which is not optimal. Let us relate more formally the matchings in a multi-sided assignment market on an m-partite graph with the matchings of the two-sided markets associated with the edges of the quotient graph.

Definition 1

Given $\gamma =(N_1,N_2,\ldots , N_m; G; \{A^{\{r,s\}}\}_{\{r,s\}\in \overline{G}})$, for each matching $\mu \in \mathcal {M}(N_1,\ldots ,N_m)$ and each pair adjacent sector $\{r,s\}\in \overline{G}$, we define a matching $\mu ^{\{r,s\}}\in \mathcal {M}(N_r, N_s)$ by

$$\begin{aligned} \{i,j\}\in \mu ^{\{r,s\}} \text{ if } \text{ and } \text{ only } \text{ if } \text{ there } \text{ exists } E\in \mu \text{ such } \text{ that } \{i,j\}\subseteq E. \end{aligned}$$

(3)

We then say that $\mu$ is the composition of $\mu ^{\{r,s\}}$ for $\{r,s\}\in \overline{G}$ and write

$$\begin{aligned} \mu =\bigoplus _{\{r,s\}\in \overline{G}}\mu ^{\{r,s\}}. \end{aligned}$$

Conversely, given a set of matchings, one for each underlying two-sided market, there may not exist a matching $\mu$ of the multi-sided assignment market that is the composition of that given set of matchings. Take for instance matchings $\mu ^{\{1,2\}}=\{(2,1'), (1,3'), (3,2')\}$, $\mu ^{\{1,3\}}=\{(1,2''), (2,1''), (3,3'')\}$ and $\mu ^{\{2,3\}}=\{(1', 2''), (2', 3''), (3', 1'')\}$ in Example 1. Since $(1',2'')\in \mu ^{\{2,3\}}$, $(2,1')\in \mu ^{\{1,2\}}$ and $(1,2'')\in \mu ^{\{1,3\}}$, there is no matching $\mu =\mu ^{\{1,2\}}\oplus \mu ^{\{1,3\}}\oplus \mu ^{\{2,3\}}$ since both 1 and 2 should be in the same coalition of partition $\mu$.

Next proposition states that whenever the composition of optimal matchings of the underlying two-sided markets results in a matching of the multi-sided market on an m-partite graph, then that matching is optimal and the core of the multi-sided assignment market is non-empty. To show this second part we need to combine payoff vectors of each underlying two-sided market $(N_r,N_s,A^{\{r,s\}})$, with $\{r,s\}\in \overline{G}$, to produce a payoff vector $x\in \mathbb {R}^N$ for the multi-sided market $\gamma$. We write $C(w_{A^{\{r,s\}}})$ to denote the core of these two-sided assignment games.

Definition 2

Given $\gamma =(N_1,N_2,\ldots , N_m; G; \{A^{\{r,s\}}\}_{\{r,s\}\in \overline{G}})$, let $x^{\{r,s\}}\in \mathbb {R}^{N_r}\times \mathbb {R}^{N_s}$ for all $\{r,s\}\in \overline{G}$. Then,

$$\begin{aligned} x= & {} \bigoplus _{\{r,s\}\in \overline{G}}x^{\{r,s\}}\in \mathbb {R}^N\; \text{ is } \text{ defined } \text{ by } \\ x_i= & {} \sum _{\{r,s\}\in \overline{G}}x_i^{\{r,s\}}, \text{ for } \text{ all } i\in N_r, r\in \{1,2,\ldots ,m\}. \end{aligned}$$

We then say that the payoff vector $x=\bigoplus _{\{r,s\}\in \overline{G}}x^{\{r,s\}}\in \mathbb {R}^N$ is the composition of the payoff vectors $x^{\{r,s\}}\in \mathbb {R}^{N_r}\times \mathbb {R}^{N_s}$. Similarly, we denote the set of payoff vectors in $\mathbb {R}^N$ that result from the composition of core elements of the underlying two-sided assignment markets by $\bigoplus _{\{r,s\}\in \overline{G}}C(w_{A^{\{r,s\}}})$.

Proposition 1

Let $\gamma =(N_1,N_2,\ldots , N_m; G; \{A^{\{r,s\}}\}_{\{r,s\}\in \overline{G}})$ be a multi-sided assignment market on an m-partite graph. If there exists $\mu \in \mathcal {M}(N_1,\ldots ,N_m)$ such that $\mu ^{\{r,s\}}$ is an optimal matching of $(N_r,N_s,A^{\{r,s\}})$ for all $\{r,s\}\in \overline{G}$, then

• 1. $\mu$ is optimal for $\gamma$ and

• 2. $\gamma$ is balanced and moreover $\bigoplus _{\{r,s\}\in \overline{G}}C(w_{A^{\{r,s\}}})\subseteq C(w_{\gamma }).$

Proof

To see that $\mu =\bigoplus _{\{r,s\}\in \overline{G}}\mu ^{\{r,s\}}$ is optimal for $\gamma$, take any other matching $\tilde{\mu }\in \mathcal {M}(N_1,\ldots ,N_m)$ and let $\tilde{\mu }^{\{r,s\}}\in \mathcal {M}(N_r,N_s)$, for $\{r,s\}\in \overline{G}$, be the matching $\tilde{\mu }$ induces in each underlying two-sided market. Then, $\tilde{\mu }=\bigoplus _{\{r,s\}\in \overline{G}}\tilde{\mu }^{\{r,s\}}$. Now, applying (1),

$$\begin{aligned} \sum _{E\in \mu }v(E)= & {} \sum _{E\in \mu }\sum _{\begin{array}{c} i\in N_r\cap E\\ j\in N_s\cap E\\ {\{r,s\}\in \overline{G}} \end{array}}v(\{i,j\})=\sum _{\{r,s\}\in \overline{G}}\sum _{\{i,j\}\in \mu ^{\{r,s\}}}v(\{i,j\}) \\\ge & {} \sum _{\{r,s\}\in \overline{G}}\sum _{\{i,j\}\in \tilde{\mu }^{\{r,s\}}}v(\{i,j\})=\sum _{E\in \tilde{\mu }}v(E), \end{aligned}$$

where the inequality follows from the assumption on the optimality of $\mu ^{\{r,s\}}$ in each market $(N_r,N_s,A^{\{r,s\}})$, for $\{r,s\}\in \overline{G}$. Hence, $\mu$ is optimal for the multi-sided market $\gamma$.

Take now, for each $\{r,s\}\in \overline{G}$, $x^{\{r,s\}}\in C(w_{A^{\{r,s\}}})$. Define the payoff vector $x\in \mathbb {R}^N$ as in Definition 2, $x_i=\sum _{\{r,s\}\in \overline{G}}x_i^{\{r,s\}}, \text{ for } \text{ all } i\in N_r,\,r\in \{1,2,\ldots ,m\}$. We will see that $x\in C(w_{\gamma })$. Given any basic coalition $E\in \mathcal {B}^N$,

$$\begin{aligned} \sum _{i\in E}x_i= & {} \sum _{r=1}^m\sum _{i\in E\cap N_r}x_i=\sum _{r=1}^m\sum _{i\in E\cap N_r}\sum _{\{r,s\}\in \overline{G}}x_i^{\{r,s\}}\\\ge & {} \sum _{r=1}^m\sum _{i\in E\cap N_r}\sum _{\begin{array}{c} \{r,s\}\in \overline{G}\\ {E\cap N_s\ne \emptyset } \end{array}}x_i^{\{r,s\}}= \sum _{\begin{array}{c} \{r,s\}\in \overline{G}\\ E\cap N_r\ne \emptyset \\ {E\cap N_s\ne \emptyset } \end{array}}\sum _{\begin{array}{c} i\in E\cap N_r\\ {j\in E\cap N_s} \end{array}}\left( x_i^{\{r,s\}}+x_j^{\{r,s\}}\right) \\\ge & {} \sum _{\begin{array}{c} \{r,s\}\in \overline{G}\\ i\in E\cap N_r \\ {j\in E\cap N_s} \end{array}}v(\{i,j\})=v(E), \end{aligned}$$

where both inequalities follow from $x^{\{r,s\}}\in C(w_{A^{\{r,s\}}})$ for all $\{r,s\}\in \overline{G}$. Notice also that if $E\in \mu$ the above inequalities cannot be strict and hence $\sum _{i\in E}x_i=v(E)$. Indeed, if $i\in E\cap N_r$, $\{r,s\}\in \overline{G}$ and $E\cap N_s=\emptyset$, then i is unmatched by $\mu ^{\{r,s\}}$ and, because of the optimality of $\mu ^{\{r,s\}}$, $x_i^{\{r,s\}}=0$. Similarly, if $i\in E\cap N_r$ and $j\in E\cap N_s$, then $\{i,j\}\in \mu ^{\{r,s\}}$ and hence $x_i^{\{r,s\}}+x_j^{\{r,s\}}=v(\{i,j\})$. $\square$

The above proposition gives a sufficient condition for optimality of a matching and for balancedness of a multi-sided assignment game on an m-partite graph. However, this condition is not necessary. The matching $\mu$ in Example 1 is optimal while $\mu ^{\{2,3\}}$ is not. The core of the market in Example 1 is empty, but one can find similar examples with non-empty core (see Example 5).

Finally, even under the assumption of the proposition, that is, when the composition of optimal matchings of the two-sided markets leads to a matching of the multi-sided market, the core may contain more elements than those produced by the composition of the cores of $(N_r,N_s,A^{\{r,s\}})$, for $\{r,s\}\in \overline{G}$ (see Atay et al. 2016 for an example in the three-sided case).

In the following section we see that the inclusion $\bigoplus _{\{r,s\}\in \overline{G}}C(w_{A^{\{r,s\}}})\subseteq C(w_{\gamma })$ becomes an equality for some particular graphs.

4 When $\overline{G}$ is cycle-free: strong balancedness

In this section we assume that the quotient graph $\overline{G}$ of the m-partite graph G does not contain cycles. We will assume without loss of generality that it is connected, since the results in that case are easily extended to the case of a finite union of disjoint cycle-free graphs.

We select a node of $\overline{G}$ as a source, that is, we select a spanning tree of $\overline{G}$. Define the distance $d=d(1,r)$ of any other node r as the number of edges in the unique path that connects this node to the source. Then, without loss of generality, we rename the nodes of $\overline{G}$ in such a way that the source has label 1 and, given two other nodes r and s, if $d(1,r)<d(1,s)$ then $r<s$. Notice that the labels of nodes at the same distance to the source are assigned arbitrarily.

A partial order is defined on the set of nodes of a tree in the following way: given two nodes r and s, we say that sfollowsr, and write $s\succeq r$, if given the unique path in the tree that connects s to the source, $\{s_{1}=1,s_2,\ldots , s_q=s\}$, it holds $r=s_p$ for some $p\in \{1,\ldots ,q-1\}$. If $r=s_{q-1}$ we say that s is an immediate follower of r. We denote by $\mathcal {S}^{\overline{G}}_{r}$ the set of followers of $r\in \{1,2,\ldots ,m\}$, we write $\hat{\mathcal {S}}_r^{\overline{G}}=\{r\}\cup \mathcal {S}^{\overline{G}}_{r}$ when we need to include sector r, and we denote by $\mathcal {I}^{\overline{G}}_r$ the set of immediate followers of $r\in \{1,2,\ldots ,m\}$.

Our main result states that an m-partite graph G where the quotient graph $\overline{G}$ is a tree is strongly balanced.

Theorem 1

Let $\gamma =(N_1,N_2,\ldots , N_m; G; \{A^{\{r,s\}}\}_{\{r,s\}\in \overline{G}})$ be a multi-sided assignment market on an m-partite graph. If $\overline{G}$ is cycle-free, then $(N,w_{\gamma })$ is balanced and

$$\begin{aligned} C(w_{\gamma })=\bigoplus _{\{r,s\}\in \overline{G}}C(w_{A^{\{r,s\}}}). \end{aligned}$$

Proof

Notice first that when $\overline{G}$ is a tree, there is a matching $\mu \in \mathcal {M}(N_{1},\ldots ,N_{m})$ that is the composition of optimal matchings $\mu ^{\{r,s\}}$ of each underlying two-sided market $(N_r,N_s, A^{\{r,s\}})$, for $\{r,s\}\in \overline{G}$. To see that, we define a binary relation on the set of agents $N=N_1\cup N_2\cup \cdots \cup N_m$. Two agents $i\in N_r$ and $j\in N_s$, with $r\le s$, are related if either $i=j$ or there exist sectors $\{r=s_1, s_2,\ldots ,s_t=s\}\subseteq \{1,2,\ldots ,m\}$ and agents $i_k\in N_{s_k}$ for $k\in \{1,2,\ldots ,t\}$ such that $\{s_k,s_{k+1}\}\in \overline{G}$ and $\{i_k,i_{k+1}\}\in \mu ^{\{s_k,s_{k+1}\}}$, for all $k\in \{1,2,\ldots ,t-1\}$. This is an equivalence relation and, because $\overline{G}$ is a tree, in each equivalence class there are no two agents of the same sector. Hence, the set $\mu$ of all equivalence classes is a matching and by its definition it is the composition of the matchings $\mu ^{\{r,s\}}$ of the two-sided markets: $\mu =\bigoplus _{\{r,s\}\in \overline{G}}\mu ^{\{r,s\}}$. Now, by Proposition 1, $\mu$ is an optimal matching for the multi-sided market $\gamma$ and $\bigoplus _{\{r,s\}\in \overline{G}}C(w_{A^{\{r,s\}}})\subseteq C(w_{\gamma })$, which guarantees balancedness. Since all two-sided assignment games have a non-empty core (Shapley and Shubik 1972), the above inclusion guarantees balancedness of the multi-sided assignment market $\gamma$.

We will now prove that the converse inclusion also holds.

Let $u=(u^1,u^2,\ldots , u^m)\in C(w_{\gamma })$. We will define, for each $\{r,s\}\in \overline{G}$, a payoff vector $(x^{\{r,s\}},y^{\{r,s\}})\in \mathbb {R}^{N_r}\times \mathbb {R}^{N_s}$. Take the optimal matching $\mu =\bigoplus _{\{r,s\}\in \overline{G}}\mu ^{\{r,s\}}$ and $E\in \mu$. Let us denote by $\overline{E}=\overline{G}_{|E}$ the subtree in $\overline{G}$ determined by the sectors containing agents in E and take as the source of $\overline{E}$ its sector $s_1$ with the lowest label. Take any leaf⁶$s_r$ of $\overline{E}$ and let $\{s_1,s_2\ldots ,s_q,s_{q+1},\ldots ,s_{r-1},s_r\}$ be the unique path in $\overline{E}$ connecting $s_r$ to the source $s_1$. Let $s_q$ be the sector in this path with the highest label among those that have more than one immediate follower in $\overline{E}$ (let us assume for simplicity that $s_q$ has two immediate followers, $s_{q+1}$ and $s_{q'+1}$). Figure 2 depicts such a subtree $\overline{E}$.

Fig. 2

A subtree $\overline{E}$ for $E\in \mu$

For each sector $s_t$ with $t\in \{1,2,\ldots ,r\}$ we denote by $i_t$ the unique agent in E that belongs to this sector. Then, we define

$$\begin{aligned} y_{i_r}^{\{s_{r-1},s_r\}}= & {} u_{i_r}^{s_r}, \end{aligned}$$

(4)

$$\begin{aligned} x_{i_{r-1}}^{\{s_{r-1},s_r\}}= & {} a_{i_{r-1}i_r}^{\{s_{r-1},s_r\}}-y_{i_r}^{\{s_{r-1}s_r\}}, \text{ and } \end{aligned}$$

(5)

$$\begin{aligned} y_{i_{r-1}}^{\{s_{r-2},s_{r-1}\}}= & {} u_{i_{r-1}}^{s_{r-1}}-x_{i_{r-1}}^{\{s_{r-1},s_r\}}. \end{aligned}$$

(6)

Iteratively, for all $t\in \{q+1,\ldots ,r-2\}$, we define

$$\begin{aligned} x_{i_{t}}^{\{s_{t},s_{t+1}\}}= & {} a_{i_{t}i_{t+1}}^{\{s_{t},s_{t+1}\}}-y_{i_{t+1}}^{\{s_{t},s_{t+1}\}}, \text{ and } \end{aligned}$$

(7)

$$\begin{aligned} y_{i_{t}}^{\{s_{t-1},s_{t}\}}= & {} u_{i_{t}}^{s_{t}}-x_{i_{t}}^{\{s_{t},s_{t+1}\}}, \end{aligned}$$

(8)

while for sector $s_q$ we define $x_{i_{q}}^{\{s_{q},s_{q+1}\}}=a_{i_{q}i_{q+1}}^{\{s_{q},s_{q+1}\}}-y_{i_{q+1}}^{\{s_{q},s_{q+1}\}}$, and, assuming $x_{i_q}^{\{s_q,s_{q'+1}\}}$ has been defined analogously from the branch $\{s_{q'+1},s_{q'+2},\ldots , s_{r'-1},s_{r'}\}$, we also define $y_{i_q}^{\{s_{q-1},s_q\}}=u_{i_q}^{s_q}-\left( x_{i_q}^{\{s_q,s_{q+1}\}}+x_{i_q}^{\{s_q,s_{q'+1}\}}\right)$. More generally, if $s_q$ has several immediate followers in $\overline{E}$, then

$$\begin{aligned} y_{i_q}^{\{s_{q-1},s_q\}}=u_{i_q}^{s_q}-\sum _{\begin{array}{c} \{s_q,s_l\}\in \overline{E}\\ s_q<s_l \end{array}}x_{i_q}^{\{s_q,s_l\}}. \end{aligned}$$

(9)

We proceed backwards until we reach $x_{i_1}^{\{s_1,s_l\}}$ for all $\{s_1,s_l\}\in \overline{E}$ with $s_1<s_l$.

In addition, if $i\in N_r$ and for some $\{r,s\}\in \overline{G}$, $r<s$, i is unmatched by $\mu ^{\{r,s\}}$, define $x_i^{\{r,s\}}=0$. Similarly, if $i\in N_r$ and for all $\{s,r\}\in \overline{G}$, $s<r$, i is unmatched by $\mu ^{\{s,r\}}$, define $y_i^{\{s,r\}}=0$.

We will first check that the payoff vectors $(x^{\{r,s\}},y^{\{r,s\}})$ we have defined are non-negative for all $\{r,s\}\in \overline{G}$. From (4) to (9) above, it follows that, for all maximal path in $\overline{E}$ starting at $s_1$, $\{s_1,s_2,\ldots , s_r\}$, and all $t\in \{ 1,2,\ldots , r-1\}$, we can express $x_{i_t}^{\{s_t,s_{t+1}\}}$ in terms of the payoffs in u to agents in following sectors in $\overline{E}$:

$$\begin{aligned} \begin{array}{rcl} x_{i_t}^{\{s_t,s_{t+1}\}}&{}=&{}a_{i_ti_{t+1}}^{\{s_t,s_{t+1}\}}-y_{i_{t+1}}^{\{s_t,s_{t+1}\}}=a_{i_ti_{t+1}}^{\{s_t,s_{t+1}\}}-(u_{i_{t+1}}^{s_{t+1}}- \displaystyle \sum _{\begin{array}{c} \{s_{t+1},l\}\in \overline{E}\\ {l > s_{t+1}} \end{array}}x_{i_{t+1}}^{\{s_{t+1},l\}})\\ &{}=&{}\cdots =a_{i_ti_{t+1}}^{\{s_t,s_{t+1}\}}+\displaystyle \sum _{\begin{array}{c} i\in N_r\cap E\\ j\in N_s\cap E\\ \{r,s\}\in \overline{E}, r,s\in \hat{\mathcal {S}}^{\overline{E}}_{s_{t+1}} \end{array}} a_{ij}^{\{r,s\}}-\displaystyle \sum _{\begin{array}{c} k\in N_r\cap E\\ {r\in \hat{\mathcal {S}}^{\overline{E}}_{s_{t+1}}} \end{array}}u_{k}^r,\end{array} \end{aligned}$$

(10)

where the first equality follows from (7) and the second from (9).

Hence, if $T=\{i_t\}\cup \{i\in E\mid i\in N_r,\,r\in \hat{\mathcal {S}}^{\overline{E}}_{s_{t+1}}\}$, we have

$$\begin{aligned} x_{i_t}^{\{s_t,s_{t+1}\}}=v(T)-u(T{\setminus }\{i_t\}). \end{aligned}$$

(11)

Notice that for $t=1$, because of efficiency of $u\in C(w_{\gamma })$, we obtain

$$\begin{aligned} \sum _{\{s_1,l\}\in \overline{E}}x_{i_1}^{\{s_1,l\}}=v(E)-\sum \limits _{\begin{array}{c} k\in E\cap N_r \\ k\ne i_1 \\ r\in \{1,\ldots ,m\} \end{array}}u_k^r=u_{i_1}^{s_1}. \end{aligned}$$

(12)

Equation (10), together with (9) gives, for all $t\in \{2,\ldots ,r\}$,

$$\begin{aligned} \begin{array}{rcl} y_{i_t}^{\{s_{t-1},s_t\}}&{}=&{}u_{i_t}^{s_t}-\displaystyle \sum _{\begin{array}{c} \{s_t,s_l\}\in \overline{E}\\ {s_t<s_l} \end{array}}x_{i_t}^{\{s_t,s_l\}}\\ &{}=&{}u_{i_t}^{s_t}-\displaystyle \sum _{\begin{array}{c} \{s_t,s_l\}\in \overline{E}\\ {s_t<s_l} \end{array}}\left( a_{i_ti_l}^{\{s_t,s_l\}}+\displaystyle \sum _{\begin{array}{c} i\in N_r\cap E\\ j\in N_s\cap E\\ {\{r,s\}\in \overline{E}, r,s\in \hat{\mathcal {S}}^{\overline{E}}_{s_{l}}} \end{array}} a_{ij}^{\{r,s\}}-\displaystyle \sum _{\begin{array}{c} k\in N_r\cap E\\ {r\in \hat{\mathcal {S}}^{\overline{E}}_{s_{l}}} \end{array}}u_{k}^r\right) \ge 0,\end{array} \end{aligned}$$

where the inequality follows from the core constraint satisfied by $u\in C(w_{\gamma })$ for coalition $T=\{i_t\}\cup \{i\in E\mid i\in N_r, r\in \mathcal {S}^{\overline{E}}_{s_{t}}\}$, that is,

$$\begin{aligned} y_{i_t}^{\{s_{t-1},s_t\}}=u(T)-v(T)\ge 0. \end{aligned}$$

(13)

Now, again making use of (4) to (12), we express $x_{i_t}^{\{s_t,s_{t+1}\}}$ in terms of the payoffs in u to agents in sectors that do not follow $s_t$ in $\overline{E}$:

$$\begin{aligned} x_{i_t}^{\{s_t,s_{t+1}\}}= & {} u_{i_t}^{s_t}-y_{i_t}^{\{s_{t-1},s_t\}}-\sum _{\begin{array}{c} \{s_t,l\}\in \overline{E}\\ {l>s_t, l\ne s_{t+1}} \end{array}}x_{i_t}^{\{s_t,l\}}\\= & {} u_{i_t}^{s_t}- a_{i_{t-1}i_t}^{\{s_{t-1},s_t\}}+x_{i_{t-1}}^{\{s_{t-1},s_t\}} -\sum _{\begin{array}{c} \{s_t,l\}\in \overline{E}\\ {l>s_t, l\ne s_{t+1}} \end{array}}x_{i_t}^{\{s_t,l\}}=\cdots \\= & {} u_{i_t}^{s_t}-a_{i_{t-1}i_t}^{\{s_{t-1},s_t\}}+x_{i_{t-1}}^{\{s_{t-1},s_t\}}-\sum _{\begin{array}{c} \{s_t,l\}\in \overline{E}\\ {s_t<l\ne s_{t+1}} \end{array}}(v(T_l)-u(T_l{\setminus }\{i_t\})), \end{aligned}$$

where the first equality follows from (9), the second from the definition of $x^{\{s_{t},s_{t+1}\}}_{i_{t-1}}$, the last equality from (11), and $T_l=\{i_t\}\cup \{i\in E\mid i\in N_r,\,r\in \hat{\mathcal {S}}_l^{\overline{E}}\}.$ Recursively applying the same argument (in first place to $x_{i_{t-1}}^{\{s_{t-1},s_t\}}$), we eventually obtain

$$\begin{aligned} x_{i_t}^{\{s_t,s_{t+1}\}}=u((T'{\setminus } T)\cup \{i_t\})-v((T'{\setminus } T)\cup \{i_t\})\ge 0, \end{aligned}$$

(14)

with $T'=\{i_1\}\cup \{i\in E\mid i\in N_r, r\in \mathcal {S}^{\overline{E}}_{s_{1}}\}$, T as defined above, and where the inequality also follows from $u\in C(w_{\gamma })$.

Once proved that for all $\{r,s\}\in \overline{G}$, $(x^{\{r,s\}},y^{\{r,s\}})$ is a non-negative payoff vector, let us check it is in $C(w_{A^{\{r,s\}}})$. If $\{i,j\}\in \mu ^{\{r,s\}}$ for some $\{r,s\}\in \overline{G}$, then i and j belong to the same basic coalition E of $\mu$ and $x_i^{\{r,s\}}+y_j^{\{r,s\}}=a_{ij}^{\{r,s\}}$ follows by definition from Eqs. (5) and (7).

Since by construction of $(x^{\{r,s\}},y^{\{r,s\}})$, see (5), this vector satisfies $x^{\{r,s\}}_{i}+y^{\{r,s\}}_{j}=a_{ij}^{\{r,s\}}$ for all $i\in N_{s}$, $j\in N_{s}$ and $\{r,s\}\in \overline{G}$, it only remains to prove that if $i\in N_r$, $j\in N_s$, with $\{r,s\}\in \overline{G}$, $r<s$, and $\{i,j\}\not \in \mu ^{\{r,s\}}$, then $x_i^{\{r,s\}}+y_j^{\{r,s\}}\ge a_{ij}^{\{r,s\}}$. Since i and j are not matched in $(N_r,N_s,A^{\{r,s\}})$, they belong to different basic coalitions in $\mu$. Let E and $E'$ be the basic coalitions containing i and j respectively. Let us consider a maximal path $\{s_1,s_2,\ldots , s_t,\ldots ,s_p\}$ in $\overline{E}$ with origin in the node in $\overline{E}$ with the lowest label (that we will name the source of the subtree $\overline{E}$) and such that there exists $t\in \{1,\ldots ,q\}$ with $r=s_t$. We write $i_1\in E\cap N_{s_1}$. Similarly, let $\{s_1',s_2',\ldots ,s_l',\ldots ,s_p'\}$ be the maximal path in $\overline{E'}$ with origin in the node in $\overline{E'}$ with the lowest label (the source) and such that there exists $l\in \{1,\ldots ,p\}$ with $s=s_l'$.

Recall from (13) that $y_{j}^{\{r,s\}}=u(R)-v(R)$, where $R=\{j\}\cup \{b\in E'\mid b\in N_k, k\in \mathcal {S}^{\overline{E'}}_{s'_{l}}\}$, and from (14) that $x_i^{\{r,s\}}=u((T'{\setminus } T)\cup \{i\})-v((T'{\setminus } T)\cup \{i\})$, where $T=\{i\}\cup \{b\in E\mid b\in N_k, k\in \mathcal {S}^{\overline{E}}_{s_{t}}\}$ and $T'=\{i_1\}\cup \{b\in E\mid b\in N_k, k\in \mathcal {S}^{\overline{E}}_{s_{1}}\}$. Since $E\cap E'=\emptyset$, $(T'{\setminus } T)\cup \{i\}$ and R are also disjoint. Then,

$$\begin{aligned} x_i^{\{r,s\}}+y_j^{\{r,s\}}=u((T'{\setminus } T)\cup \{i\}) +u(R) -v((T'{\setminus } T)\cup \{i\})-v(R)\ge a_{ij}^{\{r,s\}} \end{aligned}$$

since $v((T'{\setminus } T)\cup \{i\}\cup R)= v((T'{\setminus } T)\cup \{i\})+v(R)+a_{ij}^{\{r,s\}}$ and $u\in C(w_{\gamma })$. This completes the proof of $C(w_{\gamma })=\bigoplus _{\{r,s\}\in \overline{G}}C(w_{A^{\{r,s\}}}).$$\square$

A first remark on the computation of an optimal matching for multi-sided assignment markets is appropriate. Although the solution of the two-sided assignment problem is solvable in polynomial time, the solution of its multi-sided extension is NP-hard (see Garey and Johnson 1979). However, for a multi-sided assignment market on an m-partite graph where the quotient graph that connects the sectors is cycle-free, an optimal matching is computed in polynomial time. Indeed, from Theorem 1 it follows that the composition of optimal matchings of each underlying two-sided market yields an optimal matching of the multi-sided assignment market. Since in a market with m sectors any tree connecting the sectors has $m-1$ edges, we have $m-1$ underlying two-sided markets and we only need to solve $m-1$ bilateral assignment problems to build an optimal matching for the multi-sided market.

Now, we ask whether the class of m-partite graphs with cycle-free quotient graph is a maximal domain for strong balancedness.

A multi-sided market on a 3-partite graph with two agents in each sector is strongly balanced, that is, it has a non-empty core given any possible system of weights, even if the quotient graph contains a cycle. To prove this we only need to check that balancedness conditions in Lucas (1995) for $2\times 2\times 2$ assignment games are satisfied.

But if an m-partite graph has a cycle in its quotient graph and all sectors in the cycle contain at least three agents, then we are always able to find a system of weights such that the corresponding multi-sided assignment game has an empty core.

Corollary 1

An m-partite graph, with at least three nodes on each sector, is strongly balanced if and only if the quotient graph has no cycles.

Proof

The “if” part follows from Theorem 1. To prove the “only if” part take an m-partite graph G such that the quotient graph $\overline{G}$ has a cycle: $(N_1,N_2,N_3,\ldots ,N_p)$. Define the weights $a^{12}_{ij}$, $a^{13}_{ik}$ and $a^{23}_{jk}$, for $i,j,k\in \{1,2,3\}$ as in Example 1, and $a^{rs}_{pq}=0$ elsewhere. It is straightforward to see that if $x\in C(w_{\gamma })$, where $\gamma =(N_1,\ldots ,N_m; G; \{A^{\{r,s\}}\}_{(r,s)\in \overline{G}})$, then the restriction of x to the coalition formed by the three first agents of $N_1$, $N_2$ and $N_3$ should be in the core of the game in Example 1, which is a contradiction since it has an empty core. $\square$

The supply chain networks in Ostrovsky (2008) constitute a more general model that can be inscribed in the theory of matching with contracts, where utility may not be fully transferable among agents. These networks are somehow directed (vertical networks): each agent needs to buy some input from a preceding agent to transform it in some kind of output that serves as an input for the activity of a following agent, until the final consumer is reached. Hence, by definition, the network contains no cycles. In a generalized model in Hatfield and Kominers (2012), the network is determined by the set of feasible bilateral contracts between agents, and cycles are allowed. Nevertheless, acyclicity is needed to guarantee existence of stable allocations. Compared to that, in our model the graph that connects the agents is undirected and may contain cycles. But the main difference is that the set of agents is partitioned in sectors and it is the abscence of cycles in the quotient graph that connects the sectors what characterizes the existence of (core) stable allocations.

5 When $\overline{G}$ is cycle-free: optimal core allocations

In markets where agents are organized in sectors, it has been observed that agents may present conflict or coincidence of interests depending on whether they belong to the same sector or to different sectors. The first example is the two-sided assignment market in Shapley and Shubik (1972). Agents are partitioned in a set of buyers and a set of sellers and although one could think that there is a competition between buyers to be matched to the best sellers it turns out that there is a core allocation where all buyers get their maximum core payoff, which shows some coincidence of interests among buyers (and the same can be said for the sellers). Moreover, there is opposition of interests between the two sectors, since in this buyers-optimal core allocation, all sellers get their minimum core payoff. In the two-sided market of Shapley and Shubik (1972), the existence of the two optimal core allocations is a consequence of the lattice structure of the core. Nevertheless, Roth (1985) points out generalized bilateral markets where the same phenomena holds without an underlying lattice structure.⁷

The fact that, when $\overline{G}$ is cycle-free, the core of the multi-sided assignment game on an m-partite graph is completely described by the cores of all underlying two-sided markets allows us to deduce some properties of $C(w_{\gamma })$ from the known properties of $C(w_{A^{\{r,s\}}})$, with $\{r,s\}\in \overline{G}$. One of these consequences is that, for each sector $r\in \{1,2,\ldots ,m\}$, there is a core element $u\in C(w_{\gamma })$ where all agents in sector r simultaneously receive their maximum core payoff, which is their marginal contribution to the grand coalition. This is one property of two-sided assignment markets that does not extend to arbitrary multi-sided market, but it is preserved when sectors are connected by a tree and the value of basic coalitions is defined additively as in (1).

Proposition 2

Let $\gamma =(N_1,N_2,\ldots ,N_m; G; \{A^{\{r,s\}}\}_{\{r,s\}\in \overline{G}})$ be a multi-sided assignment market on an m-partite graph. If $\overline{G}$ is cycle-free, then for each sector $k\in \{1,2,\ldots ,m\}$ there exists $u\in C(w_{\gamma })$ such that

• 1. $u_i$ is the maximum core payoff for all $i\in N_k$ and moreover

• 2. $u_i=w_{\gamma }(N)-w_{\gamma }(N{\setminus }\{i\})$ for all $i\in N_k$.

Proof

Let us assume without loss of generality that $\overline{G}$ is a tree. Take any $k\in \{1,2,\ldots ,m\}$. For all $s\in \{1,2,\ldots ,m\}$ with $\{k,s\}\in \overline{G}$,⁸ take $(x^{\{k,s\}},y^{\{k,s\}})=(\overline{x}^{\{k,s\}},\underline{y}^{\{k,s\}})$ the element of $C(w_{A^{\{k,s\}}})$ that is optimal for all agents in $N_k$. Similarly, for all $r\in \{1,2,\ldots ,m\}$ such that $\{r,k\}\in \overline{G}$, take the element $(x^{\{r,k\}},y^{\{r,k\}})=(\underline{x}^{\{r,k\}},\overline{y}^{\{r,k\}})$ of $C(w_{A^{\{r,k\}}})$ that is optimal for the agents in $N_k$. These optimal core elements exist in any bilateral assignment market (see Shapley and Shubik 1972). Moreover, by Demange (1982) and Leonard (1983), it is known that for all $i\in N_k$, $\overline{x}_i^{\{k,s\}}=w_{A^{\{k,s\}}}(N_k\cup N_s)-w_{A^{\{k,s\}}}(N_k\cup N_s{\setminus }\{i\})$ and $\overline{y}_i^{\{r,k\}}=w_{A^{\{r,k\}}}(N_r\cup N_k)-w_{A^{\{r,k\}}}(N_r\cup N_k{\setminus }\{i\})$. Finally, for all $\{r,s\}\in \overline{G}$ with $r\ne k$ and $s\ne k$, take an arbitrary core element $(x^{\{r,s\}},y^{\{r,s\}})\in C(w_{A^{\{r,s\}}})$.

Now, if we consider the composition of the core elements defined above, we get, given $k\in \{1,2,\ldots ,m\}$, $\overline{u}^k=\bigoplus _{\{r,s\}\in \overline{G}}(x^{\{r,s\}},y^{\{r,s\}})$.

Then, for all $i\in N_k$, if $\{r,k\}\in \overline{G}$ with $r<k$,

$$\begin{aligned} \overline{u}^k_i=\overline{y}^{\{r,k\}}_i+\sum _{\begin{array}{c} \{k,s\}\in \overline{G}\\ {k<s} \end{array}}\overline{x}^{\{k,s\}}_i\ge u_i \end{aligned}$$

for all other $u\in C(w_{\gamma })$, as a consequence of Theorem 1.

Moreover, if $k\in \{1,2,\ldots ,m\}$ is such that there exists $r\in \{1,2,\ldots ,m\}$ with $\{r,k\}\in \overline{G}$ and $r<k$, and there exists $s\in \{1,2,\ldots ,m\}$ with $\{k,s\}\in \overline{G}$ and $k<s$, then

$$\begin{aligned} w_{\gamma }(N)-w_{\gamma }(N{\setminus }\{i\})= & {} \left[ w_{A^{\{r,k\}}}(N_r\cup N_k)-w_{A^{\{r,k\}}}(N_r\cup N_k{\setminus }\{i\})\right] \\+ & {} \sum _{\begin{array}{c} \{k,s\}\in \overline{G}\\ {k<s} \end{array}}\left[ w_{A^{\{k,s\}}}(N_k\cup N_s)-w_{A^{\{k,s\}}}(N_k\cup N_s{\setminus }\{i\})\right] =\overline{u}^k_i, \end{aligned}$$

for all $i\in N_k$.

Similarly, if k is a leaf of $\overline{G}$, then

$$\begin{aligned} w_{\gamma }(N)-w_{\gamma }(N{\setminus }\{i\})=w_{A^{\{r,k\}}}(N_r\cup N_k)-w_{A^{\{r,k\}}}(N_r\cup N_k{\setminus }\{i\})=\overline{u}^k_i \end{aligned}$$

for the only $r\in \{1,2,\ldots ,m\}$ such that $\{r,k\}\in \overline{G}$ and for all $i\in N_k$. Also, if k is the source of the tree $\overline{G}$, then

$$\begin{aligned} w_{\gamma }(N)-w_{\gamma }(N{\setminus }\{i\})=\sum _{\begin{array}{c} \{k,s\}\in \overline{G}\\ {k<s} \end{array}}\left[ w_{A^{\{k,s\}}}(N_k\cup N_s)-w_{A^{\{k,s\}}}(N_k\cup N_s{\setminus }\{i\})\right] =\overline{u}^k_i, \end{aligned}$$

for all $i\in N_k$.

Then, for all $k\in \{ 1, 2, \ldots , m\}$ we have $\overline{u}_{i}^{k}=w_{\gamma }(N)-w_{\gamma }(N{\setminus } i)$ for all $i\in N_{k}$. $\square$

In multi-sided assignment games on an m-partite graph with $\overline{G}$ cycle-free, unlike the case of Shapley and Shubik (1972) two-sided markets, optimal core allocations for a sector k may not be unique. Indeed, from the proof of Proposition 2, the reader will realize there is a lot of freedom of choice of core allocations for those bilateral markets in which sector k is not involved.

Notice that, for each sector $k\in \{1,2,\ldots ,m\}$ there is also a core allocation where all agents in this sector get their minimum core payoff. The proof is analogous to the one in Proposition 2: we only need to choose, for each two-sided market in which sector k takes part, the k-minimum core allocation, and for each two-sided market not involving sector k, an arbitrary core allocation. Their composition produces a minimum core allocation for sector k in the multi-sided market on an m-partite graph, as long as the quotient graph is cycle-free. When $\overline{G}$ contains cycles, optimal core allocations for all sectors may not exist (see Example 5 in the “Appendix”).

Once proved the existence of sector-optimal core allocations for an assignment market on an m-partite graph with a cycle-free quotient graph $\overline{G}$, the question arises whether some other extreme core points or some single-valued solutions of the coalitional game can be obtained in the same way by composition of the corresponding solutions in the underlying two-sided markets. Next proposition shows that indeed all extreme core allocations of the multi-sided assignment game are obtained as the composition of extreme core allocations of the underlying two-sided markets.

Proposition 3

Let $\gamma =(N_1,N_2,\ldots ,N_m;G;\{A^{\{r,s\}}\}_{\{r,s\}\in \overline{G}})$ be a multi-sided assignment market on an m-partite graph. If $\overline{G}$ is cycle-free, then any extreme core allocation $x\in Ext(C(w_{\gamma }))$ is the composition of extreme core allocations of the underlying two-sided markets, $x=\bigoplus _{\{r,s\}\in \overline{G}}x^{\{r,s\}}$, where $x^{\{r,s\}}\in Ext(C(w_{A^{\{r,s\}}}))$ for all $\{ r,s\}\in \overline{G}$.

Proof

From Theorem 1, it is straightforward to see that $x\in Ext(C(w_{\gamma }))$ satisfies $x=\bigoplus _{\{r,s\}\in \overline{G}}x^{\{r,s\}}$ for some $x^{\{r,s\}}\in C(w_{A^{\{r,s\}}})$. Assume now that $x^{\{r',s'\}}\not \in Ext(C(w_{A^{\{r',s'\}}}))$ for some $\{r',s'\}\in \overline{G}$. Then, there exist two different elements, $y^{\{r',s'\}}$ and $z^{\{r',s'\}}$, in $C(w_{A^{\{r',s'\}}})$ such that $x^{\{r',s'\}}=\frac{1}{2}y^{\{r',s'\}}+\frac{1}{2}z^{\{r',s'\}}$.

We now consider two different elements in $C(w_{\gamma })$ by composing $\bigoplus \limits _{\begin{array}{c} \{r,s\}\in \overline{G}\\ {\{r,s\}\ne \{r',s'\}} \end{array}}x^{\{r,s\}}$ either with $y^{\{r',s'\}}$ or $z^{\{r',s'\}}$,

$$\begin{aligned} x^y=\left( \bigoplus _{\begin{array}{c} \{r,s\}\in \overline{G}\\ {\{r,s\}\ne \{r',s'\}} \end{array}}x^{\{r,s\}}\right) \oplus y^{\{r',s'\}} \text{ and } x^z=\left( \bigoplus _{\begin{array}{c} \{r,s\}\in \overline{G}\\ {\{r,s\}\ne \{r',s'\}} \end{array}}x^{\{r,s\}}\right) \oplus z^{\{r',s'\}}. \end{aligned}$$

It is then straightforward to check that $x=\frac{1}{2} x^y+\frac{1}{2} x^z$, which contradicts the assumption $x\in Ext(C(w_{\gamma }))$. $\square$

However, the converse implication does not hold, that is, the composition of extreme core allocations of the underlying two-sided markets provides an element in $C(w_{\gamma })$ which may not be an extreme point (see Example 4 in the “Appendix”).

We now consider single-valued core selections that are not extreme points but usually interior core points. As a consequence of Theorem 1, the composition $\eta ^{\oplus }(w_{\gamma })=\oplus _{\{r,s\}\in \overline{G}}\eta (w_{A^{\{r,s\}}})$ of the nucleolus⁹ of the two-sided markets between connected sectors belongs to $C(w_{\gamma })$. Moreover, well-known algorithms to compute the nucleolus of a two-sided assignment game (Solymosi and Raghavan 1994; Martínez de Albéniz et al. 2014) can be used to obtain $\eta ^{\oplus }(w_{\gamma })$. However, this composition does not coincide with the nucleolus of the initial m-sided market $\gamma =(N_1,N_2,\ldots ,N_m; G; \{A^{\{r,s\}}\}_{\{r,s\}\in \overline{G}})$, as Example 3 in the “Appendix” shows.

If we select the $\tau$-value or fair-division point¹⁰ as the cooperative solution concept to distribute the profits in each bilateral market, we can propose the composition of the $\tau$-values of all connected two-sided markets, $\tau ^{\oplus }(w_{\gamma })=\oplus _{\{r,s\}\in \overline{G}}\tau (w_{A^{\{r,s\}}})$ as an allocation of the profit of the multi-sided assignment market with a tree quotient graph. Because of Theorem 1, this composition belongs to $C(w_{\gamma })$ and can be considered as a fair division solution for the m-sided market. However, different to the two-sided case, it may not coincide with the $\tau$-value of the initial m-sided market $\gamma =(N_1,N_2,\ldots ,N_m; G; \{A^{\{r,s\}}\}_{\{r,s\}\in \overline{G}})$. In fact, the $\tau$-value of a multi-sided assignment market on an m-partite graph may lie outside the core (see Example 2 in the “Appendix”), even when the quotient graph $\overline{G}$ is cycle-free.

6 Concluding remarks

We have considered multi-sided markets where agents are on an m-partite graph that induces a cycle-free network among the sectors. Basic coalitions do not need to have agents from all sectors, it is enough not to have two agents from the same sector. Moreover, the worth of a basic coalition is the addition of the worths of all its pairs that are an edge of the m-partite graph.

A similar situation is considered in Stuart (1997), although restricted to the case in which the network that connects the sectors is a chain. There, the worth of a basic coalition is also defined additively, but, as in the classical multi-sided assignment games in Kaneko and Wooders (1982) and Quint (1991), the set of basic coalitions is smaller since it is required that a basic coalition contains exactly one agent of each side. Although the core of Stuart’s multi-sided game is also non-empty, it does not contain the composition of all core elements of the underlying two sided markets.

Indeed, take $N_{1}=\{1,2,3\}$, $N_{2}=\{1',2',3'\}$ and $N_{3}=\{1'',2''\}$, and consider the chain $\overline{G}=\{\{N_{1},N_{2}\},\{N_{2},N_{3}\}\}$. Assume also that $a^{\{r,s\}}_{ij}=1$ for all $(i,j)\in N_{r}\times N_{s}$ such that $\{N_{r},N_{s}\}\in \overline{G}$, but, unlike the model we present in this paper, only triplets may have a positive value. It is easy to see that $(0.5,0.5,0.5;0.5,0.5,0.5)\in C(w_{A^{\{1,2\}}})$ and $(0,0,0;1,1)\in C(w_{A^{\{2,3\}}})$. However,

$$\begin{aligned} z=x\oplus y=(0.5,0.5,0.5;0.5,0.5,0.5;1,1)\notin C(w_{\gamma }), \end{aligned}$$

since an optimal matching consists of two triplets and hence the unassigned agents in sectors $N_{1}$ and $N_{2}$ can only receive zero payoff in the core.

Our paper answers the question about what conditions suffice so that multi-sided markets inherit the properties of two-sided markets. The answer is a cycle-free network structure with non-negative weights.

Appendix

We first consign to this “Appendix” two examples that show that for a multi-sided assignment game on a cycle-free quotient graph, the composition of the $\tau$-values (or the nucleolus) of each underlying two-sided market may not coincide with the $\tau$-value or the nucleolus of the initial multi-sided market. Similarly, the third example shows that by composition of arbitrary extreme core allocations of each two-sided market we may not obtain an extreme core allocation of the multi-sided market.

Example 2

Let us consider an assignment market $\gamma$ on a 3-partite graph such that the quotient graph is $\overline{G}=\{\{1,2\},\{2,3\}\}$ which is cycle-free. The sectors are $N_1=\{1,2\}$, $N_2=\{1',2'\}$, and $N_3=\{1'',2''\}$. The valuation matrices of the two underlying two-sided markets are

$$\begin{aligned} \begin{array}{cc}&\begin{array}{cc} 1' &{} 2'\end{array} \\ \begin{array}{c} 1 \\ 2 \end{array} &{} \left( \begin{array}{cc} 2\; &{}\; 0 \\ 5\; &{}\; 4 \end{array}\right) \end{array} \qquad \begin{array}{cc}&\begin{array}{cc} 1'' &{} 2''\end{array} \\ \begin{array}{c} 1' \\ 2' \end{array} &{} \left( \begin{array}{cc} 3\; &{}\; 4 \\ 0\; &{}\; 3 \end{array}\right) ,\end{array} \end{aligned}$$

and the value of triplets is given by the following three-dimensional matrix

$$\begin{aligned} \begin{array}{cc}&\begin{array}{cc} 1' &{} 2'\end{array} \\ \begin{array}{c} 1 \\ 2 \end{array} &{} \left( \begin{array}{cc} 5\; &{}\; 0 \\ 8\; &{}\; 4 \end{array}\right) \\ &{} 1'' \end{array}\qquad \begin{array}{cc}&\begin{array}{cc} 1' &{} 2' \end{array}\\ \begin{array}{c} 1 \\ 2 \end{array} &{} \left( \begin{array}{cc} 6 \; &{}\; 3 \\ 9\; &{} \; 7 \end{array}\right) \\ &{} 2'' \end{array}. \end{aligned}$$

The $\tau$-value of this multi-sided market game is $\tau (\gamma )=(\frac{5}{9},\frac{24}{9}; \frac{29}{9}, \frac{15}{9}; \frac{15}{9},\frac{20}{9})$ which is not in the core since $\tau _{2}+\tau _{1'}+\tau _{2''}=\frac{24}{9}+\frac{29}{9}+\frac{20}{9}=\frac{73}{9}<9=v(\{2,1',2''\})$. Hence, $\tau (\gamma )$ cannot coincide with $\tau (w_{A^{\{1,2\}}})\oplus \tau (w_{A^{\{2,3\}}})$.

Example 3

Let us consider an assignment market $\gamma$ on the following 4-partite graph related to the the quotient graph $\overline{G}=\{\{1,2\},\{2,3\},\{2,4\}\}$ which is cycle free. The sectors are $N_1=\{1,2\}$, $N_2=\{1',2'\}$, $N_3=\{1'',2''\}$, $N_4=\{1''',2'''\}$, and the valuation matrices of the two-sided markets are

The nucleolus of the three underlying two-sided markets are

$$\begin{aligned} \begin{array}{c} \eta ^{\{1,2\}}=(1.625, 0.375; 0.375, 1.625), \quad \eta ^{\{2,3\}}=(0.45, 1.55; 2.55, 0.45) \\ \text{ and } \quad \eta ^{\{2,4\}}=(0.55, 1.45; 1.45, 0.55)\end{array} \end{aligned}$$

and their composition is

$$\begin{aligned} \eta ^{\oplus }=(1.625, 0.375; 1.375, 4.625; 2.55, 0.45; 1.45, 0.55), \end{aligned}$$

while the nucleolus of the six-player game $(N, w_{\gamma })$ can be computed and is

$$\begin{aligned} \eta =(1.65,0.4; 1.6, 4.75; 2.55,0.45; 1.2, 0.4). \end{aligned}$$

Example 4

Let us consider an assignment market $\gamma$ on a 4-partite graph related to the quotient graph $\overline{G}=\{\{1,2\},\{2,3\},\{2,4\}\}$ which is cycle-free. The sectors are $N_{1}=\{1,2\}$, $N_{2}=\{1',2'\}$, $N_{3}=\{1'',2''\}$, and $N_{4}=\{1''',2'''\}$. The valuation matrices of the three underlying two-sided markets are

Take respective extreme core allocations of the three underlying two-sided markets $A^{\{1,2\}}$, $A^{\{2,3\}}$, and $A^{\{2,4\}}$: (2, 1; 0, 1), (2, 0; 0, 2), and (1, 0; 0, 1). Then, by composition we get a core allocation for the multi-sided assignment market, $x^{\oplus }=(2,1;3,1;0,2;0,1)\in C(w_{\gamma })$. But, there exist two core elements

$$\begin{aligned} y=(1.8,0.8;3.2,1.2;0,2;0,1)\in C(w_{\gamma }) \end{aligned}$$

and

$$\begin{aligned} z=(2.2,1.2;2.8,0.8;0,2;0,1)\in C(w_{\gamma }) \end{aligned}$$

such that $x^{\oplus }=\frac{1}{2}y+\frac{1}{2}z$. Hence, $x^{\oplus }\notin Ext(C(w_{\gamma }))$.

The last example shows that assumptions of Proposition 1 are not necessary for the non-emptiness of the core. In this example, the core of the multi-sided assignment game is non-empty and the matching induced on one two-sided market is not optimal. The same example shows that when $\overline{G}$ is not cycle-free, optimal core allocations for each sector may not exist.

Example 5

Let us consider an assignment market $\gamma$ on a complete 3-partite graph G where $M_1=\{1,2\}$, $M_2=\{1',2'\}$ and $M_3=\{1'',2''\}$. The valuation matrices of the three underlying two-sided markets are

$$\begin{aligned} \begin{array}{cc}&\begin{array}{cc} 1' &{} 2'\end{array} \\ \begin{array}{c} 1 \\ 2 \end{array} &{} \left( \begin{array}{cc} 4\; &{}\; \textcircled {4} \\ \textcircled {5}\; &{}\; 0 \end{array}\right) \end{array} \qquad \begin{array}{cc}&\begin{array}{cc} 1'' &{} 2'' \end{array}\\ \begin{array}{c} 1 \\ 2 \end{array} &{} \left( \begin{array}{cc} \textcircled {2} \; &{}\; 0 \\ 1\; &{} \;\textcircled {5} \end{array}\right) \end{array} \qquad \begin{array}{cc}&\begin{array}{cc} 1'' &{} 2''\end{array} \\ \begin{array}{c} 1' \\ 2' \end{array} &{} \left( \begin{array}{cc} \textcircled {4}\; &{}\; 3 \\ 0\; &{}\; \textcircled {9} \end{array}\right) ,\end{array} \end{aligned}$$

and the value of triplets is given by the following three-dimensional matrix

$$\begin{aligned} \begin{array}{cc}&\begin{array}{cc} 1' &{} 2'\end{array} \\ \begin{array}{c} 1 \\ 2 \end{array} &{} \left( \begin{array}{cc} \mathbf{10}\; &{}\; 6 \\ 10\; &{}\; 1 \end{array}\right) \\ &{} 1'' \end{array}\qquad \begin{array}{cc}&\begin{array}{cc} 1' &{} 2' \end{array}\\ \begin{array}{c} 1 \\ 2 \end{array} &{} \left( \begin{array}{cc} 7 \; &{}\; 13 \\ 13\; &{} \;\mathbf{14} \end{array}\right) \\ &{} 2'' \end{array}. \end{aligned}$$

Notice first that this market does not satisfy the sufficient condition in Proposition 1. Indeed the optimal matching is $\mu =\{(1,1',1''),(2,2',2'')\}$ but $\mu ^{\{1,2\}}=\{(1,1'), (2,2')\}$ is not optimal for $A^{\{1,2\}}$. Nevertheless, the core is non-empty. For instance, $x=(4,5;0,0;6,9)$ and $y=(4,4;1,0;5,10)$ belong to $C(w_{\gamma })$. Moreover $x_{1''}=6$ and $y_{2''}=10$ are respectively the marginal contributions of agents $1''$ and $2''$ and hence these are their maximum core payoffs. However, there is no core element where agents $1''$ and $2''$ simultaneously receive 6 and 10. Indeed, if $(x,y,4-x,4-y,6,10)$ were a core allocation, then core constraints would imply $x+(4-y)\ge 4$ and $y+(4-x)\ge 5$, which lead to the contradiction $y\le x\le y-1$. As a consequence, in this market there is no optimal core allocation for the third sector.