1 Introduction

About 15 billions of gallons of ethanol fuel were produced in the US in 2016 (World Fuel Ethanol 2017), that is half a billion more than in 2015; with more than \(90\%\) of all biofuels in the last decade being based on ethanol (Farrell et al. 2006; Balat and Balat 2009). However current ethanol production methods are unable to meet the increasing global demand of bio-ethanol production due to their low yield on feedstock whose primary value is of food and feed (Gupta and Verma 2015).

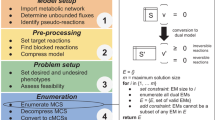
In this work, we investigate the problem associated to the overproduction of ethanol in metabolic engineered organisms. By building upon recent achievements of in silico driven engineering of bacteria strains (Patane et al. 2015; Rockwell et al. 2013; Yim et al. 2011), we perform extensive in silico optimization (Castrogiovanni et al. 2007) and analyses of eight different microorganisms for the production of ethanol as output of the metabolic network of the engineered cell. In fact, the attention given to optimization algorithms for the design of microbial strains overproducing metabolites of interest has drastically increased in the last few years (Long et al. 2015). The number of recent successes in the field of synthetic biology (Church and Regis 2014) seems indeed to shake off all but little doubt that in the near future the latter will be standard practice in the production of therapeutic drugs (Church et al. 2014), renewable bio-materials (Yim et al. 2011) and biofuels (Lee et al. 2008; Bro et al. 2006). However, the intrinsic complexity of biological systems and organisms makes of paramount importance the design of mathematical and computational approaches to fully exploit the potential of this discipline (Andrianantoandro et al. 2006). We rely on steady-state genome-scale metabolic models, such as flux balance analysis (FBA) (Kauffman et al. 2003; Palsson 2015), as it has proven to be a computational efficient and reliable modelling approach for systematic in silico analysis of many organisms (Yim et al. 2011), further allowing for straight forward implementation of -omics data sets information into the models.

Briefly, a metabolic network includes: (i) metabolic and biophysical processes occurring in the cell; (ii) chemical reactions; (iii) metabolic pathways; (iv) regulatory interactions; and models the overall biochemical metabolic properties of a cell. Mathematically, metabolic networks are modelled as flow graphs, in which metabolites (represented as graph vertices) flow through the network reactions (that is the graph edges). In particular, in FBA modelling, viable fluxes trough the metabolic network are first determined by solving constraints associated to mass-conservation within the cell, then the predicted flux through the network is obtained by maximizing a particular biological objective, e.g. biomass, or growth rate (Orth et al. 2010). In a bi-level optimization in silico framework, a meta-optimization algorithm seeks for the genetic manipulation which, applied to the metabolic network model, results in the overproduction of one or more metabolites of interest (ethanol in the case study presented in this paper).

Building upon (Patané et al. 2016), we design a multi-objective optimization algorithm tailored for the analysis of metabolic networks, and apply the latter to the problem associated with the overproduction of ethanol in FBA models of: (i) S. aureus; (ii) S. enterica; (iii) Y. pestis; (iv) S. cerevisiae; (v) C. reinhardtii; (vi) Y. lipolytica. Exploring the Pareto optimal trade-off between the production rate of ethanol and the modelled organism biological objective, we identify sets of key genetic manipulations, which lead to strains overproducing ethanol yet with sensible growth as predicted by the FBA model. Results include strains with percentage variation of ethanol production of \(+\,832.88 \% \) with respect to wild-type production rate, as well as many other Pareto optimal strains, having reduced knock-out cost and increased biomass production, potentially allowing for a sustained industrial process. We propose then unsupervised clustering as a powerful technique to map the relationship between phenotype and genotype, aiding the post-processing task by finding patterns on knocked-out genes among Pareto optimal trade-off strains.

Finally, a set of further analysis were performed, in which information on the essential genes and others constraints on the growth rate and the external simulated rich media were added, to better simulate a realistic scenario. In the same medium used in the other simulations, the maximum increase in the ethanol production is \(+\,195.24\%.\)

In silico analysis of FBA models for metabolites overproduction was firstly modelled by directly manipulating the upper and lower bounds on the reaction fluxes (Pharkya and Maranas 2006). The approach was further improved to account for improved modelling of genetic manipulations, e.g. using of genetic knockouts (Burgard et al. 2003); or modelling enzymes up/down-regulation (Rockwell et al. 2013).

Heuristic optimization techniques have been extensively applied for in silico optimization problem associated to synthetic biology in the last two decades. Example specific to the field of metabolic engineering are: genetic design through local search (GDLS) (Lun et al. 2009) in which the MILP is iteratively solved in small region of the design space; enhancing metabolism with iterative linear optimization (EMILiO) (Yang et al. 2011), that use a successive linear programming approach in order to solve efficiently a MILP obtained through the Karush–Kuhn–Tucker method. A recent survey of the state-of-the-art is given in Long et al. 2015.

The remainder of this paper is organized as follows. In Sect. 2, we review the main notions of flux balance analysis, and briefly describe how it can be applied to compute in silico prediction of the effect that genetic knockouts have on genome-scale models. We then describe the concept of Pareto optimality and the main ideas underlying our multi-objective optimization approach along with its extension in Sect. 3. In Sect. 4 we report the results regarding the overproduction of ethanol in genome-scale models for the seven organisms we consider. Finally, we conclude the paper and give final remarks in Sect. 5.

2 Genome-scale metabolic models

In this section we introduce FBA models, and modelling approach for in silico genetic manipulations that will be the used in the remainder of the paper.

Briefly FBA is a steady-state model that relies on the mass conservation assumption. Let \(S = \left( s_{ij} \right) \) be the \(m \times n\) stoichiometric matrix associated with the metabolism of an organism, where m is the number of metabolites and n is the number of reactions which build up the organism metabolism, i.e. \(s_{ij}\) is the stoichiometric coefficient of the ith metabolite in the jth reaction. Let \(v = \left( v_1, \ldots , v_n \right) \) be the vector of metabolic fluxes trough the n reaction of the network, then, the linear system \(S v = 0,\) express the mass conservation and steady state assumptions (Orth et al. 2010). The solution space of the above linear system defines the network capabilities vector space; that is the subset of v allowed from a strictly physical point of view. Of course, we cannot expect that stoichiometric information can account for the global behaviour of a cell. This is mathematically reflected by the condition \(m \ll n\) which usually leads to a high dimensional network capabilities space. Biological information is summarized into an n dimensional objective coefficient vector f experimentally tuned for modelling each specific organism, which represents the biological objective of the organism as a weighted sum of specific reactions included in the model. Although several alternatives are possible, the most used biological objective is the cell biomass production. By using FBA modelling the steady-state metabolic behaviours of the cell is hence retrieved by solving the linear programming problem

$$\begin{aligned} \begin{array}{ll} \text {maximize } &{} f^Tv \\ \text {subject to } &{} Sv=0 \\ &{} v^- \le v \le v^+ \end{array} \end{aligned}$$
(1)

where \(v^-\) and \(v^+\) are lower and upper bounds vector on the fluxes, whose actual values are based on empirical observations.

Gene knock-out analysis Gene knock-out (KO) analysis trough FBA models refer to analysing how knock-out of specific genes affects the production of specific metabolites in the cell. Mathematically, this is accomplished by introducing the Gene-protein-reaction (GPR) mapping (Palsson 2015). Briefly, the organism genes are grouped into gene sets, i.e. group of genes linked by Boolean relations accordingly to common reactions that their associated proteins catalyse. For example, a gene set of the form \(G_1\) and \(G_2\) implies that both \(G_1\) and \(G_2\) are needed for a particular reaction to be catalysed (i.e. they represent an enzymatic complex), whereas a gene set of the form \(G_1\) or \(G_2\) implies that at least one among \(G_1\) and \(G_2\) is needed for that particular reaction to be catalysed (i.e. \(G_1\) and \(G_2\) code for isoenzymes). The GPR hence relates sets of reactions to sets of genes, which code for proteins catalysing for the former sets. Namely this is introduced in the FBA model trough a matrix \(G = \left( g_{lj} \right) \), where \(g_{lj}\) is equal to 1 if and only if the lth gene set is related to the jth reaction; \(g_{lj}\) is equal to 0 otherwise. This allow us to perform in silico analysis of the effect of genetic knock-outs/knock-ins to the cell metabolism by simple manipulation of the FBA model implemented as additional linear constraints. Namely, the knockout of the lth gene set is modelled by constraining to a zero flux all the reactions j such that \(g_{lj}\) is equal to 1.

Finally, gene set knock-out Cost (KC) (Palsson 2015) is recursively defined over the form of the gene set. Briefly, if a gene set is composed by two smaller gene sets related by an “and”, then the KC of the composite gene set is the smallest KC of the two gene sets that compose it (knocking out either one these two will knock-out the enzymatic complex). If whereas the two smaller gene set are linked by means of an “or” then the KC of the gene set is the sum of the KCs of the smaller gene sets (since they are isoenzymes we need to knock-out both of them).

In the last simulation, where information on the single essential genes were added, we switched to a single gene KO approach. This required a simple further step in which from a binary vector expressing the presence of the single genes, the gene set Boolean expression were actually evaluated, to obtain their value.

Enzyme regulation analysis In enzyme regulation analysis, genetic manipulations are modelled as soft up or down regulation of specific enzymes included in the cell (Rockwell et al. 2013). In particular, the Redirector framework introduces a more biologically relevant approach for the simulation of metabolic alteration in a FBA model. Briefly (refer to (Rockwell et al. 2013) for a throughout-fully discussion about the methodology and experimental validation) the regulation of an enzyme is modelled adding all the reaction fluxes, related to that specific enzyme, to the biological objective of the FBA model. That is, up (respectively down) regulation is modelled by incentivizing (disincentivizing) the cell to perform reactions, which are catalysed by specific enzymes. In fact, fluxes added to the biological objective function are multiplied by a scalar weight, \(\beta \); a positive \(\beta \) stands for enzyme up-regulation, whereas a negative \(\beta \) models the down-regulation of that particular enzyme.

3 Multi-objective optimization and analysis

In this section, we review the basic principle of metabolic design through bioCAD tool (Patane et al. 2015) extending it with a novel approach for the analysis of the relations between the genotype and the phenotype spaces of metabolic networks.

Multi-objective optimizationMOME is built on the concept of Pareto optimality, in which the ordering relationship among real values is extended along each coordinate direction. Intuitively, Pareto optimality comes into play when for a particular design problem, it is of interest to optimize several objective functions, which are in contrast with each other. For example, there usually exists a trade-off (Conca et al. 2009) between the growth rate of a bacterium and the production rate of a particular metabolite. In fact, in order to increase the production of the latter the bacterium has to redirect its resources from the pathways involved into growth to the pathways involved into the production of the metabolite. Pareto optimality allows a rigorous analysis of the trade-offs among these two production rates.

Formally, we define a strict ordering relationship \(\prec \) for each \(x,y \in {\mathbb {R}}^k\): \(x \prec y \Longleftrightarrow x_i \le y_i \quad i=1,\ldots ,k \quad \text {and} \quad \exists \; j \; \text {s.t.} \; x_j < y_j\) , that is, if each component of x is less than or equal to its corresponding component of y, and at least one x component is strictly less than y component. Then, given a generic multi-optimization problem with objective function F an input vector x is said to dominate y with respect to F if \(F(x) \prec F(y)\). Finally, the Pareto-front is defined as the set of input vectors x such that there are no input vectors y that dominates x (Deb 2001). The goal of a multi-objective optimization algorithm is thus to find (or approximate) the Pareto front of the problem.

Analogously, a high standard deviation returned for a specific parameter indicates that either the latter is interacting with other design parameters or that it has strongly nonlinear effects on the model output.

MOME algorithm The multi-objective metabolic engineering - MOME optimization algorithm builds upon NSGA-II algorithm as for the optimization engine (Deb et al. 2012). As for being inspired by evolutionary algorithms (Deb 2001), the latter works by sampling from the optimization problem input domain an initial set of candidate solution to the optimization problem, i.e. a population, and it iteratively attempts to optimize the problem objective function, by applying to the population a set of evolutionary operators (Deb 2001).

figure a

The pseudo-code of MOME in listed in Algorithm 1. The parameters of the algorithm are: (i) pop, the size of the population; (ii) maxGen, the maximum number of generations (i.e. iterations of the algorithm main loop) to be performed; (iii) dup, the strength of the cloning operator (Ciccazzo et al. 2008); and (iv) uKC, the maximum knock-out cost allowed to be taken into account by the algorithm.

The initial population, \(P^{(0)}\), is randomly initialized by the routine InitPop, which just randomly sample the domain of the problem, by randomly applying few mutations to the wild type strain. We hence apply FBA to each strain in \(P^{(0)}\), and, accordingly to the value of the production rates of metabolite of interest, we compute rank and crowding distance for each member of the population (Deb et al. 2012). The former ensures the Pareto-orientation of our procedure, redirecting the search towards the problem Pareto front. The crowding distance whereas is a rough estimation of the population density near each candidate solution. During the optimization main loop, candidate solutions in unexplored regions of the objective space (thus having small values of crowding distance) are preferred to those which lie in “crowded” regions of the objective space. This has the purpose of obtaining good approximations of the actual Pareto front of the problem. We then initialize the generation counter, and enter the main loop, which is performed maxGen times. At the beginning of each generation the Selection procedure generate a mating pool \(Pool^{(gen)}\), by selecting individual from the current population \(P^{(gen)}\). This is done following a binary tournament selection approach. Namely, tournaments are performed until there are \( \left[ pop/2 \right] \) individuals (parents) in the mating pool. Each tournament consists of randomly choosing two individuals from \(P^{(gen)}\), and putting the best of the two individuals (in terms of rank and crowding distance) into \(Pool^{(gen)}\). Children individuals are thus generated from the parents by using binary mutation. Namely we randomly generate dup different children from each parent, generating the \(Q^{(gen)}_{dup}\). Then, we keep only the best solution of these dup children for each parent, hence defining the actual offspring set \(Q^{(gen)}\). The reason for this lies in the fact that many of the mutations allowed in an FBA model are lethal mutations, i.e. they severely compromise the bacteria growth. Of course, a greater value for dup implies that feasible mutations are more likely to be found, whereas smaller values reduce the computational burden of the optimization. In order to achieve this, we firstly ensure that each individual of \(Q^{(gen)}_{dup}\) is feasible with respect to our optimization problem (i.e. it has less than uKC knock-outs). Namely if a child is not in the allowed region, we randomly knock-in genes, until it is forced back to the feasible region. We hence evaluate the biomass and metabolites production of each new individual, and the algorithm computes new values of rank and crowding distance, for each individual. Procedure BestOutOfDup select from each of the dup children of each parent the best one and put it in the \(Q^{(gen)}\) set. Finally, procedure Best generates a new population of pop individuals, considering the current best individuals and children. Output of the optimization algorithm is the union of the populations of all the generations. We then analyse the optimization results by means of Pareto analysis, hence computing the observed Pareto fronts, i.e. the set of \(\bigcup _{gen} P^{(gen)}\) elements which are not dominated by any other element in \(\bigcup _{gen} P^{(gen)} \) (notice that \(\bigcup _{gen} P^{(gen)}\) covers only a portion of the feasible region, hence we talk about observed Pareto optimality).

Clustering Solutions when represented using, for instance, the production of a metabolite and biomass production tend to form clusters. These highlight the feasible zones of the space of solutions, assuming that an exhaustive search has been performed. Performing clustering on such solutions allows to study the characteristics of the strains that belong to a cluster and potentially identify similarities. There are several clustering techniques, however we suggest that in this context density-based clustering seems to be the preferable to centroid-based or probabilistic techniques such as k-means and expectation maximization, since clusters generally tend to have irregular shapes.

Briefly, DBSCAN distinguishes three different types of points: core, border and outliers. Core points are those points with at least k points within a distance epsilon, such points are directly reachable from the core point. a point that is not a core point is a border point if its distance from a core point is less than or equal to \(\epsilon \); those points that do not satisfy these conditions are outliers. A cluster is defined by a set of interconnected core points (forming paths of directly reachable core points) and the border points that are connected to them.

If not otherwise specified, we set the parameters of the algorithm have been set as follows: \(k=4\) and \(\epsilon =0.06\) and the data was normalized before being clustered.

4 Ethanol production

We analyse the results obtained by MOME when applied to the problem associated to overproduction of ethanol in seven different organisms, as modelled by FBA. First, we focus on gene KO analysis and discuss extensive comparisons we performed on seven different models. Then we compare the results of using genetic KO with those obtained using enzymes up/down regulation, using the Redirector modelling framework in the specific case of S. cerevisiae.

Gene KO optimization for ethanol production In this section, we present the results for the optimization of ethanol in Escherichia coli k12 mg1655 FBA model iJO1366 (Orth et al. 2011). Further we compare E. coli results with those obtained using other 7 other organisms; that is, (i) Staphylococcus aureus subsp. aureus N315 – S. aureus (model used: iSB619 (King et al. 2016; Becker and Palsson 2005), 655 metabolites, 743 reactions and 619 genes); (ii) Salmonella enterica subsp. enterica serovar Typhimurium str. LT2 – S. enterica (STM_v1_0 (King et al. 2016; Thiele 2011), 1802 metabolites , 2545 reactions and 1271 genes); (iii) Yersinia pestis CO92 – Y. pestis (iPC815 (King et al. 2016; Charusanti et al. 2011), 1552 metabolites, 1961 reactions, 815 genes); (iv) Saccharomyces cerevisiae S288C – S. cerevisiae (Yeast 7.6 (Aung et al. 2013), 2302 reactions, 909 genes); (v) Chlamydomonas reinhardtii – C. reinhardtii (iRC1080 (King et al. 2016; Chang et al. 2011), 1706 metabolites, 2191 reactions, 1086 genes); (vi) Yarrowia lipolytica – Y. lipolytica (iYL619 (King et al. 2016; Pan and Hua 2012), 843 metabolites, 1,142 reactions, 619 genes). Unless otherwise specified we set 50 as the maximum knock-out cost for each strain.

Figure 1a shows the projection on the codomain space of the feasible region explored by MOME framework and observed Pareto front for the E. coli optimization, and Table 1 shows the 10 best trade-offs found (as for values closer to theoretical maximum production). Highest production rate for ethanol found is \( 19.74\, \hbox {mmol} \, \hbox {gDW}^{-1} \, \hbox {h}^{-1} \) which is a \(+\,832.88 \% \) improvement with respect to wild-type production. This is obtained by a strain that produce biomass at a rate of f \(0.02 \, \hbox {h}^{-1}\) (i.e. \(98.06 \% \) reduction with respect to wild type biomass), and that has a knock-out cost of 14. Specific knock-outs for this strain are: frmA, (fadB or yfcX), fieF, uxuB, (nuoN and nuoM and nuoL and nuoK and nuoJ and nuoI and nuoH and nuoG and nuoF and nuoE and nuoC and nuoB and nuoA), ((pflA and pflB) or (pflA and tdcE) or (pflD and pflC) or ((pflA and pflB) and yfiD)), ppk, rfaS, tpiA, avtA (Table 1).

Fig. 1
figure 1

Results for optimization of ethanol production and biomass formation in E. coli, anaerobic condition, glucose uptake rate \(10 \, \hbox {mmol} \, \hbox {gDW}^{-1} \, \hbox {h}^{-1}\). a Pareto front (in red) and feasible strain (in black). b Clustering results for the projection of the observed Pareto front. (Color figure online)

Full size image
Table 1 Maximization of ethanol and biomass production for E. coli
Full size table

In Fig. 2 we analyse ethanol production as a function of the knock-out cost in strains explored by MOME. Intuitively, strains that are in knees of the function represent strains with an optimal trade-off between knock-out cost and ethanol production rate. Notice a single gene knock-out strain characterized by \(16.49 \, \hbox {mmol} \, \hbox {gDW}^{-1} \, \hbox {h}^{-1}\) ethanol production, i.e. \(+\,679.29 \%\) improvement with respect to wild type, and a biomass formation of \(0.23 \, \hbox {h}^{-1}\) (\(-\,77.45 \% \)). The genetic target knocked-out in this strain is: (nuoN and nuoM and nuoL and nuoK and nuoJ and nuoI and nuoH and nuoG and nuoF and nuoE and nuoC and nuoB and nuoA). Another interesting strain that this analysis reveal is the strain having a knock-out cost of 6. This produces ethanol at a rate of \(18.52 \, \hbox {mmol} \, \hbox {gDW}^{-1} \, \hbox {h}^{-1}\) (\(+\,775.22 \%\)) and has biomass formation of \(0.10 \, \hbox {h}^{-1}\) (\(-\,90.32 \%\)).

The Pareto front of the values of the objective functions (ethanol production and biomass) of the selected solutions has been clustered using DBSCAN. The results of the clustering are shown in Fig. 1b. We can identify 7 separate clusters of solutions. Cluster C3, containing 6294 solutions, provides good ethanol production without penalising biomass. On the contrary, the low biomass production of clusters C1 and C2 would not allow bacteria to survive, while clusters C4-C7 produce modest quantities of ethanol.

Fig. 2
figure 2

Pareto optimal ethanol production (in red in the figure) and feasible solutions (in blue in the figure) as an observed function of the knock-out cost. (Color figure online)

Full size image

Figure 3a, b depicts the Pareto fronts obtained for a set of prokaryote and eukaryote organisms respectively. For ease of comparisons results are normalized by using theoretical upper bounds for both ethanol and biomass production. As a comparison with the iJO1366 model we also include the E. coliiCA1273 (King et al. 2016). In contrast to the former, no trade off points between the Biomass and the Ethanol production were found by the algorithm, resulting only in points on the two axis. Since the algorithm, set with the same parameters, worked well with all the others models, these results could be caused by the inner features of the model. Among the organisms here explored, S. cerevisiae is the one for which the Pareto front computed by MOME is closest to the utopian optimization point (that is maximal biomass and maximal ethanol production). The Fig. 4a plots the whole feasible region explored by the algorithm.

On the other hand, both C. reinhardtii and S. enterica do not demonstrate good trade-off between biomass and ethanol; for only small improvements in ethanol production follows consistent decreases in the organism biomass.

Fig. 3
figure 3

Results for optimization of ethanol production and biomass formation in various Prokaryotes and Eukaryotes organisms. a Normalized Pareto fronts of prokaryote models optimizations. b Normalized Pareto fronts of eukaryote models optimizations

Full size image
Fig. 4
figure 4

Results for optimization of ethanol production and biomass formation for S. cerevisiae. a Gene set knock-out multi-objective optimization using the Yeast7.6 model. b Gene expression redirector multi-objective optimization using the iMM904 model

Full size image
Table 2 Maximization of ethanol and biomass production for S. cerevisiae using the redirector approach for enzymes regulations with the iMM904 genome-scale model
Full size table

Enzyme regulation in S. cerevisiae We show in Fig. 4b, the feasible strains and the Pareto-optimal ones found by MOME for the optimization problem associated to ethanol overproduction in S. cerevisiae using enzyme up/down regulation. Notice that a linear relationship between biomass and ethanol production is observed for Pareto-optimal strains, and that feasible strains found by MOME almost uniformly span the region from maximal biomass production (\(\approx 0.28\, \hbox {h}^{-1}\)) to null biomass production, hence discovering a number of different trade-offs S. cerevisiae strains (Table 2). These widespread results over the phenotypic space show that the enzymes regulation approach is in general more flexible than the “binary” KO one.

Table 3 Number of essential genes and lethal gene pairs present in the genome-scale metabolic models
Full size table

Ethanol production without essential genes in E. coli and S.cerevisiae We have described so far, the results of the simulations without specific constraints; those results can be considered as an utopian bound of our framework. However, without the introduction of other external constraints simulating the issues of a possible real-world application, some of the selected strains could be difficultly applied. To tackle this possible lack of plausibility we performed further simulations, reported in this section for the ethanol production considering the essential genes of the given organisms. We used the Yeast 7.6 model of S.cerevisiae and two models of E. coli, the iJO1366 and the iZ_1308 (King et al. 2016; Monk et al. 2013), the latter modelling the E. coli O157:H7 strain EDL933. In contrast to the iCA1273, this new model results are quantitative comparable with the iJO1366 ones.

Hence we then changed our framework to tackle this new task, first introducing some limitations over the genes of the models that can actually be knocked out by the algorithm. Namely, we included information on the essential genes and the lethal gene pairs of the different organism, taken from external databases. The list of the essential genes of the E. coli was taken from the EcoliWiki (Genes-EcoliWiki 2018), whereas we took the essential couples list for iJO1366 from (Suthers et al. 2009) and the one for iZ_1308 from (Aziz et al. 2015); the genes lists for the S. cerevisiae model were taken from (Heavner and Price 2015) (see Table 3). The essential genes, defined as the genes whose single KO would result in a non-viable strain of the organism, are thus always excluded in our framework, i.e. they can not be turned off by MOME. A similar approach is used for the lethal gene pairs, defined as the pairs of genes that, if knocked out at the same time, will make the strain non-viable. While the single KO of one of the genes of a couple is still allowed (if not essential), the KOs of both are not; a check of the new possible genes to be knocked out is run in every step of the mutation operator.

Since the databases always refer to single genes, in these simulations we considered the single genes in the models to obtain a direct comparison between a strain and the lists. However, it is indeed really simple to obtain the gene sets again starting from a binary vector representing the single genes of a strain, by just evaluate the Boolean expressions of all the gene sets.

Fig. 5
figure 5

Results of the gene knock-out constrained multi-objective optimization for different metabolic models and conditions. a Gene knock-out multi-objective optimization using the iJO1366 model in anaerobic condition. b Gene knock-out multi-objective optimization using the iJO1366 model in LB medium. c Gene knock-out multi-objective optimization using the iZ_1308 model in LB medium. d Gene knock-out multi-objective optimization using the Yeast7.6 model in SD medium

Full size image

In addition to this, we also introduced a strict bound on the biomass values. Referring to the Wild Type value, we force all the strain obtained to have a biomass reduction not greater than the \(10\%\). So, if a new selected KO leads the strain to a lower biomass, that gene is restored, and the mutation operator selects a new one; the procedure is repeated until a strain with a new KO, having a biomass value above the bound, is reached or until a maximum number of attempts (in general 10 trials) has been done. This new constraint also lets the algorithm to more deeply explore a reduced solution space, while forcing the algorithm to discard the strains with a low growth, which can be considered biologically unfeasible.

Table 4 Maximization of ethanol and biomass in the selected Pareto optimal strains
Full size table

Furthermore, for these new simulations we set the bounds of the external exchange reactions of the models in order to simulate the growth in a rich medium, i.e. the well-known LB medium (Aziz et al. 2015) for the E. coli models and the SD medium (Labhsetwar et al. 2017) for the S. cerevisiae model. A simulation with the same anaerobic medium used in the previous unconstrained tests was also performed.

These new simulations results are shown in Fig. 5. It is remarkable how by changing the medium setting for the same model (iJO1366, ref. to Fig. 5a, b) the phenotypic results are different in both the ethanol production and biomass value. Namely in the rich medium we have a much higher value of ethanol production even in the wild type, 25.0757 \(\hbox {mmol}\,\hbox {gDW}^{-1}\, \hbox {h}^{-1}\) against 2.116 \(\hbox {mmol}\,\hbox {gDW}^{-1}\, \hbox {h}^{-1}\) in the anaerobic medium, and a corresponding biomass value of \(3.6921\,\hbox {h}^{-1}\) against \(1.0334\,\hbox {h}^{-1}\) . Also, the progresses of the algorithm solutions are different, as it can be seen from the trends of the Pareto fronts found, even using the same parameters. These discrepancies highlight once more the importance of the external environment settings for the in silico simulations.

Finally, we considered the optimal solutions in the Pareto front and we applied on them a post processing procedure to keep only the necessary genes KOs. Starting from an optimal strain, the procedure iteratively select one gene knocked out in it and restores it obtaining a new strain. If both the biomass value and the ethanol production differences between these strains were less than a tolerance threshold, that we set at \(10^{-10}\), the gene KO can be considered superfluous, and so the gene is permanently reintroduced in the strain; otherwise it is kept knocked out. The procedures ends when all the knocked-out genes of the strain have been tested.

In the end we so have a new set of filtered and further optimized solutions, with a low number of KOs (that never involve essential genes or lethal gene pairs), and with a reasonable value of the biomass function, ensuring that we are still simulating a well behaving metabolic pathway. Some of these results are shown in Table 4; the reported strains are selected in this case as the ones with a maximum ethanol production among the strains with the same number of KOs. Usually the increase in the number of KOs will result in a potentially higher metabolite production until a maximum number is reached (cf. Fig. 2). There are indeed many other solutions with higher number of KOs, but the overall maximum production found (always labelled as S10 in the tables) can be reached with less than 10 KOs. It is notable that all the E. coli simulations reach a greater maximum ethanol production difference in percentage from the wild type than the S. cerevisiae simulation. In the anaerobic condition the maximum production rate of ethanol using the iJO1366 model is 6.2473 \(\hbox {mmol}\,\hbox {gDW}^{-1}\,\hbox {h}^{-1}\) , improving the wild type of + 195.24%. It is indeed a far lower increase if compared to the ones obtained with the unconstrained algorithm, as expected. Similarly in the LB medium the maximum ethanol production rate is 82.2582 \(\hbox {mmol}\,\hbox {gDW}^{-1}\), with a + 228.04% improvement , whereas using the iZ_1308 model the increase is + 268.68%, with a maximum production rate equals to 80.7883 \(\hbox {mmol}\,\hbox {gDW}^{-1}\,\hbox {h}^{-1}.\) In the Yeast 7.6, conversely, the maximum increase is + 8.24% and the maximum production rate is 30.1258 \(\hbox {mmol}\,\hbox {gDW}^{-1}\,\hbox {h}^{-1}\). Moreover, while these strains of the E. coli models have a biomass reduced of approximately 10%, that is the maximum allowable reduction given the constraint that we used, the strain of S. cerevisiae reduces the biomass of 6.69%, highlighting a lack of optimal trade-off points in the region of the solution space closer to the 10% threshold of biomass reduction.

5 Conclusions

In this paper, we analysed several genome-scale models by using a multi-objective optimization approach for the maximization of the ethanol production. The designed approach takes into account for finer analysis of the metabolic network models and processing of Pareto optimal strains. In particular we have also investigated the behaviour of our analysis approach in the case of ethanol production in E. coli. Here we found more than 6000 genotypically different, Pareto optimal trade-off strains. Among the others, the one with the highest production rate for ethanol improve the wild-type production rate of \(+\,886,50 \%\), with a knock-out cost of 20. Other interesting trade-off with just 1 knock-out cost were found to have produce ethanol at \(+\,679.29 \%\) improved rate with respect to the wild-type one. We have hence clustered Pareto optimal strains found in the co-domain. This was done in an effort to improve the understanding of the relationship between genotype and phenotype in this particular application scenario. Finally, another set of simulations including external information about essential genes and medium used in in vivo experimentations were performed. By including also a minimal value of the biomass function, we wanted to ensure that the strains would be still predicting a satisfying growth. The strains have on one hand a lower increases of the ethanol production, but on the other could tackle some of the biological needs of an actual cells. Applying these constraints, the maximum improvement in comparison with the wild type is \(+\,195.24\%\) . The results we have obtained in this two scenario demonstrate that our analysis approach can aid synthetic biologist in the solution of highly complex design problems, and to better analyse the behaviour of genome-scale models in terms of the effect that knock-outs have on the production rate of several metabolite of interest, both in the case of bio-fuels and enzyme targets discovery for therapeutic purposes. As well as furnishing an automatic explanation of the knock-outs performed in a particular Pareto optimal strain, obtained through the statistical analysis of the empiric distribution of knock-outs in a particular cluster of the Pareto front.