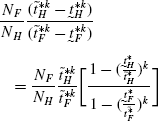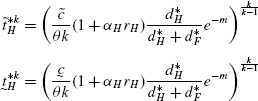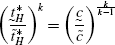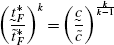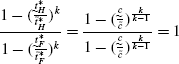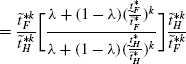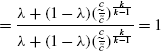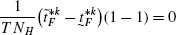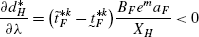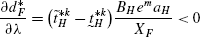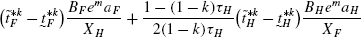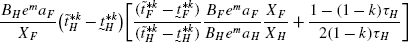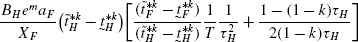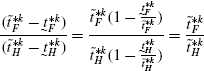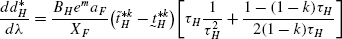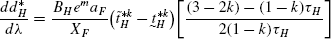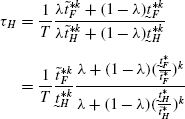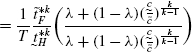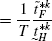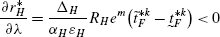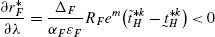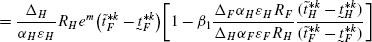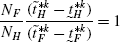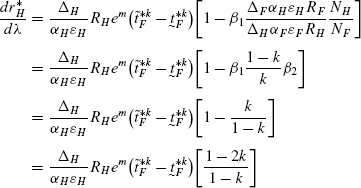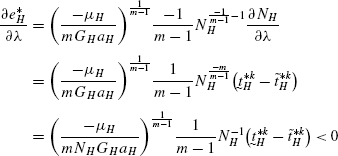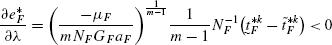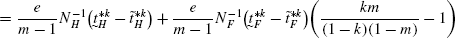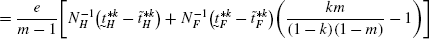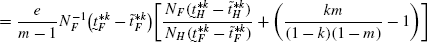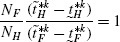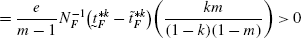Abstract
In this paper, we analyze the equilibrium responses (in terms of defense, R&D and preemption) to a potential terrorist attack in a two-country framework (Home and Foreign) using a multi-stage game with imperfect information. We highlight three different types of strategic interactions: (a) how the choice of defense, R&D and pre-emption affects the choice of the same in the other country (strategic interdependence across countries); (b) the strategic interaction between the instruments of terrorism deterrence, namely, defense, R&D and pre-emption in a given country and (c) the strategic interaction between the terrorist and the defender. Our main results are as follows: (i) defense effort in Home is a strategic complement to the defense effort in Foreign. (ii) Even without R&D sharing between countries, we find that R&D effort in one country is a strategic substitute to that in the other; (iii) similar results hold for pre-emption because of its public good nature; (iv) for a given country, defense and R&D efforts may be strategic substitutes or complements depending on the magnitude of the ratio of weighted expected damage between Foreign and Home; (v) R&D and pre-emption may be strategic substitutes or complements depending on the magnitude of the elasticity of damage and (vi) an increase in the likelihood of the terrorist being weak reduces defense effort, may increase or decrease R&D depending on the magnitude of elasticity of damage but increases pre-emptive effort in both countries.

Similar content being viewed by others
Notes
Proofs are available upon request.
A doubling of defense efforts by one induces the same by the other. However, it does not alter the probability of an attack.
In this context, all costs are opportunity costs and are expressed in terms of the domestic currency. Hence they are treated as positive quantities.
We assume that each country is endowed with a government that works for the benefit of the country. Throughout our analysis, we use the terms government and country interchangeably.
Since the governments move simultaneously at any stage (when it is their turn to move), they do not observe each others choice of effort.
Note that at this stage the governments know the terrorists effort as well as defense effort of each country because we are working through the game backwards.
This result is used in future lemmas.
If \(\sum_{i={H,F}}{p_{i}b_{i}<\sum_{i={H,F}}{\underline {c}(1+\alpha_{i}r_{i})t_{i}}}+V_{0}\), then θ 0 is the threshold valuation per unit damage of the terrorist for which it is indifferent between attacking and not attacking.
Similar results hold for \(t_{F}^{*}\).
Note that the payoff function in this context is positive. This is due to the fact that we treat all costs as opportunity costs which are in dollar terms as mentioned earlier. Further, the government minimizes the total cost/loss function (loss functions are usually positive). If the payoff function were negative the respective governments would then maximize the objective function. Since Max −V is the same as Min V, our results remain unaltered.
Similarly, F chooses d F such that it is a best response to d H . Thus in equilibrium, \(d_{H}^{*}\) and \(d_{F}^{*}\) are mutual best responses to each other as well as the equilibrium expected terrorist effort.
When R&D is decided before pre-emption, i.e. if R&D were to precede pre-emption, the countries are no longer able to free ride when deciding on R&D effort. In such a scenario, the indirect marginal effect described in Lemmas 6(c) (ii) does not come into play. Thus there is no incentive for country H to increase R H . Hence they turn out to be strategic substitutes only.
Since the strategy sets are continuous and V T is strictly concave whereas V H and V F are strictly convex (the governments in this case are minimizing their payoffs (total cost/loss function)), a unique pure strategy perfect Bayesian Nash equilibrium exists.
References
Bandyopadhyay, S., & Sandler, T. (2011). The interplay between preemptive and defensive counterterrorism measures: a two-stage game. Economica, 78(311), 546–564.
Bier, V., Oliveros, S., & Samuelson, L. (2007). Choosing what to protect: strategic defensive allocation against an unknown attacker. Journal of Public Economic Theory, 9, 563–587.
Bier, V. M., & Hausken, K. (2011). Endogenizing the sticks and carrots: modeling possible perverse effects of counterterrorism measures. Annals of Operations Research, 186, 39–59.
Church, R. L., Scaparra, M. P., & Middleton, R. S. (2004). Identifying critical infrastructure: the median and covering facility interdiction problems. Annals of the Association of American Geographers, 94(3), 491–502.
Clark, D. J., & Riis, C. (1998). Contest success functions: an extension. Economic Theory, 11, 201–204.
Dixit, A. (1987). Strategic behavior in contests. The American Economic Review, 77(5), 891–898.
Golany, B., Kaplan, H. E. H., Marmur, A., & Rothblum, U. G. (2009). Nature plays with dice—terrorists do not: allocating resources to counter strategic versus probabilistic risks. European Journal of Operational Research, 192, 198–208.
Hausken, K., Bier, V. M., & Zhuang, J. (2009). Defending against terrorism, natural disaster, and all hazards. In V. M. Bier & M. N. Azaiez (Eds.), Game theoretic risk analysis of security threats. New York: Springer.
Hausken, K., & Zhuang, J. (2011). Governments’ and terrorists’ defense and attack in a t-period game. Decision Analysis, 8(1), 46–70.
Hirshleifer, J. (2000). The macrotechnology of conflict. The Journal of Conflict Resolution, 44, 773–792.
Kunreuther, H., & Heal, G. (2004). Interdependent security. Journal of Risk and Uncertainty, 26, 231–249.
Morral, A. R., & Jackson, B. A. (2009). Understanding the role of deterrence in counterterrorism security. RAND corporation.
Nikoofal, M., & Zhuang, J. (2012). Robust allocation of a defensive budget considering an attacker’s private information. Risk Analysis. doi:10.1111/j.1539-6924.2011.01702.x
Sandler, T., & Sanders, W. (2004). An economic perspective on transnational terrorism. European Journal of Political Economy, 20, 301–316.
Sandler, T., & Siqueira, K. (2006). Global terrorism: deterrence versus pre-emption. Canadian Journal of Economics, 39, 1370–1387.
Sandler, T., & Siqueria, K. (2009). Games and terrorism: recent developments. Simulation & Gaming, 40(2), 164–192.
Scaparra, M. P., & Church, R. L. (2008). A bilevel mixed-integer program for critical infrastructure protection planning. Computers & Operations Research, 35(6), 1905–1923.
Skaperdas, S. (1996). Contest success functions. Economic Theory, 7, 283–290.
Zhuang, J., & Bier, V. M. (2007). Balancing terrorism and natural disasters defensive strategy with endogenous attacker effort. Operations Research, 55, 976–991.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: Terrorist effort
Lemma 3:
-
(a)
\(\frac{\partial t_{H}^{*}}{\partial d_{H}}<0\)
$$\begin{aligned} V_{T} =&\sum_{i={H,F}} p_{i}b_{i} \theta-\underline {c}(1+\alpha_{i}r_{i})t_{i} \end{aligned}$$(6)$$\begin{aligned} \frac{\partial V_{T}}{\partial t_{H}} =&p_{H}kt_{H}^{k-1}e^{m} \theta -\underline{c}(1+\alpha_{H}r_{H})=0 \end{aligned}$$(7)$$\begin{aligned} t_{H}^{*} =& \biggl[\frac{\underline{c}(1+\alpha _{H}r_{H})}{p_{H}e^{m}\theta k} \biggr]^{\frac{1}{k-1}} \end{aligned}$$(8)or
$$\begin{aligned} t_{H}^{*} =& \biggl[\frac{\underline{c}(1+\alpha _{H}r_{H})(d_{H}+d_{F})}{d_{F}e^{m}\theta k} \biggr]^{\frac {1}{k-1}} \end{aligned}$$(9)$$\begin{aligned} =& \biggl[\frac{\underline{c}}{\theta k}(1+\alpha_{H}r_{H}) \frac {(d_{H}+d_{F})}{d_{F}}e^{-m} \biggr]^{\frac{1}{k-1}} \end{aligned}$$(10)$$\begin{aligned} =&\overline{\gamma_{H}}h_{1H}(\cdot)h_{2H}( \cdot)h_{3H}(\cdot) \end{aligned}$$(11)Where,
$$\begin{aligned} \overline{\gamma_{H}} =& \biggl(\frac{\underline{c}}{\theta k} \biggr)^{\frac {1}{k-1}} \end{aligned}$$(12)$$\begin{aligned} h_{1H} =&(1+\alpha_{H}r_{H})^{\frac{1}{k-1}} \end{aligned}$$(13)$$\begin{aligned} h_{2H} =&\biggl(\frac{d_{H}+d_{F}}{d_{F}}\biggr)^{\frac{1}{k-1}} \end{aligned}$$(14)$$\begin{aligned} h_{3H} =&e^{\frac{-m}{k-1}} \\ =&\overline{\gamma_{H}}H_{H} \end{aligned}$$(15)Where,
$$ H_{H}=h_{1H}h_{2H}h_{3H} $$(16)Differentiating (15) with respect to d H , we get
$$\begin{aligned} \frac{\partial t_{H}^{*}}{\partial d_{H}} =&\overline{\gamma_{H}}\frac {\partial H_{H}}{\partial d_{H}} \end{aligned}$$(17)$$\begin{aligned} \ln H_{H} =&\ln h_{1H}+\ln h_{2H}+\ln h_{3H} \end{aligned}$$(18)$$\begin{aligned} \frac{1}{H_{H}}\frac{\partial H_{H}}{\partial d_{H}} =&\frac {1}{(k-1)}\frac{d_{F}}{(d_{H}+d_{F})} \frac{1}{d_{F}}=\frac{1}{k-1}\frac {1}{(d_{H}+d_{F})} \end{aligned}$$(19)Or,
$$ \frac{\partial H_{H}}{\partial d_{H}}=\frac{H_{H}}{k-1}\frac {1}{(d_{H}+d_{F})} $$(20)Or,
$$ \frac{\partial t_{H}^{*}}{\partial d_{H}}=\frac{-\overline{\gamma _{H}}H_{H}}{(1-k)}\frac{1}{(d_{H}+d_{F})}=\frac{-t_{H}^{*}}{(1-k)} \frac {1}{(d_{H}+d_{F})}<0 $$(21) -
(b)
\(\frac{\partial t_{H}^{*}}{\partial d_{F}}>0\). Similarly,
$$ \frac{\partial t_{H}^{*}}{\partial d_{F}}=\frac {t_{H}^{*}}{(1-k)}\frac{d_{H}}{(d_{H}+d_{F})d_{F}}>0, $$(22) -
(c)
\(\frac{\partial t_{H}^{*}}{\partial r_{H}}<0\). In the same vein,
$$ \frac{\partial t_{H}^{*}}{\partial r_{H}}=-\frac{t_{H}^{*}}{(1-k)}\frac{\alpha_{H}}{(1+\alpha _{H}r_{H})}<0, $$(23) -
(d)
\(\frac{\partial t_{H}^{*}}{\partial e_{H}}<0\). As before,
$$ \frac{\partial t_{H}^{*}}{\partial e_{H}}=\frac {mt_{H}^{*}}{e(1-k)}<0, $$(24)
Appendix B: Defense effort
Lemma 5:
-
(a)
\(d_{H}^{*}=\frac{1}{p_{H2}X_{H}}\).
Differentiating (2) with respect to d H , we get
$$ \frac{\partial V_{H}}{\partial d_{H}}=-\frac {d_{F}e^{m}}{(d_{H}+d_{F})^{2}}N_{H}a_{H}+ \frac {d_{F}e^{m}}{(d_{H}+d_{F})}\frac{\partial N_{H}}{\partial d_{H}}a_{H}+\gamma_{H}=0 $$(25)Differentiating (3) with respect to d H , we get
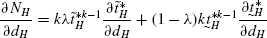 (26)$$\begin{aligned} \frac{\partial N_{H}}{\partial d_{H}} =&-\frac{k}{1-k}\frac {1}{(d_{H}+d_{F})}N_{H} \end{aligned}$$(27)
(26)$$\begin{aligned} \frac{\partial N_{H}}{\partial d_{H}} =&-\frac{k}{1-k}\frac {1}{(d_{H}+d_{F})}N_{H} \end{aligned}$$(27)Plugging (27) in (25), we get,
$$ \frac{\partial V_{H}}{\partial d_{H}}=\frac {-d_{F}e^{m}N_{H}a_{H}}{(d_{H}+d_{F})^{2}}-\frac {d_{F}e^{m}a_{H}}{(d_{H}+d_{F})}\frac{kN_{H}}{(1-k)(d_{H}+d_{F})}- \gamma _{H}=0 $$(28)Or,
$$ \frac{d_{F}e^{m}N_{H}a_{H}}{(d_{H}+d_{F})^{2}(1-k)}=\gamma _{H} $$(29)Or,
$$ (d_{H}+d_{F})^{2}=\frac{1}{(1-k)\gamma _{H}}d_{F}e^{m}N_{H}a_{H} $$(30)Or,
$$ (d_{H}+d_{F})=\bigl(B_{H}d_{F}e^{m}N_{H}a_{H} \bigr)^{\frac{1}{2}}, $$(31)where,
$$ B_{H}=\frac{1}{(1-k)\gamma_{H}} $$(32)Or,
$$ d_{H}^{*}=\bigl(B_{H}d_{F}^{*}e^{m}N_{H}a_{H} \bigr)^{1/2}-d_{F}^{*} $$(33)Similarly, for country F we have,
$$ d_{F}^{*}=\bigl(B_{F}d_{H}^{*}e^{m}N_{F}a_{F} \bigr)^{1/2}-d_{H}^{*} $$(34)$$ d_{H}^{*}=\bigl(B_{H}e^{m}N_{H}a_{H} \bigr)^{1/2}\bigl(\bigl(B_{F}d_{H}^{*}e^{m}N_{F}a_{F} \bigr)^{1/2}-d_{H}^{*}\bigr)^{1/2}-\bigl( \bigl(B_{F}d_{H}^{*}e^{m}N_{F}a_{F} \bigr)^{1/2}-d_{H}^{*}\bigr) $$(35)Or,
$$ \bigl(B_{F}d_{H}^{*}e^{m}N_{F}a_{F} \bigr)^{1/2}=\bigl(B_{H}e^{m}N_{H}a_{H} \bigr)^{1/2}\bigl(\bigl(B_{F}d_{H}^{*}e^{m}N_{F}a_{F} \bigr)^{1/2}-d_{H}^{*}\bigr)^{1/2} $$(36)Squaring both sides we get,
$$ B_{F}d_{H}^{*}e^{m}N_{F}a_{F}= \bigl(B_{H}e^{m}N_{H}a_{H}\bigr) \bigl( \bigl(B_{F}d_{H}^{*}e^{m}N_{F}a_{F} \bigr)^{1/2}-d_{H}^{*}\bigr) $$(37)Or,
$$ \bigl(B_{F}e^{m}N_{F}a_{F}+B_{H}e^{m}N_{H}a_{H} \bigr)d_{H}^{*}=B_{H}e^{m}N_{H}a_{H} \bigl(B_{F}d_{H}^{*}e^{m}N_{F}a_{F} \bigr)^{1/2} $$(38)Or,
$$ \bigl(d_{H}^{*}\bigr)^{1/2}=\frac{(B_{F}e^{m}N_{F}a_{F})^{1/2}}{1+\frac {B_{F}e^{m}N_{F}a_{F}}{B_{H}e^{m}N_{H}a_{H}}}= \frac {(B_{F}e^{m}N_{F}a_{F})^{1/2}}{1+\frac{1}{T}\frac{N_{F}}{N_{H}}} $$(39)Where
$$\begin{aligned} T =&\frac{B_{H}a_{H}}{B_{F}a_{F}} \end{aligned}$$(40)$$\begin{aligned} d_{H}^{*} =&\frac{(B_{F}e^{m}N_{F}a_{F})}{(1+\frac {N_{F}}{TN_{H}})^{2}}=\frac{(B_{F}e^{m}N_{F}a_{F})}{(1+\tau _{H})^{2}}= \frac{1}{p_{H2}X_{H}} \end{aligned}$$(41)Where,
$$\begin{aligned} p_{H2} =&\frac{1}{(B_{F}e^{m}N_{F}a_{F})} \end{aligned}$$(42)$$\begin{aligned} X_{H} =&(1+\tau_{H})^{2} \end{aligned}$$(43)$$\begin{aligned} \tau_{H} =&\frac{N_{F}}{TN_{H}} \end{aligned}$$(44)Similarly,
$$ d_{F}^{*}=\frac{B_{H}e^{m}N_{H}a_{H}}{X_{F}} $$(45)Where
$$ X_{F}=\biggl(\frac{1+\tau_{H}}{\tau_{H}}\biggr)^{2} $$(46) -
(b)
\(\frac{\partial d_{H}^{*}}{\partial d_{F}^{*}}>0\).
Differentiating (33) with respect to d F , we get
$$ \frac{\partial d_{H}^{*}}{\partial d_{F}^{*}}=\frac {1}{2}\bigl(B_{H}e^{m}N_{H}a_{H} \bigr)^{1/2}\bigl(d_{F}^{*}\bigr)^{-1/2}+ \bigl(B_{H}e^{m}a_{H}d_{F}^{*} \bigr)^{1/2}\frac {1}{2}N_{H}^{-1/2} \frac{\partial N_{H}}{\partial d_{F}^{*}}-1 $$(47)Differentiating (3) with respect to d F , we get
$$ \frac{\partial N_{H}}{\partial d_{F}^{*}}=\frac{kN_{H}}{(1-k)}\frac {d_{H}^{*}}{(d_{H}^{*}+d_{F}^{*})d_{F}^{*}} $$(48)Plugging (31), (33) and (34) into (48), we get
$$ =\frac{kN_{H}}{(1-k)\tau _{H}(B_{H}e^{m}N_{H}a_{H}d_{F}^{*})^{1/2}} $$(49)$$\begin{aligned} \frac{\partial d_{H}^{*}}{\partial d_{F}^{*}} =&\frac {1}{2}\bigl(B_{H}e^{m}N_{H}a_{H} \bigr)^{1/2}\bigl(d_{F}^{*}\bigr)^{-1/2}+ \frac{1}{2}\frac {(B_{H}e^{m}a_{H}d_{F}^{*}N_{H})^{1/2}}{(B_{H}e^{m}a_{H}d_{F}^{*}N_{H})^{1/2}}\frac {k}{1-k}\frac{1}{\tau_{H}}-1 \\ =&\frac{1}{2}\frac {(B_{H}e^{m}N_{H}a_{H})^{1/2}X_{F}^{1/2}}{(B_{H}e^{m}N_{H}a_{H})^{1/2}}+\frac {1}{2}\frac{k}{1-k} \frac{1}{\tau_{H}}-1 \\ =&\frac{1}{2}\frac{(1+\tau_{H})}{\tau_{H}}+\frac{1}{2}\frac{k}{1-k} \frac {1}{\tau_{H}}-1 \\ =&\frac{(1-k)(1+\tau_{H})+k-2(1-k)\tau_{H}}{2(1-k)\tau_{H}} \\ =&\frac{1-(1-k)\tau_{H}}{2(1-k)\tau_{H}} \end{aligned}$$(50)Therefore, after simplification we get, \(\frac{\partial d_{H}^{*}}{\partial d_{F}^{*}}>0\) if \(\tau_{H}< \frac {1}{1-k}\),
- =0:
-
if \(\tau_{H}=\frac{1}{1-k}\),
- <0:
-
if \(\tau_{H}>\frac{1}{1-k}\).
Similarly,
$$\frac{\partial d_{F}^{*}}{\partial d_{H}^{*}}>0 \quad\mbox{when } \tau _{H}>1-k $$Similarly, \(\frac{\partial d_{F}^{*}}{\partial d_{H}^{*}}=0\) when τ H =1−k and \(\frac{\partial d_{F}^{*}}{\partial d_{H}^{*}}<0\) when τ H <1−k.
Therefore, the reaction functions are stable iff:
$$\tau_{H}\in\biggl(1-k,\frac{1}{1-k}\biggr) $$ -
(c)
\(\frac{dd_{H}^{*}}{dr_{H}}<0\) for τ H ∈(τ 0,τ 1) and ≥0 elsewhere.
Differentiating (41) with respect to r H , we get
$$ \frac{\partial d_{H}^{*}}{\partial r_{H}}=\frac {B_{F}e^{m}a_{F}}{X_{H}}\frac{\partial N_{F}}{\partial r_{H}}-\frac {B_{F}e^{m}N_{F}a_{F}}{X_{H}^{2}} \frac{\partial X_{H}}{\partial r_{H}} $$(51)Note that,
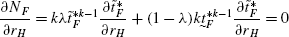 (52)
(52)Since \(\frac{\partial\tilde{t}_{F}^{*}}{\partial r_{H}}=\frac {\partial\tilde{t}_{F}^{*}}{\partial r_{H}}=0\).
Differentiating (3) with respect to r H , we get
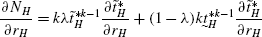 (53)
(53)Similarly, for country F we have,
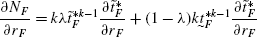 (54)
(54)Using Lemma 3(d) in (53), we get
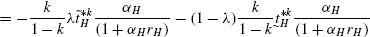 (55)$$\begin{aligned} =& -N_{H}\frac{k}{(1-k)}\frac{\alpha_{H}}{(1+\alpha_{H}r_{H})} \end{aligned}$$(56)
(55)$$\begin{aligned} =& -N_{H}\frac{k}{(1-k)}\frac{\alpha_{H}}{(1+\alpha_{H}r_{H})} \end{aligned}$$(56)Differentiating (43) with respect to r H , we get
$$\begin{aligned} \frac{\partial X_{H}}{\partial r_{H}} =&2(1+\tau_{H})\frac{\partial\tau _{H}}{\partial r_{H}} \\ =&2(1+\tau_{H}) \biggl[\frac{1}{TN_{H}}\frac{\partial N_{F}}{\partial r_{H}}- \frac{1}{T}\frac{N_{F}}{N_{H}^{2}}\frac{\partial N_{H}}{\partial r_{H}} \biggr] \end{aligned}$$(57)Using (52) and plugging (56) in (57) we get,
$$\begin{aligned} =&\frac{2(1+\tau_{H})N_{F}}{TN_{H}}\frac{k}{1-k}\frac{\alpha _{H}}{1+\alpha_{H}r_{H}} \end{aligned}$$(58)$$\begin{aligned} =&\frac{2(1+\tau_{H})\tau_{H}k\alpha_{H}}{(1-k)(1+\alpha _{H}r_{H})} \end{aligned}$$(59)Using (52) and plugging (59) in (51) we get,
$$\begin{aligned} \frac{\partial d_{H}^{*}}{\partial r_{H}} =&-\frac {B_{F}e^{m}N_{F}a_{F}}{(1+\tau_{H})^{4}}\frac{2(1+\tau_{H})k\alpha _{H}\tau_{H}}{(1-k)(1+\alpha_{H}r_{H})} \\ =&-2\frac{B_{F}e^{m}N_{F}a_{F}\tau_{H}k\alpha_{H}}{(1+\tau _{H})^{3}(1-k)(1+\alpha_{H}r_{H})}<0 \end{aligned}$$(60)$$\begin{aligned} \frac{\partial d_{F}^{*}}{\partial r_{H}} =&\frac {B_{H}e^{m}a_{H}}{X_{F}}\frac{\partial N_{H}}{\partial r_{H}}-\frac {B_{H}e^{m}N_{H}a_{H}}{X_{F}^{2}} \frac{\partial X_{F}}{\partial r_{H}} \end{aligned}$$(61)$$\begin{aligned} \frac{\partial X_{F}}{\partial r_{H}} =&2\frac{(1+\tau_{H})}{\tau _{H}} \biggl[\frac{1}{\tau_{H}}- \frac{(1+\tau_{H})}{\tau_{H}^{2}} \biggr]\frac{\partial\tau_{H}}{\partial r_{H}} \\ =&-2\frac{(1+\tau_{H})}{\tau_{H}}\frac{1}{\tau_{H}^{2}} \biggl[\tau _{H} \frac{k}{1-k}\frac{\alpha_{H}}{(1+\alpha_{H}r_{H})} \biggr] \end{aligned}$$(62)$$\begin{aligned} \frac{\partial d_{F}^{*}}{\partial r_{H}} =&-\tau_{H}^{2}\frac {B_{H}e^{m}a_{H}}{(1+\tau_{H})^{2}} \frac{kN_{H}}{1-k}\frac{\alpha _{H}}{1+\alpha_{H}r_{H}}+\frac{B_{H}e^{m}N_{H}a_{H}\tau_{H}^{4}}{(1+\tau _{H})^{4}}\frac{2(1+\tau_{H})}{\tau_{H}^{2}} \frac{k}{1-k}\frac{\alpha _{H}}{1+\alpha_{H}r_{H}} \\ =&\frac{-\tau_{H}^{2}B_{H}N_{H}e^{m}a_{H}k\alpha_{H}}{(1-k)(1+\alpha _{H}r_{H})(1+\tau_{H})^{2}} \biggl[1-\frac{2}{1+\tau_{H}} \biggr] \end{aligned}$$(63)Therefore, after some simplification we get,
$$\frac{\partial d_{F}^{*}}{\partial r_{H}}>0 \quad\mbox{when }\tau _{H}<1 $$Similarly, \(\frac{\partial d_{F}^{*}}{\partial r_{H}}=0\) when τ H =1 and \(\frac{\partial d_{F}^{*}}{\partial r_{H}}<0\) when τ H >1.
Now consider,
$$ \frac{dd_{H}^{*}}{dr_{H}}=\frac{\partial d_{H}^{*}}{\partial r_{H}}+\frac{\partial d_{H}^{*}}{\partial d_{F}^{*}}\frac{\partial d_{F}^{*}}{\partial r_{H}} $$(64)Plugging in (50), (60) and (63) in (64), we get
$$\begin{aligned} =&\frac{-2B_{F}e^{m}N_{F}a_{F}\tau_{H}k\alpha_{H}}{(1-k)(1+\tau _{H})^{3}(1+\alpha_{H}r_{H})} \\ &{}-\frac{1-(1-k)\tau_{H}}{2(1-k)\tau _{H}}\frac{B_{H}e^{m}N_{H}a_{H}k\alpha_{H}\tau_{H}^{2}}{(1-k)(1+\tau _{H})^{2}(1+\alpha_{H}r_{H})}\biggl( \frac{\tau_{H}-1}{\tau_{H}+1}\biggr) \end{aligned}$$(65)$$\begin{aligned} =& \biggl(\frac{1-\tau_{H}}{1+\tau_{H}} \biggr)\frac {B_{H}e^{m}N_{H}a_{H}k\alpha_{H}\tau_{H}^{2}(1-(1-k)\tau _{H})}{2(1-k)^{2}\tau_{H}(1+\tau_{H})^{2}(1+\alpha_{H}r_{H})} \\ &{}-\frac {2B_{F}N_{F}e^{m}a_{F}\tau_{H}k\alpha_{H}}{(1-k)(1+\tau _{H})^{3}(1+\alpha_{H}r_{H})} \end{aligned}$$(66)$$\begin{aligned} =&\frac{B_{F}e^{m}N_{F}a_{F}\tau_{H}k\alpha_{H}}{(1-k)(1+\tau _{H})^{3}(1+\alpha_{H}r_{H})} \biggl[\frac{(1-\tau_{H})(1-(1-k)\tau _{H})}{2(1-k)\tau_{H}}-2 \biggr] \end{aligned}$$(67)$$\begin{aligned} =&\frac{B_{F}e^{m}N_{F}a_{F}\tau_{H}k\alpha_{H}}{(1-k)(1+\tau _{H})^{3}(1+\alpha_{H}r_{H})} \\ &{}\times \biggl[\frac{(1-\tau_{H})(1-(1-k)\tau _{H})-4(1-k)\tau_{H}}{2(1-k)\tau_{H}} \biggr] \end{aligned}$$(68)$$\begin{aligned} =&\frac{B_{F}e^{m}N_{F}a_{F}\tau_{H}k\alpha_{H}}{(1-k)(1+\tau _{H})^{3}(1+\alpha_{H}r_{H})} \biggl[\frac{(1-k)\tau_{H}^{2}-(6-5k)\tau _{H}+1}{2(1-k)\tau_{H}} \biggr] \end{aligned}$$(69)$$\begin{aligned} \mbox{Let } y =&(1-k)\tau_{H}^{2}-(6-5k) \tau_{H}+1. \end{aligned}$$(70)Note that
$$\operatorname{sign} \biggl(\frac{dd_{H}^{*}}{dr_{H}} \biggr) = \operatorname{sign}(y). $$Differentiating (70) with respect with τ H we get,
$$ \frac{dy}{d\tau_{H}}=2(1-k)\tau_{H}-(6-5k) $$(71)Therefore,
$$\begin{aligned} \frac{dy}{d\tau_{H}} >&0 \quad\mbox{if } \tau_{H}>\frac {(6-5k)}{2(1-k)} \end{aligned}$$(72)$$\begin{aligned} \frac{dy}{d\tau_{H}} =&0 \quad\mbox{if } \tau_{H}=\frac {(6-5k)}{2(1-k)} \end{aligned}$$(73)$$\begin{aligned} \frac{dy}{d\tau_{H}} <&0\quad\mbox{if } \tau_{H}<\frac {(6-5k)}{2(1-k)} \end{aligned}$$(74)$$\begin{aligned} \frac{dy^{2}}{d\tau_{H}} =&2(1-k)>0 \end{aligned}$$(75)Therefore, y is convex, y(0)=1. Let τ 0 and τ 1 be the roots of y where τ 0<τ 1.
Therefore, ∀τ H ∈(τ 0,τ 1), y<0 and ≥0 elsewhere (see Fig. 2). Therefore, \(\frac{dd_{H}^{*}}{dr_{H}}<0\ \forall\tau_{H}\in(\tau_{0},\tau_{1})\) and ≥0 elsewhere.
-
(d)
\(\frac{dd_{H}^{*}}{de_{H}}<0\).
Differentiating (41) with respect to e H , we get
$$ \frac{\partial d_{H}^{*}}{\partial e_{H}}=\frac {mB_{F}N_{F}a_{F}e^{m-1}}{X_{H}}+\frac{B_{F}e^{m}a_{F}}{X_{H}}\frac {\partial N_{F}}{\partial e_{H}}- \frac {B_{F}e^{m}N_{F}a_{F}}{X_{H}^{2}}\frac{\partial X_{H}}{\partial e_{H}} $$(76)Differentiating (43) with respect to e H , we note that
$$ \frac{\partial X_{H}}{\partial e_{H}}=0 $$(77)Using (77) in (76) and Lemma 3(b), we get
$$\begin{aligned} =&\frac{mB_{F}N_{F}a_{F}e^{m-1}}{X_{H}}+\frac {B_{F}a_{F}N_{F}mke^{m-1}}{X_{H}(1-k)} \end{aligned}$$(78)$$\begin{aligned} =&\frac{mB_{F}N_{F}a_{F}e^{m-1}}{X_{H}} \biggl[1+\frac{k}{1-k} \biggr] \end{aligned}$$(79)$$\begin{aligned} =&\frac{mB_{F}N_{F}a_{F}e^{m-1}}{(1-k)X_{H}}<0 \end{aligned}$$(80)Differentiating (45) with respect to e H , we get
$$\begin{aligned} \frac{\partial d_{F}^{*}}{\partial e_{H}} =&\frac {mB_{H}N_{H}a_{H}e^{m-1}}{X_{F}}+\frac {B_{H}a_{H}N_{H}mke^{m-1}}{X_{F}(1-k)}\quad \biggl( \mbox{Since }\frac{\partial X_{F}}{\partial e_{H}}=0\biggr) \\ =&\frac{mB_{H}N_{H}a_{H}e^{m-1}}{(1-k)X_{F}}<0 \end{aligned}$$(81)$$\begin{aligned} \frac{dd_{H}^{*}}{de_{H}} =&\frac{\partial d_{H}^{*}}{\partial e_{H}}+\frac{\partial d_{H}^{*}}{\partial d_{F}^{*}}\frac{\partial d_{F}^{*}}{\partial e_{H}} \\ =&\frac{mB_{F}N_{F}a_{F}e^{m-1}}{X_{H}(1-k)}+\frac{(1-(1-k)\tau _{H})}{2(1-k)\tau_{H}}\frac{mB_{H}e^{m-1}N_{H}a_{H}}{X_{F}(1-k)} \\ =&\frac{mB_{F}N_{F}a_{F}e^{m-1}}{X_{H}(1-k)} \biggl[1+\frac{(1-(1-k)\tau _{H})}{2(1-k)\tau_{H}}\frac{1}{\tau_{H}} \tau_{H}^{2} \biggr] \\ =&\frac{mB_{F}N_{F}a_{F}e^{m-1}}{X_{H}(1-k)} \biggl[1+\frac{(1-(1-k)\tau _{H})}{2(1-k)} \biggr] \\ =&\frac{mB_{F}N_{F}a_{F}e^{m-1}}{X_{H}(1-k)} \biggl[\frac{(3-2k)-(1-k)\tau _{H}}{2(1-k)} \biggr] \end{aligned}$$(82)Since \(\tau_{H}<\frac{1}{1-k}\), \(\tau_{H}<\frac{(3-2k)}{(1-k)}\). Therefore, \(\frac{dd_{H}^{*}}{de_{H}}<0\)
$$\begin{aligned} \frac{\partial d_{H}^{*}}{\partial e_{F}} =&\frac {mB_{F}N_{F}a_{F}e^{m-1}}{X_{H}}+\frac{B_{F}a_{F}e^{m}N_{F}}{X_{H}} \frac {mk}{1-k}e^{-1} \\ =&\frac{mB_{F}N_{F}a_{F}e^{m-1}}{X_{H}(1-k)}=\frac{\partial d_{H}^{*}}{\partial e_{H}} \end{aligned}$$(83)$$\begin{aligned} \frac{\partial d_{F}^{*}}{\partial e_{F}} =&\frac {mB_{H}N_{H}a_{H}e^{m-1}}{X_{F}}+\frac{B_{H}a_{H}e^{m}N_{H}}{X_{F}} \frac {mk}{1-k}e^{-1} \\ =&\frac{mB_{H}N_{H}a_{H}e^{m-1}}{X_{F}(1-k)}=\frac{\partial d_{F}^{*}}{\partial e_{H}} \end{aligned}$$(84)$$\begin{aligned} \frac{dd_{F}^{*}}{de_{F}} =&\frac{\partial d_{F}^{*}}{\partial e_{F}}+\frac{\partial d_{F}^{*}}{\partial d_{H}^{*}}\frac{\partial d_{H}^{*}}{\partial e_{F}} \\ =&\frac{mB_{H}N_{H}a_{H}e^{m-1}}{X_{F}(1-k)}+\frac{\tau _{H}-(1-k)}{2(1-k)}\frac{mB_{F}N_{F}a_{F}e^{m-1}}{X_{H}(1-k)} \\ =&\frac{mB_{H}N_{H}a_{H}e^{m-1}}{X_{F}(1-k)} \biggl[1+\frac{\tau _{H}-(1-k)}{2(1-k)\tau_{H}} \biggr] \\ =&\frac{mB_{H}N_{H}a_{H}e^{m-1}}{X_{F}(1-k)} \biggl[\frac{(3-2k)\tau _{H}-(1-k)}{2(1-k)\tau_{H}} \biggr] \end{aligned}$$(85)Consider (3−2k)τ H −(1−k). This is increasing in τ H . Note that \(\tau_{H}\in(1-k,\frac{1}{1-k})\). Evaluating at τ H =1−k, we get (3−2k)(1−k)−(1−k)>0. Since m<0, we have the following:
$$ \frac{dd_{F}^{*}}{de_{F}}=\frac {mB_{H}N_{H}a_{H}e^{m-1}}{X_{F}(1-k)} \biggl[\frac{(3-2k)\tau _{H}-(1-k)}{2(1-k)\tau_{H}} \biggr]>0 $$(86) -
(e)
\(\frac{dd_{H}^{*}}{d\lambda}<0\).
Differentiating (41) with respect to λ, we get
$$ \frac{\partial d_{H}^{*}}{\partial\lambda}=\frac {B_{F}e^{m}a_{F}}{X_{H}}\frac{\partial N_{F}}{\partial\lambda}-\frac {B_{F}e^{m}N_{F}a_{F}}{X_{H}^{2}} \frac{\partial X_{H}}{\partial\lambda} $$(87)Differentiating (5) with respect to λ, we get
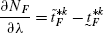 (88)
(88)Since,
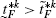 , \(\frac {\partial N_{F}}{\partial\lambda}<0\).
, \(\frac {\partial N_{F}}{\partial\lambda}<0\).Differentiating (43) with respect to λ, we get
$$ \frac{\partial X_{H}}{\partial\lambda}=2(1+\tau_{H}){\frac{\partial \tau_{H}}{\partial\lambda}} $$(89)Differentiating (44) with respect to λ, we get
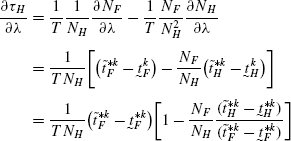 (90)
(90)We next show that,
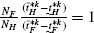 .
.
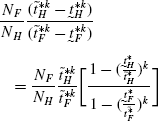 (91)
(91)Recall that,
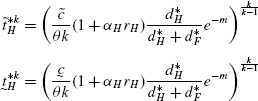
Therefore,
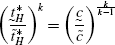 (92)
(92)Similarly,
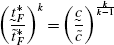 (93)
(93)Therefore,
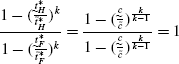 (94)
(94)Therefore,
$$\begin{aligned} =&\frac{N_{F}}{N_{H}}\frac{\tilde{t}_{H}^{*k}}{\tilde{t}_{F}^{*k}} \end{aligned}$$(95)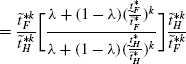 (96)
(96)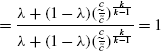 (97)
(97)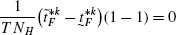 (98)
(98)Therefore, \(\frac{\partial\tau_{H}}{\partial\lambda}=0\) implies \(\frac {\partial X_{H}}{\partial\lambda}=0\).
Therefore,
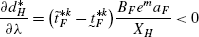 (99)
(99)Similarly,
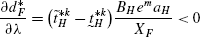 (100)$$\begin{aligned} &\frac{dd_{H}^{*}}{d\lambda}=\frac{\partial d_{H}^{*}}{\partial\lambda }+\frac{\partial d_{H}^{*}}{\partial d_{F}^{*}}\frac{\partial d_{F}^{*}}{\partial\lambda} \end{aligned}$$(101)
(100)$$\begin{aligned} &\frac{dd_{H}^{*}}{d\lambda}=\frac{\partial d_{H}^{*}}{\partial\lambda }+\frac{\partial d_{H}^{*}}{\partial d_{F}^{*}}\frac{\partial d_{F}^{*}}{\partial\lambda} \end{aligned}$$(101)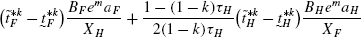 (102)
(102)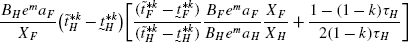 (103)
(103)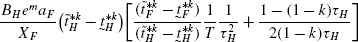 (104)
(104)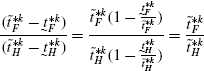 (105)
(105)Simplifying the expression within brackets and using the fact that, \(\tau_{H}=\frac{1}{T}\frac{N_{F}}{N_{H}}=\frac{1}{T}\frac{\tilde{t}_{F}^{*k}}{\tilde{t}_{H}^{*k}}\), we get the following:
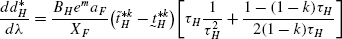 (106)
(106)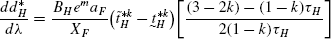 (107)
(107)Since, \(\tau_{H}\in(1-k,\frac{1}{1-k}), \tau_{H}<\frac {3-2k}{1-k}\) (since k<1). Therefore, \(\frac{dd_{H}^{*}}{d\lambda}<0\).
Appendix C: R&D effort
Lemma 6:
-
(a)
\(r_{H}^{*}=\frac{1}{\alpha_{H}} [\frac{1}{\varepsilon _{H}}\Delta_{H}\delta_{H}R_{H}-1 ]\).
Differentiating (2) with respect to r H , we get
$$\begin{aligned} \frac{dV_{H}}{dr_{H}} =&-\frac {d_{F}^{*}}{(d_{H}^{*}+d_{F}^{*})^{2}}e^{m}N_{H}a_{H} \frac {dd_{H}^{*}}{dr_{H}}+\gamma_{H}\frac{dd_{H}^{*}}{dr_{H}}+\varepsilon _{H}+\frac{d_{H}^{*}}{(d_{H}^{*}+d_{F}^{*})^{2}}e^{m}N_{H}a_{H} \frac {dd_{F}^{*}}{dr_{H}} \\ &{}+\frac{d_{F}^{*}}{(d_{H}^{*}+d_{F}^{*})}e^{m}a_{H}\frac {dN_{H}}{dt_{H}^{*}} \biggl(\frac{dt_{H}^{*}}{dd_{H}^{*}}\frac {dd_{H}^{*}}{dr_{H}}+\frac{dt_{H}^{*}}{dd_{F}^{*}} \frac {dd_{F}^{*}}{dr_{H}}+\frac{dt_{H}^{*}}{dr_{H}} \biggr)=0 \end{aligned}$$(108)Using (25) we get:
Or,
$$\begin{aligned} & \biggl[\frac {d_{H}^{*}}{(d_{H}^{*}+d_{F}^{*})^{2}}e^{m}N_{H}a_{H}+ \frac {d_{F}^{*}}{(d_{H}^{*}+d_{F}^{*})}e^{m}a_{H}N_{H} \frac{k}{(1-k)}\frac {d_{H}^{*}}{(d_{H}^{*}+d_{F}^{*})d_{F}^{*}} \biggr]\frac {dd_{F}^{*}}{dr_{H}} \\ &\quad{}-\frac{d_{F}^{*}}{(d_{H}^{*}+d_{F}^{*})}e^{m}a_{H}N_{H} \frac {k}{1-k}\frac{\alpha_{H}}{1+\alpha_{H}r_{H}}=-\varepsilon_{H} \end{aligned}$$(109)Or,
$$ \frac{d_{H}^{*}}{(d_{H}^{*}+d_{F}^{*})^{2}}\frac {e^{m}N_{H}a_{H}}{1-k}\frac{dd_{F}^{*}}{dr_{H}}-\frac {d_{F}^{*}}{(d_{H}^{*}+d_{F}^{*})} \frac{e^{m}a_{H}N_{H}k\alpha _{H}}{(1-k)(1+\alpha_{H}r_{H})}=-\varepsilon_{H} $$(110)Using (31), (32), (41) and (45) and simplifying we get:
Or,
$$ \frac{1}{B_{H}\tau_{H}(1-k)}\frac{dd_{F}^{*}}{dr_{H}}-\frac {\tau_{H}}{(1-k)(1+\tau_{H})}\frac{e^{m}a_{H}N_{H}k\alpha_{H}}{(1+\alpha _{H}r_{H})}=- \varepsilon_{H} $$(111)Plugging the expression for \(\frac{dd_{F}^{*}}{dr_{H}}\) in (111), we get
Or,
$$ \frac{B_{F}e^{m}N_{F}a_{F}k\alpha_{H}\tau _{H}(2(1-k)-(2-k)\tau_{H})}{B_{H}\tau_{H}(1-k)(1+\tau _{H})^{3}(1-k)^{2}(1+\alpha_{H}r_{H})}-\frac{\tau _{H}e^{m}a_{H}N_{H}\alpha_{H}k}{(1-k)(1+\tau_{H})(1+\alpha _{H}r_{H})}=-\varepsilon_{H} $$(112)Or,
$$ \frac{k\alpha_{H}B_{F}e^{m}N_{F}a_{F}}{B_{H}(1-k)(1+\tau _{H})(1+\alpha_{H}r_{H})} \biggl[\frac{(2-k)\tau _{H}-2(1-k)}{(1-k)^{2}(1+\tau_{H})^{2}}+\frac{\tau _{H}B_{H}e^{m}a_{H}N_{H}}{B_{F}e^{m}a_{F}N_{F}} \biggr]= \varepsilon _{H} $$(113)Or,
$$ \frac{k\alpha_{H}B_{F}e^{m}N_{F}a_{F}}{B_{H}(1-k)(1+\tau _{H})(1+\alpha_{H}r_{H})} \biggl[\frac{(2-k)\tau _{H}-2(1-k)}{(1-k)^{2}(1+\tau_{H})^{2}}+1 \biggr]=\varepsilon_{H} $$(114)Or,
$$ \frac{k\alpha_{H}B_{F}a_{F}}{B_{H}(1-k)^{3}}\frac {e^{m}N_{F}}{(1+\tau_{H})^{3}} \bigl((2-k)\tau _{H}-2(1-k)+(1-k)^{2}(1+ \tau_{H})^{2} \bigr)=\varepsilon_{H}(1+\alpha _{H}r_{H}) $$(115)Or,
$$ \frac{1}{\varepsilon_{H}}\Delta_{H}\delta_{H}R_{H}=1+ \alpha _{H}r_{H} $$(116)Where,
$$\begin{aligned} \Delta_{H} =&\frac{k\alpha_{H}B_{F}a_{F}}{B_{H}(1-k)^{3}}>0 \end{aligned}$$(117)$$\begin{aligned} \delta_{H} =&e^{m}N_{F} \end{aligned}$$(118)$$\begin{aligned} R_{H} =&\frac{(2-k)\tau_{H}-2(1-k)+(1-k)^{2}(1+\tau_{H})^{2}}{(1+\tau _{H})^{3}} \end{aligned}$$(119)Therefore, we get,
$$ r_{H}^{*}=\frac{1}{\alpha_{H}} \biggl[\frac{1}{\varepsilon_{H}} \Delta _{H}\delta_{H}R_{H}-1 \biggr] $$(120)Similarly, for country F we have,
$$ r_{F}^{*}=\frac{1}{\alpha_{F}} \biggl[\frac{1}{\varepsilon_{F}} \Delta _{F}\delta_{F}R_{F}-1 \biggr] $$(121) -
(b)
\(\frac{\partial r_{H}^{*}}{\partial r_{F}^{*}}<0\).
We first show that τ H is a constant. Plugging (3) and (5) in (44), we get
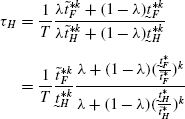 (122)
(122)Using (92) and (93) in (122), we get
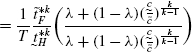 (123)
(123)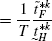 (124)
(124)Plugging (10) and (11) and simplifying, we get
$$ =\frac{1}{T} \biggl( \frac{\tilde{c}(1+\alpha _{F}r_{F}^{*})(d_{H}^{*}+d_{F}^{*})e^{-m}d_{F}^{*}}{\tilde{c}(1+\alpha _{H}r_{H}^{*})d_{H}^{*}e^{-m}(d_{H}^{*}+d_{F}^{*})} \biggr) ^{\frac {k}{k-1}} $$(125)Plugging (120) and (121) in (125) we get,
$$ \tau_{H}=\frac{1}{T} \biggl(\frac{\tau_{H}\varepsilon_{H}\Delta _{F}R_{F}\delta_{F}}{\varepsilon_{F}\Delta_{H}R_{H}\delta_{H}} \biggr)^{\frac{k}{k-1}} $$(126)After some simplification, we get the following:
$$\begin{aligned} \varPhi(\tau_{H}) =& \biggl(\frac{\varepsilon_{H}\Delta_{F}}{\varepsilon_{F}\Delta _{H}} \biggr)^{\frac{k-1}{k}}T^{\frac{2k-1}{k-1}} \end{aligned}$$(127)$$\begin{aligned} \tau_{H} =&\varPhi^{-1} \biggl( \biggl(\frac{\varepsilon_{H}\Delta_{F}}{\varepsilon _{F}\Delta_{H}} \biggr)^{\frac{k-1}{k}}T^{\frac{2k-1}{k-1}} \biggr) \end{aligned}$$(128)Since R H =f(τ H ), R H must also be a constant. Differentiating (120) with respect to r F , we get
$$ \frac{\partial r_{H}^{*}}{\partial r_{F}^{*}}=\frac{\Delta _{H}R_{H}}{\alpha_{H}\varepsilon_{H}}e^{m}\frac{\partial N_{F}}{\partial r_{F}^{*}} $$(129)Plugging (54) in (129), we get
$$ =-\frac{\Delta_{H}R_{H}}{\alpha_{H}\varepsilon_{H}}\frac{e^{m}}{(1-k)}\frac {N_{F}k\alpha_{F}}{(1+\alpha_{F}r_{F}^{*})} $$(130)Plugging (121) in (130), we get
$$ =-\frac{\Delta_{H}R_{H}}{\alpha_{H}\varepsilon_{H}}\frac{e^{m}}{(1-k)}\frac {N_{F}k\alpha_{F}}{\frac{\Delta_{F}\delta_{F}R_{F}}{\varepsilon _{F}}} $$(131)Let
$$ \frac{\Delta_{H}R_{H}\varepsilon_{F}\alpha_{F}kN_{F}}{\Delta _{F}R_{F}\varepsilon_{H}(1-k)N_{H}\alpha_{H}}=\beta_{1} $$(132)Therefore,
$$ \frac{\partial r_{H}^{*}}{\partial r_{F}^{*}}=-\beta_{1}<0 $$(133)Similarly, for country F we have,
$$ \frac{\partial r_{F}^{*}}{\partial r_{H}^{*}}=-\frac{\Delta _{F}R_{F}\varepsilon_{H}\alpha_{H}kN_{H}}{\Delta_{H}R_{H}\varepsilon _{F}(1-k)N_{F}\alpha_{F}}=-\beta_{2}<0 $$(134)Where,
$$ \beta_{2}=\frac{\Delta_{F}R_{F}\varepsilon_{H}\alpha_{H}kN_{H}}{\Delta _{H}R_{H}\varepsilon_{F}(1-k)N_{F}\alpha_{F}} $$(135)Note that,
$$ \beta_{1}\beta_{2}= \biggl(\frac{k}{1-k} \biggr)^{2} $$(136) -
(c)
\(\frac{dr_{H}^{*}}{de_{H}}>0\) when \(k>\frac{1}{2}\), <0 when \(k<\frac{1}{2}\).
Differentiating (120) with respect to e H , we get
$$ \frac{\partial r_{H}^{*}}{\partial e_{H}}=\frac{\Delta_{H}R_{H}}{\alpha _{H}\varepsilon_{H}} \biggl(me^{m-1}N_{F}+e^{m} \frac{\partial N_{F}}{\partial e_{H}} \biggr) $$(137)Differentiating (5) with respect to e H , we get
$$ \frac{\partial N_{F}}{\partial e_{H}}=\frac{N_{F}mke^{-1}}{1-k} $$(138)Plugging (138) in (137), we get
$$\begin{aligned} \frac{\partial r_{H}^{*}}{\partial e_{H}} =&\frac{\Delta_{H}R_{H}}{\alpha _{H}\varepsilon_{H}}e^{m-1} \biggl(mN_{F}+mN_{F} \frac{k}{1-k} \biggr) \\ =&\frac{\Delta_{H}R_{H}}{\alpha_{H}\varepsilon_{H}}\frac {me^{m-1}N_{F}}{1-k}<0 \end{aligned}$$(139)Similarly, for country F we have,
$$ \frac{\partial r_{F}^{*}}{\partial e_{H}}=\frac{\Delta_{F}R_{F}}{\alpha _{F}\varepsilon_{F}}\frac{me^{m-1}N_{H}}{1-k}<0 $$(140)Now consider,
$$ \frac{dr_{H}^{*}}{de_{H}}=\frac{\partial r_{H}^{*}}{\partial e_{H}}+\frac{\partial r_{F}^{*}}{\partial r_{F}^{*}}\frac{\partial r_{F}^{*}}{\partial e_{H}} $$(141)Plugging (139) and (140) in (141), we get
$$\begin{aligned} =&\frac{\Delta_{H}R_{H}}{\alpha_{H}\varepsilon_{H}}\frac {me^{m-1}N_{F}}{1-k}-\beta_{1} \frac{\Delta_{F}R_{F}me^{m-1}N_{H}}{\alpha _{F}\varepsilon_{F}(1-k)} \end{aligned}$$(142)$$\begin{aligned} =&\frac{\Delta_{H}R_{H}me^{m-1}}{\alpha_{H}\varepsilon_{H}(1-k)}N_{F} \biggl[1-\beta_{1} \frac{\Delta_{F}R_{F}N_{H}\alpha_{H}\varepsilon_{H}}{\Delta _{H}R_{H}\alpha_{F}\varepsilon_{F}N_{F}} \biggr] \end{aligned}$$(143)$$\begin{aligned} =&\frac{\Delta_{H}R_{H}me^{m-1}}{\alpha_{H}\varepsilon_{H}(1-k)}N_{F} \biggl[1-\beta_{1} \frac{(1-k)}{k}\beta_{2} \biggr] \end{aligned}$$(144)Since \(\beta_{1}\beta{2}=(\frac{k}{1-k})^{2}\)
$$\begin{aligned} =&\frac{\Delta_{H}R_{H}me^{m-1}}{\alpha_{H}\varepsilon_{H}(1-k)}N_{F} \biggl[1-\frac{k}{(1-k)} \biggr] \end{aligned}$$(145)$$\begin{aligned} =&\frac{\Delta_{H}R_{H}me^{m-1}}{\alpha_{H}\varepsilon_{H}(1-k)}N_{F} \biggl[\frac{(1-2k)}{(1-k)} \biggr] \end{aligned}$$(146)Therefore, \(\frac{dr_{H}^{*}}{de_{H}}<0\) when \(k<\frac{1}{2}\). Similarly, the other case can be shown to hold true.
-
(d)
\(\frac{dr_{H}^{*}}{d\lambda}>0\) when \(k>\frac{1}{2}\), <0 when \(k<\frac{1}{2}\).
Differentiating (120) with respect to λ, we get
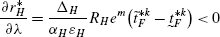 (147)
(147)Differentiating (121) with respect to λ, we get
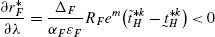 (148)$$\begin{aligned} \frac{dr_{H}^{*}}{d\lambda} =&\frac{\partial r_{H}^{*}}{\partial\lambda }+\frac{\partial r_{H}^{*}}{\partial r_{F}^{*}}\frac{\partial r_{F}^{*}}{\partial\lambda} \end{aligned}$$(149)
(148)$$\begin{aligned} \frac{dr_{H}^{*}}{d\lambda} =&\frac{\partial r_{H}^{*}}{\partial\lambda }+\frac{\partial r_{H}^{*}}{\partial r_{F}^{*}}\frac{\partial r_{F}^{*}}{\partial\lambda} \end{aligned}$$(149)Using (133), (147) and (148), we get
 (150)
(150)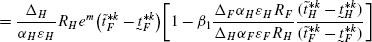 (151)
(151)Recall that,
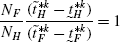
Therefore,
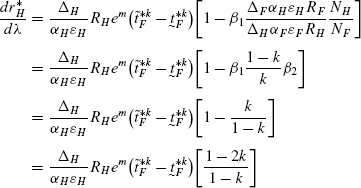 (152)
(152)Therefore, \(\frac{dr_{H}^{*}}{d\lambda}<0\) if \(k<\frac{1}{2}\). Similarly, the other case can be shown to hold true. Similar results hold for \(\frac{dr_{F}^{*}}{d\lambda}\).
Appendix D: Pre-emption
Lemma 7:
-
(a)
\(e_{H}^{*}= (\frac{-\mu_{H}}{mG_{H}N_{H}a_{H}} )^{\frac {1}{m-1}}-e_{F}^{*}\).
Differentiating (2) with respect to e H , we get
$$\begin{aligned} \frac{dV_{H}}{de_{H}} =&-\frac {d_{F}^{*}}{(d_{H}^{*}+d_{F}^{*})^{2}}e^{m}N_{H}a_{H} \biggl(\frac {dd_{H}^{*}}{dr_{H}^{*}}\frac{dr_{H}^{*}}{de_{H}}+\frac {dd_{H}^{*}}{dr_{F}^{*}} \frac{dr_{F}^{*}}{de_{H}}+\frac {dd_{H}^{*}}{de_{H}} \biggr) \\ &{}+\frac{d_{H}^{*}}{(d_{H}^{*}+d_{F}^{*})^{2}}e^{m}N_{H}a_{H} \biggl( \frac {dd_{F}^{*}}{dr_{H}^{*}}\frac{dr_{H}^{*}}{de_{H}}+\frac {dd_{F}^{*}}{dr_{F}^{*}}\frac{dr_{F}^{*}}{de_{H}}+ \frac {dd_{F}^{*}}{de_{H}} \biggr) \\ &{}+\frac {d_{F}^{*}}{(d_{H}^{*}+d_{F}^{*})}N_{H}a_{H}me^{m-1} \\ &{}+\frac{d_{F}^{*}}{(d_{H}^{*}+d_{F}^{*})}e^{m}a_{H}\frac {dN_{H}}{dt_{H}^{*}} \biggl(\frac{dt_{H}^{*}}{dd_{H}^{*}}\frac {dd_{H}^{*}}{dr_{H}^{*}}\frac{dr_{H}^{*}}{de_{H}}+ \frac {dt_{H}^{*}}{dd_{F}^{*}}\frac{dd_{F}^{*}}{dr_{H}^{*}}\frac {dr_{H}^{*}}{de_{H}}+\frac{dt_{H}^{*}}{dd_{H}^{*}} \frac {dd_{H}^{*}}{dr_{F}^{*}}\frac{dr_{F}^{*}}{de_{H}} \biggr) \\ &{}+\frac{d_{F}^{*}}{(d_{H}^{*}+d_{F}^{*})}e^{m}a_{H}\frac {dN_{H}}{dt_{H}^{*}} \biggl(\frac{dt_{H}^{*}}{dd_{F}^{*}}\frac {dd_{F}^{*}}{dr_{F}^{*}}\frac{dr_{F}^{*}}{de_{H}}+ \frac {dt_{H}^{*}}{dd_{H}^{*}}\frac{dd_{H}^{*}}{de_{H}}+\frac {dt_{H}^{*}}{dd_{F}^{*}}\frac{dd_{F}^{*}}{de_{H}}+ \frac {dt_{H}^{*}}{dr_{H}^{*}}\frac{dr_{H}^{*}}{de_{H}} \\ &{}+\frac {dt_{H}^{*}}{de_{H}} \biggr) \\ &{}+\gamma_{H} \biggl(\frac{dd_{H}^{*}}{dr_{H}^{*}}\frac {dr_{H}^{*}}{de_{H}}+ \frac{dd_{H}^{*}}{dr_{F}^{*}}\frac {dr_{F}^{*}}{de_{H}}+\frac{dd_{H}^{*}}{de_{H}} \biggr)+ \varepsilon_{H}\frac {dr_{H}^{*}}{de_{H}}+\mu_{H}=0 \end{aligned}$$(153)Using (28) and (109) and simplifying we get the following:
$$\begin{aligned} =&\frac{d_{H}^{*}}{(d_{H}^{*}+d_{F}^{*})^{2}}e^{m}N_{H}a_{H} \biggl( \frac {dd_{F}^{*}}{dr_{F}^{*}}\frac{dr_{F}^{*}}{de_{H}}+\frac {dd_{F}^{*}}{de_{H}} \biggr) \\ &{} +\frac {d_{F}^{*}}{(d_{H}^{*}+d_{F}^{*})}me^{m-1}N_{H}a_{H} \\ &{}+ \frac {d_{F}^{*}a_{H}e^{m}}{(d_{H}^{*}+d_{F}^{*})}\frac {dN_{H}}{dt_{H}^{*}} \biggl(\frac{dt_{H}^{*}}{dd_{F}^{*}} \frac {dd_{F}^{*}}{dr_{F}^{*}}\frac{dr_{F}^{*}}{de_{H}}+\frac {dt_{H}^{*}}{dd_{F}^{*}}\frac{dd_{F}^{*}}{de_{H}}+ \frac {dt_{H}^{*}}{de_{H}} \biggr) \\ =&-\mu_{H} \end{aligned}$$(154)Plugging in expressions for \(\frac{dt_{H}^{*}}{dd_{F}^{*}}\), \(\frac {dd_{F}^{*}}{dr_{F}^{*}}\), \(\frac{dr_{F}^{*}}{de_{H}}\), \(\frac {dd_{F}^{*}}{de_{H}}\) and \(\frac{dt_{H}^{*}}{de_{H}}\), we get, or
$$\begin{aligned} &\frac {d_{H}^{*}}{(d_{H}^{*}+d_{F}^{*})^{2}}e^{m}N_{H}a_{H}\biggl( \frac {B_{F}e^{m}N_{F}a_{F}k\alpha_{F}\chi_{2}}{(1+\tau_{H})^{3}(1-k)(1+\alpha _{F}r_{F}^{*})}\frac{R_{F}\Delta_{F}mN_{H}e^{m-1}(1-2k)}{\alpha _{F}\varepsilon_{F}(1-k)^{2}} \\ &\quad{}+\frac {mB_{F}N_{F}a_{F}e^{m-1}}{2X_{H}(1-k)^{2}}\bigl((3-2k)\tau _{H}-(1-k)\bigr) \\ &\quad{}+\frac{d_{F}^{*}}{(d_{H}^{*}+d_{F}^{*})}me^{m-1}N_{H}a_{H}- \frac {d_{F}^{*}kN_{H}}{(d_{H}^{*}+d_{F}^{*})^{2}(1-k)}e^{m}a_{H} \\ &\quad{}\times\biggl(\frac {d_{H}^{*}B_{F}e^{m}N_{F}a_{F}k\alpha_{F}\chi_{2}}{d_{F}^{*}(1+\tau _{H})^{3}(1-k)(1+\alpha_{F}r_{F}^{*})} \frac{R_{F}\Delta _{F}me^{m-1}N_{H}(1-2k)}{\alpha_{F}\varepsilon_{F}(1-k)^{2}}\biggr) \\ &\quad{}-\frac{d_{F}^{*}}{(d_{H}^{*}+d_{F}^{*})^{2}}e^{m}a_{H}\frac {N_{H}k}{(1-k)} \frac{d_{H}^{*}}{d_{F}^{*}}\frac {mB_{F}N_{F}a_{F}e^{m-1}}{2X_{H}(1-k)^{2}}\bigl((3-2k)\tau_{H}-(1-k)\bigr) \\ &\quad{}+ \frac {d_{F}^{*}}{(d_{H}^{*}+d_{F}^{*})}e^{m}a_{H}\frac {N_{H}mke^{-1}}{1-k}=- \mu_{H} \end{aligned}$$(155)where,
$$\chi_{2}=\frac{\tau_{H}^{2}-(4-3k)\tau_{H}+(1-k)}{2(1-k)} $$Simplifying further by plugging in (120) and (121), we get:
Or,
$$\begin{aligned} &\frac {d_{H}^{*}e^{m}N_{H}a_{H}}{(d_{H}^{*}+d_{F}^{*})^{2}}\frac {B_{F}e^{m}a_{F}N_{F}}{(1-k)^{2}} \\ &\quad{}\times\biggl(\frac{R_{F}\Delta_{F}N_{H}k\alpha _{F}me^{m-1}(1-2k)\chi_{2}}{(1+\tau_{H})^{3}(1-k)\alpha_{F}\varepsilon _{F}\frac{\Delta_{F}\delta_{F}R_{F}}{\varepsilon_{F}}}+ \frac{m((3-2k)\tau _{H}-(1-k))}{2X_{H}e} \biggr) \\ &\quad{}+\frac{d_{F}^{*}}{(d_{H}^{*}+d_{F}^{*})}me^{m-1}N_{H}a_{H} \\ &\quad{}- \frac {d_{F}^{*}}{(d_{H}^{*}+d_{F}^{*})^{2}}\frac {e^{m}a_{H}kN_{H}}{(1-k)} \biggl(\frac {d_{H}^{*}B_{F}e^{m}N_{F}a_{F}k\alpha_{F}R_{F}\Delta _{F}me^{m-1}N_{H}(1-2k)\chi_{2}}{d_{F}^{*}(1+\tau_{H})^{3}(1-k)\frac {\Delta_{F}R_{F}\delta_{F}\alpha_{F}\varepsilon_{F}(1-k)^{2}}{\varepsilon _{F}}} \biggr) \\ &\quad{}-\frac{d_{F}^{*}}{(d_{H}^{*}+d_{F}^{*})^{2}}\frac {e^{m}a_{H}N_{H}k}{1-k}\frac{d_{H}^{*}}{d_{F}^{*}} \frac {mB_{F}N_{F}a_{F}e^{m-1}}{2X_{H}(1-k)^{2}}\bigl((3-2k)\tau _{H}-(1-k)\bigr) \\ &\quad{}+\frac{d_{F}^{*}}{(d_{H}^{*}+d_{F}^{*})}\frac {e^{m-1}a_{H}kN_{H}m}{(1-k)}=-\mu_{H} \end{aligned}$$(156)Using (31), (41) and (45) and simplifying we get:
Or,
$$\begin{aligned} &\frac{e^{m-1}N_{H}a_{H}m}{(1-k)^{3}} \biggl(\frac{(1-2k)\chi _{2}}{(1+\tau_{H})^{3}(1-k)}+\frac{((3-2k)\tau_{H}-(1-k))}{2X_{H}} \biggr)+ \frac{me^{m-1}N_{H}a_{H}}{(1-k)X_{F}^{\frac{1}{2}}} \\ &\quad=-\mu_{H} \end{aligned}$$(157)Or,
$$ mN_{H}a_{H}G_{H}e^{m-1}=- \mu_{H} $$(158)This gives the following expression for e
$$ e^{*}= \biggl(\frac{-\mu_{H}}{mG_{H}N_{H}a_{H}} \biggr)^{\frac {1}{m-1}} $$(159)Where,
$$G_{H}=\frac{1}{(1-k)^{3}} \biggl(\frac{(1-2k)}{(1+\tau _{H})^{3}(1-k)^{3}}+ \frac{((3-2k)\tau_{H}-(1-k))}{2X_{H}} \biggr)+\frac {1}{(1-k)X_{F}^{\frac{1}{2}}} $$Therefore,
$$ e_{H}^{*}= \biggl(\frac{-\mu_{H}}{mG_{H}N_{H}a_{H}} \biggr)^{\frac {1}{m-1}}-e_{F}^{*} $$(160) -
(b)
\(\frac{\partial e_{H}^{*}}{\partial e_{F}^{*}}=\frac {km}{(1-k)(1-m)}-1\).
First, using the same logic as we used for \(e_{H}^{*}\), we get the following expression for country F
$$ mN_{F}a_{F}G_{F}e^{m-1}=- \mu_{F} $$(161)This gives the following expression for e
$$ e^{*}= \biggl(\frac{-\mu_{F}}{mG_{F}N_{F}a_{F}} \biggr)^{\frac {1}{m-1}} $$(162)Therefore,
$$\begin{aligned} e_{F}^{*} =& \biggl(\frac{-\mu_{F}}{mG_{F}N_{F}a_{F}} \biggr)^{\frac {1}{m-1}}-e_{H}^{*} \end{aligned}$$(163)$$\begin{aligned} \frac{\partial e_{H}^{*}}{\partial e_{F}^{*}} =& \biggl(\frac{-\mu _{H}}{mG_{H}N_{H}a_{H}} \biggr)^{\frac{1}{m-1}} \frac{1}{1-m}N_{H}^{\frac {1}{1-m}-1}\frac{\partial N_{H}}{\partial e_{F}}-1 \\ =& \biggl(\frac{-\mu_{H}}{mG_{H}N_{H}a_{H}} \biggr)^{\frac{1}{m-1}}\frac {1}{1-m}N_{H}^{\frac{1}{1-m}-1} \frac{kN_{H}m}{(1-k)e}-1 \\ =& \biggl(\frac{-\mu_{H}}{mG_{H}N_{H}a_{H}} \biggr)^{\frac{1}{m-1}}\frac {km}{(1-k)e(1-m)}-1 \\ =&\frac{km}{(1-k)(1-m)}-1 \end{aligned}$$(164)This leads to the following results.
$$ \frac{\partial e_{H}^{*}}{\partial e_{F}^{*}}=\frac {km}{(1-k)(1-m)}-1<0 $$(165)Similarly,
$$ \frac{\partial e_{F}^{*}}{\partial e_{H}^{*}}=\frac {km}{(1-k)(1-m)}-1<0 $$(166) -
(c)
\(\frac{\partial e_{H}^{*}}{\partial\lambda}>0\).
Differentiating (160) with respect to λ, we get
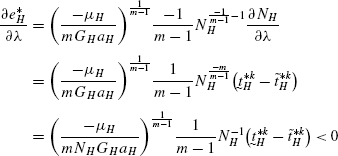 (167)
(167)Similarly,
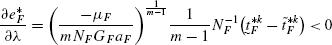 (168)$$\begin{aligned} \frac{de_{H}^{*}}{d\lambda} =&\frac{\partial e_{H}^{*}}{\partial\lambda }+\frac{\partial e_{H}^{*}}{\partial e_{F}^{*}}\frac{\partial e_{F}^{*}}{\partial\lambda} \end{aligned}$$(169)
(168)$$\begin{aligned} \frac{de_{H}^{*}}{d\lambda} =&\frac{\partial e_{H}^{*}}{\partial\lambda }+\frac{\partial e_{H}^{*}}{\partial e_{F}^{*}}\frac{\partial e_{F}^{*}}{\partial\lambda} \end{aligned}$$(169)Plugging (167) and (168) in (169), we get
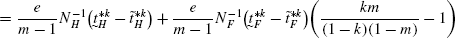 (170)
(170)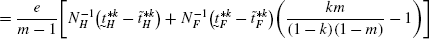 (171)
(171)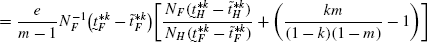 (172)
(172)Recall that,
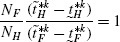
Therefore,
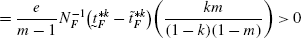 (173)
(173)Similarly, \(\frac{de_{H}^{*}}{d\lambda}>0\).
Rights and permissions
About this article
Cite this article
Roy, A., Paul, J.A. Terrorism deterrence in a two country framework: strategic interactions between R&D, defense and pre-emption. Ann Oper Res 211, 399–432 (2013). https://doi.org/10.1007/s10479-013-1431-3
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-013-1431-3




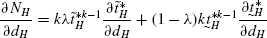
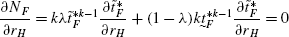
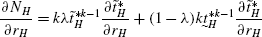
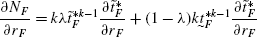
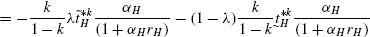

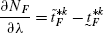
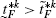 ,
, 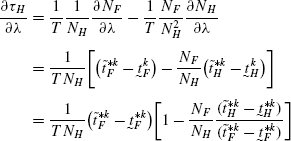
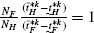 .
.