Abstract
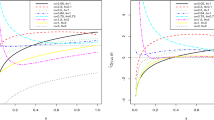
The bent line quantile regression describes the situation where the conditional quantile function of the response is piecewise linear but still continuous in covariates. In some applications, the change points at which the quantile functions are bent tend to be the same across quantile levels or for quantile levels lying in a certain region. To capture such commonality, we propose a composite estimation procedure to estimate model parameters and the common change point by combining information across quantiles. We establish the asymptotic properties of the proposed estimator, and demonstrate the efficiency gain of the composite change point estimator over that obtained at a single quantile level through numerical studies. In addition, three different inference procedures are proposed and compared for hypothesis testing and the construction of confidence intervals. The finite sample performance of the proposed procedures is assessed through a simulation study and the analysis of a real data.

Similar content being viewed by others
References
Bondell, H., Reich, B., Wang, J. (2010). Noncrossing quantile regression curve estimation. Biometrika, 97(4), 825–838.
Bunker, C., Ukoli, F., Matthews, K., Kriska, A., Huston, S., Kuller, L. (1995). Weight threshold and blood pressure in a lean black population. Hypertension, 26(4), 616–623.
Chan, K., Tsay, R. (1998). Limiting properties of the least squares estimator of a continuous threshold autoregressive model. Biometrika, 85(2), 413–426.
Chappell, R. (1989). Fitting bent lines to data, with application to allometry. Journal of Theoretical Biology, 138(2), 235–256.
Chen, L., Wei, Y. (2005). Computational issues for quantile regression. Sankhy \(\bar{a}\), 67(2):399–417.
Chernozhukov, V., Fern\(\acute{a}\)ndez-Val, I., Galichon, A. (2010). Quantile and probability curves without crossing. Econometrica, 78(3), 1093–1125.
Dette, H., Volgushev, S. (2008). Non-crossing non-parametric estimates of quantile curves. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 70(3), 609–627.
Feder, P. (1975). On asymptotic distribution theory in segmented regression problems identified case. The Annals of Statistics, 3(1), 49–83.
Fiteni, I. (2004). \(\tau \)-estimators of regression models with structural change of unknown location. Journal of Econometrics, 119(1), 19–44.
Freedman, D. (1981). Bootstrapping regression models. The Annals of Statistics, 9(6), 1218–1228.
Galvao, A. F., Kato, K., Montes-Rojas, G., Olmo, J. (2014). Testing linearity against threshold effects: uniform inference in quantile regression. Annals of the Institute of Statistical Mathematics, 66(2), 413–439.
Gutenbrunner, C., Jur\(\check{e}\), J., Koenker, R., Portnoy, S. (1993). Tests of linear hypotheses based on regression rank scores. Journal of Nonparametric Statistics, 2(4), 307–331.
Hall, P., Sheather, S. (1988). On the distribution of a studentized quantile. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 50(3), 381–391.
He, X. (1997). Quantile curves without crossing. The American Statistician, 51(2), 186–192.
He, X., Shao, Q. (1996). A general Bahadur representation of M-estimators and its application to linear regression with nonstochastic designs. The Annals of Statistics, 24(6), 2608–2630.
He, X., Shao, Q. (2000). On parameters of increasing dimensions. Journal of Multivariate Analysis, 73(1), 120–135.
Hendricks, W., Koenker, R. (1992). Hierarchical spline models for conditional quantiles and the demand for electricity. Journal of the American Statistical Association, 87(417), 58–68.
Jiang, L., Wang, H., Bondell, H. (2013). Interquantile shrinkage in regression models. Journal of Computational and Graphical Statistics, 22(4), 970–986.
Jiang, X., Jiang, J., Song, X. (2012). Oracle model selection for nonlinear models based on weighted composite quantile regression. Statistica Sinica, 22(4), 1479–1506.
Kai, B., Li, R., Zou, H. (2010). Local composite quantile regression smoothing: an efficient and safe alternative to local polynomial regression. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 72(1), 49–69.
Kai, B., Li, R., Zou, H. (2011). New efficient estimation and variable selection methods for semiparametric varying-coefficient partially linear models. The Annals of Statistics, 39(1), 305–332.
Kaufman, J., Asuzu, M., Mufunda, J., Forrester, T., Wilks, R., Luke, A., et al. (1997). Relationship between blood pressure and body mass index in lean populations. Hypertension, 30(6), 1511–1516.
Kerry, S., Micah, F., Plange-Rhule, J., Eastwood, J., Cappuccio, F. (2005). Blood pressure and body mass index in lean rural and semi-urban subjects in West Africa. Journal of Hypertension, 23(9), 1645–1651.
Kocherginsky, M., He, X., Mu, Y. (2005). Practical confidence intervals for regression quantiles. Journal of Computational and Graphical Statistics, 14(1), 41–55.
Koenker, R. (1984). A note on l-estimates for linear models. Statistics & Probability Letters, 2(6):323–325.
Koenker, R. (1994). Confidence intervals for regression quantiles. Proceedings of the 5th Prague symposium on asymptotic statistics (pp. 349–359). New York: Springer.
Koenker, R. (2005). Quantile regression. Cambridge: Cambridge University Press.
Koenker, R., Bassett, G. (1978). Regression quantiles. Econometrica, 46(1), 33–50.
Kosorok, M., Song, R. (2007). Inference under right censoring for transformation models with a change-point based on a covariate threshold. The Annals of Statistics, 35(3), 957–989.
Lee, S., Seo, M., Shin, Y. (2011). Testing for threshold effects in regression models. Journal of the American Statistical Association, 106(493), 220–231.
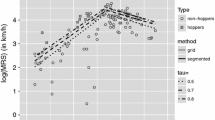
Li, C., Wei, Y., Chappell, R., He, X. (2011). Bent line quantile regression with application to an allometric study of land mammals’ speed and mass. Biometrics, 67(1), 242–249.
Liu, J., Wu, S., Zidek, J. (1997). On segmented multivariate regression. Statistica Sinica, 7(2), 97–525.
Liu, Z., Qian, L. (2010). Changepoint estimation in a segmented linear regression via empirical likelihood. Communications in Statistics—Simulation and Computation, 39(1), 85–100.
Muggeo, V. (2003). Estimating regression models with unknown break-points. Statistics in Medicine, 22(19), 3055–3071.
Oka, T., Qu, Z. (2011). Estimating structural changes in regression quantiles. Journal of Econometrics, 162(2), 248–267.
Pastor, R., Guallar, E. (1998). Use of two-segmented logistic regression to estimate change-points in epidemiologic studies. American Journal of Epidemiology, 148(7), 631–642.
Qu, Z. (2008). Testing for structural change in regression quantiles. Journal of Econometrics, 146(1), 170–184.
Robinson, D. (1964). Estimates for the points of intersection of two polynomial regressions. Journal of the American Statistical Association, 59(305), 214–224.
Su, L., Xiao, Z. (2008). Testing for parameter stability in quantile regression models. Statistics & Probability Letters, 78(16):2768–2775.
Vieth, E. (1989). Fitting piecewise linear regression functions to biological responses. Journal of the American Statistical Association, 67(1), 390–396.
Wang, J., He, X. (2007). Detecting differential expressions in genechip microarray studies: A quantile approach. Journal of the American Statistical Association, 102(477), 104–112.
Wang, J., Zhu, Z., Zhou, J. (2009). Quantile regression in partially linear varying coefficient models. The Annals of Statistics, 37(6B), 3841–3866.
Zhang, L., Wang, J., Zhu, Z. (2014). Testing for change points due to a covariate threshold in quantile regression. Statistica Sinica, 24(4), 1859–1877.
Zou, H., Yuan, M. (2008). Composite quantile regression and the oracle model selection theory. The Annals of Statistics, 36(3), 1108–1126.
Author information
Authors and Affiliations
Corresponding author
Additional information
Zhang’s research is partially supported by NNSFC Grant 11171074. Wang’s research is partially supported by NSF (National Science Foundation) CAREER Award DMS-1149355. Zhu’s research is partially supported by NSFC 11271080.
Appendix
Appendix
Lemma 1
Suppose Assumptions A1–A3 hold, then \(\hat{\varvec{\theta }}\) is a consistent estimator of \(\varvec{\theta }_{0}\).
Proof
At a fixed point u, we need to minimize the following objective function
which is equivalent to minimize
for any \(1\le k\le K\). The rest of the proof follows the similar arguments as that of Lemma 1 in Li et al. (2011) and thus is omitted. \(\square \)
Lemma 2
Suppose Assumptions A1–A3 hold, we have
where \(C_{2}\) is some positive constant.
Proof
Let
where \(\mathbf {V}_{i}\) includes all the random variables \(Y_{i}\) and \(\mathbf {W}_{i}\). Therefore, it can be rewritten as the following
where \(u_{i1}(\mathbf {V}_{i};\varvec{\theta },\varvec{\theta }_{0})=u_{i}(\mathbf {V}_{i};\) \(\varvec{\theta },\varvec{\theta }_{0})I\{X_{i}\le \min (u, u_{0})\}\), \(u_{i2}(\mathbf {V}_{i};\varvec{\theta },\varvec{\theta }_{0})=u_{i}(\mathbf {V}_{i};\varvec{\theta },\varvec{\theta }_{0})I(u_{0}\) \(< X_{i} \le u)\), \(u_{i3}(\mathbf {V}_{i};\varvec{\theta },\varvec{\theta }_{0})=u_{i}(\mathbf {V}_{i};\varvec{\theta },\varvec{\theta }_{0})I(u < X_{i} \le u_{_{0}})\) and \(u_{i4}(\mathbf {V}_{i};\varvec{\theta },\varvec{\theta }_{0})=u_{i}(\mathbf {V}_{i};\varvec{\theta },\varvec{\theta }_{0})\) \(I\{X_{i}> \max (u, u_{0})\}\).
To obtain (8), it is sufficient to show
where \(B_{i}\) represents \(u_{ij}(\mathbf {V}_{i};\varvec{\theta },\varvec{\theta }_{0})\) for \(j=1,2,3,4\). These results follow from Lemma 4.6 in He and Shao (1996), we only show the proof for \(B_{i}=u_{i1}(\mathbf {V}_{i};\varvec{\theta },\varvec{\theta }_{0})\) for instance. To verify this, we need to check the conditions (B1), (B3) and (B5\(^{'}\)) of He and Shao (1996).
For (B1), the measurability is easy to show.
For (B3), take \(r=1\), for any \(\Vert \varvec{\theta }- \varvec{\theta }_{0} \Vert \le C_{2}n^{-1/2}\), we have
For \(I_{1i}\), it is easy to obtain
For \(I_{2i}\), we have
where \(L_{1}\) is some constant, \(\mathbf {U}_{i}=(1, X_{i}, \mathbf {Z}^{T}_{i})^{T}\), \(Q_{1}(\tau _{k};\varvec{\theta },\varvec{\theta }_{0})= \min \{Q_Y(\tau _{k};\varvec{\theta }_{0}|\mathbf {W}_{i}),\) \(Q_Y(\tau _{k};\varvec{\theta }|\mathbf {W}_{i}) \}\) and \(Q_{2}(\tau _{k};\varvec{\theta },\varvec{\theta }_{0})= \max \{ Q_Y(\tau _{k};\varvec{\theta }_{0}|\mathbf {W}_{i}),\) \(Q_Y(\tau _{k};\varvec{\theta }|\mathbf {W}_{i}) \}\). Thus
Without loss of generality, we assume \(Q_{1}(\tau _{k};\varvec{\theta },\varvec{\theta }_{0})< Q_{2}(\tau _{k'};\varvec{\theta },\varvec{\theta }_{0})\) and \(Q_{1}(\tau _{k'};\varvec{\theta },\varvec{\theta }_{0})< Q_{2}(\tau _{k};\varvec{\theta },\varvec{\theta }_{0})\). Denote \(Q_{1}(\tau _{k},\tau _{k'})= \min \{Q_{1}(\tau _{k};\varvec{\theta },\varvec{\theta }_{0}), Q_{1}(\tau _{k'};\varvec{\theta },\varvec{\theta }_{0}) \}\) and \(Q_{2}(\tau _{k},\tau _{k'})= \max \{Q_{2}(\tau _{k};\varvec{\theta },\varvec{\theta }_{0}), Q_{2}(\tau _{k'};\varvec{\theta },\varvec{\theta }_{0}) \}\). Hence

where the first inequality follows from the mean value theorem with \(\xi _{k,k'}\) between \(Q_{1}(\tau _{k};\tau _{k'}) \) and \(Q_{2}(\tau _{k};\tau _{k'})\), the second inequality follows from
where \(L_{2}\) and \(L_{3}\) are some positive constants satisfying \(L_{2}= L^{2}_{1}L^{2}_{3}\). By Assumptions A3 and A4, combining (9), (10) and (11), for large n we have
It is obvious to obtain (B3) by taking \(a_{i}= \sqrt{L\Vert \mathbf {U}_{i}\Vert ^{3} \sum _{k=1}^{K}\sum _{k'=1}^{K}f_{i}(\xi _{k,k'})}\).
For (B5\(^{'}\)), let \(A_{n}=L\sum _{i=1}^{n}\Vert \mathbf {U}_{i}\Vert ^{3}\sum _{k=1}^{K}\sum _{k'=1}^{K}f_{i}(\xi _{k,k'})\). From Assumptions A2 and A3, we have \(E(A_{n})= O(n)\). For any positive constant \(C_{3}>0\), taking the decreasing sequence of positive number \(d_{n}\) satisfying \(n^{-1/2}(\log n)^4=o(d_{n})\) and \(d_{n}=o(1)\), we can show
Hence,
thus (B5’) is satisfied. This completes the proof of Lemma 2. \(\square \)
Proof of Theorem 1
Applying the Taylor expansion, we get
where
In addition, by the subgradient condition of quantile regression (pages 34–38 in Koenker 2005), we have
Combining (12), (13) and (14), we have
This results in \(\hat{\varvec{\theta }}- \varvec{\theta }_{0}= O_{p}(n^{-1/2})\). Therefore,
Following central limit theorem, by Assumption A4 and some simple calculation, we can obtain that \(n^{1/2}(\hat{\varvec{\theta }} - \varvec{\theta }_{0})\) is asymptotically normal with mean zero and variance \(\varvec{D}^{-1}\varvec{C}\varvec{D}^{-1}\). This completes the proof of Theorem 1. \(\square \)
Proof of Theorem 2
Denote
where \(\varvec{S}^{*}_{n}= \{S^{*}_{n,1},\ldots , S^{*}_{n,K}\}^{T}\), \(S^{*}_{n,k}=n^{-1/2}\sum _{i=1}^{n}p^{*}_{i}(\tau _{k};\varvec{\eta }_{k,0},u_{0}|\mathbf {W}_{i})\psi _{\tau _{k}}(e_{i,\tau _{k}})\), \(e_{i,\tau _{k}}=Y_{i}-Q_Y(\tau _{k};\varvec{\eta }_{k,0}, u_{0}|\mathbf {W}_{i})\), \(\varvec{V}^{*}_{n}\) is a \(K\times K\) matrix with the \((k,k^{'})\)th element
Following central limit theorem, we have \(\varvec{S}^{*}_{n}\ \xrightarrow {d}\ N(0,\ \varvec{V}^{*}_{n}).\) Therefore, we can obtain
To obtain the desired result, we need to show
and
It is easy to show that (15) holds since by Theorem 1,
For (16), it is sufficient to show that \(S_{n,k}=S^{*}_{n,k}+o_{p}(1)\) for any \(1\le k \le K\). Denote \( S_{n,k}(\varvec{\eta }_{k})=n^{-1/2}\sum _{i=1}^{n}p^{*}_{i}(\tau _{k}; \varvec{\eta }_{k},u_{0})\psi _{\tau _{k}}\{Y_{i}-Q_Y(\tau _{k};\varvec{\eta }_{k}, u_{0}|\mathbf {W}_{i})\}\), because we have
Because \(E(S^{*}_{n,k})=0\), following He and Shao (2000), we have
where \(C_{4}\) is some positive constant. For any \(\varvec{\eta }_k\) such that \(\Vert \varvec{\eta }_k-\varvec{\eta }_{k,0}\Vert \le C_{4}n^{-1/2}\) , by the Taylor expansion, we get
where the third equality follows from the orthogonalization between \(\varvec{p}^{*}_{i}(\tau _{k}; \varvec{\eta }_{k}, u_{0})\) and \(\mathbf {m}(\mathbf {W}_{i},\) \(u_{0})\), the fourth equality is based on \(\Vert n^{-1}\sum _{i=1}^{n}E \varvec{p}^{*}_{i}(\tau _{k}; \varvec{\eta }_{k}, u_{0}) \Vert \le \Vert n^{-1}\sum _{i=1}^{n} E \varvec{p}_{i}(\tau _{k};\varvec{\eta }_{k},\) \(u_{0}) \Vert \le o(1)\). Let \(\varvec{\eta }_{k} = \hat{\varvec{\eta }}_{k}(u_{0})\), note that \(S_{n,k}= S_{n,k}\{ \hat{\varvec{\eta }}_{k}(u_{0}) \}\). By combining (16) with (19), we obtain (16). This completes the proof of Theorem 2. \(\square \)
About this article
Cite this article
Zhang, L., Wang, H.J. & Zhu, Z. Composite change point estimation for bent line quantile regression. Ann Inst Stat Math 69, 145–168 (2017). https://doi.org/10.1007/s10463-015-0538-5
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10463-015-0538-5