Abstract
The last decade witnessed a growing interest in Bayesian learning. Yet, the technicality of the topic and the multitude of ingredients involved therein, besides the complexity of turning theory into practical implementations, limit the use of the Bayesian learning paradigm, preventing its widespread adoption across different fields and applications. This self-contained survey engages and introduces readers to the principles and algorithms of Bayesian Learning for Neural Networks. It provides an introduction to the topic from an accessible, practical-algorithmic perspective. Upon providing a general introduction to Bayesian Neural Networks, we discuss and present both standard and recent approaches for Bayesian inference, with an emphasis on solutions relying on Variational Inference and the use of Natural gradients. We also discuss the use of manifold optimization as a state-of-the-art approach to Bayesian learning. We examine the characteristic properties of all the discussed methods, and provide pseudo-codes for their implementation, paying attention to practical aspects, such as the computation of the gradients.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Machine Learning (ML) techniques have been proven to be successful in many prediction and classification tasks across natural language processing (Young et al. 2018), computer vision (Krizhevsky et al. 2012), time-series (Längkvist et al. 2014) and finance applications (Dixon et al. 2020), among the several others. The widespread of ML methods in diverse domains is found due to their ability to scale and adapt to data, and their flexibility in addressing a variety of problems while retaining high predictive ability. Recently, Bayesian methods have gained considerable interest in ML as an attractive alternative to the classical methods providing point estimations for their inputs. Despite the numerous advantages that traditional ML methods offer, they are, broadly speaking, prone to overfitting, dimming their generalization capabilities and performance on unseen data. Furthermore, an implicit consequence of the classical point estimation and modeling setup is that it delivers models that are generally incapable of addressing uncertainties. This inability is twofold, as it includes both the estimation and prediction aspects. Indeed, as opposed to the typical practice of statistical modeling and, e.g., econometrics methods, ML methods do not directly tackle aspects related to the significance and uncertainties associated with the estimated parameters. At the same time, predictions correspond to simple point estimates without reference to the confidence levels that such estimates have. Whereas some models have been developed to, e.g., provide confidence intervals over the forecasts (e.g. Gal and Ghahramani 2016), it has been observed that such models are generally overconfident. To estimate uncertainties implicitly embedded in ML models, Bayesian inference provides an immediate remedy and stands out as the main approach.
Bayesian methods have gained considerable interest as an attractive alternative to point estimation, especially for their ability to address uncertainty via posterior distribution, generalize while reducing overfitting (Hoeting et al. 1999), and for enabling sequential learning (Freitas et al. 2000) while retaining prior and past knowledge. Although Bayesian principles have been proposed in ML decades ago (e.g. Mackay 1992, 1995; Lampinen and Vehtari 2001), it has been only recently that fast and feasible methods boosted a growing use of Bayesian methods in complex models, such as deep neural networks (Osawa et al. 2019; Khan et al. 2018a; Khan and Nielsen 2018).
The most challenging task in following the Bayesian paradigm is the computation of the posterior. In the typical ML setting characterized by a high number of parameters and a considerable size of data, traditional sampling methods are prohibitive, and alternative estimation approaches such as Variational Inference (VI) have been shown to be suitable and successful (Saul et al. 1996; Wainwright and Jordan 2008; Hoffman et al. 2013; Blei et al. 2017). Furthermore, recent research advocates the use of natural gradients for boosting the optimum search and the training (Wierstra et al. 2014), enabling fast and accurate Bayesian learning algorithms that are scalable and versatile.
Recent years witnessed enormous growth in the interest related to Bayesian ML methodologies and several contributions in the field. This survey aims at summarizing the major methodologies nowadays available, presenting them from an algorithmic, empirically-oriented perspective. With this rationale, this paper aims to provide the reader with the basic tools and concepts to understand the theory behind Bayesian Deep Learning (DL) and walk through the implementation of the several Bayesian estimation methodologies available. We should note that the focus of this paper is purely on Bayesian methods. Indeed there are a number of network architectures that can resemble a Bayesian framework by, e.g., creating a distribution for the outputs, e.g., Deep Ensembles (Osband et al. 2018), Batch Ensembles (Wen et al. 2020), Layer Ensembles (Oleksiienko and Iosifidis 2022), or Variational Neural Networks (Oleksiienko et al. 2022). These solutions, based on particular network designs, are, however, not implicitly Bayesian and out of scope in our context. Other surveys and tutorials do exist on the general topic (e.g. Jospin et al. 2022; Heckerman 2008, along with several lecture notes available online), yet the focus of this paper is on algorithms and mainly devoted to VI methods. In fact, despite the wide number of VI and non-VI methods published in the last decade, a comprehensive survey embracing and discussing all of them (or perhaps the major ones) is missing, and non-experts will easily find themselves lost in their pursuit to comprehend and different notions and processing steps in different methodologies. By filling this gap, we aim to promote applications and research in this area.
1.1 The Bayesian paradigm
The Bayesian paradigm in statistics is often opposed to the pure frequentist paradigm, a major area of distinction being in hypothesis testing (Etz et al. 2018). The Bayesian paradigm is based on two simple ideas. The first is that probability is a measure of belief in the occurrence of events, rather than just some limit in the frequency of occurrence when the number of samples goes toward infinity. The second is that prior beliefs influence posterior beliefs (Jospin et al. 2022). The above two are summarized in the Bayes theorem, which we now review. Let \({\mathcal {D}}\) denote the data and \(p\left( {\mathcal {D}}\vert {{\varvec{\theta }}} \right)\) the likelihood of the data based on a postulated model with \({{\varvec{\theta }}}\in \Theta\) a k-dimensional vector of model parameters. Let \(p\left( {\varvec{\theta }} \right)\) be the prior distribution on \({{\varvec{\theta }}}\). The goal of Bayesian inference is the estimation of the posterior distribution (e.g., Gelman et al. 1995)
where \(p\left( {\mathcal {D}} \right)\) is referred to as evidence or marginal likelihood, since \(p\left( {\mathcal {D}} \right) =\int _{\Theta} p\left( {\varvec{\theta }} \right) p\left( {\mathcal {D}}\vert {{\varvec{\theta }}} \right) d{{\varvec{\theta }}}\). \(p\left( {\mathcal {D}} \right)\) acts as a normalization constant for retrieving an actual probability distribution for \(p\left( {{\varvec{\theta }}}\vert {\mathcal {D}} \right)\). In this light, as opposed to the frequentist approach, it becomes clear that the unknown parameter \({{\varvec{\theta }}}\) is treated as a random variable. The prior probability \(p\left( {\varvec{\theta }} \right)\), which intuitively expresses in probabilistic terms any knowledge about the parameter before the data has been collected, is updated in the posterior probability \(p\left( {{\varvec{\theta }}}\vert {\mathcal {D}} \right)\), mixturing prior knowledge and evidence supported by the data through the model’s likelihood. Bayesian inference is generally difficult due to the fact that the marginal likelihood is often intractable and of unknown form. Indeed, only for a limited class of models, where the prior is so-called conjugate to the likelihood, the calculation of the posterior is analytically tractable. Standard examples are Normal likelihoods and prior (resulting in Normal posteriors) or Poisson likelihoods with Gamma priors (resulting in Negative Binomial posteriors). Yet, already for the simple linear regression example, Bayesian derivation is rather tedious, and already for the logistic regression, closed-form solutions are not generally available. It is clear that in complex models, such as deep neural networks typically used in ML applications, Bayesian inference can be tackled neither analytically nor numerically (consider that the integral in the marginal likelihood is multivariate, over as many dimensions as the number of parameters).
Monte Carlo (MC) methods for sampling the posterior are certainly a possibility that has been early explored and adopted. While it still remains a valid and appropriate method for performing Bayesian inference in retractable settings, especially in high-dimensional applications, the MC approach is challenging and may become infeasible, mainly because of the need for an implicit high-dimensional sampling scheme, which is generally time-consuming and computationally demanding. As an alternative approach, VI gained much attention in recent years. VI turns the integration Bayesian problem in Eq. (1) into an optimization problem. The idea behind VI is that of targeting an approximate form of the posterior distribution, perhaps chosen within a family of well-behaved distributions, and finding the corresponding parameter that optimizes a specific objective, i.e., that is optimal under some criterion.
In the following subsection, we review the standard non-Bayesian approach for neural network parameter estimation (Sect. 1.2.1), we introduce Bayesian Neural Networks (BNNs) (Sect. 1.4), and we provide some motivation for their use, also recalling some literature about their applications (Sect. 1.3). After providing the reader an introduction to standard and Bayesian neural networks, we introduce VI in Sect. 1.5, we describe the standard framework used in Bayesian learning, and we discuss how the standard Stochastic Gradient Descent (SGD) approach can be used for solving the optimization problem therein (Sect. 1.5.1).
1.2 Standard and Bayesian Neural Networks
A Bayesian Neural Network (BNN) is an Artificial Neural Network (ANN) trained with Bayesian Inference (Jospin et al. 2022). In the following, we provide a quick overview of ANNs and their typical estimation based on Backpropagation (Sect. 1.2.1). We then describe what a Bayesian Neural Network (BNN) is (Sect. 1.4), provide motivations on why to use a BNN, over a standard ANN (Sect. 1.3), and lastly introduce VI (Sect. 1.5).
1.2.1 Artificial Neural Networks
For completeness, we review the general ingredients, principles, ideas, and standard terminology behind ANN. A comprehensive and more detailed introduction to the topic is here out of scope; the interested reader can e.g., consult the accessible book (Haykin 1998).
Neurons are elementary building blocks which can be thought of as processing units that, when combined, constitute a neural network. Each neuron processes the information presented to its input by applying a transformation to it. When affine neurons are used, the transformation corresponds to computing the weighted sum of the inputs to the neuron (received from the neurons that are connected to it or corresponding to the inputs to the neural network) and generates a value, which is further introduced to a (usually nonlinear) activation function to produce the neuron’s output (input to other neurons or the neural network output). In order to account for the need of a shift to the value needed to produce an activation response, a bias is also added as an input to the activation function, which is commonly included in the weighted sum by augmenting the input to the neuron with an additional input with a constant value of 1, associated with the corresponding bias term. While activation functions squeezing their outputs to a pre-determined range of values, like the sigmoid (with outputs in [0, 1]) or the tanh (with outputs in \([-1,1]\)) functions, have been widely used in the past, piece-wise linear functions, like the Rectified Linear Unit (ReLU) or the parametric ReLU functions (He et al. 2015), are nowadays widely adopted in building the hidden layers of neural networks. Linear and softmax activation functions are commonly used in the output layer for regression and classification problems, respectively. A common characteristic of activation functions used in neural networks is that they are differentiable with respect to their parameters over the range of their inputs. The transformation performed by an affine neuron is illustrated in Fig. 1.
Representation of the operations within the jth neuron at layer is l. Connections between this neuron and neurons in layer \(l-1\) are represented by lines corresponding to weights \(\theta ^{l}_{\cdot j}\). The inputs to the neuron \(o^{l-1}_{\cdot }\) interact with the weights \(\theta ^{l}_{\cdot j}\), computing the weighted sum \(a^{l}_{j}\). The so-called activation function \(g(\cdot )\) is applied to \(a^{l}_{j}\) leading to the output \(o^{l}_{j}\), which is sent to nodes at layer \(l+1\)
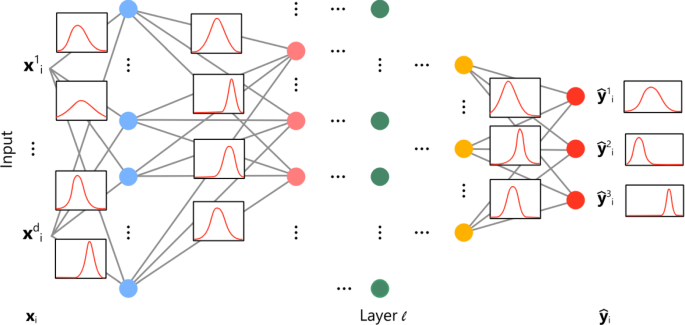
Whenever the information flow between neurons has no feedback (i.e., neurons do not process information resulting from their outputs), in the sense that information flows from the input through the neurons producing the output of the network, the network is referred to as feedforward. Neurons are arranged in layers, and a network formed by neurons in one layer is called single layer network. When more than one layer forms a neural network, layers are generally called hidden layers since they stand between the input and the output, i.e., the “tangible” information, which consists of the input samples and their classification targets/outputs. A feedforward neural network receiving as input a d-dimensional vector and producing a 3-dimensional output is shown in Fig. 2.
A feedforward network with multiple layers. Dots represent neurons across different layers (colors). The d-dimensional input vector \({\varvec{x}}_{i} = [x_{i}^{1},\dots ,x_{i}^{d}]^{T}\) is sequentially parsed to the output, from left to right, following the connections represented in grey which correspond to the weights of the network’s layers. (Color figure online)
The most relevant feature of a neural network is its capacity of learning. This corresponds to the ability to improve its outputs (performance in classification) by tuning the parameters (weights and biases) of its neurons. Learning algorithms of neural networks use a set of training data to iteratively update the parameters of a neural network such that some error measure is decreased or some performance measure is increased (see, e.g., Goodfellow et al. 2016). The data \({\mathcal {D}}\) consists of vectors \({\mathcal {D}}_{i} = \{ {\varvec{y}}_{i},{\varvec{x}}_{i} \}\), with \({\varvec{x}}_{i}\) representing an input and \({\varvec{y}}_{i}\) the corresponding target for \(i=1,\ldots ,N\). Let \({\hat{{\varvec{y}}}}_{i}\) denote the output of the network corresponding to the sample \({\varvec{x}}_{i}\), that is \({\hat{{\varvec{y}}}}_{i} = {\text {NN}}_{{\varvec{\theta }}}\left( {\varvec{x}}_{i} \right)\), with \({\text {NN}}_{{\varvec{\theta }}}\left( {\varvec{x}}_{i} \right)\) denoting a Neural Network parametrized over \({{\varvec{\theta }}}\) and evaluated at \({\varvec{x}}_{i}\). An error function \(E\left( {\mathcal {D}},{{\varvec{\theta }}} \right)\) is defined at a particular parameter \({{\varvec{\theta }}}\), which is used to guide the learning process. Several error functions have been used to this end, the most widely adopted ones being the mean-squared error (suitable for regression problems) and the cross-entropy (suitable for classification problems). The gradient of the error between the network’s outputs \({\hat{{\varvec{y}}}}_{i}\) and the targets \({\varvec{y}}_{i}\) over the entire data set (full-batch) or a subset of the data (mini-batch) is commonly used to update the network parameter values through an iterative optimization process, commonly a variant of the Backpropagation algorithm (Rumelhart et al. 1986). Widely used iterative optimization methods are the Stochastic Gradient Descent (SGD) (Robbins and Monro 1951), Root Mean Squared Propagation (RMSProp) (Tieleman and Hinton 2012) and Adaptive Moment Estimation (ADAM) (Kingma and Ba 2014).
While feedforward neural networks with affine neurons have been briefly described above, a large variety of neural networks have been proposed and used for modeling different input–output data relationships. Such networks follow the main principles as those described above (i.e., they are formed by layers of neurons, which perform transformations followed by differentiable activation functions), but they are realized by using different types of neurons and/or transformations. Examples include the Radial Basis Function (RBF) networks (Broomhead and Lowe 1988), which replace affine transformations with distance-based transformations, Convolutional Neural Networks (Homma et al. 1987), which receive a tensor input and use neurons performing convolution, Recurrent Neural Networks (e.g., Long-Short Term Memory, LSTM Hochreiter and Schmidhuber 1997 and Gated Recurrent Unit, GRU Cho et al. 2014 networks), which model sequences of their inputs by using recurrent units, and specialized types of neural networks, such as the Temporal-Augmented Bilinear Layer (TABL) network (Tran et al. 2019) based on bilinear mapping, and the Neural Bag-of-Features network (Passalis et al. 2020), extending the classical Bag-of-Features model with a differentiable processing suitable to be used in combination with other types of neural network layers.
1.3 Motivation for adopting Bayesian Neural Networks
Bayesian neural networks are interesting tools under three perspectives: (i) theoretical, (ii) methodological, and (iii) practical. In the following, we shall briefly discuss what we mean by the above three interconnected perspectives.
From a theoretical perspective, BNNs allow for differentiating and quantifying two different sources of uncertainty, namely epistemic uncertainty, and aleatoric uncertainty (see, e.g. Der Kiureghian and Ditlevsen 2009, from a ML perspective). Epistemic uncertainty is the one referring to the lack of knowledge, and it is captured by \(p\left( {{\varvec{\theta }}}\vert {\mathcal {D}} \right)\). In light of the Bayes theorem, epistemic uncertainty can be reduced with the use of additional data so that the lack of knowledge is addressed as more data are collected. After the data is collected, this results in the update of the prior belief (before the experiment is conducted) to the posterior. Thus, the Bayesian perspective allows the mixing of expert knowledge with experimental evidence. This is quite relevant in small-sample applications where the amount of collected data is inappropriate for classical statistical tools and results to apply (e.g., inference based on asymptotic theory), yet it nevertheless allows the update of the a priori belief on the parameters, \(p\left( {\varvec{\theta }} \right)\), into the posterior. On the other hand, the likelihood term captures the aleatoric uncertainty, that is the intrinsic uncertainty naturally embedded in the data, i.e., \(p\left( y\vert \theta \right)\), in the Bayesian framework is clearly distinguished and separated from the aleatoric one.
Methodologically, is remarkable the ability of Bayesian methods to learn from small data and eventually converge to, e.g., non-Bayesian maximum likelihood estimates or, more generally, to agree with alternative frequentist methods. When the amount of the collected data overwhelms the role of the prior in the likelihood-prior mixture, Bayesian methods can be clearly seen as generalizations of standard non-Bayesian approaches. Within the Bayesian methods family, certain research areas such as PAC-Bayes (Alquier 2021), Empirical Bayes (Casella 1985) and Approximate Bayes Computations (Csilléry et al. 2010) deal with such connections very tightly. In this regard, there are many examples in the statistics literature; we focus on the ML perspective. For instance, regularization, ensemble, meta-learning, Monte Carlo dropout, etc., can all be understood as Bayesian methods, and, e.g., Variational Bayes can be seen as standard linear regression (Salimans and Knowles 2013). More in general, many ML methods can be seen as approximate Bayesian methods, whose approximate nature makes them simpler and of practical use. Furthermore, as the learned posterior can be reused and re-updated once new data become available, Bayesian learning methods are well-suited for online learning (Opper and Winther 1999). In this regard, also the explicit use of the prior in Bayesian formulations is aligned with the No-Free-Lunch Theorem (Wolpert 1996) whose philosophical interpretation, among the others, is that any supervised algorithm implicitly embeds and encodes some form of prior, establishing a tight connection with Bayesian theory (Serafino 2013; Guedj and Pujol 2021).
From a practical perspective, the Bayesian approach implicitly allows for dealing with uncertainties, both in the estimated parameters and in the predictions. For a practitioner, this is by far the most relevant aspect in shifting from a standard ANN approach to BNNs. Thus, with little surprise, Bayesian methods have been well-received in high-risk application domains where quantifying uncertainties is of high importance. Examples can be found across different fields, such as industrial applications (Vehtari and Lampinen 1999), medical applications (e.g. Chakraborty and Ghosh 2012; Kwon et al. 2020; Lisboa et al. 2003), finance (e.g. Jang and Lee 2017; Sariev and Germano 2020; Magris et al. 2022a, b), fraud detection (e.g. Viaene et al. 2005), engineering (e.g. Cai et al. 2018; Du et al. 2020; Goh et al. 2005), and genetics (e.g. Ma and Wang 1999; Liang and Kelemen 2004; Waldmann 2018).
As widely recognized, the estimation of BNN is not a simple task due to the generally non-conjugacy between the prior and the likelihood and the non-trivial computation of the integral involved in the marginal likelihood. For this reason, application of BNNs is relatively infrequent, and their use is not widespread across the different domains. As of now, applying Bayesian principles in a plug-and-play fashion is challenging for the general practitioner. On top of that, several estimation approaches have been developed, and navigating through them can indeed be confusing. In this survey, we collect and present parameter estimation and inference methods for Bayesian DL at an accessible level to promote the use of the Bayesian framework.
1.4 Bayesian Neural Networks
From the description in Sect. 1.2.1, it can be seen that the goal of approximating a function relating the input to the output in classical ANNs is treated under an entirely deterministic perspective. Switching towards a Bayesian perspective in mathematical terms is rather straightforward. In place of estimating the parameter vector \({{\varvec{\theta }}}\), BNNs target the estimation of the posterior distribution \(p\left( {{\varvec{\theta }}}|{\mathcal {D}}_{x},{\mathcal {D}}_{y} \right)\), that is (Jospin et al. 2022):
which stands as a simple application of the Bayes theorem. Here we assume, as it is usually the case, that the data \({\mathcal {D}}\) is composed of an input set \({\mathcal {D}}_{x}\) and the corresponding set of outputs \({\mathcal {D}}_{y}\). In general, \({\mathcal {D}}_{x}\) is a matrix of regressors, and \({\mathcal {D}}_{y}\) is either the vector or matrix (depending on whether the nature of the output is univariate or not) of the variables that the networks aim at modeling based on \({\mathcal {D}}_{x}\). Alternatively but analogously, \({\mathcal {D}}\) can be thought as the collection of all input–output pairs \({\mathcal {D}}= \{ {\varvec{y}}_{i},{\varvec{x}}_{i} \}_{i=1}^{N}\), where N denotes the sample size, and \({\varvec{x}}_{i}\) and \({\varvec{y}}_{i}\) are the input and output vectors of observations for the ith sample, respectively. Using this notation, \({\mathcal {D}}_{x}=\{ {\varvec{x}}_{i} \}_{i=1}^{N}\) and \({\mathcal {D}}_{y}=\{ {\varvec{y}}_{i} \}_{i=1}^{N}\).
While Eq. (2) provides a theoretical prescription for obtaining the posterior distribution, in practice solving for the form of the posterior distribution and retrieving its parameters is a very challenging task. The estimation of a BNN with MC techniques and VI is discussed in the remainder of the review, here we continue the discussion towards different aspects.
Equation (2) involves all the ingredients required for performing Bayesian inference on ML models, and specifically neural networks. In the first place, Eq. (2) involves a likelihood function for the data \({\mathcal {D}}_{y}\) conditional on the observed sample \({\mathcal {D}}_{x}\) and the parameter vector \({{\varvec{\theta }}}\). The forward pass parses the input into predictions via some parameter values, such outputs (conditional on the data and the parameters) follow a prescribed likelihood function. Intuitive examples are the Gaussian likelihood (for regression) and the Binomial one (for classification). An underlying neural network is implicit in the likelihood term \(p\left( {\mathcal {D}}_{y}\vert {\mathcal {D}}_{x},{{\varvec{\theta }}} \right)\), that links the inputs to the outputs. In other words, as is the case for ANNs, the first step in designing a BNN is that of identifying a suitable neural network architecture (e.g., how many layers and of which kind and size) followed by a reasonable assumption for the likelihood function.
A major difference between ANNs and BNNs is that the latter requires the introduction of the prior distribution over the model parameters. After all, a prior must be in place for Bayesian inference to be performed; thus, priors are required in the BNN setup (Jospin et al. 2022). This means that the practitioner needs to decide on the parametric form of the prior over the parameters.
Example 1
Consider a BNN to model the variables \({\mathcal {D}}_{y} = \{ y_{i} \}_{i=1}^{N}\) where \(y_{i} \in \{ 0,1 \}\), based on the matrix of covariates \(D_{x}\). The likelihood is of a certain form and parametrized over a neural network whose weights are denoted by \({{\varvec{\theta }}}\), i.e., \({\text {NN}}_{{\varvec{\theta }}}\left( \cdot \right)\).
We can approach the above problem as a 2-class classification with \(y_{i} \in \left[ 0,1 \right]\), and derive the likelihood from the Bernoulli distribution
where \({\hat{p}}_{i} = {\text {NN}}_{{\varvec{\theta }}}\left( {\varvec{x}}_{i} \right)\) denotes the output of the network for the ith sample, that is the probability that sample i belongs to class 1. The prior (on the network parameters) can be a diagonal Gaussian \(p\left( {{\varvec{\theta }}} \right) ={\mathcal {N}}\left( {{\varvec{\theta }}}\vert 0, \tau I \right)\), where \(\tau >0\) is a scalar and I the identity matrix.
We can also approach the above problem as a regression to \({\varvec{y}}_{i} \in {\mathbb {R}}^{d}\) and derive the likelihood from the Multivariate Normal distribution
where \(\hat{{\varvec{y}}}_{i} = {\text {NN}}_{{\varvec{\theta }}}\left( {\varvec{x}}_{i} \right)\). Assuming that the covariance matrix \(\Sigma ^{-1}\) is known, the prior on \({{\varvec{\theta }}}\) could be as well a diagonal Gaussian. If \(\Sigma\) is unknown, the prior could be the product of the above Gaussian prior with, e.g., an Inverse Wishart prior distribution on \(\Sigma\). In this case, the goal of the Bayesian inference is that of estimating the joint posterior of \(\left( {{\varvec{\theta }}},\Sigma \right)\).
The inference goal is the posterior distribution. (i) If the problem has a form for which the posterior can be solved analytically, we find \(p\left( {{\varvec{\theta }}}\vert {\mathcal {D}}_{x}{\mathcal {D}}_{y} \right)\) to be of a known parametric form and identify the parameters characterizing it [standard Bayesian setting, so-called conjugacy between the prior and the likelihood, (e.g., Gelman et al. 1995)]. (ii) In general, we may proceed via MC sampling, in which case the estimation leads to a sample, of arbitrary size, approximating the true posterior. The true posterior remains unknown in its exact form, yet MC enables sampling from it and thus estimating an approximate representation (e.g., Gamerman and Lopes 2006), see Sect. 3. (iii) Alternatively, following VI, one sets a certain chosen parametric form for the posterior and optimizes its parameters for a certain objective function (e.g., Nakajima et al. 2019), see Sect. 1.5. While the actual posterior remains unknown, in VI one seeks an approximation that is optimal in some sense of optimization of a certain objective on the provided data.
Figure 3 provides an analogous representation of Fig. 2, now for a BNN. Opposed to traditional ANNs, weights in BNNs are stochastic and represented with distributions. A probability distribution over the weights is learned by updating the prior with the evidence supported by the data. Even though Fig. 3 might give the opposite impression, the posterior over the weights is, in general, a truly multivariate distribution where independence among its dimensions generally does not hold.
While the above clarifies that the estimation goal is a distribution whose, e.g., variance can be indicative of the level of confidence in the estimated parameters, the uncertainty associated with the outputs and the generation of the model outputs themselves remains unaddressed. The predictive distribution is defined as (e.g., Gelman et al. 1995)
As the posterior [Eq. (2)] is solved, the predictive distribution can also be recovered. Yet, in practice, it is indirectly sampled. Indeed, an intuitive MC-related approach for approximating the predictive distribution is that of sampling \(N_{s}\) values from the posterior to create \(N_{s}\) realizations of the neural network, each based on a different parameter sample, which are used to provide predictions. This results in a collection of predictions that approximate the actual predictive distribution. In this way, it is relatively simple to recover (approximations of) the predictive distribution from which, e.g., confidence intervals can be constructed. A way to reduce the sample forecast to single values conveying relevant information is by, e.g., using common (sampling) moment estimators (e.g., Casella and Berger 2021, Chap. 7.2.1). One may evaluate
to approximate the posterior mean through model averaging (across the different realizations \({{\varvec{\theta }}}_{j}, \,j=1,\dots ,N_{s}\) and thus different outputs) or compute
with
to approximate the covariance matrix, which is indicative of the uncertainty associated with the prediction. \(N_{s}\) corresponds to the number of samples generated from the posterior and used to generate the prediction of the network \({\text {NN}}_{{{\varvec{\theta }}}_{j}}(\cdot )\) receiving as input \({\varvec{x}}_{i}\). In classification, one may analogously approximate predictive densities for the joint probability of the different classes and average such probabilities to summarize the average probabilities of each class and implicitly the uncertainties associated with a certain class decision, which is typically determined by the predicted class of maximum probability (e.g., Osawa et al. 2019; Magris et al. 2022a):
with C being the total number of classes and \({\hat{p}}_{i,c}\) the predicted probability of class c for the sample i.
1.5 Variational Inference (VI)
Let \({\mathcal {D}}\) denote the data and \(p\left( {\mathcal {D}}\vert {{\varvec{\theta }}} \right)\) the likelihood of the data based on a postulated model with \({{\varvec{\theta }}}\in \Theta\) a k-dimensional vector of model parameters. Let \(p\left( {\varvec{\theta }} \right)\) be the prior distribution on \({{\varvec{\theta }}}\). The goal of Bayesian inference is the posterior distribution
where \(p\left( {\mathcal {D}} \right)\) is referred to as evidence or marginal likelihood, since \(p\left( {\mathcal {D}} \right) =\int _{\Theta} \left( {\mathcal {D}}\vert {{\varvec{\theta }}} \right) p\left( {\varvec{\theta }} \right) d{{\varvec{\theta }}}\). \(p\left( {{\varvec{\theta }}} \right)\) acts as a normalization constant for retrieving an actual probability distribution for \(p\left( {{\varvec{\theta }}}\vert {\mathcal {D}} \right)\). Bayesian inference is generally difficult due to the fact that the evidence is often intractable and of unknown form. In high-dimensional applications, Monte Carlo methods for sampling the posterior turn challenging and infeasible, and VI is an attractive alternative.
VI consists in an approximate method where the posterior distribution is approximated by the so-called variational distribution (e.g., Blei et al. 2017; Nakajima et al. 2019; Tran et al. 2021b). The variational distribution is a probability density \(q\left( {\varvec{\theta }} \right)\), belonging to some tractable class of distributions \({\mathcal {Q}}\) such as, e.g., the Exponential family. VI thus turns the Bayesian inference problem in Eq. (10) into that of finding the best approximation \(q^{\star} \left( {\varvec{\theta }} \right) \in {\mathcal {Q}}\) to \(p\left( {{\varvec{\theta }}}\vert {\mathcal {D}} \right)\) by minimizing the Kullback–Leibler (KL) divergence from \(q\left( {\varvec{\theta }} \right)\) to \(p\left( {{\varvec{\theta }}}\vert {\mathcal {D}} \right)\) (Kullback and Leibler 1951),
By simple manipulations of the KL divergence definition, it can be shown that
Since \(\log p\left( {\mathcal {D}} \right)\) is a constant not depending on the model parameters, the KL minimization problem is equivalent to the maximization problem of the so-called Lower Bound (LB) on \(\log p\left( {\mathcal {D}} \right)\) (e.g., Nakajima et al. 2019),
For any random vector \({{\varvec{\theta }}}\) and a function \(g\left( {\varvec{\theta }} \right)\) we denote by \({\mathbb {E}}_{f}[ g\left( {\varvec{\theta }} \right) ]\) the expectation of \(g\left( {\varvec{\theta }} \right)\) where \({{\varvec{\theta }}}\) follows a probability distribution with density f, i.e. \({\mathbb {E}}_{f}[ g\left( {\varvec{\theta }} \right) ] ={\mathbb {E}}_{{{\varvec{\theta }}}\sim f}[g\left( {\varvec{\theta }} \right) ]\). To make explicit the dependence of the LB on some vector of parameters \({{\varvec{\zeta }}}\) parametrizing the variational posterior we write \({\mathcal {L}}\left( {{\varvec{\zeta }}} \right) ={\mathcal {L}}\left( q_{{\varvec{\zeta }}} \right) = {\mathbb {E}}_{q_{{\varvec{\zeta }}}} \left[ \log p\left( {\varvec{\theta }} \right) - \log q_{{\varvec{\zeta }}}\left( {\varvec{\theta }} \right) + p\left( {\mathcal {D}}\vert {{\varvec{\theta }}} \right) \right]\). We operate within the Fixed-Form Variational Inference (FFVI) framework, where the parametric form of the variational posterior is set (e.g., Tran et al. 2021b). That is, FFVI seeks at finding the best \(q\equiv q_{{\varvec{\zeta }}}\) in the class \({\mathcal {Q}}\) of distributions indexed by a vector parameter \({{\varvec{\zeta }}}\) that minimizes the LB \({\mathcal {L}}\left( {{\varvec{\zeta }}} \right)\). In this context, \({{\varvec{\zeta }}}\) is called variational parameter. A common choice for \({\mathcal {Q}}\) is the Exponential family, and \({{\varvec{\zeta }}}\) is the corresponding natural parameter.
1.5.1 Estimation with Stochastic Gradient Descent (SGD)
A straightforward approach to maximize \({\mathcal {L}}\left( {{\varvec{\zeta }}} \right)\) is that of using a gradient-based method such as Stochastic Gradient Descent (SGD), Adaptive Moment Estimation (ADAM) (Kingma and Ba 2014), or Root Mean Squared Propagation (RMSProp) (Tieleman and Hinton 2012). The form of the basic SGD update is
where t denotes the iteration, \(\beta _{t}\) a (possibly adaptive) step size, and \({\hat{\nabla }}_{{\varvec{\zeta }}}{\mathcal {L}}\left( {{\varvec{\zeta }}} \right)\) a stochastic estimate of \(\nabla _{{\varvec{\zeta }}}{\mathcal {L}}\left( {{\varvec{\zeta }}} \right)\). The derivative, considered with respect to \({{\varvec{\zeta }}}\), is evaluated at \({{\varvec{\zeta }}}= {{\varvec{\zeta }}}_{t}\).
Under a pure Gaussian variational assumption, it is instinctive to optimize the LB for the mean vector \({{\varvec{\zeta }}}_{1} = {{\varvec{\mu }}}\) and variance-covariance matrix \({{\varvec{\zeta }}}_{2} = \Sigma\). In the wider FFVI setting with \({\mathcal {Q}}\) being the Exponential family, the LB is often optimized in terms of the natural parameter \({{\varvec{\uplambda }}}\) (Wainwright and Jordan 2008). The application of the SGD update based on the standard gradient is problematic because it ignores the information geometry of the distribution \(q_{{\varvec{\zeta }}}\) (Amari 1998), as it implicitly relies on the Euclidean distance to capture the dissimilarity between two distributions in terms of the Euclidean norm \(\vert \vert {{\varvec{\zeta }}}_{t} - {{\varvec{\zeta }}}\vert \vert ^{2}\), which can be a quite poor and misleading measure of dissimilarity (Khan and Nielsen 2018). By replacing the Euclidean norm with the KL divergence, the SGD update results in the following natural gradient update:
The natural gradient update results in better step directions toward the optimum when optimizing the distribution parameter. The natural gradient of \({\mathcal {L}}\left( {{\varvec{\uplambda }}} \right)\) is obtained by rescaling the gradient \(\nabla _{{\varvec{\uplambda }}}{\mathcal {L}}\left( {{\varvec{\uplambda }}} \right)\) by the inverse of the Fisher Information Matrix (FIM) \({\mathcal {I}}_{{\varvec{\uplambda }}}\),
where subscript in \({\mathcal {I}}^{-1}_{{\varvec{\uplambda }}}\) remarks that the FIM is expressed in terms of the natural parameter \({{\varvec{\uplambda }}}\). By replacing in the above \(\nabla _{{\varvec{\uplambda }}}{\mathcal {L}}\left( {{\varvec{\uplambda }}} \right)\) with a stochastic estimate \({\hat{\nabla }}_{{\varvec{\uplambda }}}{\mathcal {L}}\left( {{\varvec{\uplambda }}} \right)\) one obtains a stochastic natural gradient update.
Example 2
Consider a BNN to model the targets \({\varvec{y}}_{i}\), based on the covariates \({\varvec{x}}_{i}\). The likelihood, of a certain form, is parametrized over a neural network, whose weights are denoted by \({{\varvec{\theta }}}\). The prior could be a Gaussian distribution with, e.g., zero-mean, diagonal \(p\left( {\varvec{\theta }} \right) ={\mathcal {N}}\left( {{\varvec{\theta }}}\vert {\varvec{0}}, I/ \tau \right)\) or not \(p\left( {\varvec{\theta }} \right) ={\mathcal {N}}\left( {{\varvec{\theta }}}\vert {\varvec{0}}, \Sigma _{0} \right)\). \({\mathcal {Q}}\) is the set of multivariate Gaussian distributions, specified, e.g., in terms of the natural parameter \({{\varvec{\uplambda }}}\).
The objective is that of finding the corresponding variational parameter such that the LB \({\mathbb {E}}_{q_{{\varvec{\uplambda }}}} \left[ \log p\left( {\varvec{\theta }} \right) - \log q_{{\varvec{\uplambda }}}\left( {\varvec{\theta }} \right) + p\left( {\mathcal {D}}\vert {{\varvec{\theta }}} \right) \right]\) is maximized. The update of the variational parameter \({{\varvec{\uplambda }}}\) follows a gradient-based method with natural gradients. The training terminates after the LB \({\mathcal {L}}\left( {{\varvec{\uplambda }}} \right)\) does not improve for a certain number of iterations: the terminal \({{\varvec{\uplambda }}}\) provides the natural parameter of the variational posterior approximation minimizing the KL divergence to the true posterior \(p\left( {{\varvec{\theta }}}\vert {\mathcal {D}} \right)\).
2 Sampling methods
2.1 Monte Carlo Markov Chain (MCMC)
MCMC is a set of methods for sampling from a probability distribution. MCMCs have numerous applications, and especially in Bayesian statistics are a fundamental tool. The foundation of MCMC methods are Markov Chains, stochastic models describing a sequence of events in which the probability of each event depends only on the state of the previous one (Gagniuc 2017). By constructing a Markov Chain that has the desired distribution as its stationary distribution, towards which the sequence eventually converges, one can obtain samples from it, i.e., one can sample any generic probability distribution, including, e.g., a complex, perhaps multi-modal, Bayesian posterior. Early samples may be autocorrelated and not representative of the target distribution, so that MCMC methods generally require a burnout period before attaining the so-called stationary distribution. In fact, while the construction of a Markov Chain converging to the desired distribution is relatively simple, determining the number of steps to achieve such convergence with an acceptable error is much more challenging and strongly dependent on the initial setup and starting values. With burnout, the large collection of samples is practically subsampled by discarding an initial fraction of draws (e.g., 20%) to obtain a collection of approximately independent samples from the desired distribution. An accessible introduction to Markov Chains can be found in Gagniuc (2017), for a dedicated monograph on MCMC methods oriented toward Bayesian statistics and applications see, e.g., Gamerman and Lopes (2006).
Within the class of MCMC methods, some popular ones are not effective in large Bayesian problems such as BNNs. For example, the plain Gibbs sampler (Geman and Geman 1984), despite its simplicity and desirable properties (Casella and George 1992), suffers from residual autocorrelation between successive samples and becomes increasingly difficult as the dimensionality increases in multivariate distributions (e.g. Lynch 2007, Chap. 4). We review the most widespread MC approaches in the context of performing Bayesian learning for Neural Networks.
2.2 Metropolis–Hastings (MH)
The MH algorithm (Metropolis et al. 1953; Hastings 1970) is particularly helpful in Bayesian inference as it allows drawing samples from any probability distribution p, given that a function f proportional up to a constant to p can be computed. This is particularly convenient as it allows to sample a Bayesian posterior by only evaluating \(f\left( {{\varvec{\theta }}} \right) = p\left( {{\varvec{\theta }}}\vert y \right) p\left( {\varvec{\theta }} \right)\), completely excluding the normalization factor from the computations. The values of the Markov Chain are sampled iteratively, with each value depending solely on the preceding one: at each iteration, based on the current value, the algorithm picks a candidate value \({{\varvec{\theta }}}\) (proposed value), which is either accepted or rejected randomly with a probability that depends on the current and earlier values. Upon acceptance, the proposed value is used for the next iteration, otherwise is discarded, and the current value is used in the next iteration. As the algorithm proceeds and more sample values are generated, the sampled-value distribution more and more closely approximates the target distribution p.
A key ingredient in MH is the proposal density determining the drawing of the proposed value at each iteration. This is formalized by an arbitrary probability density \(g\left( {{\varvec{\theta }}}^{\star} \vert \cdot \right)\), upon which depends the probability of drawing \({{\varvec{\theta }}}^{\star}\) given the previous value \({{\varvec{\theta }}}\). g is usually assumed symmetric, and a common choice is provided by a Gaussian distribution centered on \({{\varvec{\theta }}}\). Algorithm 1 summarizes the above steps.

The acceptance ratio \(\alpha\) is representative of the likelihood of the proposed sample \({{\varvec{\theta }}}^{\star}\) over the current one \({{\varvec{\theta }}}_{t}\) according to p. Indeed, \(\alpha = f\left( {{\varvec{\theta }}}^{\star} \right) /f\left( {{\varvec{\theta }}}_{t} \right) = p\left( {{\varvec{\theta }}}^{\star} \right) /p\left( {{\varvec{\theta }}}_{t} \right)\) as f is proportional to p. A proposed sample value \({{\varvec{\theta }}}^{\star}\) that is more probable than \({{\varvec{\theta }}}_{t}\) (\(\alpha >1\)) is always accepted; otherwise, it may be rejected with probability \(\alpha\). The algorithm thus moves around the sample space, tending to stay in regions where p is of high density and, seldomly, in regions of low density. The final collection of samples follows the distribution p. As the Markov chain eventually converges to the target distribution p, initial samples may be quite incompatible with p, especially if the algorithm is initialized at a low-density region. Thus, it is customary to discard a number B of samples and retain only the subsample \(\left\{ {{\varvec{\theta }}}_{t}\right\} _{t=B}^{N}\). Note that by construction, successive samples of the Markov chain are correlated. Even though the chain eventually converges to p nearby samples are correlated, causing a reduction of the effective sample size (e.g., for \({\mathbb {E}}_{{{\varvec{\theta }}}\sim p_{{\varvec{\theta }}}}\left[ {{\varvec{\theta }}} \right]\) the central limit theorem applies but, e.g., the limiting variance is inflated by the non-zero autocorrelation in the chain).
An important feature of the MH algorithm is that it is applicable to high dimensions as it does not suffer from the course of dimensionality problem, causing an increasing rejection rate as the number of dimensions increases. This makes MH suitable for large Bayesian inference problems such as training BNNs.
2.3 Hamiltonian Monte Carlo (HMC)
HMC generates efficient transitions by using the derivatives of the density function being sampled by using approximate Hamiltonian dynamics, later corrected for performing an MH-like acceptance step (Neal 2011).
HMC augments the target probability density \(p\left( {\varvec{\theta }} \right)\) by introducing an auxiliary momentum variable \(\rho\) and generating draws from
Typically the auxiliary density is taken as a multivariate Gaussian distribution, independent of \({{\varvec{\theta }}}\):
\(\Sigma\) can be conveniently set to the identity matrix, restricted to a diagonal matrix, or estimated from warm-up draws. The Hamiltonian is defined upon the joint density \(p\left( \rho ,{{\varvec{\theta }}} \right)\):
The term \(T\left( \rho \vert {{\varvec{\theta }}} \right) = -\log p\left( \rho \vert {{\varvec{\theta }}} \right)\) is usually called kinetic energy and \(V\left( {\varvec{\theta }} \right) = - \log p\left( {\varvec{\theta }} \right)\) is called potential energy. To generate transitions to a new state, first, a value for the momentum is drawn independently from the current \({{\varvec{\theta }}}\); then, Hamilton’s equations are adopted to describe the evolution of the joint system \(\left( \rho ,{{\varvec{\theta }}} \right)\), i.e.:
By having the momentum density being independent of the target density, \(p\left( \rho \vert {{\varvec{\theta }}} \right) = p\left( \rho \right)\), \(\partial T/\partial {{\varvec{\theta }}}= {\varvec{0}}\), the transitions are governed by the derivatives
Note that \(- \partial V/\partial {{\varvec{\theta }}}\) is simply the gradient of the negative loglikelihood, which can be computed using automatic differentiation. The main difficulty is the simulation of the Hamiltonian dynamics, for which there is a variety of approaches (see, e.g. Leimkuhler and Reich 2005; Berry et al. 2015; Hoffman and Gelman 2014, ). Yet, to solve the above system of differential equations, a leapfrog integrator is generally used due to its simplicity and volume-preservation and reversibility properties (Neal 2011). The leapfrog integrator is a numerically stable integration algorithm specific to Hamiltonian systems. It discretizes time using a step size \(\varepsilon\) and alternates half-step momentum updates and full-step parameter updates:
By repeating the above steps L times, a total of \(L\varepsilon\) time is simulated, and the resulting state is \(\left( \rho ^{\star} , {{\varvec{\theta }}}^{\star} \right)\). Note that both L and \(\varepsilon\) are hyperparameters, and their tuning is often difficult in practice. In this regard, see the Generalized HMC approach of Horowitz (1991) and developments aimed at resolving the tuning of the leapfrog iterator (Fichtner et al. 2020; Hoffman and Sountsov 2022).
Instead of generating a random momentum vector right away and sampling a new state \(\left( \rho ^{\star} , {{\varvec{\theta }}}^{\star} \right)\), to account for numerical errors in the leapfrog integrator (an analysis in this regard is found in Leimkuhler and Reich 2005), a M–H step is used. The probability of accepting the proposal \(\left( \rho ^{\star} , {{\varvec{\theta }}}^{\star} \right)\) by transitioning from \(\left( \rho ,{{\varvec{\theta }}} \right)\) is
If the proposal \(\left( \rho ^{\star} , {{\varvec{\theta }}}^{\star} \right)\) is accepted, the leapfrog integrator is initialized with a new momentum draw and \({{\varvec{\theta }}}^{\star}\); otherwise, the same \(\left( \rho , {{\varvec{\theta }}} \right)\) parameters are returned to start the next iteration. The HMC procedure is summarized in Algorithm 2. Besides the difficulty of calibrating the hyperparameters L and \(\varepsilon\), HMC suffers from multimodality, yet the Hamiltonian boosts the local exploration for unimodal targets.

3 Monte Carlo Dropout (MCD)
MCD is an indirect method for Bayesian inference. Dropout has been earlier proposed as a regularization method for avoiding overfitting and improving neural networks’ predictive performance (Srivastava et al. 2014). This is achieved by applying a multiplicative Bernoulli noise on the neurons constituting the layers of the network. This corresponds to randomly switching off some neurons at each training step. The dropout rate sets the probability \(p_{i}\) of a neuron i being switched off. Though Bernoulli noise is the most common choice, note that other types of noise can be as well adopted (e.g. Shen et al. 2018). Neurons are randomly switched off only in the training phase, and the very same network configuration in terms of the activated and disabled neurons is used during backpropagation for computing gradients for weights’ calibration. On the other hand, all the neurons are left activated for predictions. Though it is intuitive that the above procedure implicitly connects to model averaging across different randomly pruned architectures obtained from a certain DL network, the exact connection between MC dropout and Bayesian inference follows a quite elaborated theory.
Gal and Ghahramani (2016) shows that a neural network of arbitrary depth and non-linearity with dropout applied before every single layer is mathematically equivalent to an approximation to the probabilistic deep Gaussian Process (GP) model (Damianou and Lawrence 2013), and (Jakkala 2021) for a recent survey. That is, the dropout objective minimizes the KL divergence between a certain approximate variational model and the deep GP. A treatment limited to multi-layer perceptron networks is provided in Gal and Ghahramani (2015).
With \({\hat{{\varvec{y}}}}\) being the output of a Neural Network with L layers whose loss function is E, for each layer \(i=1,\dots ,L\) let \(W_{i}\) denote the corresponding weight matrix of dimension \(K_{i} \times K_{i-1}\), and \({\varvec{b}}_{i}\) the bias vector of dimension \(K_{i}\). Be \({\varvec{y}}_{n}\) the target for the input \({\varvec{x}}_{n}\) for \(n=1,\dots ,N\) and denote the input and output sets respectively with \({\mathcal {D}}_{x}\) and \({\mathcal {D}}_{y}\). A typical optimization objective includes a regularization term weighted by some decay parameter \(\uplambda\), that is
Now consider a deep Gaussian process for modeling distributions over functions corresponding to different network architectures. Assume its covariance is of the form
where \(\sigma \left( \cdot \right)\) is an element-wise non-linearity, and \(p\left( {\varvec{w}} \right)\), \(p\left( b \right)\) distributions. Now let \(W_{i}\) be a random matrix of size \(K_{i} \times K_{i-1}\) for each layer i, be \({\varvec{\omega }} = \{ W_{i} \}_{i=1}^{L}\). The predictive distribution of the deep GP model can be expressed as
where \(p\left( {\varvec{\omega }}|\vert {\mathcal {D}}_{x},{\mathcal {D}}_{y} \right)\) is the posterior distribution. \(p\left( {\varvec{y}}_{n}\vert {\varvec{x}}_{n},{\varvec{\omega }} \right)\) is determined by the likelihood, while \({\hat{{\varvec{y}}}}_{n}\) is a function of \({\varvec{x}}_{n}\) and \({\varvec{\omega }}\):
\({\varvec{m}}_{i}\) are vectors of size \(K_{i}\) for each GP layer. For the intractable posterior \(p\left( {\varvec{\omega }} \vert {\mathcal {D}}_{x},{\mathcal {D}}_{y} \right)\), Gal and Ghahramani (2016) uses the variational approximation \(q\left( {\varvec{\omega }} \right)\) defined as
where the collection of probabilities \(p_{i}\) and matrices \(M_{i}\), \(i=1,\dots ,L\) constitute the variational parameter. Thus, q stands as a distribution over (non-random) matrices whose columns are randomly set to zero, and \(z_{i,j} =0\) implies that the unit j in layer \(i-1\) is dropped as an input to layer i. For minimizing the KL divergence form q to \(p\left( {\varvec{\omega }} \vert {\mathcal {D}}_{x},{\mathcal {D}}_{y} \right)\), the objective corresponds to
By use of Monte Carlo integration and some further approximations (see Gal and Ghahramani 2016, for details), the objective reads
which, up to the constant \(\frac{1}{\tau N}\), is a feasible and unbiased MC estimator of Eq. (37) where \(\hat{{\varvec{\omega }}}\) denotes a single MC draw from the posterior \(\hat{{\varvec{\omega }}}_{n} \sim q \left( {\varvec{\omega }} \right)\). By taking \(E\left( {\varvec{y}}_{n},{\hat{{\varvec{y}}}}_{n} \right) = -\log p\left( {\varvec{y}}_{n}\vert {\varvec{x}}_{n}, \hat{{\varvec{\omega }}}_{n} \right) /\tau\) Eqs. (38) and (29) are equivalent for an appropriate choice of the hyperparameters \(\tau\) and l. This shows that the minimization of the loss in Eq. (29) with dropout is equivalent to minimizing the KL divergence from q to \(p\left( {\varvec{\omega }} \vert {\mathcal {D}}_{x}, {\mathcal {D}}_{y} \right)\), thus performing VI on the deep Gaussian process.
With an SGD approach, one can maximize the above LB and estimate the variational parameters from which one can simply obtain samples from the predictive distribution \(q\left( {\varvec{y}}^{\star} \vert {\varvec{x}}^{\star} \right)\), and approximate its mean by the naive MC estimator:
\({\varvec{x}}^{\star}\) denotes a new observation, not in \({\mathcal {D}}_{x}\), for which the corresponding prediction is \({\hat{{\varvec{y}}}}^{\star}\). That is, the predictive mean is obtained by performing \(N_{s}\) forward passes through the network with Bernoulli realizations \(\{ {\varvec{z}}^{s}_{1},\dots ,{\varvec{z}}^{s}_{L} \}_{s=1}^{N_{s}}\) with \({\varvec{z}}^{s}_{i} = [{\varvec{z}}^{s}_{i,j}]_{j=1}^{K_{i}}\) for \(s=1,\dots ,N_{s}\), giving \(\{ W^{s}_{1},\dots ,W^{s}_{L} \}_{s=1}^{N_{s}}\). Such average predictions are generally referred to as MC dropout estimates. Similarly, by simple moment-matching, one can estimate the predictive variance and higher-order statistics synthesizing the properties of \(q\left( {\varvec{y}}^{\star} \vert {\varvec{x}}^{\star} \right)\).
The predictive distribution is, in general, a multi-modal distribution resulting from superposing bi-modal distributions on each weight matrix column. This constitutes a drawback of MCD, as well the implicit VI on a GP. Furthermore, the VI approximation in Eqs. (34)–(36) may be adequate or not. It is clear that even though MCD is a possibility for VI in deep-learning models, it is constrained by the very specific form in Eq. (34) of the variational posterior that implicitly corresponds to performing VI on a deep GP. Furthermore, there is evidence that MCD does not fully capture uncertainty associated with model predictions (Chan et al. 2020), and there are issues related to the use of improper priors and singularity of the approximate posterior. The latter ones are addressed and explored in Hron et al. (2018), suggesting the use of the so-called Quasi-KL divergence as a remedy. Clearly, high dropout rates drive the convergence rate slow, expand the network training time, and can cause important training data to be missed or given little relative importance. However, compared to the traditional approach for neural networks, applying dropout places no additional effort and is often of faster training than other VI methods. Furthermore, if a network has been trained with dropout, only by including an additional form of regularization acting as a prior turns the ANN into a BNN, without requiring re-estimation (Jospin et al. 2022).
4 Bayes-By-Backprop (BBB)
A common approach for estimating the variational posterior over the networks’ weights is the BBB method of Blundell et al. (2015), perhaps a breakthrough in probabilistic deep-learning as a practical solution for Bayesian inference.
The key argument in Blundell et al. (2015) is the use of the local reparametrization trick under which the derivative of an expectation can be expressed as the expectation of a derivative. It introduces a random variable \({\varvec{\varepsilon }}\) having a probability density given by \(q\left( {\varvec{\varepsilon }} \right)\) and a deterministic transform \(t\left( {{\varvec{\theta }}},{\varvec{\varepsilon }} \right)\) such that \({\varvec{w}} = t\left( {{\varvec{\theta }}},{\varvec{\varepsilon }} \right)\). The main idea is that the random variable \({\varvec{\varepsilon }}\) is a source of noise that does not depend on the variational distribution, and the weights \({\varvec{w}}\) are sampled indirectly as a deterministic transformation of \({\varvec{\varepsilon }}\), leading to a training algorithm that is analogous to that used in training regular networks. Indeed, by writing \({\varvec{w}}\) as \({\varvec{w}} = t\left( {{\varvec{\theta }}},{\varvec{\varepsilon }} \right)\), in place of evaluating
which can be complex and rather tedious, under the assumption \(q\left( {\varvec{\varepsilon }} \right) d{\varvec{\varepsilon }} = q\left( {\varvec{w}}\vert {{\varvec{\theta }}} \right) {\text {d}}{\varvec{w}}\), Blundell et al. (2015) prove that
With \(f\left( {\varvec{w}},{{\varvec{\theta }}} \right) = \log q\left( {\varvec{w}}\vert {{\varvec{\theta }}} \right) - \log p\left( {\varvec{w}} \right) p\left( y\vert {\varvec{w}} \right)\), the right side of Eqs. (41) and (42) provide an alternative approach for the estimation of the gradients of the cost function with respect to the model parameters.
In fact, upon sampling \({\varvec{\varepsilon }}\) and obtaining \({\varvec{w}}\), \(\log q\left( {\varvec{w}}\vert {{\varvec{\theta }}} \right) - \log p\left( {\varvec{w}} \right) p\left( y\vert {\varvec{w}} \right)\) is a stochastic approximation of the VI objective \({\text {KL}}\left[ q\left( {\varvec{w}}\vert {{\varvec{\theta }}} \right) \vert \vert p\left( {\varvec{w}}\vert {\mathcal {D}} \right) \right] = {\mathbb {E}}_{q\left( {\varvec{w}}\vert {{\varvec{\theta }}} \right) } \left[ \log q\left( {\varvec{w}}\vert {{\varvec{\theta }}} \right) - \log p\left( {\varvec{w}} \right) p\left( {\mathcal {D}}\vert {\varvec{w}} \right) \right]\) to be minimized.
The sampled value \({\varvec{\varepsilon }} \sim q\left( {\varvec{\varepsilon }} \right)\), resampled at each iteration, is independent of the variational parameters, while \({\varvec{w}}\) is not directly sampled but here it is a deterministic function of \({\varvec{\varepsilon }}\). Given \({\varvec{\varepsilon }}\), all the quantities in the square bracket of Eq. (42) are non-stochastic, enabling the use of backpropagation. A single draw for \({\varvec{\varepsilon }}\) approximates the right side of Eq. (41), and suffices for providing an unbiased stochastic gradient estimation of the relevant gradient on the left side. Equation (41) makes explicit the possibility of using automatic differentiation to compute the gradient of f with respect to the parameter \({{\varvec{\theta }}}\). By using a single sampled draw \({{\varvec{\theta }}}\) for approximating the expectation on the right side of Eq. (41), the only parameter in the loss is \({{\varvec{\theta }}}\), and the use of backpropagation for evaluating the gradients is straightforward. Equation (42) instead employs backpropagation in the “usual” sense, involving gradients of the cost with respect to the network parameters \({\varvec{w}}\), further rescaled by \(\partial {\varvec{w}}/\partial {{\varvec{\theta }}}\) and shifted by \(\partial f\left( {\varvec{w}},{{\varvec{\theta }}} \right) /\partial {{\varvec{\theta }}}\). Equation (42) concerns the usual backpropagation computations in terms of the network’s weights, the specific form of the partial derivative with respect to \({{\varvec{\theta }}}\) that the choice of t implies, while the last term depends on the chosen form of the variational posterior only [\({\varvec{w}}\) is here not seen as a function of \({{\varvec{\theta }}}\), as the form of Eq. (42) results from applying the multi-variable chain rule]. This results in a general framework for learning the posterior distribution over the network’s weights. The following Algorithm 3 summarizes the BBB approach.

Algorithm 3 is initialized by preliminary setting the initial values of the variational parameter \({{\varvec{\theta }}}\) and, of course, by specifying the form of the prior and the posterior along with the form of the likelihood involving the outputs of the forward pass obtained from the specified underlying network structure. The update is very similar to the one employed in standard non-Bayesian settings, where standard optimizers such as ADAM are applicable. It is the applicability of standard optimization algorithms and the use of classic backpropagation that constitute the major breakthrough element in BBB, making it a feasible approach for Bayesian learning.
To make the description more explicit and aligned with the following sections, we present the case where the variational posterior is a diagonal Gaussian with mean \({{\varvec{\mu }}}\) and covariance matrix \(\sigma ^{2} I\). In this case, the transform t takes the simple and convenient form
As \(\sigma\) is required to be always non-negative, Blundell et al. (2015) adopts the reparametrization \(\sigma = \log \left( 1+\exp \left( \rho \right) \right)\) and the variational posterior parameter \({{\varvec{\theta }}}= \left( {{\varvec{\mu }}},\rho \right)\). In this case, Algorithm 4 summarizes the BBB approach.

As for Algorithm 4, one may backpropagate the gradients of f w.r.t. \({{\varvec{\mu }}}\) and \(\rho\) directly. Alternatively, as for Algorithm 3, one may use backpropagation for computing the gradients \(\partial f\left( {\varvec{w}},{{\varvec{\theta }}} \right) /\partial {\varvec{w}}\), which are furthermore shared across the updates for \({{\varvec{\mu }}}\) and \(\rho\), or, if preferred, adopt a general automatic differentiation setup, if, e.g., the form of the variational likelihood does not allow for a simple analytic form of the gradient.
5 Exponential family and natural gradients
Assume \(q_{{\varvec{\uplambda }}}\left( {\varvec{\theta }} \right)\) belongs to an exponential family distribution. Its probability density function is parametrized as
where \({{\varvec{\uplambda }}}\in \Omega\) is the natural parameter, \(\phi \left( {\varvec{\theta }} \right)\) the sufficient statistic. \(A\left( {{\varvec{\uplambda }}} \right) = \log \int h\left( {\varvec{\theta }} \right) \exp (\phi \left( {\varvec{\theta }} \right) ^{\top} {{\varvec{\uplambda }}}) d\nu\) is the log-partition function, determined upon the measure \(\nu\), \(\phi\) and the function h. The natural parameter space is defined as \(\Omega = \{ {{\varvec{\uplambda }}}\in {\mathbb {R}}^{d}: A\left( {{\varvec{\uplambda }}} \right) < +\infty \}\). When \(\Omega\) is a non-empty open set, the exponential family is referred to as regular. Furthermore, if there are no linear constraints among the components of \({{\varvec{\uplambda }}}\) and \(\phi \left( {\varvec{\theta }} \right)\), the exponential family in Eq. (44) is said of minimal representation. Non-minimal families can always be reduced to minimal families through a suitable transformation and reparametrization, leading to a unique parameter vector \({{\varvec{\uplambda }}}\) associated with each distribution (Wainwright and Jordan 2008). The mean (or expectation) parameter \({\varvec{m}} \in {\mathcal {M}}\) is defined as a function of \({{\varvec{\uplambda }}}\), \({\varvec{m}}\left( {{\varvec{\uplambda }}} \right) = {\mathbb {E}}_{q_{{\varvec{\uplambda }}}}\left[ \phi \left( {\varvec{\theta }} \right) \right] = \nabla _{{\varvec{\uplambda }}}A\left( {{\varvec{\uplambda }}} \right)\). Moreover, for the Fisher Information Matrix \({\mathcal {I}}_{{\varvec{\uplambda }}}= -{\mathbb {E}}_{q_{{\varvec{\uplambda }}}}\left[ \nabla _{{\varvec{\uplambda }}}^{2} \log q_{{\varvec{\uplambda }}}\left( {\varvec{\theta }} \right) \right]\) it holds that \({\mathcal {I}}_{{\varvec{\uplambda }}}=\nabla ^{2}_{{\varvec{\uplambda }}}A\left( {{\varvec{\uplambda }}} \right) = \nabla _{{\varvec{\uplambda }}}{\varvec{m}} .\) Under minimal representation, \(A\left( {{\varvec{\uplambda }}} \right)\) is convex, thus the mapping \(\nabla _{{\varvec{\uplambda }}}A = {\varvec{m}}:\Omega \rightarrow {\mathcal {M}}\) is one-to-one, and \({\mathcal {I}}_{{\varvec{\uplambda }}}\) is positive definite and invertible (Nielsen and Garcia 2009). \({\mathcal {M}}\) denotes the set of realizable mean parameters. Therefore, under minimal representation we can express \({{\varvec{\uplambda }}}\) in terms of \({\varvec{m}}\) and thus \({\mathcal {L}}\left( {{\varvec{\uplambda }}} \right)\) in terms of \({\mathcal {L}}\left( {\varvec{m}} \right)\) and vice versa (Khan and Nielsen 2018).
Example 3
(The Gaussian distribution as an exponential-family member) The multivariate Gaussian distribution \({\mathcal {N}}\left( {{\varvec{\mu }}},\Sigma \right)\) with k-dimensional mean vector \({{\varvec{\mu }}}\) and covariance matrix \(\Sigma\) can be seen as a member of the exponential family [Eq. (44)]. Its density reads
where
and \(A\left( {{\varvec{\uplambda }}} \right) = -\frac{1}{4}{{\varvec{\uplambda }}}_{1}^{\top} {{\varvec{\uplambda }}}_{2}^{-1} {{\varvec{\uplambda }}}_{1}-\frac{1}{2} \log \left( -2{{\varvec{\uplambda }}}_{2} \right)\). On the other hand, \({{\varvec{\zeta }}}= \left[ {{\varvec{\zeta }}}_{1}^{\top} , {{\varvec{\zeta }}}_{2}^{\top} \right] ^{\top}\) with \({{\varvec{\zeta }}}_{1} = {{\varvec{\mu }}}= {\varvec{m}}_{1}\) and \({{\varvec{\zeta }}}_{2} = \Sigma = {\varvec{m}}_{2} - {{\varvec{\mu }}}{{\varvec{\mu }}}^{\top}\), constitutes the common parametrization of the multivariate Gaussian distribution in terms of its mean and variance–covariance matrix.
By applying the chain rule, \(\nabla _{{\varvec{\uplambda }}}{\mathcal {L}}= \nabla _{{\varvec{\uplambda }}}{\varvec{m}} \nabla _{{\varvec{m}}} {\mathcal {L}}= \nabla _{{\varvec{\uplambda }}}\left( \nabla _{{\varvec{\uplambda }}}A \right) {\mathcal {L}}= \nabla ^{2}_{{\varvec{\uplambda }}}A\left( {{\varvec{\uplambda }}} \right) {\mathcal {L}}= {\mathcal {I}}_{{\varvec{\uplambda }}}\nabla _{{\varvec{m}}} {\mathcal {L}}\), from which
The quantity \({\tilde{\nabla }}_{{\varvec{\uplambda }}}{\mathcal {L}}\) is referred to as the natural gradient of \({\mathcal {L}}\) with respect to \(\uplambda\) and it is obtained by pre-multiplying the Euclidean gradient by the inverse of the FIM (parametrized in terms of \({{\varvec{\uplambda }}}\)). In general, \({\mathcal {L}}\) can be a generic function whose derivative with respect to a parameter \({{\varvec{\uplambda }}}\) (not necessarily the natural parameter) exists. The standard reference for natural gradients computation is the seminal work of Amari (1998). Within a SGD context, the application of simple Euclidean gradients is problematic as it ignores the information geometry of the distribution \(q_{{\varvec{\uplambda }}}\). Euclidean gradients implicitly rely on the Euclidean norm to capture the dissimilarity between two distributions which can be a quite poor dissimilarity measure (Khan and Nielsen 2018). In fact, the SGD update can be obtained by writing
and setting to zero its derivative. Although the above implies that \({{\varvec{\uplambda }}}\) moves in the direction of the gradient, it remains close to the previous \({{\varvec{\uplambda }}}_{t}\) in terms of Euclidean distance. As \({{\varvec{\uplambda }}}\) is a parameter of a distribution, the adoption of the Euclidean measure is misleading. An Exponential family distribution induces a Riemannian manifold with a metric defined by the FIM (Khan and Nielsen 2018). By replacing the Euclidean metric with the Riemannian one,
the resulting update is indeed expressed in terms of the natural parameter:
generally referred to as natural gradient update. More in general, one could replace the Euclidean distance with a proximity function such as the Bregman divergence and obtain richer classes of SGD-like updates, like mirror descent (which can be interpreted as natural gradient descent), see, e.g., Nielsen (2020). A very interesting point on the limitations of plain gradient search is made in Wierstra et al. (2014) concerning the impossibility of locating, even in a one-dimensional case, a quadratic optimum. The example provided therein involves the Gaussian distribution, pivotal in VI. For an one-dimensional Gaussian distribution with mean \(\mu\) and standard deviation \(\sigma\), the gradient of \({\mathcal {L}}\) with respect to the parameters \(\mu\) and \(\sigma\) lead to the following SGD updates:
For the updates to converge and the optimum to be precisely located, \(\sigma\) must decrease (i.e., the distribution shrinks around \(\mu\)). The fact that \(\sigma\) appears in the denominator of both the updates is problematic: as it decreases, the variance of the updates increases as \(\Delta _{\mu} \propto \frac{1}{\sigma }\) and \(\Delta _{\sigma} \propto \frac{1}{\sigma }\). The updates become increasingly unstable, and a large overshooting update makes the search start all over again rather than converging. Increased population size and small learning rates cannot avoid the problem. The choice of the starting value is problematic, too: starting with \(\sigma \gg 1\) makes the updates minuscule; conversely, \(\sigma \ll 1\) makes them huge and unstable. Wierstra et al. (2014) discusses how the use of natural gradients fixes this issue that, e.g., may arise with BBVI.
Algorithm 5 summarizes the generic scheme upon the implementation of a natural gradient update. In Algorithm 5, \({{\varvec{\zeta }}}\) denotes a generic variational parameter, e.g., the natural parameter or not, while methods for evaluating \(\nabla _{\theta} {\mathcal {L}}\), \({\mathcal {I}}\), and efficiently computing its inverse \({\mathcal {I}}^{-1}\) are discussed in the following sections.

6 Black-Box methods
A major issue in VI is that it heavily relies upon model-specific computations, on which a generalized, ready-to-use, and plug-and-play optimizer is difficult to design. Black-Box methods aim at providing solutions that can be immediately applied to a wide class of models with little effort. In the first instance, the ubiquitous use of model’s gradients that traditional ML and VI approaches rely upon struggles with this principle. As Ranganath et al. (2014) describes, for a specific class of models, where conditional distributions have a convenient form and a suitable variational family exists, VI optimization can be carried out using closed-form coordinate ascent methods (Ghahramani and Beal 2000). In general, there is no close-form solution resulting in model-specific algorithms (Jaakkola and Jordan 1997; Blei and Lafferty 2007; Braun and McAuliffe 2010) or generic algorithms that involve model-specific computations (Knowles and Minka 2011; Paisley et al. 2012). As a consequence model assumptions and model-specific functional forms play a central role, making VI practical. The general idea of Black-Box VI is that of rewriting the gradient of the LB objective as the expectation of an easy-to-compute function of the latent and observed variables. The expectation is taken with respect to the variational distribution, and the gradient is estimated by using stochastic samples from it in a MC fashion. Such stochastic gradients are used to update the variational parameters following an SGD optimization approach. Within this framework, the end-user is required to develop functions only for evaluating the model log-likelihood, while the remaining calculations are easily implemented in libraries of general use applicable to several classes of models. Black-Box VI falls within stochastic optimization where the optimization objective is the maximization of the LB using noisy, unbiased, estimates of its gradient. As such, variance reduction methods have a major impact on stability and convergence, among them control variates are the most effective and of immediate implementation.
6.1 Black-Box Variational Inference (BBVI)
BBVI optimizes the LB with stochastic optimization, through an unbiased estimator of its gradients obtained from samples from the variational posterior (Ranganath et al. 2014). By using the LB definition and the log-derivative trick on the gradient of the LB with respect to the variational parameter, \(\nabla _{{\varvec{\zeta }}}{\mathcal {L}}\) can be expressed as
where \({{\varvec{\zeta }}}\) denotes the parameter of the variational distribution \(q_{{\varvec{\zeta }}}\). The above expression rewrites the gradient as an expectation of a quantity that does not involve the model’s gradients but only those of \(\log q\left( w \vert {{\varvec{\zeta }}} \right)\). A naive noisy unbiased estimate of the gradient of the LB is immediate to obtain with \(N_{s}\) samples obtained from the variational distribution,
where \({{\varvec{\theta }}}_{s} \sim q\left( {{\varvec{\theta }}}\vert {{\varvec{\zeta }}} \right)\). The above MC estimator enables the immediate and feasible computation of the LB gradients as, given a sample \({{\varvec{\theta }}}_{s}\), \(\log q\left( {{\varvec{\theta }}}_{s}\vert {{\varvec{\theta }}} \right)\) is a quantity that solely depends on the form of the variational posterior and can be of simple form. On the other hand, \(\log p\left( {\mathcal {D}},{{\varvec{\theta }}} \right) - \log q\left( {{\varvec{\theta }}}\vert {{\varvec{\theta }}} \right)\) is immediate to compute as it only requires evaluating the logarithm of the joint \(p\left( {\mathcal {D}},{{\varvec{\theta }}}_{s} \right)\) and the density of the variational distribution in \({{\varvec{\theta }}}_{s}\). This process is summarized in Algorithm 6. If sensible, one may assume that \(\log p\left( {\mathcal {D}},{{\varvec{\theta }}} \right) = \log p\left( {\mathcal {D}}\vert {{\varvec{\theta }}} \right) p\left( {{\varvec{\theta }}} \right)\) but this is not explicitly required as of Ranganath et al. (2014): there are no assumptions on the form of the model; the approach only requires the gradient of the variational likelihood with respect to the variational parameters to be feasible to compute.

In Ranganath et al. (2014), the authors employ an adaptive learning rate satisfying the Robbins Monroe conditions \(\sum _{t} \beta _{t} = \infty\) and \(\sum _{t} \beta ^{2}_{t} < \infty\), and for controlling the variance of the stochastic gradient estimator adopt Rao–Blackwellization (Rao 1945; Blackwell 1947; Robert and Roberts 2021) and use the of control variates (e.g. Lemieux 2014; Robert et al. 1999, Chap. 3) within Algorithm 6.
6.2 Natural-Gradient Black-Box Variational Inference (NG-BBVI)
We shall review the approach of Trusheim et al. (2018) boosting BBVI with natural gradients, referred to as Natural-Gradient Black-Box Variational Inference (NG-BBVI) . The FIM corresponds to the outer product of the score function with itself (see Sect. 5) and is furthermore equal to the second derivative of the KL divergence to the approximate posterior \(q\left( x\vert {{\varvec{\zeta }}} \right)\):
For the practical implementation, Trusheim et al. (2018) uses a mean-field restriction on the variational model, i.e. the joint is factorized into the product of K independent terms, where each term is in general a multivariate distribution:
The above restriction is also suggested by Ranganath et al. (2014) in order to allow for Rao–Blackwellization (Robert and Roberts 2021) as a tool to be used in conjunction with control variates (e.g. Lemieux 2014, Chap. 3) for reducing the variance of the stochastic gradient estimator. Under the above assumption, the FIM simplifies to:
which significantly simplifies the general form \(q_{{\varvec{\zeta }}}\left( {\varvec{\theta }} \right)\) while implicitly enabling Rao–Blackwellization with the variable-wise local expectations and thus reducing the variance of the FIM, estimated via a Monte Carlo approach. In fact, besides a few variational models it is difficult to compute the above expectations analytically so Trusheim et al. (2018) adopts the following naive MC estimator:
with \({{\varvec{\theta }}}_{i}^{\left( s \right) } \sim q_{{{\varvec{\zeta }}}_{i}} \left( {{\varvec{\theta }}}_{i} \right)\) denoting a sample from the ith factor of the posterior mean-field approximation. Note that the above does not introduce additional computations as the score of the samples \({{\varvec{\theta }}}_{i}^{\left( s \right) }\) is anyway required in the computation of the LB gradient. Furthermore, instead of using a plain SGD-like update, Trusheim et al. (2018) adopts an ADAM-like version, boosted with natural gradient computations. Algorithm 7 summarizes the NG-BBVI approach.

The NG-BBVI implementation is slightly more complex than the original BBVI, see Algorithm 7. The MC computation involves both the black-box stochastic gradient estimation and the estimation of the optimal control variate coefficient \(a^{\star}\). Thus the posterior samples are split into two subsets. The first one X aimed at estimating \(a^{\star}\), and the second one Y at implementing the MC estimators, independently from X, and with the control variate correction term \(a^{\star}\) earlier computed. The computation of the FIM follows immediately from Eq. (55), and the computation of \(\nabla _{{{\varvec{\zeta }}}_{k}} {\mathcal {L}}\) is analogous to BBVI. The last four lines of Algorithm 7 correspond to the implementation of the ADAM update, operators are intended to be applied element-wise, \(\beta _{1}\), \(\beta _{2}\) (exponential decay rates) are typical ADAM hyperparameters, \(\varepsilon >0\) is a small offset preventing divisions by zero.
Trusheim et al. (2018) differs from BBVI by the use of natural gradients (and the adoption of the ADAM-like update, though applicable to BBVI as well). On the other hand, the use of control variates and Rao–Blackwellization for variance reduction is found in both BBVI and NG-BBVI. As the natural gradient approach is preferable for the reasons discussed in Sect. 5, NG-BBVI is favored over BBVI.
The use of the black-box framework for computing the gradients of the LB along the MC estimator for the FIM renders NG-BBVI of general applicability and not constrained to a certain form of the variational posterior. Yet the MC-computations of the FIM are implicitly approximate, whereas for certain distributions the FIM computation can be carried out analytically and in an exact form. NG-BBVI furthermore requires the inversion of the FIM, which is a computational bottleneck. The following VON (Khan and Nielsen 2018), VADAM (Khan et al. 2018a) and VOGN (Khan et al. 2018a; Osawa et al. 2019) methods indeed fix this issue: assuming a variational posterior within the exponential distribution family, natural gradients are enabled without the direct computation of the FIM and its inverse.
7 Natural gradient methods for Exponential-family variational distributions
In the following subsections, we review methods based on Natural gradients and Exponential-family variational approximations. The following techniques are built on natural parameter updates in the natural parameter space and rely on simplified but exact FIM computations based on the natural/expectation parameter duality [Eq. (47)].
7.1 Exact gradient computations for the exponential family
The computation of the FIM required in the natural gradient computation is, in general, not trivial. In a generic perspective, not bound to a specific variational form, the sampling approach for the FIM estimation of Trusheim et al. (2018) is feasible. Yet for certain distributions, namely for those in the Exponential family class, natural gradients can be computed in an exact form with an analytical solution which furthermore does not involve the computation of the FIM.
The theoretic foundation of such a viable approach is provided in Khan and Nielsen (2018) and traces back to Eq. (47). For an Exponential family of minimal representation, the natural gradient with respect to the natural parameter \({{\varvec{\uplambda }}}\) is equal to the gradient with respect to the expectation parameter \({\varvec{m}}\). This is a powerful result that allows the computation of the natural gradient as an Euclidean gradient, avoiding the computation of the FIM and its inversion.
This section presents some baseline methods using the above duality for the natural gradient computation. Differently from BBB, BBVI, and NG-BBVI the following approaches explicitly deal with variational distributions members of the Exponential family with a focus on updating their natural parameter:
From the above updates on natural parameters, update rules for alternative and perhaps a more usual parametrization can often be obtained, see e.g. Sect. 7.2.
7.2 Natural-Gradient Variational Inference (NGVI)
NGVI constitutes a baseline methodology for natural gradient computation under a Gaussian variational distribution, upon which several other approaches have been developed.
The natural gradients in the natural parameter space can be computed under the expectation parametrization as Euclidean gradients. Khan and Nielsen (2018) shows that such gradients are of simple form and correspond to
By using the definition of natural gradients in terms of \({{\varvec{\mu }}}\) and \(\Sigma\), the update in Eq. (60) for the natural parameter \({{\varvec{\uplambda }}}_{1} = {{\varvec{\mu }}}\), \({{\varvec{\uplambda }}}_{2} = -\frac{1}{2}\Sigma ^{-1}\) rewrites as
The above two constitute the NGVI update rules for updating the mean \({{\varvec{\mu }}}\) and covariance matrix \(\Sigma\) of the variational posterior with a natural gradient update, that however does not involve the computation of the FIM as it relies on Euclidean gradients.
For a diagonal covariance matrix \(\Sigma = {\text {diag}}\left( {\sigma ^{2}} \right)\), the corresponding NGVI updates read
With respect to the NGVI update two points are important to stress out. First, at each iteration, the update for \({{\varvec{\mu }}}\) implicitly requires \(\Sigma _{t+1}\). This means that the update for \({{\varvec{\mu }}}\) follows that for \(\Sigma ^{-1}\) and that \({{\varvec{\mu }}}\) readily uses the one-step ahead updated information on \(\Sigma\). Though it may appear counter-intuitive, Lyu and Tsang (2021) and Magris et al. (2022b) show that this update is not optimal (in the terms therein discussed), while an update of the form \({{\varvec{\mu }}}_{t+1} = {{\varvec{\mu }}}_{t} + \beta \Sigma _{t}\left[ \nabla _{{\varvec{\mu }}}{\mathcal {L}} \right]\) would be. Also, note that the update for \({{\varvec{\mu }}}\) involves \(\Sigma _{t+1}\) and not \(\Sigma ^{-1}_{t+1}\), meaning that in the NGVI an online inversion of \(\Sigma ^{-1}\) is implicitly required at each iteration. Clearly, for the diagonal case, this is trivial and effortless to obtain. Second, in the full-covariance case, there is no guarantee that the updates guarantee \(\Sigma\) to be a positive-definite covariance matrix. This issue is tackled in Sect. 8. For the diagonal case, the constraint on \(\Sigma\) results in guaranteeing the positivity of the entries in the diagonal. This can be achieved via a proper reparametrization, e.g. BBVI updates \(\rho\) where \(\sigma = \log \left( 1+\exp \left( \rho \right) \right)\), or (e.g. Tan 2021) updates the Cholesky factor. Alternatively, the learning rate can be adapted to guarantee that the step size does not drive the updates \(\sigma ^{-2}\) negative (e.g., Khan and Nielsen 2018; Magris et al. 2022c).
7.3 Variational Online Newton (VON)
A computational burden in NGVI is that the gradients of the LB are still required: VON develops on NGVI but does not require the gradients of the variational objective. Furthermore, it only involves the gradient and Hessian of the model log-likelihood which can be computed with usual backpropagation.
Khan et al. (2018b) express the lower bound as
where N is the sample size, and \(f\left( {\varvec{\theta }} \right) = -\frac{1}{N} \sum _{i=1}^{N}\log p\left( {\mathcal {D}}_{i} \vert {{\varvec{\theta }}} \right)\) is negative log-likelihood of the model, i.e. standard MLE objective, where \({\mathcal {D}}_{i}\) denotes a data example, i.e. \({\mathcal {D}}_{i} = \left( {\varvec{y}}_{i},{\varvec{x}}_{i} \right)\). VON uses the theoretical results of Opper and Archambeau (2009) and Rezende et al. (2014) to express the gradients of the LB objective in terms of gradient and Hessian of \(f\left( {\varvec{\theta }} \right)\). By linearity of the expectation, the gradients of the \({\mathcal {L}}\) consist of the sum of the gradients of three expectation terms, in particular:
where \({\varvec{g}} = \nabla _{{\varvec{\theta }}}f\left( {\varvec{\theta }} \right)\) and \(H\left( {\varvec{\theta }} \right) = \nabla ^{2}_{{{\varvec{\theta }}}{{\varvec{\theta }}}} f \left( {\varvec{\theta }} \right)\) denote the gradient and Hessian of the MLE objective, respectively. With these relations the gradients of the LB objective write
and
By using these gradients in the NGVI update, one obtains
where the expectations can be again evaluated via MC sampling. By using a single draw \({{\varvec{\theta }}}_{t} \sim {\mathcal {N}}\left( {{\varvec{\theta }}}\vert {{\varvec{\mu }}}_{t}, \Sigma _{t} \right)\), the feasible update reads
To obtain a form for the update that resembles Newton’s method where the scaling matrix is estimated online, Khan et al. (2018b) defines \(S_{t} = \left( \Sigma ^{-1}_{t} -{{\varvec{\uplambda }}}I \right) /N\) and conversely \(\Sigma _{t} = \left( N\left( S_{t} +{{\varvec{\uplambda }}}I/N \right) \right) ^{-1}\), and write the final form of the VON update
Similarly, for a diagonal covariance matrix (thus under a mean-field assumption), with \(\sigma ^{2}_{t} = \left[ N\left( {\varvec{s}}_{t} +\frac{{{\varvec{\uplambda }}}}{N} \right) \right] ^{-1} = \left[ N\left( {\varvec{s}}_{t} + {\tilde{{{\varvec{\uplambda }}}}} \right) \right] ^{-1}\) and \({{\varvec{\theta }}}_{t} \sim {\mathcal {N}}\left( {{\varvec{\theta }}}\vert {{\varvec{\mu }}}_{t},{\text {diag}}\left( {\sigma ^{2}_{t}} \right) \right)\)
where the division is intended to be element-wise. Algorithm 8 summarizes the main elements of VON implementation.

In a mini-batch setting for estimating the stochastic gradient, with \({\mathcal {M}}\) denoting a mini-batch containing M samples, the stochastic estimates
enable the practical implementation of the VON update by replacing \({\varvec{g}}\) and H. To make this statement clear, think of \(f\left( {\varvec{\theta }} \right)\) as the typical negative log-likelihood of a sample (as it is an average across samples), then \({\varvec{g}}\) is the typical gradient for a sample in \({{\varvec{\theta }}}\) and, analogously, H is interpreted as the typical (average) value of the Hessian evaluated in \({{\varvec{\theta }}}\), resulting when using a single data point. Stochastic gradient estimation estimates \({\varvec{g}}\) by using a single observation \({\mathcal {D}}_{i}\) picked at random as an unbiased estimate of the actual gradient of \(f\left( {\varvec{\theta }} \right) = -\frac{1}{N} \sum _{i=1}^{N}\log p\left( {\mathcal {D}}_{i}\vert {{\varvec{\theta }}} \right)\), \({\varvec{g}} = \frac{1}{N} \sum _{i=1}^{n} \nabla _{{\varvec{\theta }}}\left[ -\log p\left( {\mathcal {D}}_{i}\vert {{\varvec{\theta }}} \right) \right]\), which would require the parsing of the entire sample. Analogously, one constructs a stochastic estimate of the Hessian with one or M observations (the higher M the lower the variance of the estimator, which is in any case unbiased).
7.4 Variational ADAM (VADAM)
The principle of Variational ADAM (VADAM) is that of augmenting the natural gradient update by incorporating a momentum factor, i.e.,
which slightly extends the form of the update in Eq. (59).
Under a Gaussian variational q, Khan et al. (2018b) expresses the momentum update as a VON update with momentum and recovers a variational version of an RMSProp update, to obtain the following updates
where \({\bar{\beta }}_{t} = \beta \frac{1-\gamma _{1}}{1-\gamma _{1}^{t}}\), \({\bar{\gamma }}_{t} = \gamma _{1} \left( 1-\gamma _{1}^{t-1} \right) \left( 1-\gamma _{1}^{t} \right)\) and \(\beta\),\(\gamma _{1}\) are learning rates. Note that in the above updates the Hessian is estimated as a squared gradient: details are provided in Sect. 7.5. These updates can be implemented and used in their actual form, yet they correspond to an ADAM-like update. Indeed the above update has the same form of an adaptive version of Polyak’s heavy ball method. Wilson et al. (2017) establishes a relation between the form of Eq. (87) and the ADAM update, and in particular that the ADAM update can be written as an adaptive version of the Polyak’s heavy ball method. Upon introducing the typical bias correction terms of ADAM, Khan et al. (2018b) expresses Eq. (87) as an ADAM update. With respect to a true ADAM update, the model weights are stochastically sampled from the posterior, resulting in a Variational version of ADAM (VADAM). For the full derivation, which is quite elaborate and extensive, refer to Khan and Nielsen (2018). Algorithm 9 summarizes the VADAM approach for a Gaussian variational posterior with diagonal covariance.

7.5 Variational Online Gauss–Newton (VOGN)
In the diagonal VON update, the Hessian drives the update for the scaling vector \({\varvec{s}}\) which determines the covariance matrix \({\text {diag}}\left( {\sigma ^{2}} \right)\). The Hessian can be negative, a situation that could turn \(\sigma ^{2}\) negative, which is meaningless. Instead of indirectly tackling the issue by using a constrained optimization approach (which could be difficult to implement), such as a controlled adaptive learning rate, or model reparametrization, Khan et al. (2018b) proposes the use of the Generalized Gauss–Newton approximation for the Hessian:
This enables a minor but important difference with respect to VON: with an initial positive value for \(\sigma ^{2}\), the above approximation will remain positive leading to valid covariance updates. This provides an algorithmic advantage over VON as constraints on \(\sigma ^{2}\) are implicitly satisfied. The above implementation of the Hessian estimation, within VON, consists in the Variational Online Gauss–Newton (VOGN) approach (Khan et al. 2018b; Osawa et al. 2019). The implementation of the above approximation is not immediate as it requires per-sample gradients. The approximation averages squared gradients evaluated on a sample-per-sample basis, as opposed to batch-gradient computation which directly computes the sum of the gradients over mini-batches (Osawa et al. 2019), which can be seen by comparing Eq. (89) with Eq. (90)
The gradient-magnitude approximation that makes use of the mini-batch squared gradient as an approximation for the Hessian,
introduces a bias in the Hessian estimation. In fact, increasing the mini-batch size is not advisable as it introduces more bias. Based on the above approximation, Khan et al. (2018b) advances an RMSProp version of the VON update.
The practical implementation of VOGN is extensively discussed in Osawa et al. (2019), where the efficient implementation of the per-sample gradient computation for certain network layers is discussed: the additional computations needed to access individual gradients bring the run-time within 2–5 times of that of ADAM. Algorithm 10 summarizes the implementation of the VOGN optimizer.

The form of Algorithm 10 slightly differs from that of VOGN/ADAM. The sampling of the random weights is analogous to that of Algorithm 9 and Algorithm 8, yet here posterior samples are built over standard-normal random numbers rather than directly sampling from the multivariate diagonal posterior by the use of the reparametrization trick. Note the index i referring to the individual samples in the mini-batch \({\mathcal {M}}\). While VOGN uses a single sample for evaluating the stochastic gradients, here \(N_{s}\) draws are averaged to reduce the approximation variance. In particular, the nested for loop computes the single-observation gradient used for the Hessian approximation, each computed in the sampled weight vector \({{\varvec{\theta }}}_{s}\). Draw-specific gradients and Hessian \({\hat{{\varvec{g}}}}_{s}\) and \({{\hat{{\varvec{h}}}}}_{s}\) are thus averaged across samples (leading to \({\hat{{\varvec{g}}}}\) and \({\hat{{\varvec{h}}}}\)) and used in the implementation of the ADAM-like update based on momentum (thus the hyperparameters \(\beta _{1}\), \(\beta _{2}\)). The pseudo-code in Osawa et al. (2019) involves an additional tempering parameter and data-augmentation factor along with details for the VOGN parallel implementation, to which we refer for further insights.
Osawa et al. (2019) furthermore discusses practical implementation aspects typical in ML such as batch normalization, data augmentation, momentum, and distributed computing. The feasibility of the VOGN update for large-scale experiments with big-data sizes and deep network architectures on standard datasets promotes VOGN as a state-of-the-art method for Bayesian DL. As a remark, among its limitations, note that VOGN applies to Gaussian variational posteriors with a diagonal covariance matrix only.
7.6 Quasi Black-Box Variational Inference (QBVI)
The BBVI framework of Ranganath et al. (2014) can benefit from the use of the natural gradients. In fact, in Trusheim et al. (2018) natural gradients are estimated via MC sampling. On the other hand Eq. (60) provides an exact framework for computing natural gradients without relying on sampling methods, applicable for the wide class of variational posteriors within the Exponential family, yet model-specific derivations, i.e. the computation of the gradients and Hessian, are involved. The QBVI approach (Magris et al. 2022c) merges the BBVI setting with the exact natural gradient computation. QBVI uses Eq. (60) to turn the computation of the natural gradients into Euclidean gradients of the LB, which are computed by the use of the score estimation, resembling the BBVI framework. On a general level, the QBVI update estimates the gradient of the LB with respect to the natural parameters as
which along with a plain SGD lead to the update rule
Here the exact computation of the natural gradient is carried out in terms of Eq. (60), so that the QBVI update for a generic variational distribution and prior (both within the exponential family) reads, for the natural parameters, as:
Similarly to Khan and Nielsen (2018), Eq. (92) uses the properties of the Exponential family distribution for the prior p, with natural parameter \({\varvec{\eta }}\), and q to simplify the first term on the right-side of Eq. (91). This results in the natural-parameter difference \({\varvec{\eta }}-{{\varvec{\uplambda }}}\), avoiding on the first instance a sampling framework for evaluating the corresponding expectation, i.e. reducing the variance of the estimate for \({\tilde{\nabla }}{\mathcal {L}}\left( {{\varvec{\uplambda }}} \right)\), regardless of the estimator used for \({\mathbb {E}}_{q_{{\varvec{\uplambda }}}}\left[ \log p\left( {\mathcal {D}}\vert {{\varvec{\theta }}} \right) \right]\).
Magris et al. (2022c) focuses on the Gaussian variational case, building the QBVI update on the NGVI update, but without using the model’s gradient and Hessian as for VON. Indeed, using Eqs. (61) and (62), Magris et al. (2022c) recovers, for a full-covariance posterior, the following updates:
where \({\varvec{v}}_{t} = \Sigma ^{-1}\left( {{\varvec{\theta }}}-{{\varvec{\mu }}}_{t} \right)\) and \({{\varvec{\mu }}}_{0}, \Sigma _{0}\) denote the mean vector and covariance matrix of the prior distribution on the model parameter \({{\varvec{\theta }}}\), respectively. The following naive MC estimator provides a simple approach for tacking the above expectations
with \({{\varvec{\theta }}}_{s} \sim q_{{\varvec{\uplambda }}}\), \(s = 1,\dots ,N_{s}\). Algorithm 12 provides the pseudo-code for the QBVI implementation.

8 Variational Inference on manifolds
In this section, we review a class of methods that pursue a theoretically different approach, i.e., manifold optimization. The major challenge in VI optimization is that of guaranteeing constraints on the variational parameter. In a Gaussian, or e.g. an Inverse Wishart, setting, this corresponds to guaranteeing updates under which the covariance matrix is Symmetric and Positive Definite (SPD).
We first introduce in general terms the concept and practice of Riemann optimization. Therefore, we provide an introduction to Riemann manifolds, the concepts of tangent vectors, tangent spaces, and Riemann gradient to finally provide a more rigorous discussion of the specific problem of performing valid covariance updated for Bayesian Inference under a Gaussian variational FFVI setting. This section addresses the most crucial aspects concerning the purpose of introducing the Manifold Gaussian Variational Bayes and Exact Manifold Gaussian Variational Bayes optimizers. As the topic is itself broad and quite technical, we intentionally provide a descriptive illustration suitable for a general audience, referring to the specialized literature for additional details and a rigorous mathematical treatment at the end of the following section.
8.1 Introduction to manifold optimization
Riemann optimization is an alternative to standard SGD that well fits problems of the kind
where \({\mathcal {L}}\) is a real-valued function of some parameter \({{\varvec{\zeta }}}\), defined on a Riemannian manifold \(\left( {\mathcal {M}},g \right)\). A manifold is a topological space that locally resembles Euclidean space near each point, in more detail, is a set that can locally be mapped one-to-one to \({\mathbb {R}}^{k}\), where k is the dimension of the manifold. g stands for a metric the manifold is equipped with.
The optimization problem aims at minimizing \({\mathcal {L}}\) by finding the parameter \({{\varvec{\zeta }}}\in {\mathcal {M}}\) that lies on the “smooth surface” of the Riemannian manifold \(\left( {\mathcal {M}},g \right)\) resembling a constrained optimization problem requiring the optimum \({{\varvec{\zeta }}}^{*}\) to lie on the Riemannian manifold, such as a sphere or the SPD set. As with SGD in Euclidean vector spaces, Riemann optimization is generally tackled with gradient descent on the surface of the manifold, based on the gradients of \({\mathcal {L}}\). Yet, because of the manifold constraint, there are important differences compared to the standard SGD approach.
The Euclidean vector space \({\mathbb {R}}^{n}\) can be interpreted as a Riemannian manifold \(\left( {\mathbb {R}}^{n},g \right)\), with g the common Euclidean metric, where the usual SGD iteratively updates the parameter \({{\varvec{\zeta }}}\) as
where
It is clear that applying the above to a generic non-Euclidean manifold \({\mathcal {M}}\) is not trivial as there is no guarantee that \({{\varvec{\zeta }}}_{t+1}\) is a valid update, i.e. that \({{\varvec{\zeta }}}_{t+1}\) lies in \({\mathcal {M}}\). Consider an optimization problem where the parameter \({{\varvec{\zeta }}}= \left( x,y,z \right)\) is required to lie on a 2-dimensional spherical manifold of radius 1, embedded in a 3-dimensional ambient space. The Riemannian manifold is \({\mathcal {M}}=\left\{ {{\varvec{\zeta }}}\in {\mathbb {R}}^{3}:\, \vert \vert {{\varvec{\zeta }}}\vert \vert _{2} = 1 \right\}\), with g being the Euclidean metric, and \({\mathcal {L}}\) corresponding to a custom loss function for an arbitrary point \({{\varvec{\zeta }}}\) on the sphere \({\mathcal {M}}\). Though partial derivatives \(\nabla _{{{\varvec{\zeta }}}}{\mathcal {L}}\) are straightforward to compute or evaluate, e.g. with backpropagation, at the current parameter value \({{\varvec{\zeta }}}_{t}\), there is no guarantee that the update rule for the Euclidean space \({{\varvec{\zeta }}}_{t+1} = {{\varvec{\zeta }}}_{t} + \beta \nabla _{{\varvec{\zeta }}}{\mathcal {L}}{{{\varvec{\zeta }}}_{t}}\) would result in an updated parameter lying on sphere \({\mathcal {M}}\). Intuitively, on the “curved” surfaces of Riemannian manifolds the updates should follow the “curved” geodesics instead of straight lines as on familiar \({\mathbb {R}}^{n}\) Euclidean spaces. To this end, Riemann Stochastic Gradient Descent (RSGD) constitutes a manifold generalization of the SGD.
8.1.1 Elements of Riemannian manifolds
In \({\mathbb {R}}^{k}\), a steepest-ascent approach updates the current iterate \({{\varvec{\zeta }}}\) in the direction where the first-order increase of the objective function \({\mathcal {L}}\) is most positive. Formally, the update direction is chosen to be the unit norm vector \({\varvec{{\varvec{\eta }}}}\) that minimizes the directional derivative
With the domain of \({\mathcal {L}}\) being the manifold \({\mathcal {M}}\), the argument \({{\varvec{\zeta }}}+t {\varvec{{\varvec{{\varvec{\eta }}}}}}\) does not make much sense in general as \({\mathcal {M}}\) is not necessarily a vector space. This leads to the notion of a tangent vector. A possibility for generalizing the directional derivative is to replace \(t \mapsto {{\varvec{\zeta }}}+ t{\varvec{{\varvec{\eta }}}}\) by a smooth curve \(\gamma\) on \({\mathcal {M}}\) passing through \({{\varvec{\zeta }}}\), i.e. \(\gamma \left( 0 \right) = {{\varvec{\zeta }}}\). A smooth mapping \(\gamma :{\mathbb {R}}\rightarrow {\mathcal {M}}:\,t\mapsto \gamma \left( t \right)\) is termed as curve in \({\mathcal {M}}\). Defining a derivative \(\gamma '\left( t \right)\) as \(\gamma '\left( t \right) := \lim _{t\rightarrow 0} \frac{\gamma \left( {{\varvec{\zeta }}}+t \right) -\gamma \left( {{\varvec{\zeta }}} \right) }{t}\) fails on a general manifold as it requires a vector space structure to compute the difference \(\gamma \left( {{\varvec{\zeta }}}+t \right) -\gamma \left( {{\varvec{\zeta }}} \right)\), however for a smooth function \({\mathcal {L}}\) on \({\mathcal {M}}\) the function \({\mathcal {L}}\circ \gamma :\, t \mapsto {\mathcal {L}}\left( \gamma \left( t \right) \right)\) is a smooth and well-defined function from \({\mathbb {R}}\) to \({\mathbb {R}}\) with a well-defined classical derivative. To sum up, let \({{\varvec{\zeta }}}\) be a point on \({\mathcal {M}}\), \(\gamma\) a curve such that \(\gamma \left( 0 \right) = {{\varvec{\zeta }}}\) and \({\mathcal {F}}_{{\varvec{\zeta }}}\left( {\mathcal {M}} \right)\) is the set of smooth real-valued functions defined in a neighborhood of \({{\varvec{\zeta }}}\) in \({\mathcal {M}}\). The mapping \({{\dot{\gamma }}}\left( 0 \right)\) from \({\mathcal {F}}_{{\varvec{\zeta }}}\left( {\mathcal {M}} \right)\) to \({\mathbb {R}}\) defined by
is called the tangent vector to the curve \(\gamma\) at \(t=0\). Note that the above definition defines \({{\dot{\gamma }}}\left( 0 \right)\) as a mapping and not as a (e.g. time) derivative as in Eq. (103), which would be general meaningless. We can now formally define the notion of a tangent vector.
A tangent vector \({{\varvec{\xi }}}_{{\varvec{\zeta }}}\) to a manifold \({\mathcal {M}}\) at a point \({{\varvec{\zeta }}}\) is a mapping from \({\mathcal {F}}_{{\varvec{\zeta }}}\left( {\mathcal {M}} \right)\) to \({\mathbb {R}}\) such that there exists a curve \(\gamma\) on \({\mathcal {M}}\) with \(\gamma \left( 0 \right) = {{\varvec{\zeta }}}\) satisfying
Such a curve \(\gamma\) is said to realize the tangent vector \({{\varvec{\xi }}}_{{\varvec{\zeta }}}\). The tangent space to \({\mathcal {M}}\) at \({{\varvec{\zeta }}}\) is the set of all tangent vectors to \({\mathcal {M}}\) at \({{\varvec{\zeta }}}\) and is denoted by \(T_{{\varvec{\zeta }}}{\mathcal {M}}\). Importantly, it can be shown that \(T_{{\varvec{\zeta }}}{\mathcal {M}}\) admits a vector space structure, i.e. \(T_{{\varvec{\zeta }}}{\mathcal {M}}\) is a vector space: it provides a local vector space approximation of the manifold. This property is useful in defining retractions used to locally transform an optimization problem on \({\mathcal {M}}\) into an optimization problem on the more friendly vector space \(T_{{\varvec{\zeta }}}{\mathcal {M}}\). To characterize which direction of motion from \({{\varvec{\zeta }}}\) produces the steepest increase in \({\mathcal {L}}\), to enable a notion of length that applies to tangent vectors, we endow the tangent space \(T_{{\varvec{\zeta }}}{\mathcal {M}}\) with an inner product \(\langle \cdot ,\cdot \rangle\), inducing the norm \(\vert \vert {{\varvec{\xi }}}_{{\varvec{\zeta }}}\vert \vert\) on \(T_{{\varvec{\zeta }}}{\mathcal {M}}\), from which the direction of the steepest ascent is given by
that is, by the unit-norm vector \({{\varvec{\xi }}}_{{\varvec{\zeta }}}^{*}\) for which directional derivative \({\text {D}}\) of \({\mathcal {L}}\) in \({{\varvec{\zeta }}}\) in the direction \({{\varvec{\xi }}}_{{\varvec{\zeta }}}^{*}\) is maximized.
A manifold whose tangent spaces are endowed with a smoothly varying inner product is called a Riemannian manifold, and the smoothly varying inner product is called the Riemann metric. With g being such a Riemann metric on \({\mathcal {M}}\), the Riemannian manifold is, strictly speaking, the couple \(\left( {\mathcal {M}},g \right)\). The Euclidean space is the particular Riemannian manifold consisting of a vector space endowed with an inner product.
The gradient of \({\mathcal {L}}\) defined on a Riemannian manifold \({\mathcal {M}}\) at \({{\varvec{\zeta }}}\) is denoted by the unique element in \(T_{{\varvec{\zeta }}}{\mathcal {M}}\) that satisfies
As in correspondence with usual Euclidean gradients, and important in the light of optimization, it can be shown that the direction of \({\text {grad}}\, {\mathcal {L}}\left( {{\varvec{\zeta }}} \right)\) is the steepest ascent direction of \({\mathcal {L}}\) at \({{\varvec{\zeta }}}\)
and that the norm of \({\text {grad}}\, {\mathcal {L}}\left( {{\varvec{\zeta }}} \right)\) gives the steepest slope of \({\mathcal {L}}\) at \({{\varvec{\zeta }}}\).
If a manifold \({\mathcal {M}}_{e}\) is endowed with a Riemann metric, one would expect that manifolds generated from \({\mathcal {M}}_{e}\) inherit its Riemann metric. Let \({\mathcal {M}}\) be a manifold embedded in \({\mathcal {M}}_{e}\) (the subscript e stands for “embedding)”. Since every tangent space \(T_{{\varvec{\zeta }}}{\mathcal {M}}\) can be regarded as a subspace of \(T_{{\varvec{\zeta }}}{\mathcal {M}}_{e}\), the Riemann metric \(g_{e}\) of \({\mathcal {M}}_{e}\) induces a Riemann metric g on \({\mathcal {M}}\) turning \({\mathcal {M}}\) into a Riemannian manifold. Endowed with this metric, \({\mathcal {M}}\) is called a Riemannian submanifold of \({\mathcal {M}}_{e}\). As it will appear clear in the next section, the submanifold idea is simple yet powerful as any element \({{\varvec{\xi }}}_{{\varvec{\zeta }}}\) in \(T_{{\varvec{\zeta }}}{\mathcal {M}}\) can be decomposed into an element of \(T_{{\varvec{\zeta }}}{\mathcal {M}}\) and its corresponding orthogonal element \(\left( T_{{\varvec{\zeta }}}{\mathcal {M}} \right) ^{\perp}\) in \(T_{{\varvec{\zeta }}}{\mathcal {M}}_{e}\):
where \({\text {Proj}}_{{\varvec{\zeta }}}\) denotes the orthogonal projection onto \(T_{{\varvec{\zeta }}}{\mathcal {M}}\), and \({\text {Proj}}^{\perp} _{{\varvec{\zeta }}}\) denotes the orthogonal projection onto \(\left( T_{{\varvec{\zeta }}}{\mathcal {M}} \right) ^{\perp}\). In this light, by properly defining the embedding ambient space \({\mathcal {M}}_{e}\), one may simplify the computation of the Riemannian gradient, and by projection determine the Riemannian gradient in the tangent space \(T_{{\varvec{\zeta }}}{\mathcal {M}}\) of the manifold \({\mathcal {M}}\) of interest:
with \({\mathcal {L}}_{e}\) being an extended version of the differentiable function \({\mathcal {L}}\) defined on \({\mathcal {M}}_{e}\) such that its restriction on \({\mathcal {M}}\) actually coincides with \({\mathcal {L}}\).
Perhaps the most simple tool to tackle Riemann optimization is the Riemann Stochastic Gradient Descent (RSGD), first proposed in (Bonnabel 2013). RSGD typically involves three steps: (i) evaluate the gradient of \({\mathcal {L}}_{e}\) in \(T_{{\varvec{\zeta }}}{\mathcal {M}}_{e}\) with respect to \({{\varvec{\zeta }}}\) at the current value \({{\varvec{\zeta }}}_{t}\), Fig. 4 (left panel), (ii) project the gradient onto the tangent space of the manifold \({\mathcal {M}}\) at \({{\varvec{\zeta }}}_{t}\), and (iii) update the parameter by performing a gradient step on the surface following the direction of \({\text {grad}}\, {\mathcal {L}}\left( {{\varvec{\zeta }}} \right)\), Fig. 4 (central panel).
The last step moves the point \({{\varvec{\zeta }}}_{t} \in {\mathcal {M}}\) in the direction of the gradient along a geodesic, onto \({{\varvec{\zeta }}}_{t+1}\), lying on the manifold. This is achieved by the so-called exponential map, mapping elements from the tangent space to \({\mathcal {M}}\). The computation of the exponential map is however a cumber-stone in practice: often a first-order approximation is used. Such first-order approximation is called retraction \(R_{{{\varvec{\zeta }}}}\left( {{\varvec{\xi }}}_{{{\varvec{\zeta }}}} \right)\), \({{\varvec{\xi }}}_{{{\varvec{\zeta }}}} \in T_{{{\varvec{\zeta }}}} {\mathcal {M}}\). Intuitively, rather than performing an exact update following the curved geodesics of the manifold, retraction first follows a straight line in the tangent space and then orthogonally projects the point in the tangent space on the manifold. Closed-form formulae for retraction on the most common manifold are available in the literature, see e.g. Absil et al. (2009) and Hu et al. (2020), and e.g. Hosseini and Sra (2015) for the SPD manifold.
The main sources we have used in writing this section are the exhaustive book of Absil et al. (2009), and the articles (Hu et al. 2020) and (Tran et al. 2021a). Classical specialized books on differential geometry are those of Kobayashi and Nomizu (1963), Do Carmo and Flaherty Francis (1992) and Boothby and Boothby (2003), while well-suited references for readers without a background in abstract topology are e.g. Tu (2011) and Do Carmo (2016) and furthermore at an introductory level e.g. Brickell and Clark (1970) and Abraham et al. (2012). We suggest referring to the literature involved in the above references for further bibliographical details, e.g. the bibliographical notes in Chapter 3 of Absil et al. (2009). An exhaustive overview of the different applications in manifold optimization in different areas can be found e.g. in Hu et al. (2020). For the first developments on SGD on Riemannian manifolds, we refer to Bonnabel (2013), further developments towards an RMSprop-like adaptive version of RSGD can be found in Kasai et al. (2019), while Riemann optimization on the lines of the popular Adam and Ada-grad are discussed in Bécigneul and Ganea (2018). Relevant for the SPD matrix manifold optimization are the results on vector transport and retraction in e.g. Jeuris et al. (2012) and Sra and Hosseini (2015), of remarkable utility for applications. In this regard, we point to Boumal et al. (2014) for a manifold optimization package available in multiple languages.
8.2 Variational Bayes on Riemannian manifolds with natural gradients
Variational Bayes on manifolds aims at maximizing the LB \({\mathcal {L}}\) under a fixed-form Gaussian variational posterior guaranteeing a positive-definite form of the covariance matrix \(\Sigma\). Thus the variational parameter \({{\varvec{\zeta }}}\) lies on the Riemannian manifold of Symmetric and Positive Definite (SPD) matrices \({\mathcal {M}}= \left\{ \Sigma \in {\mathbb {R}}^{k\times k} : \Sigma = \Sigma ^{\top} , \Sigma \succ 0\right\}\). The optimization problem of concern is thus the Riemann optimization problem
To implement the RSGD update the manifold \({\mathcal {M}}\) of SPD matrices is viewed as embedded in the Riemannian manifold \({\mathcal {M}}_{e}\). Let \(T_{{\varvec{\zeta }}}{\mathcal {M}}_{e}\) be the tangent space to \({\mathcal {M}}\) at \({{\varvec{\zeta }}}\in {\mathcal {M}}_{e}\). Aligned with the discussion in Sect. 5, we wish to perform natural gradient updates. To this end, we equip \({\mathcal {M}}_{e}\) with the Fisher–Rao metric, defined by the Fisher information matrix \({\mathcal {I}}_{{\varvec{\zeta }}}\). With such a metric, the inner product between two tangent vectors \({\varvec{{\varvec{\nu }}}}_{{\varvec{\zeta }}},{{\varvec{\xi }}}_{{\varvec{\zeta }}}\in T_{{\varvec{\zeta }}}{\mathcal {M}}_{e}\) is defined as
generalizing the usual Euclidean metric \(\langle {\varvec{\nu }}_{{\varvec{\zeta }}},{{\varvec{\xi }}}_{{\varvec{\zeta }}} \rangle = {\varvec{\nu }}_{{\varvec{\zeta }}}^{\top} {{\varvec{\xi }}}_{{\varvec{\zeta }}}\). Let \({\mathcal {L}}_{e}\) be a differentiable function defined on \({\mathcal {M}}_{e}\) such that its restriction on \({\mathcal {M}}\) corresponds to the LB \({\mathcal {L}}\). It can be shown that the steepest ascent direction at \({{\varvec{\zeta }}}\in {\mathcal {M}}_{e}\) for maximizing the objective \({\mathcal {L}}_{e}\) is the natural gradient
Note that \(\nabla _{{\varvec{\zeta }}}{\mathcal {L}}_{e}\left( {{\varvec{\zeta }}} \right)\) is the usual Euclidean gradient vector of \({\mathcal {L}}_{e}\left( {{\varvec{\zeta }}} \right)\), and that, importantly, for \({{\varvec{\zeta }}}\in {\mathcal {M}}\),
That is, the natural gradient of the extended LB \({\mathcal {L}}_{e}\) in \({\mathcal {M}}_{e}\) corresponds to the natural gradient of the LB on the relevant manifold \({\mathcal {M}}\). A framework for formally associating the natural gradient with the Riemannian gradient is provided by the lemma below, see Tran et al. (2021a) for more details.
Lemma 1
The natural gradient of the function \({\mathcal {L}}_{e}\) on the Riemannian manifold \({\mathcal {M}}_{e}\) with the Fisher–Rao metric is the Riemannian gradient of \({\mathcal {L}}_{e}\). In particular, the natural gradient at \({{\varvec{\zeta }}}\) belongs to the tangent space to \({\mathcal {L}}_{e}\) at \({{\varvec{\zeta }}}\).
This means that with respect to the embedding space \({\mathcal {M}}_{e}\), \({\tilde{\nabla }}_{{\varvec{\zeta }}}{\mathcal {L}}_{e}\left( \zeta \right)\) is the actual Riemannian gradient, lying on the tangent space \(T_{{{\varvec{\zeta }}}}{\mathcal {M}}_{e}\) of \({\mathcal {L}}_{e}\) at \({{\varvec{\zeta }}}\). Yet we need to associate the Riemannian gradient in \({\mathcal {M}}_{e}\) to the LB \({\mathcal {L}}\) in \({\mathcal {M}}\), the actual objective of RSGD optimization.
To this end, we naturally equip the submanifold \({\mathcal {M}}\) with the same Riemann metric inherited from \({\mathcal {M}}_{e}\). For \({\varvec{\nu }}_{{\varvec{\zeta }}},{{\varvec{\xi }}}_{{\varvec{\zeta }}}\) now both in \(T_{{\varvec{\zeta }}}{\mathcal {M}}_{e}\),
and we obtain the Riemannian gradient of \({\mathcal {L}}\) in \({\mathcal {M}}\) as the projection of \({\text {grad}}{\mathcal {L}}_{e}\) on \(T_{{\varvec{\zeta }}}{\mathcal {M}}\)
In a Gaussian manifold, \(T_{{\varvec{\zeta }}}{\mathcal {M}}\cong T_{{\varvec{\zeta }}}{\mathcal {M}}_{e}\), thus the projection is the identity matrix I and \({\text {grad}}\, {\mathcal {L}}_{e} = {\text {grad}}\, {\mathcal {L}}\). Indeed in Gaussian manifolds, \({\mathcal {M}}\) corresponds to the manifold of SPD matrices whereas \({\mathcal {M}}_{e} = {\mathbb {R}}^{k\times k}\): \(T_{{\varvec{\zeta }}}{\mathcal {M}}\) and \(T_{{\varvec{\zeta }}}{\mathcal {M}}_{e}\) differ by the fact that the first is the tangent space to a certain SPD matrix while the second is the tangent space of a generic \(k \times k\) symmetric matrix. In terms of projection, the difference is irrelevant, thus \({\text {Proj}}_{{\varvec{\zeta }}}{\text {grad}}\, {\mathcal {L}}_{e} = I {\text {grad}}\, {\mathcal {L}}_{e}\). Mind that, however, on a general level \({\text {Proj}}_{{\varvec{\zeta }}}\left( \cdot \right)\) can be rather difficult to compute. The above relationship between the Riemannian gradient in \({\mathcal {M}}_{e}\) and the LB \({\mathcal {L}}\) in \({\mathcal {M}}\), is established by treating \({\mathcal {M}}\) as a submanifold of \({\mathcal {M}}_{e}\). Alternatively one can derive the Riemannian gradient of \({\mathcal {L}}\) requiring \({\mathcal {M}}\) to be a so-called quotient manifold induced from a Riemannian ambient manifold. In this regard, see Tran et al. (2021a) and the references therein.
RSGD requires a proper retraction \(R_{{\varvec{\zeta }}}:\, T_{{\varvec{\zeta }}}{\mathcal {M}}\mapsto {\mathcal {M}}\) that locally maps \(T_{{\varvec{\zeta }}}{\mathcal {M}}\) onto the manifold \({\mathcal {M}}\) while preserving the first-order information of the tangent space in \({{\varvec{\zeta }}}\). This means that a step of size zero stays at the same point \({{\varvec{\zeta }}}\) and the differential of the retraction at this origin is the identity mapping (Jeuris et al. 2012). From the geodesics between two matrices in \({\mathcal {M}}\), Jeuris et al. (2012) develops the popular and convenient retraction method (actually a second-order approximation of the exponential map) for the SPD matrices manifold \({\mathcal {M}}\). This is given by
where
and updates the current value of \({{\varvec{\zeta }}}\) on \({\mathcal {M}}\) by accounting for \({{\varvec{\xi }}}\) on the tangent space \(T_{{\varvec{\zeta }}}{\mathcal {M}}\).
We now add a practically important element to the discussion, vector transport. In order to perform, among the others, the conjugate gradient algorithm, or implement the momentum method within the RSGD update, we need to relate a tangent vector at some point \({{\varvec{\zeta }}}\in {\mathcal {M}}\) to another point \({\varvec{{\varvec{\eta }}}} \in {\mathcal {M}}\). In differential geometry, this is achieved by a parallel translation, moving tangent vectors from one tangent space to the other, while preserving the length and angle of the original tangent vector, Fig. 4 (right panel). As for the exponential map, the parallel translation is often approximated by the so-called vector transport, which is easier to compute. For \({{\varvec{\xi }}}:= {{\varvec{\xi }}}_{{\varvec{\zeta }}}\) and \({\varvec{{\varvec{\eta }}}} := {\varvec{{\varvec{\eta }}}}_{{\varvec{\zeta }}}\in T_{{\varvec{\zeta }}}{\mathcal {M}}\), an effective vector transform for the manifold of interest is
with
where \({\mathcal {T}}_{{{\varvec{\zeta }}}\rightarrow {\varvec{\eta }}} \left( {{\varvec{\xi }}} \right)\) denotes the vector transport of the tangent vector \({{\varvec{\xi }}}\in T_{{\varvec{\zeta }}}{\mathcal {M}}\) to \({\varvec{\eta }} \in T_{{\varvec{\eta }}}{\mathcal {M}}\). The above vector transport can be written in a compact and computationally advantageous form as (see e.g. Sra and Hosseini 2015 for details):
with
We point out that within the above SPD matrix manifold setting relevant in Gaussian VI, \({{\varvec{\zeta }}}\), \({\varvec{\eta }}\), \({{\varvec{\xi }}}\) are matrices and the above equations are well-defined: for homogeneity in notation, we stick with the lower-case bold symbols for indicating elements of a generic space.
The above vector transport is practically relevant and essential in implementing, e.g., a momentum method on the RSGD update, that is by using a moving average of the Riemannian gradient at the previous iteration to reduce noise in the estimated gradients and boost convergence:
where \(\omega\) is a momentum-weight hyper-parameter.
Manifold optimization in the context of VI is relatively new, the main reference for this paper is Tran et al. (2021a), whose approach is reviewed in Sect. 8.3. Besides this, VI on manifolds is also discussed in Zhou et al. (2021) and Magris et al. (2022b) and appears in Lin et al. (2020). Other applications, not related to the purposes of this review, are here not covered, e.g. manifold optimization for variational autoencoders (Skopek et al. 2019). Regarding the specific Bayesian inference problem for Neural Networks, at the time of writing, we are not aware of any further works or developments.
8.3 Manifold Gaussian Variational Bayes (MGVB)
We review the (MGVB) method of Tran et al. (2021a). The variational approximation \(q_{{\varvec{\uplambda }}}\) to the true posterior is provided by a multivariate Gaussian distribution \({\mathcal {N}}\left( {{\varvec{\mu }}},\Sigma \right)\), \({{\varvec{\mu }}}\in {\mathbb {R}}^{k}\). The parameter \({{\varvec{\mu }}},\Sigma\) are jointly collected in the vector \({{\varvec{\zeta }}}= \left( {{\varvec{\mu }}},{\text {vec}}\left( \Sigma \right) \right)\), denoting the variational parameter. There are no restrictions on the structure of the variance–covariance matrix \(\Sigma\) which is a generic member of the manifold \({\mathcal {M}}\) of the SPD matrices, \({\mathcal {M}}= \left\{ \Sigma \in {\mathbb {R}}^{k\times k} : \Sigma = \Sigma ^{\top} , \Sigma \succ 0\right\}\).
The exact form of the Fisher information matrix for the multivariate normal distribution is, e.g., provided in Mardia and Marshall (1984) and reads
with \({\mathcal {I}}\left( \Sigma \right)\) being the \(k^{2} \times k^{2}\) matrix whose generic element is
The MGVB method relies on the approximation \({\mathcal {I}}\left( \Sigma \right) \approx \Sigma ^{-1}\otimes \Sigma ^{-1}\), where \(\otimes\) denotes the Kronecker product. The corresponding approximate inverse FIM reads
which leads to a convenient approximate form of the natural gradients of the lower bound with respect to \({{\varvec{\mu }}}\) and \(\Sigma\) computed as
The last equality follows from the fact that for a vector \({\varvec{v}}\in {\mathbb {R}}^{k\times k}\), \(\left( \Sigma \otimes \Sigma \right) {\varvec{v}} = {\text {vec}}\left( \Sigma {\text {vec}}^{-1}\left( {\varvec{v}} \right) \Sigma \right)\). In virtue of the natural gradient definition, the first natural gradient for \({{\varvec{\mu }}}\) is exact while the second one for \(\Sigma\) is approximate. As pointed out in Lin et al. (2020), the actual natural gradient for the above Gaussian distribution should read \(2\Sigma \nabla _{\Sigma} {\mathcal {L}}\Sigma\), as \({\mathcal {I}}\left( \Sigma \right) = 2\Sigma ^{-1}\otimes \Sigma ^{-1}\), therefore the MGVB approximation. Thus, Tran et al. (2021a) adopts the following updates for the parameters of the variational posterior:
where \(R_{\Sigma} \left( \cdot \right)\) denotes a suitable retraction for \(\Sigma\) on the manifold \({\mathcal {M}}\), and \(\beta\) is the learning rate. Momentum gradients can be used in place of natural ones. In particular Tran et al. (2021a) uses retraction in Eq. (116) and momentum gradients for the updating \(\Sigma\). In this regard, Tran et al. (2021a) adopts the parallel transport in Eq. (118) for granting that at each iteration the weighted gradient remains in the tangent space of the manifold \({\mathcal {M}}\).
The actual computation of the gradients \({\tilde{\nabla }}_{{\varvec{\mu }}}{\mathcal {L}}\) and \({\tilde{\nabla }}_{\Sigma} {\mathcal {L}}\) boils down to computing \(\nabla _{{\varvec{\mu }}}{\mathcal {L}}\) and \(\nabla _{\Sigma} {\mathcal {L}}\), which in MGVB is achieved with the black-box estimator
where
with \(q\sim {\mathcal {N}}\left( {{\varvec{\mu }}},\Sigma \right)\), \({{\varvec{\zeta }}}= \left( {{\varvec{\mu }}},{\text {vec}}\left( \Sigma \right) \right)\), and \({\mathcal {L}}\left( {{\varvec{\zeta }}} \right) \equiv {\mathcal {L}}\left( {{\varvec{\mu }}},\Sigma \right)\). In particular, the gradient of \({\mathcal {L}}\) with respect to \({{\varvec{\zeta }}}\) is estimated using \(N_{s}\) samples from the variational posterior through the unbiased estimator
where \({{\varvec{\theta }}}_{s}\sim {\mathcal {N}}\left( {{\varvec{\mu }}}_{t},\Sigma _{t} \right)\) and the h-function is evaluated in the current value of the parameters, i.e. in \({{\varvec{\zeta }}}_{t} = \left( {{\varvec{\mu }}}_{t},{\text {vec}}\left( \Sigma _{t} \right) \right)\). For a Gaussian distribution \(q \sim {\mathcal {N}}\left( {{\varvec{\mu }}},\Sigma \right)\) it can be shown that (e.g. Wierstra et al. 2014; Magris et al. 2022c):
Algorithm 12 summarizes the above process.

8.4 Exact Manifold Gaussian Variational Bayes (EMGVB)
The covariance matrix \(\Sigma\) is positive definite, its inverse exists and it is as well symmetric and positive definite. Therefore, \(\Sigma ^{-1}\) lies within the manifold \({\mathcal {M}}\) and can be updated with a suitable retraction algorithm as for \(\Sigma\) in Sect. 8.3,
Opposed to the EMGVB update, relying on the approximation \({\mathcal {I}}^{-1}\left( \Sigma \right) \approx \Sigma ^{-1}\otimes \Sigma ^{-1}\), for tackling a positive-definite update of \(\Sigma\), Magris et al. (2022b) targets at updating \(\Sigma ^{-1}\) for which its natural gradient is available in an exact form, by primarily exploiting the duality between the gradients in the natural and expectation parameter space as for Eq. (47), that circumvents the computation and the approximate form of the FIM.
In particular Eq. (47) implies that
where \({{\varvec{\uplambda }}}_{2} =-\frac{1}{2}\Sigma ^{-1}\) is the second natural parameter of the variational Gaussian posterior \(q_{{\varvec{\uplambda }}}\). This leads to the EMGVB updates
Despite the approximate MGVB update for \(\Sigma\), EMGVB updates \(\Sigma ^{-1}\) with exact natural gradient computations. Retraction and momentum gradients are computed as in MGVB but involve \(\Sigma ^{-1}\) in place of \(\Sigma\). For retraction,
with \({{\varvec{\xi }}}\) being the rescaled natural gradient \(\beta {\tilde{\nabla }}_{\Sigma ^{-1}}{\mathcal {L}}= -2\beta \nabla _{\Sigma} {\mathcal {L}}\). Instead, vector transport reads
where the weight \(0<\omega <1\) is a hyper-parameter. As for Eq. (92), by using a Gaussian prior along with a Gaussian posterior, the natural parameter difference becomes particularly simple. With \({{\varvec{\zeta }}}= \left( {{\varvec{\mu }}},\Sigma \right)\),
evaluating \({\tilde{\nabla }}_{{\varvec{\zeta }}}{\mathcal {L}}\) accounts to practically estimating \({\tilde{\nabla }}_{{\varvec{\zeta }}}{\mathbb {E}}_{q_{{\varvec{\zeta }}}}\left[ \log p\left( {\mathcal {D}}\vert {{\varvec{\theta }}} \right) \right]\) only. Whether or not one uses the results in Eqs. (141) and (142) under a Gaussian prior assumption, or prefers to use the gradient estimator based on the h-function, \(h_{{\varvec{\zeta }}}\left( {\varvec{\theta }} \right) ={\mathbb {E}}_{q_{{\varvec{\zeta }}}} \left[ \log p\left( {{\varvec{\theta }}} \right) +\log p\left( {\mathcal {D}}\vert {{\varvec{\theta }}} \right) - \log q_{{\varvec{\zeta }}}\left( {{\varvec{\theta }}} \right) \right]\), as in MGVB, a general-form for the gradients enabling the EMGVB update is provided by
where
Because of the computations of the constants \(C_{\Sigma _{t}}\) and \(c_{{{\varvec{\mu }}}_{t}}\) under the Gaussian assumption for the prior p, the MC estimators in Eqs. (143) and (144) are of reduced variance. Magris et al. (2022b) also provides analogous simplified updates under the specific assumption that the covariance matrix of q is either diagonal, block-diagonal, or full under an isotropic Gaussian prior whose mean vector is zero and prior covariance matrix \(\Sigma ^{-1}_{0}\) equal to \(\tau I\), with \(\tau >0\). Algorithm 13 summarizes the updating routine.

The reader will note that the EMGVB approach is mixing elements of the SPD (matrix) manifold (retraction and parallel transport) with the natural gradient obtained from the Gaussian manifold. A justification for the validity of the above is discussed in Magris et al. (2022b). The discrepancy between the natural gradient and the Riemannian gradient obtained from the SPD manifold, can be absorbed in the learning rate \(\beta\) and the EMGVB update obtained by manifold-consistent derivations from updating \(\left( {{\varvec{\mu }}},2\Sigma ^{-1} \right)\).
9 Conclusion
In this survey, we provided an algorithmic overview of standard, as well as, more recently introduced approaches for Bayesian learning for Neural Networks. We structured our description as an easily-accessible introduction to the basic concepts and related methodologies, focused on the core elements and their implementation, providing pseudo-codes and update rules to be used as references for a large number of Bayesian Neural Network implementations.
We provided a foreword introduction to Bayesian Neural Network, their peculiarities, and motivated their use with respect to standard non-Bayesian Artificial Neural Network. In the remainder, we focused on popular and feasible approaches for their estimation. Besides describing some effective Monte Carlo methodologies, and introducing Monte Carlo Dropout as a Bayesian tool, we presented a variety of methods based on Variational Inference and natural gradients as the main methodological ingredients in modern Bayesian inference for Neural Networks. We presented the widespread Bayes-By-Backprop optimizer, followed by two common black-box methods, namely Black-Box Variational Inference and Natural-Gradient Black-Box Variational Inference. Next, we introduced natural gradients and examined the Natural-Gradient Variational Inference, Variational Online Newton, Variational Online Gauss–Newton, and Quasi Black-Box Variational Inference approaches. Lastly, by providing an introduction to manifold optimization, we provided a discussion on methods that can implicitly deal with the positive-definite constraint over Gaussian variational specifications, presenting the Manifold Gaussian Variational Bayes and Exact Manifold Gaussian Variational Bayes solutions.
We hope that our comprehensive algorithmic treatment of the above-described methodologies will contribute to a better understanding of the connections and differences between the various Bayesian methods for Neural Networks, will support the adoption of such methods in a wide range of applications, and promote further research in this field.
References
Abraham R, Marsden JE, Ratiu T (2012) Manifolds, tensor analysis, and applications, vol 75. Springer, New York
Absil PA, Mahony R, Sepulchre R (2009) Optimization algorithms on matrix manifolds. Princeton University Press, Princeton
Alquier P (2021) User-friendly introduction to PAC-Bayes bounds. Preprint. arXiv:2110.11216
Amari SI (1998) Natural gradient works efficiently in learning. Neural Comput 10(2):251–276
Bécigneul G, Ganea OE (2018) Riemannian adaptive optimization methods. Preprint. arXiv:1810.00760
Berry DW, Childs AM, Cleve R et al (2015) Simulating Hamiltonian dynamics with a truncated Taylor series. Phys Rev Lett 114(9):090502
Blackwell D (1947) Conditional expectation and unbiased sequential estimation. Ann Math Stat 18(1):105–110
Blei DM, Lafferty JD (2007) A correlated topic model of science. Ann Appl Stat 1(1):17–35
Blei DM, Kucukelbir A, McAuliffe JD (2017) Variational inference: a review for statisticians. J Am Stat Assoc 112(518):859–877
Blundell C, Cornebise J, Kavukcuoglu K et al (2015) Weight uncertainty in neural network. In: International conference on machine learning, 2015, pp 1613–1622
Bonnabel S (2013) Stochastic gradient descent on Riemannian manifolds. IEEE Trans Autom Control 58(9):2217–2229
Boothby WM, Boothby WM (2003) An introduction to differentiable manifolds and Riemannian geometry, Revised, vol 120. Gulf Professional Publishing, Houston
Boumal N, Mishra B, Absil PA et al (2014) Manopt, a MATLAB toolbox for optimization on manifolds. J Mach Learn Res 15(42):1455–1459
Braun M, McAuliffe J (2010) Variational inference for large-scale models of discrete choice. J Am Stat Assoc 105(489):324–335
Brickell F, Clark RS (1970) Differentiable manifolds: an introduction. Van Nostrand Reinhold, London
Broomhead DS, Lowe D (1988) Multivariable functional interpolation and adaptive networks. Complex Syst 2:321–355
Cai R, Ren A, Liu N et al (2018) VIBNN: hardware acceleration of Bayesian neural networks. SIGPLAN Not 53(2):476–488
Casella G (1985) An introduction to empirical Bayes data analysis. Am Stat 39(2):83–87
Casella G, Berger RL (2021) Statistical inference. Cengage Learning, Boston
Casella G, George EI (1992) Explaining the Gibbs sampler. Am Stat 46(3):167–174
Chakraborty S, Ghosh M (2012) Applications of Bayesian neural networks in prostate cancer study. Handbook of statistics, vol 28. Elsevier, Amsterdam, pp 241–262
Chan A, Alaa A, Qian Z et al (2020) Unlabelled data improves Bayesian uncertainty calibration under covariate shift. In: International conference on machine learning, 2020, pp 1392–1402
Cho K, van Merrienboer B, Bahdanau D et al (2014) On the properties of neural machine translation: encoder–decoder approaches. In: Workshop on syntax, semantics and structure in statistical translation, 2014
Csilléry K, Blum MG, Gaggiotti OE et al (2010) Approximate Bayesian computation (ABC) in practice. Trends Ecol Evol 25(7):410–418
Damianou A, Lawrence ND (2013) Deep Gaussian processes. In: International conference on artificial intelligence and statistics, 2013, pp 207–215
Der Kiureghian A, Ditlevsen O (2009) Aleatory or epistemic? Does it matter? Struct Saf 31(2):105–112
Dixon MF, Halperin I, Bilokon P (2020) Machine learning in finance, vol 1170. Springer, Berlin
Do Carmo MP (2016) Differential geometry of curves and surfaces: revised and updated second edition. Courier Dover Publications, Mineola
Do Carmo MP, Flaherty Francis J (1992) Riemannian geometry, vol 6. Springer, Berlin
Du Y, Liu Y, Wang X et al (2020) Predicting weather-related failure risk in distribution systems using Bayesian neural network. IEEE Trans Smart Grid 12(1):350–360
Etz A, Gronau QF, Dablander F et al (2018) How to become a Bayesian in eight easy steps: an annotated reading list. Psychon Bull Rev 25(1):219–234
Fichtner A, Gebraad L, Boehm C et al (2020) Auto-tuning Hamiltonian Monte Carlo. In: EGU General Assembly conference abstracts, p 7735
Freitas JFGd, Niranjan M, Gee AH (2000) Hierarchical Bayesian models for regularization in sequential learning. Neural Comput 12(4):933–953
Gagniuc PA (2017) Markov chains: from theory to implementation and experimentation. Wiley, Hoboken
Gal Y, Ghahramani Z (2015) Dropout as a Bayesian approximation: insights and applications. In: Deep learning workshop, international conference on machine learning, 2015, p 2
Gal Y, Ghahramani Z (2016) Dropout as a Bayesian approximation: representing model uncertainty in deep learning. In: International conference on machine learning, 2016, pp 1050–1059
Gamerman D, Lopes HF (2006) Markov chain Monte Carlo: stochastic simulation for Bayesian inference. CRC Press, Boca Raton
Gelman A, Carlin JB, Stern HS et al (1995) Bayesian data analysis. Chapman and Hall/CRC, New York
Geman S, Geman D (1984) Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images. IEEE Trans Pattern Anal Mach Intell 6(6):721–741
Ghahramani Z, Beal M (2000) Propagation algorithms for variational Bayesian learning. In: Advances in neural information processing systems, 2000, vol 13
Goh AT, Kulhawy FH, Chua C (2005) Bayesian neural network analysis of undrained side resistance of drilled shafts. J Geotech Geoenviron Eng 131(1):84–93
Goodfellow I, Bengio Y, Courville A (2016) Deep learning. MIT Press, Cambridge
Guedj B, Pujol L (2021) Still no free lunches: the price to pay for tighter PAC-Bayes bounds. Entropy 23(11):1529
Hastings WK (1970) Monte Carlo sampling methods using Markov chains and their applications. Biometrika 57(1):97–109
Haykin S (1998) Neural networks: a comprehensive foundation. Prentice Hall PTR, Hoboken
He K, Zhang X, Ren S et al (2015) Delving deep into rectifiers: surpassing human-level performance on ImageNet classification. In: International conference on computer vision, 2015, pp 1026–1034
Heckerman D (2008) A tutorial on learning with Bayesian networks. Springer, Berlin, pp 33–82
Hochreiter S, Schmidhuber J (1997) Long short-term memory. Neural Comput 9(8):1735–1780
Hoeting JA, Madigan D, Raftery AE et al (1999) Bayesian model averaging: a tutorial. Stat Sci 14(4):382–417
Hoffman MD, Sountsov P (2022) Tuning-free generalized Hamiltonian Monte Carlo. In: International conference on artificial intelligence and statistics, 2022, pp 7799–7813
Hoffman MD, Blei DM, Wang C et al (2013) Stochastic variational inference. J Mach Learn Res 14:1303–1347
Hoffman MD, Gelman A et al (2014) The no-u-turn sampler: adaptively setting path lengths in Hamiltonian Monte Carlo. J Mach Learn Res 15(1):1593–1623
Homma T, Atlas LE, Marks RJ (1987) An artificial neural network for spatio-temporal bipolar patters: application to phoneme classification. In: Advances in neural information processing systems, 1987, pp 31–40
Horowitz AM (1991) A generalized guided Monte Carlo algorithm. Phys Lett B 268(2):247–252
Hosseini R, Sra S (2015) Matrix manifold optimization for Gaussian mixtures. In: Advances in neural information processing systems, 2015, vol 28
Hron J, Matthews A, Ghahramani Z (2018) Variational Bayesian dropout: pitfalls and fixes. In: International conference on machine learning, 2018, pp 2019–2028
Hu J, Liu X, Wen ZW et al (2020) A brief introduction to manifold optimization. J Oper Res Soc China 8(2):199–248
Jaakkola TS, Jordan MI (1997) A variational approach to Bayesian logistic regression models and their extensions. In: International workshop on artificial intelligence and statistics, 1997, pp 283–294
Jakkala K (2021) Deep Gaussian processes: a survey. Preprint. arXiv:2106.12135
Jang H, Lee J (2017) An empirical study on modeling and prediction of bitcoin prices with Bayesian neural networks based on blockchain information. IEEE Access 6:5427–5437
Jeuris B, Vandebril R, Vandereycken B (2012) A survey and comparison of contemporary algorithms for computing the matrix geometric mean. Electron Trans Numer Anal 39:379–402
Jospin LV, Laga H, Boussaid F et al (2022) Hands-on Bayesian neural networks—a tutorial for deep learning users. IEEE Comput Intell Mag 17(2):29–48
Kasai H, Jawanpuria P, Mishra B (2019) Riemannian adaptive stochastic gradient algorithms on matrix manifolds. In: International conference on machine learning, 2019, pp 3262–3271
Khan ME, Nielsen D (2018) Fast yet simple natural-gradient descent for variational inference in complex models. In: International symposium on information theory and its applications, 2018, pp 31–35
Khan M, Nielsen D, Tangkaratt V et al (2018a) Fast and scalable Bayesian deep learning by weight-perturbation in ADAM. In: International conference on machine learning, 2018, pp 2611–2620
Khan M, Nielsen D, Tangkaratt V et al (2018b) Fast and scalable Bayesian deep learning by weight-perturbation in ADAM. In: International conference on machine learning, 2018, pp 2611–2620
Kingma DP, Ba J (2014) ADAM: a method for stochastic optimization. arXiv preprint. arXiv:1412.6980
Knowles D, Minka T (2011) Non-conjugate variational message passing for multinomial and binary regression. In: Advances in neural information processing systems, 2011, vol 24
Kobayashi S, Nomizu K (1963) Foundations of differential geometry. Wiley, New York
Krizhevsky A, Sutskever I, Hinton GE (2012) ImageNet classification with deep convolutional neural networks. In: Advances in neural information processing systems, 2012, vol 25
Kullback S, Leibler RA (1951) On information and sufficiency. Ann Math Stat 22(1):79–86
Kwon Y, Won JH, Kim BJ et al (2020) Uncertainty quantification using Bayesian neural networks in classification: application to biomedical image segmentation. Comput Stat Data Anal 142(106):816
Lampinen J, Vehtari A (2001) Bayesian approach for neural networks—review and case studies. Neural Netw 14(3):257–274
Längkvist M, Karlsson L, Loutfi A (2014) A review of unsupervised feature learning and deep learning for time-series modeling. Pattern Recognit Lett 42:11–24
Leimkuhler B, Reich S (2005) Simulating Hamiltonian dynamics. Cambridge monographs on applied and computational mathematics. Cambridge University Press, Cambridge
Lemieux C (2014) Control variates. Statistics Reference Online, Wiley StatsRef, pp 1–8
Liang Y, Kelemen AG (2004) Hierarchical Bayesian neural network for gene expression temporal patterns. Stat Appl Genet Mol Biol 3(1):20
Lin W, Schmidt M, Khan ME (2020) Handling the positive-definite constraint in the Bayesian learning rule. In: International conference on machine learning, 2020, pp 6116–6126
Lisboa PJ, Wong H, Harris P et al (2003) A Bayesian neural network approach for modelling censored data with an application to prognosis after surgery for breast cancer. Artif Intell Med 28(1):1–25
Lynch SM (2007) Introduction to applied Bayesian statistics and estimation for social scientists, vol 1. Springer, New York
Lyu Y, Tsang IW (2021) Black-box optimizer with stochastic implicit natural gradient. In: Joint European conference on machine learning and knowledge discovery in databases, 2021. Springer, pp 217–232
Ma Q, Wang JT (1999) Biological data mining using Bayesian neural networks: a case study. Int J Artif Intell Tools 8(04):433–451
Mackay DJC (1992) Bayesian methods for adaptive models. PhD Thesis, California Institute of Technology
Mackay DJC (1995) Probable networks and plausible predictions—a review of practical Bayesian methods for supervised neural networks. Netw Comput Neural Syst 6:469–505
Magris M, Shabani M, Iosifidis A (2022a) Bayesian bilinear neural network for predicting the mid-price dynamics in limit-order book markets. Preprint. arXiv:2203.03613
Magris M, Shabani M, Iosifidis A (2022b) Exact manifold Gaussian variational Bayes. Preprint. arXiv:2210.14598
Magris M, Shabani M, Iosifidis A (2022c) Quasi black-box variational inference with natural gradients for Bayesian learning. Preprint arXiv:2205.11568
Mardia KV, Marshall RJ (1984) Maximum likelihood estimation of models for residual covariance in spatial regression. Biometrika 71(1):135–146
Metropolis N, Rosenbluth AW, Rosenbluth MN et al (1953) Equation of state calculations by fast computing machines. J Chem Phys 21(6):1087–1092
Nakajima S, Watanabe K, Sugiyama M (2019) Variational Bayesian learning theory. Cambridge University Press, Cambridge
Neal RM et al (2011) MCMC using Hamiltonian dynamics. Handb Markov Chain Monte Carlo 2(11):2
Nielsen F (2020) A note on the natural gradient and its connections with the Riemannian gradient, the mirror descent, and the ordinary gradient
Nielsen F, Garcia V (2009) Statistical exponential families: a digest with flash cards. Preprint. arXiv:0911.4863
Oleksiienko I, Iosifidis A (2022) Layer ensembles. arXiv preprint. arXiv:2210.04882
Oleksiienko I, Tran DT, Iosifidis A (2022) Variational neural networks. arXiv preprint. arXiv:2207.01524
Opper M, Archambeau C (2009) The variational Gaussian approximation revisited. Neural Comput 21(3):786–792
Opper M, Winther O (1999) A Bayesian approach to on-line learning. In: On-line learning in neural networks. Cambridge University Press, Cambridge, pp 363–378
Osawa K, Swaroop S, Khan MEE et al (2019) Practical deep learning with Bayesian principles. In: Advances in neural information processing systems, 2019, vol 32
Osband I, Aslanides J, Cassirer A (2018) Randomized prior functions for deep reinforcement learning. In: Advances in neural information processing systems, 2018, vol 31
Paisley J, Blei DM, Jordan MI (2012) Variational Bayesian inference with stochastic search. In: International conference on international conference on machine learning, 2012, pp 1363–1370
Passalis N, Tefas A, Kanniainen J et al (2020) Temporal bag-of-features learning for predicting mid price movements using high frequency limit order book data. IEEE Trans Emerg Top Comput Intell 4(6):774–785
Ranganath R, Gerrish S, Blei D (2014) Black box variational inference. In: International conference on artificial intelligence and statistics, 2014, pp 814–822
Rao CR (1945) Information and the accuracy attainable in the estimation of statistical parameters. Bull Calcutta Math Soc 38:81–91
Rezende DJ, Mohamed S, Wierstra D (2014) Stochastic backpropagation and approximate inference in deep generative models. In: International conference on machine learning, 2014, pp 1278–1286
Robbins H, Monro S (1951) A stochastic approximation method. Ann Math Stat 22(3):400–407
Robert CP, Roberts GO (2021) Rao–Blackwellization in the MCMC era. arXiv preprint. arXiv:2101.01011
Robert CP, Casella G, Casella G (1999) Monte Carlo statistical methods, vol 2. Springer, Berlin
Rumelhart DE, Hinton GE, Williams RJ (1986) Learning representations by back-propagating errors. Nature 323:533–536
Salimans T, Knowles DA (2013) Fixed-form variational posterior approximation through stochastic linear regression. Bayesian Anal 8(4):837–882
Sariev E, Germano G (2020) Bayesian regularized artificial neural networks for the estimation of the probability of default. Quant Finance 20(2):311–328
Saul LK, Jaakkola T, Jordan MI (1996) Mean field theory for sigmoid belief networks. J Artif Intell Res 4:61–76
Serafino L (2013) No free lunch theorem and Bayesian probability theory: two sides of the same coin. Some implications for black-box optimization and metaheuristics. Preprint. arXiv:1311.6041
Shen X, Tian X, Liu T et al (2018) Continuous dropout. IEEE Trans Neural Netw Learn Syst 29(9):3926–3937
Skopek O, Ganea OE, Bécigneul G (2019) Mixed-curvature variational autoencoders. Preprint. http://arxiv.org/abs/1911.08411arXiv:1911.08411
Sra S, Hosseini R (2015) Conic geometric optimization on the manifold of positive definite matrices. SIAM J Optim 25(1):713–739
Srivastava N, Hinton G, Krizhevsky A et al (2014) Dropout: a simple way to prevent neural networks from overfitting. J Mach Learn Res 15(1):1929–1958
Tan LS (2021) Analytic natural gradient updates for Cholesky factor in Gaussian variational approximation. Preprint. arXiv:2109.00375
Tieleman T, Hinton G (2012) Lecture 6.5-RMSProp, COURSERA: neural networks for machine learning. University of Toronto, Technical Report 6
Tran DT, Iosifidis A, Kanniainen J et al (2019) Temporal attention-augmented bilinear network for financial time-series data analysis. IEEE Trans Neural Netw Learn Syst 30(5):1407–1418
Tran MN, Nguyen DH, Nguyen D (2021a) Variational Bayes on manifolds. Stat Comput 31(6):71
Tran MN, Nguyen TN, Dao VH (2021b) A practical tutorial on variational Bayes. arXiv preprint. arXiv:2103.01327
Trusheim F, Condurache A, Mertins A (2018) Boosting black-box variational inference by incorporating the natural gradient. In: International conference on pattern recognition, 2018, pp 19–24
Tu LW (2011) Manifolds. In: An introduction to manifolds. Springer, Berlin, pp 47–83
Vehtari A, Lampinen J (1999) Bayesian neural networks for industrial applications. In: IEEE Midnight-Sun workshop on soft computing methods in industrial applications, 1999, pp 63–68
Viaene S, Dedene G, Derrig RA (2005) Auto claim fraud detection using Bayesian learning neural networks. Expert Syst Appl 29(3):653–666
Wainwright MJ, Jordan MI (2008) Graphical models, exponential families, and variational inference. Found Trends Mach Learn 1(1–2):1–305
Waldmann P (2018) Approximate Bayesian neural networks in genomic prediction. Genet Sel Evol 50(1):1–9
Wen Y, Tran D, Ba J (2020) BatchEnsemble: an alternative approach to efficient ensemble and lifelong learning. In: International conference on learning representations, 2020
Wierstra D, Schaul T, Glasmachers T et al (2014) Natural evolution strategies. J Mach Learn Res 15(1):949–980
Wilson AC, Roelofs R, Stern M et al (2017) The marginal value of adaptive gradient methods in machine learning. In: Advances in neural information processing systems, 2017, vol 30
Wolpert DH (1996) The lack of a priori distinctions between learning algorithms. Neural Comput 8(7):1341–1390
Young T, Hazarika D, Poria S et al (2018) Recent trends in deep learning based natural language processing. IEEE Comput Intell Mag 13(3):55–75
Zhou B, Gao J, Tran MN et al (2021) Manifold optimization-assisted Gaussian variational approximation. J Comput Graph Stat 30(4):946–957
Funding
The research received funding from the European Union’s Horizon 2020 Research and Innovation Programme under the Marie Skłodowska-Curie Project BNNmetrics (Grant Agreement No. 890690).
Author information
Authors and Affiliations
Contributions
MM and AI wrote the main manuscript test, MM prepared the figures and pseudo-codes. Both the authors reviewed the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: Nomenclature
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Magris, M., Iosifidis, A. Bayesian learning for neural networks: an algorithmic survey. Artif Intell Rev 56, 11773–11823 (2023). https://doi.org/10.1007/s10462-023-10443-1
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10462-023-10443-1