Abstract
Metaheuristic algorithms based on intelligent rules have been successfully developed and applied to solve many optimization areas over the past few decades. The sine–cosine algorithm (SCA) imitates the behaviour of transcendental functions while the sine and cosine functions are presented to explore and exploit the search space. SCA starts by random population and executes iterative evolution processes to update the standard evolutionary algorithm’s destination or the best location. SCA used linear transition rules to balance the exploration and exploitation searches while searching for the best or optimal solutions. Since Mirjalili proposed it in 2016, SCA has attracted many researchers’ attention to deal with several optimization problems in many fields due to its strengths in solving optimization tasks that include the simple concept, easiness of implementation, and rapid convergence. This paper aims to provide researchers with a relatively comprehensive and extensive overview of the Sine–Cosine optimization algorithm in the literature to inspire further research. It examines the available publications, including improvements, binary, chaotic, hybridizations, multi-objective variants, and different applications. Some optimization formulations regarding single-objective optimization problems, multi-objective optimization problems, binary-objective optimization problems, and more classifications regarding the optimization types are discussed. An extensive bibliography is also included.
Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.Avoid common mistakes on your manuscript.
1 Introduction
The rapid increase of the complicated real-life optimization problems in many fields pays many attention of researchers to develop effective and efficient optimization methodologies to cope with the urgent needing for solving the complex optimization problems, which include some natures, continuous or discrete, constrained or unconstrained, single or multi-objective, and static or dynamic. Early, many mathematical (traditional) techniques have been introduced, such as direct search and indirect search methods (Rao 2019). However, as these methods start from one initial guess and the dependency on gradient information, they often fail to reach the optimal solutions. Also, they are time-consuming while dealing with large data sizes and unstable when dealing with complex environments.
Meta-heuristic algorithms have been developed as promising alternative methods to overcome the shortages of traditional techniques by employing multiple initial guesses and avoiding the reliance on gradient information. They are established based on randomization and local search to achieve robust exploration searchability and coarser exploitation. Additionally, they have further featured such as simplicity flexibility. Metaheuristic optimization algorithms are classified into five categories such as evolutionary-based algorithms, swarm-based algorithms, physical-based algorithms, human behaviours-based algorithms, and biological behaviour-based algorithms (Dhiman and Kumar 2017; Luke 2013) (Refer to Fig. 1).
Evolutionary-based algorithms are introduced based on biological evolution that possesses reproduction, mutation, recombination, and selection. They follow the survival concept based on fitness for a population of candidates (i.e., a set of solutions) in a certain environment. Some of the prominent techniques are Genetic Programming (GP) (Koza 1992), Genetic Algorithms (GA) (Bonabeau et al. 1999), Evolution Strategy (ES) (Beyer and Schwefel 2002), Biogeography-Based Optimizer (BBO) (Simon 2008), and Differential Evolution (DE) (Storn and Price 1997). The second issue is that swarm-based techniques are inspired by the collective behaviour of bird flocking or social creatures. This behaviour simulates the interaction among the swarms within their environment. The most popular techniques are Ant Colony Optimization (Mousa et al. 2011; El-Sawy et al. 2013) (ACO), Bat-inspired Algorithm (BA) (Yang 2010a; Rizk-Allah and Hassanien 2018), Particle Swarm Optimization (PSO) (Kennedy 2011), firefly algorithm (FA) (Yang 2010b; Rizk-Allah 2014; Rizk-Allah et al. 2013), fruit fly optimization algorithm (FOA) (Han et al. 2018; Rizk-Allah 2016; Rizk-Allah et al. 2017a), Bee Colony (ABC) algorithm (Karaboga et al. 2014), Cuckoo Search (CS) (Yang and Deb 2014), Monkey Search (Mucherino and Seref 2007), Grey Wolf Optimizer (Mirjalili and Mirjalili 2014), ant lion algorithm (Mirjalili 2015), crow search algorithm (Askarzadeh 2016; Rizk-Allah et al. 2018, 2020a; Hassanien et al. 2018), Salp Swarm Algorithm (SSA) (Mirjalili et al. 2017; Rizk-Allah et al. 2018) and Spotted Hyena Optimizer (Dhiman and Kumar 2017). The physical-based algorithms are presented based on physical rules such as electromagnetic force, gravitational force, inertia force, and so on to perform the communication and movements among the agents throughout the search space. Some of this category is Simulated Annealing (SA) (Kirkpatrick et al. 1983), Colliding Bodies Optimization(CBO) (Kaveh and Mahdavi 2014), Gravitational Search Algorithm (GSA) (Rashedi et al. 2009), Black Hole (BH) (Hatamlou 2013), Charged System Search (CSS) (Kaveh and Talatahari 2010), Big-Bang Big-Crunch (BBBC) (Erol and Eksin 2006), Central Force Optimization (CFO) (Formato 2008), Ray Optimization (RO) algorithm (Kaveh and Khayatazad 2012), Small-World Optimization Algorithm (SWOA) (Du et al. 2006), Galaxy-based Search Algorithm (GbSA) (Shah 2011), Artificial Chemical Reaction Optimization Algorithm (ACROA) (Alatas 2011), Curved Space Optimization (CSO) (Moghaddam et al. 2012), and atom search algorithm (Zhao et al. 2019; Rizk-Allah et al. 2020b). The fourth category is the Human-based techniques which mimic human behaviours, where this category involving the League Championship Algorithm (LCA) (Kashan 2009), Harmony Search (HS) (Geem et al. 2001), Mine Blast Algorithm (MBA) (Sadollah et al. 2013), Tabu (Taboo) Search (TS) (Glover 1989, 1990), Teaching–Learning-Based Optimization(TLBO) (Rao et al. 2012), Group Search Optimizer (GSO) (He et al. 2006), Soccer League Competition (SLC) algorithm (Moosavian and Roodsari 2014), Imperialist Competitive Algorithm (ICA) (Atashpaz-Gargari and Lucas 2007), Seeker Optimization Algorithm (SOA) (Dai et al. 2007), and Exchange Market Algorithm (EMA) (Ghorbani and Babaei 2014). The last one is biological behaviour-based algorithms which are inspired by biological phenomena, and they include the artificial immune system (Dasgupta and (Ed.). 2012), bacterial forging optimization (Das et al. 2009), and others (Krichmar and (2012, June). 2012; Binitha and Sathya 2012). The salient features of metaheuristic algorithms are contained in their exploration and exploitation searches, where the exploration is responsible for reaching the different promising areas within the search space. In contrast, exploitation enriches the search for optimum solutions within the given region. The fine-tuning of these features is essential to attain the optimal solution for the candidate task during the searching process. On the other side, balancing these features is very difficult due to the stochastic nature of metaheuristic algorithms. Furthermore, the performance of a certain algorithm while solving the set of problems does not guarantee the superiority for the set of the issues with different natures (Omidvar et al. 2015). This fact undoubtedly becomes a challenging issue and can motivate researchers and scientists to continue developing new metaheuristic algorithms for solving more varieties of real-life problems (Yang 2011).
The sine–cosine algorithm (SCA) was initially proposed by Mirjalili (2016) in 2016, where it is inspired by the philosophy of transcendental functions via periodic behaviours using the sine and cosine functions. Like other inspiration, SCA employs mathematical mimics during the optimization process. It is assumed that multiple initial random candidate solutions fluctuated outward or toward the destination (best solution) using the sine and cosine functions. Also, some random and adaptive parameters emphasize exploration and exploitation searches through different optimisation milestones. SCA has been successfully applied and implemented in numerous areas of real-world optimization problems within diverse fields of technology and science. This paper proposes a comprehensive study of almost all perspectives regarding SCA in numerous domains along with the basic concepts, the integrated modifications, SCA versions of binary scenarios, hybridizations, and applications. Also, multiobjective versions of SCA are reviewed.
The rest sections of this paper are structured as follows. Section 2 exhibits a gentle description of the basic concepts and framework of the original SCA. Section 3 provides the variants of SCA based on different techniques and strategies. The hybridizations of SCA with different algorithms have been reviewed in Sect. 4. Section 5 provides an overview regarding some prominent applications of SCA. Section 6 highlights some research directions for future works related to SCA. Finally, the conclusion of the paper is presented in Sect. 7.
2 Preliminaries
This section provides some optimization formulations regarding single-objective optimization problems (SOOP), multi-objective optimization problems (MOOP), binary-objective optimization problems (BOOP), and more classifications regarding the optimization types.
2.1 The SOOP form
The SOOP aims to find the optimal solution for an optimization expression by considering potential decision variables’ minimum or maximum value; it can be defined mathematically.
where \({\mathbf{x}} = (x_{1} ,x_{2} ,...,x_{n} )\,\) represents the vector of \(n\) control/decision variables that belongs to the feasible set (\(FS\)), \(f({\mathbf{x}})\) define the objective function. Here \(G_{l} ({\mathbf{x}})\) and \(H_{j} ({\mathbf{x}})\) are the inequality constraints and equality constraints, respectively, \(lb_{i}\) and \(ub_{i}\) define the bounds of lower and the upper for each variable, respectively.
Definition 1 (Global minimum):
Assume the function \(f:\,FS \subseteq \,{\mathbb{R}}^{n} \to R,\,\,FS \ne \phi ,\) then the global minimum is denoted as \({\mathbf{x}}^{*}\) and equals the \(\mathop {{\text{arg min}}\,f({\mathbf{x}})}\limits_{{{\mathbf{x}}\, \in FS\,\,\,}} ,\)\(f({\mathbf{x}}^{*} ) \le f({\mathbf{x}})\)\(\forall \,{\mathbf{x}} \in FS\).
2.2 The MOOP form
The MOOP aims to simultaneously minimise multiple objective functions that have conflicting natures. In this sense, it is impossible to obtain a single solution that can optimize all objective functions simultaneously. Hence, a set of solutions known as Pareto optimal set (POS) can be obtained. The MOOP can be defined as minimization as follows:
where \(F({\mathbf{x}})\) denotes the vector of objectives.
Definition 2: The solution \(\,{\mathbf{x}}\) dominates another solution \({\mathbf{y}}\), if and only if \(\forall k,f_{k} ({\mathbf{x}}) \le f({\mathbf{y}})\) and \(\exists \,j \in\)\(:\)\(f_{j} ({\mathbf{x}}) < f_{j} ({\mathbf{y}})\). The set of non- dominated is called Pareto Optimal.
2.3 The BOOP form
The mathematical formulation of binary optimization can be expressed as follows:
where \(C\) denotes the resources \(w_{j}\) and \(p_{j}\) represents the weight, and the profit of the \(j{\text{th}}\) item, respectively.
2.4 Aspects of optimization
More details about optimization problems regarding the objective function and the decision variables can be presented (Refer to Fig. 2). In this regard, the classifications can be considered in terms of the number of objectives, restrictions or constraints, nature of functions, landscape regarding the objective functions, variables type, and determinacy in values. Consequently, the classification according to objectives involves three categories: single objective \(K = 1\), multiobjective \(K = 2,3\), and many objectives \(K > 3\) M > 1. Several real-life problems have multiobjective natures. Designing a car engine involves three objectives: maximization of the fuel efficiency, minimization of the carbon-dioxide emission, and reducing its noise level. These objectives have a conflicting nature, and a compromise concept is needed.
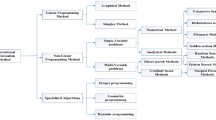
Similarly, two classes can appear when the classification is performed in terms of constraints. When there is no constraint \(G({\mathbf{x}}),\,H({\mathbf{x}}) = \phi\) (i.e., \(\phi\) denotes an empty set), it is called an unconstrained optimization problem, and when \(G({\mathbf{x}})\) and/or \(H({\mathbf{x}}) \ne \phi\), it is called a constrained problem. The function forms are classified as linear or nonlinear. Linear when the \(f({\mathbf{x}}),\) \(G({\mathbf{x}}),\,H({\mathbf{x}})\) are all linear, and then it becomes a linear programming problem (LPP). Here the term ‘programming’ means planning and/or optimization, not computing programming. However, if one of the functions (i.e., \(f({\mathbf{x}}),\)\(G({\mathbf{x}}),\,H({\mathbf{x}})\)) is nonlinear, it is called a nonlinear optimization problem.
The classification in terms of the landscape or the shape of the objective functions can be split into three classes. The problem is called unimodal when the function only has a single valley or peak with a unique global optimum. If the objective function has more than one valley or peak, it is called multimodal function, which is more difficult than unimodal as it contains local and global optima.
The design variables involve the discrete nature, and then the optimization is called discrete optimization, where if it involves integer nature, then it is named an integer programming problem. Also, discrete optimization is known as combinatorial optimization. It is very important for several fields such as graph theory, minimum spanning tree problem, routing, the travelling salesman problem, vehicle routing, knapsack problem, and airline scheduling. Suppose all the design variables take real values. In that case, it is referred to as a continuous optimization problem, and the design variables present both natures of discrete and continuous, then it is called mixed optimization problem.
The final category considers the determinacy aspect as follows. It is a deterministic optimization problem when the values for the design variables and objective/constraints are determined exactly as no noise or uncertainty in their values. When uncertainty and noise exist between the design variables and the objective functions and/or constraints, the problem becomes a stochastic optimization problem.
2.5 Optimization methodologies
Different optimisation methods must be presented to cope with the various optimization problem natures. In the following paragraph, we review some optimization techniques.
The optimization searching process for the best or the optimal solution is similar to treasure hunting. Imagine it is intended to hunt in a hilly landscape for a hidden treasure within a limited time. In one extreme, let someone is blindfolded searching for lost something, he will perform a pure random search that is not as useful as expected. In another sight, consider someone is told the place of the treasure is that at the highest peak of a known region, he will directly try to attain the highest peak by climbing up the steepest cliff. This scenario is similar to the classical hill-climbing techniques. In this regard, random walking can achieve a plausible place instead of searching in every single square inch of the large hilly region. Such random walking is the main feature of modern search methods. Also, simulated annealing is one of the modern search methods that can do treasure-hunting alone. Alternatively, if asked a group of people to search for the treasure, they can share their information (and any treasure found), and this sight is so-called swarm intelligence which corresponds to the PSO.
In this regard, the optimization algorithms have been divided into deterministic-based algorithms (DBAs) and stochastic-based algorithms (SBAs) (see Fig. 3). DBAs employ a rigorous procedure that is repeatable. DBAs start with a single starting point and depend on the gradient information, such as the Simplex method for handling LPP and Newton–Raphson method. On the other hand, the SBAs present some randomness procedures caused by random components. Due to these random components, they are classified as a stochastic algorithms. They start with single or multiple starting points, where no reliance on the gradient information is also suitable for discontinuity. Furthermore, the mixture or hybrid of DBAs and SBAs presents the third type. This hybridization aims to avoid the stuck in a local peak.
Two types have been established for stochastic-based algorithms, namely heuristic and metaheuristic. The heuristic is defined as ‘to find’ or ‘to explore using trial and error’. Thus, the heuristic algorithms do not guarantee the optimal solutions and are good enough when the best solutions are not necessarily reached and the reasonable solutions are satisfied.
The further developments in heuristic algorithms lead to metaheuristic algorithms. The term meta- means ‘beyond’ or ‘higher level’. Also, these algorithms can perform better searches than the heuristic ones. The metaheuristic algorithms employ certain tradeoffs among the randomization manner and local search. However, recent literature tends to name stochastic algorithms as metaheuristics.
2.6 Traditional SCA
Motivated by the NFL and the ever-increasing in solving daily real-life problems, many researchers have been encouraged to develop new algorithms. Several algorithms have been presented in the literature, depending on the problem type and its characteristics. Thus, no universal algorithm can work for all problems and guarantee a global solution. This fact has been denoted as ‘No Free Lunch Theorems’ (NLF theorem). NLF theorem says that algorithm A can perform better than algorithm B in searching for some cost functions, and algorithm B can outperform A for other cost functions.
SCA is a population-based algorithm inspired by the mathematical rules proposed by Mirjalili, 2016 (Mirjalili 2016). The core concept of SCA is to employ the behaviours of the mathematical sine and cosine functions for optimization searching. Like many optimization methodologies, SCA starts with the initialization step that involves a population of agents following a random fashion in generating the initial solutions. These agents are iteratively updated by using the characteristics of sine and cosine functions via some stochastic parameters. The working phases of SCA are described below.
2.6.1 Updating phase
In this phase, each solution can be evolved by updating the process that is expressed as follows.
where \(x_{i}^{(t + 1)}\), \(x_{i}^{(t)}\) are the \(i{\text{th}}\) \((i = 1,2,...,N)\) solution vectors at \((t + 1){\text{th}}\) and \(t{\text{th}}\) iteration respectively and \(x_{best}^{(t)}\) represents the fittest solution vector at the \(t{\text{th}}\) iteration. Here, \(r\) presents a uniformly random number distributed in the interval (0, 1) and performs the transition from sine to cosine forms and vice versa. Here, \(A_{2}\) a direction parameter is responsible for the movement of the current solution either towards the \(x_{best}^{(t)}\) or outside \(x_{best}^{(t)}\). The \(A_{3}\) weight parameter can emphasize the exploration manner when \(A_{3} > 1\) and enhance the exploitation when \(A_{3} < 1\).
A conceptual description of the sine and cosine functions while updating the process of the position within the range in [-2, 2] is depicted in Fig. 4. This change is performed with the \(A_{2}\) in.
2.6.2 Balancing phase
The balancing phase is responsible for maintaining a suitable balance among the diversification and intensification characteristics and thus avoiding the dilemma of premature convergence. In this sense, the parameter \(A_{1}\) can be introduced by deciding the region of the search space around the current solution, where this region can lie inside \(x_{best}^{(t)}\) and \(x_{i}^{(t)}\) or outside them. Accordingly, the parameter \(A_{1}\) contributes the exploration feature in the first half of the total number of iterations and can support the exploitation in the second half of the total number of iterations. Mathematically the parameter \(A_{1}\) can be expressed as follows
where \(l\) and \(L\) define respectively the current and maximum iterations. The framework of SCA is pointed out in Fig. 5.
2.6.3 Implementation and numerical example
To illustrate the steps of SCA, we can implement it with MATLAB code (Refer to the Appendix). Also, the simulations with test functions are provided in detail as follows to find the minimum of the function \(f(x_{1} ,x_{2} ) = x_{1}^{2} + x_{2}^{2} \,,\)\(\, - 1 \le x_{1} ,x_{2} \le 1\). We know that its global minimum \(f(x_{1} ,x_{2} ) = 0\) occurs at (0, 0). The landscape of the function is shown in Fig. 6, while its contour is provided in Fig. 7.
Solution:
1. Set the number of search agents \(N\) as 5.
2. The initialize the population of search agents randomly as
Then evaluate the objective function values for these solutions as
Find the best position \((x_{best}^{{}} )\) with its destination \(f_{best}^{{}}\) as.
\(x_{best}^{{}} = [ - 0.{746}0, 0.0{938]}\); \(f_{best}^{{}} = 0.{565347}\).
3 Begin the loop: \(l = 1\)(iteration counter)
Update the positions using Eq. (4), then the new solutions become as follows.
Solution, l=1 | [x1, x2] | F (X) |
|---|---|---|
X1 | 1.0000 −0.6297 | 1.396475 |
X2 | −1.0000 −0.7280 | 1.529987 |
X3 | 0.0095 0.0027 | 9.67E−05 |
X4 | −0.3844 1.0000 | 1.14777 |
X5 | 1.0000 1.0000 | 2 |
The next iterations can provide the following solutions by updating, evaluating, and updating the destination. The convergence behaviours of the best objective values and the average values during the five iterations for SCA are provided in Fig. 8.
Solution, l=2 | [x1, x2] | F (X) |
|---|---|---|
X1 | [−0.8403, −1.0000] | 1.706111 |
X2 | [−1.0000, −0.6850] | 1.469287 |
X3 | [−0.0011, 0.0027] | 8.69E−06 |
X4 | [−1.0000, 0.9362] | 1.876391 |
X5 | [1.0000, 1.0000] | 2 |
Solution, l=3 | [x1, x2] | F (X) |
|---|---|---|
X 1 | [0.0660, 1.0000] | 1.004355 |
X 2 | [−0.3418, −1.0000] | 1.116816 |
X 3 | [−0.0013, 0.0021] | 6.11E−06 |
X 4 | [0.3633, 1.0000] | 1.131982 |
X 5 | [1.0000, 1.0000] | 2 |
Solution, l=4 | [x1, x2] | F (X) |
|---|---|---|
X 1 | [0.1819, −0.9666] | 0.967342 |
X 2 | [−0.3972, −1.0000] | 1.157735 |
X 3 | [0.0008, 0.0023] | 5.76E−06 |
X 4 | [0.7071, 1.0000] | 1.499973 |
X 5 | [−0.8279, −0.6147] | 1.063252 |
4 Improvements and analysis
Since its introduction by Mirjalili in 2016, SCA has perceived notable attention of scientists and engineers in several disciplines worldwide. Many new improvements and ideas have been integrated and combined with the original SCA for improving its performance to deal with large varieties of optimization issues. In the following, some prominent improvements related to SCA are analyzed and reviewed along with different subtitles. The categorization scheme with some methods of SCA is presented in Fig. 9.
4.1 SCA based- opposition schemes
Many meta-heuristic algorithms begin with an initial population, where the goodness of the initialization step can help generate better solutions in the final optimization iterations. Therefore, new ways for initializing the population of SCA have been incorporated with opposition-based learning (OBL) that was presented by Tizhoosh (Tizhoosh 2005), named as OBSCA (Abdelaziz et al. 2017). Based on this situation, the searching speed can be accelerated by retaining the fitter one opposite for an individual in the population.
where \(x_{i}^{o}\) denotes the opposite vector of the \(i{\text{th}}\) solution. \(Lb\) and \(Ub\) defines the vectors of lower and upper bounds, respectively.
On the other hand, Gupta (Gupta and Deep 2019a) proposed a modified SCA (m-SCA) based on the OBL scheme to generate the opposite population to jump out from the local optima. In addition to OBL, a self-adaptive direction (SAD) is presented to exploit all the promising search regions. The SAD is combined with the classical updating rule of SCA, and the new updating solution is expressed as follows.
where \(x_{cb}\) denotes the current best of the solution \(x_{i}^{(t)}\) obtained so far and \(S_{R}\) defined the jumping rate or perturbation. The term \(S_{R} (x_{cb} - x_{i}^{(t)} )\) works as a local search using the previous information of the best solution stored in the memory. Thus, it exploits all the promising areas around the best solutions obtained.
The integration of OBL with the optimization algorithms is fruitful when the solutions are far from the promising areas of the optima, especially when the optima are in opposite directions of these solutions (Refer to Fig. 10).
4.2 SCA based- genetic operations scheme
The genetic operations are prominent operators inspired by the basics of GA. The mutation operator works to make a random change in one or several bits of the offspring. The crossover operator exchanges some of the bits in the two individuals to generate the offspring. By these operators, the exploration ability and the diversity of the population can be enhanced. Hence, some researchers have invoked these operators into SCA. To enhance the searching process and improve the convergence rate, Gupta et al. (Gupta et al. 2020a) developed a modified SCA variant (MSCA) with Gaussian mutation and a non-linear transition rule. In each generation, the solution is updated randomly using the new modified search equation (Eq. 8) or by Gaussian mutation form (Eq. 9).
The parameter \(r_{1}\) denotes the random number that is uniformly distributed in the interval (0, 1), \(\beta\) defines random number that is induced from the Logistic chaotic map, and it is defined as follows.
Here \(c\) represent a control parameter and has a fixed value (\(c = 4\)).
In Eq. (5), \(\delta\) a Gaussian mutation operator is combined into the MSCA to reduce the loss of diversity during the searching stage. The given form expresses the density function of Gaussian distribution:
where \(\sigma^{2}\) presents the variance that corresponds to each solution. This density function is reduced to generate a random number based on Gaussian distribution through a zero value for the mean to 0 and one for the standard deviation. Thus, the mutation operator that is developed to obtain a new solution \(z_{i}^{(t + 1)}\) can be considered as:
On the other side, Gupta (Gupta and Deep 2019b) proposed an improved SCA (ISCA) based on a crossover operator to avoid the slow convergence, stagnation in local optima, and skipping of true solutions when dealing with real-life problems. To alienate these issues, greedy selection strategy and crossover mechanisms are integrated into SCA. In this regard, ISCA starts the initialization step as the classical SCA, but it evolves its solutions with a new modified updating equation as follows:
where \(x_{i,pb}\) represents the current best solution obtained so far of the solution \(x_{i}^{(t)}\), and \(A_{4}\) denotes a uniform random number ranging from 0 to 1.
Afterwards, the crossover operator is performed by crossing the obtained solution \(x_{i}^{(t + 1)}\) is with the current best solution \(x_{i,pb}\) of the solution \(x_{i}^{(t)}\) by using the following equation.
where \(r_{j}\) denotes a uniform random number ranged from 0 to 1 of the \(j_{{}}^{th}\) dimension and \(CR\) presented the crossover rate that is taken as 0.3.
After implementing the crossover mechanism, the greedy selection is involved in determining the survival solution among \(x_{i,pb}\) and \(u_{i}^{(t + 1)}\), where the greedy selection is expressed as follows
where \(f(.)\) defines the objective function that is in minimization form.
4.3 SCA based-learning strategies
Chen et al. (Chen et al. 2020a) developed a memetic SCA (MSCA) variant based on several search strategies incorporating the chaotic local search strategy (CLS), Cauchy mutation operator (CM), opposition-based learning mechanism (OBL)as well as the mutation and crossover strategies (MCS)inspired from differential evolution which is synchronously developed to enhance the conventional SCA performance and balance between exploitation and exploration abilities. In this context, CLS strategy aims to strengthen the diversity of solutions, CM operates to improve the possibility of the exploration to achieve different regions of the solution space, the OBL mechanism aims to compute opposite position that may be better than the current state and the MCS can enhance the capabilities of exploration and exploitation when solving complex tasks. These strategies are equipped into the classical SCA to improve its performance and solve complicated tasks effectively.
The first modification is to use the OBL, where the opposite solution is survival if it is better than the corresponding solution based on the fitness function.
The second modification employs the CM operator that is introduced based on the Cauchy density function and distribution function, where they are presented as follows.
where \(\lambda \,(\lambda > 0)\) denotes a proportion parameter. Therefore, the CM operator is presented for updating the solution can be expressed as follows.
where C defines a distributed random number generated according to Cauchy distribution, \(x_{i}^{^{\prime}(t)}\) represents the updated solution of \(x_{i}^{(t)}\) at the current iteration after invoking the CM.
The third modification presents the CLS strategy in which the chaotic logistic function is implemented as follows.
where \(x_{i}^{^{\prime}(t)}\) defines the new vector of \(x_{i}^{(t)}\) in the \(t{\text{th}}\) iteration obtained by CLS and \(\upsilon_{c}\) is determined using the following equation:
where \(\beta_{t}\) is drawn from the chaotic map at the current iteration, where \(\beta_{1}\) is randomly created ranged in [0, 1], and \(\upsilon_{c}\) represents the mapped value that is linearly integrated with the optimal solution as the following.
where \(CF\) defines a contraction factor that is calculated as follows:
The fourth modification exhibits the MCS operator, where the mutation operator can produce a mutant vector \(\vartheta_{i}\) by eliciting randomly three vectors \(x_{a} ,x_{b} ,x_{c}\), where \(a \ne b \ne c \ne i\). This can describe as follows.
where \(F\) means a random number.
Afterward, the crossover operator crosses the mutant vector \(\vartheta_{i}\) with the target solution \(x_{best}^{(t)}\) by using the following equation.
The \(P_{c}\) is the probability factor that controls the diversity of the population and \(j_{0}\) defines the index between \(j_{0} = \{ 1,2,...,D\}\) that guarantees that \(u_{i}^{(t + 1)}\) receives at least one component from \(\vartheta_{i}\).
The four strategies that involve the CM, CLS, OBL, and MCS are worked in a sequential manner to generate new solutions and also update the destination or the best solution.
Rizk-Allah (Rizk-Allah 2018) proposed a new variant of SCA based on a multi-orthogonal search strategy (MOSS) to improve the exploration and exploitation patterns, named (MOSS). In addition, a new updating rule is based on the probability (\(p_{i}\)) factor as follows.
where \(p_{i}\) represents a mutation probability of switching among terms. Further improvement on the linear aspect of the parameter is introduced to be gradually shrunk in the nonlinear aspect.
where \(a^{\min }\) and \(a^{\max }\) are the limits for the parameter \(A_{1}\).
Furthermore, the multi-orthogonal search strategy (MOSS) is presented in a parallel form, where the generation of the solutions is as follows. The MOSS is inspired by the orthogonal design concept of a multifactor experiment that was proposed by [(Erol and Eksin 2006) to obtain a set of combinations or orthogonal array (OA). It starts by determining the levels number \(\alpha\), along with the number of factors, \(v\), and thus the OAs that is denoted by \(L_{m} (\alpha^{v} )\) can be obtained, where the index \(L\) denotes the Latin square with the number of combinations denoted by \(m\) and the number of columns denoted by \(v\), \(L_{m} (\alpha^{v} ) = [l_{i,j} ]_{m \times n}\). The \([l_{i,j} ]_{m \times n}\) denotes the \(i{\text{th}}\) combination of \(j{\text{th}}\) factor in \(L_{m} (\alpha^{v} )\). For example, the OA with \(v = 3\) and \(\alpha = 2\) is presented as follows.
To construct the OA of \(L_{m} (\alpha^{v} )\), some assumptions must be satisfied, such as \(\alpha\) must be prime, \(m = \alpha^{\beta }\), and \(\beta\) is a positive integer, such that \(v = {{(\alpha^{\beta } - 1)} \mathord{\left/ {\vphantom {{(\alpha^{\beta } - 1)} {(\alpha - 1)}}} \right. \kern-\nulldelimiterspace} {(\alpha - 1)}}\), where \(v\) is not less than the number of the variables \(n\). The main steps for constructing the OA are presented in Fig. 11.
Rizk-Allah (2019) developed a further new variant of SCA based on orthogonal parallel information, named SCA-OPI, including OBL strategy, MOSS mechanism established based on parallel and orthogonal form as it employs the orthogonal solution in constructing the OA. Also, a modified form of the parameter \(A_{1}\) is different from the previous one as it is accompanied by the index \(Q\), where it is expressed as follows.
Huang et al. (2020) developed a rationalized version of SCA based on chaotic local search (CLS) and Lévy flight techniques, named CLSCA, to solve several benchmark cases with different dimensions. In CLSCA, the Lévy flight is presented for long jumping to boost the exploratory abilities. At the same time, the CLS is adopted to perform the local search in the neighbourhood of the destination solution to enhance the exploitation tendencies of SCA.
The Lévy flight is presented to enhance the search capabilities, and it consists of the following two steps: selection of direction and generating the values for the step length, which are carried out by Lévy distribution rule as follows
where \(\mu\) is a shift parameter or the location, and \(\gamma > 0\) is a scale factor which controls the level of distribution. Lévy distribution must be expressed in the light of Fourier transformation as follows.
where \(\alpha\) denotes a scale factor ranging from −1 to 1 and \(\beta\) represents the stability index. To achieve a deeper searching ability regarding exploration and exploitation, the Lévy flight strategy can be employed to update the current location of the searched agent as follows:
where \(x_{i}^{L,(t + 1)}\) denotes the position after applying Lévy flight that is compared with \(x_{i}^{(t + 1)}\) and the best one is survival.
The second modification is in adopting the classic logistic map to improve the best searched individual (destination solution).
where \(\alpha = \left( {{{T - t + 1} \mathord{\left/ {\vphantom {{T - t + 1} T}} \right. \kern-\nulldelimiterspace} T}} \right)\) is a contraction factor?
Gupta and Deep (2019c) presented a novel variant of SCA, named HSCA, with a new searching mechanism and guidance strategy based on the temperature difference inspired by a simulated quenching algorithm. The introduced modification can be stated as follows.
The other modification is introduced based on the exponential temperature scheduling and greedy selection of the simulated to better transition from exploration to exploitation during the searching process.
Long et al. (2019) proposed an improved variant of SCA (ISCA) to deal with high-dimensional problems. In the ISCA, a modified updating rule based on inertia weight is introduced to avoid the trapping in local optima and accelerate the convergence rate. In addition, a non-linear conversion parameter is proposed based on the Gaussian function to balance the exploration and exploitation of the SCA. The modified position-updating equation is described by Eq. (2) as follows:
where \(w \in [0,\,1]\) denotes the inertia weight, where the large values \(w\) facilitate the global search and small values of \(w\) facilitates the local refinement. Hence, the value of \(w\) can is expressed in terms of a start value (\(w_{start}\)) and the end value (\(w_{end}\)) as follows.
On the other hand, the conversion parameter \(A_{1}\) is modified with nonlinearly decreasing aspect based on the Gaussian as follows.
where \(k\) indicates a nonlinear modulation index, and \(a^{start}\) and \(a^{end}\) are the initial and final values of constant \(a\), respectively.
Chen et al. (2020b) developed an improved SCA named OMGSCA based on an orthogonal learning mechanism to expand the neighbourhood searching capacities, a multi-swarm scheme to improve the exploration capabilities, and a greedy selection strategy to enhance the qualities of the agents.
Chiwen et al. (2018) presented an improved sine–cosine algorithm (ISCA) for solving global optimization problems. It involves three optimization strategies. The first one involves an exponential conversion parameter, and linear inertia weight decreased iteratively to balance the algorithm’s global and local searching ability. The second one integrates the random individuals in the neighbourhood of the optimal individuals to escape out from the local optimum easily. The final one combines the greedy strategy-based Levy mutation to enhance the local searching ability. The simulations and results evidence that the proposed algorithm can provide higher optimization accuracy with faster convergence speed.
Abdel-Baset et al. (2019) developed a novel algorithm that encompasses the merits of the SCA and Simpson method, named SCA-SM, to solve numerical integration tasks. The SCA-SM consists of two phases; the SCA phase aims to find the optimal segmentation points regarding the interval of an integrand. The second phase employs the Simpson method to find the approximate solution of the integrand. Numerical simulations show that the SCA-SM exhibits an efficient and effective route to obtain the numerical value of definite integrals with high accuracy.
Wang et al. (2020a) proposed a symmetric SCA using adaptive probability selection (SSCA-APS) to improve the ability of the SCA in the exploitation phase. The SSCA-APS employs two late stages. In the first one uses the traditional SCA, while the second stage applies three improvements as follows. These improvements include the SSCA, APS, and Gaussian perturbation-based mutation strategy. In addition, population diversity is maintained by selecting two individuals with the globally optimal individual combined through the quadratic interpolation to produce a new individual. The SSCA-APS is tested on 23 test functions, and the simulation results affirmed its competitiveness compared with some SCA variants.
Rizk-Allah (2021) presented a novel quantum-based SCA (Q-SCA) for dealing with the general systems of nonlinear equations (GSNEs). In the Q-SCA, the local quantum search (QLS) enhances the diversity of solutions and avoids the trapping in local optima. Furthermore, a new mechanism to update the solutions is presented. The Q-SCA is tested on twelve systems of GSNEs and two electrical applications. It is applied to expensive large-scale problems such as CEC 2017 benchmark as well as economic power dispatch for confirming its scalability.
In this context, the new location inside the search space of the Q-SCA is as follows:
where \(p_{i}\) defines a mutation probability to perform the switching among the terms of the equation through a random parameter \(\,r_{5}\). Furthermore, the parameter \(r_{1}\) is tuned dynamically to perform more balancing among the diversification and intensification phases, and it is expressed as follows.
On the other hand, the QLS is invoked to enhance the searching accuracy and prevent trapping into the local optimum. The steps of QLS are outlined as follows:
-
Receive the population of solutions from the SCA stage \(\{ {\mathbf{x}}_{i} \}_{i = 1}^{PS}\) and the best location (destination) \({\mathbf{x}}^{*}\).
-
Perform the quantum tools through involving the wave function \(\psi\), and the probability density function, the \(\psi\) and \(|\psi |^{2}\) of the solution \(i\) with on the \(j{\text{th}}\) dimension that moves with a \(\delta\) potential well centred at \(P_{ij}\) is described as follows.
$$ \psi (x_{ij}^{t + 1} ) = \frac{1}{{\sqrt {L_{ij}^{t} } }}\,\exp ( - {{|x_{ij}^{t + 1} - P_{ij}^{t} |} \mathord{\left/ {\vphantom {{|x_{ij}^{t + 1} - P_{ij}^{t} |} {L_{ij}^{t} }}} \right. \kern-\nulldelimiterspace} {L_{ij}^{t} }}), $$(43)$$ Q(x_{ij}^{t + 1} ) = |\psi (x_{ij}^{t + 1} )|^{2} = \frac{1}{{L_{ij}^{t} }}\,\exp ( - 2{{|x_{ij}^{t + 1} - P_{ij}^{t} |} \mathord{\left/ {\vphantom {{|x_{ij}^{t + 1} - P_{ij}^{t} |} {L_{ij}^{t} }}} \right. \kern-\nulldelimiterspace} {L_{ij}^{t} }}), $$(44)
where \({L}_{ij}^{t}\) defines the quantum search scope or the standard deviation. Then the probability distribution function \(F\) is considered by the following equation.
By the Monte Carlo technique, the search agent position \({\mathbf{x}}_{i}\) at iteration \(t + 1\) is determined as follows:
where \(u_{ij}^{t + 1}\) denotes a random number that is uniformly distributed over (0, 1) and \(L_{ij}^{t}\) is obtained as follows.
where \(C_{{}}^{t}\) is the mean of the positions of all search agents. That is
Thus the new solution can be updated according to the following equation:
where \(P_{ij}^{t}\) defines a local attractor solution chosen randomly whether from the current population or the destination \(\beta_{\min }\), and \(\beta_{\max }\) are the minimum, and maximum limits for the radius is the radius. \(\beta\) is the search radius in each iteration. Therefore, the new population is incorporated if it is better. The flowchart of the proposed Q-SCA can be shown in Fig. 12.
Wang, and Lu (2021) introduced a novel modified SCA (MSCA) by proposing a linear searching path and the empirical parameter with an effective way to avoid sinking into the local optimal. The MSCA is investigated on two kinds of tests, including 23 benchmark suits and actual engineering problem tests to prove the performance of the MSCA. Also, different dimensions (D = 30, 50, 100 and 500) are investigated. The results show that the MSCA can perform well over the original SCA and other population-based algorithms.
Li et al. (2021a) proposed the dimension-by-dimension dynamic SCA (DDSCA) for global optimization problems. In the DDSCA, dimension by dimension strategy is performed by evaluating the solution in each dimension. Then a greedy strategy is presented to form the new solution with other dimensions. Moreover, a dynamic control parameter is introduced for modifying the position of the search agents. The effectiveness of DDSCA is proved on solving 23 benchmark functions. Also, its scalability is confirmed by solving the IEEE CEC2010, where the results exhibit that the performance of the DDSCA outperforms the other algorithms. Moreover, five engineering designs also verified the efficacy of the DDSCA.
Li et al. (2021b) developed a novel dynamic SCA (DSCA) for global optimization tasks. DSCA updates the solution using a nonlinear random convergence parameter to dynamically balance SCA’s exploration and exploitation capabilities. Furthermore, a dynamic inertia weight mechanism is developed to modify the position to avoid falling into the local optimum. To evaluate the DSCA’s performance, it is conducted to solve large-scale optimization problems ranging from 200 to 5000, and also the IEEE CEC2010 functions are investigated. The simulation results affirm that the DSCA can provide better convergence precision with stronger robustness while solving the optimization suits. Moreover, two practical engineering designs are solved, and efficient results are achieved.
Rehman et al. (2021) developed a new Multi-SCA (MSCA) based on multiple swarms to diversify and intensify the searching ability to avoid the stagnation at local minima/maxima problem. Secondly, better search clusters are performed during the updating stage of MSCA to effectively offer an improved convergence towards the global minima. The MSCA is assessed by testing on unimodal, multimodal, and composite functions. Experimental simulation results confirm that the MSCA can attain superior outcomes than other state-of-the-art metaheuristic optimizers and the original SCA.
Kaur, and Dhillon (2021) proposed a hybrid hill climbed SCA (HcSCA) to handle the economic generation scheduling (EcGS) of thermal units. In the HcSCA, SCA operates in improving the exploration while the hill-climbing heuristic operates in enhancing the exploitation ability. The HcSCA is applied on EcGS with some features, including the valve-point loading effect, prohibited operating zones, ramp-rate limits, power demand constraints with losses, and generators limits. The outcomes of the HcSCA are matched with erstwhile algorithms, and the results provide a competing solution.
Tubishat et al. (2021) proposed an improved SCA (ISCA) based on two improvements. The first one incorporates the chaotic singer map within SCA to enhance the diversity of solutions, while the second improvement integrates the Simulated Annealing (SA) algorithm to improve the exploitation. The ISCA is investigated on 14 benchmark datasets from the UCI repository. The results of ISCA are compared with some optimizers, and the obtained results confirm the clear outperformance of ISCA.
Khokhar et al. (2021) proposed chaotic SCA based on two dimensions Sine Logistic map (2D-SLCSCA) for optimizing the classical PID controller for load frequency control (LFC) of an islanded microgrid (MG). Initially, the 2DSLCSCA is conducted on 8 benchmark suits, and the test results reveal that the 2DSLCSCA provides better convergence characteristics with some statistics and execution time. Finally, the 2D-SLCSCA is applied for the LFC analysis of the islanded MG. the simulation results confirm that the proposed control scheme exhibits a maximum percentage improvement compared to the other algorithms.
Si and Bhattacharya (2021) developed an improved SCA by incorporating the centroid opposition-based computing (COBC) strategy to enhance the exploration characteristic. The developed algorithm is abbreviated as COBSCA. COBSCA is applied on 28 benchmark problems from CEC2013 suits. The results of COBSCA are assessed with SCA and opposition based SCA (OBSCA), where the results reveal that the COBSCA statistically outperforms the other optimizers in dealing with the CEC2013 benchmark suite.
Al-Faisal et al. (2021) developed an SCA based on setting and controlling population size (PS) strategy. In this sense, leading PS adaptation strategies include the linear staircase reduction, reinitialization and incrementation, iterative halving, pulse wave, population diversity, and three parent crossover strategies. The investigation is performed on 23 benchmark functions. The experimental results confirm that proper selection of PS adaptation mechanism can further enhance the exploitation and exploration abilities of SCA and its variants.
4.4 Binary-based SCA
Many optimization issues cannot be addressed through a continuous version of meta-heuristics. Another scenario of optimization methodology is called Binary optimization as a class of combinatorial optimization. In Binary optimization problems, the decision variables have a distinct domain that their elements belong to {0, 1}. Meanwhile, each decision variable can be either 0 or 1 through the searching process. The problems that can model as binary formulations include the Feature Selection (FS) (Hancer et al. 2018; Ghimatgar et al. 2018), knapsack problems (KP) (He and Wang 2018; Ulker and Tongur 2017), unit commitment problem (Panwar et al. 2018).
In Hans and Kaur (2019), a hybrid SCA and ALO, named SCALO, has been presented to find the optimal subset features for dimensionality reduction. The proposed method corresponds to a sigmoid transfer function (S-shape) and Tanh transfer function (V-shape). The solution can be transformed or mapped into the binary aspect with these management-based transfer functions. This map is carried out by using V- shape/S-shaped transfer function on each dimension that obliges the solution to be binary form with the likelihood of changing from 0 to 1 and vice versa. The proposed SCALO is conducted on 18 diverse datasets, and it is compared with some of the latest metaheuristic algorithms according to some criteria. The results confirmed its significance in achieving the optimal feature.
In Abou El-Ela (2019), a novel binary Sine Cosine algorithm (BSCA) is developed to solve the unit commitment problem (UCP), which aims to find the optimal scheduling under minimization of generation costs following satisfying some restrictions such as the demand, ramp rate, spinning reserve, and other operational constraints. In this sense, the BSCA is integrated with the optimal priority list (OPL) technique to guide search space toward the effective scheduling of generators that must be considered in the services. The BSCA is tested on a 10-unit IEEE test system, and compared with other methods, the proposed BSCA gives better results as well as saves the computational efforts.
In Pinto et al. (2019), a novel binary Percentile SCA based on the binarization mechanism using the percentile concept, named BPSCOA, is introduced to deal with the multidimensional backpack problem (MKP). The BPSCOA algorithm is investigated on reference instances, where the results illustrate that the binary BPSCA obtains adequate outcomes when dealing with binary combinatorial problems (i.e., MKP).
4.5 Chaotic-based SCA
Even though SCA provides an adequate convergence rate performance, SCA still faces some shortages when dealing with complex optimization and cannot perform an effective convergence rate. So, the chaotic strategy is inserted to SCA (SCA) to mitigate these shortages and improve the capability and efficiency. The chaotic concept is generally rooted in the term ‘chaos’ that presents complex and dynamic models associated with unpredictable behaviour. The mapping function with some parameters expresses this behaviour during its simulation in the algorithm. In addition, the chaos map is characterized by the periodicity and non-repetition properties that can enable general searches with higher speeds compared to the stochastic searches that depend on probability distributions. Also, it has a sensitive dependency on the initial guess. These features are periodicity, the sensitive dependency on initial guesses, and the quasi-stochastic property. It is integrated with optimization algorithms to prevent the local optima and improve searching quality. In this regard, chaotic maps employing their dynamic performance have been vastly admitted as they can assist the optimization algorithm in supporting the search to escape from the local optimum. It is adopted by replacing the stochastic components and randomness probability distributions based on chaotic maps. Some of the chaotic maps with the mathematical formulas are listed in Table 1.
In Tahir et al. (2018), to design an improved variant of SCA, it is integrated with chaos theory and named as CSCA. In the CSCA, four chaotic maps, namely, Chebyshev, Circle, Gauss, Iterative, and intermittency, are integrated to replace the random parameters of SCA through chaotic sequences. The CSCA variants are benchmarked on 10 benchmark functions. The statistical outcomes reveal that CSCA variants outperform the standard SCA for all benchmark functions, where the Circle map provides the best performance that is overtaking the other algorithms.
In Ali and Tahir (2018), CSCA variants are proposed to manipulate the lack of the traditional SCA, such as poor convergence rate and trapping in local optima. This manipulation is performed by replacing the randomness aspect of SCA chaotic sequences. The CSCA variants are verified on large-scale problems under different dimensions, including 10, 30, 100, and 200. The results affirm that CSCA variants can achieve high-quality solutions and superior results for all the studied dimensions than the SCA.
In Liu (2018), an improved SCA (ISCA) based on the opposition strategy and Tent chaos search is presented, where an opposition strategy is adopted for better individuals. In contrast, a Tent chaos search is performed for inferior individuals. Numerical simulations illustrate that the ISCA can leap out of the local optima with higher speed. Also, better performance can be achieved while tackling high dimension benchmark functions.
4.6 Multi-objective- based SCA
During the last decades, multi-objective optimization techniques have appeared in several fields. The difficulties in solving MOOP while searching for a Pareto optimal front are behind the stuck in local fronts, slow convergence, and lack of solutions (coverage) distribution. The problem of local solution and slow convergence is a common issue for both SOOP and MOOP. The problem concerning the distribution of solutions is very important because many solutions are within the Pareto optimal front. This distribution presents the ultimate goal as it can give decision-makers or designers many alternatives during the decision-making process. The further challenge is the shape of fronts that is concave, convex, linear, separated, etc. Also, when dealing with real multiobjective problems, such as deceptive front, uncertainty isolation of the front, noisy objective functions, dynamic objective functions reliable fronts, and so on (Zhou et al. 2011).
The popular multi-objective algorithm for tackling the MOOP is Non-dominated Sorting GA2 (NSGA-2) (Deb et al. 2002), built based on non-dominated sorting technique, elite strategy, and niching operator. The NSGA-2 begins with a randomization step, and each solution joins to each group based on the non-dominated sorting strategy. Then the mutation and recombination operators are performed to create a novel one that is re-sorted again and so on.
The second popular technique is Multi-objective PSO (MOPSO) (Coello Coello and Lechuga Mopso 2002), which is established based on PSO and external archives to store and retrieve the Pareto optimal solutions. Also, it is integrated with the mutation operator for further diversity of solutions.
In Tawid and Savsani (2019), a new multi-objective variant of SCA (MO-SCA) has been purported to solve multiple objectives benchmark problems with various natures of Pareto front (i.e., convex, non-convex, and discrete), and it is also applied to solve some engineering design problems. The MOSCA utilizes elitism and crowding distance strategy to attain the optimal non-domination levels while preserving the obtained solutions’ diversity. The obtained experiments affirm that the MO-SCA can effectively generate the Pareto front.
In Ref. (Selim et al. 2019), multi-objective based on SCA (MOSCA) using fuzzy logic decision making is proposed to find the optimal size and location of multiple Distribution STATic COMpensators (DSTATCOMs) within the distribution network for minimizing the power losses, reducing the Voltage Deviation (VD), as well as maximizing the Voltage Stability Index (VSI). The fuzzy logic shows the decision maker’s preferences among the three objective functions to obtain the operating point based on ac certain membership function. The simulations are performed on the IEEE-33 bus and IEEE-69 bus distribution systems.
A novel hybrid forecasting based on multi-objective SCA (MOSCA) is introduced for Wind speed forecasting (Wang et al. 2018). The proposed algorithm includes four aspects: preprocessing, optimization, forecasting, and module evaluation. Also, the wavelet neutral network (WNN) is integrated with MOSCA to attain high accuracy and strong stability simultaneously. The presented case studies employ eight wind speed datasets encompassing two wind farms. The results reveal superior performance in terms of accuracy and stability.
Abdel-Basset et al. (2021) developed a multi-objective approach to deal with scheduling of the multiprocessor systems (MPS) based on using a modified SCA (MSCA) to optimize the makespan and energy using the Pareto dominance strategy. The algorithm is denoted as energy-aware multi-objective MSCA (EA-M2SCA). The EA-M2SCA employs a polynomial mutation to improve the performance of SCA and accelerate the convergence behaviour. The presented algorithm is compared with some of the well-established multi-objective algorithms, where the EA-M2SCA shows superior results in most test cases.
Wan et al. (2021) addressed a multiobjective SCA for remote sensing image data spatial-spectral clustering, MOSCA_SSC. The clustering task is transformed into a multiobjective optimization problem in this method. The Jeffries–Matusita (Jm) distance and the Xie–Beni (XB) index are combined with the spatial information term. The benefits of the proposed algorithm are affirmed by clustering experiments with ten UCI datasets and four real remote sensing image datasets.
Karimulla, and Ravi (2021) proposed the multi-objective optimal power flow using enhanced SCA (ESCA). The objective functions of optimal power flow include generating cost, power plant emission, losses, and voltage stability. The ESCA is evaluated on the IEEE standard 30 bus system, where the obtained results are compared with other evolutionary algorithms. The ESCA exhibit better results than the other techniques in terms of optimality and convergence speed.
5 Hybrid SCA algorithms
The optimization algorithm’s hybridization means combining two or more search techniques into a unique algorithm to establish a new framework to transcend its ancestors and find out better quality. This can provide a robust algorithm by combining these techniques’ strengths and thus can simultaneously overcome their limitations. In this section, the hybridization of SCA with different search techniques can be investigated, where some prominent algorithms of hybrid SCA are given in Table 2. A brief overview of these hybrid examples will also be exhibited as the following.
Singh and Singh (2017) developed a hybrid SCA with GWO (HGWOSCA) for solving twenty-two benchmark tests, one sine dataset, and five bio-medical dataset functions. The hybrid HGWOSCA uses SCA for the exploration in an uncertain environment while GWO for the exploitation phase. In this sense, SCA is presented to update the movement direction of the grey wolf (alpha).
Jiang et al. (2020a) proposed a hybrid SCA with gravitational search algorithm (GSA) and chaotic map, named as sine chaotic gravitational search algorithm (SCGSA), to escape from the stagnation in local optima and strength the characteristics of exploration and exploitation abilities. SCA is introduced to enhance the movement pattern of search agents in the SCGSA. The SCGSA is applied to solve CEC 2014 and some of the real constrained optimization problems.
Chegini et al. (2018) presented a new hybrid method called PSOSCALF for solving benchmark functions of the unimodal and multimodal as well as the constrained engineering problems. In the PSOSCALF, the SCA is introduced to update the solution based on sine and cosine functions to guarantee exploitation and exploration capabilities. At the same time, the Levy flight is presented as a random walk strategy and large jumps to perform effective exploration. Thus, by the introduced combination of the SCA and Levy flight, the trapped in the local minimum can be prevented, and the performance of PSOSCALF can be enhanced.
Fakhouri et al. (2020) introduced a novel hybrid evolutionary algorithm incorporating PSO with SCA and Nelder–Mead simplex (NMS), named PSOSCANMS, to solve unimodal, multimodal functions and engineering design problems. The proposed combination avoids the drawbacks of local minima trapping, the slow converge rate and the bad balancing between exploration and exploitation patterns. In PSOSCANMS, the solutions of PSO are updated by SCA and NMS. By this methodology, the consistency of exploitation and exploration can be ensured and escaped from the local minima and resolve the low converge rate problem.
Gupta et al. (2020b) developed an optimization method based on the hybridization of the SCA and grey wolf optimizer (GWO), called SC-GWO, to solve optimization benchmark problems with dimensions varied from 30 to 100 for investigating the scalability on the performance of SC-GWO. Also, some engineering designs and obtaining the optimal setting for overcurrent relays are solved. The SC-GWO starts with the SCA that integrates the social and cognitive components to improve the exploration ability. At the same time, GWO performs the second phase for maintained the balance between exploration and exploitation searches. The presented analysis and comparisons have demonstrated the superior ability of SC-GWO.
Gupta et al. (Gupta and Deep 2019d) proposed a hybrid optimization algorithm, named sine cosine artificial bee colony (SCABC), to remove the drawbacks of the traditional ABC, such as the slow convergence rate, inefficient exploration, and weak exploitation. The SCABC begins with SCA through a modified searching equation accompanied with elite guidance to detract the problem of high diversity. Then ABC is combined in sequential form with its procedures. The SCABC algorithm is validated on a well-known benchmark set of 23 tests. Some analysis metrics are considered to verify the betterment of searching ability compared to traditional ABC, SCA. Moreover, the SCABC is also applied to solve the image segmentation problems, and the performance measures affirmed its efficacy in achieving the optimum thresholds of gray images.
Nenavath et al. (2018) introduced a novel Hybrid SCA-PSO algorithm to solve optimization tasks and object tracking problems as a real thought-provoking case study. The main aim behind this hybridization is to handle the problem of SCA that is the stagnation in local minima and lacks internal memory. The personal best (\(P_{best}^{{}}\)) and global best (\(G_{best}^{{}}\)) concepts of PSO are embedded in the searching equation of traditional SCA to improve the searching process. PSO then started its phase with of SCA to enhance the exploitation searching. By this scenario, the exploitation capability is guaranteed by PSO, and SCA comprehends exploration ability. The effectiveness of SCA-PSO is shown by evaluating the performance on 23 instances, CEC 2014 and CEC 2005 benchmark problems. Statistical results have proved that the SCA-PSO is very competitive with other algorithms. Also, the SCA-PSO is applied to deal with object tracking as a real case study, where the results show that the SCA-PSO can track an arbitrary target robustly.
Nenavath and Jatoth (2018) presented a new optimization algorithm that hybridizes SCA with a Differential Evolution algorithm (DE) called SCA-DE to solve optimization problems and object tracking. The SCA-DE aims to acquire a better capability to escape from local optima faster than the classical SCA and DE. The SCA-DE is validated on three groups of benchmark functions: unimodal, multimodal, and fixed dimension multimodal. Statistical results have affirmed the efficiency of SCA-DE as it is very competitive compared with the other algorithms. Furthermore, the SCA-DE has been applied for object tracking tasks. The comparative simulations show that the SCA-DE can provide more robust tracking than the other trackers.
Zhang et al. (2020) proposed a hybrid extended ant lion optimizer (EALO) with a sine cosine algorithm (EALO-SCA) as a tracking algorithm through considering the abrupt motion. In this context, EALO is introduced with multiple elites rather than a single elite as in the standard ALO to improve the global exploration searches. On the other side, SCA is combined to perform courser local exploitation patterns. In this manner, the EALO-SCA-based tracking combines the strengths of both EALO and SCA. The extensive experimental results via qualitative and quantitative performances affirm the competitiveness of EALO-SCA compared to other trackers, particularly in dealing with abrupt motion tracking.
Issa et al. (2018) developed adaptive SCA with PSO (ASCA-PSO) to overcome the drawback of the SCA contained in the parameter setting tuning that can affect the exploitation of the enriched regions. In this sense, the SCA operates to perform the exploration searches, while PSO is merged to exploit the search space better and thus enhance the exploitation searches. The ASCA-PSO investigates unimodal and multimodal benchmark functions and pairwise local alignment as a real case problem to find the longest consecutive substrings between two biological sequences. The simulations have evidence that the ASCA-PSO has a good performance of the ASCA-PSO regarding the accuracy and computational time.
Chunquan et al. (Li et al. 2019) developed an enhanced brainstorm SCA (EBS-SCA) to improve the balance among the exploration and exploitation features, especially when dealing with complex optimization natures such as the shifted rotated problems or complex shifted. Toward this aim, the EBS is introduced through two different update equations (i.e., individual update strategies (IUS): IUS-I and IUS-II) to improve the population diversity. In this context, the EBS-SCA performs IUS-I to improve global search ability and enhance exploration patterns. At the same time, for the exploitation phase, the IUS-II strategy is presented to boost the local searching and then enhances exploitation search. The performance of EBS-SCA is investigated on 46 benchmark suites and two real-life problems. The simulations validate the EBS-SCA in terms of promising searching, scalability, and convergence speed.
Tuncer (2018) presented a novel sine–cosine-based PSO (SCSO) to optimize numerical functions. In SCSO, the particles are initialized randomly, and then personal best values are computed. Then the velocity of the particles is modified by using sine, cosine terms, and the difference between the personal best and its current candidate. The SCSO is tested on 14 numerical functions, and the results illustrate its success in numerical optimization.
Fan et al. (2020) introduced a hybrid algorithm based on fruit fly optimization algorithm (FOA) based on SCA, SCA-FOA named, to handle the non-competitiveness and falling in local optimum especially for high dimensional and practical application problems. The SCA-FOA is benchmarked on 28 functions and 10 practical problems from IEEE CEC 2011 to measure its abilities for the exploitation and exploration features. Moreover, it is applied for three engineering applications, three shifted and asymmetrical problems, and kernel extreme learning machines problems d. The simulations and observations demonstrate that its efficiency can solve real-world applications.
Support Vector Machine (SVM) (Ghaddar and Sawaya 2018) presents a prominent supervised machine learning technique aiming to achieve two phases of classification and regression by analyzing data and exploring specific hidden or visible patterns. In addition, SVM can perform a nonlinear classification task as it is dispersed the training datasets into another dimensional space and carried out linear separation to investigate any existing categories. The separation phase is performed by making a hyper plane purported at increasing the margin between the nearest points of various categories known as support vectors to explore the best separating hyper plane.
Li et al. (2018) proposed a novel SCA-SVR model to select the penalty and kernel parameters in SVR to improve the performance on unknown data. Although SVR provides a good performance in forecasting models for small and high dimensions, its parameters may significantly affect the forecasting performance of SVR. The SCA-SVR algorithm is validated with other meta-heuristics algorithms on well-known benchmark datasets. The results affirmed that the SCA-SVR model is efficient for finding the optimal values of the SVR parameters.
Abualigah and Dulaimi (2021) proposed a hybrid feature selection method based on SCA and GA, called SCAGA to deal with feature selection. The SCAGA aims to achieve better performance by balancing the exploitation and exploration strategies. The SCAGA is assessed using some criteria, including classification accuracy, mean fitness, worst fitness, best fitness, standard deviation, and the average number of features. Furthermore, the minimal features that achieve the maximum classification accuracy are obtained. The comparisons with different optimizers have shown that the SCAGA method could achieve the best overall results for the tested datasets.
Xian et al. (2021) developed a modified SCA with teacher supervision learning (TSL-SCA) for global optimization. The teacher supervision phase aims to guide the population and accelerate the convergence speed. Also, a reflective learning strategy is integrated with the standard SCA to update its position to prevent the stagnation in local minima and increase the population diversity. Furthermore, a hybrid inverse learning is introduced to enhance the ability to find an optimal global solution and increase the distributivity regarding the population. The TSL-SCA is evaluated on 33 benchmark optimization problems selected from the literature. The results have affirmed that the TSL-SCA can significantly improve the optimization accuracy and enhance the convergence speed. Furthermore, the TSL-SCA is examined on solving analogue circuit fault diagnosis of filter circuit examples.
Li et al. (2021c) developed a hybrid greedy SCA with differential evolution (DE), named (HGSCADE), to solve global optimization problems and evaluate cylindricity error. The HGSCADE integrates the opposition strategy with SCA for initializing the population. Furthermore, the HGSCADE incorporates the greedy search, DE, the success history-based parameter adaptation, the Levy flight strategy. The performance of the HGSCADE is examined on CEC2014 benchmark functions and is applied cylindricity error evaluation problem. The simulation results confirm the superiority of HGSCADE compared with the other state-of-the-art competing techniques for the benchmark problems and cylindricity error evaluation.
Sharma and Saha (2021) presented a new hybrid butterfly optimization algorithm (BOA) with SCA, named BOSCA to develop a powerful optimization method by stabilizing and enhancing the global exploration and local exploitation features. To prove the robustness and efficiency of the BOSCA, it is investigated on 25 benchmark functions. The results of BOSCA are compared with some popular algorithms, where the BOSCA is found to be superior to the compared ones. The efficiency of BOSCA is validated on real-world problems, including the gas transmission compressor design problem and an optimum capacity of gas production facilities. The results have been compared with other methods, and the BOSCA is superior to the others in dealing with these real-world optimization problems.
Altay and Alatas (2021) proposed a hybrid DE and SCA for directly and rapidly mining the reduced high-quality numerical association rules. The proposed algorithm ensures the discovered rules with high confidence. The results exhibit superior performance on the studied data sets.
Singh and Kaur (2021) addressed a new heuristic algorithm based on integrating the features of SCA with a harmony search approach (HS) called HSCAHS algorithm. The presented approach aims to reduce demerits, such as the trapping in local optima and unbalanced pattern of exploration and exploitation. SCA starts to explore the search space, while HS begins its search from SCA finds so far to augment the exploitation capabilities. The capability of the HSCAHS is verified on 18 benchmark problems, three-bar truss design, economic dispatch, rolling element bearing design, speed reducer design, multiple disc clutch brake design, and planetary gear train design problems. The simulation results reveal that the HSCAHS approach can find superior quality for most cases compared to others.
6 SCA with engineering applications
SCA is applied efficiently to back up some real-world applications in various fields such as engineering optimization tasks. In this sense, formulating the objective functions and defining the appropriate variables present major issues as this can assist efficient problem solving while addressing the engineering applications. Here, a literature survey is performed by categorizing the application areas. Many engineering areas of the SCA are classified as follows. Electrical engineering, Classification, Control Engineering, Image Processing, Industrial Engineering, Civil Engineering, and other applications. Table 3 overviews some of the prominent applications of SCA in engineering areas.
7 Discussion and directions
The numerical optimization issue is transferred to finding the optimal solutions for the mathematical model or a system through the maximization or the minimization of the accompanied objective function. Due to the complexity of many real-world tasks, developing efficient optimization methods is becoming urgent and important for optimization tasks communities. Several optimization methodologies have been introduced over the last decades based on diverse phenomena in biology or nature. For the sake of robust solving, metaheuristic algorithms (MAs) have been witnessed successfully in numerous fields due to some reasons. First, using stochastic factors allows meta-heuristics to evade the trapping in local optima and emphasize the convergence to approximate global optima. The aim is not to achieve the exact optimal solution for the candidate problem at hand but to attain a good solution with a plausible computational time. The keystone to achieving such a target mainly depends on the harmonious trade-off between exploration and exploitation fashions. Exploration is refereed to identify the regions of the search space that are most promising by the diversification the directions of searching.
Consequently, the searching is locally intensified by the fashion exploitation within the achieved promising region to obtain high-quality solutions. In this regard, the better meta-heuristic algorithm is the algorithm which can achieve a better balancing of two fashions. The existing meta-heuristics can balance these fashions differently as they can be more adapted for exploration or exploitation. In this sense, two or more techniques can be hybridized to take the strengths from each other while avoiding their drawbacks. The second reason for the successfulness of metaheuristic algorithms is their generality, ease of use and tunability for practice situations.
The hybridization of MAs gathers the power points of the combined algorithms. This combined version can be established with low or high levels of hybridization depending on the degree of interference among the schemes of the algorithms, i.e., high-level hybridization illustrates that high interference among the internal actions of hybridized algorithms with maintaining the structures of each other while low-level hybridization demonstrates that only algorithm function is diffused or transferred to another one. During the searching phases, the hybridized variant can be collaboratively exchanged or integrated its information in a sequential or parallelized manner with a master one. Thus, a high-level search can be attained that guides the search agents to improve the quality of the solution within an equitable amount of time. The MAs have been employed extensively to handle several types of optimization tasks. However, some algorithms still suffer from low convergence, and the local optima are trapped and go awry from the global optimum solution for sophisticated situations or real-life cases. This is caused due to the lack of the exploration (diversification) ability within the algorithm’s structure at hand. Thus, various diversification methodologies are implemented to counteract the drawbacks and propagate the performance of the distinguished algorithm, namely elitism and hybridization. SCA has become of a remarkable optimization tool for complicated problem solving, like other MAs. It aims to find the global solution of multidimensional functions based on sine and cosine functions through an intelligent computational manner. The SCA acquires an easy principle that can be simply implemented in a wide range of fields. The comprehensive results through this review affirm the performance attainment of SCA in terms of both quality and accuracy of solutions. This assertion is conducted by reviewing the simulations and results while comparing the SCA and the other optimization algorithms. Like the different MAs, SCA has some advantages and some unavoidable shortages. Although this algorithm has no convergence proof for its performance, it can provide competitive results over other methods in terms of convergence rate. Table 4 mentions the strengths and weaknesses of SCA. In addition, there are significant potentials for researchers and engineers to employ the advantages SCA faces involved industry applications.
8 Conclusion
A literature review regarding the SCA is introduced in this paper. This work aims to review the different improvement issues of SCA and overview various applications of SCA in all categories. The presented study confirmed that the SCA is combined with different improvements and different optimization peers, while fewer variants of MOSCA to deal with multi-objective optimized are observed. In addition, in terms of application, SCA has been applied in a wide range of applications Electrical engineering, Classification, Control Engineering, Image Processing, Industrial Engineering, Civil Engineering, and other applications. Furthermore, several works of SCA have been presented to solve different natures of mathematical optimization problems such as unconstrained optimization, constrained optimization, engineering design tasks, and pattern recognition problems. In short, SCA is very promising and effective in dealing with test problems, according to the literature review. Additionally, ease and simple implementation are the main features that encouraged many researchers to solve various optimization tasks.
In conclusion, there is still space or opportunity to improve the performance. The SCA could be enriched into various modifications, hybridizations, and variants based on the necessity for the candidate problems. Consequently, the results of this review study could be touched or implemented by other practitioners and interested researchers to illustrate different procedures or for improvement purposes through considering merits or demerits of other methods proposed by previous researchers. For possible future trends, we suggested enhancing the SCA with other meta-heuristic algorithms to exploit further benefits in solving complex and large-scale optimization problems.
In the possible future areas, we will be concerned and recommend the following aspects:
-
1)
Utilizing SCA to deal with many objectives’ optimization.
-
2)
Utilizing SCA to handle different natures of combinatorial optimization such as binary, integer, discrete, etc.
-
3)
Modifying SCA to solve real-life optimization problems, especially renewable energy and engineering design problems.
References
Abdelaziz M, Oliva D, Xiong S (2017) An improved opposition-based sine cosine algorithm for global optimization. Expert Syst Appl 90:484–500
Abdel-Baset M, Zhou Y, Hezam I (2019) Use of a sine cosine algorithm combined with Simpson method for numerical integration. Int J Math Operat Res 14(3):307–318
Abdel-Basset M, Mohamed R, Abouhawwash M, Chakrabortty RK, Ryan MJ (2021) EA-MSCA: an effective energy-aware multi-objective modified sine-cosine algorithm for real-time task scheduling in multiprocessor systems: methods and analysis. Expert Syst Appl 173:114699
Abderazek H, Hamza F, Yildiz AR, Gao L, Sait SM (2021) A comparative analysis of the queuing search algorithm, the sine-cosine algorithm, the ant lion algorithm to determine the optimal weight design problem of a spur gear drive system. Mater Test 63(5):442–447. https://doi.org/10.1515/mt-2020-0075
Abou El-Ela AA, Allam SM, Rizk-Allah RM, Doso AS (2019) Parallel binary sine cosine with optimal priority list algorithm for unit commitment. In 2019 21st International Middle East power systems conference (MEPCON) (pp. 509–514). IEEE.
Abualigah L, Dulaimi AJ (2021) A novel feature selection method for data mining tasks using hybrid sine cosine algorithm and genetic algorithm. Cluster Comput 24:1–16
Ahmadianfar I, Noshadian S, Elagib NA, Salarijazi M (2021) Robust diversity-based sine-cosine algorithm for optimizing hydropower multi-reservoir systems. Water Resour Manage 35(11):3513–3538
Alatas B (2011) Acroa: artificial chemical reaction optimization algorithm for global optimization. Expert Syst Appl 38(10):13170–80. https://doi.org/10.1016/j.eswa.2011.04.126
Al-Betar MA, Alyasseri ZAA, Awadallah MA et al (2021) Coronavirus herd immunity optimizer (CHIO). Neural Comput App 33:5011–5042. https://doi.org/10.1007/s00521-020-05296-6
Al-Faisal HR, Ahmad I, Salman AA, Alfailakawi MG (2021) Adaptation of population size in sine cosine algorithm. IEEE Access 9:25258–25277
Algabalawy MA, Abdelaziz AY, Mekhamer SF, Aleem SHA (2018) Considerations on optimal design of hybrid power generation systems using whale and sine cosine optimization algorithms. J Electr Syst Inf Technol 5(3):312–325
Ali RS, Tahir DS (2018) Analysis of scalability and sensitivity for chaotic sine cosine algorithms. Iraqi J Electric Electron Eng 14(2):139–154
Altay EV, Alatas B (2021) Differential evolution and sine cosine algorithm based novel hybrid multi-objective approaches for numerical association rule mining. Inf Sci 554:198–221
Altmemi JM, Othman RR, Ahmad R, Ali AS (2020) Implementation of sine cosine algorithm (SCA) for combinatorial testing. MS&E 767(1):012009
Amat NFIC, Yahya ZR, Rusdi NA (2019) Arabic fonts representation using sine cosine algorithm. AIP Conf Proc 2138(1):030007
Askarzadeh A (2016) A novel metaheuristic method for solving constrained engineering optimization problems: crow search algorithm. Comput Struct 169:1–12
Atashpaz-Gargari E, Lucas C (2007) Imperialist competitive algorithm: an algorithm for optimization inspired by imperialistic competition. In IEEE Congress on Evolutionary Computation, pp. 4661–7. doi: https://doi.org/10.1109/CEC.2007.4425083.
Attia AF, El Sehiemy RA, Hasanien HM (2018) Optimal power flow solution in power systems using a novel sine-cosine algorithm. Int J Electr Power Energy Syst 99:331–343
Babar MI, Ahmad A, Fayyaz S (2020) A hybrid sine cosine algorithm with SQP for solving convex and nonconvex economic dispatch problem. Mehran Univ Res J Eng Technol 39(1):31–46
Babu R, Kumar V, Shiva CK et al (2022) Application of sine-cosine optimization algorithm for minimization of transmission loss. Technol Econ Smart Grids Sustain Energy 7:6. https://doi.org/10.1007/s40866-022-00136-z
Bejarbaneh EY, Bagheri A, Bejarbaneh BY, Buyamin S, Chegini SN (2019) A new adjusting technique for PID type fuzzy logic controller using PSOSCALF optimization algorithm. Appl Soft Comput 85:105822
Belazzoug M, Touahria M, Nouioua F, Brahimi M (2019) An improved sine cosine algorithm to select features for text categorization. J King Saud Univ-Comput Inf Sci 32:454–464
Beyer H-G, Schwefel H-P (2002) Evolution strategies—a comprehensive introduction. Nat Comput 1(1):3–52. https://doi.org/10.1023/A:1015059928466
Binitha S, Sathya SS (2012) A survey of bio-inspired optimization algorithms. Int J Soft Comput Eng 2(2):137–151
Bonabeau E, Dorigo M, Theraulaz G (1999) Swarm intelligence: from natural to artificial systems. Oxford University Press Inc
Chandrasekaran K, Sankar S, Banumalar K (2020) Partial shading detection for PV arrays in a maximum power tracking system using the sine-cosine algorithm. Energy Sustain Dev 55:105–121
Chegini SN, Bagheri A, Najafi F (2018) PSOSCALF: a new hybrid PSO based on sine cosine algorithm and levy flight for solving optimization problems. Appl Soft Comput 73:697–726
Chen H, Jiao S, Heidari AA, Wang M, Chen X, Zhao X (2019) An opposition-based sine cosine approach with local search for parameter estimation of photovoltaic models. Energy Convers Manage 195:927–942
Chen H, Wang M, Zhao X (2020a) A multi-strategy enhanced sine cosine algorithm for global optimization and constrained practical engineering problems. Appl Math Comput 369:124872
Chen H, Heidari AA, Zhao X, Zhang L, Chen H (2020b) Advanced orthogonal learning-driven multi-swarm sine cosine optimization: framework and case studies. Expert Syst Appl 144:113113
Cheng J, Duan Z (2019) Cloud model-based sine cosine algorithm for solving optimization problems. Evol Intel 12(4):503–514
Cheng M-Y, Prayogo D (2014) Symbiotic organisms search: a new metaheuristic optimization algorithm. Comput Struct 139:98–112
Coello Coello CA, Lechuga Mopso MS (2002) A proposal for multiple objective particle swarm optimization. In Proceedings of the evolutionary computation on 2002. CEC ‘02. Proceedings of the 2002 congress, IEEE computer society, CEC’02, vol. 02. Washington, DC, pp. 1051–1056.
Dai C, Zhu Y, Chen W (2007) Seeker optimization algorithm. In International Conference on Computational Intelligence and Security, pp. 167–76. doi: https://doi.org/10.1007/978-3-540-74377-4_18.
Daoui A, Karmouni H, Sayyouri M, Qjidaa H, Maaroufi M, Alami B (2021) New robust method for image copyright protection using histogram features and sine cosine algorithm. Expert Syst Appl 177:114978
Das S, Biswas A, Dasgupta S, Abraham A (2009) Bacterial foraging optimization algorithm: theoretical foundations, analysis, and applications. Foundations of computational intelligence, vol 3. Springer, Berlin, Heidelberg, pp 23–55
Dasgupta D (ed) (2012) Artificial immune systems and their applications. Springer Science & Business Media
Dasgupta K, Roy PK, Mukherjee V (2020) Power flow-based hydro-thermal-wind scheduling of hybrid power system using sine cosine algorithm. Electr Power Syst Res 178:106018
Dasgupta K, Roy PK, Mukherjee V (2021) A novel oppositional learning-based chaotic sine cosine algorithm for the dynamic thermal–wind economic dispatch problem. Eng Optim. https://doi.org/10.1080/0305215X.2021.1974852
Deb K, Pratap A, Agarwal S, Meyarivan T (2002) A fast and elitist multi-objective genetic algorithm: NSGA-II. IEEE Trans Evol Comput 6(2):182–197
Devarapalli, R., & Bhattacharyya, B. (2020). A hybrid modified grey wolf optimization‐sine cosine algorithm‐based power system stabilizer parameter tuning in a multimachine power system. Optimal Control Applications and Methods.
Dhiman G, Kumar V (2017) Spotted hyena optimizer: a novel bio-inspired based metaheuristic technique for engineering applications. Adv Eng Softw 114:48–70
Du H, Wu X, Zhuang J (2006) Small-world optimization algorithm for function optimization. Springer, Berlin Heidelberg, pp 264–273
Elaziz MA, Hemedan AA, Ostaszweski M, Schneider R, Lu S (2019) Optimization ACE inhibition activity in hypertension based on random vector functional link and sine-cosine algorithm. Chemom Intell Lab Syst 190:69–77
El-Kenawy ESM, Mirjalili S, Ghoneim SS, Eid MM, El-Said M, Khan ZS, Ibrahim A (2021) Advanced ensemble model for solar radiation forecasting using sine cosine algorithm and Newton’s Laws. IEEE Access 9:115750–115765
Elnagar DI, Bakr HMA, Ziedan IE (2019) Parameter estimation of polymer electrolyte membrane fuel cell using sine-cosine algorithm. East African Scholars J Eng Comput Sci 2:2617–4480
El-Sawy AA, Zaki EM, Rizk-Allah RM (2013) A novel hybrid ant colony optimization and firefly algorithm for solving constrained engineering design problems. J Nat Sci Math 6(1):1–22
El-Sehiemy RA, Rizk-Allah RM, Attia AF (2019) Assessment of hurricane versus sine-cosine optimization algorithms for economic/ecological emissions load dispatch problem. Int Trans Electr Energy Syst 29(2):e2716
Erol OK, Eksin I (2006) A new optimization method: big bang–big crunch. Adv Eng Softw 37(2):106–111
Fakhouri HN, Hudaib A, Sleit A (2020) Hybrid particle swarm optimization with sine cosine algorithm and nelder-mead simplex for solving engineering design problems. Arab J Sci Eng. https://doi.org/10.1007/s13369-019-04285-9
Fan Y, Wang P, Heidari AA, Wang M, Zhao X, Chen H, Li C (2020) Rationalized fruit fly optimization with sine cosine algorithm: a comprehensive analysis. Expert Syst App 157:113486
Faramarzi A, Heidarinejad M, Stephens B, Mirjalili S (2020a) Equilibrium optimizer: a novel optimization algorithm. Knowl-Based Syst 191:105190
Faramarzi A, Heidarinejad M, Mirjalili S, Gandomi AH (2020b) Marine predators algorithm: a nature-inspired metaheuristic. Expert Syst Appl 152:113377
Feng Z-K, Duan J-F, Niu W-J, Jiang Z-Q, Liu Y (2022) Enhanced sine cosine algorithm using opposition learning, adaptive evolution and neighborhood search strategies for multivariable parameter optimization problems. Appl Soft Comput 119:108562
Formato RA (2008) Central force optimization: a new nature-inspired computational framework for multidimensional search and optimization. Nature Inspired Cooperative Strategies for Optimization (NICSO 2007). Springer, Berlin, Heidelberg, pp 221–238
Fu W, Wang K, Li C, Tan J (2019) Multi-step short-term wind speed forecasting approach based on multi-scale dominant ingredient chaotic analysis improved hybrid GWO-SCA optimization and ELM. Energy Convers Manage 187:356–377
Geem ZW, Kim JH, Loganathan GV (2001) A new heuristic optimization algorithm: harmony search. Simulation 76(2):60–68. https://doi.org/10.1177/003754970107600201
Ghaddar B, Sawaya JN (2018) High dimensional data classification and feature selection using support vector machines. Eur J Oper Res 265(3):993–1004
Ghimatgar H, Kazemi K, Helfroush MS, Aarabi A (2018) An improved feature selection algorithm based on graph clustering and ant colony optimization. Knowl Base Syst 159:270–2855
Ghorbani N, Babaei E (2014) Exchange market algorithm. Appl Soft Comput 19:177–187. https://doi.org/10.1016/j.asoc.2014.02.006
Glover F (1989) Tabu search-Part I. ORSA J Comput 1(3):190–206
Glover F (1990) Tabu search-Part II. ORSA J Comput 2(1):4–32
Gonidakis D, Vlachos A (2019) A new sine cosine algorithm for economic and emission dispatch problems with price penalty factors. J Inf Optim Sci 40(3):679–697
Guo W, Wang Y, Zhao F, Dai F (2019) Riesz fractional derivative elite-guided sine cosine algorithm. Appl Soft Comput 81:105481
Gupta S, Deep K (2019a) A hybrid self-adaptive sine cosine algorithm with opposition based learning. Expert Syst Appl 119:210–230
Gupta S, Deep K (2019b) Improved sine cosine algorithm with crossover scheme for global optimization. Knowl-Based Syst 165:374–406
Gupta S, Deep K (2019d) Hybrid sine cosine artificial bee colony algorithm for global optimization and image segmentation. Neural Comput App 32:1–23
Gupta S, Deep K, Moayedi H, Foong LK, Assad A (2020b) Sine cosine grey wolf optimizer to solve engineering design problems. Eng Comput 37:1–27
Gupta S, Deep K, Engelbrecht AP (2020c) A memory guided sine cosine algorithm for global optimization. Eng Appl Artif Intell 93:103718
Gupta S, Deep K (2019c) A novel hybrid sine cosine algorithm for global optimization and its application to train multilayer perceptrons. Appl Intell, 1–34.
Gupta S, Deep K, Mirjalili S, Kim, JH (2020a). A Modified Sine Cosine Algorithm with Novel Transition Parameter and Mutation Operator for Global Optimization. Expert Systems with Applications, 113395.
Han X, Liu Q, Wang H, Wang L (2018) Novel fruit fly optimization algorithm with trend search and co-evolution. Knowl-Based Syst 141:1–17
Hancer E, Xue B, Zhang M (2018) Differential evolution for filter feature selection based on information theory and feature ranking. Knowl Base Syst 140:103–119
Hans R, Kaur H (2019) Hybrid binary sine cosine algorithm and ant lion optimization (SCALO) approaches for feature selection problem. Int J Comput Mater Sci Eng. 9:1950021
Hashim FA, Houssein EH, Mabrouk MS, Al-Atabany W, Mirjalili S (2019) Henry gas solubility optimization: a novel physics-based algorithm. Futur Gener Comput Syst 101:646–667
Hassanien AE, Rizk-Allah RM, Elhoseny M (2018) A hybrid crow search algorithm based on rough searching scheme for solving engineering optimization problems. J Ambient Intell Humanized Comput. Accepted, 20–6–2018.
Hatamlou A (2013) Black hole: a new heuristic optimization approach for data clustering. Inf Sci 222:175–84. https://doi.org/10.1016/j.ins.2012.08.023
He Y, Wang X (2018) Group theory-based optimization algorithm for solving knapsack problems, Knowl. Base Syst.
He S, Wu QH, Saunders JR (2006) A novel group search optimizer inspired by animal behavioural ecology. In IEEE International Conference on Evolutionary Computation, pp. 1272–8. doi: https://doi.org/10.1109/CEC.2006.1688455.
Hekimoğlu B (2019) Sine-cosine algorithm-based optimization for automatic voltage regulator system. Trans Inst Meas Control 41(6):1761–1771
Huang H, Heidari AA, Xu Y, Wang M, Liang G, Chen H, Cai X (2020) Rationalized sine cosine optimization with efficient searching patterns. IEEE Access 8:61471–61490
Issa M, Hassanien AE, Oliva D, Helmi A, Ziedan I, Alzohairy A (2018) ASCA-PSO: adaptive sine cosine optimization algorithm integrated with particle swarm for pairwise local sequence alignment. Expert Syst Appl 99:56–70
Issaa M, Hassanien AE, Oliva D, Helmi A, Alzohairy IZA (2018) ASCA-PSO: adaptive sine cosine optimization algorithm integrated with particle swarm for pairwise local sequence alignment. Expert Syst Appl 99(1):56–70
Jahangiri M, Hadianfard MA, Najafgholipour MA, Jahangiri M, Gerami MR (2020) Interactive autodidactic school: a new metaheuristic optimization algorithm for solving mathematical and structural design optimization problems. Comput Struct 235:106268
Jiang J, Jiang R, Meng X, Li K (2020a) SCGSA: A sine chaotic gravitational search algorithm for continuous optimization problems. Expert Syst Appl 144:113118
Jiang J, Xu M, Meng X, Li K (2020b) STSA: a sine tree-seed algorithm for complex continuous optimization problems. Physica A 537:122802
Jouhari H, Lei D, Al-qaness AA, Abd Elaziz M, Ewees AA, Farouk O (2019) Sine-cosine algorithm to enhance simulated annealing for unrelated parallel machine scheduling with setup times. Mathematics 7(11):1120
Kale GA, Yüzgeç U (2022) Advanced strategies on update mechanism of sine cosine optimization algorithm for feature selection in classification problems. Eng App Artif Intell 107:104506
Karaboga D, Gorkemli B, Ozturk C et al (2014) A comprehensive survey: artificial bee colony (ABC) algorithm and applications. Artif Intell Rev 42(1):21–57
Karimulla S, Ravi K (2021) Solving multi-objective power flow problem using enhanced sine cosine algorithm. Ain Shams Eng J 12:3803–3817
Kashan AH. League championship algorithm: a new algorithm for numerical function optimization. In International Conference of Soft Computing and Pattern Recognition; 2009, pp. 43–8. doi: https://doi.org/10.1109/SoCPaR.2009.21.
Kaur G, Dhillon JS (2021) Economic power generation scheduling exploiting hill-climbed sine-cosine algorithm. Appl Soft Comput 111:107690
Kaveh A, Khayatazad M (2012) A new meta-heuristic method: ray optimization. Comput Struct 112:283–294
Kaveh A, Mahdavi V (2014) Colliding bodies optimization: a novel meta-heuristic method. Comput Struct 139:18–27. https://doi.org/10.1016/j.compstruc.2014.04.005
Kaveh A, Talatahari S (2010) A novel heuristic optimization method: charged system search. Acta Mech 213(3):267–289. https://doi.org/10.1007/s00707-009-0270-4
Kaveh A, Vazirinia Y (2020) An upgraded sine cosine algorithm for tower crane selection and layout problem. Periodica Polytechn Civil Eng 64(2):325–343
Kennedy J (2011) Particle swarm optimization. In Encyclopedia of machine learning. Springer, pp 760–766
Khadanga RK, Kumar A, Panda S (2021) A novel sine augmented scaled sine cosine algorithm for frequency control issues of a hybrid distributed two-area power system. Neural Comput App 33:1–14
Khokhar B, Dahiya S, Parmar KS (2021) Load frequency control of a microgrid employing a 2D sine logistic map based chaotic sine cosine algorithm. Appl Soft Comput 109:107564
Khrissi L, El Akkad N, Satori H, Satori K (2021) Clustering method and sine cosine algorithm for image segmentation. Evol Intell 15:1–14
Kirkpatrick S, Gelatt CD, Vecchi MP (1983) Optimization by simulated annealing. Science 220(4598):671–680
Koza JR (1992) Genetic programming: on the programming of computers by means of natural selection. MIT Press
Krichmar, JL (2012) A biologically inspired action selection algorithm based on principles of neuromodulation. In The 2012 International Joint Conference on Neural Networks (IJCNN) (pp. 1–8). IEEE.
Kuo RJ, Lin JY, Nguyen TPQ (2021) An application of sine cosine algorithm-based fuzzy possibilistic C-ordered means algorithm to cluster analysis. Soft Comput 25(5):3469–3484
Li S, Fang H, Liu X (2018) Parameter optimization of support vector regression based on sine cosine algorithm. Expert Syst Appl 91:63–77
Li C, Luo Z, Song Z, Yang F, Fan J, Liu PX (2019) An enhanced brain storm sine cosine algorithm for global optimization problems. IEEE Access 7:28211–28229
Li Y, Zhao Y, Liu J (2021a) Dimension by dimension dynamic sine cosine algorithm for global optimization problems. Appl Soft Comput 98:106933
Li Y, Zhao Y, Liu J (2021b) Dynamic sine cosine algorithm for large-scale global optimization problems. Expert Syst Appl 177:114950
Li Q, Ning H, Gong J, Li X, Dai B (2021c) A hybrid greedy sine cosine algorithm with differential evolution for global optimization and cylindricity error evaluation. Appl Artif Intell 35(2):171–191
Liu, J. (2018). Improved sine cosine algorithm with reverse-learning and adaptive tent chaos search. In 2018 14th international conference on computational intelligence and security (CIS) (pp. 187–190). IEEE.
Long W, Wu T, Liang X, Xu S (2019) Solving high-dimensional global optimization problems using an improved sine cosine algorithm. Expert Syst Appl 123:108–126
Luke S (2013) Essentials of metaheuristics, 2nd edn. Lulu
Manrique, M. L., Montoya, O. D., Garrido, V. M., Grisales-Noreña, L. F., & Gil-González, W. (2019). Sine-cosine algorithm for OPF analysis in distribution systems to size distributed generators. In Workshop on engineering applications. Springer, Cham, pp. 28–39.
Mirjalili S (2015) The ant lion optimizer. Adv Eng Softw 83:80–98
Mirjalili S (2016) SCA: a sine cosine algorithm for solving optimization problems. Knowl-Based Syst 96:120–133
Mirjalili S, Lewis A (2016) The whale optimization algorithm. Adv Eng Softw 95:51–67
Mirjalili S, Mirjalili SM (2014) Andrew Lewis, grey wolf optimizer. Adv Eng Software 69:46–61
Mirjalili S, Gandomi AH, Mirjalili SZ, Saremi S, Faris H, Mirjalili SM (2017) Salp swarm algorithm: a bio-inspired optimizer for engineering design problems. Adv Eng Softw 114:163–191
Mirjalili SM, Mirjalili SZ, Saremi S, Mirjalili S (2020) Sine cosine algorithm: theory, literature review, and application in designing bend photonic crystal waveguides. In Nature-inspired optimizers. Springer, Cham., pp. 201–217
Moghaddam FF, Moghaddam RF, Cheriet M (2012) Curved space optimization: a random search based on general relativity theory. Neural Evol Comput. abs/1208.2214.
Moosavian N, Roodsari BK (2014) Soccer league competition algorithm: a novel meta-heuristic algorithm for the optimal design of water distribution networks. Swarm Evol Comput 17:14–24. https://doi.org/10.1016/j.swevo.2014.02.002
Mousa AA, AbdEl-Wahed WF, Rizk-Allah RM (2011) A hybrid ant colony optimization approach based local search scheme for multiobjective design optimizations. J Electric Power Syst Res 81:1014–1023
Mucherino A, Seref O (2007) Monkey search: a novel metaheuristic search for global optimization. AIP Conf Proc 953:162
Nayak DR, Dash R, Majhi B, Wang S (2018) Combining extreme learning machine with modified sine cosine algorithm for detection of pathological brain. Comput Electr Eng 68:366–380
Neggaz N, Ewees AA, Elaziz MA, Mafarja M (2020) Boosting Salp swarm algorithm by sine cosine algorithm and disrupt operator for feature selection. Expert Syst Appl 145:113103
Nenavath H, Jatoth RK (2018) Hybridizing sine cosine algorithm with differential evolution for global optimization and object tracking. Appl Soft Comput 62:1019–1043
Nenavath H, Jatoth RK, Das S (2018) A synergy of the sine-cosine algorithm and particle swarm optimizer for improved global optimization and object tracking. Swarm Evol Comput 43:1–30
Omidvar MN, Li X, Tang K (2015) Designing benchmark problems for large-scale continuous optimization. Inf Sci 316:419–436
Pal PK, Deep K, Nagar AK (2019) Performance of sine-cosine algorithm on large-scale optimization problems. In: Deep K, Jain M, Salhi S (eds) Decision science in action: asset analytics (performance and safety management). Springer, Singapore
Pan JS, Yang QY, Chu SC, Chang KC (2021) Compact sine cosine algorithm applied in vehicle routing problem with time window. Telecommun Syst 78:1–20
Panwar LK, ReddyK S, Verma A, Panigrahi BK, Kumar R (2018) Binary Grey Wolf optimizer for large scale unit commitment problem. Swarm Evol Comput 38:251–266
Peng T, Zhang C, Zhou J, Nazir MS (2021) An integrated framework of Bi-directional Long-Short Term Memory (BiLSTM) based on sine cosine algorithm for hourly solar radiation forecasting. Energy 221:119887
Pinto H, Peña A, Valenzuela M, Fernández A (2019) A binary sine-cosine algorithm applied to the knapsack problem. In Computer science on-line conference (pp. 128–138). Springer: Cham.
Qu C, Zeng Z, Dai J, Yi Z, He W (2018) A modified sine-cosine algorithm based on neighborhood search and greedy levy mutation. Comput Intell Neurosci 2018:1–19
Rao SS (2019) Engineering optimization: theory and practice. John Wiley & Sons
Rao RV, Savsani VJ, Vakharia DP (2012) Teaching–learning-based optimization: an optimization method for continuous non-linear large scale problems. Inf Sci 183(1):1–15
Rashedi E, Nezamabadi-Pour H, Saryazdi S (2009) GSA: a gravitational search algorithm. Inf Sci 179(13):2232–48. https://doi.org/10.1016/j.ins.2009.03.004
Raut U, Mishra S (2020) An improved sine-cosine algorithm for simultaneous network reconfiguration and DG allocation in power distribution systems. Appl Soft Comput 92:106293
Raut U, Mishra S (2021) Enhanced sine–cosine algorithm for optimal planning of distribution network by incorporating network reconfiguration and distributed generation. Arab J Sci Eng 46(2):1029–1051
Rehman MZ, Khan A, Ghazali R, Aamir M, Nawi NM (2021) A new multi sine-cosine algorithm for unconstrained optimization problems. PLoS ONE 16(8):e0255269
Rizk-Allah RM (2014) Solving multi-objective optimization problems using modified vector evaluated firefly algorithm. Online J Math Stat 6(1):111–117
Rizk-Allah RM (2016) Hybridization of fruit fly optimization algorithm and firefly algorithm for solving nonlinear programming problems. Int J Swarm Intell Evol Comput 5(2):1–10
Rizk-Allah RM (2018) Hybridizing sine cosine algorithm with a multi-orthogonal search strategy for engineering design problems. J Comput Design Eng 5(2):249–273
Rizk-Allah RM (2019) An improved sine–cosine algorithm based on orthogonal parallel information for global optimization. Soft Comput 23(16):7135–7161
Rizk-Allah RM (2021) A quantum-based sine cosine algorithm for solving general systems of nonlinear equations. Artif Intell Rev 54(5):3939–3990
Rizk-Allah RM, Hassanien AE (2018) New binary bat algorithm for solving 0–1 knapsack problem. Complex Intell Syst 4(1):31–53
Rizk-Allah RM, Zaki Elsayed M, El-Sawy AA (2013) Hybridizing ant colony optimization with firefly algorithm for unconstrained optimization problems. Appl Math Comput 224:473–483
Rizk-Allah RM, El-Sehiemy RA, Deb S, Wang G-G (2017a) A novel fruit fly framework for multi-objective shape design of tubular linear synchronous motor. J Supercomput 73(3):1235–1256
Rizk-Allah RM, Abdel Mageed HM, El-Sehiemy RA, Abdel Aleem SHE, El Shahat A (2017b) A new sine cosine optimization algorithm for solving combined non-convex economic and emission power dispatch problems. Int J Energy Convers 5(6):180–192
Rizk-Allah RM, Hassanien AE, Slowik A (2020a) The multi-objective orthogonal opposition-based crow search algorithm for large-scale multi-objective optimization. Neural Comput App 32:1–32
Rizk-Allah RM, Hassanien AE, Oliva D (2020b) An enhanced sitting–sizing scheme for shunt capacitors in radial distribution systems using improved atom search optimization. Neural Comput App 32:1–29
Rizk-Allah RM, El-Sehiemy RA (2018) A novel sine cosine approach for single and multiobjective emission/economic load dispatch problem. In 2018 international conference on innovative trends in computer engineering (ITCE) (pp. 271–277). IEEE.
Rizk-Allah RM, Hassanien AE, Elhoseny M (2018) A new binary Salp swarm algorithm: development and application for optimization tasks. Neural Comput App. Accepted, 22–6–2018
Rizk-Allah RM, Hassanien AE, Bhattacharyya S (2018) Chaotic crow search algorithm for fractional optimization problems. Appl Soft Comput, In Press.
Sadollah A, Bahreininejad A, Eskandar H, Hamdi M (2013) Mine blast algorithm: a new population-based algorithm for solving constrained engineering optimization problems. Appl Soft Comput 13(5):2592–612. https://doi.org/10.1016/j.asoc.2012.11.026
Selim A, Kamel S, Jurado F (2019) Voltage profile enhancement using multi-objective sine cosine algorithm for optimal installation of DSTACOMs into distribution systems. 2019 10th International Renewable Energy Congress (IREC). IEEE
Shah HH (2011) Principal components analysis by the galaxy-based search algorithm: a novel metaheuristic for continuous optimisation. Int J Comput Sci Eng 6:132–140. https://doi.org/10.1504/IJCSE.2011.041221
Sharma S, Saha AK (2021) Bosca—a hybrid butterfly optimization algorithm modified with sine cosine algorithm. In Progress in advanced computing and intelligent engineering. Springer: Singapore, pp. 360–372
Shutari H, Saad N, Nor NBM, Tajuddin MFN, Alqushaibi A, Magzoub MA (2021) Towards enhancing the performance of grid-tied VSWT Via adopting sine cosine algorithm-based optimal control scheme. IEEE Access. https://doi.org/10.1109/ACCESS.2021.3119019
Si T, Bhattacharya D (2021) Sine cosine algorithm with centroid opposition-based computation. Applications of artificial intelligence in engineering. Springer, Singapore, pp 119–129
Simon D (2008) Biogeography-based optimization. IEEE Trans Evol Comput 12(6):702–713. https://doi.org/10.1109/TEVC.2008.919004
Singh N, Kaur J (2021) Hybridizing sine–cosine algorithm with harmony search strategy for optimization design problems. Soft Comput 25:1–23
Singh N, Singh SB (2017) A novel hybrid GWO-SCA approach for optimization problems. Eng Sci Technol Int J 20(6):1586–1601
Storn R, Price K (1997) Differential evolution—a simple and efficient heuristic for global optimization over continuous spaces. J Global Optim 11(4):341–359. https://doi.org/10.1023/A:1008202821328
Suid MH, Tumari MZ, Ahmad MA (2019) A modified sine cosine algorithm for improving wind plant energy production. Indonesian J Electr Eng Comput Sci 16(1):101–106
Tahir DS, Ali RS (2018) Chaotic sine-cosine optimization algorithms. Int J Soft Comput 13(3):108–122
Tawhid MA, Savsani V (2019) Multi-objective sine-cosine algorithm (MO-SCA) for multi-objective engineering design problems. Neural Comput Appl 31(2):915–929
Tizhoosh HR (2005) Opposition-based learning: a new scheme for machine intelligence. In Proceedings of the International Conference on Computational Intelligence for Modelling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce Vol. IEEE Computer Society, pp. 695–701.
Tubishat M, Ja’afar S, Idris N, Al-Betar MA, Alswaitti M, Jarrah H, Omar MS (2021) Improved sine cosine algorithm with simulated annealing and chaotic singer map for Hadith classification. Neural Comput App, 1–22.
Tuncer T (2018) SCSO: a novel sine-cosine based swarm optimization algorithm for numerical function optimization. Period Eng Nat Sci 6(2):1–9
Ulker E, Tongur V (2017) Migrating birds optimization (MBO) algorithm to solve the knapsack problem. Procedia Comput Sci 111:71–76
Wan Y, Ma A, Zhang L, Zhong Y (2021) Multiobjective sine cosine algorithm for remote sensing image spatial-spectral clustering. IEEE Trans Cybern 52:11172–11186
Wang M, Lu G (2021) A modified sine cosine algorithm for solving optimization problems. IEEE Access 9:27434–27450
Wang J, Yang W, Du P, Niu T (2018) A novel hybrid forecasting system of wind speed based on a newly developed multi-objective sine cosine algorithm. Energy Convers Manage 163:134–150
Wang GG, Deb S, Cui Z (2019) Monarch butterfly optimization. Neural Comput App 31:1995–2014. https://doi.org/10.1007/s00521-015-1923-y
Wang B, Xiang T, Li N, He W, Li W, Hei X (2020a) A symmetric sine cosine algorithm with adaptive probability selection. IEEE Access 8:25272–25285
Wang M, Wu C, Chen M, Chen B, Jiang Y (2020b) A band selection approach based on Lévy sine cosine algorithm and alternative distribution for hyperspectral image. Int J Remote Sens 41(9):3429–3445
Wu S, Mao P, Li R, Cai Z, Heidari AA, Xia J, Chen X (2021) Evolving fuzzy k-nearest neighbors using an enhanced sine cosine algorithm: case study of lupus nephritis. Comput Biol Med 135:104582
Xian H, Yang C, Wang H, Yang X (2021) A modified sine cosine algorithm with teacher supervision learning for global optimization. IEEE Access 9:17744–17766
Yang X-S (2010a) A new metaheuristic bat-inspired algorithm. Springer, Berlin Heidelberg, pp 65–74
Yang X (2010b) Firefly algorithm, stochastic test functions and design optimisation. Int J Bio-Inspired Comput 2(2):78–84. https://doi.org/10.1504/IJBIC.2010.032124
Yang X-S, Deb S (2014) Cuckoo search: recent advances and applications. Neural Comput App 24(1):169–174
Yang, XS (2011, May). Metaheuristic optimization: algorithm analysis and open problems. In International Symposium on Experimental Algorithms. Springer: Berlin, Heidelberg, pp. 21–32.
Yıldız ABS, Pholdee N, Bureerat S, Yıldız AR, Sait SM (2020) Sine-cosine optimization algorithm for the conceptual design of automobile components. Mater Test 62(7):744–748. https://doi.org/10.3139/120.111541
Yu Z, Shi X, Qiu X, Zhou J, Chen X, Gou Y (2021) Optimization of postblast ore boundary determination using a novel sine cosine algorithm-based random forest technique and Monte Carlo simulation. Eng Optim 53(9):1467–1482
Zhang H, Gao Z, Zhang J, Liu J, Nie Z, Zhang J (2020) Hybridizing extended ant lion optimizer with sine cosine algorithm approach for abrupt motion tracking. EURASIP J Image Video Process 2020(1):4
Zhang S, Fan F, Li W, Chu SC, Pan JS (2021a) A parallel compact sine cosine algorithm for TDOA localization of wireless sensor network. Telecommun Syst 78:1–11
Zhang L, Hu T, Yang Z, Yang D, Zhang J (2021b) Elite and dynamic opposite learning enhanced sine cosine algorithm for application to plat-fin heat exchangers design problem. Neural Computing and Applications, 1–14.
Zhao W, Wang L, Zhang Z (2019) A novel atom search optimization for dispersion coefficient estimation in groundwater. Futur Gener Comput Syst 91:601–610
Zhou A, Qu B-Y, Li H, Zhao S-Z, Suganthan PN, Zhang Q (2011) Multiobjective evolutionary algorithms: a survey of state of the art. Swarm Evol Comput 1:32–49
Funding
Open access funding provided by The Science, Technology & Innovation Funding Authority (STDF) in cooperation with The Egyptian Knowledge Bank (EKB).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no conflict of interest to declare.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Scientific Research Group in Egypt http://www.egyptscience.net
Appendix: The MATLAB code of the SCA
Appendix: The MATLAB code of the SCA

Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Rizk-Allah, R.M., Hassanien, A.E. A comprehensive survey on the sine–cosine optimization algorithm. Artif Intell Rev 56, 4801–4858 (2023). https://doi.org/10.1007/s10462-022-10277-3
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10462-022-10277-3