Skip to main content
SpringerLink
Log in

Persistent-homology-based machine learning: a survey and a comparative study

  • Published:
Artificial Intelligence Review Aims and scope Submit manuscript

Abstract

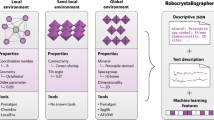
A suitable feature representation that can both preserve the data intrinsic information and reduce data complexity and dimensionality is key to the performance of machine learning models. Deeply rooted in algebraic topology, persistent homology (PH) provides a delicate balance between data simplification and intrinsic structure characterization, and has been applied to various areas successfully. However, the combination of PH and machine learning has been hindered greatly by three challenges, namely topological representation of data, PH-based distance measurements or metrics, and PH-based feature representation. With the development of topological data analysis, progresses have been made on all these three problems, but widely scattered in different literatures. In this paper, we provide a systematical review of PH and PH-based supervised and unsupervised models from a computational perspective. Our emphasizes are the recent development of mathematical models and tools, including PH software and PH-based functions, feature representations, kernels, and similarity models. Essentially, this paper can work as a roadmap for the practical application of PH-based machine learning tools. Further, we compare between two types of simplicial complexes (alpha and Vietrois-Rips complexes), two types of feature extractions (barcode statistics and binned features), and three types of machine learning models (support vector machines, tree-based models, and neural networks), and investigate their impacts on the protein secondary structure classification.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Data availability

The data and codes can be downloaded from https://entuedu-my.sharepoint.com/:f:/g/personal/xiakelin_staff_main_ntu_edu_sg/EvZ-CivdgCdCu90JpIAR3BYBmJwl--DxteRirSvLnAhFHA?e=kBPAP3.

References

  • Adams H, Emerson T, Kirby M, Neville R, Peterson C, Shipman P, Chepushtanova S, Hanson E, Motta F, Ziegelmeier L (2017) Persistence images: a stable vector representation of persistent homology. J Mach Learn Res 18:218–252

    MathSciNet  MATH  Google Scholar 

  • Adcock A, Carlsson E, Carlsson G (2016) The ring of algebraic functions on persistence bar codes. Homol, Homotopy Appli 18:381–402

    Article  MathSciNet  MATH  Google Scholar 

  • Ahmed M, Fasy BT, Wenk C (2014) Local persistent homology based distance between maps. In Proceedings of the 22nd ACM SIGSPATIAL international conference on advances in geographic information systems, ACM, pp. 43–52

  • Alfaro E, Gámez M, García N (2013) adabag: An r package for classification with boosting and bagging. J Statis Softw 54:1–35. https://doi.org/10.18637/jss.v054.i02

    Article  Google Scholar 

  • Anirudh R, Thiagarajan JJ, Kim I, Polonik W (2016) Autism spectrum disorder classification using graph kernels on multidimensional time series, arXiv preprint arXiv:1611.09897,

  • Anirudh R, Venkataraman V, Ramamurthy KN, Turaga P (2016) A Riemannian framework for statistical analysis of topological persistence diagrams. In Proceedings of the IEEE conference on computer vision and pattern recognition workshops, pp. 68–76

  • Bae W, Yoo JJ, Ye JC (2017) Beyond deep residual learning for image restoration: persistent homology-guided manifold simplification. In CVPR workshops, pp. 1141–1149

  • Bauer U (2017) Ripser: a lean C++ code for the computation of Vietoris-Rips persistence barcodes, Software available at https://github.com/Ripser/ripser

  • Bauer U, Kerber M, Reininghaus J (2014) Distributed computation of persistent homology, In: Proceedings of the 16th workshop on algorithm engineering and experiments (ALENEX)

  • Bauer U, Kerber M, Reininghaus J (2014) Distributed computation of persistent homology. In 2014 proceedings of the 16th workshop on algorithm engineering and experiments (ALENEX), SIAM, pp. 31–38

  • Bauer U, Kerber M, Reininghaus J, Wagner H (2014) PHAT–persistent homology algorithms toolbox. In International congress on mathematical software, Springer, pp. 137–143

  • Bendich P, Cohen-Steiner D, Edelsbrunner H, Harer J, Morozov D (2007) Inferring local homology from sampled stratified spaces. In foundations of computer science, 2007. FOCS’07. 48th Annual IEEE symposium on, IEEE, pp. 536–546

  • Bendich P, Edelsbrunner H, Kerber M (2010) Computing robustness and persistence for images. IEEE Trans Visual Comput Graphics 16:1251–1260

    Article  Google Scholar 

  • Bendich P, Gasparovic E, Harer J, Izmailov R, Ness L (2015) Multi-scale local shape analysis and feature selection in machine learning applications. In Neural Networks (IJCNN), 2015 international joint conference on, IEEE, pp. 1–8

  • Bendich P, Wang B, Mukherjee S (2012) Local homology transfer and stratification learning, In Proceedings of the 23th annual ACM-SIAM symposium on discrete algorithms, SIAM, pp. 1355–1370

  • Binchi J, Merelli E, Rucco M, Petri G, Vaccarino F (2014) jholes: A tool for understanding biological complex networks via clique weight rank persistent homology. Electron Notes Theoretical Comput Sci 306:5–18

    Article  MathSciNet  MATH  Google Scholar 

  • Bonis T, Ovsjanikov M, Oudot S, Chazal F (2016) Persistence-based pooling for shape pose recognition. In International workshop on computational topology in image context, Springer, pp. 19–29

  • Breiman L (2001) Random forests. Mach Learn 45:5–32. https://doi.org/10.1023/A:1010933404324

    Article  MATH  Google Scholar 

  • Breiman L, Friedman J, Stone CJ, Olshen RA (1984) Classification and regression trees. Chapman and Hall/CRC, Wadsworth Statistics/Probability

  • Bubenik P (2015) Statistical topological data analysis using persistence landscapes. J Mach Learn Res 16:77–102

    MathSciNet  MATH  Google Scholar 

  • Bubenik P (2018) The persistence landscape and some of its properties, arXiv preprint arXiv:1810.04963

  • Bubenik P, Dłotko P (2017) A persistence landscapes toolbox for topological statistics. J Symb Comput 78:91–114

    Article  MathSciNet  MATH  Google Scholar 

  • Bubenik P, Kim PT (2007) A statistical approach to persistent homology. Homol, Homotopy Appli 19:337–362

    Article  MathSciNet  MATH  Google Scholar 

  • Cai T, Liu W (2011) A direct estimation approach to sparse linear discriminant analysis. J Am Stat Assoc 106:1566–1577. https://doi.org/10.1198/jasa.2011.tm11199

    Article  MathSciNet  MATH  Google Scholar 

  • Cang ZX, Mu L, Wei GW (2018) Representability of algebraic topology for biomolecules in machine learning based scoring and virtual screening. PLoS Comput Biol 14:e1005929

    Article  Google Scholar 

  • Cang ZX, Mu L, Wu KD, Opron K, Xia KL, Wei G (2015) A topological approach to protein classificationy. Molecul Math Biol 3:140–162

    MATH  Google Scholar 

  • Cang ZX, Wei GW (2017) Analysis and prediction of protein folding energy changes upon mutation by element specific persistent homology. Bioinformatics 33:3549–3557

    Google Scholar 

  • Cang ZX, Wei GW (2017) Integration of element specific persistent homology and machine learning for protein-ligand binding affinity prediction. Int J Numerical Methods Biomed Eng 34(2):e2914

    Google Scholar 

  • Cang ZX, Wei GW (2017) TopologyNet: Topology based deep convolutional and multi-task neural networks for biomolecular property predictions. PLoS Comput Biol 13:e1005690

    Article  Google Scholar 

  • Carlsson G (2009) Topology and data. Am Math Soc 46:255–308

    Article  MathSciNet  MATH  Google Scholar 

  • Carlsson G, Ishkhanov T, Silva V, Zomorodian A (2008) On the local behavior of spaces of natural images. Int J Comput Vision 76:1–12

    Article  MathSciNet  MATH  Google Scholar 

  • Carlsson G, Singh G, Zomorodian A (2009) Computing multidimensional persistence, in Algorithms and computation, Springer, pp. 730–739

  • Carlsson G, Zomorodian A (2009) The theory of multidimensional persistence. Dis Comput Geo 42:71–93

    Article  MathSciNet  MATH  Google Scholar 

  • Carriere M, Bauer U (2018) On the metric distortion of embedding persistence diagrams into reproducing kernel hilbert spaces, arXiv preprint arXiv:1806.06924

  • Carriere M, Cuturi M, Oudot S (2017) Sliced wasserstein kernel for persistence diagrams, arXiv preprint arXiv:1706.03358

  • Cerri A, Landi C (2013) The persistence space in multidimensional persistent homology. In Discrete Geometry for Computer Imagery, Springer, 180–191

  • Chang C-C, Lin C-J (2011) LIBSVM: A library for support vector machines. ACM Trans Intell Sys Technol 27(1–27):27

    Google Scholar 

  • Chazal F, Cohen-Steiner D, Mérigot Q (2011) Geometric inference for probability measures. Found Comput Math 11:733–751

    Article  MathSciNet  MATH  Google Scholar 

  • Chazal F, Fasy B, Lecci F, Michel B, Rinaldo A, Rinaldo A, Wasserman L (2017) Robust topological inference: distance to a measure and kernel distance. J Mach Learn Res 18:5845–5884

    MathSciNet  MATH  Google Scholar 

  • Chen Y, Garcia EK, Gupta MR, Rahimi A, Cazzanti L (2009) Similarity-based classification: concepts and algorithms. J Mach Learn Res 10:747–776

    MathSciNet  MATH  Google Scholar 

  • Chevyrev I, Nanda V, Oberhauser H (2018) Persistence paths and signature features in topological data analysis, arXiv preprint arXiv:1806.00381

  • Chintakunta H, Gentimis T, Gonzalez-Diaz R, Jimenez MJ, Krim H (2015) An entropy-based persistence barcode. Pattern Recogn 48:391–401

    Article  MATH  Google Scholar 

  • Chiu MC, Pun CS, Wong HY (2017) Big data challenges of high-dimensional continuous-time mean-variance portfolio selection and a remedy. Risk Anal 37:1532–1549. https://doi.org/10.1111/risa.12801

    Article  Google Scholar 

  • Cohen-Steiner D, Edelsbrunner H, Morozov D (2006) Vines and vineyards by updating persistence in linear time. In Proceedings of the 22nd annual symposium on Computational geometry, ACM, 119–126

  • Cortes C, Vapnik V (1995) Support-vector networks. Mach Learn 20:273–297. https://doi.org/10.1023/A:1022627411411

    Article  MATH  Google Scholar 

  • Cramer JS (2004) The early origins of the logit model. Studies History Philosophy Sci Part C: Studies History Philosophy Biol Biomed Sci 35:613–626. https://doi.org/10.1016/j.shpsc.2004.09.003

    Article  Google Scholar 

  • Dey TK, Li KY, Sun J, David CS (2008) Computing geometry aware handle and tunnel loops in 3d models., ACM Trans. Graph., 27

  • Dey TK, Mandal S (2018) Protein classification with improved topological data analysis. In LIPIcs-Leibniz international proceedings in informatics, vol. 113, Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik,

  • Dey TK, Wang YS (2013) Reeb graphs: approximation and persistence. Discret Comput Geom 49:46–73. https://doi.org/10.1007/s00454-012-9463-z

    Article  MathSciNet  MATH  Google Scholar 

  • Dionysus: the persistent homology software. Software available at http://www.mrzv.org/software/dionysus

  • Di Fabio B, Landi C (2011) A Mayer-Vietoris formula for persistent homology with an application to shape recognition in the presence of occlusions. Found Comput Math 11:499–527

    Article  MathSciNet  MATH  Google Scholar 

  • Edelsbrunner H (1992) Weighted alpha shapes, tech. report, Champaign, IL, USA

  • Edelsbrunner H, Harer J (2010) Computational topology: an introduction, American Mathematical Soc.,

  • Edelsbrunner H, Letscher D, Zomorodian A (2002) Topological persistence and simplification. Discrete Comput. Geom. 28:511–533

    Article  MathSciNet  MATH  Google Scholar 

  • Edelsbrunner H, Mucke EP (1994) Three-dimensional alpha shapes. Phys Rev Lett 13:43–72

    MATH  Google Scholar 

  • Fan R-E, Chang K-W, Hsieh C-J, Wang X-R, Lin C-J (2008) Liblinear: a library for large linear classification. J Mach Learn Res 9:1871–1874

    MATH  Google Scholar 

  • Fasy BT, Kim J, Lecci F, Maria C (2014) Introduction to the r package tda, arXiv preprint arXiv:1411.1830

  • Fasy BT, Wang B (2016) Exploring persistent local homology in topological data analysis, in Acoustics, Speech and Signal Processing (ICASSP), 2016 IEEE International Conference on, IEEE, pp. 6430–6434

  • Fox NK, Brenner SE, Chandonia J-M (2014) Scope: structural classification of proteins-extended, integrating scop and astral data and classification of new structures. Nucleic Acids Res 42:D304–D309

    Article  Google Scholar 

  • Freund Y, Schapire (1997) A decision-theoretic generalization of on-line learning and an application to boosting. J Comput Syst Sci 55:119–139. https://doi.org/10.1006/jcss.1997.1504

    Article  MathSciNet  MATH  Google Scholar 

  • Friedman JH (2001) Greedy function approximation: a gradient boosting machine. Ann Stat 29:1189–1232

    Article  MathSciNet  MATH  Google Scholar 

  • Frohmader A (2008) Face vectors of flag complexes. Israel J Math 164:153–164

    Article  MathSciNet  MATH  Google Scholar 

  • Frosini P, Landi C (2013) Persistent Betti numbers for a noise tolerant shape-based approach to image retrieval. Pattern Recogn Lett 34:863–872

    Article  Google Scholar 

  • Gameiro M, Hiraoka Y, Izumi S, Kramar M, Mischaikow K, Nanda V (2013) Topological measurement of protein compressibility via persistence diagrams, preprint

  • Ghrist R (2008) Barcodes: the persistent topology of data. Bull Am Math Soc 45:61–75

    Article  MathSciNet  MATH  Google Scholar 

  • Ghrist R (2008) Barcodes: the persistent topology of data. Bull Amer Math Soc 45:61–75

    Article  MathSciNet  MATH  Google Scholar 

  • Giansiracusa N, Giansiracusa R, Moon C (2017) Persistent homology machine learning for fingerprint classification, arXiv preprint arXiv:1711.09158

  • Giusti C, Pastalkova E, Curto C, Itskov V (2015) Clique topology reveals intrinsic geometric structure in neural correlations. Proc Natl Acad Sci 112:13455–13460

    Article  MathSciNet  MATH  Google Scholar 

  • Guo W, Manohar K, Brunton SL, Banerjee AG (2018) Sparse-tda: Sparse realization of topological data analysis for multi-way classification. IEEE Trans Knowl Data Eng 30:1403–1408

    Article  Google Scholar 

  • Hadimaja MZ, Pun CS (2021) A self-calibrated regularized direct estimation for graphical selection and discriminant analysis in high dimensions. Comput Stat Data Anal 155:107105. https://doi.org/10.1016/j.csda.2020.107105

  • Han YS, Yoo J, Ye JC (2016) Deep residual learning for compressed sensing ct reconstruction via persistent homology analysis, arXiv preprint arXiv:1611.06391

  • Hastie T, Tibshirani R, Friedman J (2009) The elements of statistical learning: Data mining, inference, and prediction, in The Elements of Statistical Learning: Data Mining, Inference, and Prediction, Second Edition, Springer

  • Hiraoka Y, Nakamura T, Hirata A, Escolar EG, Matsue K, Nishiura Y (2016) Hierarchical structures of amorphous solids characterized by persistent homology. Proc Natl Acad Sci 113:7035–7040

    Article  Google Scholar 

  • Hofer C, Kwitt R, Niethammer M, Uhl A (2017) Deep learning with topological signatures. Adv Neural Inf Process Sys 30:1634–1644

    Google Scholar 

  • Horak D, Maletic S, Rajkovic M (2009) Persistent homology of complex networks. J Statis Mech: Theory Exp 2009:P03034

    MathSciNet  MATH  Google Scholar 

  • Horváth L, Kokoszka P (2012) Inference for functional data with applications, Springer. New York. https://doi.org/10.1007/978-1-4614-3655-3

  • Hylton A, Henselman-Petrusek G, Sang J, Short R (2012) Tuning the performance of a computational persistent homology package. Softw: Prac Exp 49:885–905. https://doi.org/10.1002/spe.2678

    Article  Google Scholar 

  • Kaczynski T, Mischaikow K, Mrozek M (2004) Computational homology, Springer-Verlag,

  • Kaji S, Sudo T, Ahara K (2020) Cubical Ripser: Software for computing persistent homology of image and volume data, arXiv:2005.12692

  • Kališnik S (2018) Tropical coordinates on the space of persistence barcodes. Found Comput Math 19(1):101–29

    Article  MathSciNet  MATH  Google Scholar 

  • Kasson PM, Zomorodian A, Park S, Singhal N, Guibas LJ, Pande VS (2007) Persistent voids a new structural metric for membrane fusion. Bioinformatics 23:1753–1759

    Article  Google Scholar 

  • Kusano G, Hiraoka Y, Fukumizu K (2016) Persistence weighted gaussian kernel for topological data analysis. In International conference on machine learning, pp. 2004–2013

  • Kwitt R, Huber S, Niethammer M, Lin W, Bauer U (2015) Statistical topological data analysis-a kernel perspective. Adv Neural Inf Process Syst 28:3070–3078

    Google Scholar 

  • Le T, Yamada M (2018) Riemannian manifold kernel for persistence diagrams, arXiv preprint arXiv:1802.03569

  • Lee H, Kang H, Chung MK, Kim B, Lee DS (2012) Persistent brain network homology from the perspective of dendrogram. Med Imag IEEE Trans 31:2267–2277. https://doi.org/10.1109/TMI.2012.2219590

    Article  Google Scholar 

  • Li C, Ovsjanikov M, Chazal F (2014) Persistence-based structural recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 1995–2002

  • Lin HW, Tegmark M, Rolnick D (2017) Why does deep and cheap learning work so well? J Stat Phys 168:1223–1247. https://doi.org/10.1007/s10955-017-1836-5

    Article  MathSciNet  MATH  Google Scholar 

  • Liu X, Xie Z, Yi DY (2012) A fast algorithm for constructing topological structure in large data. Homol, Homotopy Appli 14:221–238

    Article  MathSciNet  MATH  Google Scholar 

  • Makarenko N, Kalimoldayev M, Pak I, Yessenaliyeva A (2016) Texture recognition by the methods of topological data analysis, Open Engineering, 6

  • Marchese A, Maroulas V (2017) Signal classification with a point process distance on the space of persistence diagrams. Adv Data Anal Classifi, 12(3):657-82

  • Maria C (2015) Filtered complexes, in GUDHI User and Reference Manual, GUDHI Editorial Board, http://gudhi.gforge.inria.fr/doc/latest/group__simplex__tree.html

  • Merelli E, Rucco M, Sloot P, Tesei L (2015) Topological characterization of complex systems: using persistent entropy. Entropy 17:6872–6892

    Article  Google Scholar 

  • Mileyko Y, Mukherjee S, Harer J (2011) Probability measures on the space of persistence diagrams. Inverse Prob 27:124007

    Article  MathSciNet  MATH  Google Scholar 

  • Mischaikow K, Mrozek M, Reiss J, Szymczak A (1999) Construction of symbolic dynamics from experimental time series. Phys Rev Lett 82:1144–1147

    Article  Google Scholar 

  • Mischaikow K, Nanda V (2013) Morse theory for filtrations and efficient computation of persistent homology. Discret Comput Geom 50:330–353. https://doi.org/10.1007/s00454-013-9529-6

    Article  MathSciNet  MATH  Google Scholar 

  • Munkres JR (2018) Elements of algebraic topology, CRC Press

  • Murzin AG, Brenner SE, Hubbard T, Chothia C (1995) SCOP: a structural classification of proteins database for the investigation of sequences and structures. J Mol Biol 247:536–540

    Google Scholar 

  • Nanda V. Perseus: the persistent homology software. Software available at http://www.sas.upenn.edu/~vnanda/perseus

  • Nguyen DD, Cang ZX, Wu KD, Wang ML, Cao Y, Wei GW (2018) Mathematical deep learning for pose and binding affinity prediction and ranking in D3R Grand Challenges, arXiv preprint arXiv:1804.10647

  • Nguyen DD, Xiao T, Wang ML, Wei GW (2017) Rigidity strengthening: a mechanism for protein-ligand binding. J Chem Inf Model 57:1715–1721

    Article  Google Scholar 

  • Niyogi P, Smale S, Weinberger S (2011) A topological view of unsupervised learning from noisy data. SIAM J Comput 40:646–663

    Article  MathSciNet  MATH  Google Scholar 

  • Obayashi I, Hiraoka Y, Kimura M (2018) Persistence diagrams with linear machine learning models. J Appli Comput Topol 1:421–449

    Article  MathSciNet  MATH  Google Scholar 

  • Obayashi I. HomCloud: Software collection for data analysis using persistent homology, Hiraoka Laboratory https://homcloud.dev/

  • Pachauri D, Hinrichs C, Chung M, Johnson S, Singh V (2011) Topology-based kernels with application to inference problems in alzheimer’s disease. Med Imag, IEEE Trans 30:1760–1770. https://doi.org/10.1109/TMI.2011.2147327

    Article  Google Scholar 

  • Pachauri D, Hinrichs C, Chung MK, Johnson SC, Singh V (2011) Topology-based kernels with application to inference problems in alzheimer’s disease. IEEE Trans Med Imag 30:1760–1770

    Article  Google Scholar 

  • Padellini T, Brutti P (2017) Supervised learning with indefinite topological kernels, arXiv preprint arXiv:1709.07100

  • Pun CS (2021) A sparse learning approach to relative-volatility-managed portfolio selection. SIAM J Financial Math 12:410-445. https://doi.org/10.1137/19M1291674

  • Pun CS, Wong HY (2016) Resolution of degeneracy in merton’s portfolio problem. SIAM J Financial Math 7:786–811. https://doi.org/10.1137/16m1065021

    Article  MathSciNet  MATH  Google Scholar 

  • Pun CS, Wong HY (2018) A linear programming model for selection of sparse high-dimensional multiperiod portfolios. Eur J Oper Res. 273(2):754–71. https://doi.org/10.1016/j.ejor.2018.08.025

    Article  MathSciNet  MATH  Google Scholar 

  • Qaiser T, Tsang YW, Taniyama D, Sakamoto N, Nakane K, Epstein D, Rajpoot N (2018) Fast and accurate tumor segmentation of histology images using persistent homology and deep convolutional features, arXiv preprint arXiv:1805.03699

  • Ramsay JO, Silverman BW (1997) Functional data analysis, Springer. New York. https://doi.org/10.1007/978-1-4757-7107-7

  • Reininghaus J, Huber S, Bauer U, Kwitt R (2015) A stable multi-scale kernel for topological machine learning. In Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 4741–4748

  • Ren S, Wu C, Wu J (2017) Weighted persistent homology, arXiv preprint arXiv:1708.06722

  • Rieck B, Mara H, Leitte H (2012) Multivariate data analysis using persistence-based filtering and topological signatures. IEEE Trans Visual Comput Graphics 18:2382–2391

    Article  Google Scholar 

  • Robins V, Turner K (2016) Principal component analysis of persistent homology rank functions with case studies of spatial point patterns, sphere packing and colloids. Physica D 334:99–117

    Article  MathSciNet  MATH  Google Scholar 

  • Rucco M, Castiglione F, Merelli E, Pettini M (2016) Characterisation of the idiotypic immune network through persistent entropy. In Proceedings of ECCS 2014, Springer, pp. 117–128

  • Saadatfar M, Takeuchi H, Robins V, Francois N, Hiraoka Y (2017) Pore configuration landscape of granular crystallization. Nat Commun 8:15082

    Article  Google Scholar 

  • Seversky LM, Davis S, Berger M (2016) On time-series topological data analysis: New data and opportunities. In Proceedings of the IEEE conference on computer vision and pattern recognition workshops, pp. 59–67

  • Silva VD, Ghrist R (2005) Blind swarms for coverage in 2-d, in In Proceedings of Robotics: Science and Systems, p. 01

  • Singh G, Memoli F, Ishkhanov T, Sapiro G, Carlsson G, Ringach DL (2008) Topological analysis of population activity in visual cortex. J Vision 8(8):11–11. https://doi.org/10.1167/8.8.11

    Article  Google Scholar 

  • Srivastava N, Hinton G, Krizhevsky A, Sutskever I, Salakhutdinov R (2014) Dropout: A simple way to prevent neural networks from overfitting. J Mach Learn Res 15:1929–1958

    MathSciNet  MATH  Google Scholar 

  • Tausz A, Vejdemo-Johansson M, Adams H (2011) Javaplex: A research software package for persistent (co)homology. Software available at http://code.google.com/p/javaplex

  • Turner K, Mileyko Y, Mukherjee S, Harer J (2014) Fréchet means for distributions of persistence diagrams. Dis Comput Geom 52:44–70

    Article  MATH  Google Scholar 

  • Umeda Y (2017) Time series classification via topological data analysis. Inf Media Technol 12:228–239

    Google Scholar 

  • Wang B, Summa B, Pascucci V, Vejdemo-Johansson M (2011) Branching and circular features in high dimensional data. IEEE Trans Visual Comput Graphics 17:1902–1911

    Article  Google Scholar 

  • Wang B, Wei GW (2016) Object-oriented persistent homology. J Comput Phys 305:276–299

    Article  MathSciNet  MATH  Google Scholar 

  • Wang Y, Ombao H, Chung MK et al. (2014) Persistence landscape of functional signal and its application to epileptic electroencaphalogram data, ENAR Distinguished Student Paper Award

  • Wu C, Ren S, Wu J, Xia K (2018) Weighted (co) homology and weighted laplacian, arXiv preprint arXiv:1804.06990

  • Wu KD, Wei GW (2018) Quantitative toxicity prediction using topology based multi-task deep neural networks. J Chem Inf Model 58(2):520–31. https://doi.org/10.1021/acs.jcim.7b00558

    Article  Google Scholar 

  • Xia KL (2017) A quantitative structure comparison with persistent similarity, arXiv preprint arXiv:1707.03572

  • Xia KL (2018) Persistent homology analysis of ion aggregations and hydrogen-bonding networks. Phys Chem Chem Phys 20:13448–13460

    Article  Google Scholar 

  • Xia KL, Feng X, Tong YY, Wei GW (2015) Persistent homology for the quantitative prediction of fullerene stability. J Comput Chem 36:408–422

    Article  Google Scholar 

  • Xia KL, Li ZM, Mu L (2018) Multiscale persistent functions for biomolecular structure characterization. Bull Math Biol 80:1–31

    Article  MathSciNet  MATH  Google Scholar 

  • Xia KL, Wei GW (2014) Persistent homology analysis of protein structure, flexibility and folding. Int J Num Methods Biomed Eng 30:814–844

    Article  MathSciNet  Google Scholar 

  • Xia KL, Wei GW (2015) Multidimensional persistence in biomolecular data. J Comput Chem 36:1502–1520

    Article  Google Scholar 

  • Xia KL, Wei GW (2015) Persistent topology for cryo-EM data analysis. Int J Num Methods Biomed Eng 31:e02719

    MathSciNet  Google Scholar 

  • Xia KL, Zhao ZX, Wei GW (2015) Multiresolution topological simplification. J Comput Biol 22:1–5

    Article  Google Scholar 

  • Yao Y, Sun J, Huang XH, Bowman GR, Singh G, Lesnick M, Guibas LJ, Pande VS, Carlsson G (2009) Topological methods for exploring low-density states in biomolecular folding pathways. J Chem Phys 130:144115

    Article  Google Scholar 

  • Zeppelzauer M, Zieliński B, Juda M, Seidl M (2018) A study on topological descriptors for the analysis of 3d surface texture. Comput Vis Image Underst 167:74–88

    Article  MATH  Google Scholar 

  • Zhang ZF, Song Y, Cui HC, Wu J, Schwartz F, Qi HR (2015) Early mastitis diagnosis through topological analysis of biosignals from low-voltage alternate current electrokinetics, in Engineering in Medicine and Biology Society (EMBC) (2015) 37th annual international conference of the IEEE. IEEE 542–545

  • Zhou Z, Huang YZ, Wang L, Tan TN (2017) Exploring generalized shape analysis by topological representations. Pattern Recogn Lett 87:177–185

    Article  Google Scholar 

  • Zhu XJ (2013) Persistent homology: an introduction and a new text representation for natural language processing, in IJCAI, 1953–1959

  • Zhu XJ, Vartanian A, Bansal M, Nguyen D, Brandl L (2016) Stochastic multiresolution persistent homology kernel, in IJCAI, 2449–2457

  • Zielinski B, Juda M, Zeppelzauer M (2018) Persistence codebooks for topological data analysis, arXiv preprint arXiv:1802.04852

  • Zomorodian A (2010) The tidy set: a minimal simplicial set for computing homology of clique complexes, in Proceedings of the 26th annual symposium on computational geometry, ACM , pp. 257–266

  • Zomorodian A, Carlsson G (2005) Computing persistent homology. Discrete Comput Geom 33:249–274

    Article  MathSciNet  MATH  Google Scholar 

  • Zomorodian A, Carlsson G (2008) Localized homology. Comput Geom - Theory Appli 41:126–148

    Article  MathSciNet  MATH  Google Scholar 

  • Zomorodian AJ (2005) Topology for computing, vol. 16, Cambridge university press

Download references

Funding

This research is partially supported by Nanyang Technological University Startup Grants M4081840 and M4081842, Data Science and Artificial Intelligence Research Centre@NTU M4082115, and Singapore Ministry of Education Academic Research Fund Tier 1 RG109/19, Tier 2 MOE2018-T2-1-033 and MOE-T2EP20120-0013.

Author information

Authors and Affiliations

  1. School of Physical and Mathematical Sciences, Nanyang Technological University, Singapore, Singapore

    Chi Seng Pun, Si Xian Lee & Kelin Xia

Authors
  1. Chi Seng Pun
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Si Xian Lee
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Kelin Xia
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to Chi Seng Pun or Kelin Xia.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

Appendix 1: Properties of the Protein Secondary Structure

This section gives a review of some of the key properties of the secondary structure of proteins. The two main types of protein secondary structure are the alpha (\(\alpha\))-helix and the beta (\(\beta\))-pleated sheets.

The \(\alpha\)-helix has the following properties:

  1. (1)

    Bond length between immediate \(C_{\alpha }\) atom is 3.8Å.

    • This corresponds to the length of typical Betti-0 (Dim-0) bars.

  2. (2)

    Each turn is made up of 3.6 amino acid residues.

    • The formation of Betti-1 (Dim-1) bars can be explained using the slicing technique described in Xia and Wei (2014).

    • The alpha-helix structure is stabalised by the presence of hydrogen bonds between the amine hydrogen N-H and carbonyl C\(=\)O oxygen.

    • Each set of 4 \(C_{\alpha }\) atoms form a one-dimensional loop which contributes to a Betti-1 (Dim-1) bar.

  3. (3)

    Absence of Betti-2 (Dim-2) bars where no cavity is formed since there is insufficient "time" such that the loops are filled up as faces before the cavity can be formed for a single alpha helix.

The \(\beta\)-pleated sheets have the following properties:

  1. (1)

    Bond length/distance between immediate \(C_{\alpha }\) atom in the same strand is also 3.8Å.

    • This corresponds to the length of typical Betti-0 (Dim-0) bars. The bar terminates once the atoms are connected.

  2. (2)

    Each \(\beta\)-pleated sheet is a stretched out polypeptide chain made up of 3 to 10 amino acid residues.

  3. (3)

    The \(\beta\)-pleated sheets are extended structures that are stabalised by hydrogen bonds between residues in adjacent chains.

  4. (4)

    Each strand must be connected to adjacent strands where the shortest distance between \(C_{\alpha }\) and the nearest neighbour in adjacent strand is 4.1Å.

  5. (5)

    Adjacent chains run parallel or antiparallel to one another.

Principal component analysis on binned features

In this appendix, we investigate the effects of principal component analysis (PCA) on PHML for our application in Section 5. We do not involve the tree-based methods with PCA because trees process dimension reduction by their own construction.

There are signs of quite high correlation between adjacent BF as seen in Fig. 6. The use of bins unavoidably suffers from the curse of dimensionality, especially when there are limited number of samples n and \(n\ll p\), where p is the number of features. To tackle such a situation, PCA can be applied to transform features into a few uncorrelated PCs, which can be viewed as new features in a lower dimensional feature space. The downside of such an approach is that the final PCs do not have a clear interpretation to the original bins.

Fig. 6
figure 6

(a) Correlation matrix for the BFs from RC barcodes with 40 bins (where the near-zero variance variables removed). (b) Correlation matrix for the 30 PCs transformed from the same BFs. The blue regions corresponds to high positive correlation and is observed between multiple BFs, in contrast with that in the PCs, where white regions correspond to zero correlation

Full size image

In subsequent reports, the experimental results involving principal components transformed from BFs are denoted by an extension “PC". For consistency, only the first 30 PCs will be used for all transformed features using either RC or AC barcodes. The same set of PCs are used as input features for SVMs and (deep) NNs (with dropout). The settings are the same as specified in Sects. 5.2.1 and 5.2.3. Tables 4 and 5 report the corresponding results.

Table 4 Results using SVM with different simplicial complexes and principal components of BFs
Full size table
Table 5 Results using NN with different simplicial complexes and principal components of BFs
Full size table

By comparing the results in Tables 1 and 4 and Tables 3 and 5, we can see that the use of PCA on BFs does not improve the performance. It implies that the PCA transformation lost information of BFs. In conclusion, it is not recommended that ML algorithms with BFs are incorporated with PCA. However, it does not prohibit PCA from being a powerful visualization tool for the unstructured topological data.

Effects of increasing bin number for binned features

In Tables 6 and 9, the first three or four columns specify the settings of PHML and the remaining columns report the evaluation measurements. The highest overall accuracy number across different bin numbers for a given method is highlighted in red.

Table 6 Results using SVM with different simplicial complexes and BF of different bin numbers
Full size table
Table 7 Results using tree-based methods with different simplicial complexes and BF of different bin numbers. The three maxtree numbers in last two rows correspond to the cross-validated number of iterations for different bin numbers
Full size table
Table 8 Results using repeated NN with different simplicial complexes and BF of different bin numbers
Full size table
Table 9 Results using deep NN with different simplicial complexes and BF of different bin numbers
Full size table

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Pun, C.S., Lee, S.X. & Xia, K. Persistent-homology-based machine learning: a survey and a comparative study. Artif Intell Rev 55, 5169–5213 (2022). https://doi.org/10.1007/s10462-022-10146-z

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10462-022-10146-z

Keywords

Search

Navigation