Performance determination of high-purity N₂-PSA-plants

Abstract

The global demand on highly purified gases provided by energy-efficient separation processes grows steadily since decades. An example of particular industrial relevance is nitrogen generated by pressure swing adsorption from compressed air. A kinetically based separation of oxygen from nitrogen is possible by means of carbon molecular sieves (CMS) since oxygen adsorbs remarkably faster in CMS than nitrogen. Even high product purities (5–1000 ppm O₂) are easily achievable in commercial generators. However, only a few studies present experimental findings in this purity range. That comes as no surprise, since experimental conditions are not standardised and the determination of N₂-PSA performance indicators still creates an experimental challenge. Moreover, the design of the set-up remarkably influences the experimental results. Thus it is the motivation of this study to develop a multi-step strategy, comprising the definition of a reference process, the derivation of explicit and implicit performance indicators based on either flow meter readings or macroscopic material balances, a verification strategy for experimentally obtained data, and an error consideration, which advices accuracy requirements for analysers and flow meters. The effect of cycle time and operating temperature on the performance indicators is exemplarily studied at high purities by means of the proposed strategy.

1 Introduction

Pressure swing adsorption (PSA) is a well-established technology applied for the separation of multicomponent gas mixtures. Currently a huge focus is set on CO₂ capture technologies (Salazar Duarte et al. 2017; Schell et al. 2013; Ritter 2015). Nevertheless, PSA is also a well-known and frequently implemented method in traditional industrial processes such as hydrogen purification, biogas upgrading, or air separation (Dąbrowski 2001; Voss 2005; Schröter 1993). Despite many years of process employment (since the 1960s) along with experimental research and computer modelling, the PSA separation is still not fully comprehensible (Yang 2013). This statement is particularly relevant for kinetically based separation processes since any modification of the cycle organisation or slight alteration of process conditions influences the distribution of driving forces as a function of time in the production and regeneration steps. Any change affects in its ultimate consequence the local gas interstitial velocity, which again impacts for instance the local column pressure drop, the heat and mass transfer rate, and the axial dispersion of heat and mass (Vemula et al. 2015; Kvamsdal and Hertzberg 1995).

This background motivates an experimental multi-step strategy, comprising the definition of a reference process, the derivation of precise, reliable, and reproducible performance indicators based on macroscopic material balances, and a verification strategy for experimentally obtained data. A compulsory error consideration, which advices accuracy requirements for analysers and flow meters, can be an additional part of the strategy.

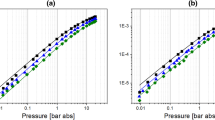
The generation of high-purity nitrogen from compressed air is selected as an object of investigation in this study. This process allows the separation of oxygen from nitrogen, which is possible by taking advantage of the remarkably faster adsorption rate of oxygen over nitrogen (Shirley and Lemcoff 2002) in PSA-plants equipped with carbon molecular sieves. Fractional uptake rates of oxygen and nitrogen in CMS are presented in Fig. 1 (Thomas and Crittenden 1998). High selectivity is attainable due to the sieving effect in intentionally narrowed micropore mouths (Patel and Patel 2014). At present, the N₂-PSA technology is commercially established for product flow rates up to several thousand Nm³/h and product purity levels up to 10 ppm of the residual oxygen concentration (Ivanova and Lewis 2012). The typical set-up of a N₂-PSA consists of two single adsorber columns (2-bed-PSA or twin-bed-PSA), which are alternating between adsorption and desorption mode, providing a semi-continuous flow of a high-pressure nitrogen stream (Jasra et al. 1991).

Fig. 1

Fractional uptake rates of oxygen and nitrogen in carbon molecular sieve (Thomas and Crittenden 1998)

Finally, the effect of cycle time and operating temperature on the performance indicators is experimentally studied for the high-purity N₂-PSA. It will be shown that accurate measurements even on the ppm-level will be possible as long as experimental due diligence obligations are respected.

2 Reference process

In order to enable data comparisons and to establish the baseline conditions for further process optimisation, firstly a reference process is proposed. The different cycle features of this reference process are displayed in Fig. 2.

Fig. 2

Scheme of the six-step cycle design (1 s/59 s/1 s/59 s)

The reference process of Fig. 2 comprises a six-step 120 s PSA cycle, which consists of (1) co- and counter-current bed pressure equalisation; (2) co-current pressurisation by feed with (4) counter-current backflow of product; (3) production; (1) co- and counter-current bed pressure equalisation; (5) counter-current blow-down; and (6) counter-current purge by product gas. A possible interruption of the blow-down respectively of the purge step, the so-called cutting step (7), is not considered for the reference process since the optimal placement of this step depends on the CMS properties and cannot be fixed independently from the selected CMS-type or even CMS-lot.

The scheme indicates a high level of process intensification. Various cycle steps run simultaneously. This allows high performance figures particularly at short cycle times, which will later be shown in the experimental part of this work.

The reference cycle is experimentally realised in a 2 × 2 l twin-bed PSA placed in a temperature adjustable climate chamber (− 5 °C/ + 100 °C, Binder). The unit is fed with dry air under a pressure of 8.1 bar abs. The adsorption process is performed under a working pressure of 8 bar abs. To control the purity level, always the product stream flow rate is adjusted in the experiments. This control strategy represents the common operation of commercial plants. The flow rate of the counter-current purge equals in every experiment exactly 40% of the adsorber volume within the selected purge time. Further data are displayed in Table 1.

Table 1 Adsorbent and adsorber column properties

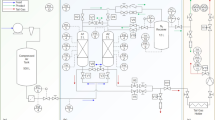
A scheme of the test unit is shown in Fig. 3. Three main sections can be recognised: the feed gas preparation and pre-treatment section (a), the twin-bed PSA plant section (b), and the product and tail gas analytics section (c). The PSA devices are connected with a 6 mm internal diameter PA12 polyamide piping resistant to oxygen diffusion.

Fig. 3

Scheme of the PSA experimental set-up

The feed gas in section (a) supplies ambient air compressed up to 11 bar abs by a compressor (KAESER Airtower 3), which is equipped with a refrigeration dryer and a hydrocyclone for moisture removal. The feed streamline further consists of a 500 l compressed air tank, followed by a 0.01 μm sieve filter and an activated carbon filter (Omega Air) for a subsequent exclusion of solid particles and oil vapour. The pressure is controlled by a Norgren pressure regulator (PC 4). A thermal mass flow meter (FM 4) from Bronkhorst, type F-112AC, is measuring the feed flow rate.

The air distribution system of the two adsorbers in section (b) contains a stainless steel perforated plate and a layer of a metal wire mesh placed at the bottom of the bed. The two stainless steel adsorber columns (A1 and A2) are packed with CMS of the type CarboTech Shirasagi CT-350 by the snowstorm filling method. A coconut fiber mat is placed at the top of the adsorbent bed to fix the bed even under strong pressure fluctuations.

Four thermocouples type K (TIR 1–4) from TMH and four pressure transmitters (PIR 1–4) from Aplisens, type PCE-28.SMART, are placed at equal intervals along the wall of columns in order to measure temperature and pressure distributions inside the packed bed. Additionally, each adsorber’s closing flange is equipped with a pressure transmitter (PIR 5, PIR 6) to track the pressure variation at the top of the packed bed. The product receiver vessel is installed together with temperature (TIR 10) and pressure (PIR 9) sensors. Moreover, temperature indicators (Aplisens CTX) are placed in the feed pipeline (TIR 3) as well as inside of the climate chamber (TIR 2) for an operating temperature control. Thermal mass flow controllers (Bronkhorst F-201AV and F-201CV) are installed for the regulation of the flow rates of product (FC 7) and purge (FC 8) streams. Two output streams—the product gas and the tail gas—are analysed in order to measure their oxygen concentration. A dual-stream oxygen analyser (Servomex MultiExact 5400) is adapted for the simultaneous measurement of trace amounts in the product gas (ppm range) by a zirconium dioxide sensor (QO2 14.1) and of the tail gas concentration by a high-precision paramagnetic sensor (QO2 14.2). A drum-type gas meter (FM 11) determines the flow rate of the tail gas (Ritter TG1/5). Due to the non-continuous flow of the tail gas stream during the PSA process cycle, the tail gas is periodically collected in a rubber holder whenever the determination of the oxygen concentration and the flow rate are required. The test unit is equipped with externally piloted pneumatic solenoid valves (V1–14) from Festo MF series, allowing the leak-tight operation in both flow directions. The system is fully automated by a PLC system (Beckhoff Automation), coded in TwinCAT 3.

Additionally, the operation scheme of particular valves in the plant during performing the reference cycle is presented in Fig. 4.

Fig. 4

Valves operation scheme in the reference cycle

3 PSA performance indicators

Multiple process variables and cycle organisation strategies give an opportunity for customising the system to individual requirements, which is the great advantage of the PSA technology. In the interest of creating a common concept of straightforward assessment and comparison of the PSA unit efficiency, so-called performance indicators (PI) are introduced to evaluate the influence of process variables and cycle design.

3.1 Derivation of the relevant performance indicators

The main goal of PI is to provide condensed information, which are needful for the plant design like production yield, adsorber sizing, and energy requirement. Table 2 (Grande 2012) itemises PI for the N₂-PSA technology—operated with a constant feed flow rate—as the purity, the productivity, the recovery, and the air demand. In commercial applications, values for the productivity and the air demand are listed for a certain purity class separately. Instead of the air demand, also the recovery could be used; however, recovery and air demand are dependent variables, carrying both the same information content. In case of the N₂-PSA technology, the air demand has been proved as the more appropriate parameter.

Table 2 Performance indicators of the N₂-PSA process.

In the N₂-PSA technology it is accepted that the product purity comprises the content of both nitrogen and argon since many industrial applications do not require an additional separation of inert gas mixtures. Consequently, the determination of the product purity is performed by assuming a binary gas mixture, where simply the difference to the oxygen concentration results in the nitrogen purity.

PSA performance indicators according to Table 2 can be obtained through two fundamental strategies: explicitly by the evaluation of the process streams throughputs, and implicitly by solving macroscopic material balances. In the first strategy, the productivity can be evaluated directly based on reading of the flow meter in the product pipeline, whereas the air demand bases on the readings of the flow meters in the feed and the product pipelines. Explicit PI determination is a very simple and low-cost method; however, its biggest disadvantage is a lack of comparison data to confirm the correctness of the measurement.

Therefore, the implicit way of the determination of performance indicators by solving macroscopic material balances is proposed as an important additional strategy for data verification. For this reason, two equations, the general (Eq. 1, GMB) and the component (here oxygen) (Eq. 2, OMB) material balances, are introduced in order to achieve the same performance information from two further independent solutions.

$$ Q_{feed} \cdot \rho_{feed} = Q_{product} \cdot \rho_{product} + Q_{{tail{\text{-}}gas}} \cdot \rho_{{tail{\text{-}}gas}} $$

(1)

$$ Q_{feed} \cdot \rho_{feed} \cdot w_{{O_{2} \,feed}} = Q_{product} \cdot \rho_{product} \cdot w_{{O_{2} product}} + Q_{{tail{\text{-}}gas}} \cdot \rho_{{tail{\text{-}}gas}} \cdot w_{{O_{2} \;tail{\text{-}}gas}} $$

(2)

Subsequently, equations for the calculation of performance indicators—the productivity (Eqs. 3, 4) and the air demand (Eqs. 5, 6)—can be derived.

$$ \frac{{Q_{product} }}{{X \cdot V_{CMS} }} = \frac{1}{{X \cdot V_{CMS} \cdot \rho_{product} }}\left( {Q_{feed} \cdot \rho_{feed} - Q_{{tail{\text{-}}gas}} \cdot \rho_{{tail{\text{-}}gas}} } \right) $$

(3)

$$ \frac{{Q_{product} }}{{X \cdot V_{CMS} }} = \frac{1}{{X \cdot V_{CMS} \cdot \rho_{product} \cdot w_{{O_{2} \;product}} }}\left( {Q_{feed} \cdot \rho_{feed} \cdot w_{{O_{2} \;feed}} - Q_{{tail{\text{-}}gas}} \cdot \rho_{{tail{\text{-}}gas}} \cdot w_{{O_{2} \;tail{\text{-}}gas}} } \right) $$

(4)

$$ \frac{{Q_{feed} }}{{Q_{product} }} = \frac{{\rho_{product} }}{{\rho_{feed} }} + \frac{{Q_{{tail{\text{-}}gas}} \cdot \rho_{{tail{\text{-}}gas}} }}{{Q_{product} \cdot \rho_{feed} }} $$

(5)

$$ \frac{{Q_{feed} }}{{Q_{product} }} = \frac{{\rho_{product} \cdot w_{{O_{2} \;product}} }}{{\rho_{feed} \cdot w_{{O_{2} \;feed}} }} + \frac{{Q_{{tail{\text{-}}gas}} \cdot \rho_{{tail{\text{-}}gas}} \cdot w_{{O_{2} \;tail{\text{-}}gas}} }}{{Q_{product} \cdot \rho_{feed} \cdot w_{{O_{2} \;feed}} }} $$

(6)

3.2 Operationalisation of performance indicators in PSA plants

PSA plants are operated in two different modes—either with a constant feed flow rate, or with a constant product flow rate. The first option is preferred in lab scale plants, whereas the second option is typically implemented in pilot and commercial plants. This has consequences for the determination of the performance indicators, as exemplarily shown in Table 3 for PIs at certain purity, obtained by explicit methods and by implicit methods (GMB) when assuming a constant density of the feed and product gas.

Table 3 Computation of performance indicators for the N₂-PSA process under either constant feed flow or constant product flow conditions

Any integration of a flow causes errors due to the limitation in scan-speed of the flow meters, which will be discussed later in detail. At this point a simple alternative shall be introduced, which consists of the collection of the fluctuating product or tail gas stream during one or more cycles in evacuated gas holders. This makes it possible to determine flow rates independent from the running process with conventional, but very precise methods under comparable constant flow conditions.

In this investigation, a PSA operation with a constant product flow rate was adjusted and thus, the tail gas flow was selected as that stream which was collected separately in a gas holder and then analysed under constant flow conditions. Referring to Table 3 it can be concluded that in case of a constant product flow rate the productivity should be determined just by a direct reading, whereas for the air demand the GMB and the OMB should be applied since the tail gas and the product flow rates are both constant in these equations. However, if for instance the feed gas flow meter would be placed between compressor and tank, the air flow measurement will not vary significantly during the cycle and an integrated flow rate can be precise enough. But the final intention of the presented experimental set-up is the verification of a mathematical PSA model, which requires a position of the feed gas flow meter as close to the adsorbers as possible.

In case of a PSA operation with a constant feed flow rate it comes to different conclusions. Assuming a collection of the product flow in a gas holder it is just possible to apply explicit methods. Only if the tail gas is additionally collected in a gas holder the utilisation of the implicit methods for calculating precise PIs is possible. If the collection of gas streams in gas holders is not feasible, accuracy limitations of integrated flow parameters have to be accepted.

3.3 Verification strategy

A perfectly determined performance indicator attains exactly the same value whether calculated from the two material balances (implicit) or directly read from the flow meters (explicit). In fact, it is necessary to accept a certain tolerance of incompatibilities between values due to inevitable measuring errors. Any exceeding significant difference in values of performance indicators are the evidence of a faulty operation of the PSA system, e.g. leakages, incorrect calibration of measuring devices, errors in transmitting electrical signals to the equipment, errors in the software code, accumulation of pollutants in valves, diffusion intake due to porous or inadequate piping or seals, or exhausted filters.

In this work, a performance indicator value is considered as to be determined correctly when the difference between the results obtained from the different calculation paths ((3)/(5) or (4)/(6) + direct readings) does not exceed a tolerance level of 1% determined as a relative error δ_exp. If δ_exp between differently calculated performance indicators is lower than 1%, obtained values are considered as correct. If δ_exp is larger than 1%, obtained values are discarded. Admittedly, this 1%-tolerance level of δ_exp seems to be set arbitrarily, however justified by laboratory experience gained in decades of quality control.

Additionally, separate performance indicators of each single adsorber column can also be calculated. This allows the disclosure of potential imbalances between the adsorber columns, which sometimes leads to an accelerated detection of operation faults.

Maintaining such a strict tolerance is the more challenging the higher the product purity is addressed. Here the accuracy of measuring devices comes to the fore since a limited measurement precision mathematically prohibits solving equations with an arbitrary low tolerance. Thus, a more detailed study on the impact of the accuracy of experimental parameters on calculated performance indicators is enclosed, which results are reported in the next sub-section.

3.4 Effect of the measurement procedure on performance results

In order to solve the balance equations (Eqs. 1 and 2), precise data of the feed, the product, and the tail gas flow rates are required. However, only one of three flows will be constant in a PSA, the others fluctuate along the cycle. In this study the product flow rate was set constant. Thus, the measurement of the feed (or tail gas) flow rate during the rapid system pressurisation/depressurisation could be burdened by a comparably high experimental error mainly due to the limitation in scan-speed of the measuring devices as presented in Fig. 5.

Fig. 5

Flow rate of process streams as a function of time in the 90 s cycle

The feed flow meter reveals 0.5 s of response time with a measurement accuracy of ± 0.6%. The mean value of the fluctuating feed flow rate shown in Fig. 5 must be calculated as an integral over the time. Anyhow, the integrated value of the feed mass flow rate is always lower than the sum of product gas mass flow rate and equalised tail gas mass flow rate. Particularly the first seconds of the adsorption cycle cannot be tracked fast enough by conventional flow meters. Consequently, the air demand determined by the explicit method is always slightly lower than determined by the implicit method, as shown in Table 4. Thus, it comes as no surprise that the relative error between explicit and implicit methods of the air demand determination does exceed the implemented 1%-tolerance level.

Table 4 Air demand of the reference process calculated according to different strategies

Therefore, in this study methods which require the feed flow rate (i.e. the implicit determination of the productivity and the explicit determination of the air demand) are not considered suitable for the precise determination of performance indicators due to their low measurement accuracy. However, the value of the explicitly determined air demand can be tracked continuously during the process cycle, therefore it can serve at least as an initial estimation of the PSA operational costs.

To reduce the experimental error, the fluctuating tail gas is collected in a gas holder¹ to be equalised over the time and then analysed on quantity and concentration parallel to the continuing operation of the test rig. So these particular data can be determined under steady-state conditions. Construction and commissioning of such devices require higher investment costs and longer start-up times due to the large number of signals integrated in the software code. Despite that, the strategy ensures high accuracy of obtained performance indicators, which is shown in Table 4. The relative error between implicit methods of determination of the air demand does not exceed the implemented 1%-tolerance level.

However, also the measurement of the tail gas flow rate is not without challenges. The tail gas must be captured by the holder vessel which leads to the generation of additional flow resistances while the gas is not directly discharged into the environment. The comparison of adsorber pressure profiles during the standard operation and the tail gas analysis is presented in Fig. 6. The magnitude of driving force for the desorption process is affected and the bed is not fully regenerated during the cycle with operation of the tail gas analysis. As a result, cyclic-steady-state conditions are disturbed and the product purity decreases slightly until the system returns to the standard operation. Therefore, continuous tracking of performance indicators by means of the implicit method is not recommended since product of lower purity will be generated.

Fig. 6

Pressure of process streams as a function of time in the 90 s cycle

3.5 Experimental error

The experimental parameters needed for the solving the balance equations (Eqs. 5 and 6) are listed in Table 5 along with their measuring accuracies provided by the manufacturers. Also, the volume of the packed bed is given; the accuracy is assumed as 0.3% according to the precision of the used calliper.

Table 5 Experimental parameters for solving the PSA system mass balances

At the beginning, a standard experiment was performed for ten times to derive an imagination of the reproducibility error of the experimental set-up. Table 6 shows the results. The reproducibility error is much lower than 1% in case of the air demand determined by the general mass balance and the oxygen mass balance.

Table 6 Reproducibility test results (20 °C/60 s)

A Monte-Carlo simulation on Eqs. 5 and 6 was implemented in order to investigate the influence of the combined measurement accuracy of all listed experimental values on the calculated performance indicator at different levels of product purity.

The statistical analysis of probabilistic data obtained by a Monte Carlo simulation in the group of 1000 data points, compared with experimentally obtained PI, is presented in Table 7. As expected, the measurement uncertainty ${\upsigma }_{\stackrel{-}{\mathrm{X}}}$ increases with the product purity, which is an obvious consequence of narrowing the measuring range of the oxygen concentration in the product.

Table 7 Comparison of Monte-Carlo simulated PI with experimentally found PI (20 °C/60 s)

The normal distribution of collected probabilistic PI around their mean values together with experimentally found results (one data point marked with a red vertical line) are presented in Fig. 7. The measured air demand is scattered around the Monte Carlo-simulated mean value—especially in the case of the 100 ppm data set, the experimentally found value is more far from the peak of the normal distribution function. However, the deliberated data point cannot be considered as incorrect, but only as less likely.

Fig. 7

Normal distribution of the air demand performance indicator at different purity levels

The distribution of the relative error δ_sim is presented in Fig. 8. The relative error δ_sim of the air demand is determined in every Monte Carlo run from the difference of Eqs. 5 and 6.

Fig. 8

Simulated distribution of the relative error δ_sim for the air demand at different purities: a 1000 ppm O₂, b 100 ppm O₂, c 10 ppm O₂

δ_sim surpasses δ_exp with a corresponding probability at every deliberated product purity level. This finding confirms, that determination and comparison of differently determined air demand values provide a very sensitive method to prove and thus to accept or to discard experimental high-purity data.

The precision of determined performance indicators depends not only on the accuracy of the measuring equipment, but also on a number of experimental systematic and random errors, which must be recognised as well, although difficult to consider in statistical analysis. From experience, some of the most common errors are:

• inaccuracy in the determination of oxygen concentration in the product; the deviation between the measured and the required values progressively expand between calibration routines of the zirconia dioxide sensor;

• inaccuracy in the determination of the tail gas flow rate; the drum-type flow meter is filled with water, which evaporates especially during the summertime—so a regular recalibration is required; moreover, the inevitable build-up of biofilms disrupts the rotation of the drum;

• insufficient homogenisation of the oxygen concentration in the tail gas; due to a non-continuous tail gas flow rate during a cycle and thus a non-uniform gas concentration caused by different oxygen levels during depressurisation, blow-down, and purge steps, a thorough gas mixing is required before sending the gas probe to the analyser.

Sensitivity studies show an increase in the standard deviation of the performance indicators along with a decreasing measurement accuracy of utilised devices in every considered purity range. Therefore, minimising the measurement error by means of using precise equipment and performing a very accurate calibration allows the collection of results with a difference smaller than the assumed δ_exp at almost every considered purity level.

4 Experimental program

In order to investigate the efficiency of high-purity N₂-PSA plants under standardised conditions, studies of three operation variables are performed—the product gas purity, the duration of the adsorption step, and the operation temperature. The purity of the product gas is adjusted by manipulation of the product stream flow rate; the duration of the adsorption step is regulated by the PLC software; and the working temperature is regulated by climate chamber settings. The PSA performance was studied in the purity range of 10–1000 ppm O₂ at cycle-times of 80–120 s and operating temperatures of 20 and 45 °C. The detailed process conditions are presented in Table 8. In order to assure cycle-steady-state conditions in the system, performance indicators are determined after at least ten hours of uninterrupted PSA unit operation.

Table 8 Experimental program and selected standardised cycle conditions

5 Results and discussion

Experimental performance indicators for three different residual oxygen concentrations are presented in Figs. 9 and 10. The temperature is fixed in these experiments at 20 °C and 45 °C, the half-cycle time varies between 40 and 60 s. As expected, in general the productivity grows and the air demand declines with decreasing purity of the product gas. However, more exciting is the influence of cycle time on the performance indicators. The trend changes for the cycle time in case of the productivity, what is particularly visible at 20 °C. At the lower purity of 1000 ppm, the productivity is promoted by short cycle times, at the higher purity of 10 ppm, it is the opposite. Also the air demand is more affected by the cycle times at higher than at lower purities. Although the arbitrary selection of three half-cycle times does not demonstrate the full picture of the influence on performance indicators, in fact, the selected half-cycle times represent very typical values applied in practice.

Fig. 9

Productivity and air demand as a function of oxygen concentration and cycle time at 20 °C

Fig. 10

Productivity and air demand as a function of oxygen concentration and cycle time at 45 °C

The main reason for this finding is probably the different flow velocity in the adsorber columns at different purities and its effect on the mass transfer and diffusion conditions (Shirley and Lemcoff 1997). Thus, the selection of the cycle time is strongly related to the desired product purity level in order to improve the overall system performance. Many PSA manufacturers already know this effect since decades, but the physical background is not fully transparent so far and thus subject of further studies by the authors in the near future.

Figures 9 and 10 also show the complexity of the influences of cycle time and temperature. Parameters exhibit different trends at different temperatures and cycle times. Thus, it can be concluded that also the temperature shows a strong effect on mass transfer and diffusion conditions (Möller et al. 2013). In case of high purity N₂ PSAs, a commercial design procedure requires either precise experimental data or instead a sophisticated mathematical model correctly representing the sensitive mass and diffusion characteristics of this kinetically driven separation process.

6 Conclusions

The experimental determination of N₂-PSA performance indicators by means of a multi-step strategy has been presented. This procedure bases on a reference process, whose performance indicators for a PSA operated with constant product flow rates were found on macroscopic material and component balances in case of the air demand, and on the direct reading of the mass flow meter in case of the productivity. An associated verification strategy for experimentally obtained data was derived which recommends the introduction of the relative error between performance indicators obtained by different experimental strategies, particularly between independent implicit or explicit, respectively between different types of independent implicit methods. From existing practical experience, a 1% tolerance value has been proved as a reasonable limit. If the deviation between independently determined performance indicators of the same type is larger than 1%, the correctness of the experimental procedure should be examined. A compulsory error consideration, which advices accuracy requirements for analysers and flow meters, is proposed as an additional part of the method. It is obvious, that this method can be also applied on every other type of pressure swing adsorption plants as for oxygen generation, biogas upgrading, hydrogen purification, nitrogen rejection, or noble gas recovery.

Experiments on the high purity level show a significant and partly contrary effect on performance indicators by operational parameters as the cycle time and the temperature. These results motivate a more realistic simulation of mass transfer effects in PSA adsorbers as being state-of-the-art today.