1 Introduction

Sigmoidal isotherms, or type V by the IUPAC classification system, are widespread in adsorption systems involving polar molecules, such as water on activated carbon. The behaviour is typically attributed to molecular clustering of the adsorbate, due to weak adsorbate—adsorbent versus strong intermolecular interactions and hence unfavourable adsorption, with subsequent pore filling. This leads to an initially convex isotherm, with an inflection to become concave and showing saturation at high pressures. Indeed, this type of isotherm is mostly associated with adsorption in mesoporous adsorbents, where condensation of the adsorbate, that is, formation of bulk liquid, in the porous structure is possible. However, type V isotherms have also been observed for a number of microporous materials, such as (silicon) aluminium phospates (ALPO and SAPO) (Henninger et al. 2010), zeolitic imidazolates, (e.g. ZIF-8) (Cousin Saint Remi et al. 2011) and metal organic frameworks (MOFs) (Küsgens et al. 2009), for which this mechanism seems somewhat unsatisfactory as by their definition the size of the micropores should preclude the existence of bulk liquid. Molecular simulations have shown that molecular clustering in micropores is possible and particularly in interconnected pore structures, such as pore channels in zeolites, this clustering can become of a scale large enough to yield typical type V behaviour (Puibasset and Pellenq 2008; Trzpit et al. 2007). From a thermodynamic viewpoint, the simplest relationship which can yield this type of isotherm for a homogeneous surface is based on the Langmuir expression, which includes molecule—molecule interactions. This can be derived through statistical thermodynamics as done by both Frumkin and Guggenheim and Fowler (Frumkin 1925; Fowler and Guggenheim 1939; Ruthven 1984):

$$bp = \frac{\theta }{{1 - \theta }}e^{{ - \frac{{2\omega \theta }}{{RT}}}}$$
(1)

where \(b\) is the isotherm constant at temperature \(T\), \(\theta\) the fractional coverage and \(\omega\) the molecule–molecule interaction energy. \(R\) and \(p\) are the gas constant and pressure, respectively. It can easily be seen that Eq. 1 reduces to the Langmuir expression if the interaction energy equals zero, as would be the basic assumption for Langmuir behaviour. The multisite-occupancy model of Nitta et al. extends the Guggenheim and Fowler model to molecules of different sizes (Nitta et al. 1984a).

Non-localised effects can be introduced, as done in the Hill—de Boer equation (Hill 1946). More recently Shigetomi et al. considered both adsorbate—fluid and fluid—fluid interactions through a Van der Waals potential in a statistical thermodynamic study of water and methanol on type A zeolite (Shigetomi et al. 1982). The resulting isotherms contained additional inflections due to these molecular interactions. Using a similar approach, it was also shown how surface heterogeneity can cause steps in isotherms; this is particularly the case where large differences exist in heats of adsorption for different sites or when dealing with bulky or branched molecules (Nitta et al. 1984a, b). In addition to models rooted in statistical thermodynamics, many other relationships exist which can yield type IV and V isotherms, but many assume multilayer adsorption and not all of them are thermodynamically consistent. The Sips isotherm for instance has theoretical merit and has been used to fit sigmoidal isotherms, but has zero slope at low pressures and thus does not converge to Henry’s Law under these conditions. Similar problems arise for the Dubinin equations, which are also routinely used to fit type IV and V isotherms. For a good overview of available models the readers is referred to Buttersack (2019). For truly microscopic insights in the origins of type IV and V behaviour, researchers have resorted to computational methods, such as molecular simulation, with great success. For typical process design and simulation however, the computational effort would be prohibitive and a macroscopic model be more appropriate.

Macroscopic models describing equilibrium adsorption behaviour are a an essential tool in designing separation processes and to this end empirical equations are often used in separations involving sigmoidal isotherms, as they are simple analytical expressions and hence have small computational demand (Van Assche et al. 2016; Cousin-Saint-Remi and Denayer 2017; Hefti et al. 2016). Their obvious drawbacks are lack of physical meaning and predictive behaviour. Discretisation with linear interpolation between isotherm points, obtained during separation experiments has been proposed as an alternative approach to modelling processes, but in the presence of steps and inflections, many experiments at different concentrations would be required (Haghpanah et al. 2012). The ability to predict this type of behaviour a priori with small computational effort using a thermodynamically consistent framework, would evidently be a great asset.

Considering the existing models to date, a statistical thermodynamic approach seems a promising route in finding a predictive model for non-type I isotherms and clearly offers the advantage of thermodynamic consistency. Moreover, no prior assumptions would be required coupled with a minimum of modelling parameters. In this context, lattice fluid (LF) based approaches, with their origins in statistical thermodynamics but with simplified partition functions, seem like a good choice (Sanchez and Lacombe 1976; Lacombe and Sanchez 1976). Indeed, their use for describing adsorption behaviour has been widely reported (Suwanayuen and Danner 1980a, b; Doghieri and Sarti 1996; Sarti and Doghieri 1998). Essentially being an equation of state, the LF leads to an expression for the residual Gibbs energy, which, through relatively straightforward calculations, can be used to predict isotherms. In recent work, we reported how, using this approach and through a limited number of physically meaningful modelling parameters, the Rigid Adsorbent Lattice Fluid (RALF) could successfully predict adsorption behaviour in both non-flexible and flexible adsorbents, namely silicalite-1 and MIL-53 (Al) (Brandani 2019; Verbraeken and Brandani 2019). Whereas in silicalite-1 only type I isotherms were presented, MIL-53 (Al) shows stepped isotherms, due to a structural change in the solid. Although not discussed, it was noticed in addition, that under certain conditions the predicted CO2 isotherms for the so-called ‘large pore’ structure of MIL-53 (Al) exhibited type V behaviour. Under the same conditions, the CO2 isotherms for the ‘narrow pore’ structure remained type I, as shown in Fig. 1. We hypothesised that this behaviour is a result from strong molecule—molecule interaction combined with a large pore volume. Under such conditions, after initial adsorption, additional molecules prefer forming clusters with previously adsorbed molecules, rather than interacting with the solid. A small number of studies using LF based approaches have shown similar predictions, but so far all studies involve adsorbents which expand upon molecule insertion (De Angelis and Sarti 2011; Galizia et al. 2012). Although LF models can clearly predict both type I and V isotherms from first principles, here we show that they can do so for a non-flexible adsorbent as well.

Fig. 1
figure 1

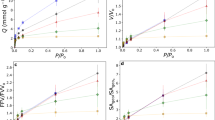
Predicted CO2 isotherms for ‘large pore’ (a) and ‘narrow pore’ (b) structures of MIL-53 (Al) at 273 K. The ‘large pore’ structure shows type V behaviour with an inflection at 47 kPa as evidenced by the root of the 2nd derivative of the isotherm. The ‘narrow pore’ structure shows strictly type I behaviour under identical conditions

Full size image

For a single adsorbate, the RALF model requires the knowledge of the characteristic parameters of the solid, which can be determined from the porosity of the solid and Henry law constants of different molecules and their adsorption energy (Brandani 2019). The adsorbate characteristic parameters are taken from bulk vapour-liquid equilibrium data (Sanchez and Lacombe 1976). To allow the model to more accurately match experimental isotherms, a correction of the packing density, \(\xi\), is introduced, which takes into account confinement constraints, allowing to match saturation capacities; an energy correction parameter, \(\kappa\), can be used to match Henry law constants (Sarti and Doghieri 1998). On the other hand, with both \(\xi = 0\) and \(\kappa = 0\), full isotherms can be predicted if the parameters of the adsorbent are known. Figure 2 shows such predictions for water and propane on silicalite-1, where the adsorbent parameters have been taken from Brandani (2019). Whilst \(\xi\) and \(\kappa\) can be used to achieve a closer match to experimental data, it is important to note that the RALF model can indeed predict a priori the different behaviour of the two adsorbates.

Fig. 2
figure 2

Predicted isotherms for propane and water on silicalite-1 at 300 K. Propane yields a type I isotherm, whereas the isotherm for water has a strong inflection, typical for type V isotherms

Full size image

Figure 3 shows the comparison between the RALF model and the Frumkin-Fowler–Guggenheim (FFG) isotherm. The FFG isotherm parameters are set to give the same Henry’s law constant and the same saturation capacity for both models (values given in the supporting information), thus leaving only the energy parameter, \(\omega\), to be determined. As \(\omega\) is increased there is the known transition to a two-phase region in the adsorbed phase, due to the emergence of a condensed liquid (evident from a discontinuity in the isotherm) (Do 1998), which is not physically meaningful in a microporous solid. This transition occurs for \(\frac{2\omega}{RT} > 4\), and it can be seen from Fig. 3 that in order to match the pressure at which a step occurs in the RALF model, the FFG isotherm has to be in this two phase regime. The RALF model on the other hand can predict the step at these low pressures without requiring a two-phase transition, i.e. the model leads to a continuous isotherm without a finite discontinuity. The continuous nature of the predicted isotherm by the RALF model stems from the fact that the model reproduces the phenomenon of molecular clustering, as opposed to formation of bulk liquid. Clustering is favoured for highly coordinating molecules, as the intermolecular energy is higher than the interaction energy of molecules with the adsorbent. The low affinity with the adsorbent in turn leads to a reduction in the adsorbed phase concentration at saturation pressure (as Fig. 3 shows, the isotherm reaches only ~ 70% of the theoretical saturation capacity). Indeed, pressures upwards of 10 MPa are required to completely fill the micropores of a hydrophobic adsorbent with water (Trzpit et al. 2007; Humplik et al. 2014). In contrast, the formation of bulk liquid as calculated by the FFG isotherm, practically saturates the micropore volume already at the saturation pressure of water. Finally, whilst qualitatively both models can give a type V isotherm, the FFG isotherm requires knowledge of some experimental data and therefore does not allow an a priori prediction.

Fig. 3
figure 3

Comparison of FFG isotherms for different values of \(\omega\), with the predicted isotherm for water on silicalite-1 at 300 K by the RALF model, shown as fractional uptake \(\theta\) versus p/p0. Normalisation is to p0 = 3.53 kPa30 and nsat = 10.03 mol kg−1; \(\omega_{2 - phase}\) corresponds to \(\frac{2\omega}{RT} = 4\)

Full size image

In this contribution we will explore which RALF model parameters determine the shape of the predicted isotherms using the parameters for silicalite-1 as our modelling adsorbent. The aim is to gain an understanding of the importance of porosity and the ratio of energy parameters in the RALF model that lead to the prediction of the two types of isotherm shape.

2 Theory

The Rigid Adsorbent Lattice Fluid and its equations have been described in great detail in Brandani (2019). In essence, the RALF model represents an equation of state based on a lattice of occupied and vacant sites, which only considers the interaction energy between occupied sites. Despite being based on a statistical thermodynamic approach, a simplification of the partition function leads to a macroscopic model with only a small number of modelling parameters. Here we will suffice by listing only the key equations of the model.

A lattice fluid representation of a pure component system is defined by only three characteristic parameters, which are related by the interaction energy between molecules of species \(j\), \(\epsilon_{j}^{*}\), close-packed volume, \(v_{j}^{*}\), and close-packed density, \(\rho_{j}^{*}\). The characteristic temperature and pressure are defined as follows (where \(\epsilon_{j}^{*}\) is a molar quantity):

$$T_{j}^{*} = \frac{{\epsilon_{j}^{*}}}{R}$$
(2)
$$P_{j}^{*} = \frac{{\epsilon_{j}^{*}}}{{ v_{j}^{*}}}$$
(3)

The parameters are related to each other through the following relationships:

$$T_{j}^{*} = \frac{{P_{j}^{*} v_{j}^{*}}}{R}$$
(4)
$$r_{j}^{0} = \frac{{M_{j}}}{{\rho_{j}^{*} v_{j}^{*}}}$$
(5)

It can be seen that \(P_{j}^{*}\) is in effect an energy density, and \(T_{j}^{*}\) a measure for the interaction energy. The parameter \(r_{j}^{0}\) is related to the close-packed density and volume through \(M_{j}\), the molecular mass, and describes the number of lattice sites occupied per molecule of species \(j\). It should be self-evident, that the pure component characteristic parameters have a physical meaning, which can be determined from existing thermodynamic data.

For any mixture, e.g. a solid—adsorbate system, the corresponding characteristic parameters follow from the pure component parameters through a set of mixing rules. The RALF model utilises the same mixing rules as used by Sanchez and Lacombe (Sanchez and Lacombe 1976; Lacombe and Sanchez 1976), which conserve the molecular volume and number of pair interactions in the closed packed state (Brandani 2019). A final rule describes the mixture interaction density, \(P^{*}\):

$$P^{*} = \mathop \sum \limits_{j} \mathop \sum \limits_{k} \phi_{j} \phi_{k} P_{jk}^{*}$$
(6)

where

$$P_{jk}^{*} = P_{kj}^{*} = \left({1 -\kappa_{jk}} \right)\sqrt {P_{j}^{*} P_{k}^{*}}$$
(7)

here, \(\phi_{j}\) is the volume fraction of component j in the lattice. The binary interaction parameter, \(\kappa_{jk}\), signifies an enhanced or reduced energy density resulting from attractive or repulsive interaction, respectively between molecules j and k, with \(\kappa_{jj} = 0\). In a purely predictive mode, \(\kappa_{jk}\) is set to zero. As described in the introduction, a final adaptation is made in RALF as compared with earlier versions of the lattice fluid model, which allows for an increase in the close-packed volume for the adsorbed phase due to confinement constraints, through \(\xi_{jA}\). This correction concomitantly leads to a reduction in both the energy density and close-packed density, whilst leaving the characteristic temperature unaffected. As we are interested in using the RALF model in a purely predictive way, in this work, \(\xi_{jA} = 0\).

$$v_{jA}^{*} = \left({1 +\xi_{jA}} \right)v_{j}^{*}$$
(8)
$$P_{jA}^{*} = \frac{{P_{j}^{*}}}{{\left({1 +\xi_{jA}} \right)}}$$
(9)
$$\rho_{jA}^{*} = \frac{{\rho_{j}^{*}}}{{\left({1 +\xi_{jA}} \right)}}$$
(10)

It is shown in Brandani (2019) how the LF equations for a system comprising a crystalline ‘rigid’ adsorbent lead to a corresponding expression for the Gibbs energy for the solid phase. For a system with a single adsorbate, the residual Gibbs energy is given by:

$$\frac{{G^{R} \left({T,P,N} \right)}}{RT} = rN\left[{- \frac{{\widetilde{\rho}}}{{\widetilde{T}}} + \frac{{\left({1 - \widetilde{\rho}} \right){ \ln }\left({1 - \widetilde{\rho}} \right)}}{{\widetilde{\rho}}} + 1} \right] + N\left({z - 1 - { \ln }z} \right)$$
(11)

Here we opt for the chemical engineering nomenclature as used in various textbooks, where the term residual refers to the departure of a thermodynamic property from that of an ideal gas at the same temperature and pressure (Smith et al. 2004; Gmehling et al. 2012).

Equation 12 is the expression for the residual Gibbs energy of the adsorbed phase given in Brandani (2019) written for a single adsorbate, given that the combinatorial term for a single adsorbate becomes zero due to the rigid nature of the solid. The reduced quantities are defined by:

$$\widetilde{T} = \frac{T}{{T^{*}}}\quad \widetilde{P} = \frac{P}{{P^{*}}}\quad \widetilde{\rho} = \frac{\rho}{{\rho^{*}}}$$

The compressibility factor is as usual, i.e. \(z = \frac{PV}{NRT } = r\frac{{\widetilde{\rho}}}{{\widetilde{\rho}\widetilde{T}}}\). For an adsorbent, the density of the mixture does not correspond to the equilibrium value as given by an Equation of State. For the compressibility factor of a single component in equilibrium, \(z^{EoS}\), the following holds:

$$z^{EoS} - 1 = r\left[{- \frac{{\widetilde{\rho}}}{{\widetilde{T}}} - \frac{{{ \ln }\left({1 - \widetilde{\rho}} \right)}}{{\widetilde{\rho}}} - 1} \right]$$
(12)

As is evident from Eq. 11, knowledge of the density of the system is essential to obtain the Gibbs energy and the chemical potentials in RALF. The volume of the adsorbent including the micropores, \(V_{s}\), is taken as the system volume and therefore the density is given by:

$$\rho = \frac{{\mathop \sum \nolimits_{j} m_{j}}}{{V_{s}}} = \frac{{m_{s}}}{{w_{s} V_{s}}} = \frac{{\rho_{s}}}{{w_{s}}}$$
(13)

where \(w_{s}\) is the weight fraction of the solid. In this paper, we are assuming that silicalite-1 behaves like a ‘frozen’ solid, that is, its density does not change with amount adsorbed. This is a reasonable assumption for small molecules, although symmetry changes and lattice distortion have been reported for larger molecules (Fyfe et al. 1984). The actual density of the solid can be obtained from diffraction data or porosimetry and the assumption of a ‘frozen’ solid means that no further relationships are required to describe this quantity. This is also the scenario used for silicalite-1 in Brandani (2019). The solid porosity, \(\varepsilon\), is naturally related to the actual density of the solid and is defined as follows:

$$\varepsilon = 1 - \widetilde{\rho}_{s} = 1 - \frac{{\rho_{s}}}{{\rho_{s}^{*}}}$$
(14)

where \(\widetilde{\rho}_{s}\) is the reduced solid density.

For the calculation of adsorption isotherms, an equilibrium condition is now required. The condition is for the chemical potentials of component j to be equal in the adsorbed and fluid phases. The subscript A is added for clarity in Eq. 15 to describe the adsorbed phase, but will be dropped from now on. Isotherms can be constructed by solving Eq. 15 for the number of moles adsorbed at any given combination of pressure and temperature.

$$\mu_{j,F} \left({P,T} \right) = \mu_{j,A} \left({N_{j},P,T} \right)$$
(15)

The expressions for the chemical potentials for both the fluid phase and adsorbed phase can be obtained by the appropriate derivations with respect to moles of component j. For the single component (and a ‘frozen’ solid) they are:

$$\frac{{\mu_{1,F}^{R}}}{RT} = \left[{- \frac{{\widetilde{\rho}_{1}}}{{\widetilde{T}_{1}}} + \frac{{\left({1 - \widetilde{\rho}_{1}} \right){ \ln }\left({1 - \widetilde{\rho}_{1}} \right)}}{{\widetilde{\rho}_{1}}} + 1} \right]r_{1}^{0} + z - 1 - { \ln }z$$
(16)
$$\frac{{\mu_{1,A}^{R}}}{RT} = - \frac{{\widetilde{\rho}}}{{\widetilde{T}}}\left({\frac{{2\mathop \sum \nolimits_{j} \phi_{j} P_{j1}^{*}}}{{P^{*}}} - 1} \right)r_{1} + \left[{\frac{{\left({1 - \widetilde{\rho}} \right){ \ln }\left({1 - \widetilde{\rho}} \right)}}{{\widetilde{\rho}}} + 1} \right]r_{1}^{0} + \left({z^{EoS} - 1} \right)\frac{{r_{1}}}{r} - { \ln }z$$
(17)

It can noted that the residual chemical potential for component j is equal to the logarithm of its fugacity coefficient, \({ \ln }\varphi_{j}\), i.e.

$$\frac{{\mu_{j}^{R}}}{RT} = \frac{1}{RT}\left({\frac{{\partial G^{R}}}{{\partial N_{j}}}} \right)_{{T,P,N_{k \ne j}}} = { \ln }\varphi_{j}$$
(18)

Finally it is worth considering that the use of a lattice fluid naturally leads to expressions for the behaviour at both infinitely high pressures yielding finite adsorbed phase concentrations, and in Henry’s law limit, thereby preserving thermodynamic consistency (Brandani 2019). The expressions under these conditions have also been given in the supporting information.

3 Parameterisation of the RALF model

In order for the RALF model to be a predictive tool, careful parametrisation of the solid and adsorbate molecules is required as explained in refs (Brandani 2019; Verbraeken and Brandani 2019). The advantage of the model is that predictions become possible with the determination of only three characteristic parameters for each species. For many molecules, these characteristic parameters have already been determined from available thermodynamic data so that determining the same parameters for the solid is the only remaining step. The solid in turn can be parameterised from available adsorption data on a number of molecules. This has been carried out for silicalite-1 in Brandani (2019) and in this work we have therefore turned our attention to this material. It is worth noting that the parametrisation of silicalite-1 was carried out using adsorption data for a number of weakly coordinating molecules, such as light alkanes, noble gases, N2, CO, etc. due to good availability of experimental data on these systems (Brandani 2019). The characteristic parameters for a number of molecules and silicalite-1 are listed in Table 1. The characteristic parameters for the molecules have been determined from bulk vapour-liquid equilibrium data, as outlined in Ref. (Sanchez and Lacombe 1976), carried out independently from this study or the determination of characteristic parameters for silicalite-1 (De Angelis et al. 2007). With the characteristic parameters in place, the RALF model can now be used as a purely predictive tool, without the need for adjustable fitting parameters. From Table 1 it can be seen that silicalite-1 is described by three characteristic parameters, which is equivalent to assuming that it can be described as a homogeneous solid, i.e. having a single characteristic adsorption site. It has been shown in various publications that this is a realistic assumption for small molecules (Zhu et al. 2000; Sun et al. 1998; Golden and Sircar 1994). This also means that any predictions of steps or inflections in isotherms are not due to surface heterogeneities.

Table 1 Characteristic parameters for silicalite-1 and a number of molecules
Full size table

4 Results

The isotherms as predicted by the RALF model for propane and water on silicalite-1 at 300 K have already been shown in Fig. 2. Here we use the model as a purely predictive tool using the parameters in Table 1, that is, no additional binary interaction or confinement parameters have been used to generate the isotherms. For comparison, Fig. 4 shows the predicted isotherm for another polar molecule under identical conditions, namely ethanol. This isotherm appears type I at first sight, but, on closer inspection, a mild inflection is also present for this molecule, albeit at very low pressure, \({\raise0.7ex\hbox{$p$} \!\mathord{\left/{\vphantom {p {p_{0}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${p_{0}}$}} < 5 \cdot 10^{- 4}\) (as a root of the second derivative exists under these conditions). The predicted inflection for water on silicalite-1 is much sharper, yet occurs well below the saturation pressure of water and this type of isotherm has indeed been found both experimentally and by molecular simulations (Puibasset and Pellenq 2008; Olson et al. 2000; Giaya and Thompson 2002; Ramachandran et al. 2006). This inflection is not always observed experimentally probably due to the presence of residual Al in the framework, i.e. the materials are not pure silica forms but variants with Si/Al below 30. This mild hydrophilicity then leads to type I isotherms for water on ZSM-5 and can also be attributed to the presence of extra framework charged defects. Similarly for ethanol, inflections at low pressures have been reported in both simulation and experimental work (Dubinin et al. 1989; Xiong et al. 2011), yet often the behaviour is regarded as type I, due to lack of data under these conditions (Oumi et al. 2002). Nonetheless, regardless of the exactness of the predictions, the inflections as shown in Figs. 2 and 4 are predicted a priori by the RALF model as a result from only a small number of input parameters. On the other hand, the isotherm for an apolar molecule such as propane is strictly type I, with no sign of any inflection.

Fig. 4
figure 4

Predicted isotherms for ethanol on silicalite-1 at 300 K. The isotherm is of type V, although it appears type I

Full size image

In order to understand the predictions by the RALF model in greater detail, we will now focus on some of the key parameters in the lattice fluid model and their effect on isotherm shape. These parameters are solid porosity, \(\varepsilon\) (or reduced density), and the characteristic parameters for the adsorbate molecules, i.e. interaction energy, \(T_{j}^{*}\), energy density, \(P_{j}^{*}\) and close packed density, \(\rho_{j}^{*}\).

Polar molecules have relatively high values for \(P_{j}^{*}\) and \(T_{j}^{*}\), as compared to apolar molecules, such as alkanes. The localised charges on polar molecules clearly endow them with an increased interaction energy in the lattice fluid. This in turn translates into strongly coordinating behaviour and a tendency to show adsorption behaviour which leads to molecular clustering. Table 1 shows values for \(P_{j}^{*}\) and \(T_{j}^{*}\) for various molecules. Similarly, the strength of the molecule’s interaction with the solid itself must be a critical parameter as to whether or not additional molecules adsorb onto the solid surface or coordinate to already adsorbed molecules. From a chemical point of view, this solid – adsorbate interaction can be effected by changing the solid’s polarity. For instance, in a zeolite this could be achieved by changing the silicon to aluminium ratio and introducing charge balancing cations. From a structural point of view, confinement of molecules in the solid is expected to have a similar effect. A large pore volume is more likely to cause clustering of polar molecules, whereas this behaviour is not expected for a dense solid with nanosized pores.

5 Solid porosity, ε

The effect of solid density or porosity on the isotherm shape is easily illustrated through the RALF predictions of ethanol adsorption at 300 K, as shown in Fig. 5. Apart from the porosity, the remaining characteristic parameters for the solid are unchanged. It can be seen that by increasing the porosity, the isotherm shape becomes increasingly type V, with a more prominent inflection, whereas when porosity is reduced to below \(\varepsilon = 0.23\), the inflection disappears altogether, leaving strictly type I isotherms. For ease of comparison, the isotherms have been normalised to the same adsorbed amount at \({\raise0.7ex\hbox{$p$} \!\mathord{\left/{\vphantom {p {p_{0}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${p_{0}}$}} = 0.02\). Figure 6 meanwhile shows the predicted isotherms for the apolar propane molecule under identical conditions. These remain type I up to a solid porosity of \(\varepsilon = 0.46\) and this shows once more that by simply changing the adsorbate the predicted shape of the isotherm can be changed for a solid with identical parameters. Obviously, decreasing the pore volume has an effect on the saturation capacity, thereby lowering the isotherms. This effect can be seen in Figs. S2 and S3 in the supporting information.

Fig. 5
figure 5

Predicted ethanol isotherms on silicalite-1 with varying solid density at 300 K. Actual density for silicalite-1 is 1786 kg m−3, which corresponds to a porosity ε = 0.31, indicated by the dashed line

Full size image
Fig. 6
figure 6

Predicted propane isotherms on silicalite-1 with varying solid density 300 K. Actual density for silicalite-1 is 1786 kg m−3, which corresponds to a porosity ε = 0.31, indicated by the dashed line

Full size image

6 Adsorbate characteristic parameters

It is clear from the results presented so far, that solid porosity is only one deciding factor for the shape of the isotherm. We will now explore the effect of the molecules’ characteristic parameters.

In order to limit our parameter space so it only covers realistic molecules, it is instructive to revisit the lattice fluid theory. Equations 4 and 5 relate the relevant characteristic parameters and it is evident that the number of lattice sites per molecule, \(r_{j}^{0}\), is directly related to the molecule’s molecular weight. In theory \(\rho_{j}^{*}\) and \(v_{j}^{*}\) could vary freely, but on inspection of the relationship between these parameters and the molecular weight of real molecules, a clear trend is visible, see Fig. 7. For linear alkanes and noble gases the relationship is practically linear, whereas it deviates somewhat from linearity for other gases and polar molecules. This indicates that a relationship exists between \(\rho_{j}^{*}\) and \(v_{j}^{*}\) for real molecules and this allows us to impose boundaries on the available parameters space.

Fig. 7
figure 7

Linear relationships of \(r_{j}^{0}\) with various molecules’ molecular weight, \(M_{j}\)

Full size image

In recognising the linear relationship between \(r_{j}^{0}\) and molecular weight, \(M_{j}\), we can write:

$$r_{j}^{0} = a \cdot M_{j} + b$$
(19)

Using Eq. 5 we can we can rewrite Eq. 19 to yield:

$$\rho_{j}^{*} v_{j}^{*} = \frac{{M_{j}}}{{a \cdot M_{j} + b}}$$
(20)

Figure 8 shows how \(\rho_{j}^{*} v_{j}^{*}\) changes for the different types of real molecules, where the same molecules have been used as in Fig. 7. It is also clear that Eq. 20 provides a satisfactory relationship between \(\rho_{j}^{*} v_{j}^{*}\) and \(M_{j}\) and that all molecules considered here are bound by \(\left({\rho_{j}^{*} v_{j}^{*}} \right)^{max}\) and \(\left({\rho_{j}^{*} v_{j}^{*}} \right)^{min}\) as found for the noble gases and small polar molecules, respectively. Based on this relationship of \(\rho_{j}^{*} v_{j}^{*}\) with \(M_{j}\), we will now explore the effect of \(\rho_{j}^{*}\), \(T_{j}^{*}\) and \(P_{j}^{*}\) on the shape of the isotherm. To do this we will now use a hypothetical molecule with a molecular weight of 0.04 kg mol−1; at given \(T_{j}^{*}\) and \(P_{j}^{*}\), \(v_{j}^{*}\) now is fixed by Eq. 4, whereas \(\rho_{j}^{*}\) is determined by Eq. 20.

Fig. 8
figure 8

The product \(\rho_{j}^{*} v_{j}^{*}\) versus \(M_{j}\) for various molecules (squares) and fits using Eq. 20

Full size image

Figure 9a shows the effect of changing \(P_{j}^{*}\) at constant \(T_{j}^{*}\) on the critical porosity for adsorbate clustering for different types of molecules (that is, changing \(\rho_{j}^{*} v_{j}^{*}\) to correspond to alkanes, noble gases, etc.). The line in Fig. 9 describes the boundary between absence and presence of an inflection in the isotherm. Whilst it is clear that \(P_{j}^{*}\) has a major effect on the location of the boundary, changing \(\rho_{j}^{*} v_{j}^{*}\) only plays a modest role. Figure 9b shows the effect of changing both \(P_{j}^{*}\) and \(T_{j}^{*}\) at a constant value for \(\rho_{j}^{*} v_{j}^{*}\). Increasing both \(P_{j}^{*}\) and \(T_{j}^{*}\) shifts the boundary for adsorbate clustering to lower porosities. This is to be expected, since these two parameters describe a molecule’s energy density and interaction energy, with higher values indicating a stronger intermolecular attraction.

Fig. 9
figure 9

Effect of \(P_{j}^{*}\) on the boundary for adsorbate clustering at different \(\rho_{j}^{*} v_{j}^{*}\) and constant \(T_{j}^{*} = 400 {\text{K}}\) (a). Effect of \(P_{j}^{*}\) on the boundary for adsorbate clustering at different \(T_{j}^{*}\) (b)

Full size image

7 Solid polarity

Changing the solid’s polarity is most easily effected by adjusting the binary interaction parameter for the adsorbate—adsorbent pair, \(\kappa_{js}\), as defined in Eq. 7. As previously discussed, this parameter is usually used to match RALF predictions to experimental isotherms, by adjusting the mixture energy density of the pair, whereas for a purely predictive model it is kept zero. In this instance however, we will illustrate the effect of changing solid polarity on the shape of the predicted isotherms by choosing a polar molecule and making \(\kappa_{js}\) non-zero, where for \(\kappa_{js} >\) and \(\kappa_{js} <\) 0, solid polarity is respectively decreased and increased. In physical terms, \(\kappa_{js} <\) 0 would indicate the presence of charged entities within the framework and would be equivalent to introducing alumina (and charge balancing cations) to an otherwise pure silica zeolite. As \(\kappa_{js}\) becomes more negative, the Si/Al ratio reduces with a concomitant increase in cation content, whose electrostatic fields create hydrophilic centres. Strong adsorption can be expected around these centres for molecules which contain, for instance, dipoles or quadrupoles. This is shown for water at 300 K in Fig. 10 and additionally for ethanol in the supporting information, Fig. S4. As can be seen when viewed in logarithmic pressure scale, the shape of the isotherms essentially remains identical, whilst the point of inflection shifts to lower pressures. On a linear scale however, the isotherms for increased solid polarity appear increasingly type I, due to the shifting and compression of the inflection. The increased polarity obviously also leads to increased Henry’s Law constants, due to greater affinity of the solid with the adsorbates. Olson et al. (2000) already qualitatively described this behaviour for water on H-ZSM-5 with varying Si/Al content and indeed experimental water isotherms on silicalite-1 reported in literature can show inflections at various pressures (Giaya and Thompson 2002; Oumi et al. 2002). The scatter in experimental results for hydrophobic silicalite-1 is usually attributed to different synthesis methods, causing differing amounts of defects, both extra-framework as well as within the zeolite crystals. This hypothesis was also confirmed using molecular simulations, where introducing small numbers of charged defects caused significant increases in amounts adsorbed at identical pressures and a drop in onset pressure for the ‘step’ in the isotherm (Trzpit et al. 2007). All in all, water—water interactions are generally always favourable over water—adsorbent ones in a silica/alumina framework, so beyond a certain adsorbed concentration (centred around charged defects), extensive clustering eventually occurs, despite entropy considerations, leading to the typical type V isotherm shape (Puibasset and Pellenq 2008).

Fig. 10
figure 10

Water isotherms for silicalite-1 (\(\varepsilon = 0.31\)) at 300 K for different values of binary interaction parameter \(\kappa_{js}\). The dashed curve for \(\kappa_{js} = 0.05\) is added to reflect a water isotherm for a truly hydrophobic solid

Full size image

8 Concluding remarks

Although the origins of type V isotherms in microporous solids have been studied for over a decade, yielding microscopic insights through molecular simulations and related computational methods, macroscopic models that can predict this behaviour a priori are rare. Predictive macroscopic models, however, are a an essential tool in designing efficient separation processes and with the advent of new exciting materials being developed that show non-trivial adsorption behaviour, the need for these models could not be higher. Here we have discussed how the simple RALF model can predict both type I and V isotherms from first principles and identified which modelling parameters are critical in determining the resulting isotherm shape. As reported previously in molecular simulation studies, the trade-off between molecule—molecule and molecule—adsorbent interaction determines the adsorption behaviour. In the LF model this is mostly described by the values for the interaction energy and energy density (\(T_{j}^{*}\) and \(P_{j}^{*}\)) of both the molecule and the solid and the porosity of the solid. The (dis)similarity between the former dictates whether molecular clustering is likely, whereas the latter acts as a geometric barrier for this behaviour. The molecule—adsorbent interaction can further be tweaked by adjusting their binary interaction parameter, \(\kappa_{js}\), but this should ultimately be a utility to match the predictions to experimentally available data.

It is impressive that a simple lattice fluid based model, where the parameters of the adsorbates can be determined from bulk fluid properties (Linstrom and Mallard), can replicate different adsorption behaviour without prior assumptions, making it a useful tool in process simulations and design.