1 Introduction

Industrial development and ongoing urbanization continue to bring about growing problems related to waste production. Wastes are a source of toxic substances which migrate unhindered through the natural environment, causing its degradation, and at the same time having an adverse effect on living organisms, including humans. One of the most dangerous groups of inorganic pollutants is the heavy metals, including among others cadmium, lead, nickel and mercury (Shafique et al. 2011).

Adsorption is one of the highly selective methods for removing heavy metals from aqueous solutions (Gupta and Bhattacharyya 2012, 2014; Khan et al. 2013). This is an economical technique which also offers numerous advantages resulting from the vast number of available adsorbents (Barakat and Kumar 2015; Ezzeddine et al. 2015; Lee et al. 2015; Li et al. 2015; Peng et al. 2015). With the development of modern technologies, a very wide range of materials have come to be used as hazardous metal adsorbents, from natural substances to highly selective synthetic systems (Cutillas-Barreiro et al. 2014; Kołodynska et al. 2012; Santhosh et al. 2015; Wysokowski et al. 2014). Alongside precipitation and hydro- or solvothermal methods, one of the basic techniques used for the synthesis of a wide range of synthetic, inorganic and inorganic/organic hybrid adsorbents is the sol–gel method (Hassan et al. 2014; Motlagh et al. 2015). Because of the mechanism of this process, it is made possible to define the physicochemical properties of materials of this type, including especially their porous structure parameters, which are extremely important for environmental applications (Fan et al. 2014a, b, c; Sriprang et al. 2014; Viltuznik et al. 2015). Both, natural and synthetic adsorbents can be modified so as to enhance their most important properties, such as surface area (Karthik and Meenakshi 2015a, b; Klapiszewski et al. 2015; Zhao et al. 2014). In many cases, simply changing the process for preparation an adsorbent or the method of modifying it may lead to an increase in its sorption capacity with respect to a specific group of pollutants (Borhade et al. 2015; Guo et al. 2014; Madrakian et al. 2014; Nguyen et al. 2015).

Much attention is also paid to the appropriate design of the adsorption process, which entails the need to carry out numerous laboratory studies with the aim of optimizing the time of contact between adsorbent and adsorbate, the pH, or the temperature (Dubey et al. 2009; Kowalczyk et al. 2013; Li et al. 2010; Mortaheb et al. 2010; Song et al. 2011). Depending on the adsorptive material itself, and also on the adsorbate, a system requires specific conditions in which the most favorable results for adsorption efficiency can be obtained.

In the literature there is very little information regarding sol–gel derived MgO–SiO2 adsorbent. Therefore, in this study, an attempt was made to apply the sol–gel route for synthesis of novel, active oxide adsorbent dedicated to the removal of hazardous metal ions from aqueous solutions. The adsorbent was analyzed in detail, particularly in terms of its porous structure parameters. As compared to other adsorbents obtained via traditional methods of water or emulsion precipitation, mechanism of sol–gel route allowed to synthesize material characterized with high purity, low bulk density and definitely improved parameters of the porous structure, including well developed surface area. Numerous sorption tests were performed, including evaluation of pH and temperature as well as sorption kinetics and isotherms.

2 Experimental

2.1 Materials and methods

2.1.1 Preparation and characterization of Mg–Si hybrid oxide adsorbent

An inorganic oxide adsorbent of MgO–SiO2 type was obtained via a modified sol–gel route using the organic magnesium precursor magnesium ethoxide, as described previously (Ciesielczyk et al. 2014). The synthesis was performed using a reactor 2 L in capacity, equipped with a heating jacket and high-speed anchor stirrer. At the first stage, a specified amount (45 g) of magnesium ethoxide was dissolved in 1500 mL of methyl alcohol. The whole system was stirred for 15 min, and after that time tetraethoxysilane (the organic silica precursor) and the catalyst of hydrolysis (25 % ammonia solution) were introduced into it simultaneously. The quantities of the reactants were selected to achieve a TEOS:magnesium ethoxide mass ratio of 1.5:1. The mixture was additionally stirred for 60 min with a stirrer speed of 300 rpm. The alcogel obtained was placed in a crystallizer to enable solvent evaporation, and was then dried at 105 °C for 48 h. The dry oxide adsorbent was classified and comprehensively analyzed. The synthesis scheme is presented in Fig. 1. The chemical composition of the synthetic powder material (content of Mg, Si and O) was analyzed using energy dispersive X-ray spectroscopy (EDS), with the use of a Princeton Gamma-Tech unit with a prism digital spectrometer. The crystalline structure of the MgO–SiO2 adsorbent was determined using the WAXS method. Diffraction patterns were taken using a TUR-M62 horizontal diffractometer equipped with an HZG-3 type goniometer over a 2θ range of 5°–80°. The morphology and microstructure of the adsorbent were analyzed using a Zeiss EVO40 scanning electron microscope. The observations enabled evaluation of the degree of dispersion, the structure of particles and their tendency towards aggregation or agglomeration. The surface area ABET (BET method) as well as pore volume and diameter (BJH method) were calculated based on data from measurements of low-temperature adsorption of nitrogen. The isotherms of nitrogen adsorption/desorption were computed at −196 °C using an ASAP 2020 apparatus (Micromeritics Instrument Co.). The FTIR spectrum was obtained using a Vertex 70 spectrophotometer (Bruker). The samples were analyzed in the form of tablets, made by pressing a mixture of anhydrous KBr (ca. 0.25 g) and 1 mg of the tested substance in a special steel ring, under a pressure of 10 MPa. Analysis was performed over a wavenumber range of 4000–400 cm−1 (at a resolution of 0.5 cm−1; number of scans: 64). Additionally, to evaluate the surface charge of the synthetic powder, the zeta potential was determined as a function of pH. Electrokinetic studies were performed in 0.001 M NaCl electrolyte using a Zeta Nano ZS instrument (Malvern Instruments Ltd.) equipped with an MPT-2 automatic titration system.

Fig. 1
figure 1

Synthesis of MgO–SiO2 inorganic oxide adsorbent via the sol–gel route (1 reactor with heating jacket, 2 pump, 3 valve, 4 crystallizer, 5 vacuum evaporator, 6 dryer)

Full size image

As a result of this process, an inorganic oxide adsorbent characterized by irregularly shaped particles, amorphous structure and mesoporous nature, with a high BET surface area, was obtained. Moreover, the synthesized adsorbent has negative surface charge over the whole pH range.

2.1.2 Sorption experiments

Sorption experiments were conducted to investigate the adsorption of Cd(II) and Pb(II) ions on the inorganic oxide adsorbent of MgO–SiO2 type. All sorption experiments were carried out in 250 mL flasks, to which an appropriate amount of adsorbent and 100 mL of the appropriate ion solution were added. Two different metal salts with the same competitive anions (Cd(NO3)2·4H2O and Pb(NO3)2) were used as metal ion precursors. This made it possible to evaluate the effectiveness of adsorption of different ions. The mixture was next stirred at 200 rpm using a magnetic stirrer (RO10, IKA Werke) for 1–240 min. Sorption behavior, including contact time, mass of adsorbent, effect of pH and sorption kinetics, was investigated in detail. To evaluate the pH effect, measurements were performed with the initial pH of the solution ranging from 1 to 9, and with the initial metal ion concentration in the range 25–100 mg/L. To obtain the desired pH, as monitored using a pH-meter (Lab 850, Schott Instruments), sodium hydroxide or nitric acid, in 0.1 M solution, was added. In order to establish the optimal mass of the adsorbent (1–20 g/L) the experiment was performed over 60 min utilizing model solutions of appropriate metal ions in an initial concentration of 50 mg/L. In the investigation of adsorption kinetics, metal ion solutions with initial concentrations of 25–100 mg/L and pH 5 were used, in a quantity of 100 mL. After adsorption, the adsorbent was separated by filtration, and the final concentration of ions in the solution was determined. To determine the stability of bonds between the adsorbate and the adsorbent, and to determine the effectiveness of removal of Cd(II) or Pb(II) ions from the surface of the adsorbent, elution tests with H2O were performed. AAS analysis was performed to evaluate the quantity of Cd(II) or Pb(II) ions present in the filtrate after the adsorption process and elution tests. The measurements were carried out to an accuracy of ±0.1 mg/L using a Z-8200 spectrometer (Hitachi). Before the analysis, a calibration curve was prepared to enable calculation of the Cd(II) and Pb(II) ion concentrations in the filtrate. Additionally, the adsorbents underwent EDS analysis following the process, to evaluate the presence of Cd(II) and Pb(II) in their structure.

Determination of the adsorption kinetics of the studied metal ions was an important part of the experiments. Calculations were performed to determine the value q t , which is needed to define various kinetic models: pseudo-first-order (Lagergren 1898) and pseudo-second-order (Ho and McKay 1999). The quantity of metal ions adsorbed per unit time (q t ) on the adsorbent surface was computed using Eq. (1):

$$q_{t} = \frac{{\left( {C_{0} - C_{t} } \right) \cdot V}}{m}$$
(1)

where C 0 and C t are the concentrations of cadmium(II) or lead(II) ions in the solution before and after sorption respectively (mg/L), V is the volume of the solution (L), and m is the mass of sol–gel derived adsorbent (g).

The standard deviation for the kinetics of the adsorption process was also determined using the formula (2):

$$SD = \sqrt {\frac{{\sum {\left[ {\left( {q_{e,\exp } - q_{e,cal} } \right)/q_{e,\exp } } \right]}^{2} }}{n - 1}}$$
(2)

where n is the number of data points, q exp are the experimental data, and q cal are the data obtained applying proper kinetic model. The higher the value of the correlation coefficient (r 2), and the smaller the standard deviation (SD), the better fit of experimental data to selected kinetic model.

To determine adsorption isotherms, tests were carried out at different concentrations (in the range of 25–500 mg/L) of metal ions. The equilibrium concentration (q e ) was calculated using the formula (3):

$$q_{e} = \frac{{\left( {C_{0} - C_{e} } \right) \cdot V}}{m}$$
(3)

where q e is the quantity of metal ions adsorbed at equilibrium (mg/g), C 0 is the initial concentration of metal ions (mg/L), C e is the equilibrium metal ions concentration (mg/L), V is the volume of the solution (L), and m is the mass of sol–gel derived adsorbent (g).

To evaluate the goodness of fit of experimental data to the model, Chi square test is used (Ding et al. 2012). It is defined by Eq. (4):

$$\lambda^{2} = \sum\limits_{i = 1}^{m} {\frac{{(q_{e,\exp } - q_{e,cal} )^{2} }}{{q_{e,\exp } }}}$$
(4)

where q e,cal is equilibrium capacity of metal ions adsorbed on sol–gel derived adsorbent and obtained from isotherm models, q e,exp is the equilibrium capacity obtained from the experimental data, and m is the number of experimental data.

3 Results and discussion

3.1 Adsorbent characterization

Firstly, the physicochemical characteristics of the sol–gel-derived MgO–SiO2 adsorbent were investigated (Table 1). Analysis of the chemical composition of the adsorbent demonstrated the presence of two dominant components in its structure: SiO2 (63.3 %) and MgO (36.5 %). Due to the methodology of synthesis the amount of moisture was limited and was no more than 10 %. The results also showed that the resulting inorganic oxide adsorbent has a completely amorphous structure, which can be transformed into crystalline by the selection of an appropriate heat treatment technique (Ciesielczyk et al. 2014). On the one hand it is possible to obtain crystalline powder adsorbent, while on the other the moisture content can be completely reduced; this determines the surface activity, translating into a quantity of reactive silanol and magnesil groups (≡Si–OH and –Mg–OH). The nature of the adsorbent dispersion presented in the SEM photograph confirms the presence of particles of varying size and of irregular shape. The inorganic oxide adsorbent has a high surface area of 612 m2/g, pore volume Vp = 1.20 mL/g and pore diameter Sp = 10.8 nm. The porous structure parameters confirm the mesoporous structure of the adsorbent.

Table 1 Physicochemical characteristic of MgO–SiO2 derived sol–gel adsorbent
Full size table

3.2 Sorption process

The efficiency of adsorption of cadmium(II) and lead(II) ions on the inorganic oxide adsorbent obtained via the sol–gel route was determined on the basis of AAS analysis.

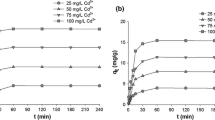
In the first stage, tests were carried out to determine the optimum time of cadmium or lead ion adsorption from model solutions in the three selected initial concentrations of 25, 50 and 100 mg/L (Fig. 2).

Fig. 2
figure 2

Quantity of cadmium(II) and lead(II) ions adsorbed versus time using model solutions with concentrations of a 25 mg/L, b 50 mg/L and c 100 mg/L (accuracy ±0.5 %) (Color figure online)

Full size image

Analysis of the relationships obtained (Fig. 2) showed that a high degree of removal of Cd(II) ions was already achieved after 1 min of adsorption. The effectiveness of adsorption reached 89.2, 87.6 and 85.3 % for model cadmium ion solutions with initial concentrations of 25, 50 and 100 mg/L respectively. This means that increasing the concentration of model Cd(II) ion solutions causes a slight decrease in the efficiency of removal of those ions. On the other hand, the longer the time of the adsorption process, the higher its efficiency, but the optimum time for adsorption of cadmium(II) ions seems to be 30 min. The same situation was observed in the case of adsorption of Pb(II) ions. This seems to be a very good result as compared with other published experimental data (Boroumand Jazi et al. 2014; Karthik and Meenakshi 2015a, b; Madrakian et al. 2014; Mahmoud and Mohamed 2014), which report that the equilibrium time for cadmium and lead removal using different adsorbents should be no shorter than 60 min. Once again a relatively high efficiency of metal ion removal (above 90 %) was observed after 1 min of adsorption. The quantity of metal ions adsorbed decreases with an increase in its initial concentration in model solution, but only for adsorption process times in the range 1–5 min. The efficiency of adsorption reaches 100 % after 10 min of the process with initial lead ion concentrations of 25 and 50 mg/L, and after 15 min using metal ions in a concentration of 100 mg/L. After that time no significant changes in the quantity of adsorbed metal ions were noted.

In both cases (Cd(II) and Pb(II) ions) the equilibrium of adsorption was reached after 5 min using an adsorbate concentration of 25 mg/L. For these model metal ion solutions, slightly better adsorption results were obtained in the case of lead(II) ions. Analogous results were recorded for higher concentrations of Cd(II) and Pb(II) ions (50 and 100 mg/L), but the time after which the equilibrium of adsorption was reached was 10 and 15 min respectively, irrespective of the metal ion type. After that time, Pb(II) ions are practically all removed from the analyzed model solutions. It was shown that the time of the adsorption process is a crucial factor determining the efficiency of removal of metal ions from their model solutions using MgO–SiO2 inorganic oxide adsorbent. The effectiveness of adsorption increases with time and in some cases decreases with increasing metal ion concentration, which also affects the time necessary to attain adsorption equilibrium. The maximum quantity of cadmium(II) and lead(II) ions adsorbed in the optimal time was achieved for the highest metal ion concentration—18.96 and 20.00 mg/g respectively.

Figure 3 shows how the adsorbent mass (MgO–SiO2) influences the efficiency of adsorption of the analyzed metal ions. The results were obtained at constant adsorption time (60 min) and an initial metal ion concentration of 50 mg/L. It was found, as expected, that by increasing the mass of oxide adsorbent the effectiveness of removal of Cd(II) and Pb(II) ions is also increased. This fact is confirmed by numerous literature reports (Mahmoud et al. 2015; Maliyekkal et al. 2010; Xiong et al. 2011) concerning different adsorbents used for the removal of cadmium and lead from aqueous solutions. The highest efficiencies of adsorption (100 %) were obtained utilizing 3 and 0.5 g of oxide adsorbent in the case of cadmium(II) and lead(II) ions respectively. The analyzed results confirmed that just 2 g/L of oxide adsorbent is enough to obtain a satisfactory efficiency of metal ion removal from model solutions, and the use of 3 g/L of adsorbent ensures 100 % effectiveness of removal of both Cd(II) and Pb(II) ions. Slightly better adsorption results were obtained in the case of lead(II) ions, especially when using a smaller quantity of oxide adsorbent (for example, for 0.25 g of adsorbent the difference in adsorption was 7 % in favor of lead). For this metal ion just 0.5 g of MgO–SiO2 oxide adsorbent ensures its complete removal from model solution.

Fig. 3
figure 3

Effect of adsorbent mass on the efficiency of Cd(II) and Pb(II) ion removal from model solutions with a concentration of 50 mg/L (adsorption time 60 min, mass of the adsorbent 5 g/L, accuracy ±0.5 %) (Color figure online)

Full size image

A key goal of the study was to evaluate the influence of the pH of the reaction system on the effectiveness of metal ion removal. As the pH was changed, different concentrations of metal ions and a constant mass of adsorbent (5 g/L) were used, and the process was carried out for 60 min. The experimental data collected (Fig. 4) clearly confirm that Cd(II) ions are adsorbed worse in acidic environments than neutral or alkaline. The difference between the effectiveness of adsorption measured at pH 1 and 9 is 38.6 %. The highest degree of cadmium(II) ion removal (100 %) was obtained by adsorption at pH 9 using a model solution with a concentration of 25 mg/L. As the concentration of adsorbate solution increased, the quantity of metal ions adsorbed decreased, irrespective of the pH value. The same situation was observed in the case of removal of lead(II) ions. These ions were better adsorbed in alkaline medium (pH 7), where their total removal from model solutions at concentrations of 25 and 50 mg/L was noted. For pH 9 an adsorption efficiency of 100 % was obtained irrespective of the solution concentration. Adsorption of lead(II) ions in an acidic medium gave much worse results, ranging from 64.3 % using a model metal ion solution with a concentration of 100 mg/L, up to 75.8 % of ions removed from model solution with a concentration of 25 mg/L. As in the case of Cd(II), increasing the concentration of lead(II) ions caused the effectiveness of the process to decrease. These results are in agreement with experimental data reported by Mahmoud et al. (Mahmoud et al. 2000; Mahmoud and Mohamed 2014; Soliman et al. 2002), who studied cadmium and lead adsorption on nano-zirconium silicate. Those authors showed that metal ion adsorption at low pH values was less favorable due to the protonation of surface functional groups, which decreases with an increase in the pH value of the contact solution. Similar observations were reported by Boroumand Jazi et al., investigating the adsorption of the same metal ions on nanoscale organo-functionalized SiO2–Al2O3 mixed oxide.

Fig. 4
figure 4

Efficiency of adsorption versus pH for analyzed metal ions using model solutions with concentrations of a 25, b 50 and c 100 mg/L (adsorption time 60 min, accuracy ±0.5 %) (Color figure online)

Full size image

It was additionally shown that the powder material synthesized via the sol–gel route has negative surface charge over the whole pH range studied. This is confirmed by the electrokinetic curve showing the zeta potential as a function of pH (Fig. 5). This is a very important fact with regard to the adsorption of positively charged metal ions, as is the quantity of active hydroxyls present on the adsorbent surface as confirmed by the FTIR spectrum of the analyzed sample. The FTIR spectrum also shows signals characteristic for sol–gel-derived MgO–SiO2 oxide adsorbent: 3650–3350 cm−1—stretching vibrations of hydroxyls; 1050 cm−1 and 890 cm−1—stretching vibrations of Si–O bonds; 645 cm−1—deformation vibrations of Si–O–Mg bonds; 630 cm−1—deformation vibrations of O–Mg–O bonds; 540 cm−1 – stretching vibrations of O–Si–O (Chabrol et al. 2010; Ciesielczyk et al. 2014; Lan et al. 2012; Vishwas et al. 2011). According to the literature (Karthik and Meenakshi 2015a, b), low pH values are unfavorable for metal ion adsorption, since in that range they are present in solution in free form as Mn+ (Cd2+ and Pb2+), hence in this case there is an electrostatic repulsion between the cation and the more positively charged surface of the adsorbent. With increasing pH, the adsorbent surface becomes more negatively charged—more OH– groups are generated (see Fig. 5)—and this fact allows metal ions, such as Cd(II) and Pb(II), to be adsorbed more effectively. In a strongly basic environment, the anions M(OH) n−m are formed, and these forms of metal ions, like cadmium or lead hydroxides, strongly interact with the surface of the inorganic oxide adsorbent, making adsorption easier. Figure 5 presents the schematic interactions between the analyzed metal ions and the MgO–SiO2 oxide adsorbent surface in different environments.

Fig. 5
figure 5

Schematic presentation of Cd(II) and Pb(II) ions’ interaction with oxide adsorbent surface at different pH values

Full size image

3.3 Desorption tests

The degree of desorption of the analyzed metals from the surface of the oxide adsorbent using water and hydrochloric acid (Table 2) takes significantly different values. Lower desorption was observed in the case of water (2.0–6.0 %). Moreover, the higher the initial concentration of metal ions in solution, the greater the efficiency of their desorption. On the other hand, hydrochloric acid removed almost all of the cadmium and lead from the adsorbent surface, especially when adsorption was carried out using metal ion solutions with concentration 25 mg/L (desorption efficiency 84.5 % for Cd(II) and 89.9 % for Pb(II)). Unlike in the case of water, the efficiency of desorption realized using HCl decreased with increasing concentration of the model metal ion solution. In the case of both desorption agents, a slightly higher desorption efficiency was noted for lead(II). This fact proves the high stability of interactions between metal ions and the adsorbent surface, and indicates the possibility of adsorbent regeneration.

Table 2 Efficiency of desorption of analyzed metal ions using water and chloric acid (desorption time 60 min)
Full size table

3.4 Sorption kinetics

Based on literature reports appropriate kinetic models were used for precise design of the adsorption process. To determine the rate constant of the adsorption process, the equations of Lagergren’s pseudo-first-order kinetic model and Ho’s pseudo-second-order kinetic model were applied.

3.4.1 Pseudo-first-order kinetic model

A linear model of pseudo-first-order adsorption kinetics is defined by Lagergren’s Eq. (5):

$$\log \left( {q_{e} - q_{t} } \right) = \log q_{e} - \frac{{k_{1} }}{2.303} \cdot t$$
(5)

where q e and q t (mg/g) are the quantities of metal ions adsorbed at equilibrium and at time t (min) respectively, and k 1 (1/min) is the rate constant for the pseudo-first-order model. The equilibrium adsorption capacity (q e ) and adsorption rate constant (k 1 ) (Table 3) can be computed experimentally by plotting log(q e  – q t ) against t. A graph of log(q e –q t ) versus t for the pseudo-first-order case is shown in Fig. 6. Table 3 gives the values of the adsorption rate constant (k 1 ) for particular concentrations of selected metal ions, calculated from the gradients in Fig. 6. It was observed that the rate constants of the adsorption processes (k 1 ) for the cadmium(II) ion concentrations studied (25 and 100 mg/L) were 0.10 and 0.11 respectively, while for lead(II) ions the values were 0.54 and 0.28. The correlation coefficient is found to increase with a rise in the concentration of the metal ions. It was confirmed that the pseudo-first-order kinetic model well describes the adsorption of lead ions on MgO–SiO2 adsorbent. However, the results for adsorption capacity (q e,cal ) obtained based on the pseudo-first-order kinetic model calculations deviated significantly from the values of the experimental capacities (q e,exp ). Much better results were obtained using the pseudo-second-order kinetic model, which is a confirmation of previously published results (Guo et al. 2014; Boroumand Jazi et al. 2014). Adsorption of cadmium and lead ions on both natural (chitosan, modified lingo-cellulosic material) and synthetic (grafted silica and silicates) adsorbents is described extremely well by a pseudo-second-order kinetic model.

Table 3 Pseudo-first and pseudo-second-order kinetic parameters obtained by using the linear methods at different cadmium(II) and lead(II) ions concentration
Full size table
Fig. 6
figure 6

Pseudo-first-order kinetic fit for adsorption of cadmium(II) and lead(II) ions on synthesized oxide adsorbent (Color figure online)

Full size image

3.4.2 Pseudo-second-order kinetic model

A linear model of pseudo-second-order adsorption kinetics is defined by Eq. (6):

$$\frac{t}{{q_{t} }} = \frac{1}{{k_{2} \cdot q_{e}^{2} }} + \frac{1}{{q_{e} }} \cdot t$$
(6)

where k 2 (g/mg min) is the rate constant for the pseudo-second-order rate equation, and q e and q t are the quantities (mg/g) of cadmium(II) ions adsorbed at equilibrium and at time t (min) respectively.

The initial adsorption rate h (g/mg min) is defined as follows:

$$h = k_{2} \cdot q_{e}^{2}$$
(7)

The values k 2 and q e may be determined from the gradient and intercept respectively of the plot of t/qt versus t. This relationship can be classed as a type 1 pseudo-second-order kinetic model. There are other subtypes of pseudo-second-order model which can also be used to compute the values k 2 and q e .

By plotting the above curves (Fig. 7) it is possible to estimate the model value of the concentration of analyzed metal ions on the adsorbent surface, and the rate constants (k 2) for saturation of the sorption capacity of the MgO–SiO2 oxide system (Table 3).

Fig. 7
figure 7

Pseudo-second-order kinetic fit for adsorption of cadmium(II) and lead(II) ions on oxide adsorbent: a type 1, b type 2, c type 3 and d type 4 (Color figure online)

Full size image

The kinetics of the adsorption of cadmium(II) and lead(II) ions from model solutions with concentrations of 25 and 100 mg/L on an inorganic oxide adsorbent are very well described by the first type of pseudo-second-order kinetic model. This is confirmed by the high value of the correlation coefficient (r 2), which reached 1.000 (Table 3) for initial cadmium(II) and lead(II) ion concentrations of 100 mg/L. A decrease in the rate constant of the adsorption process (k 2) was observed as the initial concentration of cadmium(II) ions increased, although it increased as the initial concentration of lead(II) ions increased. The adsorption capacity (q e , cal ) obtained from the type 1 pseudo-second-order kinetic equation corresponded well with the experimental capacities (q e,exp ). The parameters obtained indicate the possibility of using a type 1 pseudo-second-order model for predicting the kinetics of cadmium and lead ion adsorption on MgO–SiO2 oxide adsorbent.

For subsequent types (2–3) of pseudo-second-order kinetic models (Fig. 7; Table 3) the adsorption capacities (q e,cal ) calculated based on the selected type of kinetic model correspond closely to the experimental capacities (q e,exp ) for both Cd(II) and Pb(II) ions. With increasing concentration of metal ions, a decrease in the adsorption rate constant (k 2) and an increase in the value q e,exp were observed. It should be noted that the correlation coefficient lies in the range 0.895–0.979, which confirms a significant variance fit of the experimental data to the applied type 2 and 3 pseudo-second-order kinetic models.

For a type 4 pseudo-second-order kinetic model (Fig. 7d; Table 3) unfavorable results were obtained. The correlation coefficient was in the range 0.933–0.977 in the case of cadmium(II) ions and 0.890–0.946 for lead(II) ions. This confirms the mediocre fit of the experimental results to the applied type 4 kinetic model.

The evaluation of adsorption isotherms was a key goal of the research. Two most popular models of isotherms, Langmuir (1918) and Freundlich (1906), were used for this purpose. The results make it possible to determine the sorption capacities of the materials used and to identify the mechanism of adsorption.

Linear form of Langmuir equation is presented below:

$$\frac{{C_{e} }}{{q_{e} }} = \frac{1}{{b \cdot q_{m} }} + \frac{{C_{e} }}{{q_{m} }}$$
(8)

where C e is the equilibrium concentration of metal ions (mg/L), q e is the quantity of metal ions adsorbed per unit mass of adsorbent (mg/g), and q m (mg/g) and b (L/mg)·(L/g) are the Langmuir constants representing the maximum adsorption capacity. Mentioned parameters were estimated from graphical interpretation of C e /q e versus C e dependence (Fig. 8a).

Fig. 8
figure 8

Freundlich and Langmuir isotherm fit for adsorption of metal ions onto sol–gel derived oxide adsorbent (Color figure online)

Full size image

The linear form of the Freundlich model is given by:

$$\log q_{e} = \log K_{F} + \log C_{e}^{{\frac{1}{n}}}$$
(9)

where K F (mg/g) and n are the Freundlich constants. Values of K f and n are calculated based on log(q e ) versus log(C e ) dependence (Fig. 8b).

Figure 8 presents parameters of Freundlich and Langmuir models. Experimental data concerning adsorption of cadmium(II) and lead(II) ions onto sol–gel derived MgO–SiO2 adsorbent are better described with Langmuir isotherm model. Confirmation of this fact is relative high value of coefficient factor (r 2 = 0.992 and 0.983) and smaller λ2 values (1.19 and 1.98). In this case, adsorption may occur inside the pores as confirmed by experimental data fit to the specific model.

Maximal sorption capacity of sol–gel derived adsorbent towards cadmium(II) and lead(II) ions equals 94.05 and 102.02 mg/g respectively. The comparison of maximum monolayer adsorption capacity of Cd2+ and Pb2+ ions onto different, synthetic adsorbents is presented in Table 4.

Table 4 Adsorption capacities of different adsorbents towards removal of Cd(II) and Pb(II) ions
Full size table

As compared to sorption capacities of other materials, synthesis of MgO–SiO2 adsorbent via sol–gel route and its application in adsorption of analysed metal ions was reasoned. Material with high affinity towards removal of cadmium(II) and lead(II) ions form water solutions was obtained.

Application of Freundlich isotherm model allowed to obtain coefficient factor (r 2) 0.978 and 0.964 for adsorption of Cd2+ and Pb2+ ions respectively. It is definitely lower than this obtained applying Langmuir isotherm model. The λ2 value of 2.98 and 11.87 is also higher. Additionally, the n values were higher than 1, which prove a proper course of adsorption process and its physical nature.

4 Conclusions

Comprehensive analysis of the experimental data proved the high efficiency of sol–gel-derived MgO–SiO2 oxide adsorbent in the removal of both cadmium(II) and lead(II) ions from model aqueous solutions. This fact is indirectly related to the proposed method of its synthesis, which makes it possible to control the porous structure parameters of such oxide adsorbents (ABET = 612 m2/g, Vp = 1.20 mL/g, Sp = 10.8 nm). Additionally, it was confirmed that the adsorption process was highly dependent on the contact time of the reactants, the metal ion concentration, the adsorbent dosage, and particularly the pH.

Efficiency of adsorption of Cd(II) and Pb(II) ions on the inorganic oxide adsorbent increased with increasing time. For selected concentrations of metal ion solution, adsorption equilibrium was established after 10 min in the case of lead(II) and after 15 min for cadmium(II) ions, and 60 min was the time after which the maximum efficiency of adsorption was obtained. On the other hand, increasing the concentration of both model metal ion solutions caused a significant decrease in the effectiveness of ion removal. Moreover, as expected, it was found that increasing the mass of oxide adsorbent caused an increase in the effectiveness of removal of Cd(II) and Pb(II) ions. This is related to the increasing quantity of active sites present on the oxide adsorbent surface that can easily react with metal ions. Lead(II) ions exhibit much better affinity to the adsorbent surface, irrespective of the process conditions.

The pH of the model metal ion solution was found to be the most important factor influencing the effectiveness of the adsorption process. The lowest efficiencies, for both cadmium(II) and lead(II) ions, were obtained in an acidic environment, and with increasing alkalinity of the reaction system the adsorption affinity of MgO–SiO2 for metal ions increased. This was confirmed by an evaluation of electrokinetic stability, which proved the significant role of pH in determining the surface properties of such oxide adsorbents.

The possibility of adsorbent regeneration was confirmed by desorption tests, particularly when hydrochloric acid solution was used.

Additional kinetic studies confirmed that the results for adsorption capacity (q e,cal ) obtained based on the pseudo-first-order kinetic model calculations deviated significantly from the values of the experimental capacities (q e,exp ). Much better results were obtained using the pseudo-second-order kinetic model. Moreover, material exhibit high affinity towards removal of cadmium(II) and lead(II) ions form water solutions as confirmed by relative high values of sorption capacities, 94.05 and 102.02 mg/g respectively.

The experimental data collected and relationships established, as well as the analysis of kinetic models of the adsorption process, indicate the successful removal of both metal ions from model solutions utilizing MgO–SiO2 oxide adsorbent.