Abstract
We discuss the thermodynamics of physical adsorption of gases in porous solids. The measurement of the amount of gas adsorbed in a solid requires specialized volumetric and gravimetric techniques based upon the concept of the surface excess. Excess adsorption isotherms provide thermodynamic information about the gas-solid system but are difficult to interpret at high pressure because of peculiarities such as intersecting isotherms. Quantities such as pore density and heats of adsorption are undefined for excess isotherms at high pressure. These difficulties vanish when excess isotherms are converted to absolute adsorption. Using the proper definitions, the special features of adsorption can be incorporated into a rigorous framework of solution thermodynamics. Practical applications including mixed-gas equilibria, equations for adsorption isotherms, and methods for calculating thermodynamic properties are covered. The primary limitations of the absolute adsorption formalism arise from the need to estimate pore volumes and in the application to systems with larger mesopores or macropores at high bulk pressures and temperatures where the thermodynamic properties may be dominated by contributions from the bulk fluid. Under these circumstances a rigorous treatment of the thermodynamics requires consideration of the adsorption cell and its contents (bulk gas, porous solid and confined fluid).














Similar content being viewed by others
Notes
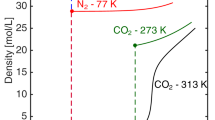
High pressure is defined as greater than 10 bar and low pressure is defined as less than 10 bar. The value of 10 bar is somewhat arbitrary and depends upon the gas and the temperature. See Sect. 2.3.1 where the difference between excess and absolute adsorption is related to the bulk density.
Abbreviations
- A, B, C:
-
Constants in Eq. (5.30)
- C i :
-
Power series coefficients for grand potential, Eq. (10.4)
- D i :
-
Power series coefficients for energy, Eq. (10.5)
- f :
-
Fugacity of gas, Pa
- f°:
-
Fugacity in perfect-gas reference state (=1 bar)
- f :
-
Molar integral Helmholtz free energy, J/mol
- f°:
-
Molar Helmholtz free energy in perfect-gas state, J/mol
- f E :
-
Excess Helmholtz free energy for nonideal solution, Eq. (5.18), J/mol
- f Eγ :
-
Excess Helmholtz free energy for activity coefficients, Eq. (5.5), J/mol
- F :
-
Helmholtz free energy of solid phase, J/kg; J in Sect. 3.3
- G :
-
Gibbs free energy of solid phase, J/kg; J in Sect. 3.3
- \(\mathcal{G}_i^*\) :
-
Standard-state factor for ith component, Eq. (4.23), (kg/mol)2
- h°:
-
Molar enthalpy in perfect-gas state, J/mol
- \(\overline{h}\) :
-
Differential enthalpy, J/mol
- H :
-
Enthalpy of solid phase, J/kg ; J in Sect. 3.3
- k B :
-
Boltzmann constant, \(1.3806 \!\times\! 10^{-23}\) J/K
- K :
-
Henry constant, mol/(kg-Pa)
- \(K_{\circ}\) :
-
Henry constant at ref. temp. \(T_{\circ}\)
- m :
-
Adsorbent capacity, mol/kg, Eq. (10.1)
- m s :
-
Mass of adsorbent, kg
- \(\Updelta m\) :
-
Weighed increase in mass of adsorbent, kg
- m E :
-
“Excess mass” from Eq. (5.6), kg/mol
- M :
-
Molecular weight of gas, kg/mol
- n :
-
Total absolute amount of adsorbate, mol/kg
- n a :
-
Specific absolute adsorption, mol/kg
- n e :
-
Specific excess adsorption, mol/kg
- n i :
-
Absolute amount of ith component, mol/kg; mol in Sect. 3.3
- n n :
-
Specific net adsorption, mol/kg
- n t :
-
Total amount of gas introduced to sample cell, mol
- n He :
-
Amount of He gas used for dead-space calibration, mol
- N :
-
Number of molecules
- P :
-
Pressure in gas phase, Pa
- \(P^{\circ}\) :
-
Reference pressure in perfect gas state, 1 bar
- \(P_{\circ}\) :
-
Pressure for helium calibration, Eq. (2.2), Pa
- q d :
-
Differential heat, J/mol
- q st :
-
Isosteric heat, J/mol
- Q :
-
Canonical partition function
- R :
-
Gas constant, 8.3145 J/(mol K)
- \(s^{\circ}\) :
-
Entropy in perfect-gas state, J/(mol K)
- s :
-
Molar integral entropy of solid phase, J/(mol K)
- \(\overline{s}\) :
-
Differential entropy of gas in solid, J/(mol K)
- S :
-
Entropy of solid phase, J/(kg K); J/K in Sect. 3.3
- \(S_s^{\circ}\) :
-
Entropy of degassed solid under full vacuum, J/(kg K)
- T :
-
Temperature, K
- \(T_{\circ}\) :
-
Reference temperature for Eq. (10.1) or temperature for helium calibration, Eq. (2.2), K
- \(u^{\circ}\) :
-
Molar energy in perfect-gas state, J/mol
- u :
-
Molar integral energy of solid phase, J/mol
- \(\overline{u}\) :
-
Differential energy in solid, J/mol
- U :
-
Energy of solid phase, J/kg; J in Sect. 3.3
- V :
-
Volume of solid phase, m3/kg; m3 in Sect. 3.3
- v p :
-
Specific pore volume, m3/kg
- v s :
-
Specific volume of solid, m3/kg
- v sk :
-
Specific skeletal volume of solid, m3/kg
- V a :
-
Volume of adsorbed phase, m3
- V d :
-
Volume of dead space, m3
- V g :
-
Volume of bulk gas phase, m3
- V p :
-
Pore volume, m3
- V s :
-
Volume of solid, m3
- V sk :
-
Skeletal volume of adsorbent, m3
- V t :
-
Volume of sample cell, m3
- x i :
-
Mole fraction of ith component in pores of solid
- y i :
-
Mole fraction of ith component in gas phase
- z :
-
Molar extensive property (u, s, etc.)
- \(\overline{z}\) :
-
Differential property (\(\overline{u}, \overline{s}\), etc.)
- Z :
-
Specific extensive property (U, S etc.)
- γ i :
-
Activity coefficient of ith component in adsorbed phase
- \(\Upgamma\) :
-
Gibbs excess adsorption per unit area, mol/m2
- μ:
-
Chemical potential, J/mol
- \(\upmu^{\circ}\) :
-
Chemical potential of adsorbate in perfect-gas state, J/mol
- μ s ′:
-
Chemical potential of solid, J/kg
- \(\Upxi\) :
-
Grand canonical partition function
- ρ:
-
Molecular density, m−3, Eq. (1.4)
- ρ g :
-
Molar density of bulk gas, mol/m3
- ρ p :
-
Pore density, mol/m3
- ψ:
-
Reduced grand potential (\(-\Upomega/RT\)), mol/kg
- \(\Upomega\) :
-
Grand potential, J/kg; J in Sect. 3.3
- i :
-
Refers to ith component
- *:
-
Refers to standard state for pure gas at same value of T and \(\Upomega\)
- id :
-
Refers to function for an ideal adsorbed solution
- e:
-
Refers to excess adsorption from liquid mixtures
- E :
-
Refers to excess function for deviation from ideal adsorbed solution
- °:
-
Refers to state of perfect gas
References
Callen, H.B.: Thermodynamics and an Introduction to Thermostatistics, 2nd ed. New York, NY: John Wiley & Sons, Inc. (1985)
Dunne, J.A., Myers, A.L., Kofke, David A.: Simulation of adsorption of liquid mixtures of N2 and O2 in a model faujasite cavity at 77.5 K. Adsorption 2, 41–50 (1996)
Dunne, J.A., Rao, M., Sircar, S., Gorte, R.J., Myers, A.L.: Calorimetric heats of adsorption and adsorption isotherms. 3. Mixtures of CH4 and C2H6 in silicalite and mixtures of CO2 and C2H6 in NaX. Langmuir 13, 4333–4341 (1997)
First, E.L., Gounaris, C.E., Wei, J., Floudas, C.A.: Computational characterization of zeolite porous networks: an automated approach. Phys. Chem. Chem. Phys. 13, 17339–17359 (2011)
First, E.L., Floudas, C.A.: MOFomics: computational pore characterization of metal-organic-frameworks. Microporous Mesoporous Mater. 165, 32–39 (2013)
Gruszkiewicz, M.S., Rother, G., Wesolowski, D.J., Cole, D.R., Wallacher, D.: Direct measurements of pore fluid density by vibrating tube densimetry. Langmuir 28, 5070–5078 (2012)
Gumma, S., Talu, O.: Gibbs dividing surface and helium adsorption. Adsorption 9, 17–28 (2003)
Gumma, S., Talu, O.: Net adsorption: a thermodynamic framework for supercritical gas adsorption and storage in porous solids. Langmuir 26, 17013–17023 (2010)
Hill, T.L.: Theory of physical adsorption. Adv. Catal. 211–258 (1952)
Keller, J.U., Staudt, R., Tomalla, M.: Volumetric-gravimetric measurements of binary gas adsorption equilibria. Berichte der Bunsengesellschaft fur physikalische Chemie 96, 28–32 (1992)
Lowell, S., Shields, J.E., Thomas, M.A., Thommes, M.: Characterization of Porous Solids and Powders: Surface Area, Pore Size, and Density. Springer, New York (2006)
Monson, P.A.: Understanding adsorption/desorption hysteresis for fluids in mesoporous materials using simple molecular models and classical density functional theory. Microporous Mesoporous Mater. 160, 47–66 (2012)
Myers, A.L., Prausnitz, J.M.: Thermodynamics of mixed-gas adsorption. AIChE J. 11, 121–127 (1965)
Myers, A.L., Sircar, S.: A thermodynamic consistency test for adsorption of liquids and vapors on solids. J.Phys.Chem. 76, 3412–3415 (1972)
Myers, A.L.: Activity coefficients of mixtures adsorbed on heterogeneous surfaces. AIChE J. 29, 691–693 (1983)
Myers, A.L.: Gravimetric measurements of adsorption from binary gas mixtures. Pure Appl. Chem. 61, 1949–1953 (1989)
Myers, A.L., Monson, P.: Adsorption in porous materials at high pressure: theory and experiment. Langmuir 18, 10261–10273 (2002)
Myers, A.L.: Prediction of adsorption of nonideal mixtures in nanoporous materials. Adsorption 11, 37–42 (2005)
Rouqerol, J., Rouqerol, F., Sing, K.S.W.: Adsorption by Powders and Porous Solids: Principles, Methodology and Applications. Academic Press, Waltham (1998)
Rowlinson, J.S., Widom, B.: Molecular Theory of Capillarity. Dover, New York (2003)
Ruthven, D.M.: Principles of Adsorption and Adsorption Processes. New York: Wiley, p. 275 (1984)
Salem, M.M.K., Braeuer, P., Szombathely, M.V., Heuchel, M., Harting, P., Quitzsch, K., Jaroniec, M.: Thermodynamics of high-pressure adsorption of argon, nitrogen, and methane on microporous adsorbents. Langmuir 14, 3376–3389 (1998)
Sarkisov, L., Monson, P.A.: Hysteresis in Monte Carlo and molecular dynamics simulations of adsorption in porous materials. Langmuir 16, 9857–9860 (2000)
Sarkisov, L., Monson, P.A.: Modeling of adsorption and desorption in pores of simple geometry using molecular dynamics. Langmuir 17, 7600–7604 (2001)
Sing, K.S.W., Everett, D.H., Haul, R.A.W., Moscou, L., Pierrotti, R.A., Rouquerol, J., Siemienewska, T.: Reporting physisorption data for gas/solid systems with special reference to the determination of surface area and porosity (Recommendations 1984). Pure Appl. Chem. 57, 603–619 (2005)
Siperstein, F.R., Myers, A.L.: Mixed-gas adsorption. AIChE J. 47, 1141–1159 (2001)
Sircar, S.: Excess properties and column dynamics of multicomponent gas adsorption. J. Chem. Soc. Faraday Trans. I 81, 1541–1545 (1985)
Sircar, S., Myers, A.L.: A thermodynamic consistency test for adsorption from binary liquid mixtures on solids. AIChE J. 17, 186–190 (1971)
Sircar, S.: Measurement of gibbsian surface excess. AIChE J. 47, 1169–1176 (2001)
Smith, J.M., Van Ness, H.C., Abbott, M.M.: Introduction to chemical engineering thermodynamics, 5th edn., McGraw-Hill, New York (1996), p 482
Specovius, J., Findenegg, G.H.: Physical adsorption of gases at high pressures: argon and methane onto graphitized carbon black. Berichte der Bunsengesellschaft für Physikalische Chemie 82, 174–180 (1978)
Valenzuela, D.P., Myers, A.L.: Adsorption Equilibrium Data Handbook. Prentice-Hall, Upper Saddle River, pp. 86, 261 (1989)
Vartuli, J.C., Roth, W.J., Leonowicz, M., Kresge, C.T., Schmitt, K.D., Chu, C.T-W., Olson, D.H., Sheppard, E.W., McCullen, S.B., Higgins, J.B., Schlenker, J.L.: A new family of mesoporous molecular sieves prepared with liquid crystal templates. J. Am. Chem. Soc. 114, 10834–10843 (1992)
Vuong, T., Monson, P.A.: Monte carlo simulation studies of heats of adsorption in heterogeneous solids. Langmuir 12, 5425–5432 (1996)
Vyas, R.K., Shashi, K.S.: Determination of micropore volume and surface area of zeolite molecular sieves by D-R and D-A equations: a comparative study. Indian J. Chem. Tech. 11, 704–709 (2004)
Acknowledgment
P. A. M. acknowledges support of this work at the University of Massachusetts by the National Science Foundation (Grant No: CBET-1158790). The authors are grateful to Matthias Thommes for some helpful discussions.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Illustrative calculations based on a mathematical model for absolute adsorption in microporous adsorbents
Complete thermodynamic information on the adsorption of a single gas is provided either by a series of adsorption isotherms, or by a single adsorption isotherm coupled with calorimetric measurement of its differential energy. Equation (10.1) provides a quantitative fit of data for adsorption in microporous materials (see Fig. 15) and is therefore suitable for calculating energy and entropy.
Isotherms for adsorption of pure gases are usually in the form n(P) for loading as a function of pressure. The calculation of thermodynamic properties requires a more general function n(P, T) for loading as a function of both pressure and temperature. It is apparent from Eq. (3.44) that an inverted form more useful for calculating thermodynamic properties would replace the independent variables P and T by n and T, with fugacity as the dependent variable:
For C(n) = 0, D(n) = 0, and f = P, this reduces to the (inverted) Langmuir equation. m is the saturation capacity parameter of the Langmuir equation corresponding to pore filling.
1.1 Henry constant
K is the Henry constant:
and K 0 in Eq. (10.1) is the Henry constant at reference temperature T 0. From Eqs. (10.1) and (10.2):
The Henry constant K decreases exponentially with increasing temperature.
1.2 Energy and entropy properties
The Langmuir equation accounts for molecules adsorbed singly in identical micropores and thus neglects entirely gas-gas interactions and variations in gas-solid interaction energy. The function C(n) in the exponential of Eq. (10.1) is a power series:
The exponential factor e C(n) in the adsorption equation modifies the grand potential by adding a truncated power series to the Langmuir result, as shown in Eq. (10.12). C(n) is dimensionless and its C i coefficients are measured at the reference temperature T 0. This series converges rapidly; typically termination after 3 or 4 coefficients provides quantitative agreement with experiment. Application of Eq. (3.44) to Eq. (10.1) yields the power series D(n) for the differential energy:
D(n), like the differential energy, is negative in sign with units of J/mol. The constant \(D_{\circ}\) is the differential energy at the limit of zero pressure. The assumption that the coefficients C i and D i in the power series are constants is equivalent to neglecting sensible heat in comparison to latent heat for the solid phase over a limited range of temperature. The energy \(\overline{u}\) is relative to h ° in the perfect-gas state at the reference temperature \(T_{\circ}\).
The integral energy from Eq. (3.48) and the differential and integral entropies from Eqs. (3.45) and (3.49) are:
where
C int(n), like C(n), is dimensionless. D int, like D(n), is a negative quantity with units of J/mol. The molar energy u is relative to the perfect-gas enthalpy h ° and the molar entropy s is relative to the perfect-gas entropy \(s^{\circ}\), both at the reference temperature \(T_{\circ}\) in Eq. (10.1). The reference pressure \(P^{\circ}\) = 1 bar in Eqs. (10.7) and (10.8).
1.3 Grand potential
Standard states for mixture equilibria are fixed by the reduced grand potential (ψ), which is obtained by integrating Eq. (3.16):
Substituting for the fugacity f from Eq. (10.1) followed by integration yields:
where the power series for ψ are:
C ψ(n) has units of mol/kg and D ψ(n) has units of J/kg. The domain of ψ is 0 ≤ n < m and the limit at low loading is:
1.4 Slope of adsorption isotherm
The calculation of differential energy or heat of adsorption of individual components of mixtures requires the slope of the adsorption isotherm evaluated at its standard state. From Eq. (10.1), the reciprocal of the dimensionless slope of an adsorption isotherm for a single gas is:
The standard state notation is simplified by writing f * i as f and n * i as n. \(T_{\circ}\) is the reference temperature for the determination of the C i coefficients in Eq. (10.1). The power series for Eq. (10.15) are:
C s (n) is dimensionless and D s (n) has units of J/mol. The limit at zero loading is:
1.5 Example
The first step is to select an isotherm measured at a reference temperature (\(T_{\circ}\)) suitable for extracting the constants m, \(K_{\circ}\), and the C i coefficients. Equation (4.21) written in the form:
exploits the near-linearity of \(\ln f\) versus 1/T at constant n to determine values of the differential energy, which are fit with the D i coefficients. An example is shown in Fig. 15, which compares Eq. (10.1) with adsorption isotherms measured at 25, 50 and 100 °C. The other isotherms at 0, 75, and 125 °C are interpolations and extrapolations.
Having fit the adsorption isotherms with Eq. (10.1), the thermodynamic functions are given by explicit equations. On Fig. 16 are plotted the integral and differential functions calculated from the equations in this Appendix. The functions {S, U, F} are integrals with respect to n of the differential functions \(\{\overline{s}, \overline{u}, \mu\}\). In addition, \(F = U - T S, \mu = \overline{u} - T\overline{s}\), and \((F/ n) = \mu + (\Upomega/n)\).
Properties for adsorption of ethylene on 13X molecular sieve at 298.15 K derived from experimental adsorption isotherms plotted on Fig. 15. Values of energy and entropy relative to perfect-gas state for gases and fully evacuated adsorbent for solid, both at 298.15 K. \(\mu = \overline{u} - T\overline{s}\). \(F = U - TS = \mu n + \Upomega\)
The μ function is the adsorption isotherm at 298.15 K. Equation (10.1) is based upon the simplification that U and S are independent of temperature, an approximation justified for the temperature range of the experimental data on Fig. 15.
All functions are negative in sign. Entropy and free energy functions are undefined at the limit of zero loading. The energy is finite at zero loading corresponding to the energy of a single molecule interacting with the solid. The grand potential \((\Upomega)\) has a finite value (−n R T) at zero loading, where \((\Upomega/n) = -RT = -2.48\) kJ/mol.
Appendix 2: Simultaneous solution of fugacity equations
2.1 Ideal solution
The objective is the solution of the fugacity Eq. (4.16) for ψ and composition x. For an ideal binary mixture with x 2 = (1 − x 1), we seek the simultaneous solution of the pair of fugacity equations at temperature T:
for which the Jacobian is:
The size of the Jacobian is equal to the number of gaseous components. Solution of the linear equations:
gives successive iterations according to Newton’s method:
If the single-gas isotherms obey Eq. (10.1), a suitable first guess is:
K i is the Henry constant for the ith component from Eq. (10.3).
Two pure-component functions are needed: n * i (ψ) (see Appendix 3) and the composite function f * i [n * i (ψ)].
2.2 Activity coefficients
Insertion of activity coefficients into Eq. (11.1) gives:
Using Eqs. (5.31), (5.32) and (5.33), the Jacobian is:
where:
Except for the more complicated form of the Jacobian, Eqs. (11.3)–(11.7) are unchanged.
Appendix 3: Inversion of grand potential function for mixture equilibria
Equation (10.12) is the function ψ(n) for single-gas adsorption but its inverse function is needed to fix the standard state. Define \(\mathcal{P}(n) \equiv \psi(n)\) and find the solution of the function \(\mathcal{H}(n)=0\):
Solve Eq. (12.1) by Newton’s method using:
with
A suitable first guess is n = m(1 − e −ψ/m). ψ increases monotonically with n and the iterative solution for the inverse function n(ψ) converges rapidly. The above notation for n is a simplification for n * i , the standard-state loading of single gas i. ψ and its standard-state properties (f * i , u * i , s * i ) are all explicit functions of n * i .
Rights and permissions
About this article
Cite this article
Myers, A.L., Monson, P.A. Physical adsorption of gases: the case for absolute adsorption as the basis for thermodynamic analysis. Adsorption 20, 591–622 (2014). https://doi.org/10.1007/s10450-014-9604-1
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10450-014-9604-1