Adsorption and desorption kinetics of benzene derivatives on mesoporous carbons

Abstract

Adsorption and desorption of benzoic and salicylic acids and phenol from a series of synthesized mesoporous carbons is measured and analyzed. Equilibrium adsorption isotherms are best described by the Langmuir–Freundlich isotherm. Intraparticle diffusion and McKay’s pore diffusion models, as well as mixed 1,2-order (MOE), integrated Langmuir kinetic equation (IKL), Langmuir–Freundlich kinetic equation and recently derived fractal-like MOE (f-MOE) and IKL models were compared and used to analyze adsorption kinetic data. New generalization of Langmuir kinetics (gIKL), MOE and f-MOE were used to describe desorption kinetics. Analysis of adsorption and desorption half-times shows simple relation to the size of carbon pores.

1 Introduction

Character of solute adsorption on mesoporous materials depends on various factors. For concentrations much below solute saturation concentration main factor becomes energetic heterogeneity, which is partly due to adsorbate properties (e.g. functional groups) and partly to surface properties (e.g. surface groups) and porous structure (Derylo-Marczewska and Jaroniec 1987). Moreover, the effect of porous structure may be also represented as the surface heterogeneity (Jaroniec and Madey 1988). However, the effect of porous structure on adsorption kinetics cannot be treated in the same way as the pore structure and solid particle size strongly affect the time solute requires to enter into the adsorbent granule. What we know now as Langmuir rate equation first appeared in the derivation of Langmuir isotherm equation for gas adsorption (Langmuir 1918). However, it has very general character and is obtained also for other sorption mechanisms (Azizian 2004; Liu and Shen 2008; Navarrete-Guijosa et al. 2003; Plazinski et al. 2009):

$$ \frac{d\theta }{dt} = v_{a} - v_{d} = k_{a} c(1 - \theta ) - k_{d} \theta $$

(1)

$$ \theta_{eq} = \frac{{Kc_{eq} }}{{1 + Kc_{eq} }} $$

(2)

where $\theta = a/a_{m}$ is the relative adsorption coverage by solute, a _m is monolayer capacity (generally, sorption capacity), adsorption rate v _a is proportional to the solute concentration, c, and available adsorbent surface (or surface sites), 1 − θ, whereas the desorption rate v _d is proportional to the amount of adsorbate on the surface, θ, and k _a , k _d are adsorption and desorption rate coefficients, “eq” corresponds to equilibrium conditions (where v _a =  v _d ) and K = k _a /k _d is adsorption equilibrium constant. Adsorbed amount and concentration are bound by the mass balance equation valid in batch conditions $\theta = (c_{o} - c)V/m$, where m is adsorbent mass and V is solution volume.

Langmuir rate Eq. (1) in batch conditions is reduced to the simple second degree polynomial with respect to the coverage θ, however, the obtained analytical solutions (Azizian 2004) were difficult to analyze and approximations led sometimes to overly simplifying conclusions (Azizian 2004; Liu and Shen 2008) e.g. concerning conditions allowing to use second order equation (Ho and McKay 1998). Recently, a simple analytical solution of Eq. (1) for adsorption conditions with initial zero coverage was presented (to avoid ambiguity it is called IKL, Integrated Kinetic Langmuir equation) (Marczewski 2010a, b). IKL was recently extended to include lateral interactions according to regular solution theory and the Kiselev association model as well as energetic heterogeneity (mRSK and LF-mRSK models) (Marczewski 2011). This model was also compared to the classic SRT model, corresponding to the same equilibrium isotherms but developed in opposition to the classic Langmuir kinetics (Ward and Findlay 1982; Zhdanov 2001; Rudzinski and Panczyk 2002a, b; Panczyk 2006; Plazinski et al. 2009). Moreover, a new “fractal-like” “approach” to MOE, IKL and SRT models provided other possible extensions to those equations (Haerifar and Azizian 2012). On the other hand, intraparticle diffusion (IDM) (Crank 1954) and pore diffusion (PDM) (McKay et al. 1996) models describe systems where adsorbate diffusion is the main factor responsible for sorption kinetics (Plazinski et al. 2009). While such models as LF-mRSK (Marczewski 2011), classic SRT (Rudzinski and Panczyk 2000; Plazinski et al. 2009; Podkoscielny and Nieszporek 2011), SRT re-interpretations (Panczyk 2006; Rudzinski and Plazinski 2008) or modifications (Azizian and Bashiri 2008) offer superior level of system description by incorporating various effects, the number of parameters makes them much more susceptible to experimental deviations and may potentially lead to partly supported conclusions. Inappropriate (too narrow) data range may have even more profound effect on data analyses allowing in fact to fit “reasonable well” almost any kind of equation. It is a well known effect, that very similar functions may have quite divergent derivatives and whereas rate profiles da/dt may be quite for various models, their integral counterparts, i.e. a(t) curves may seem vary much alike if observed over a limited data range (Marczewski 2010a, 2011) and the same is true for adsorption isotherms and corresponding adsorption energy distributions (Jaroniec and Madey 1988). Thus only the simpler equations (IKL, MOE, fractal-like MOE as well as IDM and PDM) are used here in kinetic data analysis. Moreover, the simple mathematical apparatus required for their implementation makes them much more likely to be used in practical applications.

2 Theory

2.1 Generalized integrated Langmuir kinetic equation (gIKL)

Generalization of the method used in (Marczewski 2010b) may be used to obtain solution for desorption conditions with initial zero concentration as well as a general solution for all possible initial (“o”) and equilibrium (“eq”) adsorption and desorption conditions. In this method coverage, θ, and concentration, c, are made dependent on the adsorption progress variable, F, varying from 0 (at t = 0) to 1 (at equilibrium, t → ∞):

$$ F = \frac{{c - c_{o} }}{{c_{eq} - c_{o} }} = \frac{{\theta - \theta_{o} }}{{\theta_{eq} - \theta_{o} }} $$

(3)

$$ c = c_{o} + F(c_{eq} - c_{o} )\quad {\text{and}}\quad \theta = \theta_{o} + F(\theta_{eq} - \theta_{o} ) $$

(4)

Despite nonlinear relation (2) between adsorption equilibrium coverage θ _eq and concentration c _eq , Langmuir rate Eq. (1) is essentially second order polynomial with respect to coverage or concentration (4) or adsorption progress (3) (Marczewski 2010b). However, by definition the rate becomes zero at equilibrium, i.e. F = 1 must be one the roots and we may finally write:

$$ \frac{d\theta }{dt} = (\theta_{eq} - \theta_{o} )\frac{dF}{dt}\quad {\text{and}}\quad \frac{dF}{dt} = A(1 - F)(1 - f_{L} F) $$

(5)

Eq. (5) was formulated in the way assuring compatibility with IKL (Marczewski 2010b). After integration (for $f_{L} < 1$) and by using initial conditions (t = 0, F = 0) we obtain equation which has the same form as the IKL obtained for adsorption on pure surfaces ($\theta_{o} = 0$):

$$ \ln \frac{1 - F}{{1 - f_{L} F}} = - k_{L} t\quad {\text{and}}\quad F = \frac{{1 - \exp ( - k_{L} t)}}{{1 - f_{L} \exp ( - k_{L} t)}} $$

(6)

In the above $k_{L} = A/(1 - f_{L} )$ and A > 0 is the initial adsorption/desorption relative progress rate:

$$ A = \left( \frac{dF}{dt} \right)_{F = 0} = k_{a} \frac{{c_{o} \theta_{eq} (1 - \theta_{o} ) - c_{eq} \theta_{o} (1 - \theta_{eq} )}}{{\theta_{eq} (\theta_{eq} - \theta_{o} )}} = k_{d} \frac{{c_{o} \theta_{eq} (1 - \theta_{o} ) - c_{eq} \theta_{o} (1 - \theta_{eq} )}}{{c_{eq} (1 - \theta_{eq} )(\theta_{eq} - \theta_{o} )}} $$

(7)

The rate coefficient k _L (always positive) is:

$$ k_{L} = k_{a} \frac{{c_{o} \theta_{eq} (1 - \theta_{eq} ) - c_{eq} (\theta_{o} - \theta_{eq}^{2} )}}{{(\theta_{eq} - \theta_{o} )\theta_{eq} }} = k_{d} \frac{{c_{eq} (\theta_{o} - \theta_{eq}^{2} ) - c_{o} \theta_{eq} (1 - \theta_{eq} )}}{{(\theta_{o} - \theta_{eq} )(1 - \theta_{eq} )c_{eq} }} $$

(8)

and the generalized Langmuir batch equilibrium factor f _L is:

$$ f_{L} = \frac{{\theta_{eq} (\theta_{eq} - \theta_{o} )(c_{eq} - c_{o} )}}{{c_{eq} \theta_{o} (1 - \theta_{eq} ) - c_{o} \theta_{eq} (1 - \theta_{o} )}} $$

(9)

The generalized Langmuir equilibrium batch factor f _L (9) is negative for desorption conditions ($- 1 \le f_{L} \le 0$) and positive for adsorption conditions, ($0 \le f_{L} < 1$). For adsorption kinetics with no initial coverage, gIKL (6) becomes IKL with Langmuir batch factor $f_{eq} = f_{L} = u_{eq} \theta_{eq}$, i.e. product of equilibrium coverage and equilibrium uptake $u_{eq} = (1 - c_{eq} /c_{o} )$. We may also denote gIKL for desorption with zero initial concentration as desorption IKL (dIKL) where $f_{L} = - (\theta_{eq} /\theta_{o} )(\theta_{o} - \theta_{eq} )/(1 - \theta_{eq} )$ and $k_{L} = k_{a} (c_{eq} /\theta_{eq} )(\theta_{o} - \theta_{eq}^{2} )/(\theta_{o} - \theta_{eq} )$.

However, if f _L  = 1 the second order kinetic equation, SO/PSO (Ho and McKay 1998) must be used instead of gIKL Eq. (6) (for Langmuir kinetics it is possible only if $c_{eq} \to 0$, $\theta_{eq} \to 1$, $ma_{m} = Vc_{o}$ and $K = k_{a} /k_{d} > > 1$; Marczewski 2010a, b). Adsorption progress for the SO/PSO may be then expressed as:

$$ F = \frac{{k_{2} t}}{{1 + k_{2} t}} $$

(10)

where $k_{2} = k_{a} c_{o} /\theta_{eq} \approx k_{a} c_{o}$ is the composite rate coefficient.

Most important properties of Langmuir kinetics are shown in Fig. 1 as the dependence of the (scaled) relative adsorption or desorption progress rate (it is identical to the relative adsorption/desorption rate, $(d\theta /dt)/(d\theta /dt)_{ini}$). As we can see, the relative adsorption rate for adsorption (f _L  > 0) decays quite fast and for moderate and high adsorption progress becomes quite low, i.e. the last stage of adsorption becomes quite slow. Quite differently in desorption, the rate changes initially slower and remains high, but for high progress values falls down quickly to zero.

Fig. 1

Dependence of (scaled) relative adsorption/desorption progress rate (or relative adsorption/desorption rate) on adsorption/desorption progress, F, for gIKL Eqs. (5, 6)

For any experiment “ns” with the non-standard initial conditions (θ _o  > 0 for adsorption and c _o  > 0 for desorption) we can always find such a corresponding standard experiment “s” (with θ _o  = 0 for adsorption and c _o  = 0 for desorption), that “ns” kinetics is a part of “s” kinetics. It may be shown (see the flying start technique in the Online Resource) that for such a pair of experiments the contribution of second order term (expressed as $\left| {f_{L} } \right|$) in “ns” is smaller than for “s”. The only exceptions are SO/PSO (i.e. f _L  = 1) and FO/PFO (i.e. f _L  = 0) where f _L remains constant. The same technique may be used to extend any kinetic equation insensitive to system history to non-standard initial conditions, e.g. mRSK, LF-mRSK, SRT, various empirical equations etc., however, it cannot be used for diffusion models.

In practical applications adsorption and desorption halftimes (time to F = 0.5) are useful parameters, especially for comparisons of materials or solutes.

$$ t_{1/2} = \left\{ {\begin{array}{ll} {\ln (2 - f_{L} )/k_{L} } & {{\text{if }}f_{L} < 1} \\ {1/k_{2} } & {{\text{if }}f_{L} = 1} \\ \end{array} } \right. $$

(11)

If the equilibrium concentration is close to 0 (for adsorption) or the adsorbate is almost completely released in desorption experiment, then the halftime may be determined directly from the data and becomes independent of the model used for fitting. It may be used e.g. for plotting and comparing the data in reduced time coordinates, e.g. concentration or adsorption versus reduced time, τ = t/t _1/2 (see Fig. 2 left) or versus half-log time scale ln(1 + τ) (half-log time plot) or concentration or adsorption versus τ/(1 + τ) (compact time plot) which produces straight line for SO/PSO kinetics (Marczewski 2011). The initial rate in the reduced time co-ordinates for gIKL may be expressed as $F = \tau \ln (2 - f_{L} )/(1 - f_{L} )$ and $F = \tau$ for SO/PSO.

Fig. 2

Adsorption/desorption progress, F, versus reduced time, τ = t/t _1/2 for gIKL Eq. (6) (the dashed lines correspond to the initial rates (left). Adsorption/desorption progress, F, for gIKL Eq. (6) shown in the compact time plot (right)

Initial part of adsorption/desorption kinetics presented in the reduced time plot F(τ) is compared with the initial rates (shown as dashed lines, F = τ, $\tau (\ln 2)$, $\tau (\tfrac{1}{2}\ln 3)$ for f _L  = 1, 0, −1, respectively). We may see that the desorption plot for f _L  = −1 is almost linear, whereas the plot for SO/PSO adsorption (f _L  = 1, least effect of desorption term) deviates from the initial rate very strongly. In the compact time plot for gIKL also shown in Fig. 2 (right) we can see comparison of the entire kinetic curves. For the same value of halftime and for contact time shorter than t _1/2 (i.e. τ < 1) adsorption progress is the highest (fastest adsorption) for SO/PSO, lower for FO/PFO and the lowest for desorption with f _L  = −1, however, this order is reversed if we compare kinetic curves above halftime (see also Figs. S1, S2 in the Online Resource).

2.2 Mixed-order kinetic equation

As the systems with purely Langmuirian adsorption equilibrium (no lateral interaction and no surface heterogeneity) are rare, we may expect that systems following Langmuir kinetics will be even less common. However, even systems that are quite well described by advanced models including lateral interactions and energetic heterogeneity effects, may be reasonably well fitted with IKL (Marczewski 2011). Moreover, it is well known, that many experimental systems follow quite well first order (FO/PFO) or second order kinetics (SO/PSO) (Plazinski et al. 2009; Castillejos and Rodríguez-Ramos 2011). Recently a generalization of those two empirical equations, mixed 1,2-order kinetic equation (MOE) was presented (Marczewski 2010a) and applied to adsorption of organics on mesoporous carbons. MOE is essentially IKL and gIKL (6), where the controlling parameter f ₂  = f _L is not directly related to the parameters of equilibrium isotherm but denotes the contribution of second order term to the entire kinetic behavior. Hence we may write MOE in its differential and integrated forms:

$$ \frac{dF}{dt} = (1 - f_{2} )(1 - F) + f_{2} (1 - F)^{2} $$

(12)

$$ \ln \frac{1 - F}{{1 - f_{2} F}} = - k_{1} t\quad {\text{and}}\quad F = \frac{{1 - \exp ( - k_{1} t)}}{{1 - f_{2} \exp ( - k_{1} t)}} $$

(13)

where $- 1 \le f_{2} < 1$, i.e. f ₂ may be both positive (typical adsorption behaviors like in the original MOE) and negative (typically for desorption).

As for gIKL the initial rate is $F = \tau \ln (2 - f_{2} )/(1 - f_{2} )$ for f ₂  < 1 and $F = \tau$ for SO/PSO (f ₂  = 1). Both for MOE and gIKL negative value of f ₂ or f _L (desorption) means that the rate initially will decay slower (kinetic curve will be more linear than the simple exponent for FO/PFO) but closer to the equilibrium the rate will quickly decrease, though it will remain quite significant if compared with FO and SO (see Fig. 2). However, f ₂ may be also lower than −1—though it is impossible within the pure Langmuir kinetic model. Such parameter value corresponds to a maximum on the rate profile dF/dt and an inflection point on the kinetic curve F(t) at $F = \tfrac{1}{2}(1 + f_{2} )/f_{2}$ (e.g. at F = 0.25 for f ₂  = −2) and the rate dF/dt becomes equal to the initial value at $F = (1 + f_{2} )/f_{2}$ (see Fig. 3). Such behaviors may appear e.g. for adsorption systems where lateral interactions (possibly with energetic heterogeneity effects) are important (Marczewski 2011).

Fig. 3

Adsorption/desorption rate profiles (left) and adsorption/desorption progress, F, versus reduced time, τ = t/t _1/2 for the modified MOE Eqs. (12, 13). The dashed lines correspond to the initial rates

2.3 Adsorption kinetics in non-ideal systems

Adsorption kinetics in non-ideal systems may be described by LF-mRSK model (Marczewski 2011) including energetic heterogeneity and lateral interactions. However, let us assume, that the lateral interactions do not play important role in the systems or are countered by the strong heterogeneity effects (so such effects partially cancel-out) and the adsorption equilibrium is described by the Langmuir–Freundlich (LF) isotherm:

$$ \theta_{eq} = \frac{{(Kc_{eq} )^{n} }}{{1 + (Kc_{eq} )^{n} }} $$

(14)

where 0 < n ≤ 1 is heterogeneity parameter.

Then the LF-kinetics may be represented by simple equations:

$$ \frac{d\theta }{dt} = v_{a} - v_{d} = k_{a} c(1 - \theta )^{1/n} - k_{d} \theta^{1/n} $$

(15)

$$ \left( \frac{dF}{dt} \right)_{rel} = (1 - u_{eq} F)[1 - \theta_{eq} F]^{1/n} - (1 - u_{eq} )(1 - \theta_{eq} )^{1/n} F^{1/n} $$

(16)

where the relative rate $(dF/dt)_{rel} = (d\theta /dt)/(d\theta /dt)_{ini}$ is calculated for the adsorption kinetics.

Depending on the combination of relative uptake u _eq and equilibrium coverage θ _eq as well as value of heterogeneity parameter various deviations from the IKL behavior are obtained. The most extreme deviations from IKL are obtained for θ _eq  = 0 (upward deviations) and 1 (downward deviations) with uptake affecting behavior to the lesser extent. However, when θ _eq  = 0 and u _eq  = 1 first order behavior is obtained. Model calculations for this model are presented in Fig. 4.

Fig. 4

Relative rate profiles for the LF adsorption kinetics (14–16)

By comparing gIKL and MOE rate profiles with results obtained for LF kinetics we may see, that even in the absence of lateral interactions it is difficult to distinguish kinetics on homogeneous and heterogeneous surface. Large range of both upward and downward deviations from profile linearity (i.e. FOE) may be explained by the LF-type heterogeneity or by gIKL/MOE (for homogeneous surfaces), especially for moderate values of n. Moreover, in certain conditions LF-type heterogeneity leads to pure FOE behavior. Thus it is extremely difficult to distinguish various kinetic effects by analysis of small sets of experimental data.

2.4 Fractal-like kinetic model

Recently, several new equations describing fractal-like adsorption model (Haerifar and Azizian 2012) were presented. Those equations were derived from IKL and empirical MOE as well as from SRT model by using fractal approach to kinetics (Brouers and Sotolongo-Costa 2006) introduced in order to account for complexity of adsorption systems but earlier developed by Erofeev co-workers as KEKAM theory (Avrami 1939). In this paper only fractal-like MOE (f-MOE) will be used:

$$ \ln \frac{1 - F}{{1 - f_{2} F}} = - (k_{1} t)^{p} \quad {\text{and}}\quad F = \frac{{1 - \exp ( - (k_{1} t)^{p} )}}{{1 - f_{2} \exp ( - (k_{1} t)^{p} )}}\quad {\text{if}}\,f_{2} < 1 $$

(17)

$$ F = \frac{{(k_{2} t)^{p} }}{{1 + (k_{2} t)^{p} }}\quad f_2=1 $$

(18)

where p is fractal coefficient, usually not much deviating from 1.

If we take into account the extension of IKL (6) and MOE (12, 13) to desorption, the equation form remains the same, however, f ₂ may be also negative.

This equation allows to calculate easily the adsorption or desorption half-time useful for data presentation and evaluation:

$$ t_{1/2} = \left\{ {\begin{array}{ll} {\ln (2 - f_{2} )^{1/p} /k_{1} } & {{\text{if }}f_{2} < 1} \\ {1/k_{2} } & {{\text{if }}f_{2} = 1} \\ \end{array} } \right. $$

(19)

2.5 Diffusion models

Above described models include diffusion indirectly, by assuming that its effect is similar for all adsorption sites, which may be true for strongly adsorbing molecules in wide pores. However, if the diffusion is the rate-governing phenomenon, its effect may replace the typical adsorption-related kinetics.

2.5.1 Intraparticle diffusion model (IDM)

Sorption in porous granules is often described by the classic Crank formulas corresponding to diffusion into the spherical particle (Crank 1954). If the adsorbate concentration in solution remains constant, we obtain:

$$ F = 1 - \frac{6}{{\pi^{2} }}\sum\limits_{n = 1}^{\infty } {\frac{1}{{n^{2} }}\exp ( - \pi^{2} n^{2} D_{a} t/r^{2} )} $$

(20)

where r is adsorbent particle radius and D _a is the effective diffusion coefficient:

$$ D_{a} = \frac{D}{{\tau_{p} (1 + \rho K_{H} \varepsilon_{p} )}} $$

(21)

where D is the molecular diffusion coefficient, τ _p is the dimensionless pore tortuosity factor, ρ is particle density, ε _p is particle porosity and K _H is Henry adsorption constant.

However, when the concentration of adsorbate is varying, then:

$$ F = 1 - 6(1 - u_{eq} )\sum\limits_{n = 1}^{\infty } {\frac{{\exp ( - p_{n}^{2} Dt/r^{2} )}}{{9u_{eq} + (1 - u_{eq} )^{2} p_{n}^{2} }}} $$

(22)

where p _n are non-zero roots of equation $\tan p_{n} = 3p_{n} /[3 + (1/u_{eq} - 1)p_{n}^{2} ]$.

Unluckily, those solutions correspond to non-converging series and other approximations must be used to obtain practical applications (Reichenberg 1953; Carman and Haul 1954). However, the most accurate calculations for the widest possible range of parameters may be performed by combining of the recent approximation by Haynes and Lucas (2007) and series approximations.

It may be shown (see Fig. 5), that the initial part of IDM (F ≪ 1) is always linear function of square root of time (for u _eq  = 0 derived by Boyd et al. 1947, known also as Weber-Morris kinetics, WM):

$$ F \approx (6/\pi^{1/2} )(1 - u_{eq} )(D_{a} t/r^{2} )^{1/2} $$

(23)

$$ c_{o} - c \approx (6/\pi^{1/2} )c_{o} u_{eq} (1 - u_{eq} )(D_{a} t/r^{2} )^{1/2} $$

(24)

Fig. 5

Adsorption kinetics in intraparticle diffusion model IDM (20)–(22) in reduced time-scale. Asymptotic line calculated by (23)

This relation allows us to verify the validity of IDM application when a series of sorption experiments is performed with varying mass, solution volume and adsorbate concentration—if we obtain linearity but the obtained slopes of F versus t ^1/2 do not agree across various experiments (i.e. varying D _a /r ²), it means that the process cannot be represented by this simple IDM model. While near the equilibrium IDM behavior is similar to the FOE/PFOE (asymptotic solution is known as the Boyd equation: Boyd et al. 1947), its initial adsorption rate is infinite (dF/dt ~ 1/t ^1/2). Such initial behavior is similar to the SRT, which is based on Langmuir isotherm, but uses a different kinetic equation (Rudzinski and Panczyk 2000, 2002a, b; Marczewski 2011) (please note, that re-interpretations of the classic SRT may avoid initial infinite rates, see e.g. Panczyk 2006). It is also the main difference with respect to all the equations derived from the classic kinetic Langmuir equation.

However, one also has to keep in mind, that IDM Eqs. (20)–(22) may likely fail when adsorbate concentrations are not low enough either system shows high energetic heterogeneity and adsorption phenomenon cannot be described by the Henry isotherm. Moreover, those relatively simple equations are valid only for adsorption on initially pure solids.

2.5.2 Pore diffusion model (PDM)

Another simple model describing sorption in porous solids, uses the so-called shrinking core approach (McKay et al. 1996; Castillejos and Rodríguez-Ramos 2011), with additional resistance for molecules passing from solution into the granule. The rate defined by the shrinking core approach in the reduced (dimensionless) time-scale τ _s is:

$$ \frac{dF}{{d\tau_{s} }} = \frac{{3(1 - u_{eq} F)(1 - F)^{1/3} }}{{1 - B(1 - F)^{1/3} }} $$

(25)

where adsorbate uptake u _eq is identical to the model’s capacity factor C_h, parameters B = 1 − 1/Bi, where Bi = K _f r/D _p is Biot number, D _p is pore diffusion coefficient, and K _f is external mass transfer coefficient.

Hence we obtain integrated form of McKay’s PDM equation:

$$ \tau_{s} = \frac{1}{{6u_{eq} }}\left\{ {\left( {2B - \frac{1}{X}} \right)\ln \left[ {\left| {\frac{{x^{3} + X^{3} }}{{1 + X^{3} }}} \right|} \right] + \frac{3}{a}\ln \left[ {\left| {\frac{x + X}{1 + X}} \right|} \right]} \right\} + \frac{1}{{X\sqrt 3 u_{eq} }}\left\{ {\arctan \left( {\frac{2 - X}{X\sqrt 3 }} \right) - \arctan \left( {\frac{2x - X}{X\sqrt 3 }} \right)} \right\} $$

(26)

where $x = (1 - F)^{1/3}$, $X = (1/u_{eq} - 1)^{1/3}$, $x^{3} + X^{3} = 1/u_{eq} - F$ and $1 + X^{3} = 1/u_{eq}$.

Owing to the shrinking core approach we obtain simple analytical equation, however, the side effect is the finite time to equilibrium, $\tau_{s,eq} = \tau_{s} (F = 1,B,u_{eq} )$.

The reduced experiment time, may be then calculated as $\tau = t/t_{1/2} = \tau_{s} /\tau_{s1/2}$, where ½ index denotes value at F = 0.5 and finally we obtain the experimental time $t(F) = t_{1/2} \cdot [\tau_{s} (F)/\tau_{s} (0.5)]$.

Relative rate profiles for McKay’s PDM equation (Fig. 6) show that unlike the classic IDM (Fig. 5) this equation displays finite initial rate, similarly to solutions of the Langmuir kinetic equation (but unlike the classic SRT model). However, profile shapes for PDM are mostly different than those characteristic for gIKL/MOE (Figs. 1–3) and LF-mRSK (Fig. 4), though it may be difficult to distinguish those models if the experimental data range is not sufficiently large.

Fig. 6

Relative rate profiles for McKay’s PDM (26) for constant uptake and varying Biot number (top), constant Biot number and varying uptake (bottom)

3 Results and discussion

3.1 Experimental

3.1.1 Carbon synthesis and properties

In order to verify applicability of kinetic models and equations, the experimental equilibrium and kinetic data of adsorption and desorption of benzoic acid (BA), salicylic acid (SA) and phenol (Ph) on 3 divergent mesoporous carbons W84, W85 and W87 are analyzed. Carbons were synthesized by carbonization of as-synthesized mesoporous silicas prepared with polymeric templates Pluronic PE9400 (for W85) and PE6400 (for W84 and W87) from BASF (see Table 1) in 1.6 M HCl solution by using modification of the known methods (Zhao et al. 1998; Kim et al. 2004; Derylo-Marczewska et al. 2008; Marczewski et al. 2009). Tetraethylorthosilicate (TEOS) and phenyl-triethylorthosilicate (Ph-TEOS) in 14:3 mass proportion were used as silica source and 1,3,5-trimethylbenzene (TMB) was used as pore expander. The silica ageing process was performed at 343 (W84), 373 (W87) and 393 K (W95) for 24 h. After washing and drying the as-synthesized silica, direct method of carbon synthesis was used with soft template material used as carbon source (Kim et al. 2004). Carbonization was performed with H₂SO₄ in 3 steps, first in the vacuum dryer for 12 h at 373 K and 12 h at 433 K, followed by 6 h in nitrogen atmosphere at 1,073 K. The silica skeleton was etched with NaOH (see more synthesis details in the Online Resource).

Table 1 Carbon synthesis parameters

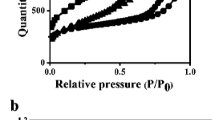
Carbon properties obtained by using nitrogen adsorption isotherms and standard calculation methods (ASAP 2405 sorption analyzer, Micromeritics Corp.) are summarized in Table 2. Nitrogen adsorption/desorption isotherms, alpha-s plots and pore size distributions (PSD) are presented in Fig. 7. Micropore volumes V _mic were determined by using standard t-plot method and total pore volumes V _t were calculated at relative pressure p/p_s = 0.98. However, primary pore volumes V _p (micro- and mesopores) and external surface areas S _ext were obtained by using alpha-s method (Fig. 7) with standard adsorption isotherm of nitrogen on carbon black Cabot BP 280 (Kruk et al. 1997). The differences between “hydraulic” pore sizes (calculated as D_h = 4V_t/S_BET) and mesopore sizes reflect micropore contribution, however, differences between sizes obtained from adsorption and desorption isotherm branches (D_d ≤ D_a) indicate narrowing of pore openings or internal pore constrictions. Moreover, analysis of PSDs shows certain bimodality for W85 and W87 (local peak at 4 nm) with large contribution of pores near and below 2 nm (especially for W85 which contains over 25 % of micropores, whereas W87 has 15 % and W84 1.5 % of micropores). However, W84 has the largest total and mesopore volumes as well as the largest specific BET and external areas, which seem to make it most suitable for relatively large adsorption and fast kinetics, although we must remember, that micropores may likely adsorb stronger than mesopores.

Table 2 Carbon properties: specific surface area, S_BET, external surface area, S_ext, total pore volume, V_p, primary pore volume, V_t, micropore volume, V_mic, mesopore size determined from adsorption and desorption (D_a, D_d) by BJH method and average hydraulic pore size D_h

Fig. 7

Nitrogen adsorption/desorption isotherms, alpha-s plots and pore size distributions (BJH method from desorption branch) for carbons W84, W85, W87

3.1.2 Adsorption from solution—equilibrium isotherms

Benzoic acid (BA), salicylic acid (SA) and phenol (Ph) were used as adsorbates. They are relatively similar acidic molecules with different solubilities and pK_a (Table 3) which are in molecular form at pH = 2. Before adsorption experiments the carbon samples were immersed in 5 ml of water and degassed under vacuum for 15 min to make all pores accessible for liquid and avoid flotation of granules (sieved to 0.1–0.5 mm). Equilibrium data was measured by cyclic increments of solute concentration for a single carbon sample (0.05 g/35 ml) at pH = 2 in a shaker bath (298 K). Every 48 h 2.5 ml samples of solution were collected and UV/Vis spectra were analyzed (Cary 100 spectrophotometer, Varian Inc., equipped with a 10 mm quartz flow cell and RSA accessory was used in all measurements). Necessary increase of concentration was calculated and appropriate amount of acidified stock solution and HCl (pH = 2) was added to keep volume and solid/liquid ratio constant.

Table 3 Properties of adsorbates, molecular weight, M _w , density, d, molar volume, pK _a and solubility, c _s . at 298 K. Benzene is shown for comparison (s: solid at 277 K)

Freundlich, Langmuir (2) and Langmuir–Freundlich (LF) isotherm Eq. (14) were used to fit the data, however, the data was not linear in log–log Freundlich plot and LF isotherm was found to represent the data most closely (see Fig. 8 and Table 4).

Fig. 8

Adsorption isotherms of BA, SA and Ph at pH = 2 on W84, W85 and W87 carbons

Table 4 Fitting parameters for LF isotherm (14) and adsorption of BA, SA and Ph on W84, W85 and W87 carbons from aqueous solution at pH = 2 and 298 K

Values of heterogeneity parameters, n, indicate at least moderate adsorption energy dispersions (0.34 ≤ n ≤ 81), with only one exception (phenol on W87). However, the data scatter for all phenol isotherms was higher than for corresponding BA and SA isotherms and this may suggest that parameters for phenol isotherms are less reliable. For all adsorbates, adsorption on W84 was the highest but mostly similar to W85, however, adsorption on W87 was much smaller than on W84 and W85. Observed heterogeneities for adsorption on W84 were higher (lower n) than for W85 (with the exception of SA), whereas those for W87 were between W84 and W85 (with the exception of Ph/W87). However, experimental data covers only a part of adsorption space and even small deviations may change fitted parameters (fitted parameters are in fact extrapolation of local behavior), while general trends become obvious from simple visual comparisons. Hence, we may easily observe (see Online Resource) that adsorption of SA was always the strongest (the same adsorption as for BA was obtained at 2–3 times lower equilibrium concentrations) and adsorption of phenol of 50 % of SA and 65 % of BA adsorption for the same solute concentration. Explanation of this behavior is mainly the Traube’s rule—the main factor affecting adsorption for similar adsorbates in the same molecular state (all adsorbates are mostly in molecular form at pH = 2) are their relative concentrations c/c _s , where c _s is saturation concentration (see Table 3) (Derylo-Marczewska and Jaroniec 1987; Derylo-Marczewska and Marczewski 1999; Moreno-Castilla 2004). Salicylic acid has the lowest solubility (half of BA solubility), whereas solubility of phenol has solubility larger by more than 1 order of magnitude and their adsorption properties may be ordered as follows: SA > BA > Ph. Moreover, intramolecular hydrogen bond formation in SA (hydroxyl and carboxyl groups in ortho position) resulting in weaker solvation effects may also be responsible for its lower solubility in water and stronger affinity to graphene-like structures in carbons (Moreno-Castilla 2004). Partial evidence of this effect may also be seen in molar volumes (as calculated from solid density data) showing that the SA molecule occupies even less space than BA, despite having an additional hydroxyl group (Table 3). It is quite different for Ph and benzene (molar volume taken from density of solid at 277 K)—the presence of hydroxyl group increases observed molar volume considerably. Of course, the density data of pure substances are only approximate measure of the space occupied in adsorption from water solution.

3.1.3 Adsorption and desorption kinetic measurements

Prior to the kinetic measurement 0.05 g carbon sample was immersed in water and degassed, then the acidified stock solution of adsorbate was added and mixed (total volume 50 ml, pH = 2). From that moment magnetic stirrer was used to limit the influence of diffusion in the bulk phase. The UV spectra (200–400 nm) were cyclically recorded for 1.3 ml solution samples collected and returned back to the adsorption vessel. After 7–24 h, 1 ml of 1 M NaOH was added and the desorption started with data collected as for the adsorption measurements for the next 13 to 20 h (total adsorption/desorption experiments lasted from 20 to 45 h). The obtained spectra were used to calculate adsorbate concentrations. The use of entire spectra instead of a single wavelength measurements is especially important in kinetic experiments with suspensions of fine particles, where flow cell window may be temporarily partially blocked by solid particles or small air bubbles (results from pressure drops caused by using peristaltic pump in RSA accessory)—such partial blockage results in a small spectrum shift that may be easily corrected when the entire spectra are available (Marczewski 2007, 2008, 2010a, 2011; Derylo-Marczewska et al. 2010a, b). It also helps to determine BA, SA and Ph concentrations in alkaline conditions, especially for BA where the side peak at 268 nm used in measurements is not separated from the main peak at 221 nm (could not be used in this concentration range)—in this case peak-shape fitting had to be used to improve calculation of concentration (see spectra in Fig. S6 in Online Resource). Similar quality of kinetic data may be also obtained with an optical fiber probe introduced into the solution (Castillejos and Rodríguez-Ramos 2011), however, authors preferred high frequency of measurements possible with single point absorbance readings (20 s) over possibility of better data correction for spectrum measurements.

Fig. 9

Bangham plots for adsorption kinetics of BA, SA and Ph on mesoporous carbons at pH = 2

3.2 Analysis of kinetic data

3.2.1 Preliminary analysis—Bangham plots

Preliminary analysis was carried out by using Bangham plots (Aharoni et al. 1979) (Fig. 9). For all adsorption systems initial part (1–20 min, in some cases up to 100 min) was linear in log(log(c _o /_c)] versus log t coordinates with slopes ranging from 0.44 to 0.49 for phenol to 0.53–0.57 for BA and 0.55–0.58 for SA (see Figures and parameters in Online Resource). Such slopes, p, near 0.5 are typical for IDM and seem to suggest initial sorption mechanism controlled by normal diffusion, whereas for p < 0.5 we system shows super diffusion and for p < 0.5—subdiffusion (Sharifi-Viand et al. 2012) with such effects attributed to disordered structure of the porous media (Havlin and Ben-Avraham 2002). However, one has to say, that the Bangham plot may be written as $u(t) = 1 - \exp [ - (kt)^{p} ]$ which is mathematically equivalent to the Avrami (1939) and fractal (Brouers and Sotolongo-Costa 2006) kinetic equations. Moreover, similar type of initial adsorption rates (a ~ t ^p) are present in the SRT model with LF heterogeneity, however, power coefficient $p = n/(1 + n)$ ≤ 0.5, where 0 < n≤1 is the heterogeneity coefficient (Marczewski 2011). All parameters for this analysis and the following sections are contained in the Online Resource.

3.2.2 IDM and PDM

Let us analyze validity of diffusion models first. IDM and PDM both seem to be promising as the porosity is the most evident property of adsorbents used in this study and Bangham slopes are near 0.5. Full IDM formula (21, 22) with Haynes-Lucas approximation (Haynes and Lucas 2007) was used in data optimization. The results are shown by using the Weber-Morris linear plots (Fig. 10).

Fig. 10

Adsorption kinetics of BA, SA and Ph on mesoporous carbons at pH = 2. Solid lines are IDM-optimizations. Time is in [min]

In the optimization, initial concentration c _o was allowed to be fitted parameter (actual value was 2.2 mmol/l for all experiments) as well as u _eq [where c _eq  = c _o (1 − u _eq )] and D _a /r ². Obtained parameters and more plots are available in the Online Resource. The data could not be very well fitted. If fitted c _o were smaller than the actual initial concentrations, c _ini , it could mean, that initial kinetics (0–1 min.) is much faster than what could be attributed to small particulate matter, adsorption on the external part of granules and initial solution mixing effect. However, for SA and BA the optimized values of c _o  > c _ini (for phenol adsorption is much smaller and deviations from the IDM are large) what indicates that IDM is not suitable model here (it predicts larger and faster initial drop of concentration than observed). Moreover, much better fitting is obtained, if both c _eq and u _eq are independently fitted. With the exception of Ph/W87 the optimized u _eq,opt  ≪ u _eq (c _eq ) corresponding to much smaller effect of solute concentration (represented in the model by u _eq ) than occurring in reality. It means that the influence of adsorption phenomena is much greater then allowed in the model [Henry isotherm does not alter IDM solution (20–22)]—nonlinearity caused by strong adsorption and local adsorption capacity limits alters the course of sorption predicted by normal diffusion laws. Due to the polydisperse nature of used carbons, average size (0.3 mm) was used to calculate effective diffusion coefficients. For BA on W84, W85 and W87, calculated D _a  = 2.9 × 10⁻⁹, 0.98 × 10⁻⁹, 4.9 × 10⁻⁹ cm²/s, respectively. For SA D _a  = 1.8 × 10⁻⁹, 0.71 × 10⁻⁹, 3.1 × 10⁻⁹ cm²/s and for phenol D _a  = 9.9 × 10⁻⁹, 2.9 × 10⁻⁹, 3.7 × 10⁻⁹ cm²/s. For comparison, estimated D _a  = 2.4 × 10⁻⁸ cm²/s for phenol adsorption on the commercial microporous Norit RS 0.8 in natural pH was reported (Castillejos and Rodríguez-Ramos 2011). Norit carbon had 73 % v/v of micropores (Nevskaia et al. 2004), what suggests that the effective diffusion in it could possibly be slower than in the mesoporous carbons. However, Norit RS 0.8 was produced from natural materials and contained some ash, whereas the structure and chemistry of W-carbons here were derived from synthetic self-organizing polymer-silica structures (effect on tortuosity factor, τ _p ) and did not contain ash (effect on K _H ). For SA effective diffusion coefficients are smaller than for BA, which may be expected based on larger size of SA. Moreover, D _a values for phenol, the smallest adsorbate molecule which should diffuse most easily, are the highest (with the exception of Ph/W87 which strongly deviates from IDM). However, diffusion is slowest on W85 which has the smallest pores and largest contribution of micropores. The same effects are obvious when comparing kinetic halftimes.

In contrast to the classic IDM, McKay’s pore diffusion model (25,26) fits experimental data much better, however, at the cost of discrepancies near equilibrium, which the model predicts to occur at a finite time, whereas the downward concentration trend of experimental data is obvious. The compact data plot (Fig. 2; adsorption or concentration versus τ/(1 + τ), where τ = t/t _0.5) which is linear for SOE kinetics is used for data presentation which allows us to better understand kinetic behaviors near the equilibrium (Fig. 11). For phenol we observe slow drift-like trend for times over 300 min resulting in the largest discrepancies, similarly to other equations.

Fig. 11

Adsorption kinetics of BA, SA and Ph on mesoporous carbons at pH = 2 in compact time plot, concentration versus τ/(1 + τ), where τ = t/t _0.5 is reduced time. Solid lines are PDM-optimizations

Fig. 12

Adsorption at pH = 2 (top) and desorption at pH = 12 (bottom) kinetics of BA, SA and Ph on mesoporous carbons at in compact time plot, concentration versus τ/(1 + τ), where τ = t/t _0.5 is reduced time. Solid lines are MOE (12, 13) optimizations

If we compare differences in fit quality between various fitting assumptions (see Figures and Tables in Online Resource), there is no improvement gained from treating c _o as fitting parameter, what confirms that the model describes well the initial kinetics (much better than IDM). However, when c _eq and u _eq are treated as independent fitting parameters, geometric average of 1−R ² values for all carbons for each of the adsorbates, decrease by 30–60 % (1.4–2.5 times). It confirms that the near-equilibrium properties of this model contradicts experimentally observed behaviors (see discussion in the Theory).

3.2.3 Generalized IKL and MOE

Equilibrium isotherms are fitted quite well (R ² > 0.99 with the exception of phenol on W85 and W87) with LF isotherm (14). The heterogeneity parameters clearly show, that this system does not adhere to the pure Langmuir model (2) with corresponding IKL kinetics (6). Moreover, preliminary tests showed that kinetic curves are well fitted with the linear plot of SOE (10) (i.e. f ₂ ≈ 1), even though the adsorbate uptakes were between 0.15 and 0.45 which is impossible in the IKL (f _L  = f _eq  = u _eq θ _eq ). Thus obtained kinetic concentration versus time data were fitted with empirical MOE (i.e. gIKL with free f _L ) and SOE as its boundary solution for f ₂ → 1 (Fig. 12).

To avoid problems with solution discontinuity between MOE and SO, kinetic halftime t _1/2 and f ₂ were used as fitting parameters, whereas the rate coefficients could be calculated by using relation (11), which is identical for gIKL and MOE.

For desorption f ₂ should be negative in the case of pure gIKL, however, in 3 out of 9 cases parameter value for adsorption was actually smaller than the positive value for desorption. Despite that, MOE fits data quite well, with the exception 1–2 initial points for adsorption and first point for desorption. Near the beginning of both experiments, it was most probably the intraparticle diffusion as well as the presence of some fine particles and adsorption on external surfaces that resulted in the much faster process than could be observed after just a few minutes. The comparison of adsorption and desorption halftimes shows, that the desorption is much faster process than adsorption (best seen by comparing corresponding halftimes). During adsorption adsorbates are neutral molecules (pH ≪ pK _a ) interacting strongly with weekly positive carbon surface, while during desorption adsorbates in solution are in anionic form and are very weakly adsorbed (carbon surface is also negatively charged) (Derylo-Marczewska and Jaroniec 1987; Derylo-Marczewska and Marczewski 1997, 1999; Moreno-Castilla 2004). However, when desorption is initiated by alkalization, H⁺ and molecular adsorbates are present initially in adsorbent pores while the solution is rich in OH⁻ ions and it is difficult to indicate the single most important factor determining desorption rate.

Despite availability of kinetic equation including LF-type heterogeneity (15, 16) (Marczewski 2011), it was not used here, because obtained kinetic parameters were not showing enough regularity or relation with the equilibrium data—clearly, data should be measured in a range of varying conditions for each single adsorbate, and due to the limited availability of obtained synthetic carbons (approx. 2 g/synthesis) it was not possible here.

3.2.4 Fractal-like kinetic model

Fractal-like kinetic MOE Eqs. (17, 18) was used in order to see if the reason of partial fit could be disordered solid structure. The result of optimizations are shown in Fig. 13 (see also Figures and Table in Online Resource)

Fig. 13

Adsorption at pH = 2 (top) and desorption at pH = 12 (bottom) kinetics of BA, SA and Ph on mesoporous carbons at in compact time plot, concentration versus τ/(1 + τ), where τ = t/t _0.5 is reduced time. Solid lines correspond to f-MOE (17, 18) optimizations

In some cases using f-MOE did not improve fitting, however, in some other cases (with strong deviations from MOE near beginning or end of kinetic curves) high improvements are noted. On average (geometric mean for all adsorption and desorption curves), indetermination coefficients 1 − R² were smaller by 40 % (1 − R ² ratio for f-MOE/MOE ~0.6). The highest improvements were noted for adsorption and desorption on W85 characterized by the highest adsorbed amounts (1 − R ² reduced by 63 %). We may attribute this improvement to the more precise data, where deviations from model are better visible. For W84 and W87 this improvement is still present, but not so pronounced (1 − R ² reduced by 24 % only). On the other hand the improvement for adsorption kinetics (1 − R ² reduced by 56 %) was much better then for desorption curves (1 − R ² reduced by 18 % only). As adsorption kinetics.

Whereas the improvement to fitting is obvious, the parameters do not change very regularly, so it is not possible to say that mechanism of these systems’ kinetics is indeed best described by the fractal-like MOE.

3.2.5 Rate of adsorption as a function of adsorbent structure and molecule size

In order to analyze overall rate of adsorption independently of kinetic mechanism, it is best to select some independent metric, e.g. kinetic halftime, which may be easily estimated if only some approximation of equilibrium concentration (or adsorption) is known. While it may be argued, that times corresponding to some other arbitrary fractional adsorption progress should be preferred, e.g. time to F = 0.90, in many systems fast adsorption is one of the most coveted properties.

If we compare geometric averages of kinetic halftimes of adsorption for the investigated systems obtained by optimization as described, for all investigated equations we obtain the same order: SA > BA > Ph (from largest to smallest and from least soluble to best soluble molecule) and W85 > W87 > W84 (from smallest to largest pores).

Best correlation of average halftimes is obtained for average mesopore size calculated from adsorption branch, D _a (see Table 2) (for MOE: R ² = 0.999) and only slightly worse for its reciprocal (for MOE: R ² = 0.994). It means that the average adsorption rate depends mainly on the mean width of mesopore adsorption channels, while the effect of local constrictions (evidenced by D _d  < D _a ) is less evident. Similarly, adsorption halftimes are partially correlated to the “hydraulic” (meso + micro) average pore size D _h and $1/D_{h}^{2}$. It does not affect directly adsorption halftimes (easily accessible pores are filled first), however, (not shown here) its effect on times corresponding to near-equilibrium states is much stronger (more in Online Resource).

It must be remembered, that estimation of kinetic halftimes depends on optimized parameters, which in fact are (in part) extrapolated values, strongly susceptible to experimental deviations and model-dependent.

If we compare quality of fit expressed as geometric mean of indetermination coefficients (1 − R ²) for all the equations used and adsorption kinetics only, we may order them as follows (no. of fitted parameters in parentheses):

$$ {\text{IDM}}\left( { 3 {\text{-par}}} \right)\left( {0.00 70} \right) > {\text{PDM}}\left( { 4 {\text{-par}}} \right)\left( {0.00 4 8} \right) > {\text{MOE}}\left( { 4 {\text{-par}}} \right)\left( {0.00 40} \right) > {\text{f-MOE}}\left( { 5 {\text{-par}}} \right)\left( {0.00 1 8} \right). $$

While the number of fitted of parameters is important, MOE—which may be also related to the properties of equilibrium isotherm—is slightly better than PDM. Moreover, as was said before IDM cannot well describe systems with strong adsorption effects, while PDM erroneously describes near-equilibrium behaviors. However, if we take into account only the desorption curves, the difference between MOE and f-MOE (large for adsorption) becomes quite small:

$$ {\text{MOE}}\left( { 4 {\text{-par}}} \right)\left( {0.00 3 8 3} \right) > {\text{f-MOE}}\left( { 5{\text{-par}}} \right)\left( {0.00 3 1 2} \right). $$

It means that the difference in fitting quality is not so much related to the number of parameters fitted, but more to the kind of kinetic equation.

4 Conclusions

Three divergent mesoporous carbons are synthesized and their properties are analyzed. They are used in adsorption of benzoic acid, salicylic acid and phenol from acidic aqueous solution. Equilibrium data is well described by the Langmuir–Freundlich isotherm equation corresponding to substantial heterogeneity. Adsorption and desorption kinetic experiments showed that the curves partially correspond to the intraparticle diffusion model (IDM) and pore diffusion model (PDM) as well as may be described by the newly extended to desorption generalized integrated Langmuir kinetic equation (gIKL) and generalized mixed 1,2-order equation (MOE). However, the best fitting quality was obtained for the fractal-like MOE (f-MOE) and f-MOE extended to desorption. None of the selected simple kinetic and equilibrium equations allowed to describe both equilibrium and kinetics with the same set of parameters. Kinetic halftimes calculated for solutes increase with solute size and decrease with increasing carbon pore size. Linear correlation of carbon-average halftimes and pore sizes or reciprocal of pore sizes obtained from adsorption data and partial correlation with “hydraulic” pore sizes is found.