Surface Curvature as a Classifier of Abdominal Aortic Aneurysms: A Comparative Analysis

Abstract

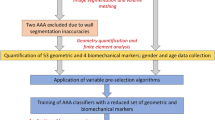
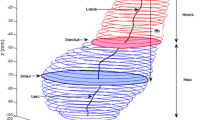
An abdominal aortic aneurysm (AAA) carries one of the highest mortality rates among vascular diseases when it ruptures. To predict the role of surface curvature in rupture risk assessment, a discriminatory analysis of aneurysm geometry characterization was conducted. Data was obtained from 205 patient-specific computed tomography image sets corresponding to three AAA population subgroups: patients under surveillance, those that underwent elective repair of the aneurysm, and those with an emergent repair. Each AAA was reconstructed and their surface curvatures estimated using the biquintic Hermite finite element method. Local surface curvatures were processed into ten global curvature indices. Statistical analysis of the data revealed that the L2-norm of the Gaussian and Mean surface curvatures can be utilized as classifiers of the three AAA population subgroups. The application of statistical machine learning on the curvature features yielded 85.5% accuracy in classifying electively and emergent repaired AAAs, compared to a 68.9% accuracy obtained by using maximum aneurysm diameter alone. Such combination of non-invasive geometric quantification and statistical machine learning methods can be used in a clinical setting to assess the risk of rupture of aneurysms during regular patient follow-ups.

Appendices

Appendix I: Definition of Global Curvature Features (i.e., Geometric Indices)

Area of a Triangular Element

$$ S_{i} = \frac{1}{2}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{a}_{i} \times \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{b}_{j} $$

where the final points of $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{a}_{i}$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{b}_{j}$ share one edge of the triangle.

Gaussian and Mean Curvatures

The roots of Eqs. (3) and (8) are defined as the local (nodal) curvatures, $k_{1i}$ and $k_{2i}.$ The local Gaussian (K) and Mean (M) curvatures are given by

$$ K_{i} = k_{1i} \cdot k_{2i} $$

$$ M_{i} = \frac{1}{2}\left( {k_{1i} + k_{2i} } \right) $$

Global Curvature Indices (Calculation Described in Detail by Martufi et al. 13)

KG :

Square root sum of the Gaussian curvature

KM :

Square root sum of the Mean curvature

GAA :

Area averaged Gaussian curvature

MAA :

Area averaged Mean curvature

K1AA :

Area averaged major principal curvature

K2AA :

Area averaged minor principal curvature

GLN :

L2 norm of the Gaussian curvature

MLN :

L2 norm of the Mean curvature

K1LN :

L2 norm of the major principal curvature

K2LN :

L2 norm of the minor principal curvature

   

Appendix II: Brief Description of Curvature Estimation by BQFE Interpolation

A BQFE interpolation has C ² continuity on the surface on which curvatures are probed by having the first and second derivatives defined at the surface nodes such that BQFE derived curvatures are more accurate than those computed with lower order continuity methods. To calculate curvatures directly from BQFE, we use Eq. (8) and the subsequent tensor products:

$$ \left( {g_{\theta \theta } g_{\theta z} - g_{\theta z}^{2} } \right)k_{n}^{2} - \left( {b_{\theta \theta } g_{zz} + g_{\theta \theta } b_{zz} - 2b_{\theta z} g_{\theta z} } \right)k_{n} + \left( {b_{\theta \theta } b_{zz} - b_{\theta z}^{2} } \right) = 0 $$

(8)

where $b_{\alpha \beta } = \sqrt {g_{\theta \theta } g_{\theta z} - g_{\theta z}^{2} } \left| {\begin{array}{*{20}c} {X_{\alpha \beta } } & {Y_{\alpha \beta } } & {Z_{\alpha \beta } } \\ {X_{\theta } } & {Y_{\theta } } & {Z_{\theta } } \\ {X_{z} } & {Y_{z} } & {Z_{z} } \\ \end{array} } \right|$ and $g_{\alpha \beta } = X_{\alpha } X_{\beta } + Y_{\alpha } Y_{\beta } + Z_{\alpha } Z_{\beta } .$

The subscripts of X, Y, and Z represent differentiation with respect to that variable. Equations (9)–(11) demonstrate how the mathematical descriptors of the BQF elements and the corresponding Cartesian coordinates of the surfaces are related to each other:

$$ \begin{aligned} X &= R\cos \theta + \mathop \sum \limits_{k} a_{k} \cos (k\omega z) \hfill \\ Y &= R\sin \theta + \mathop \sum \limits_{j} b_{j} \sin (k\omega z) \hfill \\ Z &= z \hfill \\ \end{aligned} $$

(9)

where $2\omega \pi /\left( {Z_{\hbox{max} } + Z_{\hbox{min} } } \right)$, $a_{k}$ and $b_{j}$ are constants, and k and j are the number of terms in the Fourier series used to represent the longitudinal AAA axis. For example, the derivatives with respect to ${{\uptheta}}$ and z in the X direction are given by

$$ \begin{gathered} X_{\theta } = \frac{\partial R}{\partial \theta }\cos \theta - R\sin \theta \hfill \\ X_{\theta \theta } = \frac{{\partial^{2} R}}{{\partial \theta^{2} }}\cos \theta - 2\frac{\partial R}{\partial \theta }\sin \theta - R\cos \theta \hfill \\ X_{\theta z} = \frac{{\partial^{2} R}}{\partial \theta \partial z}\cos \theta - \frac{\partial R}{\partial z}\sin \theta \hfill \\ X_{z} = \frac{\partial R}{\partial z}\cos \theta - \mathop \sum \limits_{k} \omega ka_{k} \sin (k\omega z) \hfill \\ X_{zz} = \frac{{\partial^{2} R}}{{\partial z^{2} }}\cos \theta - \mathop \sum \limits_{k} \omega^{2} k^{2} a_{k} \cos (k\omega z). \hfill \\ \end{gathered} $$

(10)

The radial coordinate R is the fitted variable and its derivatives are expressed in terms of the element shape functions N which are biquintic hermite shape functions:

$$ \begin{gathered} \frac{\partial R}{\partial \theta } = \frac{\partial \xi }{\partial \theta }\;\frac{{\partial N_{i}^{jk} }}{\partial \xi }R_{i}^{jk} \hfill \\ \frac{{\partial^{2} R}}{{\partial \theta^{2} }} = \left( {\frac{\partial \xi }{\partial \theta }} \right)^{2} \frac{{\partial^{2} N_{i}^{jk} }}{{\partial \xi^{2} }}R_{i}^{jk} \hfill \\ \frac{{\partial^{2} R}}{\partial \theta \partial z} = \frac{\partial \xi }{\partial \theta }\;\frac{\partial \eta }{\partial z}\;\frac{{\partial^{2} N_{i}^{jk} }}{\partial \xi \partial \eta }R_{i}^{jk} \hfill \\ \frac{\partial R}{\partial z} = \frac{\partial \eta }{\partial z}\;\frac{{\partial N_{i}^{jk} }}{\partial \eta }R_{i}^{jk} \hfill \\ \frac{{\partial^{2} R}}{{\partial z^{2} }} = \left( {\frac{\partial \eta }{\partial z}} \right)^{2} \frac{{\partial^{2} N_{i}^{jk} }}{{\partial \eta^{2} }}R_{i}^{jk} . \hfill \\ \end{gathered} $$

(11)

A more detailed calculation is presented by Smith et al.25