Introduction

The beat-to-beat variability of the heartbeat interval or heart rate variability (HRV) is a result of autonomic nervous system (ANS) and humoral effects on the sinus node. The ANS can be divided into sympathetic and parasympathetic (also called vagal) branches. Roughly speaking, sympathetic activity tends to increase heart rate and decrease HRV, whereas parasympathetic activity tends to decrease heart rate and increase HRV.6 The most conspicuous periodic component of HRV is the respiratory sinus arrhythmia (RSA) which is considered to range from 0.15 to 0.4 Hz. This high frequency (HF) component is mediated almost solely by the parasympathetic nervous activity.6,23 Another apparent component of HRV is the low frequency (LF) component ranging from 0.04 to 0.15 Hz. The LF component is mediated by both sympathetic and parasympathetic nervous activities6 and is substantially affected by baroreflex activity.9 There are however studies demonstrating that the normalized value of the LF component could be used to assess sympathetic efferent activity.15,31 Therefore, it is important to examine the LF component power both in absolute and normalized units.

Due to the complexity of physiologic control systems, the characteristics of HRV (e.g., powers of LF and HF components) can be assumed to vary in time. HRV dynamics have been addressed in many studies and several time-varying methods have been proposed for estimating changes in HRV spectra; for a good review on these methods and their properties see Chan et al.10 and Mainardi.25 These methods include short time Fourier transform (STFT) and wavelet transform,22,33,43 time-frequency distributions such as the Wigner distribution,26,29,34,42 and time-varying autoregressive (AR) modeling based methods.7,8,37 In addition, one fairly recent approach to model the dynamics of HRV is the point process model,4 which has been applied e.g., for dynamic estimation of RSA component and baroreflex sensitivity.11,12

HRV has been studied with relation to cardiovascular diseases, diabetic neuropathy, physical exercise, mental stress, gender and age, and sleep.1,23,40 In addition, anesthetic drugs are known to alter HRV significantly. The relationship between ANS activity, as observed through HRV analysis, and general anesthesia has been quite widely explored and the partially divergent effects of different anesthetics have been identified.23,28 The effect of general anesthesia on the ANS activity is typically evaluated by using stationary methods, i.e., by applying standard fast Fourier transform (FFT) on short data segments.14,16,18,24,27,30 In addition, the dynamics of HRV during anesthesia have been evaluated for example by using smoothed pseudo Wigner–Ville distribution19,41 and wavelet transform.20,33 However, the dynamic changes of HRV around loss and recovery of consciousness have not been studied in detail.

The aim of this study was to examine HRV changes close to loss and recovery of consciousness. Two anesthetic drugs with distinct mechanisms of action were studied; propofol (GABAergic) which is a short-acting, commonly used hypnotic agent, and dexmedetomidine (selective alpha2-agonist) which is a sedative medication increasingly used in intensive care units. Dexmedetomidine was selected because of its known sympatholytic effect due to which this drug is assumed to produce observable changes in HRV. Propofol is a commonly used and rather widely studied anesthetic, thereby producing a reference to the observed HRV changes. In the experimental part of the study, concentrations of the anesthetic drugs were increased in stages until loss of consciousness (LOC) was reached in spontaneously breathing subjects. The tests were free from any disturbances resulting from surgery, other drugs, or ventilator. Thus, the study setup was optimal for examining HRV changes during loss and recovery of consciousness.

In this paper, HRV dynamics in healthy volunteers undergoing low-dose propofol and dexmedetomidine anesthesia were assessed through standard time-domain and frequency-domain measures of HRV. The frequency-domain parameters were estimated dynamically by using a time-varying parametric spectrum estimation method originally proposed in Tarvainen et al.37 In the method, the RR interval data are modeled with a time-varying AR model, the model parameters are estimated recursively with a Kalman smoother algorithm, and time-varying spectrum estimates are obtained from the estimated model parameters. The advantages of this spectrum estimation method are high time-frequency resolution and the possibility to decompose the instantaneous spectrum estimates into separate frequency components.37 This is especially advantageous in HRV analysis, because it enables a separate estimation and investigation of the LF and HF components. In this paper, the method was further improved to take into account respiratory frequency changes in the HF component estimation. This improvement ensures that the RSA is always captured within the HF component.

Methods

A selection of time-domain and frequency-domain measures of HRV were considered. The selected analysis parameters and their computation are presented shortly in the following.

Time-Domain Measures of HRV

The time-domain parameters considered in this study were the mean RR interval (\(\overline{\hbox{RR}}\)), standard deviation of RR intervals (SDNN), and root mean square of successive differences (RMSSD). Dynamics of these parameters were computed in a 60 s moving window (moved with 1-s steps) for the whole RR interval series. The mean RR interval at time t was obtained by averaging the RR intervals within the moving window, i.e.,

$$ \overline{\hbox{RR}}(t) = \frac{1}{L}\sum_{j=1\atop t_j\in {\rm{w}}_{t}}^L \hbox{RR}_j $$
(1)

where L is the number of RR intervals within a time window w t  = [t − 30, t + 30] s and RR j is the jth RR interval observed at time t j . The SDNN at time t was similarly defined as

$$ \hbox{SDNN}(t) = \sqrt{\frac{1}{L-1}\sum_{j=1\atop t_j\in{\rm w}_{t}}^L (\hbox{RR}_j-\overline{\hbox{RR}}(t))^2}.$$
(2)

SDNN reflects the overall (both short-term and long-term) variability within the RR interval series, whereas RMSSD which was defined accordingly as

$$ \hbox{RMSSD}(t) = \sqrt{\frac{1}{L-1}\sum_{j=1\atop t_j\in {\rm w}_{t}}^{L-1} (\hbox{RR}_{j+1} - \hbox{RR}_j)^2} $$
(3)

is a measure of short-term variability. It should be noted that the number of RR intervals (L) within the time window w t may change from one time instant to another because of changes in the mean heart rate.

Frequency-Domain Measures of HRV

The frequency-domain parameters considered in this study were LF and HF component powers as well as the total spectral power. These power values as a function of time were obtained from the time-varying spectra which were estimated using the Kalman smoother spectrum estimation method. In the spectrum estimation, the data is assumed to be equidistantly sampled, and thus the RR interval series were converted into equidistantly sampled signals by using interpolation methods. The Kalman smoother spectrum estimation method is shortly described in the following (for details see Tarvainen et al.37).

In the method, the equidistantly sampled RR series was first modeled with a time-varying AR model of order p defined as

$$ x_t = -\sum_{j=1}^p a_t^{(j)}x_{t-j} + e_t $$
(4)

where x t is the modeled signal (i.e., the RR series), a (j) t is the value of jth AR parameter at time t and e t is observation error. By denoting

$$ H_t = (x_{t-1},\ldots,x_{t-p}) $$
(5)
$$ \theta_t = (-a_t^{(1)},\ldots,-a_t^{(p)})^T $$
(6)

the time-varying AR model can be written in the form

$$ x_t = H_t\theta_t + e_t $$
(7)

which is a linear observation model. Kalman smoother algorithm is based on the so-called state-space formalism which means that in addition to observation model, the evolution of the state (i.e., AR parameters) is modeled. Here a random walk model

$$ \theta_{t+1} = \theta_t + w_t $$
(8)

where w t is the state noise term, was used. Equations (7) and (8) form the state-space signal model for x t and the evolution of the AR parameters can be estimated by using the Kalman smoother algorithm.

Kalman Smoother Algorithm

The Kalman smoother algorithm consists of a Kalman filter algorithm and a fixed-interval smoother. The Kalman filtering problem is to find the linear mean square estimator \(\hat{\theta}_t\) for state θ t given the observations \(x_1,x_2,\ldots,x_t. \) Kalman filter equations can be summarized as2

$$ C_{\tilde{\theta}_{t\vert t-1}} = C_{\tilde{\theta}_{t-1}} + C_{w_{t-1}} $$
(9)
$$ K_t = C_{\tilde{\theta}_{t\vert t-1}} H_t^T(H_t C_{\tilde{\theta}_{t\vert t-1}} H_t^T +C_{e_t})^{-1} $$
(10)
$$ \hat{\theta}_t = \hat{\theta}_{t-1} + K_t(x_t-H_t\hat{\theta}_{t-1}) $$
(11)
$$ C_{\tilde{\theta}_t} = (I-K_tH_t)C_{\tilde{\theta}_{t\vert t-1}} $$
(12)

where \(\tilde{\theta}_t=\theta_t - \hat{\theta}_t\) is the state estimation error, \(\tilde{\theta}_{t\vert t-1}=\theta_t - \hat{\theta}_{t-1}\) is the state prediction error, K t is the Kalman gain vector, and \({C_{e_{t}}}\;\text{and}\;{C_{w_{t}}}\) are the observation and state noise covariances, respectively.

The fixed-interval smoothing problem is to find estimates \(\hat{\theta}_{t}^{\rm S}\) (S denotes smoothed estimates) for each state θ t given all the observations \(x_1,x_2,\ldots,x_N. \) Fixed-interval smoothing equations can be summarized as2

$$ \hat{\theta}_{t}^{\rm S} = \hat{\theta}_t + A_t (\hat{\theta}_{t+1}^{\rm S} - \hat{\theta}_t) $$
(13)
$$C_{\tilde{\theta}_t^{\rm S}} = C_{\tilde{\theta}_t}+A_t(C_{\tilde{\theta}^{\rm S}_{t+1}} - C_{\tilde{\theta}_{t+1\vert t}})A_{t}^{T} $$
(14)

where \(A_t = C_{\tilde{\theta}_t}C_{\tilde{\theta}_{t+1\vert t}}^{-1}. \) The smoother algorithm is initialized with the Kalman filter estimates, i.e., \(\hat{\theta}_{N}^{\rm S}=\hat{\theta}_N\) and \(C_{\tilde{\theta}_{N}^{\rm S}} = C_{\tilde{\theta}_N}. \) That is, the smoothed estimates \(\hat{\theta}_t^{{\rm S}}\) are obtained by first running the Kalman filter algorithm forward in time and then the smoother algorithm backwards in time.

Adaptation of the Algorithm

The terms effecting the adaptation of Kalman smoother algorithm are the state noise covariance (\({C_{w_{t}}}\)), observation noise covariance (\({C_{e_{t}}}={\sigma_{e_{t}}^{2}}\)) and the variance of the modeled signal (\({\sigma_{x_{t}}^{2}}\)). In order to control the adaptation of the algorithm, the following solution was adopted. First, the observation noise variance was estimated recursively at every step of the Kalman filter equations as

$$ \hat{\sigma}_{e_t}^2 = 0.95 \hat{\sigma}_{e_{t-1}}^2 + 0.05 \epsilon_t^2 $$
(15)

where \(\epsilon_t\) is the one step prediction error \(\epsilon_t = x_t-H_t\hat{\theta}_{t-1}. \) Secondly, the state noise covariance matrix was selected to be diagonal \({C_{w_{t}}} = {\sigma_{w_{t}}^{2}}I,\;\text{and}\;{\sigma_{w_{t}}^{2}}\) was adjusted at every step of the Kalman filter equations as

$$ \hat{\sigma}_{w_t}^2 = \hbox{UC} \hat{\sigma}_{e_t}^2/\hat{\sigma}_{x_t}^2 $$
(16)

where \(\hat{\sigma}_{x_t}^2\) is the estimated variance of the observed RR series at time t and UC is an update coefficient through which the adaptation of the algorithm is adjusted. Therefore, the adaptation of the algorithm is adjusted with a single parameter (UC) and a fixed value of UC can be used for all data.

Time-Varying Spectrum Estimation

Once the time evolution of the AR parameters is estimated with the Kalman smoother, the time-varying spectrum estimates can be obtained as

$$ P_t(f) = \frac{\hat{\sigma}_{e_t}^2/f_s}{\vert 1+\sum_{j=1}^p \hat{a}_t^{(j)} e^{-i2\pi jf/f_s}\vert^2} $$
(17)

where f s is the sampling frequency, \(\hat{a}_t^{(j)}\) is the jth AR parameter estimate at time t, and \(\hat{\sigma}_{e_t}^2\) is the variance of the estimated observation error process at time t. Note that \(\hat{\sigma}_{e_t}^2\) is not the variance estimated iteratively in the Kalman filter forward run, but it is the posterior error variance evaluated based on the smoothed estimates.

The total spectral power as a function of time can be computed from (17) as

$$ P_t^{\rm Tot.} = \sum_{f=0}^{f_s/2} P_t(f)\Updelta f $$
(18)

where \(\Updelta f\) is the frequency grid interval.

LF and HF band powers could be computed similarly by summing over the frequency points within the predefined frequency bands. However, here the LF and HF powers are computed from decomposed spectral components.

Spectral Decomposition and Component Powers

The AR spectrum given in (17) can be decomposed into components by presenting it in the factored form

$$ P_t(f) = \frac{\hat{\sigma}_{e_t}^2/f_s}{\prod_{j=1}^{p} (z-\alpha_t^{(j)})(1/z - \alpha_t^{(j)*})} $$
(19)

where \(z=e^{i2\pi f/f_{s}}, \alpha_{t}^{(j)}\) are the time-varying roots (poles) of the AR polynomial, and * denotes complex conjugate. Now, consider a pole α (j) t positioned at frequency f j . The spectrum of this single component P (j) t (f) in the vicinity of f j can be estimated by assuming the effect of other poles on the spectrum to be constant (for details see Tarvainen et al.37). Once the spectral components for each time instant t are estimated, LF and HF powers can be computed by integrating the components positioned within the defined frequency bands.

In order to capture the RSA component always within the HF band, the HF (and also LF) band limits are adjusted according to the respiratory frequency as follows. The lower limit of the HF band was fixed to be not higher than 0.15 Hz, but in the case of slowed down respiratory dynamics, the lower limit was adjusted to be 0.025 Hz below the estimated respiratory frequency (but not less than 0.125 Hz). The lower limit of the HF band was however forced to be at least 0.025 Hz higher than the peak frequency of the LF component observed at previous time step. If the difference between respiratory rate and LF peak frequency would be less than 0.025 Hz, LF and HF powers would not be computed because the separation of the components could not be trusted. The upper limit of the HF band was dynamically adjusted to be 0.125 Hz above the estimated respiratory frequency (but at least 0.4 Hz). This dynamic adjustment of the HF band ensures that the RSA component is always captured within the HF band. For other recent methods for fixing the HF band according to respiratory frequency see Bailón et al.3 and Goren et al.17 For the LF band, the lower limit was fixed to 0.04 Hz and the upper limit was between always 0.125–0.15 Hz according to the lower limit of the HF band.

The LF and HF powers are then obtained as

$$ P_{t}^{\rm LF} = \sum_{\left\{j \vert \angle\alpha_t^{(j)}\in \hbox{LF band}\right\}} \left[\sum_{f=0}^{f_s/2} P_t^{(j)}(f)\Updelta f\right] $$
(20)
$$ P_{t}^{\rm HF} = \sum_{\left\{j \vert \angle\alpha_t^{(j)}\in \hbox{HF band}\right\}}\left[ \sum_{f=0}^{f_s/2} P_t^{(j)}(f)\Updelta f\right] $$
(21)

where P (j) t (f) are the spectral components whose peak frequencies (i.e., the angles of the corresponding poles \(\angle\alpha_t^{(j)}\)) are within the specific band.

In addition to the absolute band powers, the LF and HF powers are commonly presented in normalized units (n.u.) as

$$ P_{t}^{\rm LF} (\hbox{n.u.}) = \frac{P_{t}^{\rm LF}}{P_{t}^{\rm Tot.} - P_{t}^{\rm VLF}} 100\% $$
(22)
$$ P_{t}^{\rm HF} (\hbox{n.u.}) = \frac{P_{t}^{\rm HF}}{P_{t}^{\rm Tot.} - P_{t}^{\rm VLF}} 100\% $$
(23)

where P VLF t is the power of the very low frequency (VLF) band (0–0.04 Hz). These normalized power values reveal the relative strengths of LF and HF components. In addition, the ratio between LF and HF powers is often considered as an index of sympatho-vagal balance.

Materials and Data Acquisition

Data from subjects undergoing propofol (Prop: N = 10, healthy males, age 19–28 years) and dexmedetomidine (Dex: N = 9, healthy males, age 19–26 years) anesthesia were analyzed. Originally, 20 subjects participated the tests after giving their written informed consent, but 1 subject from dexmedetomidine group was excluded from analysis because of snoring (observed in data as clear recurrent decreases in respiration related chest movements and synchronous strong increases in heart rate). The study protocol was approved by the Ethical Committee of the Hospital District of Southwest Finland (Turku, Finland) and the National Agency for Medicines.

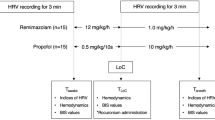
The anesthetic drug was administered intravenously using target control infusion (TCI) aiming at pseudo steady-state plasma concentrations at 10-min intervals starting from 1.0 μg/ml (Prop) or 1.0 ng/ml (Dex) and followed by 0.25–0.5 μg/ml (Prop) or 0.25–0.5 ng/ml (Dex) increases until LOC was reached. The infusion was terminated after LOC. The consciousness of the subject was tested at each concentration level and after the infusion termination by asking the subject to open his eyes. LOC was defined as no response to the “open your eyes” request and recovery of consciousness (ROC) as a meaningful response to the same request. During the recording session, subjects were not disturbed in any other way (except the “open your eyes” request); neither any compensatory maneuvers nor pharmacological interventions were performed. The study setup is illustrated in Fig. 1.

Figure 1
figure 1

Illustrative presentation of the study setup. Consciousness was tested twice at each drug level and at 1-min intervals after the infusion was terminated. The arrows on the bottom indicate these LOC-testing times and the color of the arrow indicates the result of the LOC-testing (blue = response, red = no response). The 11 epochs used later in the analysis are marked with gray vertical bars

Full size image

Electrocardiogram (ECG) along with a set of electroencephalogram (EEG) channels were recorded using a Galileo (Medtronic, Italy) EEG acquisition system. In addition, respiration signal was measured using an accelerometer for recording chest movements. The sampling rate of all the signals was 256 Hz. The R-wave time instances were extracted from the ECG by using an adaptive QRS detection algorithm. Prior to detecting the R-wave peak times, the R-waves were interpolated (Fourier interpolation at 2000 Hz) in order to improve the time resolution of the detection. The RR interval time series were then formed, and prior to spectral analysis, the RR series were interpolated (4 Hz cubic spline interpolation) to have evenly sampled data. Finally, the VLF trend components (frequencies below 0.04 Hz) were removed from the RR interval series by using a smoothness priors method.39 The respiratory frequency as a function of time was obtained as the peak frequency of the respiration signal spectrum computed in 60 s moving window using FFT.

Results

The Kalman smoother spectrum estimation was applied to the preprocessed (i.e., interpolated and detrended) RR interval series of all subjects. Standard model order selection criteria were utilized in AR model order selection and on average they suggested an order p = 16 which was then used for all data. The update coefficient of the Kalman smoother algorithm to UC = 10−5. Time-varying analysis of data from two representative subjects (Prop and Dex) is presented in Fig. 2. The vertical lines on the figure show the LOC-testing times; the three bold lines representing (1) the last LOC-test where a response from subject was obtained (pre-LOC), (2) the first LOC-test where subject did not respond (LOC), and (3) the first LOC-test (after LOC) where subject responded (ROC). The decompositions of the spectra into LF and HF components are explicit and for both subjects HF power is increased around LOC. The figure also shows a notable lengthening of RR interval (decrease in heart rate) for dexmedetomidine.

Figure 2
figure 2

HRV dynamics for representative subjects from propofol and dexmedetomidine groups. The axes from top to bottom illustrate: (1) RR interval series, (2) Kalman smoother spectra with respiratory frequency curves, (3) HF component spectra, (4) LF component spectra, and (5) LF and HF powers in decibels. The vertical lines indicate LOC-testing times

Full size image

The selected time-domain and frequency-domain measures of HRV were then computed as a function of time for every subject and for both drugs. Time-domain parameters \(\overline {\hbox{RR}},\) SDNN and RMSSD were computed from the detrended (but not interpolated) RR interval series according to (1), (2) and (3), respectively. The respiratory frequency was computed as described in “Materials and Data Acquisition” section. The total spectral power and powers of LF and HF components were computed according to (18), (20) and (21), respectively. LF and HF powers were also computed in normalized units according to (22) and (23). The LF/HF ratio was obtained as the ratio between absolute LF and HF powers.

In order to statistically evaluate the group level changes in the HRV parameters during anesthesia, the whole study setup was divided into 11 states. These states (shown in Fig. 1) were:

  1. 1.

    Baseline (2 min before infusion start)

  2. 2.

    Infusion start (middle point of first concentration level)

  3. 3.

    Infusion middle (middle point from infusion start to LOC)

  4. 4.

    Pre-LOC I (1 min before pre-LOC)

  5. 5.

    Pre-PLOC II (1 min after pre-LOC)

  6. 6.

    LOC I (1 min before LOC)

  7. 7.

    LOC II (1 min after LOC)

  8. 8.

    Infusion End (1 min after end of infusion)

  9. 9.

    ROC I (1 min before ROC)

  10. 10.

    ROC II (1 min after ROC)

  11. 11.

    ROC III (3 min after ROC).

The parameter values for each state (except for baseline) were computed by averaging the time-varying parameter values within a 60 second window. The baseline values were averaged within a 4-min window in order to have more reliable values from a state which was assumed to be physiologically static.

As a first step, each selected HRV parameter was statistically tested for any significant differences between the states. For this task the nonparametric Friedman’s test was applied separately for each parameter and for the two drugs. Sufficiently small p value for a given parameter would suggest that at least one state is significantly different from the others (i.e significantly different group median). The significance level was set to α = 0.05 and it was corrected for multiple comparisons (over all parameters and both drugs) with false discovery rate (FDR)5 to yield a threshold of p ≤ 0.0334. The results are presented in Table 1, showing that two parameters for propofol group (respiratory frequency and LF power) and three parameters for dexmedetomidine group (LF and HF powers in normalized units and LF/HF ratio) were not found to have any significant difference between the 11 states.

Table 1 Friedman’s test results for comparing state effects on the selected HRV parameters
Full size table

Pairwise comparisons between the states were then performed for each parameter and for both drugs in order to find out the most significant effects of the anesthetic drugs on HRV. At this point it was not meaningful to compare all the 11 states, but only the most essential states regarding anesthesia monitoring. Therefore, we selected states 1 (baseline), 4 (pre-LOC I), 6 (LOC I) and 9 (ROC I) for the pairwise comparisons. Pairwise comparisons between these four states were performed with Wilcoxon paired, two-sided signed rank test and the results are presented in Table 2. Results are shown only for the most meaningful comparisons. The significance level was again set to α = 0.05 and it was corrected for multiple comparisons with FDR to yield a threshold of p ≤ 0.0039. Comparisons were performed only for those parameters which were found to have significant differences between the original 11 states (see Table 1).

Table 2 Pairwise comparisons between baseline, pre-LOC I, LOC I and ROC I
Full size table

Figure 3 illustrates the group results for the HRV parameters (LF power was excluded as it did not show any significant changes between the states for either of the drugs). The plots show the group medians and the 25th and 75th percentiles for the selected states and for both drugs. Individual changes between the states are also illustrated in the graphs. For the selected states, statistical comparisons between the two drugs were performed for every parameter by using the Wilcoxon rank sum test. The significance level was set to α = 0.05 and it was corrected for multiple comparisons with FDR to yield a threshold of p ≤ 0.0015. The results of between drug comparisons are also illustrated in Fig. 3.

Figure 3
figure 3

Box plots of HRV parameters for selected states (baseline, pre-LOC I, LOC I, and ROC I) for propofol (blue) and dexmedetomidine (red). On each box, the central mark is the median, the edges of the box are the 25th and 75th percentiles, and the whiskers extend to the most extreme parameter values excluding outliers which are plotted separately. Individual changes between all the states (states 1-11) are illustrated with the lines, i.e., each line shows the parameter value at different states for one subject. The stars (*) indicate statistical differences between the two drugs (*p ≤ 0.05, **p ≤ 0.01, ***p ≤ 0.0015)

Full size image

The between state comparisons revealed the following. For propofol, a significant increase in HF power and total power, an increase in normalized HF power (p = 0.0195), and decrease in LF/HF ratio (p = 0.0137) were observed from pre-LOC I to LOC I. These parameters did not show any significant change from LOC I to ROC I. However, an increase in SDNN (p = 0.0059), an increase in RMSSD (p = 0.0137), and lengthening of RR interval (p = 0.0488) were observed from LOC I to ROC I. For dexmedetomidine, a significant lengthening of RR interval and increase in respiratory frequency were observed to take place from baseline to pre-LOC I. More importantly, HF power and total power increased from pre-LOC I to LOC I (p = 0.0195 and p = 0.0078, respectively) and decreased from LOC I to ROC I (p = 0.0117 and p = 0.0078, respectively). In addition, normalized HF power increased from pre-LOC I to LOC I (p = 0.0391), even though this parameter was not found to have any statistically significant difference between the 11 states (see Table 1).

The between drug comparisons revealed that the mean RR interval was significantly longer (lower heart rate) for dexmedetomidine at pre-LOC I, LOC I and ROC I when compared to propofol. RMSSD was higher for dexmedetomidine at pre-LOC I (p = 0.0222) and LOC I (p = 0.0275).

The changes in the HF and total spectral power around LOC and ROC observed using the Kalman smoother spectral estimation approach constitute the main finding of the study. Therefore, individual changes in these parameters around LOC and ROC were further evaluated. In addition, the identification performance of the proposed Kalman smoother spectrum estimation approach (KS1) was compared to performances of standard Kalman smoother spectrum estimation without spectral decomposition and respiratory frequency tracking (KS2) and short-time Fourier transform (STFT) computed using 120 s moving window. Figure 4 shows the individual trajectories of HF power (both in absolute and normalized units) around LOC and ROC for the dexmedetomidine group. The absolute power values are shown for the three different spectrum estimation methods. The proposed Kalman smoother and the standard Kalman smoother approach estimates differ noticeably only for four subjects (S3, S5, S7 and S9).

Figure 4
figure 4

Individual HF power trajectories (subjects S1–S9) around LOC and ROC for dexmedetomidine extracted by using the proposed Kalman smoother approach (KS1), standard Kalman smoother approach (KS2), and STFT. Pre-LOC, LOC and ROC times are illustrated with red vertical lines, whereas pre-LOC I, LOC I and ROC I states used in statistical comparisons are illustrated with gray vertical bars

Full size image

From Fig. 4, it is clear that there are big inter-individual differences in the HF power trends as well as in the duration of the LOC. However, there is a certain consistency in the HF power changes. The statistics of the HF and total power changes around LOC (Prop and Dex) and ROC (Dex) observed using the different spectrum estimation methods are presented in Table 3. Overall, the most consistent statistics are obtained with the proposed spectrum estimation method. In the propofol group, the HF power increase from pre-LOC I to LOC I is captured with the proposed method for all 10 subjects. In the dexmedetomidine group, the HF power increase from pre-LOC I to LOC I is captured for 8/9 subjects (all except S5) and the decrease from LOC I to ROC I is captured for 8/9 subjects (all except S2, for whom there is also a decrease, but it starts a bit later). Therefore, for 7/9 subjects a consistent trend in HF power (increase before LOC and decrease before ROC) is observed for dexmedetomidine by using the proposed Kalman smoother spectrum estimation method. However, by visual inspection this trend in HF power is more or less clear for 6/9 subjects (S1, S2, S3, S6, S7, and S9). For two other subjects (S5 and S8), a clear decrease in HF power is observed at ROC but they don’t show any clear increase in HF before LOC.

Table 3 Comparison of spectrum estimation methods, reproducibility of the main findings
Full size table

Discussion

The proposed Kalman smoother spectrum estimation approach was observed to produce high time-frequency resolution, and thereby it provided accurate estimation of HRV frequency-domain measures when monitoring fast changes in the level of consciousness. A more detailed comparisons of the time-frequency resolutions of Kalman smoother approach and STFT (also known as the spectrogram) have been made in Tarvainen et al.37,38 In Tarvainen et al.,37 it was also proposed that the LF and HF powers can be evaluated more accurately from the decomposed spectral components than by using predefined frequency bands. The results of this study, verify this proposition by showing that the decomposition can have a significant effect on certain HRV measures even in the group level. In this paper, the Kalman smoother approach was further improved to take into account changes in respiratory frequency when defining the frequency band for the HF component. This improvement ensures that the RSA component is fully included in the HF band and the parasympathetic activity will not be underestimated.

The aim of the study was to examine HRV changes close to loss and recovery of consciousness in two anesthetic drugs, and thereby to evaluate the usefulness of HRV analysis in anesthesia monitoring. The most promising HRV parameters for monitoring purposes were thus identified. In addition, it was important to identify the different cardiovascular effects of the two anesthetics in order to use HRV for supporting anesthesia monitoring in clinical practice.

The results showed an increase in HF power (indicating increase in vagal control of HR) prior to LOC for both drugs (propofol and dexmedetomidine). For dexmedetomidine, a strong decrease in heart rate was also observed prior to LOC. The relative increase of vagal control over sympathetic control of HR was overall larger for dexmedetomidine showing on average strong decrease in heart rate (62/45 bpm in baseline/LOC), strong increases in RMSSD (53/238 ms in baseline/LOC), absolute HF power (700/3180 ms2 in baseline/LOC), and normalized HF power (47/84% in baseline/LOC). However, only the decrease in heart rate was found to be statistically different between the two drugs. These findings are in line with the well-described cardiovascular effects of dexmedetomidine. The main causes of these effects are its centrally mediated sympatholytic effect (i.e., attenuation of sympathetic tone) in combination with peripherally mediated vasoconstriction.13 The augmented parasympathetic outflow has been attributed to the direct activation of alfa2-adrenoceptors in the dorsal motor nucleus of the vagus nerve and nucleus tractus solitarius.36

The most promising HRV parameter for anesthesia monitoring purposes was the absolute HF power which increased from pre-LOC to LOC (202/669 ms2 increase for Prop/Dex). Also the total power increased from pre-LOC to LOC, but this was due to the increase in HF component. For dexmedetomidine, the HF power and total power decreased again from LOC to ROC (−357 and −1318 ms2, respectively), and thus they could be used also for predicting ROC. For propofol, on the other hand, the most significant change between LOC and ROC was in SDNN which increased by 22 ms. The individual trajectories of HF power around LOC and ROC were further examined for dexmedetomidine in Fig. 4 and Table 3, which showed that for 6/9 subjects the HF power trend was consistent around LOC and ROC. In conclusion, these preliminary findings suggest that the HF component power of HRV could be utilized in monitoring loss and recovery of consciousness during dexmedetomidine anesthesia.

The proposed Kalman smoother spectrum estimation method outperformed the standard Kalman smoother approach and STFT in identification of LOC and ROC. As the standard Kalman smoother approach we considered the proposed method without the spectral decomposition and respiratory frequency tracking. The respiratory frequency tracking did not actually have any effect on the identification of LOC and ROC because respiratory frequencies of all subjects around these time points were within the default HF frequency band (0.15–0.4 Hz). The respiratory frequency was however just below 0.15 Hz in baseline for two subjects. The fact that the respiratory dynamics within the study population stayed mainly within the normal range does not reduce the importance of respiratory tracking. Quite the contrary, dynamic adjustment of the HF band according to respiratory dynamics is an important point when developing time-varying HRV analysis methods that need to be reliable and need to operate in real time automatically.

Spectral decomposition, on the other hand, had a noticeable effect on the HF power estimates in few subjects. The two evident causes for this are; (1) a strong LF component spreads partly into the HF band (Fig. 4, S7) and (2) the respiratory frequency is close to either of the HF band limits, and therefore part of the HF component power spreads outside the HF band (Fig. 4, S5). In the first case, the HF power will be overestimated, and in the second case underestimated, if spectral decomposition is not used in HF power computation. The disadvantage of the STFT is the relatively low time-frequency resolution compared to the Kalman smoother approach. Therefore, STFT could not identify LOC and ROC as reliably as the proposed method.

There are several previous studies showing an overall decrease in HRV during propofol anesthesia.16,20,21,27,33,35,41 Such a reduction was not observed in the present study, which is probably because the depth of anesthesia was low and it lasted only for a short time, whereas in most of the previous studies higher concentrations of anesthetics (i.e., deeper anesthesia) were used. It should also be noted that in many previous studies subjects have been mechanically ventilated which was not the case in this study. Mechanical ventilation can have influence on HRV because it produces a non-physiological condition in which pulmonary pressures are reversed compared to spontaneous breathing, and therefore normal RSA may be disturbed.

HRV changes related to dexmedetomidine induced anesthesia have not been studied as widely. In Penttilä et al.,32 intravenous infusion of dexmedetomidine was followed by a decrease in heart rate and increase in HF variability with maximal effect at 10 min. In Hogue et al.,18 infusion of dexmedetomidine was followed by a decrease in heart rate and LF power in unanesthesized subjects, but no change was observed in HF power. In the present study, heart rate decreased and HF power increased after the infusion until LOC which supports the results of Penttilä et al.32 Furthermore, in Feld et al.,14 a decrease in LF and HF powers accompanied by decrease in LF/HF ratio was observed during dexmedetomidine anesthesia. Our results did not show any clear decrease in LF or HF power after LOC, but this is probably due to the relatively short lasting anesthesia in the present study.

The limitations of this study include the rather small number of subjects. For anesthesia monitoring purposes during clinical practice, the methods should be further tested with more subjects and also in different experimental conditions (deeper anesthesia, ventilated subjects etc.). In addition, the rather high inter-individual variability in the HRV parameters (even between the healthy young male subjects tested in this study) is a clear limitation. The Kalman smoother algorithm applied in this paper was based on a linear model, but it would be interesting to further investigate if nonlinear modeling of the RSA could improve the identification of LOC and ROC. Finally, the Kalman smoother algorithm applied in this paper is not suitable for real-time monitoring, but a fixed-lag smoother algorithm could be used for real-time functionality.