Decomposition and Description of the Nasal Cavity Form

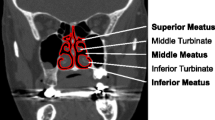
Abstract

Patient-specific studies of physiological flows rely on anatomically realistic or idealized models. Objective comparison of datasets or the relation of specific to idealized geometries has largely been performed in an ad hoc manner. Here, two rational procedures (based respectively on Fourier descriptors and medial axis (MA) transforms) are presented; each provides a compact representation of a complex anatomical region, specifically the nasal airways. The techniques are extended to furnish average geometries. These retain a sensible anatomical form, facilitating the identification of a specific anatomy as a set of weighted perturbations about the average. Both representations enable a rapid translation of the surface description into a virtual model for computation of airflow, enabling future work to comprehensively investigate the relation between anatomic form and flow-associated function, for the airways or for other complex biological conduits. The methodology based on MA transforms is shown to allow flexible geometric modeling, as illustrated by a local alteration in airway patency. Computational simulations of steady inspiratory flow are used to explore the relation between the flow in individual vs. averaged anatomical geometries. Results show characteristic flow measures of the averaged geometries to be within the range obtained from the original three subjects, irrespective of averaging procedure. However the effective regularization of anatomic form resulting from the shape averaging was found to significantly reduce trans-nasal pressure loss and the mean shear stress in the cavity. It is suggested that this may have implications in attempts to relate model geometries and flow patterns that are broadly representative.

Appendix

Implicit Function

In brief, the interpolating surface is defined as the zero-level iso-surface of an implicit function $f(\mathbf{x}).$ Setting $f(\mathbf{x})=0$ on sampled points of the cross-section stack, defines the on-surface constraints. A gradient is formed in the implicit function by introducing further constraints at a constant close distance normal to the curve, known as off-surface constraints, with $f(\mathbf{x})<-\lambda$ inside the curves and $f(\mathbf{x})>\lambda$ outside the curves, where λ is a constant. Interpolation of these constraints leads to the solution of the unknown coefficients $\mathbf{c}$ from a linear system given by $f(\mathbf{x}_{i})= \sum^{n}_{j=1}\mathbf{c}_{j}\phi(\mathbf{x}_{i}-\mathbf{x}_{j}),$ for $i=1,\ldots,n,$ where n is the number of constraints. Here the weighting function is given by the cubic RBF (RBF), hence $\phi(\mathbf{x}_{i}-\mathbf{x}_{j})= |\mathbf{x}_{i}-\mathbf{x}_{j}|^{3},$ where $|\cdot|$ denotes the Euclidean norm, $\mathbf{x}_{i}$ are the position vectors the function is evaluated at and $\mathbf{x}_{j}$ are the interpolation constraints, for $\mathbf{x}_{j}=(x_{j},y_{j},z_{j});\quad j=1,\ldots,n.$ This choice of RBF is such that it minimises curvature variation.

The zero-level iso-surface of the implicit function that defines the virtual model surfaces is extracted using the marching tetrahedra approach5 with linear interpolation to give an initial triangulation, which was then projected onto the true zero-level iso-surface.

To reduce the computational time in the implicit function formulation as well as the marching tetrahedra method, a partition-of-unity approach15,37 is used. This divides the global domain of interest into smaller overlapping sub-domains where the problem can be solved locally. The local solutions are combined together by using weighting functions that act as smooth blending functions to obtain the global solution.

Medial Axis

The approach used in this work is the following: a two-dimensional closed curve is defined with edge, E. A medial axis S is then defined as the set of points whose closest distance, D, from the nearest boundary is locally maximum.22 The local value of D, denoted by d _ij , is obtained for a uniform sampling grid centered at the center of mass of E and made up of $n_{\zeta_{1}} \times n_{\zeta_{2}}$ points p _ij , where $i=1,\ldots,n_{\zeta_{1}},j=1,\ldots,n_{\zeta_{2}},\zeta_{1}$ and $\zeta_{2}$ are orthogonal axes of the sampling grid, and $\zeta_{1}$ is chosen as the major axis of E. The grid is typically formed by choosing $n_{\zeta_{1}} = 1000$ and maintaining the spacing yields $n_{\zeta_{2}} \approx 400$ for the middle section of the nasal cavity. If an interrogation point p _ij on the grid is inside E then d _ij  > 0 and if outside d _ij  < 0. Hence, a value of d _ij  = 0 signifies that p _ij lies on E. If the points on the grid are given an out-of-plane distance proportional to d _ij , the object would resemble a hilly landscape where S would be the resultant connected crests (or ridgeline).11 The local maximum is extracted using a 3 × 3 local mask and results in a cluster of points that are then connected, ensuring that different branches are identified. Finally interpolation is performed to yield smooth fitting curves that are the medial axes and represent the supporting frame of E.

This procedure is sensitive to the resolution of the evaluation grid, generating spurious or insignificant branches if overly fine. This sensitivity arises if the piecewise linear segments that form E are comparable or larger than the grid scale, and hence at the junction of each segment a MA is formed. High grid sampling is however needed to accurately capture the medial axes. An automatic pruning method is adopted such that each branch is checked to identify spurious terminal branches by calculating its gradient $g= \frac{\text{length\;of\;branch}}{\text{branch calibre at root}}.$ A criterion for the classification of a branch as spurious can be set based on the value of g. In the present case, a limit of g ≤ 1.1 was found to be robust in determining whether branches should be removed, although the choice is somewhat arbitrary and different values may be required for other datasets. Other pruning methods are described in Weeks et al.,40 Tam and Heidrich,35 and Aujay et al.33 which may be beneficial for other applications. For example an alternative approach is to consider branch lengths, such that if shorter than a given value they can be considered as small features and removed without significantly altering the object.

The pruning acts as a filter, reducing the level of detail by incrementally removing features of the smallest magnitude. This will therefore also progressively reduce the surface area and volume of the object. A small uniform inflation of the medial axes calibre is hence required, to account for the volume lost due to the pruning procedure. This inflation does not effectively change the surface area of the geometry boundary due to the high aspect ratio of the sections. Details of the surface areas and volumes of the cases studied are detailed in Tables 1 and 2.

Fourier Descriptor

Let us consider a closed curve γ(l) that can be expressed as a signal g(l), where l is the perimeter-length at a certain location and 0 ≤ l ≤ L, such that the signal has period L. The discrete Fourier expansion of g(l) is formulated by sampling at m equally spaced points to yield $g(k);k=0, \ldots,m-1.$ The discrete Fourier transform (DFT) is given by

$$c(n)=\frac{1}{m}\sum_{k=0}^{m-1}g(k) e^{-i2\pi nk/m} \quad 0 \le n \le m-1 $$

(1)

where $i=\sqrt{-1}.$ The real and complex components of c(n) are the FDs, denoted as R(n) and I(n), respectively. The amplitude, or energy, of the nth mode in the series expansion is given by $\sqrt{R(n)^2+I(n)^2}.$ To reconstruct g(k) the inverse discrete Fourier transform (IDFT) is used, which is given by

$$ g(k)=\sum_{n=0}^{m-1}c(n) e^{i2\pi nk/m} \quad 0 \le k \le m-1 $$

(2)

Signals of the closed curve may be formulated by considering the change in angular direction,42 however in this work the location in fixed Cartesian coordinate frame38 is used. The advantage in providing a signal in terms of the angular direction variation along the curve is that only one signal is required, while if using a Cartesian coordinate approach an orthogonal signal for each axis is required. In this work the Cartesian coordinate approach is used since it allows a closed contour to be reconstructed after filtering, averaging or other signal manipulations that is not possible otherwise. A brief description of this approach is now given.

A curve can be described as the change of location coordinates as a function of l, hence implementable directly in ${\mathbb{R}^{3}}$ even when the planar cross-sections are not aligned to the Cartesian axes. The signal that describes the curve is given by g(l) = (x(l) − x(0), y(l) − y(0), z(l) − z(0)), providing an orthogonal signal for each axis that allows for independent signal modification if desired. It is important to note that since the signals are periodic, a reconstructed closed curve in ensured.