Skip to main content
SpringerLink
Log in

Rotation-based finite elements: reference-configuration geometry and motion description

  • Research Paper
  • Published:
Acta Mechanica Sinica Aims and scope Submit manuscript

Abstract

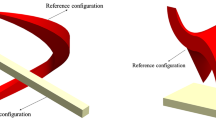
Infinitesimal-rotation finite elements allow creating a linear problem that can be exploited to systematically reduce the number of coordinates and obtain efficient solutions for a wide range of applications, including those governed by nonlinear equations. This paper discusses the limitations of conventional infinitesimal-rotation finite elements (FE) in capturing correctly the initial stress-free reference-configuration geometry, and explains the effect of these limitations on the definition of the inertia used in the motion description. An alternative to conventional infinitesimal-rotation finite elements is a new class of elements that allow developing inertia expressions written explicitly in terms of constant coefficients that define accurately the reference-configuration geometry. It is shown that using a geometrically inconsistent (GI) approach that introduces the infinitesimal-rotation coordinates from the outset to replace the interpolation-polynomial coefficients is the main source of the failure to capture correctly the reference-configuration geometry. On the other hand, by using a geometrically consistent (GC) approach that employs the position gradients of the absolute nodal coordinate formulation (ANCF) to define the infinitesimal-rotation coordinates, the reference-configuration geometry can be preserved. Two simple examples of straight and tapered beams are used to demonstrate the basic differences between the two fundamentally different approaches used to introduce the infinitesimal-rotation coordinates. The analysis presented in this study sheds light on the differences between the incremental co-rotational solution procedure, widely used in computational structural mechanics, and the non-incremental floating frame of reference formulation (FFR), widely used in multibody system (MBS) dynamics.

Graphic Abstract

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. Specht, B.: Modified shape functions for the three-node plate bending element passing the patch Test. Int. J. Numer. Meth. Eng. 26(3), 705–715 (1988)

    Article  MATH  Google Scholar 

  2. Noor, A.K.: Bibliography of monographs and surveys on shells. Appl. Mech. Rev. 43(9), 223–234 (1990)

    Article  MathSciNet  Google Scholar 

  3. A.K. Noor, S.H. Belytschko, J.C. Simo, Analytical and computational models of shells, in Proceedings of the Symposium, ASME Winter Annual Meeting, San Francisco, CA, United States, 1989

  4. Cammarata, A., Pappalardo, C.M.: On the use of Component mode synthesis methods for the model reduction of flexible multibody systems within the floating frame of reference formulation. Mech. Syst. Signal Process. 142, 106745 (2020). https://doi.org/10.1016/j.ymssp.2020.106745

    Article  Google Scholar 

  5. Guo, X., Zhang, D.G., Li, L., et al.: Application of the two-loop procedure in multibody dynamics with contact and constraint. Sound Vib. 427, 15–27 (2018)

    Article  Google Scholar 

  6. García-Vallejo, D., Alcayde, A., López-Martínez, J., et al.: Detection of communities within the multibody system dynamics network and analysis of their relations. Symmetry 11, 1525 (2019). https://doi.org/10.3390/sym11121525

    Article  Google Scholar 

  7. Duan, Y.C., Zhang, D.G., Hong, J.Z.: Partition method for impact dynamics of flexible multibody systems based on contact constraint. Appl. Math. Mech. (Engl. Ed.) 34, 1393–1404 (2013)

    Article  MathSciNet  Google Scholar 

  8. Shabana, A.A.: Dynamics of Multibody Systems, 5th edn. Cambridge University Press, Cambridge (2020)

    Book  MATH  Google Scholar 

  9. Belytschko, T., Hsieh, B.J.: Nonlinear transient finite element analysis with convected coordinates. Int. J. Numer. Methods Eng. 7, 255–271 (1973)

    Article  MATH  Google Scholar 

  10. Belytschko, T., Glaum, L.W.: Applications of higher order corotational stretch theories to nonlinear finite element analysis. Comput. Struct. 1, 175–182 (1979)

    Article  MATH  Google Scholar 

  11. Belytschko, T., Schwer, L.: Large displacement transient analysis of space frames. Int. J. Numer. Methods Eng. 11, 65–84 (1977)

    Article  MATH  Google Scholar 

  12. Gerstmayr, J., Schoberl, J.: A 3D finite element method for flexible multibody systems. Multibody Syst. Dyn. 15(4), 305–320 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  13. Nada, A.A.: Flexible robotic manipulators: modeling, simulation and control with experimentation, [PhD Thesis], Cairo University, Cairo, Egypt, 2007.

  14. Cook, R.D., Malkus, D.S., Plesha, M.E., et al.: Concepts and Applications of Finite Element Analysis, 4th edn. Wiley, New York (2001)

    MATH  Google Scholar 

  15. Hutton, D.V.: Fundamentals of Finite Element Analysis, 1st edn. McGraw-Hill, New York (2003)

    Google Scholar 

  16. Segerlind, L.J.: Applied Finite Element Analysis, 1st edn. Wiley, New York (1976)

    MATH  Google Scholar 

  17. Seshu, P.: Textbook of Finite Element Analysis, 1st edn. PHI Learning Private Limited, New Delhi (2004)

    MATH  Google Scholar 

  18. Shames, I.H., Dym, C.L.: Energy and Finite Element Methods in Structural Mechanics. Hemisphere Publishing, New York (1985)

    MATH  Google Scholar 

  19. Zeng, P.: Finite Element Analysis and Applications. Tsinghua University Press, Beijing, China (2004)

    Google Scholar 

  20. Zienkiewicz, O.C., Taylor, R.L., Zhu, J.Z.: Finite Element Method: Its Basis and Fundamentals, 7th edn. Butterworth-Heinemann, Waltham, MA (2017)

    MATH  Google Scholar 

  21. Farin, G.: Curves and Surfaces for CAGD, A Practical Guide, 5th edn, Morgan Kaufmann, Publishers, San Francisco, 1999

  22. Gallier, J.: Geometric Methods and Applications: For Computer Science and Engineering. Springer, New York (2011)

    Book  MATH  Google Scholar 

  23. Goetz, A.: Introduction to Differential Geometry. Addison Wesley, Reading (1970)

    MATH  Google Scholar 

  24. Kreyszig, E.: Differential Geometry. Dover, New York (1991)

    MATH  Google Scholar 

  25. Piegl, L., Tiller, W.: The NURBS Book, 2nd edn. Springer, Berlin (1997)

    Book  MATH  Google Scholar 

  26. Rogers, D.F.: An Introduction to NURBS with Historical Perspective. Academic Press, San Diego, CA (2001)

    Google Scholar 

  27. Chen, Y., Zhang, D.G., Li, L.: Dynamic analysis of rotating curved beams by using absolute nodal coordinate formulation based on radial point interpolation method. Sound Vib. 441, 63–83 (2019)

    Article  Google Scholar 

  28. Dmitrochenko, O., Mikkola, A.: Digital nomenclature code for topology and kinematics of finite elements based on the absolute nodal co-ordinate formulation. Proc. Inst. Mech. Eng. Part K J. Multi-body Dyn. 225(1), 34–51 (2011)

    Google Scholar 

  29. Fotland, G., Haskins, C., Rølvåg, T.: Trade study to select best alternative for cable and pulley simulation for cranes on offshore vessels. Syst. Eng. 23(2), 1–12 (2019). https://doi.org/10.1002/sys.21503

    Article  Google Scholar 

  30. Hewlett, J.: Methods for real-time simulation of systems of rigid and flexible bodies with unilateral contact and friction, [PhD Thesis], McGill University, 2019

  31. Hewlett, J., Arbatani, S., Kovecses, J.: A fast and stable first-order method for simulation of flexible beams and cables. Nonlinear Dyn. 99, 211–1226 (2020)

    Article  Google Scholar 

  32. Htun, T.Z., Suzuki, H., Garcia-Vallejo, D.: Dynamic modeling of a radially multilayered tether cable for a remotely-operated underwater vehicle (ROV) based on the absolute nodal coordinate formulation (ANCF). Mech. Mach. Theory (2020). https://doi.org/10.1016/j.mechmachtheory.2020.103961

    Article  Google Scholar 

  33. I.M. Khan, K.S. Anderson, Divide-and-conquer-based large deformation formulations for multi-flexible body systems, Proceedings of the ASME 9th International Conference on Multibody Systems, Nonlinear Dynamics, and Control, vol. 7B, Portland, Oregon, USA, pp. V07BT10A002-1–V07BT10A002-10, 2013

  34. Kłodowski, A., Rantalainen, T., Mikkola, A., et al.: Flexible multibody approach in forward dynamic simulation of locomotive strains in human skeleton with flexible lower body bones. Multibody Syst. Dyn. 25(4), 395–409 (2011)

    Article  MATH  Google Scholar 

  35. Laflin, J.J., Anderson, K.S., Khan, I.M., et al.: New and extended applications of the divide-and-conquer algorithm for multibody dynamics. J. Comput. Nonlinear Dyn. 9(4), 041004-1-041004–8 (2014)

    Google Scholar 

  36. Li, S., Wang, Y., Ma, X., et al.: Modeling and simulation of a moving yarn segment: based on the absolute nodal coordinate formulation. Math. Probl. Eng. 2019, 6567802 (2019). https://doi.org/10.1155/2019/6567802

  37. Nachbagauer, K.: Development of shear and cross section deformable beam finite elements applied to large deformation and dynamics problems, [PhD Thesis], Johannes Kepler University, Linz, Austria, 2013

  38. Nachbagauer, K., Pechstein, A.S., Irschik, H., et al.: A new Locking-free formulation for planar, shear deformable, linear and quadratic beam finite elements based on the absolute nodal coordinate formulation. Multibody Syst. Dyn. 26(3), 245–263 (2011)

    Article  MATH  Google Scholar 

  39. Orzechowski, G.: Analysis of beam elements of circular cross section using the absolute nodal coordinate formulation. Arch. Mech. Eng. 59(3), 283–296 (2012)

    Article  MathSciNet  Google Scholar 

  40. Orzechowski, G., Frączek, J.: Integration of the equations of motion of multibody systems using absolute nodal coordinate formulation. Acta Mech. Autom. 6(2), 75–83 (2012)

    Google Scholar 

  41. Orzechowski, G., Frączek, J.: Nearly incompressible nonlinear material models in the large deformation analysis of beams using ANCF. Nonlinear Dyn. 82(1–2), 451–464 (2015)

    Article  MathSciNet  Google Scholar 

  42. Shabana, A.A.: ANCF tire assembly model for multibody system applications. J. Comput. Nonlinear Dyn. 10(2), 024504-1-024504–4 (2015)

    Google Scholar 

  43. Shabana, A.A.: Computational Continuum Mechanics, 3rd edn. Wiley & Sons, Chichester (2018)

    Book  MATH  Google Scholar 

  44. Sun, J., Tian, Q., Hu, H., et al.: Axially variable-length solid element of absolute nodal coordinate formulation. Acta. Mech. Sin. 35, 653–663 (2019). https://doi.org/10.1007/s10409-018-0823-7

    Article  MathSciNet  Google Scholar 

  45. Tian, Q., Chen, L.P., Zhang, Y.Q., et al.: An efficient hybrid method for multibody dynamics simulation based on absolute nodal coordinate formulation. J. Comput. Nonlinear Dyn. 4(2), 021009-1-021009–14 (2009)

    Google Scholar 

  46. Tian, Q., Sun, Y.L., Liu, C., et al.: Elastohydro-dynamic lubricated cylindrical joints for rigid–flexible multibody dynamics. Comput. Struct. 114–115, 106–120 (2013)

    Article  Google Scholar 

  47. Yu, L., Zhao, Z., Tang, J., et al.: Integration of absolute nodal elements into multibody system. Nonlinear Dyn. 62, 931–943 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  48. Yamano, A.A., Shintani, A., Ito, T., et al.: Influence of boundary conditions on a flutter-mill. Sound Vib. 478, 115359 (2020)

    Article  Google Scholar 

  49. Zhang, Y., Wei, C., Zhao, Y., et al.: Adaptive ancf method and its application in planar flexible cables. Acta. Mech. Sin. 34, 199–213 (2018). https://doi.org/10.1007/s10409-017-0721-4

    Article  MathSciNet  MATH  Google Scholar 

  50. Shabana, A.A.: Geometrically accurate floating frame of reference finite elements for the small deformation problem. Proc. Inst. Mech. Eng. Part K J. Multi-body Dyn. 232(2), 286–292 (2017)

    Google Scholar 

  51. Shabana, A.A.: Geometrically accurate infinitesimal-rotation spatial finite elements. Proc. Inst. Mech. Eng. Part K J. Multi-body Dyn. 232(1), 182–187 (2018)

    Google Scholar 

  52. Zhang, Z.G., Wang, T.F., Shabana, A.A.: Development and implementation of geometrically accurate reduced-order models: convergence properties of planar beams. J. Sound Vib. 439, 45–478 (2019)

    Article  Google Scholar 

  53. Shabana, A.A.: ANCF consistent rotation-based finite element formulation. J. Comput. Nonlinear Dyn. 11(1), 014502-1-014502–4 (2016)

    Google Scholar 

  54. Zheng, Y.H., Shabana, A.A.: A two-dimensional shear deformable ANCF consistent rotation-based formulation beam element. Nonlinear Dyn. 87(2), 1031–1043 (2017)

    Article  Google Scholar 

  55. Boresi, A.P., Chong, K., Lee, J.D.: Elasticity in Engineering Mechanics, 3rd edn. Wiley, New Jersey (2011)

    MATH  Google Scholar 

  56. Holzapfel, G.A.: Nonlinear Solid Mechanics: A Continuum Approach for Engineering. Wiley, Chichester (2000)

    MATH  Google Scholar 

  57. Ogden, R.W.: Non-linear Elastic Deformations, 1st edn. Wiley, New York (1984)

    MATH  Google Scholar 

  58. Chandrupatla, T.R., Belegundu, A.D.: Introduction to Finite Elements in Engineering, 4th edn. Pearson Education, New Jersey (2012)

    MATH  Google Scholar 

  59. Zienkiewicz, O.C.: The Finite Element Method, 3rd edn. McGraw Hill, New York (1977)

    MATH  Google Scholar 

  60. Shabana, A.A.: Definition of ANCF finite elements. ASME J. Comput. Nonlinear Dyn. 10, 054506-1-054506–5 (2015)

    Google Scholar 

  61. Omar, M.A., Shabana, A.A.: A two-dimensional shear deformable beam for large rotation and deformation problems. J. Sound Vib. 243(3), 565–576 (2001)

    Article  Google Scholar 

  62. Mackenzie, D.: Curing ill surfaces, SIAM News, April 2011.

  63. Shabana, A.A., Ling, H.: Noncommutativity of finite rotations and definitions of curvature and torsion. ASME J. Comput. Nonlinear Dyn. 14, 0910051–09100510 (2019)

    Google Scholar 

  64. Bonet, J., Wood, R.D.: Nonlinear Continuum Mechanics for Finite Element Analysis. Cambridge University Press, Cambridge (1997)

    MATH  Google Scholar 

  65. Bower, A.F.: Applied Mechanics of Solids, 1st edn. CRC Press, Boca Raton (2009)

    Book  Google Scholar 

  66. Spencer, A.J.M.: Continuum Mechanics. Longman, London, England (1980)

    MATH  Google Scholar 

  67. Logan, D.L.: A First Course in the Finite Element Method, 6th edn. Cengage Learning, New Delhi (2017)

    Google Scholar 

  68. Gibson, S.F.F., Mirtich, B.: A Survey of Deformable Modeling in Computer Graphics. Mitsubishi Electric Research Laboratories, http://www.merl.com, TR97-19, 1997.

  69. Metaxas, D.N.: Physics-Based Deformable Models: Applications to Computer Vision, Graphics, and Medical Imaging. Springer, New York (2012)

    Google Scholar 

  70. Metaxas, D., Terzopoulos, D.: Shape and nonrigid motion estimation through physics-based synthesis. IEEE Trans. Pattern Anal. Mach. Intell. 15, 580–591 (1993)

    Article  Google Scholar 

  71. Qin, H., Terzopoulos, D.: D-NURBS: a physics-based framework for geometric design. IEEE Trans. Visual Comput. Graphics 2(1), 85–96 (1996)

    Article  Google Scholar 

  72. Terzopoulos, D., Metaxas, D.: Dynamic 3D models with local and global deformations: deformable superquadrics. IEEE Trans. Pattern Anal. Mach. Intell. 13, 703–714 (1991)

    Article  Google Scholar 

  73. Chu, S.C., Pan, K.C.: Dynamic response of a high-speed slider crank mechanism with an elastic connecting rod. ASME J. Eng. Ind. 92, 542–550 (1975)

    Article  Google Scholar 

  74. Shabana, A.A.: Automated analysis of constrained inertia-variant flexible systems. ASME J. Vib. Acoust. 107, 431–440 (1985)

    Article  Google Scholar 

  75. Cottrell, J.A., Hughes, T.J.R., Bazilevs, Y.: Isogeometric Analysis. Wiley, Chichester (2009)

    Book  MATH  Google Scholar 

Download references

Acknowledgements

This research was supported, in part, by the National Science Foundation (Grant 1852510). The authors would like also to thank Ph.D. graduate student Mr. Ahmed Eldeeb of University of Illinois at Chicago for providing some of the figures and data presented in this paper.

Author information

Authors and Affiliations

  1. Department of Mechanical and Industrial Engineering, University of Illinois At Chicago, Chicago, IL, 60607, USA

    Ahmed A. Shabana

  2. Faculty of Mechanical Engineering and Automation, Zhejiang Sci-Tech University, Hangzhou, 310018, China

    Lingmin Xu

Authors
  1. Ahmed A. Shabana
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Lingmin Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ahmed A. Shabana.

Additional information

Executive Editor: Gui-Lin Wen

Appendix

Appendix

The ANCF mass matrix of straight beam can be written as:

$$ \begin{aligned} {\mathbf{M}}_{As} & = \rho t\iint {{\mathbf{S}}_{A}^{{\text{T}}} {\mathbf{S}}_{A} {\text{d}}x{\text{d}}y} \\ & = m\left[ {\begin{array}{*{20}c} {13/35} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} \\ 0 & {13/35} & {} & {} & {} & {} & {} & {} & {} & {} & {} & {} \\ {11l/210} & 0 & {l^{2} /105} & {} & {} & {} & {} & {} & {{\text{symmetric}}} & {} & {} & {} \\ 0 & {11l/210} & 0 & {l^{2} /105} & {} & {} & {} & {} & {} & {} & {} & {} \\ 0 & 0 & 0 & 0 & {h^{2} /36} & {} & {} & {} & {} & {} & {} & {} \\ 0 & 0 & 0 & 0 & 0 & {h^{2} /36} & {} & {} & {} & {} & {} & {} \\ {9/70} & 0 & {13l/420} & 0 & 0 & 0 & {13/35} & {} & {} & {} & {} & {} \\ 0 & {9/70} & 0 & {13l/420} & 0 & 0 & 0 & {13/35} & {} & {} & {} & {} \\ { - 13l/420} & 0 & { - l^{2} /140} & 0 & 0 & 0 & { - 11l/210} & 0 & {l^{2} /105} & {} & {} & {} \\ 0 & { - 13l/420} & 0 & { - l^{2} /140} & 0 & 0 & 0 & { - 11l/210} & 0 & {l^{2} /105} & {} & {} \\ 0 & 0 & 0 & 0 & {h^{2} /72} & 0 & 0 & 0 & 0 & 0 & {h^{2} /36} & {} \\ 0 & 0 & 0 & 0 & 0 & {h^{2} /72} & 0 & 0 & 0 & 0 & 0 & {h^{2} /36} \\ \end{array} } \right] \\ \end{aligned} $$
(46)

For the planar straight beam with the coordinate system located at the end point, the mass moment of inertia is

$$ J = {\mathbf{e}}_{Aso}^{{\text{T}}} {\mathbf{M}}_{As} {\mathbf{e}}_{Aso} = m\left( {4l^{2} { + }h^{2} } \right)/12, $$
(47)

where \({\mathbf{e}}_{Aso}\) is the vector of element nodal coordinates defined with respect to the coordinate system located at the end point. If the coordinate system is located at the center for the straight beam, the mass moment of inertia is

$$ J = {\mathbf{e}}_{Asc}^{{\text{T}}} {\mathbf{M}}_{As} {\mathbf{e}}_{Asc} = m\left( {l^{2} + h^{2} } \right)/12, $$
(48)

where \({\mathbf{e}}_{Asc}\) is the vector of element nodal coordinates defined with respect to the coordinate system located at the center of the element. When the ANCF element is used, the tapered geometry is accounted for by stretching the transvers gradient vector [43].

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Shabana, A.A., Xu, L. Rotation-based finite elements: reference-configuration geometry and motion description. Acta Mech. Sin. 37, 105–126 (2021). https://doi.org/10.1007/s10409-020-01030-6

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10409-020-01030-6

Keywords

Search

Navigation