1 Introduction

Gas flow in porous media can be observed in various engineering devices such as catalytic converters and fuel cells. Because of their large effective surface area, porous media are used to facilitate surface reactions such as dissociation of \(\mathrm {H}_2\) in electrodes of proton exchange membrane fuel cells (PEMFCs). In order to improve the performance of such devices, it is important to understand transport phenomena in porous media.

Gas flow through a porous medium is usually analyzed by using Darcy’s law (1856), which states that the discharge rate through a porous medium is proportional to the pressure gradient \(\nabla p\) and the permeability K and is inversely proportional to the coefficient of viscosity \(\mu\) of gas. Darcy’s law can be written as

$$\begin{aligned} U_\mathrm s=-\frac{K}{\mu }\nabla p, \end{aligned}$$
(1)

where p is the gas pressure and \(U_\mathrm s\) is the superficial velocity, which is defined as the volume flow rate through a unit cross-sectional area of the solid plus fluid of a porous medium (Bird et al. 2007). The superficial velocity \(U_\mathrm s\) is not the velocity of the gas traveling through the pores. The average velocity U of the gas traveling through the pores has the following relation with the superficial velocity \(U_\mathrm s\):

$$\begin{aligned} U=\frac{U_\mathrm s}{\varepsilon }, \end{aligned}$$
(2)

where \(\varepsilon\) is the porosity of the porous medium. In order to estimate gas flow rate through a porous medium, evaluating its permeability correctly is important. In previous studies, the following empirical models for permeability have been proposed:

$$\begin{aligned} K_{\mathrm {B-K}}& = \displaystyle \frac{d_{\mathrm p}^2}{150}\frac{\varepsilon ^3}{\left( 1-\varepsilon \right) ^2}, \end{aligned}$$
(3)
$$\begin{aligned} K_{\mathrm {C-K}} & = \displaystyle \frac{d_{\mathrm p}^2}{180}\frac{\varepsilon ^3}{\left( 1-\varepsilon \right) ^2}, \end{aligned}$$
(4)
$$\begin{aligned} K_{\mathrm {R-G}} & = \displaystyle \frac{d_{\mathrm p}^2}{5.6}\frac{\varepsilon ^{5.5}}{1.05}, \end{aligned}$$
(5)

where \(d_\mathrm p\) is the effective average diameter of packed particles of the porous medium, \(K_{\mathrm {B-K}}\), \(K_{\mathrm {C-K}}\), and \(K_{\mathrm {R-G}}\) are the Blake–Kozeny model (Blake 1922; Kozeny 1927), the Carman–Kozeny model (Carman 1937, 1938, 1956; Kozeny 1927), and the Rumpf–Gupte model (Rumpf and Gupte 1971), respectively. The Blake–Kozeny and the Carman–Kozeny models were derived by regarding a porous medium as a bundle of capillary tubes and by considering laminar flow in tubes (Dullien 1979; Bird et al. 2007). The Rumpf–Gupte model was derived by finding the relationship between the friction factor of the porous medium and the porosity by dimensional analysis (Dullien 1979). The constants in these models were determined to fit experimental data on packed beds. In the derivation of these models, the effect of the mean free path of molecules in gaseous flow was neglected. The pores of porous media used in the above-mentioned devices may be in the micro-/nanoscale range, e.g., those of porous media used for electrodes of PEMFCs may be as small as the mean free path of gas molecules. The Knudsen number of gas flow in such porous media is on the order of unity, and hence, the gas is in nonequilibrium because of a lack of intermolecular collisions. Such kind of gas flow is called “high Knudsen number flow” and cannot be treated as a continuum. Since the effect of the mean free path was neglected in the derivation of the above-mentioned permeability models, these models are not applicable to gas flow in such porous media with micro-/nanoscale pores.

In the case where the pore size of porous media is much smaller than the mean free path of gas molecules, i.e., in the case where the Knudsen number is much larger than unity, gas molecules collide with the pore walls much more frequently than with other gas molecules, and thus, the effect of molecule–molecule collisions is negligible. Due to the diffuse reflections at the pore wall, gas molecules diffuse gradually. This phenomenon is called “Knudsen diffusion” and the pressure-driven gas transport in such a high Knudsen number system is governed by Knudsen diffusion. Knudsen (1909) obtained the expression for Knudsen diffusivity in a cylindrical tube. Evans et al. (1980) investigated effective Knudsen diffusivity in porous media, which are represented by packing solid spherical particles, by performing Monte Carlo simulations of molecular motion in porous media. Tomadakis and Sotirchos (1991) also investigated the effective Knudsen diffusivity by performing Monte Carlo simulations, porous media being represented by randomly arranged solid fibers, which can interpenetrate one another.

In the case where the pore size is comparable with the mean free path of gas molecules, gas flow in the porous medium is in the slip or transition flow regime and both the contributions of Knudsen diffusion and viscous flow appear. Knudsen (1909) found that as the averaged pressure is reduced, the gaseous mass flux through capillaries for a given pressure drop decreases at first due to the decrease of gas density, but reaches a minimum value when the Knudsen number is about unity, and then starts to increase. This is caused by the appearance of velocity slip at the capillary wall and Knudsen diffusion. A similar phenomenon will appear in porous media. As the average pressure \(\bar{p}\) decreases, the gas permeability K of a porous medium will increase and deviate from its liquid permeability \(K_0\), which is equal to the gas permeability K in the continuum limit. Klinkenberg (1941) derived the following expression for the effective gas permeability:

$$\begin{aligned} K=K_0\left( 1+\frac{b}{\bar{p}} \right) , \end{aligned}$$
(6)

where b is called the Klinkenberg coefficient. For a large pressure, the gas permeability K is equal to the liquid permeability \(K_0\). This phenomenon is called the “Klinkenberg effect” and is induced by the appearance of velocity slip at the pore walls and Knudsen diffusion. For low permeability porous media, Jones (1972) found that the Klinkenberg coefficient b and the liquid permeability \(K_0\) have the relation, \(b \propto K_0^{-0.36}\). Bravo (2007) developed the generalized model of the Klinkenberg coefficient b for the whole range of the Knudsen number. In his model, the Klinkenberg coefficient b is a function of the Knudsen number. It explains the pressure dependence of the Klinkenberg coefficient b as was seen in experiments, whereas in earlier models the Klinkenberg coefficient b was considered independent of pressure.

For transition flow in porous media, Mason et al. (1967) proposed the dusty gas model, in which the solid body of a porous medium is regarded as large molecules fixed in space and these imaginary molecules are considered to constitute a dusty gas component of the gas mixture. In the dusty gas model, the mass flux of one gas component is given by the sum of diffusive flux and viscous flux, where the diffusive flux is the combined flux of molecular diffusion and Knudsen diffusion. Beskok and Karniadakis (1999) proposed the expression

$$\begin{aligned} \mu _\mathrm e=\mu _\mathrm 0 \frac{1}{1+a\,\mathrm{Kn}} \end{aligned}$$
(7)

for the effective viscosity \(\mu _\mathrm e\) in the transition flow regime and validated it by comparing with the linearized Boltzmann solution and with the results obtained by the direct simulation Monte Carlo (DSMC) method (Bird 1994) (see also Karniadakis et al. 2005). Here, \(\mu _0\) is the viscosity in the continuum limit and Kn is the Knudsen number given by \(\mathrm{Kn}=\lambda _\mathrm {mol}/L\), \(\lambda _\mathrm {mol}\) is the mean free path of gas molecules, and L is the characteristic length of the flow. Michalis et al. (2010) performed DSMC simulations of hard sphere gas flow between parallel plates and found that the numerical factor a has the value of 2 for length-to-width ratio of 20 over the entire transition flow regime. Kalarakis et al. (2012) incorporated the effect of rarefaction on the viscosity, Eq. (7), into the dusty gas model and derived the expression of the effective permeability with the form of the Klinkenberg equation, Eq. (6). They showed that the permeability of a porous medium obtained in the gas flow simulations by the lattice Boltzmann method incorporating the effective gas viscosity in the transition flow regime agrees well with that obtained by the DSMC simulations. Dreyer et al. (2014) investigated the gas diffusion process in high-porosity nanoscale porous media by using the DSMC method and compared the DSMC results with those of the dusty gas model. Christou and Dadzie (2016) investigated the effect of the Knudsen number for the velocity profile in a Berea porous structure, which was obtained with micro-CT, by performing DSMC simulations.

The objectives of the present study are to investigate governing factors of molecular transport due to the pressure gradient through porous media with pores ranging from nanometer to micrometer by performing numerical simulations of gas flow through porous media and to construct an expression to estimate pressure-driven gas transport through such porous media by using the present simulation results and by considering the effects of Knudsen diffusion and viscous flow with a velocity slip.

2 Numerical method

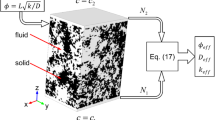
In this study, porous media were represented by randomly arranging solid spherical particles as shown in Fig. 1. Although random arrangement causes interpenetration among neighboring particles, it was allowed in the present study. Steady gas flows in the porous media driven by a steady pressure gradient in the y direction were studied. The surface reaction was neglected here. The lengths of the computational domain in the x and z directions were set to be 3 times as long as the diameter \(d_{\mathrm p}\) of the solid particles and that in the y direction was set to be 30 times as long as \(d_{\mathrm p}\). The centers of spherical particles with the diameter \(d_{\mathrm p}\) were placed randomly in the region of \(1.5 d_{\mathrm p}< y < 28.5 d_{\mathrm p}\). In the present simulation, the diameter \(d_\mathrm p\) of the solid particles is varied from 10 to 2000 nm.

Fig. 1
figure 1

Porous medium represented by randomly arranged solid spherical particles

Full size image

The gas treated here was \(\mathrm H_2\). The hard sphere model (Bird 1994) for intermolecular collisions was used in the present simulation. \(\mathrm H_2\) molecules were treated as hard spheres with diameters of \(d_\mathrm m = 0.274\) nm and masses of \(m = 3.3476\times 10^{-27}\) kg. The molecular diameter \(d_\mathrm m\) was determined from the value of the viscosity \(\mu\) of \(\mathrm H_2\), \(\mu =8.8\times 10^{-6}\) Pa s, in the case of the temperature of \(T = 293\) K and the pressure of \(p=101,325\) Pa by using the relations \(\mu =(1/2)\rho \bar{C}\lambda _\mathrm {mol}\) and \(\lambda _\mathrm {mol}=1/\sqrt{2}n\pi d_\mathrm m^2\), where \(\rho\) is the gas density and given by \(\rho =mn\), n is the number density of molecules, \(\bar{C}\) is the mean molecular speed and given by \(\bar{C}=\sqrt{8k_\mathrm BT/\pi m}\), and \(k_\mathrm B\) is the Boltzmann constant. The mean free path \(\lambda _\mathrm {mol}\) for intermolecular collisions is given by \(\lambda _\mathrm {mol}=119.3\) nm in the case of \(\mathrm H_2\) with the temperature of \(T = 293\) K and the pressure of \(p=101,325\) Pa.

In the case where the diameter \(d_\mathrm p\) of solid spherical particles is as small as the mean free path \(\lambda _\mathrm {mol}\), the pore size will also be as small as the mean free path \(\lambda _\mathrm {mol}\). Since the Knudsen number of gas flow through such porous media will be on the order of unity, such high Knudsen number flow cannot be treated as a continuum, and the governing equation of the gas flow is the Boltzmann equation rather than the Navier–Stokes equations. In order to analyze high Knudsen number gas flows such as rarefied gas flows or micro-/nanoscale gas flows, several methods have been developed, such as the DSMC method (Bird 1994), the lattice Boltzmann method with the Bhatnagar–Gross–Krook (BGK) collision operator (Nie et al. 2002; Zhang et al. 2005; Guo and Zheng 2008), the linearized Boltzmann equation (Ohwada et al. 1989; Doi 2010), and the information preservation (IP) scheme (Fan and Shen 1999, 2001). In the present work, the DSMC method, which is the stochastic solution of the Boltzmann equation (Nanbu 1980), was used for numerical simulations of gas flows in porous media. The DSMC method has been used to simulate gas flow in micro-/nanoscale porous media (Saito et al. 1995; Tomarikawa et al. 2011; Kalarakis et al. 2012; Oshima et al. 2012; Dreyer et al. 2014; Christou and Dadzie 2016).

In the present DSMC simulation, the computational domain was divided into cells, the length of which was about the same or smaller than the mean free path \(\lambda _\mathrm {mol}\) of gas molecules. The motions and collisions of molecules were traced, and hence, time evolution of the flow field was simulated. Intermolecular collisions in the same cell were calculated stochastically using the maximum collision number method (Nanbu 1992, 2000). Except for the cases treated in Fig. 2, the gas pressure at the inlet was set at 1 atm and the mean free path at the inlet, \(\lambda _\mathrm {mol, inlet}\), was 119.3 nm. In the cases of \(d_\mathrm p=10\)–500 nm, the computational domain with the size \(3d_\mathrm p \times 30d_\mathrm p \times 3d_\mathrm p\) was divided into \(10\times 100\times 10\) cubic cells. In those cases, the cell size \(l_\mathrm {cell}\) was given by \(0.3d_\mathrm p\) (=3–150 nm), which was about the same or smaller than the mean free path. In the cases of \(d_\mathrm p=1000\) nm and \(d_\mathrm p=2000\) nm, the computational domain was divided into \(15\times 150\times 15\) cubic cells and \(30\times 300\times 30\) cubic cells, respectively. In those cases, the cell size \(l_\mathrm {cell}\) was 200 nm. It is slightly larger than the mean free path but much smaller than the particle diameter \(d_\mathrm p\). Therefore, this choice of the cell size is also reasonable to describe gas flow through the porous medium, which is represented by the arrangement of particles. Since gas molecules can flow only through a void region in the porous medium, the volume of a void region in each cell needs to be calculated for intermolecular collision judgment in the DSMC simulations. In order to calculate it, we considered grid points, which were equally spaced in the x, y, and z directions in each cell. The spacing between grid points in x, y, and z directions was 10 times smaller than the cell size. The effective volume \(V_\mathrm {cell}\) of a cell, i.e., the volume of the void region in the cell, is given by

$$\begin{aligned} V_\mathrm {cell}=\left( l_\mathrm {cell} \right) ^3 \left( 1- \frac{N_\mathrm {solid}}{N_\mathrm {grid}} \right) , \end{aligned}$$
(8)

where \(N_\mathrm {solid}\) is the number of grid points in the solid region in the cell and \(N_\mathrm {grid}\) is the total number of grid points in the cell and was equal to 1000 in the present simulations.

The post-collisional velocities of molecules impinging on the solid wall were determined by using the diffuse reflection model with wall temperature. The accommodation coefficient on the wall was set at unity. The gas temperatures at the inlet and at the outlet were set at 293 K, and the surface temperature of solid spherical particles was also set at 293 K. The gas pressures at the inlet and the outlet were set in accordance with the condition of each case considered in the present simulations. However, the pressure at the outlet was always set to be lower than that at the inlet in order to generate a negative pressure gradient of \(\mathrm dp/\mathrm dy\). The periodic boundary condition was applied for the boundaries in both the x and z directions. In the present simulation, the arrangement of solid spheres was also considered to be repeated periodically in both the x and z directions. Therefore, if a molecule goes out of the computational domain through a point in a void region on one periodic boundary, it will necessarily re-enter the computational domain through the corresponding point in the void region on the opposite boundary.

The time step was set at \(\varDelta t=\alpha _t \tau _\mathrm {mol, inlet}\), where \(\tau _\mathrm {mol, inlet}\) is the mean free time for intermolecular collisions at the inlet. In all cases considered here, the pressure at the inlet is the highest in the computational domain. Therefore, the mean free time at the inlet will be the smallest in the domain. This is the reason why we adopted the mean free time at the inlet, \(\tau _\mathrm {mol, inlet}\), as the reference time length. The coefficient \(\alpha _t\) was set so that the time step \(\varDelta t\) was much smaller than the mean free time for intermolecular collisions, i.e., \(\alpha _t \ll 1\), and the moving distance of molecules would be much smaller than the cell size \(l_\mathrm {cell}\), i.e., \(\bar{C}\varDelta t \ll l_\mathrm {cell}\). Since \(\varDelta t=\alpha _t \tau _\mathrm {mol, inlet}\) and \(\tau _\mathrm {mol, inlet}=\lambda _\mathrm {mol, inlet}/\bar{C}\), the latter condition for \(\alpha _t\) results in \(\alpha _t \ll l_\mathrm {cell}/\lambda _\mathrm {mol, inlet}\). Since \(\lambda _\mathrm {mol, inlet}=119.3\) nm and \(l_\mathrm {cell}\) was set at \(0.3d_\mathrm p\) for \(d_\mathrm p=10\)–500 nm and was set at 200 nm for \(d_\mathrm p=1000\) and 2000 nm, \(\alpha _t\) was set at 0.01, 0.015, 0.02, 0.05, 0.05, 0.1, 0.1, and 0.1 for \(d_\mathrm p=10\), 20, 50, 100, 200, 500, 1000, and 2000 nm, respectively. In the case where the gas pressure at the inlet was set at 1 atm, the mean free time at the inlet was \(\tau _\mathrm {mol, inlet}=6.8\times 10^{-11}\) s.

In the DSMC method, the velocities of incoming molecules are determined stochastically from the velocity distribution at the corresponding boundary. Even if the velocity distribution is assumed to be Maxwellian, the flow velocity at that boundary is required to determine the velocity distribution. However, in the present case of pressure-driven flow, the flow velocity at the inlet or the outlet boundaries cannot be known before the numerical simulation is performed because the flow velocity is an outcome of applied pressure gradient and selected parameters of porous media. Therefore, in the present study, the tentative conditions of flow velocities at these boundaries were given first, and the velocities of incoming molecules from these boundaries were determined by using these conditions. The resultant flow velocity \(U_{\mathrm {B}}\) at the inlet or the outlet boundaries is given by

$$\begin{aligned} U_{\mathrm {B}}=\frac{J_+-J_-}{n}, \end{aligned}$$
(9)

where \(J_+\) and \(J_-\) are the molecular number fluxes through that boundary in the \(+y\) direction and in the \(-y\) direction, respectively, and n is the number density of molecules at that boundary. After commencement of the numerical simulation, the boundary condition of the flow velocity at that boundary has to be frequently adjusted to correspond to \(U_{\mathrm {B}}\). However, if \(U_\mathrm B\) obtained at the \((i-1)\)th step is used as the boundary condition for the ith step, the solution will not easily become stable. Ikegawa and Kobayashi (1988) proposed a technique to adjust the tentative boundary condition \(U_\mathrm {B.C.}\) of the flow velocity by using the average of the values \((J_+-J_-)/n\) of the two preceding time steps as follows:

$$\begin{aligned} U^i_{\mathrm {B.C.}}=\frac{J^{i-1}_+ + J^{i-2}_+ - J^{i-1}_- - J^{i-2}_-}{2n}, \end{aligned}$$
(10)

where the superscripts i, \(i-1\), and \(i-2\) indicate the values at the ith, \((i-1)\)th, and \((i-2)\)th time steps, respectively. Saito et al. (1995) improved this method and proposed the following technique to adjust the tentative boundary condition:

$$\begin{aligned} U^i_{\mathrm {B.C.}}=(1-\alpha )U^{i-1}_\mathrm {B.C.}+\frac{\alpha }{3n}\sum ^{i-1}_{k=i-3}\left( J^k_+-J^k_-\right) , \end{aligned}$$
(11)

where \(\alpha\) is the relaxation coefficient. In the present simulations, we adopted Eq. (11) to adjust the boundary condition of the flow velocity at both the inlet and the outlet boundaries. The relaxation coefficient \(\alpha\) was set at 0.01.

After the gas flow through the porous medium had reached the steady state, the flow properties such as gas density, gas velocity, gas pressure, and gas temperature were sampled in each cell. Since the flow in the vicinity of the edge of the assembly of solid particles has properties different from those in the bulk of porous medium which we want to know, the flow properties in the region \(3d_{\mathrm p} \le y \le 27d_{\mathrm p}\) were adopted as those in the porous medium. The porosity of the porous medium was also calculated from the volume fraction of gas in the region \(3d_{\mathrm p} \le y \le 27d_{\mathrm p}\).

3 Results and discussion

3.1 The validity of Darcy’s law in the case of a nanoscale porous medium

In the present study, we defined the flow velocity U as the average velocity of gas molecules traveling through a porous medium as follows:

$$\begin{aligned} U=\frac{\displaystyle \sum \nolimits ^{N_\mathrm {smp}}_{k=1}\left( \displaystyle \sum \nolimits ^{N^{(k)}}_{j=1} c_{y,j}^{(k)}\right) }{\displaystyle \sum \nolimits ^{N_\mathrm {smp}}_{k=1}N^{(k)}}, \end{aligned}$$
(12)

where \(c_{y,j}^{(k)}\) is the y component of the velocity of the jth simulated molecule within the sampling region \((3d_\mathrm p \le y \le 27d_\mathrm p)\) at the kth sampled time step, \(N^{(k)}\) is the number of simulated molecules in the sampling region at the kth sampled time step, and \(N_\mathrm {smp}\) is the number of sampling operations. The pressure gradient \(\mathrm dp/\mathrm dy\) is calculated by dividing the pressure difference between the inlet and the outlet by the length of the region, \(d_{\mathrm p} \le y \le 29d_{\mathrm p}\), where solid particles are arranged, as follows:

$$\begin{aligned} \frac{\mathrm dp}{\mathrm dy}=\frac{p_\mathrm {out}-p_\mathrm {in}}{28d_\mathrm p}, \end{aligned}$$
(13)

where \(p_\mathrm {in}\) and \(p_\mathrm {out}\) are the gas pressures at the inlet and the outlet, respectively. The reason why the total length of the computational domain, \(30d_\mathrm p\), is not used here is because the pressure p does not change in the regions of \(0<y<d_\mathrm p\) and \(29d_\mathrm p<y<30d_\mathrm p\) due to nonexistence of solid particles. Figure 2 shows the effect of the pressure gradient on the flow velocity U for various cases of particle diameter \(d_\mathrm p\) and porosity \(\varepsilon\). The average pressure \(\bar{p}=(p_\mathrm {in}+p_\mathrm {out})/2\) was set at 0.95 atm for all the cases considered in Fig. 2. The pressures at the inlet and the outlet were set in accordance with the set value of \(\mathrm dp/\mathrm dy\). In Fig. 2, the flow velocity U is proportional to the pressure gradient \(\mathrm dp/\mathrm dy\) for all the cases considered here. From Eqs. (1) and (2), Darcy’s law with respect to the flow velocity U is given by

$$\begin{aligned} U=-\frac{K}{\mu \varepsilon }\nabla p. \end{aligned}$$
(14)

Thus, Darcy’s law states that the flow velocity U of gas traveling through a porous medium is proportional to permeability K and pressure gradient \(\nabla p\) and is inversely proportional to the coefficient of viscosity \(\mu\) and porosity \(\varepsilon\). In a set of cases with the same porosity \(\varepsilon\) and the same particle diameter \(d_\mathrm p\) in Fig. 2, the same arrangement of particles was used, and hence, the Knudsen number and the permeability are also the same among those cases. Since the gas is common to all the cases considered here, \(\mu\) is also common to those. Consequently, Fig. 2 shows that the flow velocity U is proportional to pressure gradient \(\mathrm dp/\mathrm dy\) under the conditions of constant porosity \(\varepsilon\), constant permeability K, and constant viscosity \(\mu\). Namely, Darcy’s law holds for all the cases considered here.

Fig. 2
figure 2

Relation between the flow velocity U and the pressure gradient. U is plotted in the ranges of a \(0\le U \le 40 \text{ m/s}\) and b \(0\le U \le 4\, \text{ m/s}\) (\(\bar{p}=(p_\mathrm {in}+p_\mathrm {out})/2=0.95\) atm)

Full size image

The Reynolds numbers and the Knudsen numbers for the cases of the highest flow velocity among the cases with the same porosity \(\varepsilon\) and the same particle diameter \(d_\mathrm p\) are also shown in Fig. 2. In the present study, the Reynolds number Re and the Knudsen number Kn are defined as

$$\begin{aligned} \mathrm{Re}=\frac{\rho U \lambda _\mathrm {wall}}{\mu }, \end{aligned}$$
(15)

and

$$\begin{aligned} \mathrm{Kn}=\frac{\lambda _\mathrm {mol}}{\lambda _\mathrm {wall}}, \end{aligned}$$
(16)

respectively. Here, \(\lambda _{\mathrm {mol}}\) is the mean free path for molecule–molecule collisions, i.e., the so-called the mean free path, and \(\lambda _\mathrm {wall}\) is the mean free path for molecule–wall collisions, which is defined as the average distance that a molecule travels between successive molecule–wall collisions.

For the definitions of the Reynolds and the Knudsen numbers, we chose the mean free path \(\lambda _{\mathrm {wall}}\) for molecule–wall collisions as the characteristic length. This is because the pore size in a porous medium is difficult to be determined and because the mean free path \(\lambda _{\mathrm {wall}}\) for molecule–wall collisions is expected to represent the characteristic length of the inner channel of the porous medium such as the pore size or the channel diameter. The validity of this expectation will be confirmed in Sect. 3.4. The mean free paths \(\lambda _{\mathrm {mol}}\) and \(\lambda _{\mathrm {wall}}\) are given by

$$\begin{aligned} \lambda _\mathrm {mol}=\frac{\bar{C}}{\nu _\mathrm {mol}}, \end{aligned}$$
(17)

and

$$\begin{aligned} \lambda _\mathrm {wall}=\frac{\bar{C}}{\nu _\mathrm {wall}}, \end{aligned}$$
(18)

respectively. Here, \(\nu _\mathrm {mol}\) and \(\nu _\mathrm {wall}\) are the molecule–molecule and the molecule–wall collision frequencies, respectively. Therefore, Eq. (16) results in

$$\begin{aligned} \mathrm{Kn}=\frac{\nu _\mathrm {wall}}{\nu _\mathrm {mol}}. \end{aligned}$$
(19)

Yonemura (2008) pointed out that the Knudsen number Kn, which is defined by \(\mathrm{Kn}=\lambda _\mathrm {mol}/L\) using the characteristic length L of the flow, represents essentially the ratio of the molecule–wall collision frequency to the molecule–molecule collision frequency, \(\nu _\mathrm {wall}/\nu _\mathrm {mol}\), although the value of \(\nu _\mathrm {wall}/\nu _\mathrm {mol}\) may differ from Kn to some extent in most cases. For instance, in the case of gas flow through the cylindrical tube of diameter L, the value of \(\nu _\mathrm {wall}/\nu _\mathrm {mol}\) is equal to Kn, while in the case of gas flow between two parallel plates which are separated by a distance L, that is equal to 0.5 Kn, and furthermore in the case of gas flow in the spherical region of diameter L, that is equal to 1.5 Kn. Thus, the value of \(\nu _\mathrm {wall}/\nu _\mathrm {mol}\) is always proportional to Kn and is not largely different from Kn. Therefore, we can say that the physical meaning of \(\nu _\mathrm {wall}/\nu _\mathrm {mol}\) is essentially the same with that of Kn. The definition of the Knudsen number in the present study, Eq. (16), comes from such a consideration. Here, \(\lambda _\mathrm {wall}\) was obtained by using \(\nu _\mathrm {wall}\), which was counted in the present DSMC simulations. The mean free path \(\lambda _{\mathrm {mol}}\) for molecule–molecule collisions for \(\bar{p}=0.95\) atm is 125.5 nm.

Thus, from Fig. 2, it is confirmed that even in the case of a nanoscale porous medium, i.e., even in the case of high Knudsen number, Darcy’s law holds at least for \(\mathrm{Re}<0.1\). In the following sections, we investigate the flow velocity U for various porous media with various porosities and particle sizes under the condition of the fixed pressure gradient. Nevertheless, applying the same pressure gradient for various porous media in the present DSMC simulations is not easy. For example, in the case of \(d_\mathrm p=1000\) nm, the pressure gradient \(\mathrm dp/\mathrm dy\) becomes \(-0.3619~\mathrm {Pa/nm}\) under the conditions of \(p_\mathrm {in}=1.0\) atm and \(p_\mathrm {out}=0.9\) atm. In order to apply the same pressure gradient in the case of \(d_\mathrm p=10\) nm, the pressure difference has to be set at 0.001 atm, i.e., the inlet and the outlet pressures have to be set at \(p_\mathrm {in}=0.9505~\mathrm {atm}\) and \(p_\mathrm {out}=0.9495~\mathrm {atm}\), respectively, because the length of the computational domain is changed according to the diameter \(d_\mathrm {p}\). In the DSMC simulation, such a small pressure difference might be buried in statistical fluctuations resulting from its stochastic approach. Consequently, the flow velocity cannot be evaluated accurately in such a case. Therefore, we use Darcy’s law to evaluate the flow velocity in the case of such a small pressure difference.

From this point forward, in all cases, the inlet and the outlet pressures are set at \(p_\mathrm {in}=1.0\) atm and \(p_\mathrm {out}=0.9\) atm, respectively. Since the pressure gradient \(\mathrm dp/\mathrm dy\) becomes \(-0.3619\) Pa/nm in the case of \(d_\mathrm p=1000\) nm, \(\mathrm dp/\mathrm dy\) for other cases of different particle size \(d_\mathrm p\mathrm {[nm]}\) can be given by \(-0.3619(1000/d_\mathrm p[\mathrm {nm}])\) Pa/nm. The flow velocity U for \(\mathrm dp/\mathrm dy=-0.3619\) Pa/nm was estimated by multiplying the obtained flow velocity by \(d_\mathrm p[\mathrm {nm}]/1000\). Such conversion of the flow velocity U was performed under the condition of a very low Reynolds number, \(\mathrm{Re}<0.1\).

The smallest value of flow velocity before the conversion was \(U=0.37\) m/s, which was obtained in the case of \(\varepsilon =0.3\) and \(d_\mathrm p=10\) nm. In the case of such a small flow velocity, sampling was repeated a lot so that the total number of sampled molecules

$$\begin{aligned} N_\mathrm {total}=\sum ^{N_\mathrm {smp}}_{k=1}N^{(k)} \end{aligned}$$

becomes large enough. In the case of \(\varepsilon =0.3\) and \(d_\mathrm p=10\) nm, sampling was repeated one million times and 1,609,095,123 simulated molecules were sampled. The magnitude of fluctuation of calculated flow velocity U can be estimated to be \((1/\sqrt{N_\mathrm {total}})\sqrt{k_\mathrm B T/m}\), and hence, the estimated magnitude of fluctuation of U is 0.0274 m/s, and consequently, the error is 7.4% in this case. This is the case of the maximum error. In the case of larger flow velocity, the error is smaller.

3.2 Knudsen diffusion in porous media

In order to construct an expression to estimate molecular transport through porous media, we would like to start by considering the case in which the size of pores is much smaller than the mean free path \(\lambda _\mathrm {mol}\) for molecule–molecule collisions. Since the mean free path \(\lambda _\mathrm {wall}\) for molecule–wall collisions is as large as the pore size, the number of molecule–molecule collisions is negligible compared with the number of molecule–wall collisions. Molecules colliding with the wall rebound in random directions. Since the molecule–molecule collisions are negligible, the pressure gradient does not induce molecular transport directly. However, the pressure gradient induces the gradient of the molecular concentration. The chaotic molecular motions after molecule–wall collisions induce a net molecular flux from the more concentrated region to the less concentrated one. This phenomenon is called Knudsen diffusion. In the case of a cylindrical capillary tube with radius R, the Knudsen diffusion coefficient \(D^{\mathrm K}_{\mathrm {cylinder}}\) is given by (Knudsen 1909; Cunningham and Williams 1980)

$$\begin{aligned} D^{\mathrm K}_{\mathrm {cylinder}}=\frac{2}{3}R{\bar{C}}. \end{aligned}$$
(20)

The molar flux \(N^\mathrm {K}_{\mathrm {cylinder}}\) due to Knudsen diffusion under the pressure gradient is given by (Cunningham and Williams 1980)

$$\begin{aligned} N^\mathrm K_{\mathrm {cylinder}}=-D^{\mathrm K}_{\mathrm {cylinder}}\frac{1}{R_\mathrm gT}\nabla p, \end{aligned}$$
(21)

where \(R_\mathrm g\) is the universal gas constant. Dividing Eq. (21) by the molar concentration c, the flow velocity \(U^\mathrm K_\mathrm {cylinder}\) in a capillary tube is given by

$$\begin{aligned} U^\mathrm K_{\mathrm {cylinder}}=-D^{\mathrm K}_{\mathrm {cylinder}}\frac{\nabla p}{p}, \end{aligned}$$
(22)

where the relation \(N^\mathrm K_\mathrm {cylinder}=cU^\mathrm K_\mathrm {cylinder}\) and the equation of state of an ideal gas, \(p=cR_\mathrm gT\), are used.

Let us regard a porous medium as a bundle of tortuous capillary tubes, as shown in Fig. 3. Here, \(d_{\mathrm t}\) is the diameter of the capillary tubes, \(l_{\mathrm t}\) is their tortuous length, l is the straight-line length of the porous medium, \(\varepsilon\) is the porosity of the porous medium, and U is the flow velocity in the porous medium in the direction of the macroscopic pressure gradient, not in the direction of the local pressure gradient, and \(U_\mathrm t\) is the flow velocity along the center line of a tortuous tube. From Eqs. (20) and (22), the velocity \(U_{\mathrm t}\) induced by Knudsen diffusion and the pressure gradient is given by

$$\begin{aligned} U_{\mathrm t}=-\frac{1}{3}d_{\mathrm t}{\bar{C}}\frac{1}{\bar{p}}\frac{p_{\mathrm {out}}-p_{\mathrm {in}}}{l_{\mathrm t}}. \end{aligned}$$
(23)

Considering the time required for gas to pass through the porous media, we have the following relation between l, \(l_{\mathrm t}\), U, and \(U_{\mathrm t}\):

$$\begin{aligned} \frac{l_{\mathrm t}}{U_{\mathrm t}}=\frac{l}{U}. \end{aligned}$$
(24)

By substituting Eq. (24) in Eq. (23), the flow velocity U is given by

$$\begin{aligned} U & = -\frac{1}{3}d_{\mathrm t}{\bar{C}}\frac{1}{\bar{p}}\frac{p_{\mathrm {out}}-p_{\mathrm {in}}}{l}\left( \frac{l}{l_{\mathrm t}}\right) ^2 \nonumber \\ & = -\frac{1}{3}d_{\mathrm t}{\bar{C}}\frac{1}{\bar{p}}\frac{p_{\mathrm {out}}-p_{\mathrm {in}}}{l}\tau , \end{aligned}$$
(25)

where \(\tau\) is “tortuosity” defined as follows:

$$\begin{aligned} \tau =\left( \frac{l}{l_{\mathrm t}} \right) ^2. \end{aligned}$$
(26)
Fig. 3
figure 3

Concept of the tube bundle model for a porous medium

Full size image

However, it is unclear how to determine the diameter \(d_\mathrm t\) of tortuous capillary tubes because porous media have a very complicated structure. In the case of a straight cylindrical tube, the mean free path \(\lambda _\mathrm {wall}\) for molecule–wall collisions in equilibrium gas is exactly equal to the tube diameter. Therefore, in the present work, we use \(\lambda _\mathrm {wall}\) as the tube diameter. Considering the importance of molecule–wall collisions in the Knudsen diffusion, this replacement may be reasonable. The validity of this replacement will be discussed in Sect. 3.4. Consequently, we have

$$\begin{aligned} U=-\frac{1}{3}\tau \lambda _{\mathrm {wall}}{\bar{C}} \frac{\nabla p}{p}. \end{aligned}$$
(27)

The tortuosity \(\tau =(l/l_\mathrm t)^2\) still remains unknown. Many tortuosity models for electric, hydraulic, or diffusive conductivity have been proposed by empirical, analytical, and numerical approaches (Ghanbarian et al. 2013). In porous media with micro-/nanoscale pores, however, both contributions of viscous flow and Knudsen diffusion appear, and hence, the tortuosity of such porous media is unclear. Zalc et al. (2004) calculated the diffusive tortuosity by using the mean-square displacement method and test-particle method. Asinari et al. (2007) also calculated the diffusive tortuosity by using the lattice Boltzmann method. In order to estimate the tortuosity, let us compare the flow velocities obtained in the DSMC simulations with the values of

$$\begin{aligned} -\frac{1}{3}\lambda _{\mathrm {wall}}{\bar{C}} \frac{\nabla p}{p} \end{aligned}$$
(28)

obtained under the same conditions. Figure 4 shows the ratios of the flow velocities obtained in the DSMC simulations to the values of Eq. (28). Here, \(\lambda _{\mathrm {wall}}\)’s obtained in the DSMC simulations were used to give the values of Eq. (28). If the tortuosity \(\tau\) is equal to these ratios, the flow velocity estimated by using Eq. (27) will agree with the flow velocity obtained in the DSMC simulations. As mentioned above, the mean free path \(\lambda _{\mathrm {mol}}\) for molecule–molecule collisions for the case of \(\bar{p}=0.95\) atm is 125.5 nm. On the other hand, the mean free path \(\lambda _{\mathrm {wall}}\) for molecule–wall collisions is \(0.96d_\mathrm p\) for \(\varepsilon =0.5\), \(0.73d_\mathrm p\) for \(\varepsilon =0.4\), and \(0.55d_\mathrm p\) for \(\varepsilon =0.3\). Since Eq. (27) is for estimation of the flow velocity for very high Knudsen numbers much larger than 10, the tortuosity must agree with these ratios over the ranges of \(d_\mathrm p<13\) nm for \(\varepsilon =0.5\), \(d_\mathrm p<17\) nm for \(\varepsilon =0.4\), and \(d_\mathrm p<23\) nm for \(\varepsilon =0.3\). In Fig. 4, the three dashed lines, which represent the values of \(0.9\varepsilon\) for \(\varepsilon =0.3\), 0.4, and 0.5 from the bottom up, agree well with the ratios obtained for \(\varepsilon =0.3 (\Box )\), \(\varepsilon =0.4 (\circ )\), \(\varepsilon =0.5 (\Diamond )\), respectively, for very small particle diameter \(d_\mathrm p\). Therefore, in the present study we adopt the tortuosity,

$$\begin{aligned} \tau =0.9\varepsilon , \end{aligned}$$
(29)

for the case of low porosity, \(0.3<\varepsilon <0.5\). On the other hand, the ratios obtained for the higher porosities, \(\varepsilon >0.6\), are much less than \(0.9\varepsilon\) for very small particle diameter \(d_\mathrm p\). This may be because the concept of the tube bundle model is not appropriate in the case of high porosity since the arrangement of solid particles is coarse. In the present study, we consider only the cases of low porosity, \(0.3<\varepsilon <0.5\).

Fig. 4
figure 4

Ratio of the flow velocity U obtained in the DSMC simulations to the value of Eq. (28)

Full size image

In Fig. 5a, b, the flow velocities U estimated by using Eq. (27) and \(\tau =0.9\varepsilon\) are compared with those obtained in the DSMC simulations on a log-log scale and on a linear scale, respectively. For reference, the flow velocities estimated by using the three empirical models, i.e., the Blake–Kozeny model given by Eq. (3), the Carman–Kozeny model given by Eq. (4), and the Rumpf–Gupte model given by Eq. (5), are also shown in Fig. 5a. In Fig. 5b, the Knudsen numbers estimated by using Eq. (16) are also shown. Here, the porosity is set at \(\varepsilon =0.49\), the pressure gradient is set at \(\mathrm dp/\mathrm dy=-0.3619~\mathrm {Pa/nm}\), and the diameter of solid particles \(d_{\mathrm p}\) is varied from 10 to 2000 nm. Note that, in Fig. 5a, the marks with the same values on the horizontal axis represent the data for the same particle diameter \(d_\mathrm p\). The solid line in each figure represents a set of points such that the estimated velocity is equal to the velocity obtained in the DSMC simulations. Therefore, if a mark for some model is on this solid line, it shows that the velocity estimated by using that model agrees with that obtained in the DSMC simulation. In cases of conventional empirical models, the smaller the particle diameter \(d_\mathrm p\) becomes, the more greatly the estimated velocity deviates from that obtained in the DSMC simulation. This is because in the case of smaller \(d_{\mathrm p}\), the Knudsen number becomes the same or more than unity and the effect of rarefaction becomes stronger, whereas the effect of the Knudsen number is not considered in these conventional models. Therefore, these conventional models are not appropriate for nanoscale porous media. On the other hand, the velocities estimated by using Eq. (27) agree well with those obtained in the DSMC simulations for \(d_\mathrm p<200\) nm, i.e., for \(\mathrm{Kn}>0.6\). Thus, it is confirmed that a good estimation of the flow velocity in porous media can be made by using Eq. (27) in the high Knudsen number regime of \(\mathrm{Kn}>0.6\). However, for \(d_\mathrm p>200\) nm, i.e., for \(\mathrm{Kn}<0.6\), the larger the particle diameter \(d_\mathrm p\) becomes, the more greatly the velocity estimated by using Eq. (27) deviates from that obtained in the DSMC simulation. This is because as the Knudsen number becomes smaller, the effects of molecule–molecule collisions, i.e., the characteristics of gas as a continuum, becomes stronger, whereas the effects of molecule–molecule collisions were not considered when deriving Eq. (27). In the next section, we will modify Eq. (27) by considering the characteristics of gas as a continuum.

Fig. 5
figure 5

Comparison of flow velocities estimated by using conventional models and Eq. (27) with those obtained in the DSMC simulations: a on a log–log scale; b on a linear scale (\(\varepsilon =0.49\), \(\tau =0.9\varepsilon\), \(d_\mathrm p=10{-}2000~\mathrm {nm}\), \(\bar{p}=0.95~\mathrm {atm}\), \(\mathrm dp/\mathrm dy=-0.3619~\mathrm {Pa/nm}\))

Full size image

3.3 Construction of an expression to estimate gas flow velocity in porous media considering Knudsen diffusion and viscous flow

As discussed in the previous section, although Eq. (27) is valid in the case of a Knudsen number higher than unity, it is not applicable in the case of a Knudsen number much smaller than unity. Here, in order to remedy the shortcoming of our expression, i.e., Eq. (27), we will modify it by considering the contribution of molecule–molecule collisions.

In the limit of a small Knudsen number, molecules frequently collide with each other and gas behaves as a continuum. Under a pressure gradient of \(\nabla p\), gas is pushed by the difference between the gas pressures on both its sides and is set in motion. If the gas moves with respect to the porous medium, momentum will be transferred from the gas to the porous medium due to the normal and the viscous tangential stresses and the gas will be subjected to its reaction force. The gas flow becomes steady when the reaction force from the porous medium balances out the force exerted on the gas by the pressure gradient. In the case of laminar flow in a long cylindrical tube under a steady pressure gradient, the flow maintaining such a balance is called “Poiseuille flow.” As can be inferred from “Poiseuille flow,” in the case of a Knudsen number much smaller than unity and a low Reynolds number, molecular transport under a steady pressure gradient is governed by the viscosity of the gas. Therefore, such a regime is called the “viscous regime” (Cunningham and Williams 1980). On the other hand, in the case of a Knudsen number much higher than unity, molecule–molecule collisions are negligible and the Knudsen diffusion is dominant. Such a regime is called the “Knudsen regime” (Cunningham and Williams 1980).

In the case of gas flow in a cylindrical capillary, there are several expressions of molecular transport which are suggested as valid for the viscous and Knudsen regimes and for the entire transition regime between these two extremes. For example, Knudsen (1909) and Wakao et al. (1965) constructed an expression to estimate the molar flux of gas in a cylindrical capillary by superposing the molar fluxes due to Knudsen diffusion and due to viscous flow. Knudsen (1909) proposed a semiempirical expression to describe the molar flux \(N_\mathrm {cylinder}\) of gas in a cylindrical capillary as follows:

$$\begin{aligned} N_\mathrm {cylinder}=-\left( a^{\mathrm K} {p} + b^{\mathrm K} \frac{1+c^{\mathrm K}_1{p}}{1+c^{\mathrm K}_2 p} \right) \frac{1}{R_\mathrm gT}\nabla p, \end{aligned}$$
(30)

where \(a^\mathrm K\), \(b^\mathrm K\), \(c^\mathrm K_1\), and \(c^\mathrm K_2\) are coefficients that depend on the nature of the gas and the capillary (Cunningham and Williams 1980). The first term of Eq. (30) represents the viscous flow, and the second term represents the Knudsen diffusion. Dividing Eq. (30) by the molar concentration c, we have

$$\begin{aligned} U_\mathrm {cylinder}=-\left( a^{\mathrm K} {p} + b^{\mathrm K} \frac{1+c^{\mathrm K}_1{p}}{1+c^{\mathrm K}_2 p} \right) \frac{\nabla p}{p}, \end{aligned}$$
(31)

where \(N_\mathrm {cylinder}=cU_\mathrm {cylinder}\) and \(p=cR_\mathrm gT\) are used. By considering the case of large p, from comparison of Eq. (31) with the Hagen–Poiseuille law

$$\begin{aligned} \pi R^2 U_\mathrm {cylinder}=-\frac{\pi R^4}{8\mu }\nabla p, \end{aligned}$$
(32)

where R is the radius of the cylindrical capillary, it is found that \(a^\mathrm K\) is given by

$$\begin{aligned} a^\mathrm K=\frac{R^2}{8\mu } \end{aligned}$$
(33)

and represents the viscous flux coefficient. By considering the case of \(p \rightarrow 0\), it is found from the comparison of Eq. (31) with Eq. (22) that the coefficient \(b^\mathrm K\) is the Knudsen diffusivity \(D^\mathrm K_\mathrm {cylinder}\) for a cylindrical tube as follows (Cunningham and Williams 1980):

$$\begin{aligned} b^\mathrm K=D^\mathrm K_\mathrm {cylinder}=\frac{2}{3}R\bar{C}. \end{aligned}$$
(34)

The coefficients \(c^\mathrm K_1\) and \(c^\mathrm K_2\) are to describe the slip flow in the transition regime. Knudsen obtained the values of \(c^\mathrm K_1\) and \(c^\mathrm K_2\) to fit his experimental data as follows:

$$\begin{aligned} {\begin{matrix} c^{\mathrm K}_1=2.00\left( \displaystyle\frac{8}{\pi }\right) ^{\frac{1}{2}} \left( \displaystyle\frac{R}{\mu {\bar{C}}}\right) , \\ c^{\mathrm K}_2=2.47\left( \displaystyle\frac{8}{\pi }\right) ^{\frac{1}{2}} \left( \displaystyle\frac{R}{\mu {\bar{C}}}\right) . \end{matrix}} \end{aligned}$$
(35)

Wakao et al. (1965) also proposed an expression to estimate the molar flux in a cylindrical capillary of radius R as follows:

$$\begin{aligned} N_\mathrm {cylinder}=-\left[ \phi D^\mathrm K_\mathrm {cylinder}+\left( 1-\phi \right) \left( \frac{R^2}{8\mu }p+\frac{\pi }{4}D^\mathrm K_\mathrm {cylinder} \right) \right] \frac{1}{R_\mathrm gT}\nabla p, \end{aligned}$$
(36)

where

$$\begin{aligned} \phi =\frac{\text {wall collision frequency}}{\text {total collision frequency}}. \end{aligned}$$
(37)

Dividing Eq. (36) by the molar concentration c, we have

$$\begin{aligned} U_\mathrm {cylinder}=-\left[ \phi D^\mathrm K_\mathrm {cylinder}+\left( 1-\phi \right) \left( \frac{R^2}{8\mu }p+\frac{\pi }{4}D^\mathrm K_\mathrm {cylinder} \right) \right] \frac{\nabla p}{p}. \end{aligned}$$
(38)

Using our definition of Knudsen number, i.e., Eq. (16), the ratio \(\phi\) is given by

$$\begin{aligned} \phi & = \frac{\nu _\mathrm {wall}}{\nu _\mathrm {wall}+\nu _\mathrm {mol}}\nonumber \\ & = \frac{\nu _\mathrm {wall}/\nu _\mathrm {mol}}{\nu _\mathrm {wall}/\nu _\mathrm {mol}+1}\nonumber \\ & = \frac{(\bar{C}/\lambda _\mathrm {wall})/(\bar{C}/\lambda _\mathrm {mol})}{(\bar{C}/\lambda _\mathrm {wall})/(\bar{C}/\lambda _\mathrm {mol})+1}\nonumber \\ & = \frac{\lambda _\mathrm {mol}/\lambda _\mathrm {wall}}{\lambda _\mathrm {mol}/\lambda _\mathrm {wall}+1}\nonumber \\ & = \frac{\mathrm{Kn}}{\mathrm{Kn}+1}. \end{aligned}$$
(39)

The first term of Eq. (38) represents the Knudsen diffusion, the second term represents the viscous flow, i.e., the Poiseuille flow, and the third term represents the contribution of the velocity slip on the capillary wall. In the case of \(\mathrm{Kn}\gg 1\), i.e., in the case of \(\phi \approx 1\), Eq. (38) results in Eq. (22) and represents the flow velocity only due to Knudsen diffusion, whereas in the case of \(\mathrm{Kn}\ll 1\), i.e., in the case of \(\phi \approx 0\), Eq. (38) represents Poiseuille flow with a velocity slip. However, since the viscous flux coefficient \(R^2/8\mu\) is proportional to \(R^2\) and \(D^\mathrm {K}_\mathrm {cylinder}\) is proportional to R, the contribution of the velocity slip will become negligible in the case of \(\mathrm{Kn}\ll 1\)

Let us apply the above expressions to gas flow in porous media. In Sect. 3.2, a porous medium was regarded as a bundle of tortuous capillary tubes with a diameter of \(\lambda _\mathrm {wall}\). The Knudsen diffusivity for such a tube is given by

$$\begin{aligned} D^\mathrm K_\mathrm {tube}=\frac{1}{3}\lambda _\mathrm {wall}\bar{C}. \end{aligned}$$
(40)

Therefore, Eq. (27) is given by

$$\begin{aligned} U=-\tau D^\mathrm K_\mathrm {tube}\frac{\nabla p}{p}. \end{aligned}$$
(41)

The coefficient \(D^\mathrm K_\mathrm {tube}\) corresponds to \(b^\mathrm K\) in Knudsen’s expression, Eq. (31), and \(D^\mathrm K_\mathrm {cylinder}\) in Wakao’s expression, Eq. (38). Supposing that the tortuosity for the viscous flow with a velocity slip is the same as the tortuosity \(\tau\) for Knudsen diffusion since both flows go through the same channel in the porous medium, we can modify Eq. (41) by adding the contribution of viscous flow with a velocity slip as in Knudsen’s expression and Wakao’s expression. Referring to Knudsen’s expression, Eq. (41) is modified as

$$\begin{aligned} U & = -\tau \left( D^\mathrm K_\mathrm {tube}\frac{1+c^{\mathrm K}_1p}{1+c^{\mathrm K}_2p}+\frac{(\lambda _\mathrm {wall}/2)^2}{8\mu }p \right) \frac{\nabla p}{p}\nonumber \\ & = -\tau \left( \frac{1}{3}\lambda _{\mathrm {wall}}{\bar{C}} \frac{1+c^{\mathrm K}_1p}{1+c^{\mathrm K}_2p} +\frac{\lambda _{\mathrm {wall}}^2}{32\mu }p \right) \frac{\nabla p}{p},\nonumber \\ c^{\mathrm K}_1 & = 2.00\left( \frac{8}{\pi } \right) ^\frac{1}{2}\left( \frac{\lambda _\mathrm {wall}}{2\mu \bar{C}} \right) ,\nonumber \\ c^{\mathrm K}_2 & = 2.47\left( \frac{8}{\pi } \right) ^\frac{1}{2}\left( \frac{\lambda _\mathrm {wall}}{2\mu \bar{C}} \right) . \end{aligned}$$
(42)

Note that the mean free path \(\lambda _\mathrm {wall}\) for molecule–wall collisions is used as the diameter 2R of the tortuous capillary tube. Similarly, referring to Wakao’s expression, Eq. (41) is modified as

$$\begin{aligned} U=-\tau \left[ \phi \frac{1}{3}\lambda _{\mathrm {wall}}{\bar{C}}+\left( 1-\phi \right) \left( \frac{\lambda _{\mathrm {wall}}^2}{32\mu }p + \frac{\pi }{12}\lambda _{\mathrm {wall}}{\bar{C}}\right) \right] \frac{\nabla p}{p}. \end{aligned}$$
(43)

Since the viscosity varies depending on the Knudsen number under conditions of rarefaction, let us replace the viscosity \(\mu\) in Eq. (43) by the effective viscosity \(\mu _\mathrm e\) which reflects the dependence on the Knudsen number. The effective viscosity \(\mu _\mathrm e\) is given by

$$\begin{aligned} \mu _\mathrm e=\mu \frac{1}{1+a\,\mathrm{Kn}} \end{aligned}$$
(44)

(Michalis et al. 2010; Kalarakis et al. 2012), where a is a numerical factor. Equation (43) results in

$$\begin{aligned} U & = -\tau \left[ \phi \frac{1}{3}\lambda _{\mathrm {wall}}{\bar{C}}+\left( 1-\phi \right) \left( \frac{\lambda _{\mathrm {wall}}^2}{32\mu _\mathrm e}p + \frac{\pi }{12}\lambda _{\mathrm {wall}}{\bar{C}}\right) \right] \frac{\nabla p}{p}\nonumber \\ & = -\tau \left[ \phi \frac{1}{3}\lambda _{\mathrm {wall}}{\bar{C}}+\left( 1-\phi \right) \left( \frac{\lambda _{\mathrm {wall}}^2}{32\mu }\left( 1+a\, \mathrm{Kn} \right) p + \frac{\pi }{12}\lambda _{\mathrm {wall}}{\bar{C}}\right) \right] \frac{\nabla p}{p}. \end{aligned}$$
(45)

Using \(p=nk_\mathrm BT\), \(\bar{C}=\sqrt{8k_\mathrm B T/\pi m}\), \(\rho =mn\), \(\mu =(1/2)\rho \bar{C}\lambda _\mathrm {mol}\), and \(\mathrm{Kn}=\lambda _\mathrm {mol}/\lambda _\mathrm {wall}\), Eq. (45) can be rewritten as

$$\begin{aligned} U=-\tau \frac{\lambda _\mathrm {wall}^2}{32\mu }\left[ \phi \frac{128}{3\pi }\mathrm{Kn}+\left( 1-\phi \right) \left\{ 1+\left( a+\frac{32}{3} \right) \mathrm{Kn} \right\} \right] \nabla p .\end{aligned}$$
(46)

Here, let us call Eq. (42) the Knudsen-type expression for porous media and call Eq. (46) the Wakao-type expression for porous media.

In Fig. 6a, b, the flow velocities U estimated by using expressions proposed here and those obtained in the DSMC simulations are compared on a log–log scale and on a linear scale, respectively. In the present study, the numerical factor a in the Wakao-type expression for porous media was set at 2 because the factor a in Eq. (44) was found by Michalis et al. (2010) to have the value of 2 in the case of a gas flow of hard sphere molecules between parallel plates. The cases treated in Fig. 6 are the same as those treated in Fig. 5. The porosity was set at \(\varepsilon =0.49\), the pressure gradient was set at \(\mathrm dp/\mathrm dy=-0.3619\) Pa/nm, and the diameter of solid particles \(d_\mathrm p\) was varied from 10 to 2000 nm. Here, the gas viscosity \(\mu\) in Eqs. (42) and (46) was given by \(\mu =(1/2)\rho \bar{C}\lambda _\mathrm {mol}\). Although the flow velocity estimated by using the expression Eq. (27) considering only Knudsen diffusion deviates from that obtained in the DSMC simulation for a Knudsen number lower than 0.6, the flow velocities estimated by using the Knudsen-type expression, Eq. (42), and by using the Wakao-type expression, Eq. (46), agree well with those obtained in the DSMC simulations over the whole range of Knudsen numbers considered here due to the consideration of both contributions of Knudsen diffusion and viscous flow with a velocity slip.

Fig. 6
figure 6

Comparison of flow velocities estimated by using the three expressions proposed in the present study with those obtained in the DSMC simulations: a on a log–log scale; b on a linear scale. (\(\varepsilon =0.49\), \(\tau =0.9\varepsilon\), \(d_\mathrm p=10{-}2000~\mathrm {nm}\), \(\bar{p}=0.95~\mathrm {atm}\), \(\mathrm dp/\mathrm dy=-0.3619~\mathrm {Pa/nm}\))

Full size image

In Fig. 7a, b, the flow velocities U estimated by using the Knudsen-type expression, Eq. (42), and by using the Wakao-type expression, Eq. (46), are compared with those obtained in the DSMC simulations for the cases of various porosities \(\varepsilon\) and various particle diameters \(d_\mathrm p\) on a log–log scale and on a linear scale, respectively. The flow velocities estimated by using both expressions proposed here agree well with those obtained in the DSMC simulations. This result indicates that both expressions proposed here well describe gas transport in porous media from nanometer to micrometer scale.

Fig. 7
figure 7

Comparison of flow velocities estimated by using the Knudsen-type expression and by using the Wakao-type expression with those obtained in the DSMC simulations for the cases of various porosities \(\varepsilon\): a on a log–log scale; b on a linear scale. (\(\tau =0.9\varepsilon\), \(d_\mathrm p=10{-}1000~\mathrm {nm}\), \(\bar{p}=0.95~\mathrm {atm}\), \(\mathrm dp/\mathrm dy=-0.3619~\mathrm {Pa/nm}\))

Full size image

The superficial velocity is given by the Knudsen-type expression for porous media as follows:

$$\begin{aligned} U_\mathrm s & = \varepsilon U\nonumber \\ & = -\varepsilon \tau \left( \frac{1}{3}\lambda _{\mathrm {wall}}{\bar{C}} \frac{1+c^{\mathrm K}_1p}{1+c^{\mathrm K}_2p} +\frac{\lambda _{\mathrm {wall}}^2}{32\mu }p \right) \frac{\nabla p}{p}. \end{aligned}$$
(47)

Using \(p=nk_\mathrm BT\), \(\bar{C}=\sqrt{8k_\mathrm B T/\pi m}\), \(\rho =mn\), \(\mu =(1/2)\rho \bar{C}\lambda _\mathrm {mol}\), and \(\mathrm{Kn}=\lambda _\mathrm {mol}/\lambda _\mathrm {wall}\), this results in

$$\begin{aligned} U_\mathrm s=-\varepsilon \tau \frac{\lambda _{\mathrm {wall}}^2}{32} \left( 1+\frac{128}{3\pi }\mathrm{Kn}\frac{1+c_1^\mathrm Kp}{1+c_2^\mathrm Kp} \right) \frac{\nabla p}{\mu }. \end{aligned}$$
(48)

From this equation and Darcy’s law, the permeability of porous medium is given by

$$\begin{aligned} K=K_0 \left( 1+\frac{128}{3\pi }\mathrm{Kn}\frac{1+c_1^\mathrm Kp}{1+c_2^\mathrm Kp} \right) , \end{aligned}$$
(49)

where \(K_0\) is the permeability in the continuum limit, \(\mathrm{Kn}\rightarrow 0\), and given by

$$\begin{aligned} K_0=\varepsilon \tau \frac{\lambda _{\mathrm {wall}}^2}{32}. \end{aligned}$$
(50)

Since the permeability can be rewritten as

$$\begin{aligned} K=K_0 \left( 1+\frac{\displaystyle \frac{128}{3\pi }\cdot \displaystyle \frac{1+c_1^\mathrm Kp}{1+c_2^\mathrm Kp}\mathrm{Kn}\cdot p}{p} \right) , \end{aligned}$$
(51)

this has the form of the Klinkenberg equation (1941). The Klinkenberg coefficient b for the Knudsen-type expression for porous media is given by

$$\begin{aligned} b=\frac{128}{3\pi }\cdot \frac{1+c_1^\mathrm Kp}{1+c_2^\mathrm Kp}\mathrm{Kn}\cdot p. \end{aligned}$$
(52)

The coefficients \(c_1^\mathrm K\) and \(c_2^\mathrm K\) depend on the nature of the gas and the material of porous medium (Cunningham and Williams 1980). In the case where the coefficients \(c_1^\mathrm K\) and \(c_2^\mathrm K\) are given as shown in Eq. (42), using \(p=nk_\mathrm BT\), \(\bar{C}=\sqrt{8k_\mathrm B T/\pi m}\), \(\rho =mn\), \(\mu =(1/2)\rho \bar{C}\lambda _\mathrm {mol}\), and \(\mathrm{Kn}=\lambda _\mathrm {mol}/\lambda _\mathrm {wall}\), we have

$$\begin{aligned} c_1^\mathrm Kp & = \sqrt{\frac{\pi }{2}}\frac{1}{\mathrm{Kn}},\end{aligned}$$
(53)
$$\begin{aligned} c_2^\mathrm Kp & = 1.235\sqrt{\frac{\pi }{2}}\frac{1}{\mathrm{Kn}}. \end{aligned}$$
(54)

The superficial velocity \(U_\mathrm s\), the permeability of porous medium K, and Klinkenberg coefficient b are given by the Knudsen-type expression for porous media as follows:

$$\begin{aligned} U_\mathrm s & = -\varepsilon \tau \frac{\lambda _{\mathrm {wall}}^2}{32} \left( 1+\frac{128}{3\pi }\mathrm{Kn}\frac{1+\sqrt{\displaystyle \frac{\pi }{2}}\displaystyle \frac{1}{\mathrm{Kn}}}{1+1.235\sqrt{\displaystyle \frac{\pi }{2}}\displaystyle \frac{1}{\mathrm{Kn}}} \right) \frac{\nabla p}{\mu }, \end{aligned}$$
(55)
$$\begin{aligned} K & = K_0\left( 1+\frac{128}{3\pi }\mathrm{Kn}\frac{1+\sqrt{\displaystyle \frac{\pi }{2}}\displaystyle \frac{1}{\mathrm{Kn}}}{1+1.235\sqrt{\displaystyle \frac{\pi }{2}}\displaystyle \frac{1}{\mathrm{Kn}}} \right) , \end{aligned}$$
(56)
$$\begin{aligned} b & = \frac{128}{3\pi }\cdot \frac{1+\sqrt{\displaystyle \frac{\pi }{2}}\displaystyle \frac{1}{\mathrm{Kn}}}{1+1.235\sqrt{\displaystyle \frac{\pi }{2}}\displaystyle \frac{1}{\mathrm{Kn}}} \mathrm{Kn}\cdot p, \end{aligned}$$
(57)

where \(\mathrm{Kn}\cdot p\) is given by

$$\begin{aligned} \mathrm{Kn}\cdot p & = \frac{\lambda _\mathrm {mol}}{\lambda _\mathrm {wall}}\cdot nk_\mathrm BT\nonumber \\ & = \frac{1}{\lambda _\mathrm {wall}}\cdot \frac{1}{\sqrt{2}n\pi d_\mathrm m^2}\cdot nk_\mathrm BT\nonumber \\ & = \frac{1}{\lambda _\mathrm {wall}}\cdot \frac{1}{\sqrt{2}\pi d_\mathrm m^2}\cdot k_\mathrm BT, \end{aligned}$$
(58)

and hence, it depends only on the temperature in the case of hard sphere molecules since \(\lambda _\mathrm {wall}\) is constant for the same porous medium as is shown in Sect. 3.4. This suggests that the Knudsen number contributes to the Klinkenberg coefficient b for the Knudsen-type expression for porous media. Thus, the Klinkenberg coefficient b for the Knudsen-type expression for porous media monotonically increases from \(11.00\,\mathrm{Kn}\cdot p\) to \(13.58\,\mathrm{Kn}\cdot p\) as Kn increases from 0 to infinity.

On the other hand, the superficial velocity is given by the Wakao-type expression for porous media as follows:

$$\begin{aligned} U_\mathrm s=-\varepsilon \tau \frac{\lambda _\mathrm {wall}^2}{32}\left[ \phi \frac{128}{3\pi }\mathrm{Kn}+\left( 1-\phi \right) \left\{ 1+\left( a+\frac{32}{3} \right) \mathrm{Kn} \right\} \right] \frac{\nabla p}{\mu }. \end{aligned}$$
(59)

From this equation and Darcy’s law, the permeability of porous medium is given by

$$\begin{aligned} K=K_0\left[ \phi \frac{128}{3\pi }\mathrm{Kn}+\left( 1-\phi \right) \left\{ 1+\left( a+\frac{32}{3} \right) \mathrm{Kn} \right\} \right] . \end{aligned}$$
(60)

From Eq. (39), this permeability of porous medium can be rewritten in the form of the Klinkenberg equation as follows:

$$\begin{aligned} K=K_0\left[ 1+\frac{\left\{ \displaystyle \frac{128}{3\pi } \cdot \displaystyle \frac{\mathrm{Kn}}{\mathrm{Kn}+1}+\left( a+\displaystyle \frac{32}{3}-1 \right) \cdot \displaystyle \frac{1}{\mathrm{Kn}+1} \right\} \mathrm{Kn}\cdot p}{p}\right] . \end{aligned}$$
(61)

Consequently, the Klinkenberg coefficient b for the Wakao-type expression for porous media is given by

$$\begin{aligned} b=\left[ \displaystyle \frac{128}{3\pi } \cdot \displaystyle \frac{\mathrm{Kn}}{\mathrm{Kn}+1}+\left( a+\displaystyle \frac{32}{3}-1 \right) \cdot \displaystyle \frac{1}{\mathrm{Kn}+1}\right] \mathrm{Kn}\cdot p. \end{aligned}$$
(62)

Thus, the Knudsen number also contributes to the Klinkenberg coefficient b for the Wakao-type expression for porous media. In the case of \(a=2\), the coefficient b monotonically increases from \(11.66\,\mathrm{Kn}\cdot p\) to \(13.58\,\mathrm{Kn}\cdot p\) as Kn increases from 0 to infinity.

3.4 Estimation of mean free path \(\lambda _{\mathrm {wall}}\) for molecule–wall collisions

In the previous section, the validity of the Knudsen-type expression, Eq. (42), and the Wakao-type expression, Eq. (46), both of which are proposed in the present study, were confirmed for gas transport in porous media with micro-/nanoscale pores. However, the mean free paths \(\lambda _{\mathrm {wall}}\) for molecule–wall collisions obtained from the results of the DSMC simulations were used in both expressions. In order to use both expressions to estimate gas transport in porous media, it is necessary to know \(\lambda _{\mathrm {wall}}\) without the aid of DSMC simulation. In this section, we consider how to estimate \(\lambda _{\mathrm {wall}}\).

Let us consider the void region of a porous medium, whose volume available for flow and total wetted surface area are V and S, respectively. This region is filled with a gas of molecular number density n. Since the mean free path \(\lambda _{\mathrm {wall}}\) for molecule–wall collisions is defined as the average distance that a molecule travels between successive molecule–wall collisions, \(\lambda _{\mathrm {wall}}\) can be given by

$$\begin{aligned} \lambda _{\mathrm {wall}}=\frac{\text {total distance that all molecules travel}}{{\text{total number of molecule}{-}{\text{wall collisions}}}}. \end{aligned}$$
(63)

In the case where the gas flow velocity U is much smaller than the mean molecular speed \(\bar{C}\) of gas molecules, the number of molecule–wall collisions per unit time is given by \((1/4)n{\bar{C}}S\). On the other hand, the total distance that all molecules travel per unit time is given by \(nV\bar{C}\). Therefore, the mean free path \(\lambda _{\mathrm {wall}}\) for molecule–wall collisions is given by

$$\begin{aligned} \lambda _{\mathrm {wall}} & = \displaystyle \frac{nV{\bar{C}}}{\displaystyle \frac{1}{4}n{\bar{C}}S} \nonumber \\ & = \displaystyle \frac{4V}{S}. \end{aligned}$$
(64)

Dividing the numerator and the denominator of Eq. (64) by the total volume of the porous medium including both solid and void regions, \(\lambda _{\mathrm {wall}}\) is four times as large as the ratio of the porosity \(\varepsilon\) to the wetted surface area \(S_\mathrm {v}\) per unit volume of porous medium as follows:

$$\begin{aligned} \lambda _{\mathrm {wall}} & = \displaystyle \frac{4V/(\text{volume } \text{ of } \text{ porous } \text{ medium})}{S/(\text{volume } \text{ of } \text{ porous } \text{ medium})}, \nonumber \\ & = \displaystyle \frac{4\varepsilon }{S_\mathrm {v}}. \end{aligned}$$
(65)

Interestingly, the mean free path \(\lambda _\mathrm {wall}\) for molecule–wall collisions, which is defined at the microscopic level, results in the macroscopic hydraulic diameter \(D_\mathrm {H}\) for the case when the porous medium is regarded as a conduit. Here, \(D_\mathrm {H}\) is given by (Dullien 1979)

$$\begin{aligned} D_\mathrm H=\frac{4\times \text {void volume of porous medium}}{\text {surface area of channels in porous medium}}. \end{aligned}$$
(66)

Thus, if we know the porosity \(\varepsilon\) and the wetted surface area \(S_\mathrm v\) per unit volume of porous medium, we can estimate the value of \(\lambda _\mathrm {wall}\).

In the case where a porous medium is a packed column of spherical particles of diameter \(d_\mathrm p\) without interpenetration of particles, \(\varepsilon\), \(S_\mathrm v\), and \(\lambda _\mathrm {wall}\) are easily obtained by

$$\begin{aligned} \varepsilon & = 1-V_\mathrm pN\nonumber \\ & = 1-\frac{1}{6}\pi d_\mathrm p^3 N, \end{aligned}$$
(67)
$$\begin{aligned} S_{\mathrm{v}} & = \frac{S_\mathrm p N}{V_\mathrm p N / (1-\varepsilon )} \\ & = \frac{\pi d_\mathrm p^2}{ \displaystyle\frac{1}{6}\pi d_\mathrm p^3}(1-\varepsilon ) \\ & = \frac{6}{d_\mathrm p}(1-\varepsilon ), \end{aligned}$$
(68)
$$\begin{aligned} \lambda _\mathrm {wall} & = \frac{4\varepsilon }{S_\mathrm v}\nonumber \\ & = \frac{4\varepsilon }{\displaystyle \frac{6}{d_\mathrm p}(1-\varepsilon )}\nonumber \\ & = \frac{2}{3}\frac{\varepsilon }{1-\varepsilon }d_\mathrm p, \end{aligned}$$
(69)

where N is the number of particles per unit volume of porous medium, \(V_\mathrm p\) is the volume of a particle and given by \(V_\mathrm p=(1/6)\pi d_\mathrm p^3\), and \(S_\mathrm p\) is the surface area of a particle and given by \(S_\mathrm p=\pi d_\mathrm p^2\). However, in the porous medium treated in the present DSMC simulations, particles were arranged randomly and were interpenetrating one another. For such a porous medium, \(\varepsilon\), \(S_\mathrm v\), and N are given by (Weissberg 1963; Weissberg and Prager 1970)

$$\begin{aligned} \varepsilon & = \mathrm e^{-V_\mathrm p N}, \end{aligned}$$
(70)
$$\begin{aligned} S_\mathrm v & = \varepsilon S_\mathrm p N , \end{aligned}$$
(71)
$$\begin{aligned} N & = -\frac{1}{V_\mathrm p}\log {\varepsilon }, \end{aligned}$$
(72)

respectively. Consequently, \(\lambda _\mathrm {wall}\) for the porous medium used in the present study is given by

$$\begin{aligned} \lambda _\mathrm {wall} & = \frac{4\varepsilon }{S_\mathrm v}\nonumber \\ & = \frac{4}{S_\mathrm p N}\nonumber \\ & = -\frac{4}{\displaystyle \frac{S_\mathrm p}{V_\mathrm p}\log {\varepsilon }}\nonumber \\ & = -\frac{2}{3}\frac{d_\mathrm p}{\log {\varepsilon }}. \end{aligned}$$
(73)

Equations (69) and (73) show that the mean free path \(\lambda _\mathrm {wall}\) for molecule–wall collisions depends on the porosity \(\varepsilon\) and the diameter \(d_\mathrm p\) of solid particles, i.e., the parameters determining the channel configuration of the porous medium, but does not depend on the molecular number density, the gas pressure, the gas temperature, and the nature of gas such as viscosity.

In Fig. 8, \(\lambda _\mathrm {wall}\)’s estimated by using Eq. (73) are compared with \(\lambda _\mathrm {wall}\)’s obtained in the DSMC simulations, which were used in Eq. (27), the Knudsen-type expression Eq. (42), and the Wakao-type expression Eq. (46) in Sects. 3.2 and 3.3, for the cases of various porosities \(\varepsilon\) and various diameters \(d_\mathrm p\) of solid particles. The estimated \(\lambda _\mathrm {wall}\)’s are in good agreement with those obtained in the DSMC simulations. Since Eq. (73) is derived from Eq. (65) for the porous media treated in the present study, this agreement shows that the estimation of \(\lambda _\mathrm {wall}\) by using Eq. (65) is valid.

Fig. 8
figure 8

Comparison of \(\lambda _\mathrm {wall}\)’s estimated by using Eq. (73) with those obtained in the DSMC simulations for the cases of various porosities and various diameters of spherical particles (\(d_\mathrm p=10{-}1000~\mathrm {nm}\), \(\bar{p}=0.95~\mathrm {atm}\))

Full size image

As mentioned above, the mean free path \(\lambda _\mathrm {wall}\) for molecule–wall collisions depends only on the channel configuration of a porous medium and is estimated to be equivalent to the hydraulic diameter \(D_\mathrm H\) for the porous medium. Therefore, our choice of \(\lambda _\mathrm {wall}\) as the characteristic length for both Knudsen and Reynolds numbers is valid, and furthermore, using \(\lambda _\mathrm {wall}\) as the tube diameter in our tube bundle model for porous media is reasonable.

Lastly, let us check the validity of the flow velocities estimated by using the Knudsen-type expression Eq. (42) and by using the Wakao-type expression Eq. (46) together with the mean free path \(\lambda _\mathrm {wall}\) for molecule–wall collisions estimated theoretically by using Eq. (65). Actually, \(\lambda _\mathrm {wall}\) was estimated by using Eq. (73) here because Eq. (73) is derived from Eq. (65) so as to be specialized for the porous medium treated in the present study. In Fig. 9a, b, the flow velocities U estimated by using the Knudsen-type expression Eq. (42) and by using the Wakao-type expression Eq. (46) together with \(\lambda _\mathrm {wall}\) estimated theoretically by using Eq. (65) are compared with those obtained in the DSMC simulations for the cases of various porosities \(\varepsilon\) and various particle diameters \(d_\mathrm p\) on a log–log scale and on a linear scale, respectively. The flow velocities estimated by using both expressions with theoretically estimated \(\lambda _\mathrm {wall}\) agree well with those obtained in the DSMC simulations.

Thus, if we know the porosity \(\varepsilon\) and the wetted surface area \(S_\mathrm v\) per unit volume of a porous medium, we can make a good estimate of the gas flow velocity U and the superficial velocity \(U_\mathrm s\), i.e., the volume flux, by using the Knudsen-type expressions, Eqs. (42) and (48), or the Wakao-type expressions, Eqs. (46) and (59), together with Eq. (65) for porous media with pores ranging from nanometer to micrometer and porosity of \(0.3<\varepsilon <0.5\).

Fig. 9
figure 9

Comparison of flow velocities estimated by using the Knudsen-type expression and by using the Wakao-type expression together with theoretically estimated \(\lambda _\mathrm {wall}\) with those obtained in the DSMC simulations for the cases of various porosities \(\varepsilon\): a on a log–log scale; b on a linear scale (\(\tau =0.9\varepsilon\), \(d_\mathrm p=10{-}1000~\mathrm {nm}\), \(\bar{p}=0.95~\mathrm {atm}\), \(\mathrm dp/\mathrm dy=-0.3619~\mathrm {Pa/nm}\))

Full size image

4 Conclusion

In this study, a porous medium was represented by arranging solid spherical particles randomly. Using that, gas flow through a porous medium with micro-/nanoscale pores was reproduced by performing DSMC simulations. Using the results obtained in the DSMC simulations, the two expressions to estimate gas flow velocity through a porous medium were proposed. The results are summarized as follows:

  1. 1.

    From the results of the DSMC simulations, it was found that the gas flow velocity through a porous medium increases in proportion to increasing pressure gradient at least for \(\mathrm{Re}<0.1\). This result shows that Darcy’s law holds even in the case of a porous medium with micro-/nanoscale pores.

  2. 2.

    The gas flow velocity estimated by using conventional models for permeability, i.e., the Blake–Kozeny, the Carman–Kozeny, and the Rumpf–Gupte models, more greatly deviated from that obtained in the DSMC simulations as the particle size of a porous medium became smaller from micrometer to nanometer scale.

  3. 3.

    We regarded the porous medium as a bundle of tortuous capillary tubes with a diameter of \(\lambda _\mathrm {wall}\), where \(\lambda _\mathrm {wall}\) is the mean free path for molecule–wall collisions. At first, considering only Knudsen diffusion, the expression to estimate gas flow velocity U through a porous medium was constructed as follows:

    $$\begin{aligned} U=-\frac{1}{3}\tau \lambda _\mathrm {wall}\bar{C}\frac{\nabla p}{p}. \end{aligned}$$

    In the case where \(\tau\) is set at \(\tau =0.9\varepsilon\), the flow velocity estimated by using this expression agreed well with that obtained in the DSMC simulations for particle diameter \(d_\mathrm p<200\) nm, i.e., for \(\mathrm{Kn}>0.6\). However, for \(d_\mathrm p>200\) nm, i.e., for \(\mathrm{Kn}<0.6\), the larger the particle diameter became, the more greatly the velocity estimated by using this expression deviated from that obtained in the DSMC simulations.

  4. 4.

    Our expression shown in the previous item is not applicable to the case of a Knudsen number much smaller than unity. This is because viscous flow is not considered in that expression. Referring to Knudsen’s expression and Wakao’s expression proposed to estimate gas flux through a straight cylindrical capillary, our expression was modified by adding the contribution of viscous flow with a velocity slip. The obtained sets of expressions for the flow velocity U, the superficial velocity \(U_\mathrm s\), the permeability K, and the Klinkenberg coefficient b are as follows:

    The Knudsen-type expressions for porous media:

    $$\begin{aligned}&U=-\tau \left( \frac{1}{3}\lambda _{\mathrm {wall}}{\bar{C}} \frac{1+c^{\mathrm K}_1p}{1+c^{\mathrm K}_2p} +\frac{\lambda _{\mathrm {wall}}^2}{32\mu }p \right) \frac{\nabla p}{p},\\&U_\mathrm s=-\varepsilon \tau \frac{\lambda _{\mathrm {wall}}^2}{32} \left( 1+\frac{128}{3\pi }\mathrm{Kn}\frac{1+c_1^\mathrm Kp}{1+c_2^\mathrm Kp} \right) \frac{\nabla p}{\mu },\\&K=K_0 \left( 1+\frac{128}{3\pi }\mathrm{Kn}\frac{1+c_1^\mathrm Kp}{1+c_2^\mathrm Kp} \right) ,\\&b=\frac{128}{3\pi }\cdot \frac{1+c_1^\mathrm Kp}{1+c_2^\mathrm Kp}\mathrm{Kn}\cdot p,\\&c^{\mathrm K}_1=2.00\left( \frac{8}{\pi } \right) ^\frac{1}{2}\left( \frac{\lambda _\mathrm {wall}}{2\mu \bar{C}} \right) ,\\&c^{\mathrm K}_2=2.47\left( \frac{8}{\pi } \right) ^\frac{1}{2}\left( \frac{\lambda _\mathrm {wall}}{2\mu \bar{C}} \right) . \end{aligned}$$

    The Wakao-type expressions for porous media:

    $$\begin{aligned} &U=-\tau \frac{\lambda _\mathrm {wall}^2}{32\mu }\left[ \phi \frac{128}{3\pi }\mathrm{Kn}+\left( 1-\phi \right) \left\{ 1+\left( a+\frac{32}{3} \right) \mathrm{Kn} \right\} \right] \nabla p,\\&U_\mathrm s=-\varepsilon \tau \frac{\lambda _\mathrm {wall}^2}{32}\left[ \phi \frac{128}{3\pi }\mathrm{Kn}+\left( 1-\phi \right) \left\{ 1+\left( a+\frac{32}{3} \right) \mathrm{Kn} \right\} \right] \frac{\nabla p}{\mu },\\&K=K_0\left[ \phi \frac{128}{3\pi }\mathrm{Kn}+\left( 1-\phi \right) \left\{ 1+\left( a+\frac{32}{3} \right) \mathrm{Kn} \right\} \right] ,\\&b=\left[ \phi \displaystyle \frac{128}{3\pi } +\left( 1-\phi \right) \left( a+\displaystyle \frac{32}{3}-1 \right) \right] \mathrm{Kn}\cdot p,\\&\phi =\frac{\mathrm{Kn}}{\mathrm{Kn}+1}. \end{aligned}$$

    Here, the Knudsen number Kn is given by \(\mathrm{Kn}=\lambda _\mathrm {mol}/\lambda _\mathrm {wall}\) and \(K_0\) is the permeability in the continuum limit and given by \(K_0=\varepsilon \tau (\lambda _\mathrm {wall}^2/32)\).

  5. 5.

    We derived the expression to estimate the mean free path \(\lambda _\mathrm {wall}\) for molecule–wall collisions as follows:

    $$\begin{aligned} \lambda _\mathrm {wall}=\frac{4\varepsilon }{S_\mathrm v}. \end{aligned}$$

    The mean free paths \(\lambda _\mathrm {wall}\) for molecule–wall collisions estimated by using this expression agreed well with those obtained in the DSMC simulations, and hence, the validity of this expression was confirmed. This expression suggests that the mean free path \(\lambda _\mathrm {wall}\) for molecule–wall collisions depends only on the channel configuration of a porous medium and is equivalent to the hydraulic diameter for the porous medium. Therefore, our choice of \(\lambda _\mathrm {wall}\) as the characteristic length for both Knudsen and Reynolds numbers is valid, and furthermore, using \(\lambda _\mathrm {wall}\) as the tube diameter in our tube bundle model for porous media is reasonable.

  6. 6.

    The flow velocities estimated by using the Knudsen-type expression and by using the Wakao-type expression together with \(\lambda _\mathrm {wall}\) estimated in such a way as mentioned in the previous item agreed well with those obtained in the DSMC simulations for the range of the porosity of \(0.3<\varepsilon <0.5\) and the pore size from nanometer to micrometer scale. Thus, if we know the porosity \(\varepsilon\) and the wetted surface area \(S_\mathrm v\) per unit volume of a porous medium, we can make a good estimate of the gas flow velocity and the volume flux by using these expressions proposed here together with the estimated mean free path \(\lambda _\mathrm {wall}\) for molecule–wall collisions for porous media with pores ranging from nanometer to micrometer and porosity of \(0.3<\varepsilon <0.5\).