1 Introduction

Recent years have seen a tremendous acceleration of research related to the dynamics of fluids inside nanochannels. Nanofluidics holds great promises for designing novel applications, largely in the context of nanobiotechnology (Eijkel and van den Berg 2005; Abgrall and Nguyen 2008; Schoch and Han et al 2008). The additional functionality of such devices is based on the fact that the geometric dimension of the channel becomes comparable to some intrinsic length scale of the (complex) fluid to be investigated, such as the size of dissolved biomolecules (e.g., DNA, proteins) and the electrostatic screening length (Debye length) of electrolytes.

One of the primary requirements for a successful operation of such nanochannel-based fluidic devices is a thorough understanding of the dynamics of the (typically aqueous) solvent in the absence of dissolved macromolecules. To this end, several groups investigated the spontaneous filling of hydrophilic nanochannels driven by capillarity (Tas and Haneveld et al. 2004; Han and Mondin et al. 2006; Thamdrup et al. 2007; van Delft and Eijkel et al. 2007; Haneveld et al. 2008; Mortensen and Kristensen 2008). The general finding of all those experiments is that the filling dynamics of typically pure simple fluids follows the classical Lucas–Washburn law (Lucas 1918; Washburn 1921), in which the meniscus advances proportional to the square root of time. However, in most instances, it was found that the prefactor in that algebraic law was reduced compared to the theoretical expectations, which was attributed to various possible effects including an electrokinetic counter flow (Tas et al. 2004) (later disputed by others; Mortensen and Kristensen 2008), the presence of bubbles (Thamdrup et al. 2007), elastic deformations of the channel wall, and an increased dynamic contact angle (Han et al. 2006). One of the most important problems is that most experiments do not allow for distinguishing between confinement effects arising from a variation of the macroscopic materials properties (viscosity, surface tension) and retarding effects on the moving meniscus, e.g., due to wall roughness, pinning, and slip.

For complex fluids such as mixtures, one may expect additional effects due to preferential molecular interactions of the different species with the channel walls. It is well-known that the “surface fields” arising from such specific interactions affect the phase behavior of confined fluids (Binder 2008). Such effects are technologically exploited in selective membranes (e.g., reverse osmosis) to filter out specific components. In particular, recent interest in concentrating ethanol–water mixtures for bio-fuel applications raised renewed interest in the physical mechanisms underlying the chemical selectivity in processes such as membrane pervaporation (Fritz and Hofmann 1998; Vane 2005; Huang et al. 2008), where water suppressed from passing nanoscopic pores. Artificial nanochannels allowing for detailed optical characterization may serve as model systems to investigate these mechanisms in more detail.

In this study, we investigate the dynamics of capillarity-driven filling of nanochannels with a thickness of 6 and 16 nm with ethanol and water and various mixtures thereof, i.e., we vary systematically the surface tension and the viscosity of the fluid. Multiple beam interferometry based on the partially reflective mirrors embedded into the channel walls allows us to visualize the liquid inside the channel with high resolution following techniques which have been well-established in the context of measurements with the surface forces apparatus (Israelachvili 1992; Heuberger 2001; Becker and Mugele 2003).

2 Theoretical background

The Lucas–Washburn law is based on the balance of capillary forces sucking the liquid into the nanochannel and viscous drag opposing that motion. Assuming that the channel width w is much larger than its thickness d, macroscopic capillarity tells that the moving meniscus has a negative curvature \( \kappa = 2\cos \theta /d, \) where θ is the contact angle. Combined with the surface tension σ, this gives rise to a negative Laplace pressure \( \Updelta p_{\text{L}} = \sigma \kappa \) at the meniscus. The pressure drop between the meniscus and the inlet of the channel (where the pressure is p 0 = 0) drives the fluid flow. Assuming d ≪ w along with the standard no-slip boundary condition at the solid–liquid interface, this pressure drop is counteracted by the hydraulic resistance \( R_{\text{H}} = 12\mu x/d^{3} , \) where μ is the viscosity of the liquid and x is the position of the meniscus measured from the inlet. Relating the total flux (per unit width) \( Q = d\,\dot{x} \) and the total pressure drop \( \Updelta p = \Updelta p_{\text{L}} \) by Ohm’s law, leads to

$$ \dot{x} = {\frac{\sigma d\cos \theta }{6\mu }} \cdot {\frac{1}{x}} = {\frac{\alpha }{2}} \cdot {\frac{1}{x}}, $$
(1)

where the prefactor α is given by

$$ \alpha = {\frac{\sigma d\cos \theta }{3\mu }}. $$
(2)

The classical Lucas–Washburn equation for x(0) = 0 is derived from Eq. 1.

$$ x(t) = \sqrt {\alpha \cdot t} $$
(3)

The \( \sqrt t \)-dependence thus generically results from the fact that a constant driving force is balanced by a viscous drag force that increases linearly with the meniscus position. Deviations of the driving force (e.g., due to some additional friction of the moving contact line or a variation of σ) or of the absolute value of the hydrodynamic resistance (e.g., due to a variation of μ or of the flow profile as in the electroviscous effect) leave this basic structure unaffected and are hence only reflected in variations of the prefactor α, which are difficult to interpret since various factors such as actual contact angle and exact local height of the channel are not accessible in typical experiments. A systematic variation of the two bulk parameters σ and μ, however, may shed some additional light.

3 Experimental setup and methods

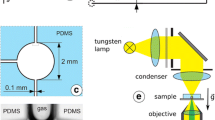
The experiments were performed in nanochannels with a length of l c = 500 μm and a width of 10 μm. Two batches of nanochannels were fabricated with average thickness of d = 6 and 16 nm, respectively. The manufacturing process as well as the characterization of the channels has been described in (van Delft et al. 2007). The typical roughness of the channel walls was determined to ≈1 nm (root means square) by atomic force microscopy (AFM). The contact angles of pure water and ethanol were found to be \( \theta_{{{\text{H}}_{ 2} {\text{O}}}} \) = 30° and θ EtOH = 0°, respectively, as measured on the wafer surfaces prior to anodic bonding of the chip. The layout of the chip incorporating the nanochannels as well as microchannels for introducing liquids and access holes for connecting to macroscopic tubes and syringe pumps is shown in Fig. 1a. Partially transparent Ag mirrors with a thickness of 45 nm are embedded into the top and bottom walls of the chip, separated from the nanochannel by SiO x spacer layers with a thickness of approximately 1 μm each. These mirrors form a Fabry–Pérot interferometer as sketched in Fig. 1b. The experiments are based on measuring the optical transmission through this device, which displays a series of distinct transmission peaks, using an optical microscope (Zeiss Axioskop) equipped with a digital video camera (PCO Pixelfly). Monochromatic light was generated from a white light fiber laser source (Fianium) (compared to the previously used Xe arc lamp (van Delft et al. 2007), this source offers superior intensity and stability over time) and a grating monochromator (Newport). From the position of these peaks, we determine the thickness of the nanochannel. Note from Fig. 1c that only the odd interference orders displaying an antinode of the electric field in the center (i.e., at the position of the nanochannel) are sensitive to the refractive index of the liquid. To visualize the filling dynamics of the nanochannels, we illuminated the nanochannels with a wavelength on the right wing of one of the odd transmission peaks. When liquid enters the nanochannel, the position of the transmission peak shifts to the right hand side by an amount that is proportional to the change in optical thickness \( \Updelta d_{\text{opt}} = \Updelta n \cdot d = (n_{\text{liq}} - n_{\text{air}} ) \cdot d, \) where n liq and n air are the refractive indices of the liquid and air, respectively. For a fixed wavelength, this shift gives rise to a variation of the transmitted intensity, which allows a precise localization of the meniscus position even for the very thin channels of this study. More details of the optical setup and the methods can be found in (Heuberger 2001; Becker and Mugele 2005; van Delft et al. 2007).

Fig. 1
figure 1

Schematic layout of nanochannels and interferometry setup. a Layout of the chip (top view) including microchannels and connection holes to interface the chip to the external tubing. b Illustration of integrated interferometer (vertical cross section) with nanochannel (white; thickness not to scale) in between mirrors (black lines) at 1 μm distance. Left: illustration of optical standing waves. c Optical transmission T vs. incident wavelength λ for an empty nanochannel (black solid) and next to a spacer layer between nanochannels (red dashed). Insets: zoomed view of odd and even interference fringe (see text)

Full size image

4 Results

Figure 2 shows a series of video snapshots obtained during filling with water. While the optical contrast becomes maximum for the empty channels, the filled channels are hardly visible due to nearly perfect matching of the refractive index. The filling process is characterized by a rather sharp advancing meniscus and the occasional inclusion of air bubbles that typically dissolve on the time scale of a few seconds. Data for other liquids look very similar (Occasionally, we found a partial step in the refractive index followed by a gradual relaxation within a few seconds to the bulk refractive index n H20, as described already in van Delft. However, this behavior was not very consistent and disappeared after filling and drying the channel several times.).

Fig. 2
figure 2

Video snapshots for various states of channel filling. Channels appear dark in the empty state and become (almost) invisible in the filled state. Channel width: 10 μm

Full size image

In the following, we focus only on the dynamics of the meniscus. Figure 3 shows the position of the menisci of water and ethanol filling 6 nm and 16 nm channels, respectively, plotted versus the square root of time. Each curve in this figure represents an average over approximately 25 individual channel filling events obtained by averaging over several adjacent nanochannels as well as several subsequent runs with the same channel. In between the runs the nanofluidic chip was dried in a vacuum oven at an elevated temperature of approximately 200°C. (One may worry that contamination accumulates inside the nanochannels in each filling and drying cycle. This is indeed the case. After several runs an increasing number of channels gets partially or totally blocked. Such channels are easily identified in the video data and are excluded from the analysis. The remaining channels display a rather consistent behavior.)

Fig. 3
figure 3

Positions of menisci with respect to the square root of time for water and ethanol in nanochannels with a thickness of 6 nm and 16 nm

Full size image

The data follow the qualitatively expected behavior: for both liquids the position increases with \( \sqrt t . \) The filling speed decreases with decreasing channel thickness and for each channel thickness the filling speed of ethanol is slower than that of water, reflecting the approximately three times lower surface tension of ethanol at similar viscosity (μ EtOH = 1.20; \( \mu_{{{\text{H}}_{ 2} {\text{O}}}} \)=1.03 mPa s). The observed filling speeds (V) range from 185 to 382 μm/s, which correspond to the capillary numbers \( Ca = \mu V/\sigma = 4.28 \times 10^{ - 6}-1.59 \times 10^{-5}\ll 1.\)

Figure 4a and b show the same type of data for various concentrations of water–ethanol mixtures in the 6 and 16 nm channel, respectively. It turns out that the filling speed does not vary monotonously with the composition of the liquid. Upon adding ethanol to the water, the speed first decreases, reaching a minimum at around 50–50 composition and then increases again toward the pure ethanol behavior. This behavior is consistently found for both channel thicknesses. Figure 5 shows the prefactor α in Eq. 3 according to the concentration of mixture, as determined from the experimental data (symbols) along with the values calculated based on the bulk properties (solid lines). The comparison between the experimental measurements and the theoretical expectations shows that the former are systematically 10–30% lower than the latter.

Fig. 4
figure 4

Positions of menisci with respect to the square root of time for water–ethanol mixtures of various concentrations in nanochannels with a thickness of (a) 6 nm and (b) 16 nm. X volume fraction of ethanol

Full size image
Fig. 5
figure 5

Comparison of experimental filling rate (α1/2) with theoretical prediction (based on bulk properties) for various mixtures in nanochannels with a thickness of 6 and 16 nm. X EtOH volume fraction of ethanol, symbols experiment, solid lines theoretical prediction

Full size image

Let us first address the non-monotonous behavior. At first glance, this result may seem surprising. However, it is in fact consistent with the bulk behavior of water–ethanol mixtures (see also Fig. 5). While the surface tension monotonously decreases from 72 mJ/m2 for pure water to 23 mJ/m2 for pure ethanol, the viscosity first increases from 1 mPa s to the maximum of ≈2.9 mPa s for a 50–50 mixture and then decreases again to 1.2 mPa s for pure ethanol. (This anomaly is, in fact, believed to be related to the imperfect mixing of water and ethanol on the molecular scale (Dixit 2002 et al.)). Since cos θ varies only between 0.87 and 1 within the range of contact angles between 30° and 0°, the behavior of the prefactor in Eq. 2 is determined by the ratio σ/μ. The concentration-dependence of σ and μ gives rise to the minimum of this ratio at X EtOH = 56%.

In fact, Eq. 2 suggests that the data obtained for different composition and channel thickness should all collapse onto a single curve if we plot the dimensionless quantities \( \xi = x/l_{\text{c}} \) versus \( \sqrt \tau = \sqrt {\alpha t/l_{c}^{2} }. \) This master plot of all experimental data in this study is shown in Fig. 6 (where we used a linear interpolation of cos θ Y with XEtOH between 0.87 and 1). Indeed, the data do collapse to a reasonable degree of accuracy. The water–ethanol mixtures in our experiments thus behave completely as expected based on their bulk behavior. Within the experimental accuracy, we find no indication of confinement-induced effects with respect to the dependence of the fluid parameters viscosity and surface tension.

Fig. 6
figure 6

Dimensionless plots of the positions of menisci versus the square root of time in nanochannels with a thickness of (a) 6 nm and (b) 16 nm. X volume fraction of ethanol

Full size image

Finally, we want to comment on the observed reduction in absolute value of α. In fact, various partially contradicting observations have been reported in the literature regarding the deviation between experimental filling speeds and the expectations based on the Lucas–Washburn equation. It is clear from various experimental data that the roughness of channel walls affects the dynamics of the menisci. Our video recordings clearly show that the motion of the menisci is affected by occasional temporary pinning due to roughness and heterogeneity of the channel walls. For an average channel thickness of 6 nm, a wall roughness of 1 nm root means square gives rise to tremendous variations of the local channel thickness and thus of the local hydraulic resistance. A quantitative analysis of this effect within the framework of classical hydrodynamics is possible provided that the exact channel geometry is known. The lateral variation of the transmitted intensity for the empty and filled channels does in principle contain this information (on a lateral scale given by the lateral optical resolution). Unfortunately, however, a careful analysis of the lateral intensity profiles shows that the static roughness is dominated by the roughness of the interface between the Ag mirrors and the spacer layers rather than actual channel roughness. A detailed analysis of the channel geometry therefore requires additional experimental efforts beyond the scope of this work.

Here, we simply want to argue that despite the 1/h 3-dependence it is unlikely that the thickness dependence of the hydraulic resistance is responsible for the 10–30% reduction of α observed. For a channel of length L in two dimensions with variable thickness \( h(x) = h_{0} + \Updelta h\sin qx, \) the hydraulic resistance is given by

$$ R_{\text{H}} = {\frac{\Updelta p}{Q}} = 12\mu \int\limits_{0}^{L} {{\frac{{{\text{d}}x}}{{h(x)^{3} }}}} \approx {\frac{12\mu L}{{h_{0}^{3} }}}\left( {1 + 3\left( {{\frac{\Updelta h}{{h_{0} }}}} \right)^{2} + {\frac{45}{8}}\left( {{\frac{\Updelta h}{{h_{0} }}}} \right)^{4} } \right). $$
(4)

For Δh = 1.4 nm (corresponding to 1 nm root mean square) and h 0 = 6 nm, this produces an increase of the R H to 16%, for h 0 = 16 nm, it is only 2.3%. We consider these numbers are the upper limits of increase of R H by the roughness effect: the correlation length of the roughness in our channels (as seen from the AFM pictures, see van Delft et al. 2007) is much smaller than the width of the nanochannel, and hence liquid can always easily ‘flow around’ any local minimum of the film thickness. This conclusion is further corroborated by numerical studies by (Hu et al. 2003; Baviere et al. 2006) showing that roughness effects are negligible in microchannels with periodic rough elements if the distance between rough elements is large enough compared with their heights. Hence, we do not believe that the roughness dependence of the hydraulic resistance can explain the substantial reduction of prefactor.

Another possibility that should be taken into account is the presence of stagnant layers on the solid surface. The conventional fluid dynamic picture assumes that the liquid immediately adjacent to the solid does not move; the so-called no-slip boundary condition. Since liquid consist of discrete molecules rather than a continuum, this boundary condition can produce one immobile layer of molecules stuck to the surface. As a result, the effective thickness of the channel available for the Poiseuille flow is reduced by two molecular diameters (one on each wall), which amounts to approximately 0.6 nm for H2O in the present experiments. Owing to the h −3 dependence of the hydraulic resistance, this effect could account for reductions of α up to 30% in the 6 nm channels. While such effects have been demonstrated convincingly in earlier work (Chan and Horn 1985; Becker and Mugele 2003), the current experiments do not allow us to make a definite statement.

5 Discussion and conclusion

Our experiments show that the filling dynamics of nanochannels with mixtures of ethanol and water follows the behavior expected based on bulk properties. This observation is striking since one might expect that specific interactions of ethanol and water molecules with the SiO x channel walls would affect the dynamics of fluid flow in channels with a thickness of merely 20–50 water molecules. Yet, like in earlier studies of significantly wider nanochannels (from 27 to 73 nm; Han et al. 2006) surface effects do not seem to play a major role. Han et al. had reported reasonably consistent filling dynamics of 40% ethanol–water mixtures in a 27 nm deep and 900 nm wide nanochannel compared to pure water and ethanol. In contrast to us, these authors reported that the filling proceeds somewhat faster than expected. They attributed this to a dynamic contact angle in excess of the static one, which is surprising since a larger angle in fact leads to a reduced Laplace pressure—if the concept is at all appropriate with channels of a few nanometers thickness.

The observation that the nanochannels do not display any selectivity with respect to water or ethanol is in fact consistent with the numerical studies of other alcohol–water mixtures as well as the typical findings in membrane science (Fritz and Hofmann 1998; Vane 2005; Huang et al. 2008). Despite the strong surface fields, heterogeneity and clustering in alcohol–water typically seems to occur on a scale of no more than ≈10 molecules, corresponding to lateral scales of about 1 nm (Dixit et al. 2002; Guo et al. 2003; Wakisaka and Matsuura 2006). In the presence of a liquid–solid interface, specific adsorption of one species in combination with such clustering probably leads to surface enhanced layers with a thickness of order 1–2 nm. From the absence of any composition-dependent effect in our nanochannels, one may conclude that the influence of these surface layers is insufficient to ‘bridge the gap’ of a 6 nm channel. A systematic investigation of the chemical selectivity of nanopores (e.g., as in pervaporation membranes) thus requires even thinner nanochannels.

Having seen that the filling rates scale with the bulk viscosity and surface tension as expected based on the bulk properties, we are still left with the challenge to explain the reduced absolute filling rate. The present experiments cannot provide a definite answer because they suffer from two deficiencies. First, we have no means of characterizing in situ the wettability of the channels. Second, capillarity-driven filling has the fundamental problem that it does not allow for distinguishing between variations of either the driving forces or the retarding forces. In fact is likely that the wettability does change with time and with the number of consecutive filling cycles. One may argue that wettability changes might be more pronounced for water, which was already partial wetting before bonding the channels, than for ethanol, was completely wetting. Yet, a definite answer requires experiments with additional controls, such as the recent suggestion by Dimitrov et al. (2007, 2008). These authors proposed (and verified using molecular dynamics simulations) that it should be possible to decouple the effect of driving capillary force and of hydraulic resistance including possible wall-slip by following the filling dynamics for variable external driving pressure. Despite the high pressures required, such experiments should be feasible and would probably add important insight to this fundamental problem.