A chaotic serpentine mixer efficient in the creeping flow regime: from design concept to optimization

Abstract

Motivated by the three-dimensional serpentine channel (Liu et al. in J Microelectromech Syst 9:190–197, 2000), we introduce a chaotic serpentine mixer (CSM) and demonstrate a systematic way of utilizing a mapping method to find out an optimal set of design variables for the CSM. One periodic unit of the mixer has been designed to create two streamlines portraits crossing each other. As a preliminary study, flow characteristics and mixing in the original serpentine channel has been reinvestigated. The working principle of the CSM is demonstrated via a particle-tracking method. From the design principle and the flow characteristics of the CSM, we choose three key design variables with an influence on mixing. Then, simulations for all possible combinations of the variables are carried out. At proper combinations of the variables, almost global chaotic mixing is observed in the Stokes flow regime. The design windows obtained can be used to determine an optimal set of the variables to fit with a specific application.

1 Introduction

A micromixer is one of the key components in lab-on-a-chip devices (Reyes et al. 2002) that integrate laboratory functions in biology or chemistry on a single chip while handling extremely small liquid volumes. Under typical operating conditions, flow in these devices is laminar and molecular diffusion across the channels is slow, which makes efficient mixing in microfluidic devices difficult to achieve. To overcome this problem, as successfully applied to the development of macro-scale mixers, the theory of chaotic mixing (Aref 1984; Ottino 1989) is recently extensively applied. By incorporating chaotic advection, which refers to a kinematic phenomenon in which motion of fluid particles is chaotic in Lagrangian sense even though the velocity field is simple from the Eulerian viewpoint, one can achieve enhanced mixing even in the creeping flow regime where inertia is negligible.

Micromixers can be classified into two types, active and passive mixers, depending on the way of manipulating fluids to be mixed. In active microfluidic mixing (Lin et al. 2004; Bottausci et al. 2004; Sritharan et al. 2006; Kang et al. 2007a, b; den Toonder et al. 2008; Phelan et al. 2008), one introduces active controls over the flow field using moving parts, varying pressure gradients, acoustic waves, or electro-magnetic fields, etc. However, a passive mixer utilizes no external actuation except for the mechanism (e.g., pressure head or pump) used to drive flow into a fluidic system. Passive micromixers (Liu et al. 2000; Chen and Meiners 2004; Stroock et al. 2002; Kim et al. 2004, 2005; Kang et al. 2008; Schönfeld and Hardt 2004; Schönfeld et al. 2004) make use of a specific three-dimensional structure to induce, in a periodic (or aperiodic) manner, lateral motion of fluids that yields chaotic mixing in a laminar flow. For more information, we refer to review papers on micromixers (Ottino and Wiggins 2004; Hessel et al. 2005; Nguyen and Wu 2005).

In this study, we are especially concerned with a passive mixer, called the three-dimensional serpentine channel originally proposed by Liu et al. (2000). The serpentine channel, consisting of repeating “C-shaped” structure, shows chaotic mixing only if inertia is significant. In this work we demonstrate that since there is no mechanism (e.g., stretching and folding or stretching, cutting, and stacking) to lead to chaotic mixing, this mixer shows no mixing at all in the absence of inertia. Chaotic mixing above a critical Reynolds number is due to enhanced vortical flows leading to folding of material. As reported by Liu et al. (2000), the serpentine channel has a number of advantages such as the simple two-layer structure and minimizing the chances of clogging and shear-induced damage to bio-molecules, which makes it attractive for use in a wider of microfluidic applications. In the Stokes flow regime, however, one cannot achieve mixing at all due to the symmetry of the channel geometry, which is a severe drawback for general use of the design. Other micromixers utilizing rectangular channels with bends have been proposed to achieve better mixing in a wider range of operating conditions (Kim et al. 2005; Park et al. 2008; Chen and Meiners 2004).

As far as the flow induced by the three-dimensional serpentine channel is concerned, recently, Park and Kwon (2008) numerically investigated the flow characteristics of the original channel geometry and several variants of the channel. The function of the rectangular channel with “C-shaped” bends was turned out to induce rotational motion of fluid elements in the channel, which is significantly influenced by the shape of the bend and the aspect ratio of the rectangular channel. According to their study, the aspect ratio is the most important design variable determining the amount of rotation of fluid elements and thereby governing the performance of mixers relying on such mechanisms as splitting, rotation, and lamination.

Motivated by the previous researches on flow characteristics and mixing in the serpentine channel and its variants, we propose a chaotic serpentine mixer (CSM), which is simple in design and able to induce efficient chaotic mixing even in the Stokes flow regime without inertia. The mixer consists of two functional units (also called mixing protocols) repeating periodically and constituting one spatial period of the mixer. The two units have the functions of splitting fluid elements and creating two asymmetric rotational flows (either co-rotating or counter-rotating) with crossing streamlines in an overall sense. Therefore, the mixer can be thought to be fitted within the linked twist map (LTM) framework (Ottino and Wiggins 2004; Wiggins and Ottino 2004; Sturman et al. 2006). A mapping method is employed to analyze mixing and optimize the mixer. The mapping method had already been validated and applied to various micromixers (Kang et al. 2008; Singh et al. 2008). The progress of mixing is characterized by a measure of mixing called the intensity of segregation. Given design concept for a micromixer, a systematic approach to determine an optimal set of design variables will be discussed as well.

This paper is organized as follows. First, we investigate the flow characteristics and mixing in the serpentine channel proposed by Liu et al. (2000) to demonstrate the role of the typical geometric unit on which the design of the CSM is based. Next discussed is the working principle of the CSM with an emphasis on the kinematics of flow in the creeping flow regime. To do this, the deforming interface between two fluids is tracked. Then, results of mixing analysis will be introduced. Finally, we discuss the results of parameter studies for the key design variables chosen and eventually provide design windows for the mixer.

2 Modeling and numerical methods

2.1 Flow problem

To numerically analyze the progress of mixing, we follow the same approach, based on the mapping method, as used in our previous works (Kang et al. 2008; Singh et al. 2008). In mixing analysis of a mixer with a periodic protocol, generally, a computational domain is defined for a flow analysis such that the periodicity of the velocity field is warranted within the domain, and then the computational domain is discretized to solve the governing equations for the flow field using a proper numerical method. It is assumed that the representative velocity field of each mixing protocol is spatially periodic. This assumption is good enough to investigate mixing in a micromixer composed of composite mixing protocols with their own peculiar flow portraits. Therefore, one needs to know the velocity field in one periodic unit with periodicity constraints. Then, this velocity field is used to create a mapping matrix of a mixing protocol. The obtained mapping matrices is repeatedly reused to analyze mixing in a micromixer to the period up to which one wants to analyze.

We made several assumptions for simplicity of analysis. Two fluids to be mixed are assume to be incompressible and Newtonian with the same viscosity. Here, we are only concerned with distributive mixing without molecular diffusion purely governed by the flow kinematics, i.e., the case with an infinite Péclet number. We restrict our interests in flow characteristics and mixing to those in the creeping flow regime, neglecting inertia. Note that, only in the preliminary study on the three-dimensional serpentine channel flow introduced in Sect. 3, we take into account the effect of inertia due to its significance.

The periodic velocity field is obtained by solving the Stokes equations represented by

$$ \nabla p - \mu \nabla^2{\varvec{u}}={\bf 0}\quad {\text{in}}\ \Upomega, $$

(1)

$$ \nabla \cdot {\varvec{u}}=0\quad \hbox{in}\ \Upomega, $$

(2)

where ${\varvec{u}}$ the velocity, p the pressure, and μ the viscosity. The boundary conditions and constraint equations are

$$ {\varvec{u}}={\bf 0}\quad \hbox{on}\ \Upgamma_w, $$

(3)

$$ Q=-\int_{\Upgamma_i}{\varvec{u}}\cdot{\varvec{n}}\rm{dS}\quad \hbox{on}\ \Upgamma_i, $$

(4)

$$ {\varvec{u}}_i={\varvec{u}}_o\quad \hbox{on}\ \Upgamma_i\ {\text{and}}\ \Upgamma_o, $$

(5)

where Q is the imposed flow rate through the inlet, ${\varvec{n}}$ the outward unit normal vector at the boundary Γ _i , ${\varvec{u}}_i$ the velocity at the inlet node, and ${\varvec{u}}_o$ the velocity at the outlet node. In the above equations, Ω, Γ _w , Γ _i , and Γ _o denote the entire bounded domain, the solid wall boundaries, the inlet boundary, and the outlet boundary, respectively. To obtain the periodic velocity field, we discretize the computational domain into 27-node brick elements using a commercial mesh generation package, NX I-DEAS™, and use a toolkit for the finite element method (TFEM) (Hulsen 2008) to solve a set of governing equations. We use biquadratic interpolation for the velocity and bilinear interpolation for the pressure, the so-called Q2/Q1 element. The constraints for the flow rate and the periodic velocity, Eqs. 4 and 5, are enforced using Lagrange multipliers in a similar way as described in the previous work (Kang et al. 2007a). The resulting matrix equation is solved using a parallel sparse matrix solver, PARDISO (Schenk and Gärtner 2004) on a symmetric multiprocessing (SMP) machine with four quad-core processors.

2.2 Mapping method

Repetitive mixing of viscous liquids in laminar flows corresponds to the situation where a specified mixing operation is repeated during a number of times on a specified mass of material, an excellent example being the baker’s transformation (Ottino 1989). Spencer and Wiley (1951) suggested that the distribution of material in such flows can be handled quite well by the use of a matrix method.

The mapping method uses this idea as follows: a distribution matrix ${\varvec{\varphi}}$ is formed to store information about the distribution of fluid from one cross-section to the next, which arises in spatially periodic flows. A cross-sectional area of a channel with the length L is subdivided into N discrete cells of the same size. During flow, fluid elements from a donor cell are transferred to different recipient cells. The fraction of material that is transferred from the donor cell to a recipient cell gives the distribution coefficient of the donor cell with respect to that of the recipient cell. Thus, the transport of materials in the area consisting of N cells results in a distribution matrix of the order N × N. The coefficient $\varphi_{ij}$ of the matrix equals the fraction of sub-domain Ω _j at z = L that is found in the sub-domain Ω _i at z = 0 to the area of Ω _j at z = 0, defined by

$$ \varphi _{{ij}}=\frac{{\int_{\Upomega _{j} |_{{z=L}} \cap \Upomega _{i} |_{{z=0}} \hbox{dA}}}}{{\int {\Upomega _{j} |_{{z=0}} \hbox{dA}}}} $$

(6)

To calculate φ _ij , the boundary of a cell should be tracked in time, which in fact is not an easy task to carry out in practical applications. Recently, Singh et al. (2008) proposed an alternative approach to overcome this difficulty. Since the new mapping method is based on a particle tracking scheme rather than area tracking requiring an adaptive interface tracking, it is much simpler to implement and leads to almost same accuracy in results as the original method.

To approximate the coefficients of the mapping matrix (or distribution matrix), we introduce K passive particles distributed uniformly at each cell and track the position of the particles from the inlet (z = 0) to the end of a periodic channel (z = L). The position of the particles ${\varvec{x}}$ are tracked in time until it reach the end of a periodic channel geometry. Given velocity field in a mixer geometry, the position is updated by solving an ordinary differential equation:

$$ \frac{{\hbox{d}}{\varvec{x}}}{\hbox{d}t}={\varvec{u}}({\varvec{x}},t), \quad {\varvec{x}}|_{t=0}={\varvec{x}}_0, $$

(7)

where t is the time and ${\varvec{x}}_0$ the initial position of a particle. To integrate the differential equation, Eq. 7, we employ the fourth-order Runge-Kutta Bulirsch-Stoer scheme with the adaptive step size selection (Galaktionov et al. 2000).

Using the distributions of particles at the inlet and the outlet, we can calculate components of a mapping matrix ${\varvec{\Upphi}}.$ If the number of initial particles in the donor sub-domain Ω _j is M _j and, after tracking, the number of the particles found in the recipient sub-domain Ω _i is M _ij , then the component Φ _ij is defined by

$$ \Upphi_{ij}=\frac{{M_{ij}}}{{M_j}}. $$

(8)

In other words, the coefficient Φ _ij is the measure of the fraction of total flux of the sub-domain Ω _j donated to the sub-domain Ω _i . If the numbers of particles K are large enough then Φ _ij approaches to φ _ij . Figure 1 schematically represents how a component of a mapping matrix is calculated.

Fig. 1

Computing the mapping matrix coefficient Φ _ij . The sub-domain Ω _j at z = 0 is covered with a number of particles and the particles are tracked along the down-channel direction z to the next position z = L to determine the number of particles received by the recipient cell Ω _i to the initial number of particles of Ω _j . In this illustration, M _j  = 25 and M _ij  = 9, so Φ _ij  = 0.36

The elegance of this approach is that if one wants to analyze mixing-related scalar quantities, like the concentration vector ${\varvec{C}} \in {{\mathbb{R}}}^{N}$ with a given initial distribution ${\varvec{C}}^0$ at the inlet, then the concentration after one period ${\varvec{C}}^1$ can be obtained by simply multiplying the mapping matrix ${\varvec{\Upphi}}$ by the initial concentration vector ${\varvec{C}}^0$, i.e., ${\varvec{C}}^1=\Upphi {\varvec{C}}^0$. For repetitive mixing, the same operation is repeated multiple times to the same mass, and hence the concentration evolution after n periods is obtained by ${\varvec{C}}^n ={\varvec{\Upphi}}^n {\varvec{C}}^0$. For a sufficiently large number n and chaotic system, the matrix ${\varvec{\Upphi}}^n$ will not be sparse and in some cases the matrix becomes a dense one which requires huge memory. Instead of studying ${\varvec{\Upphi}}^n$, the evolution of the concentration after n periods ${\varvec{C}}^n$ is computed in sequence as follows:

$$ {\varvec{C}}^{i+1}={\varvec{\Upphi}}{\varvec{C}}^i, \hbox{hence } {\varvec{C}}^n=\underbrace{{\varvec{\Upphi}}({\varvec{\Upphi}} (\ldots ({\varvec{\Upphi}}}_{n \,\hbox{times}}{\varvec{C}}^0))). $$

(9)

Thus, the mapping matrix ${\varvec{\Upphi}}$ is calculated only once and is utilized a number of times to study the evolution of concentration in the flow field. For validation of the mapping method and other details, we refer to our previous paper (Singh et al. 2008) and references therein.

2.3 Measure of mixing

To characterize the progress of mixing and compare the performance of mixers with different sets of design variables, we employ the intensity of segregation (Danckwerts 1953), defined by

$$ I=\frac{{\sigma_c^2}}{{\bar{c}(1-\bar{c})}}, $$

(10)

where $\sigma_c^2$ is the variance in the concentration c over the entire domain Ω defined as:

$$ \sigma_c^2=\langle\left(c({\varvec{x}})-\bar{c}\right )^2 \rangle _\Upomega, $$

(11)

where $c({\varvec{x}})$ denotes the concentration, which is dimensionless with $0{\le}c({\varvec{x}})\le 1$, ${\varvec{x}}$ a position vector, and $\bar{c}$ the average concentration in the domain. The denominator of Eq. 10 is the variance of a completely segregated system, where c is either 0 or 1. Thus the intensity of segregation I is 1 when segregation is complete, while I = 0 when the concentration is uniform ($c=\bar{c}$ in the whole domain). The maximum value of the denominator is 0.25, which occurs in equal volume mixing, i.e., when $\bar{c}=0.5$. Even though the value of $\bar{c}$ may vary with the relative fraction of the fluids to be mixed, the value of I always varies from unity to zero with the progress of mixing. In this study, the amount of each fluid introduced through the inlet is assumed to be same, i.e., the case of equal volume mixing.

In discrete space, we can define a discrete intensity of segregation (I _d ) using the discrete concentration C _i at the i-th cell for distributive mixing without diffusion. The number of cells (or sub-domains) used to compute the discrete intensity of segregation is chosen equal to the number of cells N used to compute the mapping matrix. The cells are uniform in size, thus the discrete intensity of segregation can be simplified as follows:

$$ I_d=\frac{{1}}{{\bar{C}(1-\bar{C})}}\frac{{1}}{ {N}}\sum^N_{i=1}(C_i-\bar{C})^2, $$

(12)

where the average concentration $\bar{C}$ is

$$ \bar{C}=\frac{{1}}{{N}}\sum^N_{i=1}C_i. $$

(13)

The intensity of segregation (I _d ) is a measure of the deviation of the local concentration from the ideal situation, a homogeneous state of the mixture.

3 Three-dimensional serpentine channel

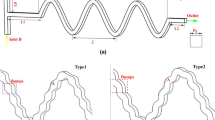
As a preliminary study, first, we carry out flow and mixing analysis for the three-dimensional serpentine channel (Liu et al. 2000), intending to understand flow and mixing characteristics in detail. Figure 2 shows the periodic unit of the channel with a “C-shaped” structure. Liu et al. (2000) experimentally demonstrated that chaotic mixing can be achieved in this device, once inertia is significant.

Fig. 2

Periodic unit of the three-dimensional serpentine channel with a “C-shaped” structure proposed by Liu et al. (2000). Here, L = 4W and W = 2H, where W is the width of the channel, L the length, and H the height, therefore the aspect ratio of the channel is 0.5

Since, in the operating condition of the channel (Liu et al. 2000), inertia is not negligible, the steady Navier–Stokes equations should be solved to obtain the periodic velocity fields. The momentum balance equation is given by

$$ \rho({\varvec{u}}\cdot\nabla{\varvec{u}})=-\nabla p+\mu \nabla^2{\varvec{u}}\quad \hbox{in}\,\Upomega, $$

(14)

where ρ is the density. The other equations required to solve a flow problem are the same as Eqs. 2–5. A particle tracking method is used to observe the manifold of the deforming interface. To characterize the progress of mixing dependent on the effect of inertia, the mapping method introduced in the previous section is employed to calculate the evolution of the scalar concentration C on which the quantification of mixing is based.

3.1 Flow characteristics

To gain insights on the function of the typical channel geometry, the “C-shaped” structure, flows at four Reynolds numbers, Re = 0.01, 10, 30, and 50, are analyzed. For this purpose, we first obtain the periodic velocity field using the finite element method, then track interfaces between two fluids introduced through the inlet to the exit of one periodic unit. Here, non-dimensional equations are solved. The Reynolds number is defined by Re = UD _h/ν, where U is the average velocity at the inlet, D _h the hydraulic diameter of the channel, and ν the kinematic viscosity of the fluid. The channel geometry is discretized by 36,000 27-node brick elements. The non-linear matrix equation is solved by an iteration scheme combining both the Picard and the Newton–Raphson method.

An interfacial line consisting of 500 passive particles (with different colors depending on their vertical locations) has been tracked down to the outlet using a fourth-order Runge–Kutta method. Figure 3 depicts the evolution of the interfaces at the four Reynolds numbers with fluids moving from left to right. Clearly, the embedded colors to the interfaces allow us to see the deformation pattern dependent on the Reynolds number. In the creeping flow regime (see Fig. 3a), the vertical interface rotates in clockwise direction during the first half period, followed by the same amount of counterclockwise rotation during the next half period, resulting in no change in the shape of the interface at the outlet. As the Reynolds number increases, however, the vertical interfacial line is deformed to a curved one at the outlet surface by vortical flows. At an even higher Reynolds number, Re = 50, the interface becomes more complicated by the combined effect of rotational flows and back flows due to inertia (see Fig. 3d). Figure 4 shows the velocity vectors at two cross sections, z = 0 and z = 0.5L, at Re = 50.

Fig. 3

Deformation of the interface (composed of 500 points) between two fluids flowing from left to right for the four Reynolds numbers, a Re = 0.01, b Re = 10, c Re = 30, and d Re = 50. The points constituting an interface are labeled with different colors depending on their vertical locations (color figure online)

Fig. 4

Cross-sectional velocity vectors at two axial locations, a z = 0 and b z = 0.5L, at the Reynolds number Re = 50. The contours represent the magnitude of the axial velocity component w

Poincaré sections at the two Reynolds numbers, Re = 10 and Re = 50, are depicted in Fig. 5. At Re = 10, two KAM (Kolmogorov–Arnold–Moser) boundaries are clearly observed implying poor mixing at this Reynolds number. At a higher Reynolds number Re = 50, the two KAM boundaries are completely disappeared and the flow system is now globally chaotic. The complex flow pattern occurring in Re ≥ 50 is thought to be the main cause of enhanced mixing in this mixing device, as observed experimentally by Liu et al. (2000), but with a higher pressure drop. Similar examples in which micromixing relies on vortices in curved channels are also reported in Schönfeld and Hardt (2004).

Fig. 5

Poincaré sections at two Reynolds numbers, a Re = 10 and b Re = 50

It should be noted that, in the Stokes flow regime, the shape of a bend in the channel determines the direction of a rotational motion. As recently reported by Park and Kwon (2008), the amount of rotation after one bend is determined by the aspect ratio of the channel. In the case of the serpentine channel with the aspect ratio of 1, fluid elements rotate approximately 90° during half-period. The lower the aspect ratio, the smaller the amount of rotation. Due to this reason, the aspect ratio will be chosen as one of key design variables in the parameter study for the new mixer, which will be introduced in Sect. 4.

3.2 Mixing analysis

To the best of our knowledge, until now, detailed mixing analysis on the serpentine channel geometry depicted in Fig. 2 has been done only by our group (Singh et al. 2008). In what follows, results of mixing analysis will be introduced.

We study the progress of mixing for the four Reynolds numbers, Re = 0.01, 10, 30, and 50. The mapping matrices for the four cases are calculated using the periodic velocity field obtained and the numerical scheme described in Sect. 2. In this study, we have used 200 × 200 cells covering a cross sectional area of interest to analyze mixing and introduced 16 × 16 particles at each cell to evaluate the mapping coefficients Φ _ij .

Figure 6 shows the the progress of mixing visualized by the concentration C along the down-channel positions after 1, 2, 3, 4, 5, and 10 periods for the four Reynolds numbers. As the Reynolds number increases, stretching and folding of interfaces become more vigorous. It is evident that the flow at Re = 50 is capable of producing the best mixing among the four cases, while at the lowest Reynolds number, Re = 0.01, one cannot mix the two fluids at all. The onset of chaos in the whole cross-section requires a minimum cross-over Reynolds number. Depicted in Fig. 7 is the characterization of mixing in terms of the intensity of segregation for the four Reynolds numbers. From Figs. 6 and 7, we can conclude that the change from regular to chaotic mixing occurs around Re = 50.

Fig. 6

Evolution of the concentration at several down-channel positions after 1, 2, 3, 4, 5, and 10 period at the four Reynolds numbers, a Re = 0.01, b Re = 10, c Re = 30, and d Re = 50

Fig. 7

Plot of the intensity of segregation I _d along the normalized axial position z/L at the Reynolds numbers Re = 0.01, 10, 30, and 50. Here, L is the length of one periodic unit of the serpentine channel

4 The chaotic serpentine mixer (CSM)

4.1 Design concept

In this section, we introduce the design principle of the CSM which shows chaotic mixing in the creeping flow regime, while maintaining the advantages of the original serpentine channel. Repeated stretching and folding of fluid elements is the key mechanism leading to chaotic mixing. According to the theory of the link twist maps (LTMs; for more details see Ottino and Wiggins (2004); Wiggins and Ottino (2004); Sturman et al. (2006)), a necessary condition for chaos is the crossing of streamlines which should occur at different times in a time-periodic flow. In three-dimensional spatially periodic flows, especially, two successive flow portraits generated by two mixing protocols should show intersecting streamlines, when projected onto a same plane, say (x,y)-plane. Many macro- and micro-scale mixing devices fit within the LTM framework. Examples include the partitioned pipe mixer (PPM) (Khakhar et al. 1987), the rotated arc mixer (RAM) (Metcalfe et al. 2006), the staggered herring bone mixer (SHM) (Stroock et al. 2002), the barrier embedded micromixer (BEM) (Kim et al. 2004), etc. In the Stokes flow regime, the three-dimensional serpentine channel creates two rotational flows, but with opposite direction. Since there is no notable mechanism leading to chaotic mixing in this channel, chaotic mixing occurs only above the critical Reynolds number. If one is able to improve the geometry of the original serpentine channel such that it can create two crossing streamlines portraits, the resulting flow field can induce stretching and folding, leading to chaos even in the Stokes flow regime.

From the preliminary study on the serpentine channel flow, we learned that a bend in a rectangular channel generates rotational motion with the sense of a rotational motion affected by the shape of the bend. The CSM is inspired by the flow characteristics of the serpentine channel and the principle of the linked twist maps (LTMs), and has two repeating functional units (see Fig. 8). A repeating unit of the mixer has a simple two-layer structure consisting of two “L-shaped” structures and bypass channels, which can possibly be fabricated using such a mass-production technique as micro injection molding or hot embossing. The “L-shaped” bends in the channel creates helical flows rotating either clockwise or counterclockwise depending on its shape. The bypass channels play a role of offsetting the centers of rotational flows, generating the two rotational flows with crossing streamlines. Since the sense of rotation of the two flow portraits plays an important role in the progress of mixing, we study mixing in both counter-rotating (Fig. 8a) and co-rotating (Fig. 8b) designs. In the schematic drawings of the streamlines depicted in Fig. 8, dashed and solid lines indicate streamlines during the first and second half periods in a repeating unit, respectively.

Fig. 8

Chaotic serpentine mixer consisting of “L-shaped”structure and bypass channel. a Counter-rotating design and b co-rotating design. The streamlines portraits are shown at the lower-right corner of each of the figures. The arrows in the streamlines indicated the direction of the rotational flows viewed from the exit of the channel. Here, W ₁ is the width of the “L-shaped” channel, W ₂ the width of the bypass channel, and H the height of one layer of the channel. The length of one period is L = 8W ₁

4.2 Flow characteristics

In this study, we restrict our interests to the flow kinematics of the CSM in the creeping flow regime. Therefore, we need to solve the Stokes equations with proper boundary conditions and constraint equations described in Sect. 2. Numerical scheme to solve the governing equations is similar to that used in the three-dimensional serpentine channel flow.

To numerically visualize the flow characteristics of two designs of the CSM, we track the interface between two fluids using a fourth-order Runge-Kutta scheme and create manifolds of the deforming interface as before. Figure 9 shows the manifolds of deforming interfaces in two cases, illustrating detailed flow characteristics, split and rotation of the interface, for the two designs. The initial interfacial line consists of 500 passive particles with embedded colors depending on their vertical locations. In the two typical examples, we use the following geometrical parameters: α = H/W ₁ = 1, β = W ₂/(W ₁ + W ₂) = 1/3, and L = 8W ₁. The first variable α is the aspect ratio of the “L-shaped” channel and β is the ratio of the width of the bypass channel to the whole width of the rectangular channel. The two geometrical parameters α and β are key design variables influencing flow kinematics and resulting mixing, together with the sense of rotation, which will be discussed shortly.

Fig. 9

Deformation of the interfacial line composed of 500 points between two fluids depending on the sense of rotation of the two mixing protocols. a Counter-rotating design and b co-rotating design. The points constituting an interface are labeled with different colors depending on their vertical locations (color figure online)

First, the flow kinematics of the counter-rotating design (see Fig. 8a) is to be examined. The flow portraits in this channel reveals a clockwise rotational motion, followed by a counterclockwise rotation (viewed from the exit). At the first bend, as shown in Fig. 9a, the vertical interface is splitted into two: one rotates almost 180° during the half-period and the other just passes through the bypass channel. After the first half-period, the two splitted streams merge together and the number of the interfaces is now two. During the next half-period, the two interfaces again experience split and rotation by the same mechanism as in the first half, thus the number of interfaces becomes four at the exit. One can clearly see the topological change (due to split and rotation) of the interface via the colors embedded to the interfaces. The flow characteristics due to repeated split and rotation is thought to be an excellent mechanism inducing chaotic mixing.

Figure 9b shows the manifold of the interface for the co-rotating design (see Fig. 8b). During the first half-period, the deformation of the interface is the same as that occurring in the counter-rotating design, giving rise to two interfaces. At the second half-period, however, there is no splitting in the two interfaces due to the rotational motion with the same sense as in the first half-period. There are only two interfaces at the exit. Therefore, mixing will be less effective than that of the counter-rotating design. It should be noted that this is not a general conclusion, which needs to be investigated further by parameter studies for the chosen design variables.

4.3 Parameter study

In the previous section, we showed the working principle of the CSM via a particle tracking method. Now, we conduct parameter studies for the both designs, aiming to optimize the mixer and to provide design guides for practical applications. From the flow characteristics of the CSM, we choose three design variables: the sense of rotation of two rotational flows, the aspect ratio of the channel (α), and the ratio of the bypass channel to the whole width (β). The sense of rotation is either counter-rotating or co-rotating. The aspect ratio α varies from 0.25 to 1.25 with an increment of 0.25. The third variable β changes from 1/4 to 5/12 with an increment of 1/12. So, we need to conduct mixing analysis for 30 cases.

Using the velocity fields obtained, we create mapping matrices for all the cases and calculate the distributions of the concentration C at each period. We divide a cross-section into 200 × 200 rectangular cells with equal size, and at each cell we introduce 100 particles to calculate mapping coefficients. As representative examples, we introduce the results of mixing analysis for the counter- and co-rotating designs with a fixed β = 1/3 at the five aspect ratios, α = 0.25, 0.5, 0.75, 1, and 1.25.

Figure 10 depicts the progress of mixing in the counter-rotating design. Compared with the interface evolution shown in Fig. 9a, after one period, the mixing pattern with α = 1 and β = 1/3 reflects the shape of the interface. At lower values of the aspect ratio, α = 0.25 and 0.5, mixing is not globally chaotic and unmixed islands are observed. When α ≥ 0.75, mixing seems to be globally chaotic without any noticeable island. Interestingly, the mixing patterns in this region (α ≥ 0.75) look quite similar to each other indicating saturation in mixing above a critical value of the aspect ratio α _c  ∼ 0.75. Since the rotation angle of fluid elements due to a “L-shaped” bend is constrained by a threshold value of approximately 180°, mixing becomes saturated above the critical aspect ratio. The progress of mixing is characterized by the intensity of segregation I _d . Figure 11 shows the evolution of I _d along the normalized down-channel position (z/L) at the five values of α. When α ≥ α _c , clearly, one can observe a transition to globally chaotic mixing and the saturation in mixing characterized by I _d .

Fig. 10

Progress of mixing in the counter-rotating design, visualized by the evolution of the concentration C after 1, 2, 3, 4, 5, 10, and 20 period with different values of the aspect ratio, a α = 0.25, b α = 0.5, c α = 0.75, d α = 1, and e α = 1.25, with a fixed β = 1/3. Figures in the first row show the initial concentration distributions

Fig. 11

Plot of the intensity of segregation I _d for the counter-rotating design with β = 1/3 for the five values of α. The abscissa is the axial distance z scaled by the length of one period L

As for the co-rotating design, the progress of mixing is depicted in Fig. 12. The evolution of the concentration C is quite different from that in the counter-rotating design. The concentration distribution after one period with α = 1 and β = 1/3 reflects the interfaces at the exit shown Fig. 9b, but with an additional interfacial line due to merging of the two fluids (in this study, yellow and black fluids). At α = 0.5 mixing is globally chaotic. At α = 0.25 mixing is chaotic, but with several unmixed islands. At higher values of the aspect ratio, α = 0.75, 1, and 1.25, however, mixing becomes poor due the existence of three big islands (see Fig. 12c–e). In this particular case, the optimal value of α seems to exist around 0.5. Comparing Fig. 13 with Fig. 11, even at the optimal condition in the co-rotating design, the progress of mixing is not as fast as the cases showing chaotic mixing in the counter-rotating design.

Fig. 12

Progress of mixing in the co-rotating design, visualized by the evolution of the concentration C after 1, 2, 3, 4, 5, 10, and 20 period with different values of the aspect ratio, a α = 0.25, b α = 0.5, c α = 0.75, d α = 1, and e α = 1.25, with β = 1/3

Fig. 13

Plot of the intensity of segregation I _d for the co-rotating design with β = 1/3 for the five values of α. The abscissa is the axial distance z scaled by the length of one period L

Now, the remaining task is to optimize each of the two designs and make design guides to achieve good mixing (evaluated from the measure of mixing I _d ) for both designs. For this purpose, we have also calculated the concentration distributions for other cases with different values of β by changing α. The objective function for optimization is to minimize the intensity of segregation I _d at the final step (in this study chosen to be the 20th period). As shown in Fig. 14, using the results of mixing analysis, we plot the intensity of segregation I _d as a function of α and β for the two designs. Instead of finding out one set of the design variables minimizing the objective function, we provide windows in which I _d is less than a cut-off value I ^* _d (chosen to be I ^* _d  = 0.1 in this study) and one can have good mixing evaluated by the measure of mixing used. In the two plots shown in Fig. 14, a combination of the variables within the area, where I _d  ≤ I ^* _d , guarantees globally chaotic mixing. In the case of the counter-rotating design, we have a wider range of the variables to achieve enhanced mixing, which means that the counter-rotating design is more flexible one to be applied to a variety of applications.

Fig. 14

Design windows for a the counter-rotating design and b the co-rotating design. For a fixed threshold value of the intensity of segregation (I ^* _d  = 0.1), one can expect good mixing in the areas with I ^* _d  < I ^* _d (here areas with blue color) (color figure online)

In summary, the counter-rotating design allows us to choose the design variables in a wider range to achieve enhanced mixing compared with the co-rotating design. In the case of counter-rotating design, the higher α and the lower β, the better mixing. Even though it is not shown in this paper, in the course of the parameter study, we found that one of the key flow characteristics, splitting of the interface, was missing in cases with higher β and lower α (in upper left region in Fig. 14a) leading to poor mixing. While, in the co-rotating design, one can have good mixing only within limited values of the variables, around α = 0.5 and β = 1/3.

5 Summary and conclusion

We proposed a chaotic micromixer called the chaotic serpentine mixer (CSM) efficient in the creeping flow regime and demonstrate a systematic approach to find out an optimal set of design variables for the mixer.

As a preliminary study, we numerically reinvestigate the flow characteristics and mixing of the original serpentine channel. The critical Reynolds number Re _c , showing transition from regular to chaotic mixing, has been found to be approximately Re _c  = 50. Since there is no mechanism inducing chaotic advection in the Stokes flow regime, chaotic mixing is possible to occur only above the critical Reynolds number with the help of complicated secondary flows.

The working principles of the CSM, based on the linked twist maps (LTMs) principle, are demonstrated through the manifolds of deforming interfaces showing repeated split and rotation. The counter-rotating design shows enhanced mixing performance in a broad range of the chosen design variables, while the co-rotating design shows chaotic mixing only in a limited range of the variables. The design windows provided by the parameter studies can be utilized as a design tool to determine a proper set of the design variables to fit with a specific application in a microfluidic device. Finally, it is worthwhile to mention that this paper presents a good example to optimize a new micromixer design before fabricating real devices by incorporating the mapping method and an optimization scheme.