Introduction

Modern sustainable forestry aims to increase naturalness in forest management. In order to manage forests by emulating natural processes, it is necessary to gain insight into patterns and processes that occur naturally in forests (Law et al. 2009; Petritan et al. 2012). Despite the increasing number of studies conducted in natural forests, long-term studies on spatiotemporal patterns are relatively scarce in the literature (Hessburg et al. 2000; Wolf 2005; LeMay et al. 2009). Forests are very complex natural systems, consisting of many organisms influencing each other in space and time. Their complexity results from the heterogeneity of their structure, modified by various natural and human-induced processes. In general, the term “forest structure” refers to patterns and relationships among forest components. Forest structure and natural processes are not independent, and both are recognized as important drivers of forest dynamics. The impact of biological processes is manifested in the form of the spatial pattern of trees, while simultaneously the spatial distribution of trees determines the properties of the system, affecting its structure (Stoll and Prati 2001; McIntire and Fajardo 2009; Picard et al. 2009; Pretzsch 2010; von Gadov et al. 2012). Thus, analysis of the spatial pattern allows ecologists to get insight into the processes and mechanisms standing behind the development of the forest over time. Spatial patterns observed in forests may be explained in terms of self-organization rules, resulting from different factors affecting growth and development of trees and consequently forests (Stoll and Prati 2001; Gray and He 2009; von Gadov et al. 2012; Hai et al. 2014; Ledo et al. 2014).

A fundamental process in forest development is tree mortality process. This process affects the forest structure through the influence on the distribution of living trees, tree regeneration and their future growth as well as creates canopy gaps (Stoll and Newbery 2005; Aakala et al. 2012; Silver et al. 2013). It also affects the resource availability (water, nutrients), and thus, it influences species composition of the forest (Das et al. 2011; Aakala et al. 2012; Silver et al. 2013). The death of tree, however, involves many factors (e.g., competition, pathogen and insect attack, environmental stress, air pollution). Competition has been well-documented driver of mortality process, and its role in forest dynamics has been frequently manifested by regular spacing of survived trees (Kenkel 1988; Bravo-Oviedo et al. 2006; LeMay et al. 2009; Das et al. 2011; Pommerening and Särkkä 2013; Silver et al. 2013; Larson et al. 2015). Because competition intensity varies over time, different developmental stages of forest can be characterized by different spatial pattern of trees and different spatial mingling of tree species in mixed stands (Kenkel 1988; LeMay et al. 2009; Larson et al. 2015). Density-dependent mortality is especially well documented in young forests (e.g., Kenkel 1988). In old-growth forests, where demographic processes are rather stabilized, density-dependent competition plays rather minor role in mortality process since old-growth forests has been frequently characterized by random or close to random spatial arrangement of trees (e.g., Szwagrzyk 1992; Szwagrzyk and Czerwczak 1993; Paluch and Bartkowicz 2004; Das et al. 2011). Random distribution would indicate the lack of intertree relations but more likely such pattern results from the fact that natural processes responsible for clumping of spacing trees are just not strong enough to produce statistically significant results (Szwagrzyk 1992; Gray and He 2009). Other factors, e.g., disturbance events, insect outbreaks, also seem to be important in structuring old-growth forests.

While regular arrangement of trees in the forest has been attributed mostly to competition, their aggregated pattern has been frequently observed in nature (e.g., Wiegand and Moloney 2004; Yu et al. 2009; Shen et al. 2013). This type of spatial pattern results from many factors, e.g., specific dispersal mechanisms and associated seed dispersal limitation, habitat heterogeneity, local disturbance events or clonal growth (Stoll and Prati 2001; Stoll and Newbery 2005; Wiegand and Moloney 2004; Shen et al. 2013). To distinguish the importance of habitat heterogeneity and other clustering mechanisms is of vital importance in modern ecology, but such studies are still very scarce in the literature (Velázquez et al. 2016). In mixed forests, spatial structure of different species plays an important role in the process of their coexistence (Stoll and Newbery 2005; Wiegand and Moloney 2004; Raventós et al. 2010; Shen et al. 2013). Species coexistence has been commonly described by the theory of spatial segregation (Raventós et al. 2010). Interspecific segregation is usually due to the niche differentiation or habitat filtering (Raventós et al. 2010; Velázquez et al. 2016), and usually it is related to intraspecific aggregation. However, Wilson (2011) indicated twelve theories of different importance explaining the coexistence of different species in plant populations. Analyzing species diversity of woodlands that comprise more than two tree species has been still challenging.

Information from the long-term repeatedly measured stem-mapped plots (spatiotemporal analysis) is assumed to be crucial for better understanding of stand development and forest dynamics due to the fact that spatial patterning of individuals, live and dead may change over time. An extension of spatial analyses to include changes in time makes it possible to describe changes in the forest structure due to competition, local disturbances, etc. Long-term studies of forest structures are, however, limited because of cost and time constraints and some of them have used chronosequences rather than real-time series (Getzin et al. 2008; LeMay et al. 2009). In the present paper, we evaluated changes in intra- and interspecific spatial patterns of tree species from an existing medium-term field experiment established in a multi-species, uneven-aged and uneven-sized natural Scots pine-dominated forest. Mortality events over the 14-year period were also described in the spatial context. In our study, we examined: (1) spatial patterns of all living trees regardless of the species, (2) spatial patterns of conspecifics, (3) species associations between the most abundant tree species, i.e., Scots pine, pedunculate oak, common birch and black alder, and (4) spatial pattern of trees that have died over the analyzed 14-year period of forest development. Specifically, we tested the hypotheses that trees in mixed uneven-aged Scots pine forest show random distribution (H1), but spatial pattern of individual tree species can be more complex due to differences in their ecology, particularly light requirements (H2). We also hypothesized that low intraspecific competition of different tree species results in their spatial segregation (H3). Moreover, we tested the hypothesis of density-independent mortality (H4) as the predominant demographic process in old-growth Scots pine forests.

Due to scarcity of uneven-aged Scots pine forests, our study will provide valuable insights into the structure, diversity and succession of such forests. Such knowledge is thus crucial for the proper conservation and sustainable management of mixed, uneven-aged Scots pine-dominated forests.

Object and methods

Study area

The study was carried out in the Kaliszki Forest Reserve situated in the Kampinoski National Park (52°15′N and 20°50′E), central Poland. The temperate climate is intermediate between maritime and continental and is characterized by relatively short, cold winters and warm, moderately humid summers (Walter et al. 1975). The mean annual precipitation is 500 mm, mean temperature is 8.0 °C, and the growing season lasts 214 days. It has moderately favorable natural conditions for Scots pine regeneration, with fresh moderately gleyed podzolic soil developed from alluvial slightly loamy sands with the modern type ectohumus. The terrain of the study plot is flat, with small variation in altitude (up to 2 m) and the lowest altitude located in the central part of the transect. The stand consists of Scots pine (Pinus sylvestris L.), pedunculate oak (Quercus robur L.), common birch (Betula pendula L.), black alder (Alnus gutinosa (L.) Gaertner) and aspen (Populus tremula L.). The average age of the overstory formed by pine was assumed to be 142 years in the year of the first survey (Tarasiuk and Zwieniecki 1990). The understory consists of uneven-aged Scots pine, pedunculate oak, common birch, black alder and aspen, all of natural origin. Crown density is partly disconnected, but no severe disturbances have been noticed in the past few decades. This reserve covers 105.82 ha, and it has been excluded from any management since 1979 (Tarasiuk and Zwieniecki 1990).

Measurements and data collection

Measurements were carried out on a 700-m-long and 20-m-wide transect (1.40 ha in total) being the representative for all reserve. The transect has been established in 1980 to analyze the dynamics of the social structure of natural regeneration of Scots pine under the canopy of old trees (Tarasiuk and Zwieniecki 1990) and vitality structure of the understory (Zwieniecki and Tarasiuk 1993). We decided to use the data collected over 14-year period to conduct spatial analysis of changes in trees distribution despite rather unfortunately stretched study plot. The fact that long-term studies on spatial structure dynamics in uneven-aged forest in temperate zone are relatively scarce in the literature supported our decision.

On the transect all live trees were recorded, and the collected data included diameter at breast height (DBH, cm), tree species and the position of each tree in the local coordinate system (x, y). Only trees of DBH ≥ 4.5 cm and tree species with the abundance greater than 10 trees were included into further analyses. Measurements were conducted twice, in 1993 and 2007. We also reported the status of each tree (dead or live) at the beginning and at the end of the examined period.

Univariate spatial analyses

The univariate analyses were conducted for all live trees pooled and for each tree species separately. The relevant ecological question focused on whether trees were distributed in any systematic way (e.g., regularly or clumped), or whether they were just randomly dispersed in the forest. We used the pair correlation function, g(r), as the summary statistic, which quantifies spatial relationships between pairs of trees of the same type at a different spatial scale (Illian et al. 2008; Szmyt 2014; Wiegand and Moloney 2014). It is a derivative of the commonly used Ripley’s K-function, but its character is non-cumulative. It presents an expected number of points in a ring at distance r from the arbitrary point of the pattern, divided by the intensity of the pattern, and it may be calculated from (Illian et al. 2008):

$$g(r) = \rho (r) \cdot \lambda^{ - 2}$$
(1)

where ρ(r) is the second-order product density and λ is the intensity of the process. If the pattern is random, then g(r) = 1. If pairs of trees are more abundant at a certain distance r than expected from the null model of complete spatial randomness (CSR), then the pattern shows a tendency for aggregation and g(r) > 1. In contrast, g(r) < 1 indicates that pairs of trees at distance r are less abundant than in the case of the null model (CSR), which denotes regular distribution in space (Illian et al. 2008; Law et al. 2009; Szmyt 2014).

Bivariate analyses

A bivariate point pattern involves two types of points, e.g., different tree species in the forest. Relevant ecological questions here involved the detection of independence or two possible interactions between two tree species: attraction and repulsion (segregation) (Wiegand and Moloney 2014). We used a bivariate pair correlation function, g 12(r), that represents the expected density of trees of species 2 at distance r from an arbitrary tree of species 1, divided by the intensity of trees of species 2. It is estimated from:

$$g_{12} (r) = \rho_{12} (r) \cdot \lambda_{1}^{ - 1} \lambda_{2}^{ - 1}$$
(2)

where ρ 12(r) is the second-order product density and λ 1 and λ 2 are the intensities of trees of pattern 1 and 2, respectively. Function g 12(r) = 1 indicates no interaction between trees of different tree species (spatial independence), while g 12(r) > 1 means that there is a larger number of trees of type 2 at distance r from a focal tree of type 1 than expected from the null model of independence, indicating a spatial attraction effect between the two tree species. Similarly, g 12(r) < 1 indicates that there is a smaller number of trees of type 2 at distance r from a focal tree type 1, indicating repulsion (small scale) or segregation (large scale) effects.

The bivariate analyses were conducted here for live trees of the following tree–species pairs: pine–alder (referred to in the text as P–A), pine–birch (P–B), pine–oak (P–O), oak–birch (O–B), oak–alder (O–A) and birch–alder (B–A).

Random mortality analysis

When testing the random mortality hypothesis, we assigned the marks “dead” (pattern 1) or “live” (pattern 2) to each tree in the forest. The major interest in this analysis is in revealing the spatial correlation structure of the marking process conditional on the univariate pattern (combined dead and live individuals). We applied different summary statistics to address specific questions on spatial pattern of dead trees (g 11), spatial correlation between dead and live trees (g 12) and neighborhood around dead trees, namely: Are they densely or sparsely populated (g 1,1+2 − g 2,1+2) (Raventós et al. 2010; Larson et al. 2015)? The last statistic is especially suitable to detect density-dependent mortality, because it compares the density of pre-mortality trees (univariate pattern of dead and live trees) around dead trees with density of pre-mortality trees around live individuals.

Null models

Complete spatial randomness (referred to as CSR), commonly applied as the initial null model (hypothesis) in spatial analysis for univariate analyses, is the simplest model assuming a lack of interaction between trees in the forest. It means that trees are distributed randomly and independently of the other trees. It assumes also that the intensity of the pattern (tree density) is constant across the plot (Wiegand and Moloney 2014).

The heterogeneous Poisson null model (HP) is a suitable null model when the intensity of a pattern varies with location of trees generating the pattern. The heterogeneous density may be caused by external factors, e.g., soil variation or seed dispersal. In such cases, the CSR model is not suitable for the exploration of tree–tree interactions. The HP model is thus an alternative to account for the exploration of large-scale variation in habitat quality. The constant intensity for the CSR model is replaced by the intensity function varying with tree location, but the independence of tree position on the plot remains. Practically, this can be done by displacing the known tree locations within the neighborhood with a certain radius R. It removes potential patterns for distances r < R, but it leaves the large-scale pattern untouched, which makes it possible to explore only the interaction between trees, not confounded by a large-scale effect (e.g., soil variation). We used the nonparametric kernel intensity function with the radius R = 10 m (Wiegand and Moloney 2014).

The Thomas cluster null model (TH) is the simplest point process that creates an aggregated pattern with a single scale of clustering. The Thomas process consists of a number of randomly and independently distributed clusters, which position of the centers follows the Poisson process with intensity κ. The number of points that belong to a certain cluster follows the Poisson distribution with the mean μ = λ/κ (λ-intensity of points of the pattern). The location of points in a given cluster relative to the cluster center has a bivariate Gaussian distribution with variance σ 2 (Wiegand et al. 2009; Diggle 2014; Wiegand and Moloney 2014).

Spatial independence is the fundamental null model for the bivariate pattern in contrast to attraction or repulsion. The model assumes that two patterns (e.g., two tree species) are generated by two independent mechanisms. The absence of interaction between two types of points corresponds to the absence of interaction between two patterns. In our study, we used parametric point process models to fit the second pattern (species 2) and used realizations of the fitted point process model (Thomas cluster or heterogeneous Poisson models) to randomize the pattern of the second component, while keeping the pattern of species 1 unchanged (Wiegand and Moloney 2014). Parameters of TH model were estimated during the univariate analysis of each tree species.

In the random mortality hypothesis, we applied random labeling as the suitable null model. This model randomly assigns marks (dead or live) to trees with equal probability among all of them and independently of their location. This model assumes that mortality is a random process over a given pattern of trees (Yu et al. 2009). Positive (negative) departures of g 11 from the random labeling null model indicate that dead trees are clumped (dispersed). Positive (negative) values of g 12 relative to the null model indicated attraction (segregation) between dead and live trees. Under random labeling, g 1,1+2 = g 2,1+2(r). If g 1,1+2 > g 2,1+2, it means that dead trees are located in places of higher tree pre-mortality densities (negative density dependence), while g 1,1+2 < g 2,1+2 indicates a positive density dependence (Jacquemyn et al. 2007; Yu et al. 2009; Raventós et al. 2010; Larson et al. 2015).

Testing significance of departures from the null models

For a given species or species pairs, we contrasted the summary statistics to that expected under the suitable null model described above. First, we used Monte Carlo simulations to test significant departures from the expectation using 199 simulations of a point process underlying the null model, each of which generates a pair correlation function. The upper and lower bounds of simulation, referred to as the critical region, were evaluated from the 5th lowest and 5th largest values of the summary statistics, which corresponds to the error rate α = 0.05. Departures lying outside the critical region are assumed to be significant. Despite problems with simultaneous testing of many spatial scales, such testing is suitable in the exploratory context we focused on (Jacquemyn et al. 2007; Illian et al. 2008; Wiegand and Moloney 2014). However, we combined envelope tests with the goodness-of-fit tests (referred to as GoF) for formal inference (Loosmore and Ford 2006). All GoF tests were performed at the distance of 10 m. All point process analyses were conducted using Programita (ver. 2014) software (Wiegand and Moloney 2004; Wiegand et al. 2010).

Results

Forest stand demography

During 14 years of stand development, the number of trees (DBH > 4.5 cm) decreased by 20% from 1230 trees in 1993–986 trees in 2007 (Table 1). The number of stems of most tree species declined, with the greatest reduction observed for pedunculate oak (− 28%), and the smallest, but positive change was observed for common birch (+3.8%). The initial (1993) mean tree diameter for the stand was 17.42 cm (range 4.55–56.95 cm) (Table 1) with the coefficient of variation of 70%. After 14 years the mean diameter for the stand increased to 20.99 cm, but the range of diameters as well as their variation decreased slightly. In terms of the average stand basal area (BA), we observed a small increase from 31.22 to 33.71 m2 (Table 1).

Table 1 Species abundance, mean diameter at the breast height (DBH) and stand basal area (BA) in the Kaliszki Forest Reserve, Kampinoski National Park, during the examined period (STDDBH—standard deviation of DBH; CVDBH—coefficient of variation of DBH)
Full size table

In both surveys, Scots pine was the most abundant tree species, and population size of this tree species decreased by 22% over 14-year period. It was the species with the largest diameters of trees, 56.95 cm in 1997 and 59.85 cm in 2007, and the highest DBH variation (Table 1). The highest decline in stem number was observed in the case of common oak, and it was by 28% during the examined period (Table 1). The average DBH of oaks was 53.8 and 52 cm in 1993 and 2007, respectively (Table 1). DBH variability was lower than in the case of pine, and it amounted to 51% in 1993 and 49% in 2007. The least abundant tree species in the forest was black alder, and the number of trees of this tree species declined by 25% over the 14-year period (Table 1). Trees showed the mean diameter of 17.30 cm (CV = 53%) and 19.95 cm (CV = 48%) in 1993 and 2007, respectively (Table 1). Birch was the only species that slightly increased in number (by 3.8%) during 14 years of forest development (Table 1). Birch was characterized by the smallest mean diameter, 14.28 and 16.93 cm in 1993 and 2007, respectively. It showed the lowest DBH variability: 44% in 1993 and 42% in 2007 (Table 1).

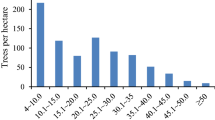
Figures 1 and 2 present the diameter distribution for all live trees pooled and separately for tree species, respectively. Both structures follow the pattern (J-shaped distribution) connected with old-growth forests—abundant young individuals and small number of oldest trees.

Fig. 1
figure 1

DBH distribution for live trees pooled (DBH ≥ 4.5 m) in the uneven-aged Scots pine-dominated forest in 1993 (left panel) and 2007 (right panel) surveys

Full size image
Fig. 2
figure 2

DBH distribution for tree species growing in the uneven-aged Scots pine-dominated forest in 1993 (left) and 2007 (right)

Full size image

Univariate analyses: intraspecific interactions

Live trees from both forest surveys showed significant departures from the homogenous null model of CSR. Results showed that the pair correlation function did not approach the value of 1 for any spatial scale investigated. Such a shape of g(r) provides evidence for heterogeneous density of trees. In fact, the applied heterogeneous Poisson null model fitted the data from 1993 surveys very well (p GoF = 0.12, Fig. 3). Thus, we did not find any evidence for non-random distribution of live trees at the beginning of the analyzed period. Contrary to that, trees from the 2007 survey showed significant departures from the HP model toward regularity in tree distribution at the distances of 1.5–6.5 m (p GoF = 0.01, Fig. 3).

Fig. 3
figure 3

Univariate pair correlation function g(r) for all live trees pooled in 1993 (a) and 2007 (b) censuses with HP null model. Solid thick line—empirical g(r), solid thin line—g(r) for the null model, dashed lines—95% confidence envelopes based on 199 Monte Carlo simulations

Full size image

Univariate analysis conducted for each tree species separately showed clear evidence for a more complex spatial pattern than the random type.

Scots pine

In the 1993 survey, the HP null model described the distribution of Scots pine very well (p GoF = 0.19), indicating their random distribution (Fig. 4). In 2007 we found evidence for small-scale clustering of pines (p GoF = 0.02). The application of the TH model showed that trees were distributed in 86 clusters with the average size of ~ 9 m. The average cluster consisted of about seven trees (Fig. 4).

Fig. 4
figure 4

Univariate pair correlation function g(r) for Scots pine from 1993 (a) and 2007 (b) censuses with HP null model (a, b inset) and the Thomas cluster null model (b). Explanation—refer to Fig. 3

Full size image

Common birch

The cluster model described the data for birch much better than the HP model if it concerned both data sets from the two surveys (Fig. 5). In 1993 trees were distributed in 25 clusters with the average size of ~ 9 m and with 7 trees per cluster. In 2007 the TH model fit well the data (p GoF = 0.75). The number of clusters decreased slightly to 21 clusters with an average size of ~ 12 m. The number of trees within the average cluster remained similar as before (Fig. 5).

Fig. 5
figure 5

Univariate pair correlation function g(r) for common birch from 1993 (a) and 2007 (b) censuses with HP null model (insets) and the Thomas cluster null model. Explanation—refer to Fig. 3

Full size image

Pedunculate oak

While data from the 1993 survey could be described by the HP model relatively well (p GoF = 0.16), indicating the random arrangement of oaks, in 2007 it was not the case, since oaks showed a weak tendency toward regularity at the spatial scale of 1.5–3 m. This regularity diminished with increasing spatial scales (Fig. 6).

Fig. 6
figure 6

Univariate pair correlation function g(r) for pedunculate oak from 1993 (a) and 2007 (b) censuses with HP null model. Explanation—refer to Fig. 3

Full size image

Black alder

The pair correlation function for living trees in 1993 showed significant departures from the HP null model at small distances, r < 2 m, indicating small-scale clustering (p GoF = 0.04, Fig. 7). The Thomas cluster model fit the data much better (p GoF = 0.89, Fig. 7). Estimated parameters showed that alder was distributed in four clumps with the average size of 12.5 m and ~ 20 trees per cluster. In 2007 small-scale clustering was still observed (p GoF = 0.84, Fig. 7), but the number of clusters dropped to three clusters of average size approximated to 19 m. The number of trees per cluster (~ 20 trees) was very similar to that in the earlier survey.

Fig. 7
figure 7

Univariate pair correlation function g(r) for black alder from 1993 (a) and 2007 (b) censuses with HP null model (insets) and the Thomas cluster null model. Explanation—refer to Fig. 3

Full size image

Bivariate analysis: interspecific interactions

The bivariate analyses of the data from 1993 pointed out that the most common bivariate spatial pattern was spatial segregation, followed by independence (Table 2). Spatial independence (no correlations) was stated for pine versus oak (P–O) and oak versus alder (O–A) species pairs. Clear repulsion (small scale) or segregation (large scale) between species was observed for pine versus alder (P–A), alder versus birch (A–B) and oak versus birch (O–B) species combinations. A more complex spatial structure was detected for pine and birch (Table 2). Birches were more abundant than expected from the independence null model around pines (P–B) at distances > 5 m, providing evidence for medium-scale attraction between these tree species. At the smallest distances (< 1 m), both species showed mutual repulsion (Table 2).

Table 2 Distance intervals (meters), at which two species showed independence, attraction or repulsion (segregation) in 1993 based on 95% confidence envelopes
Full size table

After 14 years of stand development, bivariate analysis indicated very similar results (Table 3). Spatial segregation was still a predominant interaction type between tree species in the forest. Also spatial correlation between pine and birch did not change much and birch was still more abundant around pine than it may have been expected; however, the repulsion between these two species increased slightly up to 2 m (Table 3).

Table 3 Distance intervals (meters), at which two species showed independence, attraction or repulsion (segregation) in 2007 based on 95% confidence envelopes
Full size table

Spatial context of mortality

Trees that died in the analyzed 14-year period were more aggregated than expected under random labeling at the distances of 1–9 m (p GoF = 0.01, Fig. 8, inset). Bivariate analysis concerning the spatial correlation between dead and surviving trees showed a clear positive relationship, which means that surviving trees were more abundant around dead trees than it may have been expected under the null model (p GoF = 0.01, Fig. 8). A positive association was observed at short distances of 1–5.5 m. The third test statistic, g 1,1+2 − g 2,1+2, indicated that pre-mortality neighbors were more crowded around dead trees than survivors, demonstrating the density-dependent mortality (p GoF = 0.01, Fig. 9). It was detected for the spatial scale of 1–9 m.

Fig. 8
figure 8

Univariate (inset) and bivariate pair correlation function for dead trees (inset) and spatial relationships between dead and surviving trees. Solid thick line—observed g-function, solid thin line—confidence envelopes based on 199 simulations of random mortality (random labeling)

Full size image
Fig. 9
figure 9

Spatial aspect of the density-dependent mortality. Values of g 1,1+2 − g 2,1+2 > 0 and above the confidence envelope indicate density-dependent character of mortality. Solid thick line—observed g-function, solid thin line—confidence envelopes based on 199 simulations of random mortality (random labeling)

Full size image

Discussion

Demographic changes

Our results showed that the old-growth uneven-aged Scots pine forests were characterized by a highly differentiated diameter structure. However, they follow, in general, the negative exponential curve that is often used to describe the structure of virgin or old-growth natural forests (Westphal et al. 2006). However, Kucbel et al. (2012) reported bimodal diameter structures in old-growth beech forests. Stand demography over 14 years of forest development changed only slightly in respect to the stem number and stand basal area. Scots pine was the most stable element of the stand, being simultaneously predominant, despite the fact that its abundance over 14 years decreased by 22%. Other tree species also decreased their abundance, with the exception of birch, which increased slightly its stem number (+3.8%). As it was indicated by diameter structures, trees from smaller diameter classes (DBH < 15 cm) were subject to mortality at a greater rate than large trees.

Spatial patterns of conspecifics (H1 and H2 hypotheses)

Point pattern analysis of the initial distribution (1993) of pooled live trees revealed a lack of significant deviations from random expectations. After 14 years of stand development, our results indicted only a minor change in spatial arrangement of trees in favor of their regularity. Trends toward regularity have been assumed as the evidence for density-dependent mortality, which is in accordance with our results from mortality analysis and with previous studies of other authors (see Kenkel 1988; Getzin et al. 2006; Das et al. 2011; Aakala et al. 2012). In the literature one can find various patterns of tree distribution in old-growth forest. Lutz et al. (2014) observed a random distribution of live trees in old-growth Pseudotsuga-Tsuga forests. Similarly, Aakala et al. (2012) found a random pattern in an old-growth red pine forests. Akhavan et al. (2012) discovered an aggregated pattern of living trees in oriental beech forests in Iran. Szwagrzyk (1992) found no evidence for density-dependent competition leading to a clear uniform distribution of survived trees in Pinus sylvestris–Fagus sylvatica forests in the Carpathian foothills. Similar results to ours have been obtained in a stratified Scots pine forest with an admixture of oak, birch and alder located in the Niepołomice Forest, southern Poland (Paluch and Bartkowicz 2004). LeMay et al. (2009) discovered only slight or no changes in spatial patterns of trees in uneven-aged Douglas fir stands in Canada. On the contrary, Getzin et al. (2006) reported a clear shift from the aggregated pattern of Douglas fir trees in an immature stand, through random in a mature stand toward small-scale aggregation in the old-growth phase. Wolf (2005) detected the change in the spatial pattern of trees over a 50-year period in a mixed deciduous forest.

Our results indicated that spatial pattern of individual tree species in an uneven-aged Scots pine forest showed minor changes over 15-year period of succession. Tree species present in the examined old-growth Scots pine forest may be assigned to two groups according to their light requirements. One group consisted of Scots pine and silver birch (high light-demanding trees) and the second—pedunculate oak and black alder (low-shade-tolerant trees). Birch and alder differed from pine and oak significantly in terms of their spatial pattern, showing clustering after factoring out the large-scale effect on their distribution. The most likely mechanism of aggregation of birch reflects the colonization process through small-scale gap dynamics. Eichhorn (2010) found a similar small-scale clumping pattern of Betula platyphylla in Kamchatka, while Kang et al. (2014) reported a random distribution of the same species. They stated that randomness in tree dispersion of birch was attributed to wind dispersal of small seeds. The second light-demanding species, pine, showed initially the random pattern that changed toward clustering with forest aging. At least two reasons for the non-random pattern of pine at the end of observation period could be assumed. First—similar to that for birch—young pines filled up small gaps created by the death of single old pines. The second is associated with competition in locally dense parts of forest causing death of some pines and promoting small clustering of survivors. In case of oak, the initially random distribution shifted toward a more uniform pattern with forest aging. This tree species experienced the highest reduction in population size over the examined period; thus, intraspecific competition may explain the change in spatial pattern of oak. A clustered pattern of young and small-sized trees in old-growth forests has been often discovered, see Aldrich et al. (2003), McDonald et al. (2003), Youngblood et al. (2004), Fajardo and McIntire (2007), Getzin et al. (2006), LeMay et al. (2009), Pommerening and Särkkä (2013), Petritan et al. (2012). Constant small-scale clumped distribution of black alder in our study can be attributed to its clonal growth. This mechanism was assumed to be responsible for clumping distribution of aspen in aspen-white pine forest (Peterson and Squiers 1995). Szwagrzyk and Czerwczak (1993) reported a clumped pattern of lime due to sprouting in an old-growth mixed forest in East-Central Europe. Aldrich et al. (2003) presented interesting study on changes in spatial pattern of different tree species over 60 years in old-growth hardwood forest in USA. They found that spatial pattern of trees shifted from initially random distribution to regular one at the end of analyzed period. That shift they attributed to density-dependent mortality and ingrowth. Moreover, they reported that light-demanding tree species changed their aggregated pattern toward more random, while shade-tolerant species became more aggregated over time (Aldrich et al. 2003). A limited change in the spatial pattern, from clustered to random or even regular, was observed by Gray and He (2009) in boreal mixed stands in Canada. It suggested the important role of intraspecific competition in governing the spatial distribution of tree populations.

Predicted hypothesis of more complex spatial patterns of individual tree species than in case of the all forest community taken together (H2) was supported by our results. Random distribution of all living trees in old-growth Scots pine forest (H1) was only partly supported by our study and the initial random pattern shifted toward more uniform over 14-year period.

Interspecific relations (H3 hypothesis)

The existence of a spatial structure in the univariate component patterns does not necessarily indicate an interaction between components. An opposite situation, when two univariate patterns do not show any spatial structure, but the bivariate pattern does, is also possible (Wiegand and Moloney 2014). Our results supported this statement. The prevailing bivariate pattern in our study was spatial segregation followed by spatial independence. Spatial attraction was observed only for the pine-birch species combination and only at certain distances (5–10 m). Mechanisms of spatial segregation include differences related to habitat requirements of different tree species, strong interspecific competition, limited seed dispersal as well as strong intraspecific aggregations due to low intraspecific competition (Raventós et al. 2010). Spatial segregation of pine–alder, alder–birch and oak–birch combinations can be explained by different ecological requirements of these species. Since alder prefers moister habitats than birch or pine, these tree species tend to avoid each other by occupying microsites with different moisture regimes. The negative association of oak and birch may be also explained by their different light requirements. Birch, being a much more light-demanding and fast-growing tree species, fills up gaps much easier than oak, a low-shade-tolerant tree species. Hypothesis that different ecological niche requirements and low intraspecific competition promote species coexistence in mixed forests has been commonly accepted in previous studies (Szwagrzyk and Czerwczak 1993; Condit et al. 2000; Stoll and Prati 2001; Stoll and Newbery 2005; Raventós et al. 2010; Wang et al. 2010; Dimov et al. 2013; Ledo et al. 2014; Hai et al. 2014; Wiegand and Moloney 2014). Paluch and Bartkowicz (2004) reported negative relationships for pine and birch, which was rather in contradiction to our results showing their mutual attraction except for a small spatial scale where repulsion was noted. Although both species differed in terms of their conspecific spatial patterns, pine was more frequently surrounded by birches than it could have been expected. Pommerening and Särkkä (2013) observed positive interactions between oak and hornbeam (light-demanding vs. light-intolerant species) in the Bialowieża Forest. Spatial independence—observed in our study for pine and oak, oak and alder—was the dominant type of spatial relationships in the forests analyzed by Szwagrzyk and Czerwczak (1993) and Szwagrzyk et al. (1997). Spatial interactions between tree species did not change significantly over the 14-year period.

Our hypothesis predicting spatial segregation of different tree species (spatial segregation theory) due to intraspecific aggregations of individual tree species is supported by results of our study.

Random mortality hypothesis (H4 hypothesis)

Dying of trees in a forest has been assumed as a complex event. It is difficult to evaluate the risk of death of trees, because many factors affect the growth and survival of trees (Paluch and Bartkowicz 2004). Among them spatial relationships between trees seem to play a significant role in mortality process. Many studies conducted in forests of different species composition reported the importance of density-dependent processes, such as competition (e.g., Bravo-Oviedo et al. 2006; LeMay et al. 2009; Das et al. 2011; Larson et al. 2015). Usually, the evidence for density-dependent mortality was a more uniform distribution of survivors (Kenkel 1988; Szwagrzyk and Szewczyk 2001; Little 2002; Stoll and Bergius 2005). However, in old-growth forests the death of tree can be frequently attributed to other factors than density-induced competition, and surviving trees can be distributed in a manner other than regular (Szwagrzyk 1992; Das et al. 2008, 2011; Gray and He 2009; Bagchi et al. 2011; Akhavan et al. 2012; Aakala et al. 2012; Larson et al. 2015). Our results confirmed, however, the negative density-dependent character of tree mortality in uneven-aged Scots pine-dominated forest and dead trees occurred preferably in areas with higher pre-mortality densities (see results of g 1,1+2 − g 2,1+2 statistic). This is in agreement with results obtained by Yu et al. (2009) and Lutz et al. (2014). Larson et al. (2015) found that initial neighborhoods of dying trees did not differ more than neighborhoods of surviving trees. The clumped distribution of dead trees found in our study (g11 statistic) is partly in accordance with results obtained by Salas et al. (2006), Raventós et al. (2010), Silver et al. (2013) or Larson et al. (2015). Yu et al. (2009) also found a mostly aggregated structure of dead trees in a Mongolian pine forest in China. Larson et al. (2015) reported the difference in the distribution of dead trees between young and old-growth stands, and the latter showed a more often random distribution than aggregated. Lutz et al. (2014) found a random or aggregated distribution of dead trees in an old-growth Pseudotsuga-Tsuga forest. Chokkalingam and White (2000) discovered a large variety of distribution types of dead trees in old-grown hardwood and mixed forests in the USA. They found a random, clumped and even regular arrangement of such trees. A mostly random distribution of dead trees in the old-growth red pine forests was found by Aakala et al. (2012). Spatial relationships between dead and live trees in our study (g 12 statistic) are partly consistent with previous findings from other old-growth forests. Larson et al. (2015) found positive interactions only in the case of young forests, while in old growths the relationships were random. The lack of relationships between dead and live trees was found by Lutz et al. (2014), both for all living trees and for individual tree species. However, our findings are contradictory to results reported by Raventós et al. (2010) and Yu et al. (2009), who discovered a negative relationship (spatial segregation) between dead and survived trees.

Thus, our results did not support our initial hypothesis assuming density-independent mortality in old-growth Scots pine forest. However, one should keep in mind that trees that die are on average in more crowded places and other factors, biotic and mechanical ones, may also play important role in mortality process.

Conclusion

Our study allowed us to point out the following:

  • an uneven-aged, naturally regenerated Scots pine forest can be characterized by a complex spatial structure resulting from both a heterogeneous tree density and different types of interactions between individuals, both the same and different tree species;

  • species-specific methods of regeneration as well as different ecology of tree species can be important factors affecting species composition in the uneven-aged Scots pine forest;

  • a low intraspecific competition, reflected in the aggregated pattern of conspecifics, may lead to spatial segregation of tree species, promoting their coexistence in multi-species and multi-generation pine forests;

  • death of trees in the examined uneven-aged Scots pine-dominated forest was the density-dependent process, and competition played an important role in modifying forest development over 14 years of succession.

In general, our study showed that factors associated with tree-to-tree interactions, species-specific ecological requirements (e.g., light requirements, regeneration methods) as well as density-dependent mortality should be incorporated in realistic models of forest development, helping to manage the forest ecosystems toward their greater structural complexity assuring their sustainability in a changing environment.