1 Introduction

Since the 1980s, foreign direct investment (FDI) has grown at a remarkable rate, reaching a peak in global FDI inflows of almost 1,400 billion US$ in 2000 (UNCTAD 2006). This boom in FDI has led to a substantial interest to investigate its causes and consequences, both empirically and theoretically. Despite the considerable progress that has been made, one important weakness of the vast part of the empirical literature has been the reliance on the two-country framework and hence the exclusion of third-country effects or spatial linkages in the analysis. The assumption that the FDI decision by, for instance, a Dutch multinational firm into France is independent of the Dutch FDI decision into any other host country is, however, deficient for basically two reasons. First, by focussing on a bilateral context some of the basic stylized facts about FDI, like the surge in horizontal FDI and the existence of export platforms, can not be explained, if only because in general a country pair is relatively small as compared to the rest of the world (Neary 2008; Baltagi et al. 2007). Second, excluding third-country effects or spatial linkages can lead to serious econometric problems. Indeed, the omission of third-country effects may lead to biased, inconsistent or inefficient parameter estimates, a too high R 2 statistic or incorrect inferences (see Anselin (1988) for an overview of the econometric problems in the presence of spatial effects). Given these potential weaknesses, the aim of this paper is to test for the relevance of these spatial linkages. As such, our paper is among the few to date to take spatial linkages with respect to FDI into account.

In contrast to most of the literature—which analyses US FDI—our paper focuses on Dutch outbound FDI stocks. Being home to some of Europe’s largest multinational firms, the Netherlands is one of the Organisation for Economic Cooperation’s (OECD) main “exporters” of FDI. Our sample covers up to 18 OECD host countries over the period 1984–2004. We employ spatial econometrics and use a spatial lag model as the main vehicle for our research. The reason to opt for a spatial lag model is that such a model can be grounded on recent FDI theories.Footnote 1 Space also enters our empirical analysis through the market size and a corporate income tax variable. Our estimation results illustrate that third-country effects are indeed important for Dutch FDI. By and large, we find support to the presence of spatial linkages in Dutch outbound FDI.

The remainder of the paper is organised as follows. We start in Sect. 2 with a brief discussion of the literature on FDI and spatial econometrics. Section 3 describes our data set and provides the empirical specifications. Section 4 presents our main findings. First, we present the full sample results as well as European sub-sample results for the spatial lag model. Second, for 12 of our 18 host countries we estimate the spatial lag model when the FDI data are split into industry and services FDI. Third, and although not linked to FDI theory, we also present the estimation results when one opts for a spatial error instead of a spatial lag model. Finally, Sect. 5 concludes.

2 FDI and spatial linkages: analytical considerations and related literature

2.1 FDI and the lack of space

In recent years, the theoretical and empirical research on the causes and consequences of FDI has been booming (Markusen 2002; Barba Navaretti and Venables 2004; Helpman 2006). But despite the considerable progress that has been made, the research still remains largely confined to a two-country setting where FDI between home country x and host country i is solely determined by x and i’s characteristics only. This focus on a bilateral setting is problematic. To start with, these bilateral models are at odds with basic stylized facts about FDI. As Neary (2008) for instance argues two-country models cannot explain why in an era of falling trade costs, (horizontal) FDI has surged within the European Union (EU). One way to explain these kind of empirical FDI puzzles is to take third-country effects into account like in the export-platform models of Ekholm et al. (2007). In these models the (distance weighted) market size of third countries can help to solve the puzzle of Neary (2008) by allowing for the possibility that a country becomes a host country for FDI because it can be used by the multinational firm as a base to export to other (nearby) markets. Also from a theoretical perspective, the recent FDI literature can be criticized for its assumption that when analyzing the FDI decisions of individual firms the economic landscape is taken as given. How the location decision of a single firm could be determined by the location decisions of other firms is mostly not an issue. From the new economic geography literature (Fujita et al. 1999), we know that if agglomeration effects matter one cannot assume the spatial distribution of other firms to be taken as given. A few papers have incorporated FDI into a new economic geography framework and these papers show how agglomeration effects and FDI decisions interact (see, for instance, Brakman et al. (2009, chap. 8); Ekholm and Forslid (2001); Hoffmann and Markusen (2008); Baldwin and Okubo (2006)). Both the empirical and theoretical objections to a bilateral FDI setting boil down to the recommendation that geography or spatial interdependencies have to be included in the analysis (see for a similar observation Baltagi et al. (2007) and Blonigen et al. (2007)). From an empirical perspective this means that third-country effects should be taken into account.

With respect to FDI, there are a limited number of empirical papers that include third-country effects. Apart from some work on the export-platform case (Ekholm et al. 2007), agglomeration effects are a key element in the seminal papers by Head et al. (1995) and Head and Mayer (2004) that investigate the location decisions of Japanese multinational firms across the United States and Europe respectively. In the latter study for instance, and clearly inspired by the new economic geography literature, agglomeration effects are captured by a market potential variable that includes not only the market size (GDP) of the FDI host, but also the (distance weighted) GDPs of other locations. Furthermore, in the empirical literature on FDI and corporate income taxation, Krogstrup (2004, 2005) and Garretsen and Peeters (2007) also include a market potential variable to show that more centrally located or core countries can allow themselves to ceteris paribus have higher corporate income tax rates. Notwithstanding the inclusion of third-country effects, these papers focus only on particular aspects as to whether and how space might matter. A more systematic treatment of spatial interdependencies calls for an approach where the third-country effects are not a priori limited to one channel (e.g. market potential) and/or a few specific (host) locations but where instead as few as possible restrictions should be placed on the data when it comes to the way spatial interdependencies might determine the FDI to or from a specific country. It is here that spatial econometrics can be a very useful tool to improve our understanding of FDI patterns (see also Keller and Shiue (2007)).

2.2 Related literature and the grounding of spatial linkages on FDI theory

To our knowledge there are to date only a few papers that use spatial econometrics to test for the relevance of third-country effects in FDI behaviour, notably Coughlin and Segev (2000); Baltagi et al. (2007); Blonigen et al. (2004, 2007, 2008). Overall, and even though the evidence is mixed, these papers find evidence that spatial interdependencies matter. While controlling for standard determinants of FDI, Coughlin and Segev (2000) use a sample of inward FDI to 29 Chinese regions to estimate a spatial error model and find evidence of (positive) spatial autocorrelation. Using a far more advanced econometric approach and with US outbound FDI between 1989 and 1999 as their dependent variable, Baltagi et al. (2007) allow for spatial effects by including among their set of regressors the spatially weighted exogenous variables and by testing for spatial autocorrelation. They also try to link their findings to a theoretical model of FDI (see our discussion of Table 1 below). Their main empirical finding is that third-country effects are significant. Blonigen et al. (2007, 2008) estimate for a sample of US FDI data a spatial lag model and thereby examine whether spatial autoregression is important. The main difference from an empirical perspective between these two last studies is that the former does so for US inbound FDI and the latter for US outbound FDI. In their analysis of US inbound FDI from OECD countries during 1980–2000, Blonigen et al. (2008) inter alia find that the United States receives more FDI from home countries that are close to large third-country markets.

Table 1 Basic FDI models and expected sign for the spatial lag and market potential
Full size table

For our present purposes, the study on US outbound FDI by Blonigen et al. (2007) is the most important one because our empirical specification is modelled upon their work and their estimation results will provide a benchmark when discussing our own results. In addition, and based in turn on Baltagi et al. (2007), they also argue how in particular a spatial lag specification can be grounded upon FDI theory. In our view this connection between FDI theory and the spatial lag model is quite important. It means that the inclusion of a spatial lag has a foundation in economic theory, and this is not the case or at least far more problematic for the other workhorse model in spatial econometrics, a spatial error model. In a spatial error set-up, distance weighted shocks to FDI in one host country may spill over to another host country, but FDI theory simply provides little to no guidance whether or not to expect (positive or negative) spatial autocorrelation. For the spatial lag model and in particular for the spatial lag coefficient, FDI theory does, however, provide some guidance. Following theoretical work by Markusen (2002) and Egger and Pfaffermayr (2004), Baltagi et al. (2007, Table 1, p. 263) for instance come up with four categories of FDI or multinational firm strategies: vertical FDI, horizontal FDI, export-platform FDI, and complex (vertical) FDI. The first three categories are well-known and the fourth refers to a situation where, in a three-country model, a multinational firm from home country x not only has production plants in host country i but also in third country j (slicing up the value chain).

As summarized in Table 1, based on Blonigen et al. (2007, p. 1308), the spatial lag coefficient can therefore be linked to specific FDI theories. Combined with expected sign of the market potential variable (the distance-weighted sums of other countries’ GDP that captures the market size effect), Blonigen et al. (2007) show that this in principle provides for testable hypotheses when it comes to grounding the results for the spatial lag coefficient for FDI on FDI theory, see Table 1. In principle, because their as well as our data set only contains aggregate annual outbound FDI and thereby is the summation of all FDI decisions undertaken by firms in a given year neglecting that these various FDI decisions may result from rather different motives. The spatial lag coefficient may for instance be on average not different from zero but this could simply be the result of export-platform and complex vertical FDI effects cancelling out.

With (pure) horizontal FDI, and assuming sufficiently high trade costs between countries, a firm from host country x can serve foreign markets i and j by exports or by setting up production in i and j. The possibility to circumvent trade costs provides an incentive for horizontal or market seeking FDI (as opposed to exporting), but the cost of setting up production in countries i and j discourages FDI. In this case, the decision by the firm from country x whether or not to engage in FDI in country i has no bearing on its decision whether to do so in country j. This means that the spatial lag is assumed not to be significant. The spatial lag allows for the fact that FDI from x into host i is affected by the FDI going from x to j taking the distance between i and j into account. Similarly, for the FDI decision of an x firm to start to produce in country i, the market size of other countries j is also not an issue with pure horizontal FDI, hence the 0-entry for the market potential variable in Table 1.

From basic FDI theory we also expect for (pure) vertical FDI from home country x to host country i that the market size of countries j(≠i), and thus the market potential, not to be relevant because vertical FDI is driven by factor cost differences between countries and not by market size considerations. With (pure) vertical FDI, FDI theory predicts that the home country firm seeks to set up (part of the) production in the country with lowest factor costs. This implies that vertical FDI from country x to country j will be at the expense of vertical FDI from x to host country i. This means that one expects a negative spatial lag for (pure) vertical FDI.

With export platform FDI and now assuming that trade costs between potential host countries i and j are lower than between home country x vis-a-vis i and j, firms from country x may decide to engage in FDI by setting up production in host country i, thereby circumventing the trade costs between the countries x and i and thereby using the FDI as a platform to export from i to the market in country j. In this case, the market potential variable is expected to have a positive impact on FDI because larger (and nearby) markets in countries j(≠i) make country i a more attractive location for FDI. The spatial lag is, however, expected to be negative for export platform FDI from x to host country i because setting up a plant in another country is costly (production takes place under increasing returns to scale) and serving the combined markets i and j is more efficient from a single FDI location. This means that an increase in export platform motivated FDI from home country x to third country j ceteris paribus means less FDI from x to i. This is even more so if the distance between i and j is small, hence the minus sign for the spatial lag in Table 1.

In models of complex (vertical) FDI, where FDI from home country x implies that part of the production takes place in host countries i and j, multinational firms “slice up the value chain” of their production process by seeking out (low cost) suppliers in multiple (nearby) countries. If nearby countries i and j share similar supply (network) characteristics, multinational firms may find it profitable to set up production in i given that they already produce from (nearby) country j as well. In terms of Table 1 (last row), this means that FDI from home country x to third country j is a complement for FDI from home country x to host country i even more so if i and j are neighbouring countries. For this fourth group of FDI models one expects a geographical clustering of FDI for supply reasons. Whether the market potential matters in this category of FDI models, is open to debate (compare for instance Table 1 in Blonigen et al. (2004) with Table 1 in Blonigen et al. (2007)). If the market potential captures agglomeration effects, we would expect a + sign; however, if it captures demand or market-size reasons only, we would expect a 0-signs for the market potential. This explains the 0/+-sign in Table 1.

As to the actual estimation results in Blonigen et al. (2007), for their sample of 35 host countries for the period 1983–1998 and based on what is essentially a gravity model of US outbound FDI to which a spatial lag is added, they find that the “traditional” gravity-type of host country determinants of FDI like GDP, population and bilateral distance are rather robust to the inclusion of the spatial lag variable. They also conclude, perhaps most importantly, that the inclusion of country-fixed effects renders the spatial lag variable insignificant in most cases. This also holds true for the other spatial or geography variable in their analysis, the aforementioned market potential variable. And when the spatial effects turn out to be significant this is very sensitive to the particular (sub-)sample of countries chosen. This last observation makes it rather difficult to relate the findings to any of the basic theoretical models of FDI from Table 1. Their finding that spatial effects by and large cease to be significant when country-fixed effects are included suggests that spatial effects, if at all relevant, are primarily cross-sectional which is quite an important finding and one that extends beyond the FDI literature as such. Or to quote Blonigen et al. (2007, p. 1316) on this: “spatial interactions are relatively stable over time. In fact there’s an analogy in the international trade literature in Feenstra’s (2002) finding that third-country interdependence in gravity model estimation delineated by Anderson and van Wincoop (2003) can be adequately accounted for a panel setting with country-level fixed effects. In our data, the inclusion of country dummies substantially eliminates the statistical and economic significance of the spatial terms.” One of the main aims of our inquiry into Dutch outbound FDI is to find out whether spatial effects are indeed no longer relevant when one controls for country-fixed effects. This is really an important issue because without controlling for fixed effects any alleged evidence in favour of spatial dependence in FDI, in this case through the spatial lag model, might simply be due to spatial heterogeneity across our set of countries. The inclusion of country-fixed effects is meant to capture this last effect.

3 Data and empirical specification

3.1 Data

For our spatial econometric analysis, we use a panel of annual data on Dutch outbound FDI into 18 OECD host country destinations for the period 1984–2004. The Netherlands as a home country of FDI is an interesting case to consider. Being home to some of Europe’s largest multinational enterprises, the Netherlands is one of the OECD’s main exporters of FDI. Indeed, ranked by FDI outbound positions, the Netherlands was ranked fifth worldwide in 2005, after much larger countries like the United States, the United Kingdom, France and Germany (UNCTAD 2006). Related studies (see Sect. 2) have thus focused on the United States as a parent country. The fact that the Netherlands, and as opposed to the United States, is not only part of the EU but also located in the heart of the EU makes it interesting to look at Dutch outward FDI as well. Also, a large part of FDI flows in the EU are intra-EU flows and this is also true for Dutch FDI. This may imply that Dutch FDI may very well be driven by other motives than US FDI to host countries in the EU.

We limit ourselves to host country destinations within the OECD for two reasons. First, these countries account for the lion’s share of Dutch outbound FDI. On average, these 18 OECD countries accounted for more than 82% of Dutch FDI activity, with the United States, the United Kingdom, Belgium, Germany and Switzerland being the main host country destinations (averaged across our sample period the United States is the most important host country for Dutch FDI, more recently the United Kingdom has become the prime host country for Dutch FDI). Second, focusing on the OECD is also likely to limit vertical specialisation as a primary motive for FDI. This allows us to better disentangle the factors behind spatial interdependence. FDI is measured as real FDI stocks and Dutch FDI stocks are aggregated investment data collected by the Netherlands’ Central Bank (DNB), which we convert into millions of real euros using a price index for gross fixed capital formation.Footnote 2 Our data on FDI exclude FDI positions from foreign firms that headquarter in the Netherlands for tax purposes only without truly being active in the Netherlands. In some of our estimations, we will use data on sectoral FDI; that is to say, we split our Dutch FDI data into industry and services FDI. Unfortunately, sectoral FDI data for the Netherlands are only sufficiently available for the rather crude break-down of FDI into these two sectors (see Sect. 4.2) and only for 12 of our 18 host countries, see Table 6 in the Appendix.

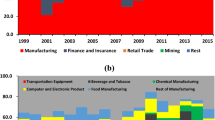
Figure 1 plots the development of the Dutch FDI outbound position in the 18 host countries in our sample period, both as a percentage of GDP and in absolute terms. Irrespective of the measure used, the Dutch outbound position has risen significantly over time.

Fig. 1
figure 1

Dutch outbound FDI position to 18 host countries

Full size image

For the set of explanatory variables in our basic specification, we included data on the following variables (see Table 7 in the Appendix for data definitions and data sources). Host country real GDP data are taken from the Penn World Tables (PWT). Trade costs are measured by the inverse of the openness measure reported by the PWT, which itself is equal to exports plus imports divided by GDP. The quality of government is measured by a composite index, calculated as the mean value of the variables “corruption”, “law and order” and “bureaucracy quality”. This index is developed by the Quality of Government Institute, see Teorell et al. (2006), and uses data collected by the PRS Group. Labour productivity per hour worked is taken from the Groningen Growth and Development Centre database. To control for distance, we use great circle distances between capital cities (measured in kilometres), which are drawn from the CEPII database.Footnote 3 In order to investigate the relevance of neighbouring corporate income tax rates for FDI positions, we use a dummy variable. The tax dummy equals 1 if the statutory tax rate of the respective country is larger than the distance-weighted average of the statutory tax rates of the other countries and 0 otherwise. The statutory tax rates are drawn from Devereux et al. (2002). The inclusion and specification of the tax variable is merely meant to measure in a very simple manner the possibility that, in line with the standard tax competition literature, a relatively higher tax rate may put a downward pressure on the inflow of FDI. This may be relevant because the Netherlands is a tax exemption country. The distance weighting is meant to capture the idea that if a Dutch firm thinks about setting up a plant in southern Europe as to the chances the FDI going to Portugal the tax rate of Spain vis-a-vis Portugal is more relevant than the tax rate of Sweden. In our estimations (see Sect. 4.1) we also used alternative tax rates. Finally, the market potential variable is measured as the distance weighted average of GDP of all host countries in the sample (in our empirical specifications below we also checked whether the estimation results are sensitive to the inclusion of host GDP in the market potential variable). The summary statistics of the variables in our data are given in Table 2.

Table 2 Descriptive statistics of the variables
Full size table

3.2 Empirical specification

Our benchmark model, see Eq. (1), is a gravity model which is still the workhorse model for empirical research on (bilateral) FDI (see Barba Navaretti and Venables (2004, chap. 6) for an overview). Unless indicated otherwise all variables are in logs (Blonigen and Davies 2004) and, still ignoring spatial econometrics for the moment, the main differences with a standard bilateral FDI gravity model specification are as follows. First, home (=Dutch) variables are not included since invariably the Netherlands is the home country and these variables thus only vary in our sample over time (and not in a cross-sectional sense), and the time-series variation is dealt with by including a time trend (in our case only a quadratic trend turned out to be significant). Second, in our benchmark specification geography or space is already allowed to play a role through the inclusion of the market potential variable and the tax-dummy. For the latter variable, capturing whether a host country has a higher corporate income tax rate than the other countries (weighted by distance), we expect a negative sign. For the market potential variable the expected sign is not clear-cut, see Table 1. If Dutch outbound FDI is mainly driven by export-platform considerations or agglomeration economies, we expect that the market potential variable enters with a positive sign. But FDI theory tells us that if FDI is predominantly of the “pure” horizontal or vertical type, or captures market-size effects only, there is no reason to expect market potential to matter.

Both the tax variable and the market potential variable are included among the set of Host Variables in Eq. (1). We also included, see Sect. 3.1 for more information on the data (expected sign between brackets): host GDP (+), host population (−), trade costs, as measured by the inverse of openness (−), quality of government (+), labour productivity (+) and bilateral distance (−). The distance variable only enters the specification when we do not control for country-fixed effects.Footnote 4 We will estimate (1) with and without country-fixed effects.

$$ {\text{FDI}} = \alpha_{0} + \alpha_{1} \;{\text{Host}}\;{\text{Variables}} + \varepsilon $$
(1)

In spatial econometrics, there are two basic options to test for spatial effects or spatial linkages (Anselin 1988): a spatial lag and a spatial error model. As we explained in Sect. 2, our preferred option is to estimate a spatial lag model where, very much like in non-spatial models with a lagged dependent variable, one seeks to establish whether there is spatial autoregression in the data. This is captured in Eq. (2) by the ρWFDI term, where W is a distance matrix, which identifies the geographical relationship among host countries (see below), and ρ is the coefficient to be estimated, which is assumed to lie between −1 and +1. This spatial lag variable allows us to establish if Dutch FDI to Spain (the dependent variable) is (positively/negatively) affected by the Dutch FDI to other host countries weighted by the distance between Spain and the other host countries.

$$ {\text{FDI}} = \alpha_{0} + \alpha_{1} \;{\text{Host}}\;{\text{Variables}} + \rho W{\text{FDI}} + \varepsilon $$
(2)

As is standard in spatial econometrics, the weighting matrix W is row standardized so that each row in W sums to unity. The term WFDI therewith has the “simple interpretation of row-sums being a proximity-weighted average of FDI into alternative countries” (Blonigen et al. 2007, p. 1311). To be more specific on the W matrix for any year y, W Y is defined as:

$$ W_{Y} = \left[ {\begin{array}{*{20}c} 0 & {w(d_{i,j} )} & {w_{Y} (d_{i,k} )} \\ {w_{Y} (d_{j,i} )} & 0 & {w_{Y} (d_{j,k} )} \\ {w_{Y} (d_{k,i} )} & {w_{Y} (d_{k,j} )} & 0 \\ \end{array} } \right] $$

where w(d i,j ) defines the functional form of the weights between any two pair of host countries i and j. We choose a simple inverse distance function, where the shortest distance within the sample gets a weight of unityFootnote 5 and all other distances within the sample a weight that declines to w(d i,j ) = 262/d i,j , where d i,j is the distance between host country i and j. Equation (2) will be estimated by maximum likelihood. It is one thing to test for spatial linkages by estimating a spatial lag model while it is quite another thing to establish whether it makes sense to do so. From the point of FDI theory we already briefly discussed in Sect. 2 (Table 1) how the spatial lag coefficient ρ could be linked to various FDI models. From an econometrical point of view and with the “non-spatial” model (1) as benchmark we will test for this in the next section.

4 Estimation results

4.1 Full sample and European sub-sample results

Table 3 gives the estimation results for the full sample (1984–2004, 18 OECD host countries, see Table 6 in the Appendix for a list of the countries included) for Dutch outbound FDI as well as for sub-samples of the European and euro-area countries. Columns (1) and (2) show the results for Eq. (1), columns (3) and (4) do the same for the spatial lag model from Eq. (2), and columns (5) and (6) give the estimation results when we include only Dutch FDI to respectively the European and euro area countries among the 18 host countries.

Table 3 Spatial analysis of Dutch outbound FDI—full sample and sub-samples
Full size table

Turning first to the results for the benchmark model in columns (1) and (2), we focus on the results with country-fixed effects because it turns out that the pooled OLS estimation without fixed effects had to be rejected in favour of the fixed effects model. The standard gravity model variables (host GDP, host population and, without fixed effects, bilateral distance) are significant and the coefficients have the expected sign. The same is true for labour productivity (LPROD) and the quality of government (QOG). The home country time-series variation in FDI is captured by a time trend. The results for the tax variable reveal that ceteris paribus Dutch FDI is discouraged if a host country has a relatively high corporate income tax rate.Footnote 6

Since we are mainly concerned with the relevance of space for Dutch FDI, the estimation results for the market potential variable (host MP) are of particular interest. The host MP coefficient indicates that Dutch outbound FDI is stimulated if the host country has a large market potential, that is to say if it is surrounded by countries with (distance weighted) relatively large GDP levels. In the specification of the MP variable in Table 3, host GDP (weighted by internal distance) is included in the MP variable. From Blonigen et al. (2007) we know that the inclusion of host GDP may influence the results in that it increases the size (and significance) of the MP coefficient. We re-ran our regressions for the MP variable without the host GDP as part of the host’s market potential but this did not change our results.

Before we discuss the estimation results for the spatial lag model, we first establish that spatial dependence is present in the data for Dutch FDI. As a first pass, we tested for spatial autocorrelation for our main variable, real FDI stocks, by Moran’s I. The corresponding coefficient of 0.601 (p-value: 0.000) indicates that there is indeed spatial autocorrelation. More importantly, when testing for spatial dependence for model specification as shown by column (2) in Table 3, we find clear evidence of spatial dependence. The test results for Lagrange multipliers clearly show that we can opt for a spatial lag model. The LM-coefficient for the spatial lag model is 7.173 (p-value: 0.007).

Columns (3) and (4) in Table 3 show the estimation results for the spatial lag model. As far as the standard FDI determinants are concerned, the results are in general more in line with the underlying theory and more significant for the fixed effects specification (see for instance the results for the market potential variable). Given our discussion at the end of Sect. 2.2 as to whether the inclusion of country-fixed effects renders the spatial lag coefficient ρ insignificant because of the time-invariance of spatial dependence, a comparison of columns (3) and (4) leads to two important conclusions. First, the inclusion of fixed effects implies that the spatial lag coefficient decreases substantially (from 0.44 to 0.07). This finding is in line with Blonigen et al. (2007) and it signals that indeed spatial autoregression is picked up by the fixed effects. Second, despite the inclusion of fixed effects the spatial lag coefficient is still clearly significant (at the 1% level). This leads us to conclude that at least for Dutch FDI spatial effects are not fully of a cross-sectional nature. This is in contrast with the results by Blonigen et al. (2007). When it comes to the grounding of the estimation results from column (4), our preferred spatial lag specification, on FDI theory and the hypotheses outlined in Table 1, the combination of a positive spatial lag coefficient with a positive market potential coefficient could be compatible with a FDI model of complex vertical FDI with agglomeration economies.

From related studies, we know that the results might be sensitive to the selection of host countries. As a first attempt to see how robust our results for Dutch FDI are to variations in our set of 18 host OECD countries we re-estimate our basic spatial lag model (see column (4) in Table 3) for two different sub-samples. We split our sample in two different ways. First, we exclude the non-European countries (Australia, Canada, Japan and the United States) from our sample. This results into a “European” sub-sample, including 14 European countries. On average, these 14 countries account for 61% of Dutch outbound FDI in the period 1984–2004. The second sub-sample is even smaller and contains 10 euro area countries only, accounting for 33% of Dutch FDI. The reason to look only at Dutch FDI to other European countries is to acknowledge the potential relevance of the EU single market (and EMU). We only show the results for the fixed effects specification in columns (5) and (6), because this specification is to be preferred over the pooled OLS estimation without country dummies. It turns out that our results are indeed to some extent sensitive to sample selection. Turning first to the sub-sample of European countries, column (5) in Table 3 shows that the spatial lag coefficient for Europe is negative (and only significant at the 10% level), while the spatial lag coefficient for the euro area (see column 6) is still positive. More importantly, in both sub-samples the spatial lag coefficient remains significant, even though we controlled for fixed effects. Turning to the other spatial variables of interest, i.e. the market potential variable and the tax-dummy, it follows that the market potential variable remains significant and positive for our sub-samples. Again, with Table 1 in mind, our results could be compatible with a FDI model of complex vertical FDI with agglomeration economies. As to the different outcome for the spatial lag coefficient for the Europe and euro area sub-samples a breakdown of the data shows that this result is driven by Dutch FDI to the United Kingdom and Sweden (both countries belong to the Europe but not the euro area sample). Without these two countries, the spatial lag for the Europe sample is also positive. It turns out that Dutch FDI to the United Kingdom and Sweden is more strongly oriented to services FDI (compared to the overall sample) and this, as we will see in the next sub-section (see Table 4 below), may help to account for the negative spatial lag for the Europe sample as a whole in Table 3.

Table 4 Spatial analysis of sectoral Dutch outbound FDI
Full size table

Overall, the estimation results in Table 3 lead us to conclude that:

  • Spatial linkages matter for Dutch FDI because the spatial lag coefficient is significant (and positive), also and rather crucially when we control for fixed effects.

  • In the model specifications with fixed effects and compared to the benchmark model in column (2), the standard determinants of FDI are quite robust to the inclusion of a spatial lag.

  • Controlling for country-fixed effects reduces the importance of the spatial lag coefficient (indicating that spatial autoregression does to a large extent not vary across time).

  • Apart from the results for the spatial lag, there is also evidence that space matters through other channels, e.g. for the market potential and tax variables.

4.2 Sectoral FDI and a spatial error model

In modern FDI theory, a firm’s decision whether or not to engage in FDI basically has two dimensions. First, there is dimension of location. With horizontal or market-seeking FDI the trade-off between trade costs and (plant and firm level) economies of scale determines if the firms prefers FDI over exporting. With vertical FDI, the main variables of interest are factor price differences between the home and the potential host countries, economies of scale and trade costs (compare Barba Navaretti and Venables (2004), chaps. 3 and 4). As to the organizational dimension, once the firm has decided to engage in off-shoring it still has to figure out whether if it wants to do so through FDI or outsourcing. In reality, the location and organization issue are of course intertwined (Helpman 2006). The fact is that firm and also sector characteristics determine the outcome of this decision process. But characteristics like economies of scale, skill-intensity or asset-specificity may differ across sectors and that is why it is useful to disaggregate our Dutch FDI data. Ideally, we would like estimate the spatial lag model for a wide range of sectors but data availability dictates a basic (but still in our view relevant) split between industry and services FDI. We have the corresponding data for 12 of our 18 host countries (see Table 7 in the Appendix) and the estimation results are shown in Table 4.

Columns (1)–(3) give the “no spatial” results for total FDI for 12 host countries, the industry FDI and the services FDI respectively. By and large, and with one or two exceptions (see for instance the insignificance of the labour productivity coefficient for the industrial FDI sample) the results for these specifications are rather similar. The market potential variable is positive and significant in all 3 cases but somewhat larger for the industry FDI. The main focus of Table 4 is again the spatial lag coefficient ρ. Note first that we included country-fixed effects in all specifications. For the total of 12 countries (column 4) and much like in Table 3, the spatial lag is significant (at 1% level) and has a positive sign. This is also true for industry FDI (column 5) but not for services FDI (column 6). The spatial lag for services FDI has a negative sign and borders on insignificance (significant at 10% level). Even though the level of sectoral aggregation is still quite high, these results indicate that a sectoral differentiation is important in order to understand the role of spatial linkages. Taken at face value the difference in the spatial lag coefficient for industry and services FDI suggests that Dutch industrial (services) FDI to host country i is a complement (substitute) for Dutch FDI to other host countries j. Future research should try to further disaggregate the FDI data to be able to better disentangle and distinguish between the motives for FDI. As with Table 3 (column 4), the inclusion of fixed effects does not render the spatial linkages insignificant thereby re-enforcing the conclusion that spatial dependence is not merely a reflection of spatial heterogeneity in the case of Dutch FDI. Finally, note that the negative spatial lag coefficient for services could help to explain why we found a negative spatial lag coefficient for the Europe sub-sample in Table 3 (column 5) above. Recall that this last result was due to the Dutch FDI to the United Kingdom and Sweden and FDI to these 2 countries relatively strongly aimed at services FDI.

So far, we have only been concerned with spatial linkages through the estimation of a spatial lag model for FDI, the main reason being that this model can be linked to FDI theory. We have, however, also estimated a spatial error model because we have a priori no reason to expect that spatial linkages in the case of Dutch FDI would only show up in our data by estimating the spatial lag model (2). In addition, the FDI studies by Coughlin and Segev (2000) and Baltagi et al. (2007) suggest that a spatial error model may be relevant as well. Equation (3) gives the basic specification for the spatial error model. By estimating (3) one tests for the significance of spatial autocorrelation. If the λ-coefficient is significant, there is spatial autocorrelation implying that a shock in the Dutch FDI to host country j(≠i) will have an impact on Dutch FDI to host country i, where the size of the impact depends on the distance between the two host countries i and j as measured by the distance matrix W and where the distance matrix W is defined as specified in Sect. 3.2. Equation (3) will be estimated by maximum likelihood.

$$ {\text{FDI}} = \alpha_{0} + \alpha_{1} \;{\text{Host}}\;{\text{Variables}} + \varepsilon ,{\text{ where }}\varepsilon = \lambda W\varepsilon + \mu $$
(3)

Table 5 displays the estimation results for the spatial error specification for the various samples that have been introduced previously.Footnote 7 Country-fixed effects were included in all specifications reported in Table 5. Our main interest is now the spatial error coefficient λ.

Table 5 Spatial error specifications of Dutch outbound FDI
Full size table

Irrespective of which countries or sectors are included in our sample, the spatial error coefficient is invariably significant and positive. Hence, we can conclude that Dutch outbound FDI is characterized by spatial autocorrelation. But this conclusion is entirely data-driven and from the perspective of FDI one has no clear-cut theoretical foundation for this result. Or to quote Blonigen et al. (2007) on this, the spatial error model is “silent with respect to evidence of the substitution or complementarity of FDI across countries and therefore does not inform theory” (Blonigen et al. 2007, p. 1309). It does, however, point to the fact that apart from channels identified by FDI theory (recall Table 1) there must be other channels through which shocks to Dutch FDI to third country j can influence the Dutch FDI to country host country i. Footnote 8

5 Conclusions

In this paper, and informed by FDI theory, a spatial lag model was introduced to test for the relevance of third-country effects in Dutch outbound FDI. Our paper is related to a few other papers that have used spatial econometrics in this context, i.e. Coughlin and Segev (2000), Baltagi et al. (2007), Blonigen et al. (2004, 2007, 2008). While Coughlin and Segev (2000) use a sample of inward FDI to Chinese regions, the other studies focus on (in- or outbound) US FDI. In contrast, the present paper is concerned with Dutch outbound FDI. The Dutch case is interesting as both within and outside the EU the Netherlands is one of the main exporters of FDI. Our approach is similar to the one in Blonigen et al. (2007) in that we first and foremost estimate a spatial lag model and we also try to find out whether spatial effects are still relevant when one controls for fixed effects.

Our results suggest that spatial linkages matter for Dutch outbound FDI. In most specifications, the spatial lag is (highly) significant. Stronger still, while we find evidence that some of the spatial autoregression is picked up by country-fixed effects, our spatial lag coefficient remains significant despite the inclusion of fixed effects. Having said this, our results turn out to be somewhat sensitive to sample selection which, together with the fact that we have to use aggregate FDI data, makes it not straightforward to link our estimation results entirely to a specific FDI model. Nevertheless, most of our results are compatible with complex FDI with agglomeration economies. Sub-sample results for industry and services FDI, for a subset of European host countries as well as for a spatial error specification of Dutch FDI all reinforce our conclusion that spatial linkages or third-country effects matter for Dutch FDI. At the same time, our results suggest that more work needs to be done to disentangle the channels through which these third-country effects operate and how these channels may vary across space and time. The availability and use of more disaggregated FDI data should be very helpful in this respect.