Optimality conditions and Mond–Weir duality for a class of differentiable semi-infinite multiobjective programming problems with vanishing constraints

Abstract

In this paper, the class of differentiable semi-infinite multiobjective programming problems with vanishing constraints is considered. Both Karush–Kuhn–Tucker necessary optimality conditions and, under appropriate invexity hypotheses, sufficient optimality conditions are proved for such nonconvex smooth vector optimization problems. Further, vector duals in the sense of Mond–Weir are defined for the considered differentiable semi-infinite multiobjective programming problems with vanishing constraints and several duality results are established also under invexity hypotheses.

1 Introduction

Multiobjective optimization (also known as multiobjective programming, vector optimization, multicriteria optimization) is an area of mathematical programming that is concerned with extremum problems involving more than one objective function to be optimized simultaneously. The difficulty of multiobjective programming lies in the fact that the objectives of vector optimization problems are in conflict with each other and an improvement of one objective may lead to the reduction of other objectives. A multiobjective optimization model provides the mathematical framework to deal with such situations. Because multiobjective optimization problems arise in different scientific applications, many researches have focused on developing optimality conditions and duality results for such mathematical programming problems and also methods for their solution. The available literature on optimality conditions and various types of duality for multiobjective programming problems is very rich (see, for example, several monographs on multiobjective programming which have been published in recent past, that is, Chen et al. 2005; Chankong and Haimes 1983; Jahn 2004; Luc 1989; Miettinen 1999; Mishra et al. 2016; Sawaragi et al. 1985; Yu 1985).

A semi-infinite multiobjective optimization problem is the simultaneously minimization of finitely many scalar objective functions subject to an arbitrary (possibly infinite) set of constraint functions. Fundamental theoretical aspects and a wide range of applications of both scalar and multiobjective semi-infinite programming problems have been studied intensively by many researchers (see, for example, Antczak 2016; Antczak et al. 2016; Antczak and Verma 2017; Jayswal and Mishra 2015; Jayswal et al. 2013; Jayswal and Singh 2019; López and Still 2007; Verma 2017; Zheng and Yang 2007; Zalmai and Zhang 2007, 2010, 2012 and others).

A particular form of a mathematical programming problem which attracted the attention of the optimization community over more than the past decade is a so-called optimization problem with vanishing constraints. Such an extremum problem has been recently introduced and studied by Achtziger and Kanzow (2008), motivated by several real-world applications, mainly for topology design problems in mechanical structures as described in their work. Since optimization problems with vanishing constraints, in their general form, are quite a new class of mathematical programming problems, very few works have only been published on this subject so far (see, for example, Achtziger et al. 2013; Dorsch et al. 2012; Dussault et al. 2018; Guu et al. 2017; Hoheisel and Kanzow 2007, 2008, 2009; Hu et al. 2019; Izmailov and Solodov 2009; Mishra et al. 2015, 2016). Recently, Tung (2020) established the optimality and duality results for the considered multiobjective semi-infinite programming with vanishing constraints under convexity assumptions. However, to the best our knowledge there are no works on optimality conditions and duality results for nonconvex differentiable semi-infinite multiobjective programming problems with vanishing constraints in the literature.

Therefore, the main purpose of this paper is to derive both necessary and sufficient optimality conditions and several duality results for a class of differentiable semi-infinite multiobjective optimization problems with vanishing constraints. Namely, we consider the semi-infinite multiobjective programming problem with vanishing constraint which is characterized by both an infinite number of inequality and equality constraints. Then, for the considered differentiable semi-infinite multiobjective programming problem with vanishing constraints, we prove two types Karush–Kuhn–Tucker necessary optimality conditions for a feasible solution to be a weak Pareto solution by using the semi-infinite version of Motzkin’s theorem of the alternative. We also extend the definition of a S-stationary point given in the literature for scalar optimization problem with vanishing constraints to the case of a differentiable semi-infinite multiobjective optimization problems with vanishing constraints. Then, we formulate the foregoing necessary optimality conditions for such smooth vector optimization problems in terms of such stationary points. Further, we prove the sufficiency of the foregoing necessary optimality conditions under assumptions that the functions constituting the considered differentiable semi-infinite multiobjective optimization problem with vanishing constraints are invex (with respect to the same function $\eta$). The second part of the paper is devoted to proving several duality results in the sense of Mond–Weir between the considered differentiable semi-infinite multiobjective optimization problem with vanishing constraint and its vector Mond–Weir dual problem. We prove several Mond–Weir duality results between the aforesaid vector optimization problems also under appropriate invexity hypotheses.

2 Preliminaries and problem formulation

The following convention for equalities and inequalities will be used in the paper.

For any $x=\left( x_{1},x_{2},...,x_{n}\right) ^{T}$, $y=\left( y_{1},y_{2},...,y_{n}\right) ^{T}$ in $R^{n}$, we define:

• (i) $x=y$ if and only if $x_{\alpha }=y_{\alpha }$ for all $\alpha =1,2,...,n$;

• (ii) $x>y$ if and only if $x_{\alpha }>y_{\alpha }$ for all $\alpha =1,2,...,n$;

• (iii) $x\geqq y$ if and only if $x_{\alpha }\geqq y_{\alpha }$ for all $\alpha =1,2,...,n$;

• (iv) $x\ge y$ if and only if $x\geqq y$ and $x\ne y.$

In this paper, we will use the same notation for row and column vectors when the interpretation is obvious.

Further, the cardinality of the index set J is denoted by $\left| J\right|$. The notation $\left\langle \cdot ,\cdot \right\rangle$ is used in the paper to denote the inner product. The convex (linear, canonical) hull of a nonempty set A is the intersection of all convex sets (linear subspaces, convex cones containing the origin) containing it, and coincides with the set of all the convex (linear, nonegative) combinations of its elements. For any set $A\subseteq R^{n}$, the symbols intA, clA, convA, spanA, coneA stand for its interior, closure, convex hull, linear hull, and the convex cone (containing the origin) generated by A (called the convex conic hull of A and it is the smallest convex cone containing A), respectively.

It is known that, for any sets $A_{1},A_{2}\in R^{n}$,

$$\begin{aligned} span\left( A_{1}\cup A_{2}\right)= & {} spanA_{1}+spanA_{2}, \end{aligned}$$

(1)

$$\begin{aligned} cone\left( A_{1}\cup A_{2}\right)= & {} coneA_{1}+coneA_{2}\text {.} \end{aligned}$$

(2)

Proposition 1

(Florenzano and Le Van 2001) The convex cone span$\left( A\right)$ generated by a subset A of $R^{n}$ is precisely the set of all positive linear combinations of finitely many elements of A.

Further, let us denote by $A^{-}$ and $A^{s-}$ the negative polar and the strictly negative polar of a set A, that is,

$$\begin{aligned}&A^{-}:=\left\{ y\in R^{n}:\left\langle y,x\right\rangle \leqq 0\text {, } \forall x\in A\right\} , \end{aligned}$$

(3)

$$\begin{aligned}&A^{s-}:=\left\{ y\in R^{n}:\left\langle y,x\right\rangle <0\text {, }\forall x\in A\right\} . \end{aligned}$$

(4)

Now, we give the definition of a differentiable vector-valued invex function which is a generalization of the concept of invexity introduced by Hanson (1981) for scalar smooth optimization problems to the differentiable vectorial case (see, for example, Osuna-Gómez et al. 1998).

Definition 2

Let $f=\left( f_{1},...,f_{p}\right) :R^{n}\rightarrow R^{p}$ be a differentiable function on $R^{n}$ and $u\in R^{n}$. If there exist a vector-valued function $\eta :R^{n}\times R^{n}\rightarrow R^{n}$ such that the inequalities

$$\begin{aligned} f_{i}(x)-f_{i}(u)\geqq \nabla f_{i}\left( u\right) \eta \left( x,u\right) (>),\quad , i=1,...,p \end{aligned}$$

(5)

hold for all $x\in R^{n}$ ($x\ne u$), then f is said to be a differentiable vector-valued (strictly) invex at u on $R^{n}$ (with respect to $\eta$). Each function $f_{i}$, $i=1,...,p$, satisfying (5 ) is said to be differentiable (strictly) invex at u on $R^{n}$ (with respect to $\eta$).

If the inequalities (5) are satisfied at any point u, then f is said to be a differentiable vector-valued (strictly) invex function on $R^{n}$ (with respect to $\eta$).

If X is a nonempty subset of $R^{n}$ and the inequalities (5) are satisfied at $u\in X$ for all $x\in X$, then f is said to be differentiable vector-valued (strictly) invex at u on X (with respect to $\eta$).

In order to define an analogous class of differentiable vector-valued (strictly) incave functions, the direction of the inequalities in Definition 2 should be changed to the opposite one.

In the paper, we consider the following constrained semi-infinite vector optimization problem defined by:

$$\begin{aligned} \begin{array}{cll} f(x)=\left( f_{1}\left( x\right) ,...,f_{p}\left( x\right) \right) \rightarrow V\text {-min} \\ \quad \text {subject to}\quad g_{t}(x)\leqq 0\text {, }t\in T, \\ h_{s}\left( x\right) =0\text {, }s\in S, \\ H_{j}\left( x\right) \geqq 0\text {, }j\in J=\left\{ 1,...,w\right\} , \\ \quad G_{j}\left( x\right) H_{j}\left( x\right) \leqq 0\text {, }j\in J\text {,} \end{array} \end{aligned}$$

(SIMPVC)

where $f_{i}:R^{n}\rightarrow R$, $i\in I=\left\{ 1,...,p\right\}$, $g_{t}:R^{n}\rightarrow R$, $t\in T$, $h_{s}:R^{n}\rightarrow R$, $s\in S$, $H_{j}:R^{n}\rightarrow R$, $G_{j}:R^{n}\rightarrow R$, $j\in J$, are assumed to be continuously differentiable functions on $R^{n}$. Moreover, T and S are arbitrary, not necessarily finite (but nonempty) sets. We call (SIMPVC) a semi-infinite multiobjective programming problem with vanishing constraints.

For the purpose of simplifying our presentation, we will next introduce some notations which will be used frequently throughout this paper.

Let

$$\begin{aligned}&\Omega :=\left\{ x\in R^{n}:g_{t}(x)\leqq 0\text {, }t\in T\text {, } h_{s}\left( x\right) =0\text {, }s\in S\text {, }\right. \\&\quad \left. H_{j}\left( x\right) \geqq 0\text {, }G_{j}\left( x\right) H_{j}\left( x\right) \leqq 0\text {, }j\in J\right\} \end{aligned}$$

be the set of all feasible solutions in the considered vector optimization problem (SIMPVC). Further, for a given feasible solution ${\overline{x}}$, we denote the index set $T\left( {\overline{x}}\right)$ of all active constraints $g_{t}$ at this solution as follows

$$\begin{aligned} T\left( {\overline{x}}\right) =\left\{ t\in T:g_{t}\left( {\overline{x}}\right) =0\right\} \text {.} \end{aligned}$$

In multicriteria optimization problems, the concept of (weak) Pareto optimality (or (weak) efficiency) has an important role in all optimal decision problems with noncomparable criteria.

Definition 3

A feasible point ${\overline{x}}$ is said to be a weak Pareto solution (a weakly efficient solution) for (SIMPVC) if there is no other $x\in \Omega$ such that

$$\begin{aligned} f(x)<f({\overline{x}})\text {.} \end{aligned}$$

Definition 4

A feasible point ${\overline{x}}$ is said to be a Pareto solution (an efficient solution) for (SIMPVC) if there is no other $x\in \Omega$ such that

$$\begin{aligned} f(x)\le f({\overline{x}})\text {.} \end{aligned}$$

Now, for any feasible solution ${\overline{x}}$, let us denote the following index sets

$$\begin{aligned} J_{+}\left( {\overline{x}}\right)= & {} \left\{ j\in J:H_{j}\left( {\overline{x}} \right) >0\right\} \text {,} \\ J_{0}\left( {\overline{x}}\right)= & {} \left\{ j\in J:H_{j}\left( {\overline{x}} \right) =0\right\} \text {.} \end{aligned}$$

Further, let us divide the index set $J_{+}\left( {\overline{x}}\right)$ into the following index subsets:

$$\begin{aligned} J_{+0}\left( {\overline{x}}\right)= & {} \left\{ j\in J:H_{j}\left( {\overline{x}} \right)>0\text {, }G_{j}\left( {\overline{x}}\right) =0\right\} \text {,} \\ J_{+-}\left( {\overline{x}}\right)= & {} \left\{ j\in J:H_{j}\left( {\overline{x}} \right) >0\text {, }G_{j}\left( {\overline{x}}\right) <0\right\} \text {.} \end{aligned}$$

Similarly, the index set $J_{0}\left( {\overline{x}}\right)$ can be partitioned into the following three index subsets:

$$\begin{aligned} J_{0+}\left( {\overline{x}}\right)= & {} \left\{ j\in J:H_{j}\left( {\overline{x}} \right) =0\text {, }G_{j}\left( {\overline{x}}\right) >0\right\} \text {,} \\ J_{00}\left( {\overline{x}}\right)= & {} \left\{ j\in J:H_{j}\left( {\overline{x}} \right) =0\text {, }G_{j}\left( {\overline{x}}\right) =0\right\} \text {,} \\ J_{0-}\left( {\overline{x}}\right)= & {} \left\{ j\in J:H_{j}\left( {\overline{x}} \right) =0\text {, }G_{j}\left( {\overline{x}}\right) <0\right\} \text {.} \end{aligned}$$

Note that the first subscript indicates the sign of $H_{j}$ at ${\overline{x}}$ , whereas the second subscript stands for the sign of $G_{j}$ at ${\overline{x}}$. We would like to point out also that the above index sets substantially depend on the chosen point ${\overline{x}}$.

Definition 5

The (Bouligand) tangent cone (or contingent cone) to the feasible set $\Omega$ of (SIMPVC) at ${\overline{x}}\in \Omega$ is the set $T_{C}\left( \Omega ;{\overline{x}}\right)$ defined by

$$\begin{aligned}&T_{C}\left( \Omega ;{\overline{x}}\right) :=\left\{ d\in R^{n}:\exists \left( x_{k}\right) \subseteq \Omega \text {,}\left( \alpha _{k}\right) \subset R_{+} \text { such that }\alpha _{k}\downarrow 0\wedge x_{k}\rightarrow {\overline{x}} \wedge \frac{x_{k}-{\overline{x}}}{\alpha _{k}}\rightarrow d\right\} \\&\quad =\left\{ d\in R^{n}:\exists d_{k}\rightarrow d\text {, }\alpha _{k}\downarrow 0\text { such that }{\overline{x}}+\alpha _{k}d_{k}\in \Omega \text { }\forall k\in N\right\} \end{aligned}$$

Achtziger and Kanzow (2008) defined the linearized cone and the modified linearized cone called the VC-linearized cone for the scalar optimization problem with vanishing constraints.

Definition 6

(Achtziger et al. 2013) The linearized cone to the feasible set $\Omega$ of (SIMPVC) at ${\overline{x}}\in \Omega$ is the set $L\left( {\overline{x}}\right)$ defined by

$$\begin{aligned}&L\left( {\overline{x}}\right) :=\left\{ d\in R^{n}:\left\langle \nabla g_{t}\left( {\overline{x}}\right) ,d\right\rangle \leqq 0\text {, }t\in T\left( {\overline{x}}\right) \text {, }\left\langle \nabla h_{s}\left( {\overline{x}} \right) ,d\right\rangle =0\text {, }s\in S\text {,}\right. \\&\left. \left\langle \nabla H_{j}\left( {\overline{x}}\right) ,d\right\rangle =0 \text {, }j\in J_{0+}\text {, }\left\langle \nabla H_{j}\left( {\overline{x}} \right) ,d\right\rangle \geqq 0\text {, }j\in J_{00}\cup J_{0-}\text {, } \left\langle \nabla G_{j}\left( {\overline{x}}\right) ,d\right\rangle \right. \\&\left. \qquad \leqq 0 \text {, }j\in J_{+0}\right\} \text {.} \end{aligned}$$

Definition 7

(Achtziger et al. 2013) The VC-linearized cone to the feasible set $\Omega$ of (SIMPVC) at ${\overline{x}}\in \Omega$ is the set $L_{VC}\left( {\overline{x}}\right)$ defined by

$$\begin{aligned}&L_{VC}\left( {\overline{x}}\right) :=\left\{ d\in R^{n}:\left\langle \nabla g_{t}\left( {\overline{x}}\right) ,d\right\rangle \leqq 0\text {, }t\in T\left( {\overline{x}}\right) \text {, }\left\langle \nabla h_{s}\left( {\overline{x}} \right) ,d\right\rangle =0\text {, }s\in S\text {,}\right. \\&\left. \left\langle \nabla H_{j}\left( {\overline{x}}\right) ,d\right\rangle =0 \text {, }j\in J_{0+}\text {, }\left\langle \nabla H_{j}\left( {\overline{x}} \right) ,d\right\rangle \geqq 0\text {, }j\in J_{00}\cup J_{0-}\text {, } \left\langle \nabla G_{j}\left( {\overline{x}}\right) ,d\right\rangle \right. \\&\left. \qquad \leqq 0 \text {, }j\in J_{00}\cup J_{+0}\right\} \text {.} \end{aligned}$$

In order to prove the Karush–Kuhn–Tucker necessary optimality conditions, we need the constraint qualification. We use the Abadie constraint qualification and its modification for differentiable optimization problems with vanishing constraints introduced by Achtziger and Kanzow (2008).

Definition 8

(Achtziger and Kanzow 2008) (Abadie constraint qualification). It is said that the Abadie constraint qualification (ACQ) holds at ${\overline{x}}\in \Omega$, if and only if,

$$\begin{aligned} L\left( {\overline{x}}\right) =T_{C}\left( \Omega ;{\overline{x}}\right) \text {.} \end{aligned}$$

(6)

Definition 9

(Achtziger and Kanzow 2008) (VC-Abadie constraint qualification). It is said that the VC-Abadie constraint qualification (VC-ACQ) holds at ${\overline{x}}\in \Omega$, if and only if,

$$\begin{aligned} L^{VC}\left( {\overline{x}}\right) \subseteq T_{C}\left( \Omega ;{\overline{x}} \right) \text {.} \end{aligned}$$

(7)

Next, we recall the semi-infinite version of Motzkin’s theorem of the alternative given in Zalmai and Zhang (2007) (see also Goberna and López 1998 ).

Lemma 10

Let A and B be compact subset in $R^{n}$ and C an arbitrary set in $R^{n}$. Further, assume that the set $cone\left( B\right) +span\left( C\right)$ is closed. Then, either the system

$$\begin{aligned} \left\{ \begin{array}{ccc} \left\langle a,d\right\rangle <0 &{}\quad \text {for all} &{} a\in A\text {,} \\ \left\langle b,d\right\rangle \leqq 0 &{}\quad \text {for all} &{} b\in B\text {,} \\ \left\langle c,d\right\rangle =0 &{}\quad \text {for all} &{} c\in C\text { } \end{array} \right. \end{aligned}$$

has a solution $d\in R^{n}$, or there exist integers p, v and w with $0\leqq v\leqq n+1$, $0\leqq w\leqq n+1$, such there there exist p points $a^{i}\in A$, v points $b^{t}\in B$, w points $c^{s}\in C$, p non-negative scalars $\lambda _{i}$, $i\in \left\{ 1,...,p\right\}$ with $\sum _{i=1}^{p}\lambda _{i}=1$, scalars $\mu _{t}$ with $\mu _{t}\geqq 0$ for $t\in \left\{ 1,...,v\right\}$ and scalars $\xi _{s}$, $s\in \left\{ 1,...,w\right\}$, such that

$$\begin{aligned} \sum _{i=1}^{p}\lambda _{i}a^{i}+\sum _{t=1}^{v}\mu _{t}b^{t}+\sum _{s=1}^{w}\xi _{s}c^{s}=0\text {,} \end{aligned}$$

or equivalently,

$$\begin{aligned} 0\in conv\left( A\right) +cone\left( B\right) +span\left( C\right) \text {,} \end{aligned}$$

but never both.

Now, we show that weakly efficiency of a feasible solution ${\overline{x}}$ in (SIMPVC) implies the inconsistency of a certain semi-infinite system of linear inequalities and equalities.

Lemma 11

Let ${\overline{x}}\in \Omega$ be a weak efficient solution in (SIMPVC). Further, we assume that the Abadie constraint qualification (ACQ) holds at ${\overline{x}}$ for (SIMPVC). Then, the system

$$\begin{aligned} \left\{ \begin{array}{ccc} \left\langle \nabla f_{i}\left( {\overline{x}}\right) ,d\right\rangle <0 &{}\quad \text {for all} &{} i=1,...,p\text {,} \\ \left\langle \nabla g_{t}\left( {\overline{x}}\right) ,d\right\rangle \leqq 0 &{}\quad \text {for all} &{} t\in T\left( {\overline{x}}\right) \text {, } \\ \left\langle \nabla h_{s}\left( {\overline{x}}\right) ,d\right\rangle =0 &{}\quad \text {for all} &{} s\in S\text {,} \\ \left\langle \nabla H_{j}\left( {\overline{x}}\right) ,d\right\rangle =0 &{}\quad \text {for all} &{} j\in J_{0+}\left( {\overline{x}}\right) \text {,} \\ \left\langle -\nabla H_{j}\left( {\overline{x}}\right) ,d\right\rangle \leqq 0 &{}\quad \text {for all} &{}\quad j\in J_{00}\left( {\overline{x}}\right) \cup J_{0-}\left( {\overline{x}}\right) \text {,} \\ \left\langle \nabla G_{j}\left( {\overline{x}}\right) ,d\right\rangle \leqq 0 &{}\quad \text {for all} &{} j\in J_{+0}\left( {\overline{x}}\right) . \end{array} \right. \end{aligned}$$

(8)

has no solution $d\in R^{n}$.

Proof

By assumption, ${\overline{x}}$ is a weak efficient solution in (SIMPVC). Then, by Definition 3, there is no other $x\in \Omega$ such that

$$\begin{aligned} f\left( x\right) <f\left( {\overline{x}}\right) \text {,} \end{aligned}$$

or equivalently,

$$\begin{aligned} f_{i}\left( x\right) <f_{i}\left( {\overline{x}}\right) ,\quad \forall i\in I \text {.} \end{aligned}$$

(9)

Now, we show that there is no $d\in T\left( \Omega ;{\overline{x}}\right)$ such that

$$\begin{aligned} \left\langle \nabla f_{i}\left( {\overline{x}}\right) ,d\right\rangle <0,\quad \forall i\in I. \end{aligned}$$

(10)

We proceed by contradiction. Suppose, contrary to the result, that there is $d\in T\left( \Omega ;{\overline{x}}\right)$ such that (10) holds. Since $d\in T_{C}\left( \Omega ;{\overline{x}}\right)$, by Definition 5, there exist $\left( d_{k}\right) \subset R^{n}$, $\left( \alpha _{k}\right) \subset R$ such that $\alpha _{k}>0$ for all $k\in N$ and, moreover,

$$\begin{aligned} \alpha _{n}\downarrow 0\text {, }d_{k}\rightarrow d\text {, }{\overline{x}} +\alpha _{k}d_{k}\in \Omega \quad \forall k\in N. \end{aligned}$$

(11)

By assumption, each objective function $f_{i}$, $i\in I$, is continuously differentiable at ${\overline{x}}$. Thus,

$$\begin{aligned} f_{i}\left( {\overline{x}}+\alpha _{k}d_{k}\right) =f_{i}\left( {\overline{x}} \right) +\alpha _{k}\left\langle \nabla f_{i}\left( {\overline{x}}\right) ,d_{k}\right\rangle +o\left( \alpha _{k}\left\| d_{k}\right\| \right) ,\quad \forall i\in I. \end{aligned}$$

(12)

Hence, (12) yields

$$\begin{aligned} \frac{f_{i}\left( {\overline{x}}+\alpha _{k}d_{k}\right) -f_{i}\left( {\overline{x}}\right) }{\alpha _{k}}=\left\langle \nabla f_{i}\left( {\overline{x}}\right) ,d_{k}\right\rangle +\frac{o\left( \alpha _{k}\left\| d_{k}\right\| \right) }{\alpha _{k}\left\| d_{k}\right\| } \left\| d_{k}\right\| ,\quad \forall i\in I. \end{aligned}$$

(13)

If $k\rightarrow \infty$, then

$$\begin{aligned} \left\langle \nabla f_{i}\left( {\overline{x}}\right) ,d_{k}\right\rangle + \frac{o\left( \alpha _{k}\left\| d_{k}\right\| \right) }{\alpha _{k}\left\| d_{k}\right\| }\left\| d_{k}\right\| \rightarrow \left\langle \nabla f_{i}\left( {\overline{x}}\right) ,d\right\rangle <0,\quad \forall i\in I. \end{aligned}$$

(14)

By (13) and (14), we conclude that, for each $i\in I$, there exists $k_{i}^{*}>0$ such that $\frac{f_{i}\left( {\overline{x}}+\alpha _{k}d_{k}\right) -f_{i}\left( {\overline{x}}\right) }{\alpha _{k}}<0$, for any $k>k_{i}^{*}$. Let us set $k^{*}:=\max \left\{ k_{i}^{*}:i\in I\right\}$. This means that

$$\begin{aligned} f_{i}\left( {\overline{x}}+\alpha _{k}d_{k}\right) <f_{i}\left( {\overline{x}} \right) ,\quad \forall i\in I. \end{aligned}$$

(15)

Because by (11) ${\overline{x}}+\alpha _{k}d_{k}\in \Omega$, (15) is a contradiction to (9). Thus, (10) holds or, in other words, by (4), we have shown that

$$\begin{aligned} \left( \underset{i\in I}{\bigcup }\nabla f_{i}\left( {\overline{x}}\right) \right) ^{s-}\cap T\left( \Omega ;{\overline{x}}\right) =\varnothing . \end{aligned}$$

(16)

By assumption, the Abadie constraint qualification (ACQ) holds. Combining (6) and (16), we get

$$\begin{aligned} \left( \underset{i\in I}{\bigcup }\nabla f_{i}\left( {\overline{x}}\right) \right) ^{s-}\cap L\left( {\overline{x}}\right) =\varnothing . \end{aligned}$$

(17)

By the definition of the linearized cone (see Definition 6), (10) and (17) imply that the system (8) has no solution $d\in R^{n}$. $\square$

Lemma 12

Let ${\overline{x}}\in \Omega$ be a weak efficient solution in (SIMPVC). Further, we assume that the VC-Abadie constraint qualification (VC-ACQ) holds at ${\overline{x}}$ for (SIMPVC). Then, the system

$$\begin{aligned} \left\{ \begin{array}{c@{\quad }c@{\quad }c} \left\langle \nabla f_{i}\left( {\overline{x}}\right) ,d\right\rangle <0 &{} \text {for all} &{} i=1,...,p\text {,} \\ \left\langle \nabla g_{t}\left( {\overline{x}}\right) ,d\right\rangle \leqq 0 &{} \text {for all} &{} t\in T\left( {\overline{x}}\right) \text {, } \\ \left\langle \nabla h_{s}\left( {\overline{x}}\right) ,d\right\rangle =0 &{} \text {for all} &{} s\in S\text {,} \\ \left\langle \nabla H_{j}\left( {\overline{x}}\right) ,d\right\rangle =0 &{} \text {for all} &{} j\in J_{0+}\left( {\overline{x}}\right) \text {,} \\ \left\langle -\nabla H_{j}\left( {\overline{x}}\right) ,d\right\rangle \leqq 0 &{} \text {for all} &{} j\in J_{00}\left( {\overline{x}}\right) \cup J_{0-}\left( {\overline{x}}\right) \text {,} \\ \left\langle \nabla G_{j}\left( {\overline{x}}\right) ,d\right\rangle \leqq 0 &{} \text {for all} &{} j\in J_{00}\left( {\overline{x}}\right) \cup J_{+0}\left( {\overline{x}}\right) \end{array} \right. \end{aligned}$$

(18)

has no solution $d\in R^{n}$.

Now, we prove the Karush–Kuhn–Tucker necessary optimality conditions for weak efficiency of a feasible solution in (SIMPVC) to be its weak Pareto solution.

Theorem 13

(Karush–Kuhn–Tucker necessary optimality conditions). Let ${\overline{x}}\in \Omega$ be a weak efficient solution in (SIMPVC). Further, we assume that the Abadie constraint qualification (ACQ) holds at ${\overline{x}}$ for (SIMPVC) and the set

$$\begin{aligned}&\Gamma \left( {\overline{x}}\right) :=cone\left( \left\{ \nabla g_{t_{k}}( {\overline{x}}):t_{k}\in T\left( {\overline{x}}\right) \text {, } k=1,...,q\right\} \cup \right. \\&\quad \left. \left\{ -\nabla H_{j}({\overline{x}}):j\in J_{00}\left( {\overline{x}} \right) \cup J_{0-}\left( {\overline{x}}\right) \right\} \cup \left\{ \nabla G_{j}({\overline{x}}):j\in J_{+0}\left( {\overline{x}}\right) \right\} \right) \\&\quad +span\left( \left\{ \nabla h_{s_{m}}({\overline{x}}):s_{m}\in S,\text { } m=1,...,r\right\} \cup \left\{ \nabla H_{j}({\overline{x}}):j\in J_{0+}\left( {\overline{x}}\right) \right\} \right) \end{aligned}$$

is closed. Then, there exist integers $0\leqq q,r\leqq n+1$ and Lagrange multipliers ${\overline{\lambda }}_{i}\geqq 0$, $\sum _{i=1}^{p}{\overline{\lambda }}_{i}=1$, $\overline{\mu }_{t_{k}}\geqq 0$, $t_{k}\in T\left( {\overline{x}}\right)$, with ${\overline{\mu }}_{t_{k}}>0$ for $1\leqq k\leqq q$ , $\overline{\xi }_{s_{m}}\in R$, $s_{m}\in S$, $1\leqq m\leqq r$, ${\overline{\vartheta }}^{H}\in R^{w}$, ${\overline{\vartheta }}^{G}\in R^{w}$ such that the following conditions

$$\begin{aligned}&\sum _{i=1}^{p}{\overline{\lambda }}_{i}\nabla f_{i}({\overline{x}} )+\sum _{k=1}^{q}{\overline{\mu }}_{t_{k}}\nabla g_{t_{k}}({\overline{x}} )+\sum _{m=1}^{r}{\overline{\xi }}_{s_{m}}\nabla h_{s_{m}}({\overline{x}} )\nonumber \\&\qquad -\sum _{j=1}^{w}{\overline{\vartheta }}_{j}^{H}\nabla H_{j}({\overline{x}} )+\sum _{j=1}^{w}\overline{\vartheta }_{j}^{G}\nabla G_{j}({\overline{x}})=0 \text {,} \end{aligned}$$

(19)

$$\begin{aligned}&{\overline{\mu }}_{t}g_{t}({\overline{x}})=0\text {, }t\in T, \end{aligned}$$

(20)

$$\begin{aligned}&{\overline{\vartheta }}_{j}^{H}H_{j}\left( {\overline{x}}\right) =0\text {, }j\in J\text {,} \end{aligned}$$

(21)

$$\begin{aligned}&{\overline{\vartheta }}_{j}^{G}G_{j}\left( {\overline{x}}\right) =0\text {, }j\in J\text {,} \end{aligned}$$

(22)

$$\begin{aligned}&{\overline{\vartheta }}_{j}^{H}=0\text {, }j\in J_{+}\left( {\overline{x}}\right) \text {, }{\overline{\vartheta }}_{j}^{H}\geqq 0\text {, }j\in J_{00}\left( {\overline{x}}\right) \cup J_{0-}\left( {\overline{x}}\right) \text {, }{\overline{\vartheta }}_{j}^{H}\text { free, }j\in J_{0+}\left( {\overline{x}}\right) \text { ,}\nonumber \\ \end{aligned}$$

(23)

$$\begin{aligned}&{\overline{\vartheta }}_{j}^{G}=0\text {, }j\in J_{00}\left( {\overline{x}} \right) \cup J_{0+}\left( {\overline{x}}\right) \cup J_{0-}\left( {\overline{x}} \right) \cup J_{+-}\left( {\overline{x}}\right) \text {, }{\overline{\vartheta }} _{j}^{G}\geqq 0\text {, }j\in J_{+0}\left( {\overline{x}}\right) \quad \end{aligned}$$

(24)

hold.

Proof

By assumption, ${\overline{x}}\in \Omega$ is a weak Pareto solution in (SIMPVC) and the Abadie constraint qualification (ACQ) holds at ${\overline{x}}$ for (SIMPVC). We set

$$\begin{aligned} A= & {} \left\{ \nabla f_{i}({\overline{x}}):i=1,...,p\right\} \text {,} \\ B= & {} \left\{ \nabla g_{t_{k}}({\overline{x}}):t_{k}\in T\left( {\overline{x}} \right) ,\text { }k=1,...,q\right\} \cup \left\{ -\nabla H_{j}({\overline{x}} ):j\in J_{00}\left( {\overline{x}}\right) \cup J_{0-}\left( {\overline{x}} \right) \right\} \\&\quad \cup \left\{ \nabla G_{j}({\overline{x}}):j\in J_{+0}\left( {\overline{x}} \right) \right\} , \\ C= & {} \left\{ \nabla h_{s_{m}}({\overline{x}}):s_{m}\in S,\text { } m=1,...,r\right\} \cup \left\{ \nabla H_{j}({\overline{x}}):j\in J_{0+}\left( {\overline{x}}\right) \right\} \text {.} \end{aligned}$$

Hence, by Lemma 11, it follows that the system (8) has no solution $d\in R^{n}$. By assumption, the set $\Gamma \left( {\overline{x}}\right) =cone\left( B\right) +span\left( C\right)$ is closed. Then, by the semi-infinite version of Motzkin’s theorem of the alternative, it follows that $0\in conv\left( A\right) +cone\left( B\right) +span\left( C\right)$, that is,

$$\begin{aligned}&0\in conv\mathop {\bigcup }\limits _{i=1}^{p}\nabla f_{i}({\overline{x}})+cone\left( \mathop {\bigcup }\limits _{k=1}^{q}\left\{ \nabla g_{t_{k}}({\overline{x}}):t_{k}\in T\left( {\overline{x}}\right) \right\} \right. \nonumber \\&\quad \left. \cup \mathop {\bigcup }\limits _{j\in J_{00}\left( {\overline{x}}\right) \cup J_{0-}\left( {\overline{x}}\right) }\left( -\nabla H_{j}({\overline{x}})\right) \cup \mathop {\bigcup }\limits _{j\in J_{+0}\left( {\overline{x}}\right) }\nabla G_{j}( {\overline{x}})\right) \nonumber \\&\qquad + span\left( \mathop {\bigcup }\limits _{m=1}^{r}\left\{ \nabla h_{s_{m}}({\overline{x}} ):s_{m}\in S\right\} \cup \mathop {\bigcup }\limits _{j\in J_{0+}\left( {\overline{x}} \right) }\nabla H_{j}({\overline{x}})\right) \text {.} \end{aligned}$$

(25)

Thus, by (1) and (2), (25) gives

$$\begin{aligned}&0\in conv\mathop {\bigcup }\limits _{i=1}^{p}\nabla f_{i}({\overline{x}} )+cone\mathop {\bigcup }\limits _{k=1}^{q}\left\{ \nabla g_{t_{k}}({\overline{x}} ):t_{k}\in T\left( {\overline{x}}\right) \right\} \\&\quad +span\mathop {\bigcup }\limits _{m=1}^{r}\left\{ \nabla h_{s_{m}}({\overline{x}} ):s_{m}\in S\right\} \\&\quad + cone\mathop {\bigcup }\limits _{j\in J_{00}\left( {\overline{x}}\right) \cup J_{0-}\left( {\overline{x}}\right) }\left( -\nabla H_{j}({\overline{x}})\right) +span\mathop {\bigcup }\limits _{j\in J_{0+}\left( {\overline{x}}\right) }\nabla H_{j}( {\overline{x}})+cone\mathop {\bigcup }\limits _{j\in J_{+0}\left( {\overline{x}}\right) }\nabla G_{j}({\overline{x}})\text {.} \end{aligned}$$

In other words, there exist Lagrange multipliers $\overline{\lambda }\in R^{p}$, ${\overline{\mu }}\in R^{m}$, ${\overline{\xi }}\in R^{q}$, ${\overline{\vartheta }}^{H}\in R^{w}$ and $\overline{\vartheta }^{G}\in R^{w}$ such that the conditions (19)–(24) are fulfilled. $\square$

Remark 14

Note that the Karush–Kuhn–Tucker necessary optimality conditions proved in the paper are more general than the similar results established by Tung (2020). This is a consequence of, for example, the fact that they have been established for a more general semi-infinite multiobjective programming problem with vanishing constraints than in Tung (2020). In fact, we consider a semi-infinite multiobjective programming problem with vanishing constraint which is characterized by both an infinite number of inequality and equality constraints whereas a semi-infinite vector optimization problem considered in Tung (2020) is characterized by an infinite number of inequality constraints only.

Now, we generalize to the vectorial case the Karush–Kuhn–Tucker necessary optimality conditions established by Achtziger and Kanzow (2008) for a differentiable scalar optimization problem with vanishing constraints under the VC-ACQ assumption. Therefore, we call them the VC-Karush–Kuhn–Tucker necessary optimality conditions.

Theorem 15

(VC-Karush–Kuhn–Tucker necessary optimality conditions) Let ${\overline{x}}$ be a weak efficient solution in (SIMPVC). Further, we assume that the VC-Abadie constraint qualification (VC-ACQ) holds at ${\overline{x}}$ for (SIMPVC) and the set

$$\begin{aligned}&\Gamma _{VC}\left( {\overline{x}}\right) :=cone\left( \left\{ \nabla g_{t_{k}}( {\overline{x}}):t_{k}\in T\left( {\overline{x}}\right) \text {, } k=1,...,q\right\} \cup \right. \\&\quad \left. \left\{ -\nabla H_{j}({\overline{x}}):j\in J_{00}\left( {\overline{x}} \right) \cup J_{0-}\left( {\overline{x}}\right) \right\} \cup \left\{ \nabla G_{j}({\overline{x}}):j\in J_{00}\left( {\overline{x}}\right) \cup J_{+0}\left( {\overline{x}}\right) \right\} \right) \\&\quad +span\left( \left\{ \nabla h_{s_{m}}({\overline{x}}):s_{m}\in S,\text { } m=1,...,r\right\} \cup \left\{ \nabla H_{j}({\overline{x}}):j\in J_{0+}\left( {\overline{x}}\right) \right\} \right) . \end{aligned}$$

is closed. Then, there exist integers $0\leqq q,r\leqq n+1$ and Lagrange multipliers ${\overline{\lambda }}_{i}\geqq 0$, $\sum _{i=1}^{p}{\overline{\lambda }}_{i}=1$, $\overline{\mu }_{t_{k}}\geqq 0$, $t_{k}\in T\left( {\overline{x}}\right)$, with ${\overline{\mu }}_{t_{k}}>0$ for $1\leqq k\leqq q$ , $\overline{\xi }_{s_{m}}\in R$, $s_{m}\in S$, $1\leqq m\leqq r$, ${\overline{\vartheta }}^{H}\in R^{w}$, ${\overline{\vartheta }}^{G}\in R^{w}$ such that the following conditions

$$\begin{aligned}&\sum _{i=1}^{p}{\overline{\lambda }}_{i}\nabla f_{i}({\overline{x}} )+\sum _{k=1}^{q}{\overline{\mu }}_{t_{k}}\nabla g_{t_{k}}({\overline{x}} )+\sum _{m=1}^{r}{\overline{\xi }}_{s_{m}}\nabla h_{s_{m}}({\overline{x}} )-\sum _{j=1}^{w}{\overline{\vartheta }}_{j}^{H}\nabla H_{j}({\overline{x}} )\nonumber \\&\qquad +\sum _{j=1}^{w}\overline{\vartheta }_{j}^{G}\nabla G_{j}({\overline{x}})=0 \text {,} \end{aligned}$$

(26)

$$\begin{aligned}&{\overline{\mu }}_{t}g_{t}({\overline{x}})=0\text {, }t\in T({\overline{x}}), \end{aligned}$$

(27)

$$\begin{aligned}&{\overline{\vartheta }}_{j}^{H}H_{j}\left( {\overline{x}}\right) =0\text {, }j\in J\text {,} \end{aligned}$$

(28)

$$\begin{aligned}&{\overline{\vartheta }}_{j}^{G}G_{j}\left( {\overline{x}}\right) =0\text {, }j\in J\text {,} \end{aligned}$$

(29)

$$\begin{aligned}&{\overline{\vartheta }}_{j}^{H}=0\text {, }j\in J_{+}\left( {\overline{x}}\right) \text {, }{\overline{\vartheta }}_{j}^{H}\geqq 0\text {, }j\in J_{00}\left( {\overline{x}}\right) \cup J_{0-}\left( {\overline{x}}\right) \text {, }{\overline{\vartheta }}_{j}^{H}\text { free, }j\in J_{0+}\left( {\overline{x}}\right) \text { ,} \end{aligned}$$

(30)

$$\begin{aligned}&{\overline{\vartheta }}_{j}^{G}=0\text {, }j\in J_{0+}\left( {\overline{x}} \right) \cup J_{0-}\left( {\overline{x}}\right) \cup J_{+-}\left( {\overline{x}} \right) \text {, }\overline{\vartheta }_{j}^{G}\geqq 0\text {, }j\in J_{00}\left( {\overline{x}}\right) \cup J_{+0}\left( {\overline{x}}\right) \end{aligned}$$

(31)

hold.

Remark 16

Note that VC-Karush–Kuhn–Tucker necessary optimality conditions for (SIMPVC) established in Theorem 15 are weaker than the standard Karush–Kuhn–Tucker necessary optimality conditions for this vector optimization problem established in Theorem 13 (see Achtziger and Kanzow 2008).

Various stationarity concepts are widely studied in the literature and known to be important optimality conditions for optimization problems with vanishing constraints (see, for example, Dorsch et al. 2012; Hoheisel and Kanzow 2007; Hoheisel et al. 2012; Khare and Nath 2019; Kazemi and Kanzi 2018). Therefore, we now generalize one of such concepts of a stationary condition. Namely, we extend the definition of a so-called KKT condition given by Achtziger and Kanzow (2008) (see also Hoheisel and Kanzow 2008; Kazemi and Kanzi 2018 ) for a scalar optimization problem with vanishing constraint and also the concept of a S-stationary point given by Khare and Nath (2019) for a scalar optimization problem with vanishing constraint to the semi-infinite vectorial case. We also introduce the concept of a ”VC-S-stationary point” for the necessary optimality condition established in Theorem 15. Note that these stationary conditions differ only for the multipliers associated with the indices in $J_{00}\left( {\overline{x}}\right)$.

Definition 17

The feasible solution ${\overline{x}}\in \Omega$ is called a S-stationary point of (SIMPVC) iff there exist integers $1\leqq q,r\leqq n+1$ and Lagrange multipliers ${\overline{\lambda }}\in R^{p}$ , $\overline{\mu }\in R^{q}$, ${\overline{\xi }}\in R^{r}$, $\overline{ \vartheta }^{H}\in R^{w}$ and ${\overline{\vartheta }}^{G}\in R^{w}$ with ${\overline{\lambda }}\ge 0$, ${\overline{\mu }}\geqq 0$, ${\overline{\vartheta }} _{j}^{H}=0$, $j\in J_{+}\left( {\overline{x}}\right)$, ${\overline{\vartheta }} _{j}^{H}\geqq 0$, $j\in J_{00}\left( {\overline{x}}\right) \cup J_{0-}\left( {\overline{x}}\right)$, ${\overline{\vartheta }}_{j}^{H}$ free, $j\in J_{0+}\left( {\overline{x}}\right)$, $\overline{\vartheta }_{j}^{G}=0$, $j\in J_{00}\left( {\overline{x}}\right) \cup J_{0+}\left( {\overline{x}}\right) \cup J_{0-}\left( {\overline{x}}\right) \cup J_{+-}\left( {\overline{x}}\right)$, ${\overline{\vartheta }}_{j}^{G}\geqq 0$, $j\in J_{+0}\left( {\overline{x}} \right)$ such that

$$\begin{aligned}&\sum _{i=1}^{p}{\overline{\lambda }}_{i}\nabla f_{i}({\overline{x}} )+\sum _{k=1}^{q}{\overline{\mu }}_{t_{k}}\nabla g_{t_{k}}({\overline{x}} )+\sum _{m=1}^{r}{\overline{\xi }}_{s_{m}}\nabla h_{s_{m}}({\overline{x}} )\nonumber \\&\qquad -\sum _{j=1}^{w}{\overline{\vartheta }}_{j}^{H}\nabla H_{j}({\overline{x}} )+\sum _{j=1}^{w}\overline{\vartheta }_{j}^{G}\nabla G_{j}({\overline{x}})=0 \text {.} \end{aligned}$$

(32)

Definition 18

The feasible solution ${\overline{x}}\in \Omega$ is called a VC-S-stationary point of (SIMPVC) iff there exist integers $1\leqq q,r\leqq n+1$ and Lagrange multipliers ${\overline{\lambda }} \in R^{p}$, ${\overline{\mu }}\in R^{q}$, ${\overline{\xi }}\in R^{r}$, ${\overline{\vartheta }}^{H}\in R^{w}$ and ${\overline{\vartheta }}^{G}\in R^{w}$ with ${\overline{\lambda }}\ge 0$, ${\overline{\mu }}\geqq 0$, $\overline{ \vartheta }_{j}^{H}=0$, $j\in J_{+}\left( {\overline{x}}\right)$, ${\overline{\vartheta }}_{j}^{H}\geqq 0$, $j\in J_{00}\left( {\overline{x}}\right) \cup J_{0-}\left( {\overline{x}}\right)$, ${\overline{\vartheta }}_{j}^{H}$ free, $j\in J_{0+}\left( {\overline{x}}\right)$, ${\overline{\vartheta }}_{j}^{G}=0$, $j\in J_{0+}\left( {\overline{x}}\right) \cup J_{0-}\left( {\overline{x}}\right) \cup J_{+-}\left( {\overline{x}}\right)$, ${\overline{\vartheta }}_{j}^{G}\geqq 0$, $j\in J_{00}\left( {\overline{x}}\right) \cup J_{+0}\left( {\overline{x}} \right)$ such that

$$\begin{aligned}&\sum _{i=1}^{p}{\overline{\lambda }}_{i}\nabla f_{i}({\overline{x}} )+\sum _{k=1}^{q}{\overline{\mu }}_{t_{k}}\nabla g_{t_{k}}({\overline{x}} )+\sum _{m=1}^{r}{\overline{\xi }}_{s_{m}}\nabla h_{s_{m}}({\overline{x}} )\nonumber \\&\qquad -\sum _{j=1}^{w}{\overline{\vartheta }}_{j}^{H}\nabla H_{j}({\overline{x}} )+\sum _{j=1}^{w}\overline{\vartheta }_{j}^{G}\nabla G_{j}({\overline{x}})=0 \text {.} \end{aligned}$$

(33)

Remark 19

It is worth mentioning that when $p=1$, Definition 17 is the definition of a S-stationary point given by Achtziger and Kanzow (2008) (as a KT-condition), Khare and Nath (2019) for a differentiable scalar optimization problem with vanishing constraints. Moreover, it is also named “strongly stationary condition” (Hoheisel and Kanzow 2007; Kazemi and Kanzi 2018). The VC-S-stationary condition for differentiable scalar optimization problems with vanishing constraints can be found, for example, in Mishra et al. (2016).

Now, using the above concepts of stationary points, we formulate the necessary optimality conditions established in Theorems 13 and 15 in terms of the foregoing stationary points.

Theorem 20

(A Karush–Kuhn–Tucker type S-stationary condition) Let ${\overline{x}}$ be a weak efficient solution in (SIMPVC). Further, we assume that the Abadie constraint qualification with vanishing constraints (VC-ACQ) holds at ${\overline{x}}$ for (SIMPVC) and the set $\Gamma \left( {\overline{x}}\right)$ is closed. Then, ${\overline{x}}$ is a S-stationary point of (SIMPVC).

Theorem 21

(A VC-Karush–Kuhn–Tucker type VC-S-stationary condition) Let ${\overline{x}}$ be a weak efficient solution in (SIMPVC). Further, we assume that the VC-Abadie constraint qualification with vanishing constraints (VC-ACQ) holds at ${\overline{x}}$ for (SIMPVC) and the set $\Gamma _{VC}\left( {\overline{x}}\right)$ is closed. Then, ${\overline{x}}$ is a VC-S-stationary stationary point of (SIMPVC).

Now, we prove the sufficient optimality conditions for a feasible solution to be a weak Pareto solution (a Pareto solution) in the considered multiobjective programming problem (MPVC) with vanishing constraints under appropriate invexity hypotheses. Before proving this result, we define the following index sets:

$$\begin{aligned}&S^{+}\left( {\overline{x}}\right) :=\left\{ s\in S:{\overline{\xi }} _{s}>0\right\} \text {,} \\&S^{-}\left( {\overline{x}}\right) :=\left\{ s\in S:{\overline{\xi }} _{s}<0\right\} \text {,} \\&J_{G}\left( {\overline{x}}\right) :=J_{00}\left( {\overline{x}}\right) \cup J_{+0}\left( {\overline{x}}\right) \text {,} \\&J_{0+}^{H+}\left( {\overline{x}}\right) :=\left\{ j\in J_{0+}\left( {\overline{x}}\right) :{\overline{\vartheta }}_{j}^{H}\geqq 0\right\} \text {,} \\&J_{0+}^{H-}\left( {\overline{x}}\right) :=\left\{ j\in J_{0+}\left( {\overline{x}}\right) :{\overline{\vartheta }}_{j}^{H}<0\right\} \text {,} \\&J_{H}^{+}\left( {\overline{x}}\right) :=J_{00}\left( {\overline{x}}\right) \cup J_{0-}\left( {\overline{x}}\right) \cup J_{0+}^{H+}\left( {\overline{x}}\right) \text {,} \\&J_{0+}^{G+}\left( {\overline{x}}\right) :=\left\{ j\in J_{0+}\left( {\overline{x}}\right) :{\overline{\vartheta }}_{j}^{G}>0\right\} \text {.} \end{aligned}$$

Theorem 22

Let ${\overline{x}}\in \Omega$ be a S-stationary point in (SIMPVC) and let the following assumptions be satisfied:

• (a) $\Omega _{G^{+}}\left( {\overline{x}}\right) :=\underset{j\in J_{+0}\left( {\overline{x}}\right) }{\bigcup }\left\{ x\in \Omega \backslash \left\{ {\overline{x}}\right\} :G_{j}\left( x\right) >0\right\} =\varnothing$ or $J_{+0}^{G+}\left( {\overline{x}}\right) =\varnothing$,

• (b) $J_{0+}^{H-}\left( {\overline{x}}\right) =\varnothing$.

Further, we assume that each objective function $f_{i}$, $i\in I$, is invex at ${\overline{x}}$ on $\Omega$ with respect to $\eta$, each inequality constraint $g_{t_{k}}$, $t_{k}\in T\left( {\overline{x}}\right)$, $k=1,...,m$ , is (strictly) invex at ${\overline{x}}$ on $\Omega$ with respect to $\eta$ , each function $h_{s_{m}}$, $s_{m}\in S^{+}\left( {\overline{x}}\right)$, is invex at ${\overline{x}}$ on $\Omega$ with respect to $\eta$, each function $-h_{s_{m}}$, $s_{m}\in S^{-}\left( {\overline{x}}\right)$ is invex at ${\overline{x}}$ on $\Omega$ with respect to $\eta$, each function $-H_{j}$, $t\in J_{H}^{+}\left( {\overline{x}}\right)$, is invex at ${\overline{x}}$ on $\Omega$ with respect to $\eta$, each function $H_{j}$, $J_{0+}^{-}\left( {\overline{x}}\right)$, is invex at ${\overline{x}}$ on $\Omega$ with respect to $\eta$, each constraint $G_{j}$, $j\in J_{+0}\left( {\overline{x}}\right)$ , is invex at ${\overline{x}}$ on $\Omega$ with respect to $\eta$. Then ${\overline{x}}$ is a weak Pareto solution (a Pareto solution) of (SIMPVC).

Proof

We proceed by contradiction. Suppose, contrary to the result, that ${\overline{x}}$ is a weak Pareto solution of (SIMPVC). Hence, by Definition 3, there exists ${\widetilde{x}}\in \Omega$ such that

$$\begin{aligned} f\left( {\widetilde{x}}\right) <f\left( {\overline{x}}\right) . \end{aligned}$$

(34)

Using invexity hypotheses, by Definition 2, the inequalities

$$\begin{aligned}&f_{i}(x)-f_{i}({\overline{x}})\geqq \nabla f_{i}({\overline{x}})\eta \left( x, {\overline{x}}\right) \text {, }\quad i\in I\text {,} \end{aligned}$$

(35)

$$\begin{aligned}&g_{t_{k}}(x)-g_{t_{k}}({\overline{x}})\geqq \nabla g_{t_{k}}({\overline{x}})\eta \left( x,{\overline{x}}\right) \text {, }t_{k}\in T\left( {\overline{x}} \right) \text {, }\quad k=1,..,m, \end{aligned}$$

(36)

$$\begin{aligned}&h_{s_{m}}(x)-h_{s_{m}}({\overline{x}})\geqq \nabla h_{s_{m}}({\overline{x}})\eta \left( x,{\overline{x}}\right) ,\text { }s_{m}\in S^{+}\left( {\overline{x}} \right) \text {,} \end{aligned}$$

(37)

$$\begin{aligned}&-h_{s_{m}}(x)+h_{s_{m}}({\overline{x}})\geqq -\nabla h_{s_{m}}({\overline{x}} )\eta \left( x,{\overline{x}}\right) ,\text { }s_{m}\in S^{-}\left( {\overline{x}} \right) \text {,} \end{aligned}$$

(38)

$$\begin{aligned}&-H_{j}(x)+H_{j}({\overline{x}})\geqq -\nabla H_{j}({\overline{x}})\eta \left( x, {\overline{x}}\right) ,\text { }j\in J_{H}^{+}\left( {\overline{x}}\right) \text {, } \end{aligned}$$

(39)

$$\begin{aligned}&H_{j}(x)-H_{j}({\overline{x}})\geqq \nabla H_{j}({\overline{x}})\eta \left( x, {\overline{x}}\right) ,\text { }j\in J_{0+}^{-}\left( {\overline{x}}\right) \text { ,} \end{aligned}$$

(40)

$$\begin{aligned}&G_{j}(x)-G_{j}({\overline{x}})\geqq \nabla G_{j}({\overline{x}})\eta \left( x, {\overline{x}}\right) \text {, }j\in J_{+0}\left( {\overline{x}}\right) \end{aligned}$$

(41)

hold for all $x\in \Omega$. Therefore, they are also fulfilled for $x= {\widetilde{x}}\in \Omega$. Using ${\widetilde{x}}$, ${\overline{x}}\in \Omega$ together with the Karush–Kuhn–Tucker necessary optimality conditions (27)–(31), we get, respectively,

$$\begin{aligned} g_{t_{k}}({\widetilde{x}})\le 0= & {} g_{t_{k}}({\overline{x}})\text {, }t_{k}\in T\left( {\overline{x}}\right) \text {, }k=1,..,m\text {,} \end{aligned}$$

(42)

$$\begin{aligned} h_{s_{m}}({\widetilde{x}})= & {} h_{s_{m}}({\overline{x}}),\text { }s_{m}\in S^{+}\left( {\overline{x}}\right) \cup S^{-}\left( {\overline{x}}\right) \text {.} \end{aligned}$$

(43)

From assumption b), it follows that $H_{j}({\widetilde{x}})\geqq 0$, ${\overline{\vartheta }}_{j}^{H}<0$, $j\in J_{0}^{H-}\left( {\overline{x}}\right) =\varnothing$. Thus,

$$\begin{aligned} \left. \begin{array}{c} H_{j}({\widetilde{x}})\geqq 0\text {, }\overline{\vartheta }_{j}^{H}=0\text {, } j\in J_{+}\left( {\overline{x}}\right) \\ H_{j}({\widetilde{x}})\geqq 0\text {, }\overline{\vartheta }_{j}^{H}\geqq 0 \text {, }j\in J_{H}^{+}\left( {\overline{x}}\right) \end{array} \right\} \Longrightarrow -\sum _{j=1}^{w}\overline{\vartheta }_{j}^{H}H_{j}( {\widetilde{x}})\leqq 0\text {.} \end{aligned}$$

(44)

Using ${\widetilde{x}}\in \Omega$ together with assumption a), we have

$$\begin{aligned} \left. \begin{array}{c} (G_{j}({\widetilde{x}})\leqq 0\text {, }\overline{\vartheta }_{j}^{G}\geqq 0 \text { }j\in J_{+0}\left( {\overline{x}}\right) \text { or }j\in J_{+0}^{G+}\left( {\overline{x}}\right) =\varnothing ) \\ G_{j}\left( {\widetilde{x}}\right) \in R\text {, }{\overline{\vartheta }} _{j}^{G}=0\text {, }j\in J_{00}\left( {\overline{x}}\right) \cup J_{0+}\left( {\overline{x}}\right) \cup J_{0-}\left( {\overline{x}}\right) \cup J_{+-}\left( {\overline{x}}\right) \end{array} \right\} \nonumber \\ \Longrightarrow \sum _{j=1}^{w}\overline{\vartheta }_{j}^{G}G_{j}( {\widetilde{x}})\leqq 0\text {.} \end{aligned}$$

(45)

Thus, (44) and (45) together with the Karush–Kuhn–Tucker necessary optimality conditions (28) and (29) yield

$$\begin{aligned} -\sum _{j=1}^{w}\overline{\vartheta }_{j}^{H}H_{j}({\widetilde{x}})\leqq -\sum _{j=1}^{w}\overline{\vartheta }_{j}^{H}H_{j}({\overline{x}})\text {,} \end{aligned}$$

(46)

$$\begin{aligned} \sum _{j=1}^{w}{\overline{\vartheta }}_{j}^{G}G_{j}({\widetilde{x}})\leqq \sum _{j=1}^{w}{\overline{\vartheta }}_{j}^{G}G_{j}({\overline{x}}). \end{aligned}$$

(47)

Multiplying (39)–(41) by the corresponding Lagrange multipliers, adding both sides of the resulting inequalities and then using (46) and (47), we obtain, respectively,

$$\begin{aligned} -\sum _{j=1}^{w}{\overline{\vartheta }}_{j}^{H}\nabla H_{j}({\overline{x}})\eta \left( {\widetilde{x}},{\overline{x}}\right) \leqq 0\text {,} \end{aligned}$$

(48)

$$\begin{aligned} \sum _{j=1}^{w}{\overline{\vartheta }}_{j}^{G}\nabla G_{j}({\overline{x}})\eta \left( {\widetilde{x}},{\overline{x}}\right) \leqq 0\text {.} \end{aligned}$$

(49)

Combining (34)–(38) and (42)–(43), respectively, then multiplying the resulting inequalities by the corresponding Lagrange multipliers, taking into account Lagrange multipliers equal to 0, adding both sides of the resulting inequalities and combining some of the resulting inequalities with (48) and (49), we get that the inequality

$$\begin{aligned}&\left[ \sum _{k=1}^{p}{\overline{\lambda }}_{k}\nabla f_{k}({\overline{x}})+\sum _{ \text { }k=1}^{m}\overline{\mu }_{t_{k}}\nabla g_{t_{k}}({\overline{x}} )+\sum _{m=1}^{r}\overline{\xi }_{s_{m}}\nabla h_{s_{m}}({\overline{x}} )\right. \\&\quad \left. -\sum _{j=1}^{w}\overline{\vartheta }_{j}^{H}\nabla H_{j}( {\overline{x}})+\sum _{j=1}^{w}{\overline{\vartheta }}_{j}^{G}\nabla G_{j}( {\overline{x}})\right] \eta \left( {\widetilde{x}},{\overline{x}}\right) <0 \end{aligned}$$

holds, which is a contradiction to the Karush–Kuhn–Tucker necessary optimality condition (26). The proof of Pareto optimality is similar and, therefore, it is omitted in the paper. Thus, the proof of this theorem is completed. $\square$

In order to illustrate the results established in this section, we consider the following example of a nonconvex differentiable semi-infinite vector optimization problem with vanishing constraints.

Example 23

Consider the following differentiable semi-infinite multiobjective programming problem with vanishing constraints

$$\begin{aligned} \begin{array}{cll} &{}f(x)=\left( \ln \left( x_{1}^{2}+x_{2}^{2}+1\right) \text { , }\arctan \left( x_{1}\right) -\arctan \left( x_{2}\right) \right) \rightarrow \min \\ &{}g_{t}(x)=\arctan \left( x_{1}\right) -\arctan \left( x_{2}\right) +1-t\leqq 0 \text {, }t\in T={\mathbb {N}} \\ &{}H_{1}\left( x\right) =\arctan \left( x_{1}\right) -\arctan \left( x_{2}\right) \geqq 0\text {,} \\ &{}G_{1}\left( x\right) H_{1}\left( x\right) =\left( x_{1}^{2}+x_{2}^{2}\right) \left( \arctan \left( x_{1}\right) -\arctan \left( x_{2}\right) \right) \leqq 0\text {.} \end{array} \end{aligned}$$

(SIMPVC1)

Note that $\Omega =\left\{ \left( x_{1},x_{2}\right) \in R^{2}:\arctan \left( x_{1}\right) -\arctan \left( x_{2}\right) =0\text { }\wedge \right.$

$\ \left. \left( x_{1}^{2}+x_{2}^{2}\right) \left( \arctan \left( x_{1}\right) -\arctan \left( x_{2}\right) \right) \leqq 0\right\}$ and ${\overline{x}}=\left( 0,0\right)$ is such a feasible solution at which the Karush–Kuhn–Tucker necessary optimality conditions (19)–(24) are satisfied. Indeed, if we set ${\overline{\lambda }}=\left( \overline{ \lambda }_{1},{\overline{\lambda }}_{2}\right)$, ${\overline{\lambda }}_{1}\in R_{+}$, ${\overline{\lambda }}_{2}=1$, ${\overline{\mu }}_{1}=1$, ${\overline{\vartheta }}_{1}^{H}=2$ and $\overline{\vartheta }_{1}^{G}\in R_{+}$, then the Karush–Kuhn–Tucker necessary optimality conditions (19)–(24 ) are fulfilled with these Lagrange multipliers. Further, it can be shown, by Definition 2, that all functions constituting (SIMPVC1) are invex at ${\overline{x}}$ on $\Omega$ with respect to the same function $\eta :\Omega \times \Omega \rightarrow R^{2}$ defined by

$$\begin{aligned} \eta \left( x,{\overline{x}}\right) =\left[ \begin{array}{c} \arctan \left( x_{1}\right) -\arctan \left( {\overline{x}}_{1}\right) \\ \arctan \left( x_{2}\right) -\arctan \left( {\overline{x}}_{2}\right) \end{array} \right] \text {.} \end{aligned}$$

Further, note that $J_{00}\left( {\overline{x}}\right) =\left\{ 1\right\}$ and, moreover, both assumptions a) and b) in Theorem 22 are satisfied. Since all hypotheses of Theorem 22 are fulfilled, ${\overline{x}} =\left( 0,0\right)$ is a weak Pareto solution of (SIMPVC1).

Remark 24

Note that it is not possible to prove weakly efficiency of ${\overline{x}} =\left( 0,0\right)$ in (SIMPVC1) considered in Example 23 under convexity hypotheses. This is a consequence of the fact that not all functions constituting (SIMPVC1) are convex. However, the optimality criteria established in the paper are applicable in the considered case, since the functions involved in (SIMPVC1) are invex with respect to the same function $\eta$, for example, with respect to that one given in Example 23. As it follows even from Example 23, in fact, optimality criteria established in the paper are applicable for a larger class of differentiable semi-infinite multiobjective programming problems with vanishing constraints than the class of convex ones.

Now we give the example of a differentiable semi-infinite multiobjective programming problem with vanishing constraints for which the sufficient optimality conditions for efficiency in vector optimization problems of such a type actually existing in the literature fail.

Example 25

Consider the following differentiable semi-infinite multiobjective programming problem with vanishing constraints

$$\begin{aligned} \begin{array}{cll} &{}f(x)=\left( \ln \left( x_{1}^{2}+x_{2}^{2}+1\right) \text { , } x_{1}^{2}+x_{2}^{2}+10x_{2}^{3}+x_{2}\right) \rightarrow \min \\ &{}g_{t}(x)=x_{1}^{3}+x_{1}-10x_{2}^{3}-x_{2}+1-t\leqq 0\text {, }t\in T= {\mathbb {N}}\text {,} \\ &{}H_{1}\left( x\right) =\ln \left( x_{1}^{2}+x_{2}^{2}+1\right) \geqq 0\text {,} \\ &{}G_{1}\left( x\right) H_{1}\left( x\right) =-\left( x_{1}^{3}+x_{1}\right) \ln \left( x_{1}^{2}+x_{2}^{2}+1\right) \leqq 0\text {.} \end{array} \end{aligned}$$

(SIMPVC2)

Then, we have that $\Omega =\left\{ \left( x_{1},x_{2}\right) \in R^{2}:x_{1}^{3}+x_{1}-10x_{2}^{3}-x_{2}+1-t\leqq 0\text {, }t\in T={\mathbb {N}}\text { }\wedge \text { }\right.$ $\left. \ln \left( x_{1}^{2}+x_{2}^{2}+1\right) \geqq 0\text { }\wedge \text { }-\left( x_{1}^{3}+x_{1}\right) \ln \left( x_{1}^{2}+x_{2}^{2}+1\right) \leqq 0\right\}$ and ${\overline{x}}=\left( 0,0\right)$ is such a feasible solution at which the Karush–Kuhn–Tucker necessary optimality conditions (19)–(24) are satisfied. Further, note that the inequality constraint functions $g_{t}$, $t\in T={\mathbb {N}}$, are invex because they have no stationary points (see Ben-Israel and Mond 1986). However, the constraint functions $g_{t}$, $t\in T={\mathbb {N}}$, are not quasi-convex. In fact, if we take $x=\left( 2,1\right)$ and ${\overline{x}}=\left( 0,0\right)$ , then $g_{t}\left( x\right) -g_{t}\left( {\overline{x}}\right) <0$ but $\nabla g_{t}\left( {\overline{x}}\right) \left( x-{\overline{x}}\right) >0$ for each $t\in T={\mathbb {N}}$, so that $g_{t}$, $t\in T={\mathbb {N}}$, are not quasi-convex. This means that it is not possible to use the sufficient conditions established in Tung (2020) in order to find (weak) Pareto solutions in (SIMPVC2). Now, we show that the sufficient optimality conditions established in this paper are applicable for such nonconvex vector optimization problems. In fact, the objective function is strictly invex at ${\overline{x}}$ on $\Omega$ and all constraints functions are invex at ${\overline{x}}$ on $\Omega$ with respect to the same function $\eta :\Omega \times \Omega \rightarrow R^{2}$ defined by

$$\begin{aligned} \eta \left( x,{\overline{x}}\right) =\left[ \begin{array}{c} x_{1}^{3}+x_{1}-\left( {\overline{x}}_{1}^{3}+{\overline{x}}_{1}\right) \\ 10x_{2}^{3}+x_{2}-\left( 10{\overline{x}}_{2}^{3}+{\overline{x}}_{2}\right) \end{array} \right] . \end{aligned}$$

Further, note that $J_{00}\left( {\overline{x}}\right) =\left\{ 1\right\}$ and, therefore, both assumptions a) and b) in Theorem 22 are satisfied. Since all hypotheses of Theorem 22 are fulfilled, ${\overline{x}}=\left( 0,0\right)$ is a Pareto solution in (SIMPVC2).

As it follows even from this example, the sufficient conditions for (weakly) efficiency established in the paper are applicable also for some of differentiable semi-infinite multiobjective programming problems with vanishing constraints for which the sufficient optimality conditions established in Tung (2020) fail.

3 Mond–Weir duality

In this section, we formulate two vector dual problems in the sense of Mond–Weir related to the considered differentiable semi-infinite multiobjective programming problem (SIMPVC) with vanishing constraints.

For $x\in \Omega$, we define the following vector dual problem in the sense of Mond–Weir related to the considered semi-infinite vector optimization problem (SIMPVC) with vanishing constraints as follows:

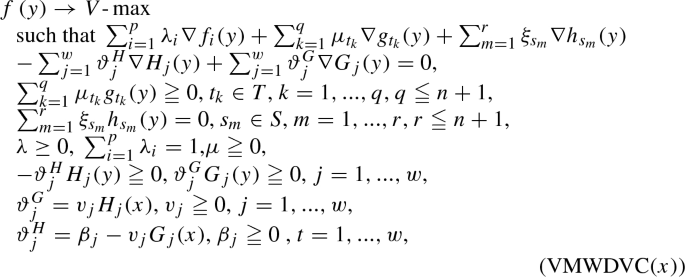
where all functions are defined in the similar way as for (SIMPVC).

Let

$$\begin{aligned} Q\left( x\right) =\left\{ \left( y,\lambda ,\mu ,\xi ,\vartheta ^{H},\vartheta ^{G},v,\beta \right) :\text {verifying the constraints of (VMWDVC}\left( x\right) \text {)}\right\} \end{aligned}$$

be the set of all feasible solutions in (VMWDVC$\left( x\right)$). Further, we define the set $Y\left( x\right)$ as follows: $Y\left( x\right) =\left\{ y\in X:\left( y,\lambda ,\mu ,\xi ,\vartheta ^{H},\vartheta ^{G},v,\beta \right) \in Q\left( x\right) \right\}$.

Remark 26

In the Mond–Weir dual problem (VMWDVC$\left( x\right)$) given above, the significance of $v_{j}$ and $\beta _{j}$ is the same as the one in Theorem 1 (Achtziger and Kanzow 2008).

Now, on the line Hu et al. (2019), we define the following vector dual problem in the sense of Mond–Weir related to the considered vector optimization problem (SIMPVC) with vanishing constraints as follows:

where the set Q of all feasible solutions in (VC-VMWDVC) is defined by $Q=\bigcap \nolimits _{x\in \Omega }Q\left( x\right)$. Further, let us define the set $Y_{p}$ by $Y=\left\{ y\in X:\left( y,\lambda ,\mu ,\xi ,\vartheta ^{H},\vartheta ^{G},v,\beta \right) \in Q\right\}$.

Theorem 27

(Weak duality): Let x and $\left( y,\lambda ,\mu ,\xi ,\vartheta ^{H},\vartheta ^{G},v,\beta \right)$ be any feasible solutions for (SIMPVC) and (VC-VMWDVC), respectively. Further, we assume that each objective function $f_{i}$, $i\in I$, is invex at y on $\Omega \cup Y$ with respect to $\eta$, each inequality constraint $g_{t_{k}}$, $t_{k}\in T$, $k=1,...,q$, is invex at y on $\Omega \cup Y$ with respect to $\eta$, $g_{t_{k}}$, $t_{k}\in T$, $k=1,...,m$, is invex at y on $\Omega \cup Y$ with respect to $\eta$, each function $h_{s_{m}}$, $s_{m}\in S^{+}\left( x\right)$, is invex at y on $\Omega \cup Y$ with respect to $\eta$, each function $-h_{s_{m}}$, $s_{m}\in S^{-}\left( x\right)$ is invex at y on $\Omega \cup Y$ with respect to $\eta$, each function $-H_{j}$, $t\in J_{H}^{+}\left( x\right)$, is invex at y on $\Omega \cup Y$ with respect to $\eta$, each function $H_{j}$, $J_{0+}^{-}\left( x\right)$ , is invex at y on $\Omega \cup Y$ with respect to $\eta$, each constraint $G_{j}$, $j\in J_{+0}\left( x\right)$, is invex at y on $\Omega \cup Y$ with respect to $\eta$. Then, $f\left( x\right) \nless f\left( y\right)$.

Proof

We proceed by contradiction. Suppose, contrary to the result, that

$$\begin{aligned} f\left( x\right) <f\left( y\right) . \end{aligned}$$

(50)

Since $\lambda \ge 0$, (50) gives

$$\begin{aligned} \sum _{i=1}^{p}\lambda _{i}\nabla f_{i}(x)<\sum _{i=1}^{p}\lambda _{i}\nabla f_{i}\left( y\right) . \end{aligned}$$

(51)

Using invexity hypotheses, by Definition 2, the inequalities

$$\begin{aligned}&f_{i}(x)-f_{i}(y)\geqq \nabla f_{i}(y)\eta \left( x,y\right) \text {, } i\in I\text {,} \end{aligned}$$

(52)

$$\begin{aligned}&g_{t_{k}}(x)-g_{t_{k}}(y)\geqq \nabla g_{t_{k}}(y)\eta \left( x,y\right) \text {, }t_{k}\in T\text {, }k=1,..,m, \end{aligned}$$

(53)

$$\begin{aligned}&h_{s_{m}}(x)-h_{s_{m}}(y)\geqq \nabla h_{s_{m}}(y)\eta \left( x,y\right) , \text { }s_{m}\in S^{+}\left( y\right) \text {,} \end{aligned}$$

(54)

$$\begin{aligned}&-h_{s_{m}}(x)+h_{s_{m}}(y)\geqq -\nabla h_{s_{m}}(y)\eta \left( x,y\right) , \text { }s_{m}\in S^{-}\left( y\right) \text {,} \end{aligned}$$

(55)

$$\begin{aligned}&-H_{j}(x)+H_{j}(y)\geqq -\nabla H_{j}(y)\eta \left( x,y\right) ,\text { }j\in J_{H}^{+}\left( x\right) \text {,} \end{aligned}$$

(56)

$$\begin{aligned}&H_{j}(x)-H_{j}(y)\geqq \nabla H_{j}({\overline{x}})\eta \left( x,y\right) , \text { }j\in J_{0+}^{-}\left( x\right) \text {,} \end{aligned}$$

(57)

$$\begin{aligned}&G_{j}(x)-G_{j}(y)\geqq \nabla G_{j}({\overline{x}})\eta \left( x,y\right) \text {, }j\in J_{+0}\left( x\right) \end{aligned}$$

(58)

hold. By $x\in \Omega$ and $\left( y,\lambda ,\mu ,\xi ,\vartheta ^{H},\vartheta ^{G},v,\beta \right) \in Q$, we have, respectively,

$$\begin{aligned}&\sum _{k=1}^{q}\mu _{t_{k}}g_{t_{k}}(x)\leqq \sum _{k=1}^{q}\mu _{t_{k}}g_{t_{k}}(y)\text {,} \end{aligned}$$

(59)

$$\begin{aligned}&\sum _{i=1}^{r}\xi _{s_{m}}h_{s_{m}}(x)\leqq \sum _{i=1}^{r}\xi _{s_{m}}h_{s_{m}}(y)\text {,} \end{aligned}$$

(60)

$$\begin{aligned}&\left. \begin{array}{c} H_{j}(x)>0\text {, }\vartheta _{j}^{H}=\beta _{j}-v_{j}G_{j}(x)\geqq 0\text {, }j\in J_{+}\left( x\right) \\ H_{j}(x)=0\text {, }\vartheta _{j}^{H}=\beta _{j}-v_{j}G_{j}(x)\in R\text {, } j\in J_{0}\left( x\right) \end{array} \right\} \Longrightarrow \sum _{j=1}^{w}\vartheta _{j}^{H}H_{j}(x)\geqq 0 \text {,} \nonumber \\\end{aligned}$$

(61)

$$\begin{aligned}&\left. \begin{array}{c} G_{j}(x)>0\text {, }\vartheta _{j}^{G}=v_{j}H_{j}(x)=0\text {, }j\in J_{0+}\left( x\right) \\ G_{j}(x)=0\text {, }\vartheta _{j}^{G}=v_{j}H_{j}(x)=0\text {, }j\in J_{00}\left( x\right) \\ G_{j}\left( x\right)<0\text {, }\vartheta _{j}^{G}=v_{j}H_{j}(x)=0\text {, } j\in J_{0-}\left( x\right) \\ G_{j}(x)=0\text {, }\vartheta _{j}^{G}=v_{j}H_{j}(x)\geqq 0\text {, }j\in J_{+0}\left( x\right) \\ G_{j}(x)<0\text {, }\vartheta _{j}^{G}=v_{j}H_{j}(x)\geqq 0\text {, }j\in J_{+-}\left( x\right) \end{array} \right\} \Longrightarrow \sum _{j=1}^{w}\vartheta _{j}^{G}G_{j}(x)\leqq 0 \text {.} \end{aligned}$$

(62)

Multiplying (52)–(58) by the corresponding Lagrange multipliers and then adding both sides of the resulting inequalities, we get, respectively,

$$\begin{aligned}&\sum _{k=1}^{p}\lambda _{k}\nabla f_{k}(x)-\sum _{k=1}^{p}\lambda _{k}\nabla f_{k}\left( y\right) \geqq \sum _{k=1}^{p}\lambda _{k}\nabla f_{k}\left( y\right) \eta \left( x,y\right) \text {,} \end{aligned}$$

(63)

$$\begin{aligned}&\sum _{k=1}^{q}\mu _{t_{k}}g_{t_{k}}(x)-\sum _{k=1}^{q}\mu _{t_{k}}g_{t_{k}}(y)\geqq \sum _{k=1}^{q}\mu _{t_{k}}\nabla g_{t_{k}}(y)\eta \left( x,y\right) \text {,} \end{aligned}$$

(64)

$$\begin{aligned}&\sum _{m=1}^{r}\xi _{s_{m}}h_{s_{m}}(x)-\sum _{m=1}^{r}\xi _{s_{m}}h_{s_{m}}(y)\geqq \sum _{m=1}^{r}\xi _{s_{m}}\nabla h_{s_{m}}(y)\eta \left( x,y\right) \text {,} \end{aligned}$$

(65)

$$\begin{aligned}&-\sum _{j=1}^{w}\vartheta _{j}^{H}H_{j}(x)+\sum _{j=1}^{w}\vartheta _{j}^{H}H_{j}(y)\geqq -\sum _{j=1}^{w}\vartheta _{j}^{H}\nabla H_{j}(y)\eta \left( x,y\right) \text {,} \end{aligned}$$

(66)

$$\begin{aligned}&\sum _{j=1}^{w}\vartheta _{j}^{G}G_{j}(x)-\sum _{j=1}^{w}{\overline{\vartheta }} _{j}^{G}G_{j}(y)\geqq \sum _{j=1}^{w}\vartheta _{j}^{G}\nabla G_{j}(y)\eta \left( x,y\right) \text {.} \end{aligned}$$

(67)

Hence, using again $\left( y,\lambda ,\mu ,\xi ,\vartheta ^{H},\vartheta ^{G},v,\beta \right) \in Q$ together with (61) and (62), we get, respectively,

$$\begin{aligned}&-\sum _{j=1}^{w}\vartheta _{j}^{H}H_{j}(x)\leqq -\sum _{j=1}^{w}\vartheta _{j}^{H}H_{j}(y)\text {,} \end{aligned}$$

(68)

$$\begin{aligned}&\sum _{j=1}^{w}\vartheta _{j}^{G}G_{j}(x)\leqq \sum _{j=1}^{w}\vartheta _{j}^{G}G_{j}(y)\text {.} \end{aligned}$$

(69)

Combining (51), (59), (60), (63)–(67), (68) and (69), we get that the inequality

$$\begin{aligned}&\left[ \sum _{k=1}^{p}\lambda _{k}\nabla f_{k}\left( y\right) +\sum _{k=1}^{q}\mu _{t_{k}}\nabla g_{t_{k}}(y)+\sum _{i=1}^{r}\xi _{s_{m}}\nabla h_{s_{m}}(y)-\right. \\&\quad \left. \sum _{j=1}^{w}\vartheta _{j}^{H}\nabla H_{j}(y)+\sum _{j=1}^{w}\vartheta _{j}^{G}\nabla G_{j}(y)\right] \eta \left( x,y\right) <0 \end{aligned}$$

holds, contradicting the feasibility of $\left( y,\lambda ,\mu ,\xi ,\vartheta ^{H},\vartheta ^{G},v,\beta \right)$ in (VC-VMWDVC). This completes the proof of this theorem. $\square$

If the stronger assumptions are imposed on the functions constituting (SIMPVC), then the following result is true:

Theorem 28

(Weak duality): Let x and $\left( y,\lambda ,\mu ,\xi ,\vartheta ^{H},\vartheta ^{G},v,\beta \right)$ be feasible any feasible solutions in (SIMPVC) and (VC-VMWDVC), respectively. Further, we assume that each objective function $f_{i}$, $i\in I$, is strictly invex at y on $\Omega \cup Y$ with respect to $\eta$, each inequality constraint $g_{t_{k}}$, $t_{k}\in T$, $k=1,...,q$, is invex at y on $\Omega \cup Y$ with respect to $\eta$, $g_{t_{k}}$, $t_{k}\in T$, $k=1,...,m$, is invex at y on $\Omega \cup Y$ with respect to $\eta$, each function $h_{s_{m}}$, $s_{m}\in S^{+}\left( y\right)$, is invex at y on $\Omega \cup Y$ with respect to $\eta$, each function $-h_{s_{m}}$, $s_{m}\in S^{-}\left( y\right)$ is invex at y on $\Omega \cup Y$ with respect to $\eta$, each function $-H_{j}$, $t\in J_{H}^{+}\left( x\right)$ , is invex at y on $\Omega \cup Y$ with respect to $\eta$, each function $H_{j}$, $J_{0+}^{-}\left( x\right)$, is invex at y on $\Omega \cup Y$ with respect to $\eta$, each constraint $G_{j}$, $j\in J_{+0}\left( x\right)$, is invex at y on $\Omega \cup Y$ with respect to $\eta$. Then, $f\left( x\right) \nleqslant f\left( y\right)$.

Theorem 29

(Strong duality): Let ${\overline{x}}\in \Omega$ be a (weak) Pareto solution of (SIMPVC) and a suitable constraint qualification (for example, the VC-ACQ constraint qualification) be satisfied at ${\overline{x}}$. Then, there exist Lagrange multipliers ${\overline{\lambda }}\in R^{p}$, ${\overline{\mu }}\in R^{m}$, ${\overline{\xi }} \in R^{q}$, ${\overline{\vartheta }}^{H}\in R^{w}$, ${\overline{\vartheta }} ^{G}\in R^{w}$ and ${\overline{v}}\in R^{w}$, ${\overline{\beta }}\in R^{w}$ such that $\left( {\overline{x}},{\overline{\lambda }},\overline{\mu },{\overline{\xi }},{\overline{\vartheta }}^{H},\overline{\vartheta }^{G},{\overline{v}}, {\overline{\beta }}\right)$ is feasible in (VC-VMWDVC). If also all hypotheses of the weak duality theorem (that is, Theorem 27 (Theorem 28)) are satisfied, then $\left( {\overline{x}},{\overline{\lambda }},{\overline{\mu }}, \overline{\xi },{\overline{\vartheta }}^{H},{\overline{\vartheta }}^{G}, {\overline{v}},{\overline{\beta }}\right)$ is a weakly efficient solution (an efficient solution) of a maximum type in (VC-VMWDVC).

Proof

By assumption, ${\overline{x}}$ is a weak Pareto solution of (SIMPVC) and the VC-ACQ constraint qualification is satisfied at ${\overline{x}}$. Then, by the standard Karush–Kuhn–Tucker necessary optimality conditions (see, for example, Singh 1987), there exist Lagrange multipliers ${\overline{\lambda }}\in R^{p}$, $\overline{\mu }\in R^{m}$, ${\overline{\xi }}\in R^{q}$ and ${\overline{v}}\in R^{w}$, ${\overline{\beta }}\in R^{w}$ such that the condition

$$\begin{aligned}&\sum _{i=1}^{p}{\overline{\lambda }}_{i}\nabla f_{i}({\overline{x}} )+\sum _{t=1}^{q}{\overline{\mu }}_{t_{k}}\nabla g_{t_{k}}({\overline{x}} )+\sum _{m=1}^{r}{\overline{\xi }}_{s_{m}}\nabla h_{s_{m}}({\overline{x}}) \nonumber \\&\quad -\sum _{j=1}^{w}{\overline{v}}_{j}\nabla H_{j}({\overline{x}} )+\sum _{j=1}^{w}{\overline{\beta }}_{j}\nabla \left( H_{j}G_{j}\right) ( {\overline{x}})=0 \end{aligned}$$

(70)

holds. If we set

$$\begin{aligned} {\overline{\vartheta }}_{j}^{G}= & {} {\overline{v}}_{j}H_{j}({\overline{x}}),\ j=1,...,w \text {,} \end{aligned}$$

(71)

$$\begin{aligned} {\overline{\vartheta }}_{tj}^{H}= & {} \overline{\beta }_{tj}-{\overline{v}}_{j}G_{j}( {\overline{x}}),\ j=1,...,w \end{aligned}$$

(72)

in (70), then there exist ${\overline{\lambda }}\in R^{p}$, ${\overline{\mu }}\in R^{m}$, ${\overline{\xi }}\in R^{q}$, ${\overline{\vartheta }}^{H}\in R^{w}$ and $\overline{\vartheta }^{G}\in R^{w}$ such that the Karush–Kuhn–Tucker necessary optimality conditions (26)–(31) are satisfied. Thus, the feasibility of $\left( {\overline{x}},\overline{ \lambda },{\overline{\mu }},{\overline{\xi }},{\overline{\vartheta }}^{H}, {\overline{\vartheta }}^{G},{\overline{v}},{\overline{\beta }}\right)$ in (VC -VMWDVC) follows from the VC-Karush–Kuhn–Tucker necessary optimality conditions (26)–(31) and also from (71) and (72).

Now, we prove that $\left( {\overline{x}},\overline{\lambda },{\overline{\mu }}, {\overline{\xi }},\overline{\vartheta }^{H},{\overline{\vartheta }}^{G}, {\overline{v}},\overline{\beta }\right)$ is a weakly efficient solution of a maximum type in (VC-VMWDVC). We proceed by contradiction. Suppose, contrary to the result, that $\left( {\overline{x}},{\overline{\lambda }}, \overline{\mu },{\overline{\xi }},{\overline{\vartheta }}^{H},\overline{ \vartheta }^{G},{\overline{v}},{\overline{\beta }}\right)$ is not a weakly efficient solution of a maximum type in (VC-VMWDVC). Then, by definition, there exists $\left( {\widetilde{y}},\widetilde{\lambda },{\widetilde{\mu }}, {\widetilde{\xi }},\widetilde{\vartheta }^{H},{\widetilde{\vartheta }}^{G}, {\widetilde{v}},\widetilde{\beta }\right) \in Q$ such that the inequality

$$\begin{aligned} f\left( {\widetilde{y}}\right) >f\left( {\overline{x}}\right) \text {.} \end{aligned}$$

holds, which is a contradiction to the weak duality theorem (Theorem 27). Hence, we conclude that $\left( {\overline{x}}, {\overline{\lambda }},{\overline{\mu }},\overline{\xi },{\overline{\vartheta }} ^{H},\overline{\vartheta }^{G},{\overline{v}},{\overline{\beta }}\right)$ is a weakly efficient solution of a maximum type in (VC-VMWDVC). The proof of efficiency of a maximum type in (VC-VMWDVC) is similar and, therefore, it is omitted in the paper. $\square$

The next two theorems give sufficient conditions for ${\overline{y}}$, where $\left( {\overline{y}},{\overline{\lambda }},\overline{\mu },{\overline{\xi }}, {\overline{\vartheta }}^{H},\overline{\vartheta }^{G},{\overline{v}},{\overline{\beta }}\right)$ is a feasible solution of the (VC-VMWDVC), to be a weak Pareto solution (a Pareto solution) of (SIMPVC).

Theorem 30

(Converse duality): Let x be any feasible solution of (SIMPVC) and $\left( {\overline{y}},{\overline{\lambda }}, {\overline{\mu }},\overline{\xi },{\overline{\vartheta }}^{H},\overline{ \vartheta }^{G},{\overline{v}},{\overline{\beta }}\right)$ be a weak efficient solution of a maximum type in Mond–Weir dual problem (VC-VMWDVC) such that ${\overline{y}}\in \Omega$. Further, we assume that each objective function $f_{i}$, $i\in I$, is invex at ${\overline{y}}$ on $\Omega \cup Y$ with respect to $\eta$, each inequality constraint $g_{t_{k}}$, $t_{k}\in T$, $k=1,...,q$ , is invex at ${\overline{y}}$ on $\Omega \cup Y$ with respect to $\eta$, each function $h_{s_{m}}$, $s_{m}\in S^{+}\left( {\overline{y}}\right)$, is invex at ${\overline{y}}$ on $\Omega \cup Y$ with respect to $\eta$, each function $-h_{s_{m}}$, $s_{m}\in S^{-}\left( {\overline{y}}\right)$ is invex at ${\overline{y}}$ on $\Omega \cup Y$ with respect to $\eta$, each function $-H_{j}$, $t\in J_{H}^{+}\left( x\right)$, is invex at ${\overline{y}}$ on $\Omega \cup Y$ with respect to $\eta$, each function $H_{j}$, $J_{0+}^{-}\left( x\right)$, is invex at ${\overline{y}}$ on $\Omega \cup Y$ with respect to $\eta$, each constraint $G_{j}$, $j\in J_{+0}\left( x\right)$, is invex at ${\overline{y}}$ on $\Omega \cup Y$ with respect to $\eta$. Then ${\overline{y}}$ is a weak Pareto solution of (SIMPVC).

Proof

We proceed by contradiction. Suppose, contrary to the result, that ${\overline{y}}\in \Omega$ is not a weak Pareto solution of (SIMPVC). Hence, by Definition 3, there exists ${\widetilde{x}}\in \Omega$ such that

$$\begin{aligned} f\left( {\widetilde{x}}\right) <f\left( {\overline{y}}\right) . \end{aligned}$$

(73)

From invexity hypotheses, by Definition 2, the inequalities

$$\begin{aligned}&f_{i}({\widetilde{x}})-f_{i}({\overline{y}})\geqq \nabla f_{i}({\overline{y}})\eta \left( {\widetilde{x}},{\overline{y}}\right) \text {, }i\in I\text {,} \end{aligned}$$

(74)

$$\begin{aligned}&g_{t_{k}}({\widetilde{x}})-g_{t_{k}}({\overline{y}})\geqq \nabla g_{t_{k}}( {\overline{y}})\eta \left( {\widetilde{x}},{\overline{y}}\right) \text {, } t_{k}\in T\left( {\overline{y}}\right) \text {, }k=1,..,m, \end{aligned}$$

(75)

$$\begin{aligned}&h_{s_{m}}({\widetilde{x}})-h_{s_{m}}({\overline{y}})\geqq \nabla h_{s_{m}}( {\overline{y}})\eta \left( {\widetilde{x}},{\overline{y}}\right) ,\text { }s_{m}\in S^{+}\left( {\overline{y}}\right) \text {,} \end{aligned}$$

(76)

$$\begin{aligned}&-h_{s_{m}}({\widetilde{x}})+h_{s_{m}}({\overline{y}})\geqq -\nabla h_{s_{m}}( {\overline{y}})\eta \left( {\widetilde{x}},{\overline{y}}\right) ,\text { }s_{m}\in S^{-}\left( {\overline{y}}\right) \text {,} \end{aligned}$$

(77)

$$\begin{aligned}&-H_{j}({\widetilde{x}})+H_{j}({\overline{y}})\geqq -\nabla H_{j}({\overline{y}} )\eta \left( {\widetilde{x}},{\overline{y}}\right) ,\text { }j\in J_{H}^{+}\left( {\widetilde{x}}\right) \text {,} \end{aligned}$$

(78)

$$\begin{aligned}&H_{j}({\widetilde{x}})-H_{j}({\overline{y}})\geqq \nabla H_{j}({\overline{y}})\eta \left( {\widetilde{x}},{\overline{y}}\right) ,\text { }j\in J_{0+}^{-}\left( {\widetilde{x}}\right) \text {,} \end{aligned}$$

(79)

$$\begin{aligned}&G_{j}({\widetilde{x}})-G_{j}({\overline{y}})\geqq \nabla G_{j}({\overline{y}})\eta \left( {\widetilde{x}},{\overline{y}}\right) \text {, }j\in J_{+0}\left( {\widetilde{x}}\right) \end{aligned}$$

(80)

hold. By ${\widetilde{x}}$, ${\overline{y}}\in \Omega$, we have, respectively,

$$\begin{aligned}&g_{t_{k}}({\widetilde{x}})\leqq 0=g_{t_{k}}({\overline{y}})\text {, }t_{k}\in T\left( {\overline{y}}\right) \text {, }k=1,..,m\text {,} \end{aligned}$$

(81)

$$\begin{aligned}&h_{s_{m}}({\widetilde{x}})=h_{s_{m}}({\overline{y}}),\text { }s_{m}\in S^{+}\left( {\overline{y}}\right) \cup S^{-}\left( {\overline{y}}\right) \text {,} \end{aligned}$$

(82)

$$\begin{aligned}&\left. \begin{array}{c} H_{j}({\widetilde{x}})>0\text {, }\overline{\vartheta }_{j}^{H}=\overline{\beta }_{j}-{\overline{v}}_{j}G_{j}({\widetilde{x}})\geqq 0\text {, }j\in J_{+}\left( {\widetilde{x}}\right) \\ H_{j}({\widetilde{x}})=0\text {, }\vartheta _{j}^{H}=\overline{\beta }_{j}- {\overline{v}}_{j}G_{j}({\widetilde{x}})\in R\text {, }j\in J_{0}\left( {\widetilde{x}}\right) \end{array} \right\} \Longrightarrow \sum _{j=1}^{w}\overline{\vartheta }_{j}^{H}H_{j}( {\widetilde{x}})\geqq 0\text {,} \qquad \quad \end{aligned}$$

(83)

$$\begin{aligned}&\left. \begin{array}{c} G_{j}({\widetilde{x}})>0\text {, }\overline{\vartheta }_{j}^{G}={\overline{v}} _{j}H_{j}({\widetilde{x}})=0\text {, }j\in J_{0+}\left( {\widetilde{x}}\right) \\ G_{j}({\widetilde{x}})=0\text {, }\overline{\vartheta }_{j}^{G}={\overline{v}} _{j}H_{j}({\widetilde{x}})=0\text {, }j\in J_{00}\left( {\widetilde{x}}\right) \\ G_{j}\left( {\widetilde{x}}\right)<0\text {, }\overline{\vartheta }_{j}^{G}= {\overline{v}}_{j}H_{j}({\widetilde{x}})=0\text {, }j\in J_{0-}\left( \widetilde{x }\right) \\ G_{j}({\widetilde{x}})=0\text {, }\overline{\vartheta }_{j}^{G}={\overline{v}} _{j}H_{j}({\widetilde{x}})\geqq 0\text {, }j\in J_{+0}\left( {\widetilde{x}} \right) \\ G_{j}({\widetilde{x}})<0\text {, }\overline{\vartheta }_{j}^{G}={\overline{v}} _{j}H_{j}({\widetilde{x}})\geqq 0\text {, }j\in J_{+-}\left( {\widetilde{x}} \right) \end{array} \right\} \Longrightarrow \sum _{j=1}^{w}\overline{\vartheta }_{j}^{G}G_{j}( {\widetilde{x}})\leqq 0\text {.} \end{aligned}$$

(84)

Hence, using (83) and (84) together with $\left( {\overline{y}}, {\overline{\lambda }},{\overline{\mu }},\overline{\xi },{\overline{\vartheta }} ^{H},\overline{\vartheta }^{G},{\overline{v}},{\overline{\beta }}\right) \in Q$, we obtain

$$\begin{aligned} -\sum _{j=1}^{w}\overline{\vartheta }_{j}^{H}H_{j}({\widetilde{x}})\leqq & {} -\sum _{j=1}^{w}\overline{\vartheta }_{j}^{H}H_{j}({\overline{y}})\text {,} \end{aligned}$$

(85)

$$\begin{aligned} \sum _{j=1}^{w}{\overline{\vartheta }}_{j}^{G}G_{j}({\widetilde{x}})\leqq & {} \sum _{j=1}^{w}{\overline{\vartheta }}_{j}^{G}G_{j}({\overline{y}}). \end{aligned}$$

(86)

Combining (73)–(77), multiplying by the corresponding Lagrange multipliers and then adding both sides of the resulting inequalities, we obtain, respectively,

$$\begin{aligned}&\sum _{i=1}^{p}{\overline{\lambda }}_{i}\nabla f_{i}({\overline{y}})\eta \left( {\widetilde{x}},{\overline{y}}\right) \leqq 0\text {,} \end{aligned}$$

(87)

$$\begin{aligned}&\sum _{\text { }k=1}^{m}{\overline{\mu }}_{t_{k}}\nabla g_{t_{k}}({\overline{y}} )\eta \left( {\widetilde{x}},{\overline{y}}\right) \leqq 0\text {,} \end{aligned}$$

(88)

$$\begin{aligned}&\sum _{m=1}^{r}{\overline{\xi }}_{s_{m}}\nabla h_{s_{m}}({\overline{y}})\eta \left( {\widetilde{x}},{\overline{y}}\right) \leqq 0\text {.} \end{aligned}$$

(89)

Multiplying (78)–(80) by the corresponding Lagrange multipliers, adding both sides of the resulting inequalities and then using (85) and (86), we get, respectively,

$$\begin{aligned}&\sum _{j=1}^{w}{\overline{\vartheta }}_{j}^{H}\nabla H_{j}({\overline{y}})\eta \left( {\widetilde{x}},{\overline{y}}\right) \leqq 0\text {,} \end{aligned}$$

(90)

$$\begin{aligned}&\sum _{j\in J_{G}\left( {\overline{y}}\right) }{\overline{\vartheta }} _{j}^{G}\nabla G_{j}({\overline{y}})\eta \left( {\widetilde{x}},{\overline{y}} \right) \leqq 0\text {.} \end{aligned}$$

(91)

Combining (87)–(91), we get that the inequality

$$\begin{aligned}&\left[ \sum _{i=1}^{p}{\overline{\lambda }}_{i}\nabla f_{i}({\overline{y}})+\sum _{ \text { }k=1}^{m}\overline{\mu }_{t_{k}}\nabla g_{t_{k}}({\overline{y}} )+\sum _{m=1}^{r}\overline{\xi }_{s_{m}}\nabla h_{s_{m}}({\overline{y}}) \right. \\&\quad \left. -\sum _{j=1}^{w}\overline{\vartheta }_{j}^{H}\nabla H_{j}( {\overline{y}})+\sum _{j\in J_{G}\left( {\overline{y}}\right) }{\overline{\vartheta }}_{j}^{G}\nabla G_{j}({\overline{y}})\right] \eta \left( \widetilde{x },{\overline{y}}\right) <0 \end{aligned}$$

holds, which is a contradiction to the first constraint of (VC-VMWDVC). This completes the proof of this theorem. $\square$

If we assume stronger assumptions, then the following result is true:

Theorem 31

(Converse duality): Let x be any feasible solution of (SIMPVC) and $\left( {\overline{y}},{\overline{\lambda }}, {\overline{\mu }},\overline{\xi },{\overline{\vartheta }}^{H},\overline{ \vartheta }^{G},{\overline{v}},{\overline{\beta }}\right)$ be an efficient solution of a maximum type in Mond–Weir dual problem (VC-VMWDVC) such that ${\overline{y}}\in \Omega$. Further, we assume that each objective function $f_{i}$, $i\in I$, is strictly invex at ${\overline{y}}$ on $\Omega \cup Y$ with respect to $\eta$, each inequality constraint $g_{t_{k}}$, $t_{k}\in T$ , $k=1,...,q$, is invex at ${\overline{y}}$ on $\Omega \cup Y$ with respect to $\eta$, each function $h_{s_{m}}$, $s_{m}\in S^{+}\left( {\overline{y}} \right)$, is invex at ${\overline{y}}$ on $\Omega \cup Y$ with respect to $\eta$, each function $-h_{s_{m}}$, $s_{m}\in S^{-}\left( {\overline{y}} \right)$ is invex at ${\overline{y}}$ on $\Omega \cup Y$ with respect to $\eta$, each function $-H_{j}$, $t\in J_{H}^{+}\left( x\right)$, is invex at ${\overline{y}}$ on $\Omega \cup Y$ with respect to $\eta$, each function $H_{j}$, $J_{0+}^{-}\left( x\right)$, is invex at ${\overline{y}}$ on $\Omega \cup Y$ with respect to $\eta$, each constraint $G_{j}$, $j\in J_{+0}\left( x\right)$, is invex at ${\overline{y}}$ on $\Omega \cup Y$ with respect to $\eta$. Then ${\overline{y}}$ is a Pareto solution of (SIMPVC).

The next theorem gives sufficient conditions for a feasible point of the primal problem (SIMPVC) to be a weak Pareto solution (a Pareto solution) by using the Mond–Weir dual problem (VC-VMWDVC).

Theorem 32

(Strict converse duality): Let ${\overline{x}}$ be any feasible solution of (SIMPVC) and $\left( {\overline{y}},\overline{\lambda },{\overline{\mu }}, {\overline{\xi }},\overline{\vartheta }^{H},{\overline{\vartheta }}^{G}, {\overline{v}},\overline{\beta }\right)$ be a feasible solution of (VC -VMWDVC) such that $f\left( {\overline{x}}\right) =f\left( {\overline{y}}\right)$. Further, we assume that each objective function $f_{i}$, $i\in I$, is (strictly) invex at ${\overline{y}}$ on $\Omega \cup Y$ with respect to $\eta$ , each inequality constraint $g_{t_{k}}$, $t_{k}\in T$, $k=1,...,q$, is invex at ${\overline{y}}$ on $\Omega \cup Y$ with respect to $\eta$, each function $h_{s_{m}}$, $s_{m}\in S^{+}\left( {\overline{y}}\right)$, is invex at ${\overline{y}}$ on $\Omega \cup Y$ with respect to $\eta$, each function $-h_{s_{m}}$, $s_{m}\in S^{-}\left( {\overline{y}}\right)$ is invex at ${\overline{y}}$ on $\Omega \cup Y$ with respect to $\eta$, each function $-H_{j}$, $t\in J_{H}^{+}\left( {\overline{x}}\right)$, is invex at ${\overline{y}}$ on $\Omega \cup Y$ with respect to $\eta$, each function $H_{j}$, $J_{0+}^{-}\left( {\overline{x}}\right)$, is invex at ${\overline{y}}$ on $\Omega \cup Y$ with respect to $\eta$, each constraint $G_{j}$, $j\in J_{+0}\left( {\overline{x}}\right)$, is invex at ${\overline{y}}$ on $\Omega \cup Y$ with respect to $\eta$. Then ${\overline{x}}$ is a weak Pareto solution (a Pareto solution) of (SIMPVC) and $\left( {\overline{y}},{\overline{\lambda }},\overline{\mu },{\overline{\xi }},{\overline{\vartheta }}^{H}, \overline{\vartheta }^{G},{\overline{v}},{\overline{\beta }}\right)$ is a weak efficient solution (an efficient solution) of a maximum type in (VC -VMWDVC).

Proof

We proceed by contradiction. Suppose, contrary to the result, that ${\overline{x}}\in \Omega$ is not a weak Pareto solution of (SIMPVC). Hence, by Definition 3, there exists ${\widetilde{x}}\in \Omega$ such that

$$\begin{aligned} f\left( {\widetilde{x}}\right) <f\left( {\overline{x}}\right) \text {.} \end{aligned}$$

(92)

Combining (92) with the assumption $f\left( {\overline{x}}\right) =f\left( {\overline{y}}\right)$, we get $f\left( {\widetilde{x}}\right) <f\left( {\overline{y}}\right)$. The rest of this proof is similar to the proof of Theorem 30. Weak efficiency of a maximum type of $\left( {\overline{y}},{\overline{\lambda }},{\overline{\mu }}, \overline{\xi },{\overline{\vartheta }}^{H},{\overline{\vartheta }}^{G}, {\overline{v}},{\overline{\beta }}\right)$ in (VC-VMWDVC) follows from the weak duality theorem - Theorem 27 (or Theorem 28 in the case efficiency of a maximum type). $\square$

4 Conclusion

In the paper, both necessary and sufficient optimality have been proved for the considered differentiable semi-infinite multiobjective programming problem with vanishing constraints. Namely, two types of Karush–Kuhn–Tucker necessary optimality conditions have been established for such smooth vector optimization problems and, moreover, they have also been specified in terms of S-stationary points which their definitions have been introduced in the paper for the differentiable semi-infinite multiobjective programming problem with vanishing constraints. Further, sufficient optimality conditions have been established for such smooth semi-infinite vector optimization problems under invexity hypotheses. Furthermore, several duality results in the sense of Mond–Weir between the considered differentiable semi-infinite multiobjective programming problem with vanishing constraints and its vector Mond–Weir dual problem defined in the paper for such extremum problems have been proved also under appropriate invexity assumptions. The sufficient optimality conditions and duality results presented here have been established for differentiable semi-infinite multiobjective programming problems with vanishing constraints in which the involved functions are invex (with respect to the same function $\eta$). Thus, similar results established previously in the literature for scalar smooth optimization problems with vanishing constraints in which the involved functions are convex have been extended to a new class of nonconvex differentiable semi-infinite multiobjective optimization problems with vanishing constraints. Further, it has been illustrated that the results established in the paper are applicable for some of differentiable semi-infinite multiobjective programming problems with vanishing constraints for which the similar results existing actually in the literature for such extremum problems can fail.

It seems that the techniques employed in this paper can be used in proving similarly results for other classes of mathematical programming problems with vanishing constraints. We shall investigate these problems in the subsequent papers.