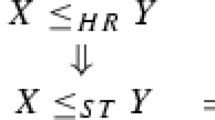Abstract
The univariate distorted distributions were introduced in risk theory to represent changes (distortions) in the expected distributions of some risks. Later, they were also applied to represent distributions of order statistics, coherent systems, proportional hazard rate and proportional reversed hazard rate models, etc. In this paper we extend this concept to the multivariate setup. We show that, in some cases, they are a valid alternative to the copula representation, especially when the marginal distributions may not be easily handled. Several examples illustrate the applications of such representations in statistical modeling. They include the study of paired (dependent) ordered data, joint residual lifetimes, order statistics and coherent systems






Similar content being viewed by others
References
Ahmadi J, Nagaraja HN (2020) Conditional properties of a random sample given an order statistic. Stat Pap 61:1971–1996
Arias-Nicolás P, Ruggeri F, Suárez-Llorens A (2016) New classes of priors based on stochastic orders and distortion functions. Bayesian Anal 11:1107–1136
Barlow RE, Proschan F (1975) Statistical theory of reliability and life testing. International Series in Decision Processes, Holt, Rinehart and Winston Inc, New York
Durante F, Foschi R, Sarkoci P (2010) Distorted copulas: constructions and tail dependence. Commun Stat-Theory Methods 39:2288–2301
Durante F, Foschi R, Spizzichino F (2008) Threshold copulas and positive dependence. Stat Probab Lett 78:2902–2909
Durante F, Mesiar R, Papini PL, Sempi C (2007) \(2\)-increasing binary aggregation operators. Inf Sci 177:111–129
Durante F, Sempi C (2016) Principles of copula theory. CRC/Chapman & Hall, London
Embrechts P (2009) Copulas: a personal view. J Risk Insur 76:639–650
Fermanian JD, Wegkamp MH (2012) Time-dependent copulas. J Multivar Anal 110:19–29
Joe H (2005) Asymptotic efficiency of the two-stage estimation method for copula-based models. J Multivar Anal 94:401–419
Joe H (2014) Dependence modeling with copulas. CRC/Chapman & Hall, Boca Raton, FL
Klüppelberg C, Resnick SI (2008) The Pareto copula, aggregation of risks and the emperor’s socks. J Appl Probab 45:67–84
Koenker R (2005) Quantile Regression. Cambridge University Press
Liu P, Schied A, Wang R (2021) Distributional transforms, probability distortions, and their applications. Mathematics of Operations Research (in press)
Longobardi M, Pellerey F (2019) On the role of dependence in residual lifetimes. Stat Probab Lett 153:56–64
López-Díaz M, Sordo MA, Suárez-Llorens A (2012). On the Lp-metric between a probability distribution and its distortion. Insurance: Mathematics and Economics 51, 257–264
Mai J-F, Scherer M (2017) Simulating copulas, 2nd edn. World Scientific, Singapore
Morillas PM (2005) A method to obtain new copulas from a given one. Metrika 61:169–184
Navarro J (2018) Distribution-free comparisons of residual lifetimes of coherent systems based on copula properties. Stat Pap 59:781–800
Navarro J, Balakrishnan N (2010) Study of some measures of dependence between order statistics and systems. J Multivar Anal 101:52–67
Navarro J, Calì C (2019) Inactivity times of coherent systems with dependent components under periodical inspection. Appl Stoch Models Bus Ind 35:871–892
Navarro J, Durante F (2017) Copula-based representations for the reliability of the residual lifetimes of coherent systems with dependent components. J Multivar Anal 158:87–102
Navarro J, del Águila Y, Sordo MA, Suárez-Llorens A (2013) Stochastic ordering properties for systems with dependent identically distributed components. Appl Stochastic Models Bus Ind 29:264–278
Navarro J, del Águila Y, Sordo MA, Suárez-Llorens A (2016) Preservation of stochastic orders under the formation of generalized distorted distributions. Methodol Comput Appl Probab 18:529–545
Navarro J, Durante F, Fernández-Sánchez J (2021) Connecting copula properties with reliability properties of coherent systems. Appl Stochast Models Bus Ind 37:496–512
Navarro J, Longobardi M, Pellerey F (2017) Comparison results for inactivity times of \(k\)-out-of-\(n\) and general coherent systems with dependent components. Test 26:822–846
Navarro J, Samaniego FJ, Balakrishnan N (2010) The joint signature of coherent systems with shared components. J Appl Probab 47:235–253
Navarro J, Sordo MA (2018) Stochastic comparisons and bounds for conditional distributions by using copula properties. Depend Modeling 6:156–177
Nelsen RB (2006) An introduction to copulas, 2nd edn. Springer, New York
Omelka M, Gijbels I, Veraverbeke N (2009) Improved kernel estimation of copulas: weak convergence and goodness-of-fit testing. Ann Stat 37:3023–3058
Shaked M, Shanthikumar JG (2007) Stochastic orders. Springer Series in Statistics, Springer, New York
Sklar A (1959) Fonctions de répartition à \(n\) dimensions et leurs marges. Publications de l’Institut de Statistique de l’Université de Paris 8:229–231
Sordo MA, Castaño-Martínez A, Pigueiras G (2016). A family of premium principles based on mixtures of TVaRs. Insurance: Mathematics and Economics 70, 397–405
Sordo MA, Suárez-Llorens A (2011). Stochastic comparisons of distorted variability measures. Insurance: Mathematics and Economics 49, 11–17
Sumarjaya IW (2017). A survey of kernel-type estimators for copula and their applications. Journal of Physics: Conference Series 893 012027.https://doi.org/10.1088/1742-6596/893/1/012027
Taylor MD (2016) Multivariate measures of concordance for copulas and their marginals. Depend Modeling 4:224–236
Valdez EA, Xiao Y (2011) On the distortion of a copula and its margins. Scand Actuar J 4:292–317
Wang S (1996) Premium calculation by transforming the layer premium density. ASTIN Bull 26:71–92
Yaari ME (1987) The dual theory of choice under risk. Econometrica 55:95–115
Acknowledgements
The authors would like to thank the anonymous reviewers for the careful reading and several useful suggestions. JN is partially supported by Ministerio de Ciencia e Innovación of Spain under grant PID2019-103971GB-I00/AEI/10.13039/501100011033, CC and ML are partially supported by the GNAMPA research group of INDAM (Istituto Nazionale di Alta Matematica) and CC, ML and FD are also partially supported by MIUR-PRIN 2017, Project “Stochastic Models for Complex Systems” (No. 2017JFFHSH)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Appendix
Appendix
Proof of proposition 1
For every \(i=1,\dots ,n\), \(G_i\) is continuous and, hence, its range \(Ran(G_i)\) contains the interval (0, 1). Let D be the distribution function of \((G_1(X_1),\dots ,G_n(X_n))\). Then it can be checked that D satisfies properties (i), (ii) and (iii) of Definition 1. Thus, \(D\in {\mathcal {D}}_n\).
Moreover, for every \((x_1,\dots ,x_n)\) in \({\mathbb {R}}^n\), it follows that
where in the second equality we use that \(G_i\) is strictly increasing in the support of \(X_i\). Hence is \(F\equiv MDD(G_1,\dots ,G_n)\).\(\square\)
Proof of proposition 2
Since F is continuous, (1) holds for a unique copula C. Thus, for every \((x_1,\dots ,x_n)\) in \({\mathbb {R}}^n\), it follows that
For every \(i=1,\dots ,n\), since \(G_i\) is continuous, there exists \(u_i\in (0,1)\) such that \(x_i=G_i^{-1}(u_i)\), where \(G_i^{-1}\) is quasi–inverse of G (see, e.g., Durante and Sempi 2016). Thus, it follows that
which is the desired assertion. \(\square\)
Proof of proposition 3
Clearly, if (2) holds for some distribution functions \(G_1,\dots ,G_n\) and \(D\in {\mathcal {D}}_n\), then
for \(i=1,\dots ,n\) and
since \(D \in {\mathcal {D}}_n\). Moreover, F is right-continuous in each variable since D is continuous and \(G_1,\dots ,G_n\) are right-continuous.
Let us consider now \((x_1,\dots ,x_n)\in {\mathbb {R}}^n\) and \((y_1,\dots , y_n)\in {\mathbb {R}}^n\) such that \(x_i\le y_i\) for \(i=1,\dots ,n\). Then we define \(u_i=G_i(x_i)\) and \(v_i=G_i(y_i)\) for \(i=1,\dots ,n\). As \(G_i\) is a distribution function, we have \(0\le u_i\le v_i\le 1\) for \(i=1,\dots ,n\). Therefore
since D satisfies property (iii) in Definition 1. Therefore, F is a proper multivariate distribution function. \(\square\)
Proof of Proposition 5
The joint distribution function of \((X_1,\dots ,X_m)\) can be written as
for all \((x_1,\dots ,x_m)\in {\mathbb {R}}^m\). Then (5) is obtained from (2) taking into account that \(G_i(+\infty )=1\) for any distribution function \(G_i\) and \(i=m+1,\dots ,n\). Finally, (5) implies \(D_{1,\dots ,m}\in {\mathcal {D}}_m\). \(\square\)
Proof of Proposition 7
The conditional PDF of \((X_2|X_1=x_1)\) can be written as
for all \(x_1,x_2\) such that \(f_1(x_1)>0\). Then by using (7) and the fact that
where \(D_1(u):=D(u,1)\) and \(D'_1(u)=\partial _1 D(u,1)\), we obtain
Thus, the conditional distribution function can be obtained as
Now, if we assume \(\lim _{v\rightarrow 0^+}\partial _1D(G_1(x_1),v)=0\), then
Hence, (8) holds. \(\square\)
Proof of Proposition10
First we note that \(\Pr (X_i>t)\ge \Pr (X_1>t,\dots ,X_n>t)>0\) for \(i=1,\dots ,n\). So we can consider the survival functions \(\bar{F}_{1,t},\dots ,\bar{F}_{n,t}\) of the marginal residual lifetimes at time t. Then we note that \({\bar{F}}_t\) can be written as
for \(x_1,\dots ,x_n\ge 0\). Now we use the following copula representation for \({\bar{F}}\) (obtained from Sklar’s theorem) \({\bar{F}}(x_1,\dots ,x_n)={\hat{C}}({\bar{F}}_1(x_1),\dots ,{\bar{F}}_n(x_n)),\) where \({\hat{C}}\) is a continuous survival copula of \({\bar{F}}\). Hence
and (10) holds for the function \(D_t\) in (11). Hence \({\hat{D}}_t\in {\mathcal {D}}_n\). \(\square\)
Survival function of \({\mathbf {X}}^{(n)}_t\) given by (12) We aim at calculating the survival function of
To this end, consider that
for \(x_1,\dots ,x_{n-1}\ge 0\). Hence it can be written as
where \(\bar{F}_{1,t},\dots ,\bar{F}_{n-1,t}\) are the survival functions of the univariate residual lifetimes,
for \({\mathbf {u}}=(u_1,\dots ,u_{n})\in [0,1]^n\) and \(D^{(n,\le )}_t\in {\mathcal {D}}_{n-1}\). \(\square\)
Proof of Proposition 11
The distortion function for \(n=3\) can be obtained as follows for \(0\le u_1\le u_2 \le u_3\le 1\). If we assume \(F(x)=x\) for \(x\in [0,1]\), then
where \(A_i=\{ X_i\le u_1\}\), \(A_{i,j}=\{ X_i\le u_2\}\cap \{ X_j \le u_2\}\), and \(A_{1,2,3}=\{ X_1\le u_3\}\cap \{ X_2 \le u_3\}\cap \{ X_3 \le u_3\}\) for \(i,j\in \{1,2,3\}\). Hence
where \(B_1=A_1\cap A_{1,2}\cap A_{1,2,3}\), \(B_2=A_2\cap A_{1,2}\cap A_{1,2,3}\), \(B_3=A_3\cap A_{1,2}\cap A_{1,2,3}\), \(B_4=A_1\cap A_{1,3}\cap A_{1,2,3}\), \(B_5=A_2\cap A_{1,3}\cap A_{1,2,3}\), \(B_6=A_3\cap A_{1,3}\cap A_{1,2,3}\), \(B_7=A_1\cap A_{2,3}\cap A_{1,2,3}\), \(B_8=A_2\cap A_{2,3}\cap A_{1,2,3}\), and \(B_9=A_3\cap A_{2,3}\cap A_{1,2,3}\). Hence, the formula for D is obtained by applying the inclusion-exclusion formula to (21) taking into account that all these probabilities can be computed from C. For example
and
\(0\le u_1\le u_2 \le u_3\le 1\). The other probabilities can be obtained in a similar way. Clearly, this procedure can also be applied to the n dimensional case (but the expression for D gets really involved).
Proof of Proposition 12
Let \({\mathcal {C}}_1,\dots , {\mathcal {C}}_s\) and \({\mathcal {C}}^*_1,\dots , {\mathcal {C}}^*_{s^*}\) be the minimal cut sets of T and \(T^*\), respectively. Hence the joint distribution \(F(x,y)=\Pr (T\le x, T^*\le y)\) can be written as
where \(A_i:=\{\max _{k\in {\mathcal {C}}_i}X_k \le x\}\), \(A^*_j:=\{\max _{k\in {\mathcal {C}}^*_j}X_k \le y\}\) and \(B_{i,j}:=A_i\cap A^*_j\). Now, we can apply the inclusion-exclusion formula to the union of the sets \(B_{i,j}\). Moreover we note that, if \(x\le y\), then
where \({\mathcal {C}}^*_j-{\mathcal {C}}_i ={\mathcal {C}}^*_j\cap \mathcal {{\bar{C}}}_i\) (\({\bar{A}}\) is the complementary set of the set A), \(C_{{\mathcal {C}}_i,{\mathcal {C}}^*_j}(u,v):=C(u_1,\dots ,u_n)\), \(u_k=F(x)\) if \(k\in {\mathcal {C}}_i\), \(u_k=F(y)\) if \(k\in {\mathcal {C}}^*_j-{\mathcal {C}}_i\), and \(u_k=1\) if \(k\notin {\mathcal {C}}_i\cup {\mathcal {C}}^*_j\). Similar expressions can be obtained for the other probabilities in the inclusion-exclusion formula as \(\Pr (B_{i,j}\cap B_{\ell ,r})\), \(\dots\) and for \(x>y\). Hence, we obtain (19). \(\square\)
Rights and permissions
About this article
Cite this article
Navarro, J., Calì, C., Longobardi, M. et al. Distortion representations of multivariate distributions. Stat Methods Appl 31, 925–954 (2022). https://doi.org/10.1007/s10260-021-00613-2
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10260-021-00613-2