Abstract
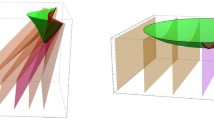
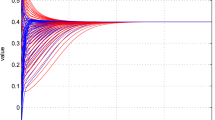
The temporal development of a single mode Rayleigh-Taylor instability consists of three stages: the linear, free fall and terminal velocity regimens. The purpose of this paper is to report on new phenomena observed in the approach to terminal velocity. Our numerical study shows an unexpected nonuniform approach to terminal velocity. The nonuniformity applies especially to the spikes, which are fingers of heavy fluid falling into the light fluid, but it also applies to the rising bubblesof light fluid. For spikes especially, our results call into question the meaningfulness of a terminal velocity for moderate values of the Atwood number A. After a short time period of pseudo-terminal plateau, the spike velocity increases to a significantly higher maximum, followed by a decrease. This phenomena appears to be due to a slow evolution in the shape of the spike and bubble. We find a relation between the spike (bubble) acceleartion and the tip curvature. In correlation with an increase in the spike velocity, the main body of the spike becomes narrower and the tip curvature increases. Our numerical results are by the Front Tracking method. The very late time simulations considered here required stabilization by a small value for the viscosity, so that the compressible Navier-Stokes equations govern the dynamics.
Similar content being viewed by others
References
Abarzhi, S.I. Stable Steady Flows in Rayleigh-Taylor Instability. Phys. Rev. Lett., 1998, 81(2): 337–340
Alon, U., Hecht, J., Mukamel, D., Shvarts, D. Scale Invariant Mixing Rates of Hydrodynamically Unstable Interfaces. Phys. Rev. Lett., 1994, 72: 2867–2870
Alon, U., Hecht, J., Ofer, D., Shvarts, D. Power Laws and Similarity of Rayleigh-Taylor and Richtmyer-Meshkov Mixing Fronts at all Density Ratios. Phys. Rev. Lett., 1995, 74: 534–538
Alon, U., Shvarts, D. Two-phase Flow Model for Rayleigh-Taylor and Richtmyer-Meshkov Mixing. In: Young, R., Glimm, J., Boston, B. eds., Proceedings of the Fifth International Workshop on Compressible Turbulent Mixing, World Scientific, Singapore, 1996
Birkhoff, G., Carter, D. Rising Plane Bubbles. J. Math. Mech., 1957, 6: 769
Chandrasekhar, S. Hydrodynamic and Hydromagnetic Stability. Oxford University Press, Oxford, 1961
Cheng, B., Glimm, J, Sharp, D.H. A 3-D RNG Bubble Merger Model for Rayleigh-Taylor Mixing. Submitted to: Chaos, 2001, SUNYSB-AMS-01-04 State Univ. of New York at Stony Brook
Dimonte, G., Schneider, M. Turbulent Rayleigh-Taylor Instability Experiments with Variable Acceleration. Pys. Rev. E, 1996, 54: 3740–3743
Garabedian, P. On Steady-state Bubbles Generated by Taylor Instability. Proc. R. Soc. London A, 1957, 241: 423–431
Gardner, C.L., Glimm, J, McBryan, O., Menikoff, R., Sharp, D., Zhang, Q. The Dynamics of Bubble Growth for Rayleigh-Taylor Unstable Interfaces. Pys. Fluids, 1988, 31: 447–465
Glimm, J., Grove, J.W., Li, X.L., Oh, W., Sharp, D.H. A Critical Analysis of Rayleigh-Taylor Growth Rates. J. Comp. Phys., 2001, 169: 652–677; LANL Report No. LA-UR-99-5582
Glimm, J., Grove, J.W., Li, X.L., Shyue, K.M., Zhang Q., and Zeng Y. Three Dimensional Front Tracking. SIAM J. Sci. Comp., 1998, 19: 703–727
Glimm, J., Li, X. On the Validation of the Sharp-Wheeler Bubble Merger Model from Experimental and Computational Data. Pys. Fluids, 1998, 31: 2077–2085
Glimm, J., Li, X.L., Menikoff, R., Sharp, D.H., Zhang Q. A Numerical Study of Bubble Interactions in Rayleigh-Taylor Instability for Compressible Fluids. Pys. Fluids A, 1990, 2(11): 2046–2054
Glimm, J., Sharp, D.H. Chaotic Mixing as a Renormalization Group Fixed Point. Phys. Rev. Lett., 1990, 64: 2137–2139
Glimm, J., Sharp, D.H. Stochastic Partial Differential Equations: Selected Applications in Continuum Physics. In: Carmona, R.A. and Rozovskii, B.L. eds., Stochastic Partial Differential Equations: Six Perspectives, Mathematical Surveys and Monographs, American Mathematical Society, Providence, 1997
Hecht, J., Alon, U., Shvarts, D. Potential Flow Models of Rayleigh-Taylor and Richtmyer-Meshkov Bubble Fronts. Phys. Fluids, 1994, 6: 4019–4030
Layzer, D. On the Instability of Superimposed Fluids in a Gravitational Field. Astrophys. J., 1995, 122:1–12
Li, X.L., Jin, B.X., Glimm, J. Numerical Study for the Three Dimensional Rayleigh-Taylor Instability Using the TVD/AC Scheme and Parallel Computation. J. Comp. Phys., 1996, 126: 343–355
Lin, A. Late Time Phenomena of Single Mode Rayleigh-Taylor Instability. Ph.D. Thesis, State Univ. of New York at Stony Brook, 2000
Read, K.I. Experimental Investigation of Turbulent Mixing by Rayleigh-Taylor Instability. Physica D, 1984, 12: 45–58
Taylor, G.I. The Instability of Liquid Surfaces when Acceleratedin a Direction Perpendicular to Their Planes I. Proc. R Soc. London A, 1950, 201: 192–196
Thommen, Hans U. Numerical Integration of the Navier-stokes Equations. Z. Angew. Math. Phys., 1966, 17: 369–384
Zhang, Q. Validation of the Chaotic Mixing Renormalization Group Fixed Point. Phys. Lett. A, 1990, 151: 18–22
Zhang, Q. The Motion of Single Bubble or Spike in Rayleigh-Taylor Unstable Interfaces. Impact Comput. Sci. Engrg., 1991, 3: 277–304
Author information
Authors and Affiliations
Corresponding author
Additional information
Supported by the MICS program of the U.S. Department of Energy DE-FG02-90ER25084, DE-AC02-98CH10886, the Department of Energy Office of Inertial Fusion, the Army Research Office, grant DAAL-03-91-0027 and the National Science Foundation, grant DMS-0102480.
Rights and permissions
About this article
Cite this article
Glimm, J., Li, Xl. & Lin, AD. Nonuniform Approach to Terminal Velocity for Single Mode Rayleigh-Taylor Instability. Acta Mathematicae Applicatae Sinica, English Series 18, 1–8 (2002). https://doi.org/10.1007/s102550200001
Received:
Issue Date:
DOI: https://doi.org/10.1007/s102550200001