Spatial calcium kinetics after a traumatic brain injury

Abstract

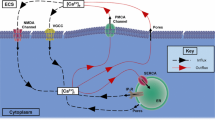
Accurate modelling of intracellular calcium ion ($Ca^{2+}$) concentration evolution is valuable as it is known to rapidly increase during a Traumatic Brain Injury. In the work presented here, our older non-spatial model dealing with the effect of mechanical stress upon the $Ca^{2+}$ transportation in a neuron is spatialized by considering the brain tissue as a solid continuum with the $Ca^{2+}$ activity occurring at every material point. Starting with one-dimensional representation, the brain tissue geometry is progressively made realistic and under the action of pressure or kinematic impulses, the effect of dimensionality and material behaviour on the correlation between the stress and concomitant $Ca^{2+}$ concentration is investigated. The spatial calcium kinetics model faithfully captures the experimental observations concerning the $Ca^{2+}$ concentration, load rate, magnitude and duration and most importantly shows that the critical location for primary injury may not be the most important location as far as secondary injury is concerned.

A Appendix: 1D analytical solution

Consider a viscoelastic bar of length L as shown in Fig. 2, one end of which is fixed, while at the other end a constant stress of magnitude $\sigma ^*(t)=\sigma ^*$ is applied. The standard linear solid viscoelastic relaxation law in terms of the elastic modulus for a uniaxial case can be written as,

$$\begin{aligned} E(t)=E_\infty +E_1e^{-E_1t/\eta _1}, \end{aligned}$$

(A.1)

where the material constants $E_{\infty }$, $E_1$, and $\eta _1$ are defined as,

$$\begin{gathered} E_{\infty } = \frac{{9G_{\infty } K}}{{3K + G_{\infty } }},\quad E_{1} = \frac{{27G_{1} K^{2} }}{{(3K + G_{\infty } )(3K + G_{\infty } + G_{1} )}},\quad {\text{and}} \hfill \\ \eta _{1} = \frac{{9K - E_{\infty } }}{{9K - E_{\infty } - E_{1} }} \times E_{1} \tau _{1} \hfill \\ \end{gathered}$$

(A.2)

where $G_{\infty }$ and $G_1$ are the shear modulus corresponding to the long time and relaxation time, $\tau _1$. K denotes the bulk modulus. For the ease of calculations, we normalize the variables as follows,

$$\begin{aligned} \begin{aligned}&\ \tau =\frac{E_0t}{\eta _1}, \qquad \xi = \frac{\sqrt{\rho E_0}}{\eta _1}x=M\frac{x}{L}, \qquad \Sigma = \frac{\sigma }{\sigma ^*}, \\&\quad {\mathbb {U}} = \frac{\sqrt{\rho E_0}}{\eta _1}u=M\frac{u}{L}, \quad \text {and} \qquad \epsilon =\frac{E_0\varepsilon }{\sigma ^*} = \frac{E_0}{\sigma ^*} \frac{\partial {\mathbb {U}}}{\partial \xi } \end{aligned} \end{aligned}$$

(A.3)

where $\tau$, $\xi$, $\Sigma$, ${\mathbb {U}}$, $\epsilon$ are the non-dimensionalized time t, space co-ordinate x, stress $\sigma$, displacement u and strain $\epsilon$, respectively, and $E_0 = E_\infty + E_1$. The factors $\eta _1/E_0$ and $\eta _1/\sqrt{\rho E_0}$ used to normalize time and length, respectively, represent the characteristic time and length offered by the material model. The space co-ordinate and displacement scaled by the length of the bar are related to their dimensionless counterparts $\xi$ and ${\mathbb {U}}$ through non-dimensional parameter $M = L\sqrt{\rho E_0}/\eta _1$. M compares the length of the bar to the material characteristic length.

Using Eqs. (3, 4, and A.3), the normalized equation of motion in the x-direction, the constitutive law, the relaxation law and the boundary conditions can be expressed as follows,

$$\begin{aligned}&\text {Equation of Motion:}\quad&\frac{\partial \Sigma }{\partial \xi }=\frac{E_0}{\sigma ^*}\times \frac{\partial ^2{\mathbb {U}}}{\partial \tau ^2}, \end{aligned}$$

(A.4)

$$\begin{aligned}&\text {Constitutive Law:}\quad&\Sigma (\tau )=\int \limits _{0}^{\eta _1\tau /E_0}{\mathbb {E}}(\tau -{\tilde{\tau }}){\dot{\epsilon }}({\tilde{\tau }})d\tau , \end{aligned}$$

(A.5)

$$\begin{aligned}&\text {Relaxation Law:}\quad&{\mathbb {E}}(\tau ) = 1-\psi +\psi e^{-\psi \tau }, \end{aligned}$$

(A.6)

$$\begin{aligned}&\text {Boundary Conditions:}\quad&{\mathbb {U}}(0,\tau )=0,\ \text {and}\quad \Sigma (M,\tau )=1 \end{aligned}$$

(A.7)

where $\psi =E_1/E_0$. Note that the, the non-dimensional time ‘$\tau$’ used here must not be confused with the viscoelastic relaxation time ‘$\tau _1$’ used in Eq.(6).

The wave equation given by Eq. (A.4) in conjunction with Eqs.(A.5–A.7) can be solved analytically using Laplace transforms. In the transformed domain, the Eqs.(A.4–A.7) can be rewritten as,

$$\begin{aligned}&\frac{\partial ^2\bar{{\mathbb {U}}}}{\partial \xi ^2} = \frac{s}{\bar{{\mathbb {E}}}(s)}\bar{{\mathbb {U}}}, \end{aligned}$$

(A.8)

$$\begin{aligned}&{\bar{\Sigma }}=s\bar{{\mathbb {E}}}(s){\bar{\epsilon }}, \end{aligned}$$

(A.9)

$$\begin{aligned}&\bar{{\mathbb {E}}}(s)=\frac{s+\psi -\psi ^2}{s(s+\psi )}, \end{aligned}$$

(A.10)

$$\begin{aligned}&\bar{{\mathbb {U}}}(0,s)=0,\quad \text {and}\quad {\bar{\Sigma }}(M,s)=1/s. \end{aligned}$$

(A.11)

Following the procedure given by Christensen (2012), the general solution of Eqs. (A.8–A.11) can expressed as,

$$\begin{aligned} \bar{{\mathbb {U}}}(\xi ,s) = \sum \limits _{n=1}^{\infty }{\bar{C}}_n(s){\mathbb {U}}^n(\xi ) + \bar{{\mathbb {V}}}(\xi ,s), \end{aligned}$$

(A.12)

where ${\mathbb {U}}^n(\xi ) = sin[(2n-1)\pi \xi /2M]$ is the $n^{th}$ eigenvalue in the solution for an equivalent elastic bar, and $\bar{{\mathbb {V}}}(\xi ,s)=(\sigma ^*\xi )/(s^2\bar{{\mathbb {E}}}(s)E_0)$ is the quasi-static solution for the viscoelastic bar. The coefficients ${\bar{C}}_n(s)$ are obtained by substituting the expression of $\bar{{\mathbb {U}}}(\xi ,s)$ given in Eq. (A.12) into the governing equation in Eq. (A.8), and invoking the orthogonality of the elastic eigenvalues ${\mathbb {U}}^n(\xi )$. Combining the displacement solution with the constitutive law in Eq. (A.9) and the relaxation law in Eq. (A.10), we obtain the stress distribution over the length of the bar in Laplace domain as,

$$\begin{aligned} \begin{aligned}&\ {\bar{\Sigma }}(\xi ,s)=\frac{1}{s}+ \frac{4}{\pi }\sum \limits _{n=1}^\infty \left[ \frac{(-1)^n}{(2n-1)} \times \right. \\&\ \left. \frac{s(s+\psi )}{s^3 + \psi s^2 + \frac{(2n-1)^2\pi ^2}{4M^2}s + \frac{(2n-1)^2\pi ^2}{4M^2}\psi (1-\psi )} \times cos\Big \{\frac{(2n-1)\pi \xi }{2M}\Big \}\right] \end{aligned} \end{aligned}$$

(A.13)

Although an analytical inversion cannot be derived in a generalised fashion, by electing a specific value for M, substituting for $\psi$ according to the material properties, and choosing to truncate the convergent infinite series after a finite number of terms enables us to invert the expression in the RHS of Eq. (A.13). We perform this operation on MAPLE for the values of M discussed in Sect. 3, thus obtaining the stress evolution with time, plotted in Fig. 3 a, b and c.