Mechanical stresses associated with flattening of human femoropopliteal artery specimens during planar biaxial testing and their effects on the calculated physiologic stress–stretch state

Abstract

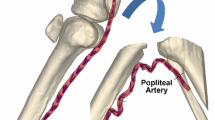
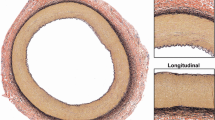
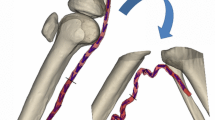
Planar biaxial testing is commonly used to characterize the mechanical properties of arteries, but stresses associated with specimen flattening during this test are unknown. We quantified flattening effects in human femoropopliteal arteries (FPAs) of different ages and determined how they affect the calculated arterial physiologic stress–stretch state. Human FPAs from 472 tissue donors (age 12–82 years, mean 53 ± 16 years) were tested using planar biaxial extension, and morphometric and mechanical characteristics were used to assess the flattening effects. Constitutive parameters for the invariant-based model were adjusted to account for specimen flattening and used to calculate the physiologic stresses, stretches, axial force, circumferential stiffness, and stored energy for the FPAs in seven age groups. Flattened specimens were overall 12 ± 4% stiffer longitudinally and 19 ± 11% stiffer circumferentially when biaxially tested. Differences between the stress–stretch curves adjusted and non-adjusted for the effects of flattening were relatively constant across all age groups longitudinally, but increased with age circumferentially. In all age groups, these differences were smaller than the intersubject variability. Physiologic stresses, stretches, axial force, circumferential stiffness, and stored energy were all qualitatively and quantitatively similar when calculated with and without the flattening effects. Stresses, stretches, axial force, and stored energy reduced with age, but circumferential stiffness remained relatively constant between 25 and 65 years of age suggesting a homeostatic target of 0.75 ± 0.02 MPa. Flattening effects associated with planar biaxial testing are smaller than the intersubject variability and have little influence on the calculated physiologic stress–stretch state of human FPAs.

Appendix

1.1 Cauchy stresses

The components of the isochoric Cauchy stress tensor $\bar{\varvec{t}}$ associated with each of the residual, physiologic, and flattening deformations can be calculated by taking the appropriate derivatives in Eq. 3 and using a form of strain energy function defined by Eqs. 1 and 2. This produces Cauchy stresses in the form

$$\begin{aligned} & \bar{t}_{rr} = C_{\text{gr}} \lambda_{r}^{2} = C_{\text{gr}} \frac{1}{{\lambda_{z}^{2} \lambda_{\theta }^{2} }} , \\ & \bar{t}_{\theta \theta } = C_{\text{gr}} \lambda_{\theta }^{2} + C_{1}^{\text{smc}}\langle \lambda_{\theta }^{2} - 1\rangle e^{{C_{2}^{\text{smc}} \left( {\lambda_{\theta }^{2} - 1} \right)^{2} }} \lambda_{\theta }^{2} + 2C_{1}^{\text{col}} \langle I_{4}^{\text{col}} - 1\rangle e^{{C_{2}^{\text{col}} \left( {I_{4}^{\text{col}} - 1} \right)^{2} }} \lambda_{\theta }^{2} \sin^{2} \gamma , \\ & \bar{t}_{zz} = C_{\text{gr}} \lambda_{z}^{2} + C_{1}^{\text{el}} \langle\lambda_{z}^{2} - 1\rangle e^{{C_{2}^{\text{el}} \left( {\lambda_{z}^{2} - 1} \right)^{2} }} \lambda_{z}^{2} + 2C_{1}^{\text{col}}\langle I_{4}^{\text{col}} - 1\rangle e^{{C_{2}^{\text{col}} \left( {I_{4}^{\text{col}} - 1} \right)^{2} }} \lambda_{z}^{2} \cos^{2} \gamma , \\ \end{aligned}$$

with

$$I_{4}^{\text{col}} = \lambda_{z}^{2} \cos^{2} \gamma + \lambda_{\theta }^{2} \sin^{2} \gamma$$

where $r, \theta , z$ are used to point out that these directions align with the radial, circumferential, and longitudinal directions of the artery in vivo. When considering specimen flattening, stretches $\lambda_{r} , \lambda_{\theta } , \lambda_{z}$ need to be substituted with λ₁, λ₂, λ₃. When considering residual deformations, they need to be substituted with $\lambda_{\rho } , \lambda_{\vartheta } , \lambda_{\zeta }$. Finally, when considering physiologic deformations, these stretches need to be substituted with $\lambda_{r}^{\text{phys}} ,\lambda_{\theta }^{\text{phys}} , \lambda_{z}^{\text{phys}}$.

1.2 Obtaining through-thickness values of stretch and stress

Through-thickness average values of stretch and stress were calculated by integrating them over the current volume and dividing the result by the total current volume. In Cartesian coordinates, since the stretches and the stresses vary through specimen thickness, this takes the form:

$$\begin{aligned} & \lambda_{2,3}^{\text{ave}} = \frac{{\iiint {\lambda_{2,3} {\text{d}}v}}}{{\iiint {{\text{d}}v}}} = \frac{{\mathop \smallint \nolimits_{0}^{{L_{1} }} \lambda_{2,3} {\text{d}}x_{1} }}{{\mathop \smallint \nolimits_{0}^{{L_{1} }} {\text{d}}x_{1} }} = \frac{{\mathop \smallint \nolimits_{0}^{{L_{1} }} \lambda_{2,3} {\text{d}}x_{1} }}{{L_{1} }} , \\ & t_{22,33}^{\text{ave}} = \frac{{\iiint {t_{22,33} {\text{d}}v}}}{{\iiint {{\text{d}}v}}} = \frac{{\mathop \smallint \nolimits_{0}^{{L_{1} }} t_{22,33} {\text{d}}x_{1} }}{{\mathop \smallint \nolimits_{0}^{{L_{1} }} {\text{d}}x_{1} }} = \frac{{\mathop \smallint \nolimits_{0}^{{L_{1} }} t_{22,33} {\text{d}}x_{1} }}{{L_{1} }} , \\ \end{aligned}$$

where L₁ is the thickness of the flattened specimen. Similarly in the cylindrical coordinates:

$$\begin{aligned} \lambda_{\theta }^{\text{avg}} & = \frac{{\iiint {\lambda_{\theta }^{\text{phys}} r{\text{d}}r{\text{d}}\theta {\text{d}}z}}}{{\iiint {r{\text{d}}r{\text{d}}\theta {\text{d}}z}}} = \frac{{\mathop \smallint \nolimits_{{r_{i} }}^{{r_{o} }} \lambda_{\theta }^{\text{phys}} r{\text{d}}r}}{{\mathop \smallint \nolimits_{{r_{i} }}^{{r_{o} }} r{\text{d}}r}} , \\ t_{\theta \theta }^{\text{avg}} & = \frac{{\iiint {t_{\theta \theta }^{\text{phys}} r{\text{d}}r{\text{d}}\theta {\text{d}}z}}}{{\iiint {r{\text{d}}r{\text{d}}\theta {\text{d}}z} }} = \frac{{\mathop \smallint \nolimits_{{r_{i} }}^{{r_{o} }} t_{\theta \theta }^{\text{phys}} r{\text{d}}r}}{{\mathop \smallint \nolimits_{{r_{i} }}^{{r_{o} }} r{\text{d}}r}} . \\ \end{aligned}$$

1.3 Kinematics of the residual and physiologic deformations

The stress-free (reference) configuration (Fig. 1a) is defined in terms of cylindrical coordinates $\left( {R,\varTheta ,Z} \right)$ as

$$R_{i} \le R \le R_{o} ,\quad 0 \le \varTheta \le 2\pi - \alpha ,\quad 0 \le Z \le L,$$

where R_i, R_o, α, and L are the inner and outer radii, opening angle, and the length of the stress-free arterial segment, respectively. The deformation gradient $\varvec{F}_{\text{res}}$ takes this configuration into the load-free state (Fig. 1b) geometrically defined as

$$\rho_{i} \le \rho \le \rho_{o} ,\quad 0 \le \vartheta \le 2\pi ,\quad 0 \le \zeta \le \xi ,$$

in which

$$\rho = \rho \left( R \right),\quad \vartheta = \frac{2\pi }{2\pi - \alpha }\varTheta ,\quad \zeta = \lambda_{\zeta } Z .$$

In cylindrical coordinates, $\varvec{F}_\text{res}$ is then given by

$$\varvec{F}_{\text{res}} = {\text{diag}}\left[ {\frac{\partial \rho }{\partial R},\frac{\rho }{R}\frac{\partial \vartheta }{\partial \varTheta },\frac{\partial \zeta }{\partial Z}} \right] = {\text{diag}}\left[ {\lambda_{\rho } ,\lambda_{\vartheta } ,\lambda_{\zeta } } \right] ,$$

where $\lambda_{\rho }$, λ_ϑ, and λ_ζ are the radial, circumferential, and longitudinal residual stretches, respectively, with λ_ϑ given by (Ogden 1997; Holzapfel et al. 2000; Humphrey 2002; Sommer and Holzapfel 2012; Kamenskiy et al. 2014)

$$\lambda_{\vartheta } = \frac{\rho }{R}{\rm K}$$

(9)

and ${\rm K} = \frac{2\pi }{2\pi - \alpha }$ is a measure of the circumferential opening angle. Assuming incompressibility, one can write

$$\rho_{o}^{2} - \rho_{i}^{2} = \frac{1}{{{\rm K}\lambda_{\zeta } }}\left( {R_{o}^{2} - R_{i}^{2} } \right) ,$$

(10)

and similarly

$$\rho_{o}^{2} - \rho^{2} = \frac{1}{{{\rm K}\lambda_{\zeta } }}\left( {R_{o}^{2} - R^{2} } \right) .$$

(11)

By substituting R form Eq. 11 in Eq. 9, the circumferential residual stretch λ_ϑ can be calculated at each point through thickness as a function of $\rho ,R_{o} ,{\rm K}, \lambda_{\vartheta }^{o} ,\lambda_{\zeta }$, given by Eq. 6.

Further, deformation $\varvec{F}_\text{load}$ takes the load-free configuration to the loaded (current) configuration (Fig. 1c) which in cylindrical coordinates is defined as

$$r_{i} \le r \le r_{o} ,\quad 0 \le \theta \le 2\pi ,\quad 0 \le z \le l ,$$

where

$$r = r\left( \rho \right), \theta = \vartheta , z = \lambda_{z} \zeta .$$

$\varvec{F}_{\text{load}}$ is given by

$$\varvec{F}_{\text{load}} = {\text{diag}}\left[ {\frac{\partial r}{\partial \rho },\frac{r}{\rho }\frac{\partial \theta }{\partial \vartheta },\frac{\partial z}{\partial \zeta }} \right] = {\text{diag}}\left[ {\lambda_{r} ,\lambda_{\theta } ,\lambda_{z} } \right] ,$$

in which $\lambda_{\theta } = \frac{r}{\rho }$ is the circumferential stretch. Assuming incompressibility, similar to Eq. 11

$$r_{o}^{2} - r^{2} = \frac{1}{{\lambda_{z} }}\left( {\rho_{o}^{2} - \rho^{2} } \right).$$

(12)

The total deformation gradient with respect to the stress-free configuration is then given by

$$\varvec{F}_{\text{phys}} = \varvec{F}_{\text{load}} \varvec{F}_{\text{res}} ,$$

in which the circumferential stretch is calculated as

$$\lambda_{\theta }^{\text{phys}} = \lambda_{\vartheta } \lambda_{\theta } = \frac{\rho }{R}{\rm K} \times \frac{r}{\rho } = \frac{r}{R}{\rm K}$$

By substituting $\rho_{o}^{2} - \rho^{2}$ from Eq. 10 in Eq. 12, one can find $\lambda_{\theta }^\text{phys}$ as a function of $r,R_{o} , {\rm K}, \lambda_{\vartheta }^{o} ,\lambda_{\zeta } ,\lambda_{z}$, given by Eq. 7

1.4 Equilibrium and boundary conditions

The total Cauchy stress in Eq. 3 (i.e., $\varvec{t} = - p\varvec{I} + \bar{\varvec{t}}$) contains both volumetric and isochoric parts (Ogden 1997; Humphrey 2002; Holzapfel and Ogden 2010a). Constitutive parameters define the isochoric stress tensor $\bar{\varvec{t}}$ (Sect. 2.2), but the volumetric component $- p\varvec{I}$ needs to be determined from the equilibrium and boundary conditions (Humphrey 2002; Holzapfel and Ogden 2010a).

Assuming quasi-static motions (Humphrey 2002), in the absence of body forces, for each of the deformations depicted in Fig. 1, the equilibrium equation is

$$\text{div}\,\varvec{t} = 0,$$

(13)

where $\text{div}$ represents the spatial divergence. Equation 13 can then be used to find the Lagrange multiplier $p$ in Eq. 3, along with the unknown stretches.

For the deformation associated with the specimen flattening, Eq. 13 reduces to Ogden (1997) $t_{11} = 0 ,$ and from Eq. 3, the volumetric part of the Cauchy stress can then be determined as $p = \bar{t} _{11} .$

In the load-free configuration, the only nontrivial component of Eq. 13 is (Humphrey 2002; Holzapfel and Ogden 2010a)

$$\text{div}\,\varvec{t} = 0 \Rightarrow \frac{{\partial t_{\rho \rho } }}{\partial \rho } + \frac{{t_{\rho \rho } - t_{\vartheta \vartheta } }}{\rho } = 0$$

which reduces to

$$t_{\rho \rho } \left( \rho \right) = \mathop \int \limits_{{\rho_{i} }}^{\rho } \frac{{\bar{t} _{\vartheta \vartheta } - \bar{t} _{\rho \rho } }}{\rho }d\rho ,$$

(14)

for $t_{\rho \rho } \left( {\rho_{i} } \right) = 0$. The Lagrange multiplier can then be calculated at each point through the thickness of the artery by substituting t_ρρ into Eq. 3, i.e.,

$$p\left( \rho \right) = \bar{t} _{\rho \rho } - t_{\rho \rho } .$$

In addition, since axial force vanishes in the load-free configuration due to release of longitudinal pre-stretch, the axial global equilibrium can be written as (Humphrey 2002; Holzapfel and Ogden 2010a)

$$F_{\zeta } = 2\pi \mathop \int \limits_{{\rho_{i} }}^{{\rho_{o} }} t_{\zeta \zeta } \rho {\text{d}}\rho = 0 ,$$

(15)

where F_ζ denotes the axial force. The above equation can be further reduced to (Humphrey 2002)

$$F_{\zeta } = \pi \mathop \int \limits_{{\rho_{i} }}^{{\rho_{o} }} \left( {2\bar{t} _{\zeta \zeta } - \bar{t} _{\rho \rho } - \bar{t} _{\vartheta \vartheta } } \right)\rho {\text{d}}\rho = 0 .$$

(16)

Equations 14 and 16 combined with the boundary condition $t_{\rho \rho } \left( {\rho_{o} } \right) = 0$ are then solved together to calculate the unknown stretches $\lambda_{\vartheta }^{o}$ and $\frac{\xi }{L}$ in Eq. 6

Similar to Eq. 14, for the loaded configuration (Fig. 1c), one can write

$$t_{rr} \left( r \right) = \mathop \int \limits_{{r_{i} }}^{r} \frac{{\bar{t} _{\theta \theta } - \bar{t} _{rr} }}{r}{\text{d}}r - P_{i} ,$$

(17)

where P_i is the internal luminal pressure, and the Lagrange multiplier is determined according to

$$p\left( r \right) = \bar{t} _{rr} - t_{rr} .$$

Furthermore, assuming no pressure on the outer surface of the artery, one can find

$$t_{rr} \left( {r_{o} } \right) = \mathop \int \limits_{{r_{i} }}^{{r_{o} }} \frac{{\bar{t} _{\theta \theta } - \bar{t} _{rr} }}{r}{\text{d}}r - P_{i} = 0 ,$$

(18)

which can be used to find $\lambda_{\theta }^{o}$ in Eq. 7. Finally, the axial force in the loaded configuration can be calculated from (Humphrey 2002)

$$F_{z} = \pi \mathop \int \limits_{{r_{i} }}^{{r_{o} }} \left( {2\bar{t} _{zz} - \bar{t} _{rr} - \bar{t} _{\theta \theta } } \right)r{\text{d}}r .$$

(19)

1.5 Variability of the mechanical properties within age groups

The four-fiber family constitutive parameters adjusted for the effects of flattening and representing the 25th and 75th percentiles within each age group are summarized in Tables 2 and 3, respectively.

Table 2 Parameters for the four-fiber family constitutive model describing the isochoric behavior of human FPAs in seven age groups at the 25th percentile. Parameters are adjusted for the effects of flattening. Here, n is the sample size in each group that was used to derive these parameters. The coefficient of determination R² = 0.99 for all age groups

Table 3 Parameters for the four-fiber family constitutive model describing the isochoric behavior of human FPAs in seven age groups at the 75th percentile. Parameters are adjusted for the effects of flattening. Here, n is the sample size in each group that was used to derive these parameters. The coefficient of determination R² = 0.99 for all age groups