1 1 Introduction

Pressure ulcers are localized areas of soft tissue breakdown resulting from sustained mechanical loading. The wounds either start in the skin, from which they may extend towards deeper tissue layers, or they arise in deep tissue layers and progress towards the skin. The current paper focuses on deep tissue injury, recently defined as pressure-related injury to subcutaneous tissues while the skin is still intact (Donnelly 2005). The reason for this is that those deep pressure ulcers, often starting in skeletal muscle tissue overlying bony prominences, develop much faster and yield more extensive ulceration than superficial ulcers. In addition, these ulcers are hard to detect. When they become visible at the skin surface, extensive tissue degeneration may already have occurred in deeper tissue layers. Spinal cord injured patients are especially vulnerable for these wounds (Bours et al. 2002; Garber and Rintala 2003; McKinley et al. 1999). Pressure ulcer prevalence rates for this group are very high (30–60%), and a recent study in the United States (Garber and Rintala 2003) has shown that 56% of these ulcers are deep pressure ulcers.

1.1 1.1 Problem

To develop good, objective methods for early detection of deep tissue injury and to develop a method to identify patients at risk of getting a pressure ulcer, it is necessary to understand the way tissues react on mechanical loading. It is generally accepted that external loading is the primary cause of pressure ulcers, but the subsequent pathway leading to damage is still unclear. The most often adhered hypothesis is that tissue compression inhibits capillary perfusion, leading to ischaemia, and after removal of the load to reperfusion injury (Grisotto et al. 2000; Kosiak 1961; Peirce et al. 2000). However, disturbance of the metabolic equilibrium due to impaired lymph circulation and compromised interstitial fluid transport have also been proposed as aetiological factors (Miller and Seale 1981; Reddy 1990). More recently, it has been shown that cellular deformation in itself can produce damage to muscle cells, increasing in time and with magnitude of compression (Bouten et al. 2001; Breuls et al. 2003). The individual contributions of these pathways and their interactions are unknown. Bosboom et al. (2003) and Stekelenburg et al. (2006) have observed that in the initial stages of muscle damage, healthy and damaged cells form an alternating pattern, suggesting an important role for the microstructure in the load transmission. It might also be that dying cells protect healthy cells.

Stekelenburg et al. (2007) demonstrated in animal studies that 2 h of compressive loading, inducing both cellular deformation and ischaemia, led to damage in muscle tissue that was still visible after 24 h, while 2 h of pure ischaemia resulted in signs of damage that disappeared within an hour after load removal. She hypothesized that deformation initiates damage, but that ischaemia causes the damage to grow faster than would otherwise be the case.

1.2 1.2 Objective

The objective of the current study is to increase the understanding of the underlying mechanisms in the onset of deep pressure ulcers. This means that the study focuses on skeletal muscle tissue. Our hypothesis is that the aetiology is dominated by the interplay between cellular deformation and deformation-induced ischaemia. In our opinion, it is very important to understand transport properties and metabolic processes, and in particular how they are influenced by tissue compression.

1.3 1.3 Approach

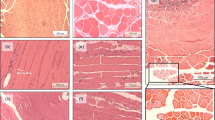
It became evident from earlier observations that in order to understand the way damage develops in tissues, the microstructure of the tissue should be studied. The pattern of interspersed healthy and dead cells (Fig. 1) Stekelenburg et al. (2006) found after compression suggests that whether or not a cell becomes damaged cannot be predicted by considering each cell as an individual, but that cell-cell interactions and the typical muscle microstructure should be taken into account. It is also clear that oxygen and nutrients are not evenly spread over tissues, but that there is a spatial component in the distribution. Moreover, in experiments, it is difficult to separate the individual contributions of deformation and ischaemia to damage development. That is why it was decided to develop a microstructural model of skeletal muscle tissue, which is a combination of a solid mechanics model to determine tissue deformations and stresses, and a transport model that describes the spatial distribution of oxygen in the tissue. The questions addressed in the present paper are if cessation of oxygen consumption in dead cells is beneficial for the remaining cells in the tissue, and if a change in mechanical properties upon cell death affects damage development in other cells.

Fig. 1
figure 1

Transverse cross-section of skeletal muscle after 2 h of mechanical loading, stained with Gomori’s trichrome: the damage pattern is a mixture of healthy (dark) and necrotic fibres (light, arrows) (Stekelenburg et al. 2006, with permission)

Full size image

2 2 Materials and methods

To answer these questions, a finite element model was developed that describes deformation, diffusion and damage in a cross-section of skeletal muscle tissue. An outline of the model is presented in Fig. 2. To assess tissue injury at a certain predefined compression level, the mesh is compressed and the diffusion model is solved to obtain the steady state oxygen distribution with the (partially) collapsed capillaries as oxygen supplies. Damage is only assessed at the predefined compression level, because the actual process of applying tissue deformation is too fast for any hypoxic damage to occur. Damage grows in time until one cell dies. This changes the mechanical properties of the cell, the oxygen distribution in the tissue and the rate of damage growth in the remaining cells, making a reevaluation of the total loop necessary. This is repeated until all cells are dead or no more cells die within a reasonable amount of time.

Fig. 2
figure 2

Outline of finite element model: left Compression is applied to a mesh consisting of cells, ecm and capillaries, resulting in decreased capillary-cross-sections that determine the oxygen supply for the diffusion model. Healthy cells are oxygen sinks in the oxygen diffusion model, in which the partial oxygen pressures (pO2) are calculated. When the resulting pO2’s remain above a threshold, the tissue remains healthy, but if they fall below a threshold, damage starts to accumulate (see right). This leads to cell death for some cells, of which the properties change subsequently. This has consequences for both the deformation and diffusion, necessitating another loop of the model if not all cells have died yet. Right In the damage model, damage in each cell is updated according to the current extent of hypoxia. When the damage in all cells is still below the threshold for cell death, time is updated and damage accordingly until damage does exceed the death threshold in one or more cells

Full size image

The mesh is a representative volume element consisting of cells (muscle fibres), extracellular matrix (ecm), and holes representing capillaries (Fig. 3). Cells and ecm are modelled with extended quadratic, triangular, plane strain, Updated Lagrange elements. Since pilot studies with changing mechanical properties of dead cells revealed that the necessary large deformations led to problems due to distorted elements, the effect of the change in mechanical properties is evaluated on a smaller mesh, only one quarter of the one shown in Fig. 3.

Fig. 3
figure 3

Mesh and boundary conditions for deformation model: the mesh consists of cells (light grey), ecm (dark grey) and capillaries (holes, white). Movement in vertical direction is suppressed along the lower boundary of the mesh, and a downward displacement is prescribed on the upper boundary

Full size image

The model is solved with the finite element package Sepran (Segal 1984), using an HSL solver (HSL 2002) for the deformation part and an iterative generalised minimum residual solver for the diffusion part.

2.1 2.1 Deformation

In the deformation part, the impulse balance (Eq. 1) is solved with a hyperelastic constitutive law for both ecm and cells (Eq. 2):

$$\vec \nabla \cdot \sigma = \vec 0$$
$$\sigma = \kappa {{\ln \left( J \right)} \over J}{\rm{I}} + {G \over J}\left( {{\rm{B}} - {J^{{2 \over 3}}}{\rm{I}}} \right)$$

In these equations, σ is the Cauchy stress, B is the Finger tensor, defined as F · F c with F the deformation tensor, G is the shear modulus (156 kPa), and κ is the compression modulus (598 kPa). Cells and ecm were given the same initial material properties. After a cell has died, both its shear and compression modulus are reduced to 2/3 of their original values.

Deformation is applied in the form of unconfined compression (Fig. 3). A constant pressure (−0.5 kPa) is defined inside the holes, accounting for the hydrostatic pressure exerted by the blood in these vessels. The resulting deformed areas of the capillary cross-sections are determined and used in the calculation of boundary conditions for the diffusion model.

2.2 2.2 Diffusion

The curves surrounding the capillary holes are considered as the layers of ecm surrounding the capillaries, and the oxygen pressure there (pO cap2 ) is expressed as a function of the capillary cross-section (A cap). This capillary cross-section is assumed to determine the size of the erythrocyte flux and therefore the amount of oxygen delivered to the tissue. The small percentage of dissolved oxygen in the blood is neglected (3%, Guyton and Hall 2000).

The erythrocyte flux (Q ery) is equal to the blood flow (Q blood) multiplied by the discharge hematocrit (H D) (Goldman and Popel 2000), which is the erythrocyte content:

$${Q_{{\rm{ery}}}} = {Q_{blood}}{H_{\rm{D}}}$$

The blood flow is proportional to the capillary cross-section (A cap) squared and inversely proportional to the apparent viscosity (η a) according to Poiseuille’s law:

$${Q_{{\rm{blood}}}} \sim {{A_{{\rm{cap}}}^2} \over {{\eta _{\rm{a}}}}}$$

The apparent viscosity is again strongly dependent on blood vessel cross-section and the discharge hematocrit, for which Pries et al. (1994) and Pries (1996) developed an elaborate viscosity law which was substituted in Eq. (4). Since capillary cross-sections constitute only a small part of the range of cross-sections for which this viscosity law applies, and the discharge hematocrit was assumed to be constant, the resulting relation was simplified by fitting it with a parabolic relation between erythrocyte flux and cross-section to the relevant range of cross-sections.

Assuming that pO cap2 is proportional to the erythrocyte flux and equal to 5.3 kPa when the capillary is not deformed (A 0cap ), the following equation is obtained:

$$p{\rm{O}}_2^{{\rm{cap}}} = \left\{ {\matrix{ {5.3{{\left( {{{{A_{{\rm{cap}}}}} \over {A_{{\rm{cap}}}^0}}} \right)}^{2.5}}} & {{\rm{if}}{{{A_{{\rm{cap}}}}} \over {A_{{\rm{cap}}}^0}} > 0.25} \cr 0 & {{\rm{if}}{{{A_{{\rm{cap}}}}} \over {A_{{\rm{cap}}}^0}} \le 0.25} \cr } } \right.$$

The second part of this equation accounts for the fact that despite their high deformability, erythrocytes cannot pass through a capillary with a cross-section that has fallen below a critical value (Potter and Groom 1983; Xakellis et al. 1991), which was set to 25% of the original capillary cross-section.

The oxygen pressures calculated with Eq. (5) are used as essential boundary conditions to solve the steady state diffusion equation, with oxygen consumption in the cells as a negative source term:

$$\vec \nabla \cdot \left( {D\vec \nabla P} \right) - {{{V_{\rm{m}}}P} \over {{K_m} + P}} = 0$$

The first term represents the oxygen diffusion in the tissue, with D the oxygen diffusion coefficient (2.41 × 10−3 mm2 s−1, Bentley et al. 1993), \({\vec \nabla }\) the gradient operator, and P the partial oxygen pressure.

The second term describes oxygen consumption for which Michaelis-Menten kinetics was assumed (Goldman and Popel 2000; Lo et al. 2003), with K m the oxygen tension at which the consumption rate is half maximum (0.25 kPa, Honig and Gayeski 1982; Richmond et al. 1999), and V m the maximum rate of oxygen consumption. The value of V m was chosen such (order of magnitude 102 kPa s−1) that the oxygen pressures in the cells were at a physiological level.

Since it is known that the density of mitochondria is much higher directly beneath the cell membrane than between the myofibrils in a skeletal muscle cell (Kunz 2001; Kuznetsov et al. 1998; Philippi and Sillau 1994), the oxygen consumption in a small layer under the sarcolemma was made higher than in the remainder of the cell. This subsarcolemmal area is defined as the region within 1µm of the cell membrane (Philippi and Sillau 1994), where V m was made four times higher than V m in the rest of the cell, with K m equal in both cell regions. This ensures a more homogeneous oxygen distribution within the cell.

Steady state is assumed because the characteristic diffusion time is much shorter than the characteristic time needed for a pressure ulcer to develop. When the diffusion model has been solved at the predefined compression level, damage due to a lack of oxygen can be evaluated.

2.3 2.3 Damage

Up to a certain duration of ischaemia, the injury is reversible, but it will become irreversible if the ischaemic period lasts too long. For skeletal muscle cells, it is known that they have an ischaemic tolerance time of approximately 4 h (Blaisdell 2002).

It is assumed that cell damage (Dm cell) starts to accumulate when the partial oxygen pressure falls below a threshold value of γ (0.13 to 0.32 kPa, Guyton and Hall 2000; Richmond et al. 1999), according to the following equation:

$$D{m_{{\rm{cell}}}}\left( t \right) = {{{s_{{\rm{cell}}}}} \over {{A_{{\rm{cell}}}}}}\sum\limits_{e = 1}^{Nel} {\left\{ {\matrix{ {{A_e}\int {_t} \left( {{{\gamma - {P_e}} \over \gamma }} \right){\rm{d}}t} \hfill & {{\rm{if }}{P_e} < \gamma } \hfill \cr 0 \hfill & {{\rm{if }}{P_e} \ge \gamma } \hfill \cr } } \right.} $$

The damage is calculated as an area-weighted average of the damage in the Nel individual elements of the cell with partial oxygen pressure P e, and area A e. A cell is the area of the total cell, and t is the time in hours. When the accumulated damage Dm cell exceeds 1, the cell dies. This definition of damage is based upon the assumption that the oxygen need in a cell is proportional to its size, in agreement with the size-dependent consumption of the cells in the present model.

The cell-specific sensitivity parameter s cell is introduced because it is known that some cells die after only 3 h of ischaemia, while others can survive 5 h of complete ischaemia. Each cell in the mesh is assigned an s cell between 1/6 and 1/3, corresponding to cell death after respectively 6 to 3 h of complete ischaemia. The distribution of these sensitivities is random, but the amount of cells with a particular sensitivity corresponds to data from Labbe et al. (1987).

Cellular damage Dm cell is allowed to grow until it reaches the threshold for cell death in one cell (or in more cells simultaneously). The mechanical properties of these dead cells change, and they stop consuming oxygen. The deformation and diffusion state are reevaluated (without further compression), and thereafter damage continues to grow.

3 3 Results

3.1 3.1 Effect of cessation of consumption after cell death

The mesh shown in Fig. 3 was subjected to unconfined compression until its height was reduced with 22, 20, 18, 16, 14, 12, or 10%. In each of these deformed states, hypoxic damage was assessed as a function of time. Two cases are considered to see whether cessation of consumption in dead cells influences the course of damage development. In case stopy, a cell stops consuming oxygen after it has died, while in case stopn it continues consuming oxygen after death. In both cases, the mechanical properties of dead cells do not change.

A compression of only 10% was too small to produce any dead cells within 72 h in both cases. For larger deformations, the first cell of course dies at the same time in both cases, but thereafter cell death is delayed or even prevented in case stopy compared to case stopn (Fig. 4). The difference between the two cases becomes larger after more cells have died (compare the different panels in Fig. 4), and it is more pronounced at lower compression levels.

Fig. 4
figure 4

Compression versus time curves for hypoxic cell death in cases stopy (consumption stops in dead cells) and stopn (dead cells continue to consume oxygen): The graphs show from top to bottom the time it takes for respectively 3, 11 and all of the cells to die at compression levels up to 22%. In case stopy, cells die later than in case stopn. This effect is more pronounced after more cells have died and at lower compression levels

Full size image

The time course of the partial oxygen pressures in a cell shows an increase after a cell has died with which it shared one or more capillaries.

3.2 3.2 Effect of decrease in stiffness after cell death

The effect of changing mechanical cell properties upon cell death was studied at compression levels of 19, 17, 15, 13, 11 and 9% on a mesh with four cells. The mechanical properties of a cell are either adapted after cell death (case propy), or kept unchanged (case propn).

The results show that there is indeed a difference in damage accumulation between cases propy and propn when the compression is more than 11% (Fig. 5). Smaller deformations do not lead to more than 1 dead cell within the considered 72 h. For compression levels of 15% or higher, case propy delays cell death after the first two cells have died. However, at a compression of only 13%, only two cells die, and in case propn this takes longer than in case propy.

Fig. 5
figure 5

Compression versus time curves for hypoxic cell death in cases propy (mechanical properties change in dead cells) and propn (mechanical properties do not change in dead cells): The graphs show from top to bottom the time it takes for respectively 1, 2, 3 and all of the cells to die at compression levels up to 19%. For high compression levels, cells eventually die later in case propy than in case propn

Full size image

Results on other meshes or with other distributions of the cell sensitivities are similar. For smaller deformations or when only a few of the cells have died yet, case propn can be somewhat more favourable than propy, but in the end, case propy turns out more advantageous.

Studying capillary cross-sections in time reveals that the exact position of a capillary determines whether its cross-section will become smaller or larger when a particular cell becomes less stiff than before.

4 4 Discussion

Two questions have been addressed regarding deformation-induced hypoxic damage development in skeletal muscle tissue. The finite element model presented above was used to evaluate the influence of both a cessation of consumption and a decrease in cell stiffness after cell death on further damage development.

The results show a dramatic increase in cell death at large compressions, and a much slower damage development for low compression levels. They also demonstrate that a cessation of oxygen consumption after cell death is beneficial for the remaining cells, since more oxygen becomes available for these cells. This effect gradually increases with time, when more cells have died so the amount of extra oxygen available becomes larger and larger. It is also more pronounced at lower compression levels, since in the high compression states the oxygen supply to the tissue is so small due to almost completely collapsed capillaries that a redistribution does not make much difference.

The second issue addressed in this paper was the influence of a change in mechanical properties of a cell after it had died. We hypothesized that a cell becomes less stiff when it dies because it loses its structural integrity. This indeed leads to changes in damage accumulation. For smaller deformations or only a few dead cells, changed material properties are sometimes disadvantageous for tissue viability, but when more cells have already died, weakening of dead cells delays further cell death in comparison to the case where mechanical properties remain unchanged.

4.1 4.1 Model mechanics

The inhomogeneities introduced in the mesh by changing material properties of dead cells led to distorted elements in large meshes. This prohibited the evaluation of damage in these meshes at the large compression levels that are relevant for pressure ulcer development, and forced the use of smaller meshes with less cells. Therefore, the above discussed findings are only preliminary and the effect of changing properties has to be tested further. However, the current results suggest that weakening of cells initially leads to a redistribution of strains that compresses some capillaries more, while others become a little bit less collapsed. The exact locations of capillaries and dead cells are both important determinants for further damage growth in the cells. After more cells have died, most of the capillaries will probably be more open than with the stiffer, viable cells. This will then delay further cell deaths, making the weakening of dead cells protective for other cells in the end.

The initial material properties used in the model are identical for both ecm and cells. This choice has been made since the layer of ecm is so thin in reality that its properties will hardly influence the overall mechanical properties. The values of the shear and compression moduli were chosen such that the stresses in compression resembled those predicted by the model fitted by Bosboom et al. (2001).

The amount with which a cell’s stiffness is reduced after it has died is arbitrary, but enough to show that remodelling indeed influences damage development in muscle tissue. There are reports though, stating that overall muscle stiffness increases after prolonged compression (Gefen et al. 2005; Linder-Ganz and Gefen 2004), which is strange considering the fact that the structure of the cytoskeleton is disrupted. A possible explanation for this observation is the formation of oedema after load removal.

4.2 4.2 Oxygen transport

In the model presented in this paper, no up- or downstream effects of compression on blood flow were taken into account, nor were autoregulatory mechanisms. The latter include responses to metabolic alterations, which might be interesting to implement in the future if metabolism is more accurately modeled. Literature about the compartment syndrome is concerned with the former effects (Reneman et al. 1980; Mellander and Albert 1994; Shrier and Magder 1995), but extension to 3 dimensions would be necessary, and including the effects of increased tissue pressure on different parts of the circulation would divert the model’s focus to these complicated mechanisms. To explore concepts of damage development, 2 dimensions are thought to be sufficient. For now, it was assumed that an external mechanical load simply exerted its effect on perfusion via collapse of capillaries, which is often stated to be one of the main causes of pressure ulcers (Kosiak 1961; Nola and Vistnes 1980; Bogie et al. 1995; Thompson 2005).

For the effect of the capillary collapse on the oxygen supply, a simplified description was used since the aim was to study the importance of hypoxic damage due to ischaemia in the aetiology of deep pressure ulcers, and not to model the oxygen transport on the microlevel of a muscle as realistically as possible.

Oxygen buffering and transport by myoglobin has also been left out of consideration. Although this might influence the appearance of hypoxic tissue areas (Beard et al. 2001, Ji et al. 2006), it will probably not alter the pattern of cell death at different compression levels. It might explain the rather large value of the maximum oxygen consumption compared to literature values (Goldman and Popel 2000, 2001; Philippi and Sillau 1994) that was necessary to get realistic tissue oxygen pressures.

4.3 4.3 Damage

A lack of oxygen is the only factor contributing to cell injury in the present model, although ischaemia can also lead to damage through acidosis, a lack of nutrient supply or impaired removal of waste products. The cell death threshold in this study is equal to the amount of damage accumulated after 3 to 6 h of complete hypoxia, corresponding to cell sensitivities of 1/3 to 1/6 respectively. The number of cells with a certain sensitivity was chosen such that complete collapse of all the capillaries led to approximately the same time course of cell death as did the study by Labbe et al. (1987), who measured the amount of necrotic fibres due to complete ischaemia in canine skeletal muscle. In the present damage calculations, the oxygen lack can therefore be seen as a measure of the severity of ischaemia, and the damage as the resulting ischaemic damage.

The model is meant to study the consequences of muscle tissue injury on further damage development rather than exactly predict the time of tissue injury. Therefore, a simple linear fit to the data from Labbe et al. (1987) to construct the damage law was thought to be sufficient.

Evaluation of damage in the present model does not include recovery, while it is known that ischaemic damage to skeletal muscle cells can be reversed if reperfusion starts in time (Blaisdell 2002; Stekelenburg et al. 2007). It is also known however that reperfusion can deteriorate the damage (Chan et al. 2004; Logue et al. 2005), which is very interesting in view of the advised shifting of position every few hours to prevent pressure ulcers.

The introduction of two regions in the cell with different oxygen consumption rates to account for the inhomogeneous mitochondrial distribution in the cell led to a more homogeneous oxygen distribution within the cells. This more realistic situation proved to be beneficial during the simulated ischaemia, i.e. damage was delayed.

Although the compression versus time curves from the model resemble those found in the literature (Reswick and Rogers 1976; Sacks 1989; Kosiak 1959), they are shifted somewhat to the right. This means that the model predicts that damage occurs after longer periods of deformation than the experimental curves in literature indicate. This is easily explained by the fact that skeletal muscle cells can tolerate ischaemia for approximately 4 h (Blaisdell 2002), so there will not be much ischaemic cell death after less than 4 h of mechanical loading. This indicates that there has to be something more, e.g. that compression makes cells more sensitive for ischaemia-induced damage, or that compression in itself is harmful for cells. This is supported by animal studies by Stekelenburg et al. (2007). In future research, we will incorporate hypothetical damage-producing mechanisms for these ideas to try to elucidate the pathway through which cell deformation and ischaemia cooperate to produce damage.