Towards in vivo aorta material identification and stress estimation

Abstract

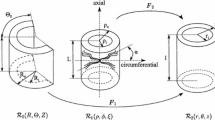
This paper addresses the problem of constructing a mechanical model for the abdominal aorta and calibrating its parameters to in vivo measurable data. The aorta is modeled as a pseudoelastic, thick-walled, orthotropic, residually stressed cylindrical tube, subjected to an internal pressure. The model parameters are determined by stating a minimization problem for the model pressure and computing the optimal solution by a minimization algorithm. The data used in this study is in vivo pressure–diameter data for the abdominal aorta of a 24-year-old man. The results show that the axial, circumferential and radial stresses have magnitudes in the span 0 to 180 kPa. Furthermore, the results show that it is possible to determine model parameters directly from in vivo measurable data. In particular, the parameters describing the residual stress distribution can be obtained without interventional procedures.

Appendix

Equilibrium conditions in cylindrical coordinates are well known and are presented in standard textbooks when written in terms of the Cauchy stress. However, we use the first Piola–Kirchhoff stress and two sets of base vectors as explained in the section on deformation. Therefore, an explicit derivation of Eqs. (7), (8) and (9) seems appropriate.

The divergence of a tensor T, denoted divT is defined by

$$ {\left( {{\text{div}}{\user2{T}}} \right)} \cdot {\mathbf{c}} = {\text{div}}{\left( {{\user2{T}}^{{\text{T}}} {\mathbf{c}}} \right)} $$

(32)

for any constant vector c. The left-hand side of Eq. (32) is the divergence of a vector field and is assumed well defined.

Taking an arbitrary vector c = c _i j _i ( αφ) we may write

$$ {\user2{T}}^{{\text{T}}} {\mathbf{c}} = T_{{iK}} c_{i} {\mathbf{j}}_{K} {\left( \phi \right)}. $$

Thus, T _iK c _i are the components of the vector T ^T c in cylindrical coordinates. The divergence of a vector in such coordinates is well known, and we have from the definition of divergence of a tensor in Eq. (32) that

$$ {\left( {{\text{div}}{\user2{T}}} \right)} \cdot {\mathbf{c}} = \frac{\partial } {{\partial s}}{\left( {T_{{i1}} c_{i} } \right)} + \frac{{T_{{i1}} c_{i} }} {s} + \frac{1} {s}{\left( {\frac{\partial } {{\partial \phi }}{\left( {T_{{i2}} c_{i} } \right)}} \right)} + \frac{\partial } {{\partial _{z} }}{\left( {T_{{i3}} c_{i} } \right)}. $$

(33)

Since c is constant we have

$$ \frac{{\partial c_{i} }} {{\partial \phi }}{\mathbf{j}}_{i} {\left( {\alpha \phi } \right)} = c_{i} \frac{{\partial {\mathbf{j}}_{i} {\left( {\alpha \phi } \right)}}} {{\partial \phi }}. $$

(34)

Furthermore, one concludes from definitions of base vectors

$$ \begin{array}{*{20}c} {{\frac{{\partial {\mathbf{j}}_{1} {\left( {\alpha \phi } \right)}}} {{\partial \phi }} = \alpha {\mathbf{j}}_{2} {\left( {\alpha \phi } \right)},}} &{{\frac{{\partial {\mathbf{j}}_{2} {\left( {\alpha \phi } \right)}}} {{\partial \phi }} = - \alpha {\mathbf{j}}_{1} {\left( {\alpha \phi } \right)}.}} \\ \end{array} $$

(35)

Equations (34) and (35) imply

$$ \begin{array}{*{20}c} {{\frac{{\partial c_{1} }} {{\partial \phi }} = c_{2} \alpha ,}} &{{\frac{{\partial c_{2} }} {{\partial \phi }} = c_{1} \alpha ,}} \\ \end{array} $$

which we introduce into Eq. (33) and use

$$ \begin{array}{*{20}c} {{\frac{{\partial c_{3} }} {{\partial \phi }} = 0,}} &{{\frac{{\partial c_{i} }} {{\partial z}} = 0,}} &{{\frac{{\partial c_{i} }} {{\partial s}} = 0}} \\ \end{array} $$

to obtain

$$ \begin{array}{*{20}l} {{{\left( {{\text{div}}{\user2{T}}} \right)} \cdot {\mathbf{c}}} \hfill} & { = \hfill} & {{{\left( {\frac{{\partial T_{{11}} }} {{\partial s}} + \frac{{T_{{11}} }} {s} + \frac{1} {s}\frac{{\partial T_{{12}} }} {{\partial \phi }} - \frac{{T_{{22}} }} {s}\alpha + \frac{{\partial T_{{13}} }} {{\partial z}}} \right)}c_{1} + } \hfill} \\ {{} \hfill} & {{} \hfill} & {{{\left( {\frac{{\partial T_{{21}} }} {{\partial s}} + \frac{{T_{{21}} }} {s} + \frac{1} {s}\frac{{\partial T_{{22}} }} {{\partial \phi }} + \frac{{T_{{12}} }} {s}\alpha + \frac{{\partial T_{{23}} }} {{\partial z}}} \right)}c_{2} + } \hfill} \\ {{} \hfill} & {{} \hfill} & {{{\left( {\frac{{\partial T_{{31}} }} {{\partial s}} + \frac{{T_{{31}} }} {s} + \frac{1} {s}\frac{{\partial T_{{32}} }} {{\partial \phi }} + \frac{{\partial T_{{33}} }} {{\partial z}}} \right)}c_{3} .} \hfill} \\ \end{array} $$

Since c is arbitrary Eqs. (7), (8) and (9) now follow. For a different derivation of these equations, see Warne and Warne (1999a, 1999b).