1 Introduction

Wind stress and surface heating are generally the two most important factors driving physical processes within lakes (Wüest and Lorke 2003). Water movements forced by the wind produce turbulent mixing which combines with surface heating or cooling to determine the vertical structure of the lake and mediate the vertical fluxes of scalars which, in turn, have major impacts on lake ecology. In order to understand fully the functioning of lakes, it is, therefore, important to have a detailed understanding of how atmospheric forcing affects the system, especially in an era of climate change.

Following the autumnal overturn, the water column stability of temperate lakes becomes minimal and vertical homogeneity tends to persist throughout the winter months, except when the surface temperature falls below 4 °C to induce an inverse temperature gradient. In such conditions of minimal stability, momentum introduced by the surface wind stress can penetrate vertically through a lake, and thus influence mixing near the bed. During summer, when a lake is thermally stratified, the thermocline acts to inhibit the downward penetration of direct vertical mixing. At the same time, however, wind stress acts to induce oscillatory internal wave motions (seiches), which extend down through the water column to the bottom boundary layer (BBL). In the summer regime, seiches are widely observed to be the most energetic large-scale motions in stratified lakes and are responsible for driving turbulence and, thus, mixing in the deeper waters (Imberger 1998). They promote vertical fluxes of nutrients, cause sediment re-suspension within the BBL, and also redistribute water masses within a lake; all of which can influence primary productivity and water quality (Gloor et al. 2000; Ostrovsky et al. 1996; MacIntyre et al. 1999). Internal seiches have also been shown to have implications for the distributions of variables such as dissolved oxygen in the metalimnion (Eckert et al. 2002) and in the BBL (Nishri et al. 2000), and the dominance of metalimnetic communities of cyanobacteria (Pannard et al. 2011).

As the summer season progresses, the evolving density structure, together with wind forcing over a wide range of frequencies, allows internal seiches to develop into a number of modes whose frequencies increase with the intensifying seasonal stratification (Wiegand and Chamberlain 1987; Simpson et al. 2011). As the frequency of an individual seiche mode changes, it may be affected by resonance in which the seiche period matches that of the wind forcing (Thorpe 1974; Antenucci et al. 2000). Such resonance can lead to an increase in turbulent kinetic energy and mixing within the water column without an increase in the magnitude of the wind stress.

In this contribution, we examine the changes which occur in the efficiency of energy input by wind stress to a temperate lake, Windermere, during the spring transition from a mixed water column to the summer stratified regime. The efficiency of energy transfer is a useful measure of the ability of a lake to extract energy imposed from wind stress, which can vary temporally and can be used to characterise differences between lakes. Our study is based on a new analysis of a data set which was previously used to investigate turbulent dissipation in the BBL and pycnocline of Windermere (Simpson et al. 2015). An interesting feature of the previous study was the observation of a marked increase in the mean kinetic energy of water column flow during the observation period without a corresponding increase in wind stress forcing. It is this feature that has prompted a more detailed investigation of the energetics of Windermere. In this new analysis, the rate of working by surface wind stress on the surface layer of the lake is related to the downward energy flux in the atmosphere to determine the changes in the efficiency of energy transfer to the lake and its relation to changes in the natural period of the dominant seiche. The new results are combined with the dissipation measurements from the previous study in order to estimate the fraction of energy input that is dissipated in the BBL, and we calculate changes in the potential energy anomaly to provide an estimate of the proportion of energy used in mixing the water column.

2 Study site

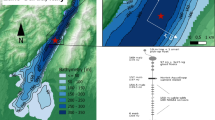
Our study is based on measurements in the south basin of Windermere (Fig. 1, English Lake District; 54.343° N, −2.941° E), the largest natural lake in England. Windermere has been a focus for studies in physical limnology since the pioneering work of Clifford Mortimer who made careful measurements of the changes in water column temperatures and used them to clarify the role of seiche motions in lakes (Mortimer 1952), a study which stimulated a rigorous theoretical analysis of internal seiches by Heaps and Ramsbottom (1966).

Fig. 1
figure 1

Bathymetric map, with contours in metres, of Windermere South Basin (after Ramsbottom 1976) showing the location of the instruments (filled circle; depth ∼40 m) used in the investigation

Full size image

The south basin of Windermere, which is separated from the north basin by a shallow (2 m) sill, is long (∼10 km) and narrow (width, <1 km) with a surface area of ∼6.7 km2, a maximum depth of 42 m, and a mean depth of 16.8 m. The axis of the lake is approximately north to south and the winds are primarily steered by the terrestrial topography along the axial direction of the lake. Our observations in Windermere covered the period DOY (day of year) 99 (April 2) to 155 (June 4) in 2013.

3 Observational methods

Measurements of water motions and density structure were made with a combination of acoustic Doppler current profilers (ADCPs) and a chain of temperature sensors moored at the location shown in Fig. 1. The water column observations were complemented by measurements of the wind velocity above the lake surface from a raft-mounted meteorological station located close to the moored instruments near the centre of the lake. A full account of the instrument deployment and set-up is given in Simpson et al. (2015).

Measurements of the water column profile of velocity were obtained at the lake centre from a bottom-mounted 600-kHz ADCP (Teledyne RDI Workhorse) recording average profiles at intervals of Δt = 60 s based on 50 sub-pings, which were averaged to yield the components of horizontal velocity with a root mean square (rms) uncertainty of ∼1 cm s−1, and with a vertical bin size of Δz = 1 m. The velocity profiles extended from ∼2.1 mab (meters above bed) to a level ∼3.5 m below the lake surface. The validity of data from the top bin was established by checking continuity with the bins immediately below. Additional measurements of turbulence in the BBL and in the pycnocline were made using fast sampling ADCPs (1200 kHz, Teledyne RDI Workhorse), where an average of two sub-pings was recorded at intervals of 1 s giving an rms uncertainty of ∼0.4 cm s−1. The data were used to provide estimates of the dissipation of turbulent kinetic energy via the structure function (SF) method (Wiles et al. 2006); the results and analysis details are reported in Simpson et al. (2015). Here, we make further use of the BBL results in relation to the energy budget of the lake.

The chain of temperature sensors was made up of 20 Starmon thermistor microloggers recording every 60 s. The sensors were spaced at intervals of Δz = 1.5 m above 30 m depth and of Δz = 3.5 m below. The temperature data was recorded with a resolution of 0.01 °C and an accuracy of ∼0.1 °C. Wind speed and direction were measured at time intervals of 240 s by an automatic water quality monitoring station (AWQMS), specific details of which is provided in Woolway et al. (2015).

4 Analysis

4.1 Rate of working by the wind stress

The wind stress components (τ x, τ y) acting on the lake surface are determined from the wind observations via the quadratic drag law:

$$ \left({\tau}_{\mathrm{x}},{\tau}_{\mathrm{y}}\right)={C}_{\mathrm{d}}{\rho}_{\mathrm{a}} W\left( U, V\right), $$
(1)

where C d is the drag coefficient, calculated as a function of wind speed (Large and Pond 1981), ρ a is the air density, U and V are the components of the wind corrected to anemometer height, and W is the corresponding wind speed. We assume that the stress is continuous across the air-water interface and rotate coordinates to obtain the along axis and transverse components of the stress. Similarly, water column velocities are converted to axial and transverse components by rotating coordinates by 9° clockwise. The total rate of working (RW) by the axial, τ y, and transverse, τ x, components is then given by:

$$ \kern0.5em RW={RW}_{\mathrm{y}}+{RW}_{\mathrm{x}}={\tau}_{\mathrm{y}} v+{\tau}_{\mathrm{x}} u, $$
(2)

where (v, u) are the near-surface, axial, and transverse water velocity components which we take from the uppermost ADCP bin with valid data (see above). The total rate of working is a useful measure as it can be used to quantify the energy input of the wind to surface waters. It is positive when the surface current is directed in the same direction as the wind stress but can also be negative at times when the wind is directed in the opposite direction to that of surface currents, as can occur during seiche induced motions.

As a reference for the rate of energy input to a lake from the atmosphere, we use P 10, the rate of working in a horizontal plane above the lake (Lombardo and Gregg 1989):

$$ {P}_{10}={C}_{\mathrm{d}}{\rho}_{\mathrm{a}}\overline{W^3}, $$
(3)

which is obtained from the wind speed (averaged over 20 min), corrected to a height of 10 m (Large and Pond 1981).

4.2 Total BBL dissipation

The rate of turbulent kinetic energy dissipation, ε, in the BBL was determined from ADCP measurements using the SF method (Wiles et al. 2006). The resultant estimates of dissipation, which are averages over a vertical span (∼2 mab), were extrapolated using “law of the wall” (LOW) scaling to determine the total dissipation in the BBL. In the LOW regime, close to the boundary, dissipation varies inversely with height above the bed (z) according to:

$$ \epsilon (z)=\frac{u_{\ast}^3}{\kappa z}, $$
(4)

where \( {u}_{\ast }=\sqrt{\tau /\rho} \) is the friction velocity based on the frictional stress τ imposed on the bed by the flow and κ is the von Karman’s constant (∼0.41). The total dissipation in the BBL \( {\widehat{\epsilon}}_{\mathrm{BBL}} \) (NB units are W m−2) is then estimated by:

$$ {\widehat{\epsilon}}_{\mathrm{BBL}}=\rho {u}_{\ast}^3{\int}_{z_0}^{z_{\mathrm{t}}}\frac{1}{\kappa z} dz, $$
(5)

where ρ is the density of water, z 0 is the roughness length, and z t is the top of the boundary layer. The measured mean dissipation between levels z 1 and z 2 is:

$$ {\overline{\epsilon}}_{12}=\frac{\rho {u}_{\ast}^3}{\left({z}_2-{z}_1\right)}{\int}_{z_1}^{z_2}\frac{1}{\kappa z} dz, $$
(6)

so that the ratio of the total dissipation ϵ BBL to \( {\overline{\epsilon}}_{12} \) is given by

$$ \frac{{\widehat{\epsilon}}_{\mathrm{BBL}}}{{\overline{\epsilon}}_{12}}=\frac{\left({z}_2-{z}_1\right)\ \log \left({\mathrm{z}}_{\mathrm{t}}/{z}_0\right)}{ \log \left({z}_2/{z}_1\right)}. $$
(7)

4.3 Depth-uniform and depth-varying kinetic energy

The axial components of the water column velocities were used to determine the depth-mean KE dm and depth-varying KE dv components of kinetic energy as:

$$ \begin{array}{l}{KE}_{\mathrm{dm}}=\frac{1}{2}\rho\ {\left\langle v\right\rangle}^2;\left\langle v\right\rangle =\frac{1}{h}{\int}_{-\mathrm{h}}^0 v(z)\ dz\hfill \\ {}{KE}_{\mathrm{dv}}={\int}_{-\mathrm{h}}^0\frac{1}{2}\rho\ \left\langle {\widehat{v}}^2\right\rangle dz;\widehat{v}(z)= v(z)-\left\langle v\right\rangle, \hfill \end{array} $$
(8)

where h is the depth of the water column. Square brackets signify time averages and v(z) represents the along-lake velocity.

4.4 Internal seiche periods

In order to determine the periods of the internal seiche modes of the lake, the vertical density gradient, derived from the temperature profile data, was used to obtain the profile of N 2, the square of the buoyancy frequency, which is defined as:

$$ {N}^2=-\frac{g}{\rho}\frac{\partial \rho}{\partial z}, $$
(9)

where g is the acceleration due to gravity (m s−2) and \( \frac{\partial \rho}{\partial z} \) is the density gradient. The buoyancy frequency profile N 2(z) was then utilised in the equation for the complex amplitude of the vertical velocity ψ(z) (Gill 1982):

$$ \frac{d^2\psi}{{d z}^2}+\left\{\frac{N^2(z)}{c^2}\right\}\psi =0 $$
(10)

with boundary conditions ψ = 0 at the surface z = 0 and at the bottom z = −h. The eigenvalues of this equation for the first few vertical modes were found numerically using an established MATLAB code (Klink 1999), which also calculates the corresponding modal structure ψ n(z) for mode n from which the horizontal velocity modal structure U n(z) is derived. The eigenvalue is the phase velocity c n of mode n which is used to determine the seiche period T n = 2L/c n where L is the “effective length” of the basin, i.e. the length of a rectangular basin of constant depth. An initial estimate of L was refined by comparing with the seiche period determined independently from the cross-spectrum between the axial velocity at each level and that at the lowest bin level (See Simpson et al. 2011). Forming the co-spectrum improves the signal-to-noise ratio as the flow close to the bed tends to be dominated by seiche motions and is relatively free from “noise” associated with less regular motions further up in the water column.

4.5 Evolution of thermal stratification

As a measure of the strength of water column stratification, we use the potential energy anomaly, ϕ (Simpson 1981), which is defined as:

$$ \phi =\frac{1}{h}{\int}_{-\mathrm{h}}^0\left(\overline{\rho}-\rho (z)\right) gzdz;\overline{\rho}=\frac{1}{h}{\int}_{-\mathrm{h}}^0\rho (z) dz, $$
(11)

where the density profile ρ(z) is derived from the temperature data. ϕ is a measure of the energy required (in J m−3) to mix fully the water column; it is zero in mixed conditions and increases with water column stability. Note that ϕ reflects changes in \( \overline{\rho} \) and ρ(z).

5 Results

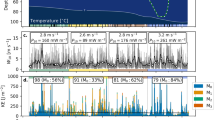
An overview of the velocity and temperature measurements in Windermere is presented in Fig. 2 along with the wind speed data. The 600-kHz ADCP data and that from the temperature loggers are continuous except for two breaks to download data (at DOY 113 and a brief lacuna on DOY 127 that affected only the temperature profiles). The water column was initially unstratified with an almost uniform temperature close to 4 °C (Fig. 2b). Stratification started to develop after DOY 110, although stronger winds, exceeding 10 m s−1 at times during the period DOY 127–134 (Fig. 2a), delayed the development of stronger stratification until the end of the observation period when the surface to bottom temperature difference reached ∼6 °C.

Fig. 2
figure 2

Wind speed, temperature, and water velocity for Windermere South Basin. Panels show observations covering all three deployment periods (dep. 1–3) for a wind speed W (m s−1) above the lake surface, b water column temperature (°C), c axial velocity component (m s−1), and d transverse velocity component (m s−1)

Full size image

With the onset of stratification, a number of marked changes occurred in the velocity structure. There was a general increase in the magnitude of the axial velocities (Fig. 2c) and the development of a marked vertical structure, which are both characteristic of internal seiche motions. In the initial, unstratified regime, the transverse flow (Fig. 2d) was of a magnitude similar to that of the axial flow; but with the developing stratification, the axial flow became dominant with rms velocities ∼2.5 times greater than those of the transverse motion. In the following sections, we utilise the flow data to elucidate some aspects of the mechanical energy budget of Windermere.

5.1 Rate of working by the surface stress

The wind stress, along and across the lake (Fig. 3a), is determined from Eq. (1) using the wind speed and direction measurements. As a measure of the near-surface flow, we use the velocities measured from the highest ADCP bin in the water column with good data, which was located at 3.5 m below the surface. The axial velocity component (Fig. 3b) exhibits a significant increase in the strength of the flow as stratification develops with speeds reaching 0.1 m s−1 towards the end of the record. By contrast, the transverse component (Fig. 3b), which was of comparable magnitude to the axial flow in the initial mixed regime, becomes relatively much weaker with the onset of stratification.

Fig. 3
figure 3

a Components of surface wind stress: axial (blue) and transverse (red). b Near-surface flow at 3.5-m depth: axial v (blue), transverse u (red) offset by −0.15 m s−1. c Components of rate of working RW, axial RW y (blue), and transverse RW x (red). d Along-lake wind component V

Full size image

Combining the wind stress and near-surface velocity (Eq. (2)) provides an estimate of the axial rate of working, RW y, (Fig. 3c), which makes a dominant contribution to RW throughout the observation period. RW y is seen to be predominantly positive, i.e. energy is generally being input to the lake flow, with strong positive peaks at times of high wind stress whose magnitude appear to increase with time. Note that the input of KE may be negative when the surface flow is opposed by the wind stress. Specifically, if the wind stress is opposing the surface flow, it will reduce the KE content of the lake. In this way, energy may be extracted from the mean circulation of the lake and/or from the seiche motions, thus reducing the potential for stirring. The observed increase in RW y in our observations is clearly not due to an increase in wind speed and wind stress which, if anything, decrease over the recording period. In order to illustrate the relation of RW and the resulting lake motions to wind forcing, we show, in Fig. 4, RW alongside P 10, the rate of working by the wind in a horizontal plane above the lake along with the depth-uniform and depth-varying components of the kinetic energy and the observed dissipation in the BBL. There is a close correspondence between the time course of P 10 and RW with maxima in the two variables coinciding.

Fig. 4
figure 4

a P 10 downward energy flux in the atmosphere. b Rate of working RW at 3.5 m depth. c Lake kinetic energy: depth-varying (red), depth-uniform (blue). d Total bottom boundary layer (BBL) dissipation as log (\( {\widehat{\epsilon}}_{\mathrm{BBL}} \)(W m−2)); heavy black line indicates lacunas during mooring servicing

Full size image

Changes in the kinetic energy of the flow are also closely related to P 10 and RW (Fig. 4c). During the mixed regime, the depth-uniform and depth-varying components are of similar magnitude but, as stratification develops, there is a marked increase in the depth-varying component without a corresponding change in the depth-uniform energy. During the last 10 days of the recording period, the spectral peak associated with the lowest mode internal seiche accounted for >60% of the total kinetic energy in the near-bed flow (Simpson et al. 2015).

5.2 Efficiency of energy input

To explore the transfer of energy from the atmosphere to the lake, we undertook a regression analysis of RW on P 10 for the periods before and after stratification. The results (Fig. 5) indicate a significant relation between the two variables but with a much greater slope b of the regression after stratification is established (b = 0.0064; t = 17.7, df = 832) than in the homogeneous regime (b = 0.0013; t = 62.9; df = 2957). The higher t value in stratified conditions than in the mixed regime is indicative of a considerably closer relation between RW and P 10. The slope of the regression b represents the efficiency, Eff, of energy transfer to the lake which is seen to increase markedly, by a factor of about 5, between mixed and stratified regimes. It should be noted that the increased input of energy to the lake, apparent in Fig. 5, is related to a marked change in the response of the surface flow to wind forcing. The plot of RW versus P 10 involves the stress in both variables since RW = τ y v and P 10 = C d ρ a W 2 W = τ × W. Since the along-lake components are dominant in both wind and near-surface flow, we might expect the observed relation between RW and P 10 to be essentially determined by the correlation of v and the along-lake wind component V, i.e. leaving out the stress in both cases. A clear visual correlation between these variables can be seen during the stratified regime in the time series plots of Fig. 3b and d. This correlation is explored further in the regression analysis of Fig. 6, which shows a marked contrast between the stratified and mixed regimes. Under stratified conditions (Fig. 6a), the slope of the regression line is substantially larger (by a factor ∼3) than in the preceding mixed regime (Fig. 6b), and the statistical confidence of the regression is also much higher (stratified: t = 39; df = 2955; mixed: t = 14; df = 938).

Fig. 5
figure 5

Relationship between the rate of working (RW) and the wind energy flux (P 10) for mixed (blue) and stratified (red) regimes

Full size image
Fig. 6
figure 6

Near-surface (3.5 m) axial velocity v versus along-lake wind component V with lines representing regression for a increasingly stratified conditions after DOY 113 (regression slope b = 0.0067; t = 39; df = 2955) and b in the preceding vertically-mixed regime from DOY 99.5 to DOY 112.5 (slope b = 0.0024; t = 14; df = 938)

Full size image

To investigate further the changes in the downward momentum flux occurring with the development of a stably stratified water column, we have determined Eff for each 7-day interval during the recording period. The result is shown in Fig. 7 along with the period T 1 of the lowest internal mode, determined by normal mode analysis of the density profile, and validated from cross spectral analysis of the ADCP data. As T 1 decreases from large values (>100 h) in the initial very weak stratification to more robust stability, Eff is seen to increase markedly reaching a value of ∼0.01 around DOY 143. This behaviour is suggestive of an approach to resonance between the wind stress forcing at the diurnal frequency and the dominant, lowest mode of the lake as T 1 approaches 24 h (Fig. 7). Analysis of the axial and transverse wind stress time series reveals that there was a significant diurnal contribution to the wind forcing during our observations as can be seen in the “equal variance” plot of the power spectrum, calculated using standard power spectrum analysis techniques (Emery and Thompson 1998), of the axial wind stress in Fig. 8. Full resonance requires not only the matching of the period of the forcing with the natural period of the lake but also the presence of adequate wind stress forcing at the resonant period. In Fig. 7c, we show the amplitude of the wind stress forcing averaged over an interval of 3 days. The maximum Eff around DOY 143 occurs when the seiche period is almost exactly diurnal and there is a maximum in the diurnal wind stress forcing and RW. The subsequent reduction in Eff appears to be a consequence of the seiche period diverging, for a while, from diurnal together with a reduction in the amplitude of diurnal forcing. Figure 7 demonstrates that we only encountered one period of exact matching of forcing and natural periods when the forcing in the diurnal band (∼0.04 Pa) was adequate to produce a resonant response.

Fig. 7
figure 7

a Period of the lowest seiche mode v1h1 derived from temperature profiles. b Efficiency of energy transfer to the lake, Eff. c 72-h fits of the diurnal component of wind stress. The grey horizontal line in a indicates the diurnal (24 h) period and the vertical line in all three panels indicates the transition between mixed and stratified regimes

Full size image
Fig. 8
figure 8

Power spectra P(f) of axial (black) and transverse (red) wind stress components for the stratified regime (DOY 110–155) plotted in “equal variance” format (degrees of freedom, df = 12). The vertical blue line indicates a period of 24 h. c/h refers to cycles per hour and f is the frequency (freq)

Full size image

5.3 Dissipation in the BBL

Estimates of the turbulent kinetic energy dissipation, ε, for the BBL were obtained, during three separate deployments (dep. 1–3 in Fig. 2), from the fast-sampling bottom-mounted 1200-kHz ADCP using the SF method. The mean values of ε over a sampling interval of 2 m were extrapolated to yield estimates of \( {\widehat{\epsilon}}_{\mathrm{BBL}} \), the total dissipation in the BBL (W m−2), by applying Eq. (7) with z 0 = 0.5 mm and z t = 4 m. z 0 is based on an estimate of the drag coefficient (C d = 2 × 10−3) in Simpson et al. (2015), and the height of the boundary layer z t = 4 m is based on examination of the velocity profiles which show no significant variation with height above 4 m. However, in view of the 1/z dependence in the LOW, the extrapolation is rather insensitive to the parameter z t. The resulting BBL dissipation (Fig. 4d) appears to be related to RW and P 10 with a considerable degree of correspondence between maxima. Regression analysis confirms that there is a significant relation between ε BBL and both RW and P 10 in mixed and stratified regimes (Table 1). The results indicate that the fraction of RW dissipated in the BBL was ∼9% in the mixed regime (deployment 1) with the closest relation between the variables at zero time lag.

Table 1 Regression of dissipation in the bottom boundary layer (BBL) ϵ BBL on the rate of working (RW) and the wind energy flux (P 10) for mixed (deployment 1) and stratified (deployment 3) regimes. The final column indicates the time lag for an optimum fit to the data
Full size table

When stratification was well established (deployment 3), the fraction of RW dissipated in the BBL increased to ∼15% at a time lag of ∼70 min, which indicates the time required for the near-bed motions to respond to changes in RW under stratified conditions. The corresponding regressions on P 10 show similar trends with the fraction of P 10 dissipated in the boundary layer increasing by a factor of ∼2.5 after the establishment of stratification when the optimum time lag was ∼90 min.

5.4 Development of stratification

Changes in the stratification parameter, ϕ, in the competition between heating and stirring by the wind can be represented (Simpson 1981) by the equation:

$$ \frac{\partial \phi}{\partial t}=\frac{\alpha g\overset{\cdot }{Q}}{2{c}_{\mathrm{p}}}-\delta {C}_{\mathrm{d}}{\rho}_{\mathrm{a}}\frac{\overline{W^3}}{h}=\frac{\alpha g\overset{\cdot }{Q}}{2{c}_{\mathrm{p}}}-\frac{\delta {P}_{10}}{h}, $$
(12)

where α is the thermal expansion coefficient of water, \( \overset{\cdot }{Q} \) is the rate of surface heat input derived from changes in the water column heat content, c p is the specific heat capacity of water at constant pressure, ρ a is the density of air, h is the water column depth, and δ is a constant. Alternatively, we may use the rate of working by the surface stress RW in place of P 10:

$$ \frac{\partial \phi}{\partial t}=\frac{\alpha g\overset{\cdot }{Q}}{2{c}_{\mathrm{p}}}-\frac{\delta_{\mathrm{RW}}}{h} RW, $$
(13)

with a new constant δ RW which represents the fraction of RW used in mixing the water column. Integrating this equation from the onset of stratification at t = 0, we have ϕ as a function of time:

$$ \phi (t)=\frac{g}{2}{\int}_0^{\mathrm{t}}\frac{\alpha \overset{\cdot }{Q}}{c_{\mathrm{p}}}\ dt-\frac{\delta_{\mathrm{RW}}}{h}{\int}_0^t RW(t)\mathrm{dt}={\phi}_{\mathrm{heat}}-{\delta}_{\mathrm{RW}}{RW}_{\mathrm{t}\mathrm{ot}}/ h. $$
(14)

Notice that, because α for freshwater varies widely with temperature, it must be included inside the integral for the heating term. The time course of the buoyancy input term ϕ heat and the stirring term RW tot/h, both averaged over 24 h, are shown in Fig. 9 along with the corresponding average of the observed stratification ϕ(t). A regression of the observed ϕ(t) on the heating term and the total stirring RW tot/h yields:

$$ \phi (t)=0.01+0.80{\phi}_{\mathrm{heat}}-0.21{RW}_{\mathrm{tot}}/ h, $$
(15)

with significant coefficients for the heating (t = 10.5, df = 47) and stirring terms (t = 6.5, df = 47). The coefficient of the stirring term δ RW has a value of 0.21, which indicates that a substantial fraction of the input power RW is used in working against buoyancy forces to bring about mixing. For heat arriving by downward transfer, the coefficient of the buoyancy term should be unity since without stirring ϕ = ϕ heat . The fact that the regression coefficient for the buoyancy term (0.80 ± 0.0.15; t = 10.5; df = 47) is significantly less than unity at 0.2% suggests that some of the heat observed in the water column at the central site may have arrived by lateral advective processes rather than entering locally through the surface. A hindcast of ϕ(t) using the regression (Eq. (15)) and shown by the dashed line in Fig. 9 reproduces the observed variation of stratification (as calculated from Eq. (11)) with an rms deviation from the observed ϕ(t) of <1 J m−3.

Fig. 9
figure 9

Time series of the development of thermal stratification showing the integrated rate of working RW tot/h (grey line), the integrated buoyancy input as heat ϕ heat (red line), and the potential energy anomaly, ϕ,from observations (blue line) and from multiple regression (dashed black line)

Full size image

6 Summary and discussion

The response of a temperate lake to wind stress forcing has been investigated in a series of observations by moored acoustic Doppler current profilers and a vertical string of temperature sensors. The results have enabled us to determine new estimates of several pivotal components of the mechanical energy budget of a lake which should lead to further improvements in our understanding of lake and shallow sea processes.

Near-surface measurements of the axial current have been combined with the along-lake stress imposed by the wind to estimate RW, the rate of working by the wind on the lake surface. A comparison, by regression, of RW with P 10, the downward energy flux in the atmosphere, yields estimates of Eff, the efficiency of energy transfer to the lake. During the spring transition, there was a striking increase in Eff from ∼0.0013 in vertically homogeneous conditions to an average of 0.0064 in the first 40 days of the stratified regime.

It is important to recognise that, since both RW and P 10 involve multiplying the near-surface velocity and wind speed, respectively, the relation between them arises almost entirely from the correlation of the axial near-surface velocity with the along-lake wind velocity V, a result confirmed by regression analysis of v on V which shows comparable slope and statistical confidence to that obtained in the RW and P 10 regression.

As mentioned above, a striking feature of the observations was that the increase in Eff and RW during the observation period was accompanied by a growth in the depth-varying kinetic energy of the motion, while there was no corresponding increase in the wind stress forcing. The largest values of Eff (∼0.01) were observed when, with increasing stratification, the period of the lowest-mode internal seiche came very close to 24 h, thus creating the conditions for a resonant response to the diurnal variation of the wind stress. The combination of plots of the seiche period and the amplitude of the diurnal component of wind stress forcing (Fig. 7) provide strongly suggestive evidence that a resonant response is occurring. Moreover, substantial movements of the isotherms are apparent in Fig. 2b on DOY 143, the time of a resonant response, although we should note that the observational site in the centre of the lake, being close to the node of a v1h1 seiche, is not ideally located to see vertical displacements of the isotherms but optimal for velocity measurements.

Some of the seiche motions observed in Windermere have periods that are long; therefore, it is reasonable to ask whether they will be significantly modified by the Earth’s rotation (Bernhardt and Kirillin 2013). While Earth’s rotation is important for motion in an unbounded domain, in a narrow lake such as Windermere, the transverse velocities are necessarily small and so the axial component of the Coriolis term is negligible and so does not affect the longitudinal dynamics. Hence, the period of oscillations is the same as in the non-rotating case. The transverse component of the Coriolis term is, of course, important and is reasonable for the transverse slope of the pycnocline.

Parallel measurements of energy dissipation ε BBL in the BBL indicate that, in the stratified regime, ∼15% of the rate of working by wind stress is accounted for by boundary layer dissipation with a corresponding figure for the mixed regime of ∼9%. The evolution of water column stratification was found to conform to a ϕ model of heating-stirring in which the fraction of RW used in mixing was found to be δ RW∼0.21 ± 0.06 (confidence limits shown, and elsewhere in the text, as ±2 standard deviations).

The response of lakes to wind forcing has been described in the scientific literature (Woolway et al. 2017), and a number of studies have investigated the influence of surface wind stress to induce vertical mixing (MacIntyre et al. 1999), the vertical transport of wind energy (Imboden and Wüest 1995), the role of seiches (Watson 1904; Wedderburn 1907; Mortimer 1974; Lemmin et al. 2005; Simpson et al. 2011), and wind resonance (Antenucci and Imberger 2003). To date, however, the temporal variability of wind-induced mixing and energy dissipation in lakes has received comparatively little attention and there are rather few published estimates of the components of the mechanical energy budget. A significant exception is the study by Wüest et al. (2000) of Lake Alpnach in Switzerland, a basin that does not differ greatly in area and depth from Windermere. Their investigation was based on a series of 130 temperature microstructure profiles, taken on nine occasions, along with continuous wind and thermistor profile measurements during a 1-month period in summer when the lake was strongly stratified. Profiles of the dissipation rate were obtained from the fine structure temperature measurements by fitting the Batchelor spectrum to the observations. The campaign average of all the profiles was then used to deduce estimates of the fraction of P 10 that was dissipated in different regions of the lake. The estimated quantities do not align precisely with our results but there are some useful points of comparison. The authors estimate that 0.70% of P 10 is dissipated or used in mixing in the waters below the surface layer (6-m depth). This value for the total energy consumption below 6 m is similar to our estimate of the rate of working by the wind stress 3.5 m below the surface, where we found an average value for RW of 0.64% of P 10 in stratified conditions.

For the total dissipation of turbulent kinetic energy in the BBL, Wüest et al. (2000) estimate 0.38% of P 10 which is a factor of ∼4 larger than was observed in the Windermere where we found that ε BBL = 0.15 RW ∼ 0.085 % of P 10. The difference here may be partly explained by the occurrence of the relatively high local dissipation rate ϵ (W kg−1) observed in the pycnocline of Windermere (See Simpson et al. 2015), which generally exceeded the corresponding dissipation rate 2.5 m above the bed in the BBL, a feature that was not apparent in the Alpnach microstructure results. On the other hand, the mixing power, used in working against buoyancy forces under stratified conditions in Windermere, was ∼0.05% of P 10 which is close to the value of ∼0.06% of P 10 in Lake Alpnach.

In our results, we found suggestive evidence of resonant behaviour in both the efficiency of energy input and the kinetic energy of depth-varying motions. Resonant responses of internal seiche modes to wind forcing have been observed previously (Münnich et al. 1992; Münnich 1996; Antenucci and Imberger 2003; Pannard et al. 2011; Rozas et al. 2014). In Lake Kinneret, Antenucci and Imberger (2003) observed resonances, analogous to those in our observations, occurring in spring and autumn, when, due to changes in stratification, the first mode seiche period became ∼24 h and, hence, matched the diurnal component of the wind. Resonance interactions have also been observed in experiments (Wake et al. 2007), which demonstrated that resonance could excite harmonics of the fundamental frequency. In assessing the frequency and importance of these types of resonant events, it should be remembered that the matching of the forcing and natural frequencies is a necessary but not sufficient condition for enhanced seiche growth which also requires adequate wind forcing at the resonant frequency, which may, or may not, be present. Specifically, the key point is that as well as matching of the forcing and natural periods, there has to be some level of forcing at the resonant frequency. For example, in the sustained resonance reported by Rozas et al. (2014), there was highly consistent diurnal forcing for most of the 12-day period of observation, although the winds were limited in strength. In the present case of Windermere, the diurnal forcing varied considerably along with significant departures from resonant matching as can be seen in Fig. 7. In ideal resonance, within an undamped frictionless system, any forcing at the resonant frequency would produce an infinite growth of amplitudes. However, motion in a lake is damped so that oscillations typically die out in a few cycles. In these circumstances, resonance will not be apparent until a threshold level of forcing is available. In a series of laboratory experiments, Boegman and Ivey (2012) showed that, after an initial period of rapid growth, the first mode seiche becomes modified by progressive non-linear internal waves which lead to dissipation and mixing and, hence, a limit on the amplitude of the seiche.

An interesting feature of the regression analysis of lake stratification in Windermere is that the coefficient of the buoyancy input term was significantly less than unity (0.8 ± 0.15). This result suggests a component of heat transport to the deep water of the lake by intrusion of mixed water produced by internal wave breaking around the lake margins at the depth of the pycnocline (Wain et al. 2013). Specifically, as the ϕ model does not consider lake hypsometry and we have only a local model of processes in the centre of the lake, processes occurring in the surrounding shallower area, which may impact the lake centre through the transfer of heat and pre-mixed water by advection or diffusion, are not considered. Thus, as the buoyancy input term is considerably less than unity, this indicates that there is additional heat in the water column in the lake centre than had come through the surface locally, indicating some influence of lateral transfer.

The values of the efficiency of wind mixing δ RW in Windermere (0.21 ± 0.06) indicate that a substantial part of the energy input RW is being directed to mixing. The corresponding estimate of δ for a regression using P 10, instead of RW, to represent wind stirring is δ = 5.1 (±3.9) × 10−4. This result, which has already been quoted above in percentage form in relation to the estimates of Wüest et al. (2000), may also be compared with a similar analysis for the development of stratification in the shelf seas (Simpson et al. 1978; Simpson and Bowers 1981), which yielded δ = 9.1 (±3.4) × 10−4. A lower value of δ in a lake is seen as reflecting the influence of much smaller fetch and the influence of sheltering by terrestrial topography, both of which have been described as important factors which influence lake thermal dynamics (France 1997; Tanentzap et al. 2008).

In conclusion, we would contend that the observational methods and analysis used in this study represent a significant step towards the goal of determining key components of a full water-column energy budget for lakes and shallow seas. In order to evaluate RW closer to the surface, more detailed measurements of the near-surface velocity profile will be required. There is also a clear need for fuller dissipation profile measurements covering the pycnocline and the BBL, a requirement which would be facilitated by an increase in the range of ADCP p-p coherent measurements which, to date, has been limited by phase ambiguity.

It should be noted that our conclusions are based on measurements from a single location in a lake, which cannot be regarded as representative of the entire basin. We consider, however, that in view of the near-rectilinear configuration of Windermere that our measurements were reasonably representative of the physical processes operating in a large proportion of the central area of the lake, but future investigations should consider additional observations to account for the spatial variability that may exist in the velocity structure (Hodges et al. 2000; Rueda et al. 2003; Appt et al. 2004; Becherer and Umlauf 2011). Given these extensions of the measurements, there are good prospects for better determinations of energy budgets and consequent improvements in our understanding of lake and shallow sea processes.