Sensitivity of tidal motion in well-mixed estuaries to cross-sectional shape, deepening, and sea level rise

Abstract

For well-mixed estuaries, key physical mechanisms are identified and quantified that cause changes in characteristics of the semi-diurnal sea surface elevation and lateral velocity due to modifications of the lateral bottom profile, channel deepening, and sea level rise. This is done by decomposing solutions of a new analytical model into components relating to different physical processes. The default geometry and parameter values are representative for the Ems estuary, with a converging width and a reflective landward boundary. The default Gaussian lateral bottom profile is modified to obtain profiles with the same cross-sectional area, but with a different skewness or steepness. Results show that a steeper lateral bottom profile leads to amplification of the sea surface elevation. The width convergence is shown to influence the resonance characteristics. Channel deepening and sea level rise result in amplification of the sea surface elevation until a resonance peak is reached. When flooding is incorporated, the amount of sea level rise at which maximum tidal amplification occurs is found to be about two times lower. When using a symmetric Gaussian bottom profile, the lateral tidal flow is determined by Coriolis deflection of longitudinal flow and lateral density gradients caused by differential salt advection. However, an additional lateral tidal flow component incorporating the effect of continuity related to sea level variations and longitudinal gradients in longitudinal flow is shown to become increasingly important for skewed lateral bottom profiles. Furthermore, the lateral flow due to the lateral density gradient is enhanced for bottom profiles with increased steepness.

1 Introduction

Tides are an important, and often dominant constituent of the water motion in partially to well-mixed estuaries. It is well known (cf. Defant 1961) that they are mainly forced by co-oscillation with tides present in the sea or ocean adjacent to these estuaries and that their characteristics strongly depend on estuarine shape and friction (Prandle and Rahman 1980). A distinctive characteristic of tidal currents in estuaries is that they are modified by their interaction with the density field. An important mechanism is differential advection of salt: as longitudinal currents are large in channels and weak over shoals, they cause differential advection of the longitudinal estuarine salinity gradient, which results in a lateral density gradient driving a transverse tidal flow (Nunes and Simpson 1985).

Knowledge of tidally induced sea surface variations and currents is important for navigation, design of coastal defence structures and ecology. The latter is because tidal currents instigate net transport and mixing of, e.g., salt, sediment and nutrients, and thereby may cause zones of high turbidity (Allen et al. 1980) where oxygen values will be low (Talke et al. 2009b). Field data (see Jiang et al. 2012, Schuttelaars et al. 2013 and Winterwerp et al. 2013) indicate that tidal characteristics in many estuaries have changed during the last decades, probably in response to anthropogenic measures such as large-scale deepening of navigation channels and construction of jetties and groynes. Tides also change on longer time scales due to, e.g., sea level rise and changes in tidal forcing related to altered tidal motion in seas and oceans (Van der Spek 1997; Hall et al. 2013; Mudersbach et al. 2013).

Over the years, different types of models have been developed and analysed to quantify the behaviour of estuarine tides. Detailed numerical models allow for accurate simulations of tides in estuaries like, e.g., Chesapeake Bay (Zhong et al. 2008), the Yangtze (Hu et al. 2009) and the Scheldt (De Brye et al. 2010). Alternatively, highly idealised models have proven to be successful in yielding basic process knowledge. Moreover, such models are fast and flexible, and thus allow for extensive sensitivity analyses. Cross-sectionally averaged models (Defant 1961; Prandle and Rahman 1980; Friedrichs 2010; Toffolon and Savenije 2011, and references therein) revealed the importance of friction, width convergence and reflection in determining the longitudinal distribution of amplitude and phase of tidal constituents. Width-averaged models (Ianniello 1977; Chernetsky et al. 2010; Schuttelaars et al.2013 provided additional insight into the vertical and longitudinal distribution of tidal currents, while Friedrichs and Hamrick (1996) and Huijts et al. (2009) studied the distribution of tidal currents over estuarine cross-sections with models that assume local longitudinally uniform conditions. Li and Valle-Levinson (1999) investigated the dependence of depth-averaged (2DH) longitudinal and transverse tidal velocity on lateral depth profiles. A three-dimensional, semi-analytical model for tides in a semi-enclosed basin was presented and analysed by Winant (2007), and for a system of connected basins by Waterhouse et al. (2011).

This study aims at gaining further physical insight into the dynamics of estuarine tides and it has three specific goals. The first is to assess the dependence of the sea surface elevation on the width convergence and the shape of the lateral bottom profile. The second goal is to assess the relative contribution of changes in sea surface elevation due to projected climate change (sea level rise and altering tidal forcing at the seaward boundary) and due to anthropogenic measures, like deepening of a fairway. Here, the hypothesis to be tested is that on time scales of 50–100 years, changes in tides due to climate change cannot be ignored with respect to those induced by, e.g. deepening of fairways. The third goal is to quantify the effect of changing the lateral bottom profile shape on the lateral tidal velocity, and to identify the underlying physical processes. A specific hypothesis that will be tested is that the structure of lateral and vertical tidal flow is strongly affected by lateral density gradients and a contribution from three-dimensional continuity. This hypothesis is based on discrepancies between modelled and measured transverse tides found in the study of Huijts et al. (2009). Gaining this information is important because lateral flow advects longitudinal tidal momentum, thereby affecting the mean transport of water in the longitudinal direction (see Lerczak and Geyer 2004).

To meet these goals, a modified version of the model of Winant (2007) will be presented and analysed. This three-dimensional analytical model is designed such that it accounts for all basic processes that determine the dynamics of co-oscillating tides in narrow estuaries (width small compared to the Rossby radius of deformation). The necessary modifications include an exponential width convergence of the estuary and a module that accounts for lateral density gradients as a result of differential advection. Moreover, the turbulence closure scheme is adjusted, such that it accounts for partial slip at the bed and for an eddy viscosity that depends on the local depth. Also, asymmetrical lateral depth profiles will be considered.

The model is applied to a prototype estuary that represents the upper Ems estuary on the border of Germany and The Netherlands. The Ems faces a multitude of problems related to ecology and navigation and it has undergone large-scale deepening between 1980 and 2005. Measured sea surface heights for 2005 were used in this study. Additionally, measurements of tidal flow through a single cross-section at 16 km upstream from Knock were conducted using an ADCP in 2012. These measurements are used to verify output of the three-dimensional analytical model used in this study.

In Section 2, the model equations and their analytical solutions will be presented. The different experiments are described in Section 3. Results for a default configuration are discussed first in Section 4. After that, the sensitivity of tidal elevations and velocities to changes in width convergence and bottom profile shape are considered. Subsequently, the effect of adding sea level rise and deepening of the navigation channel on the tidal elevations is considered. In Section 5, modelled tides are compared with observed tides in the Ems to explore the validity of the analysis and limitations of the analytical model are discussed. Finally, Section 6 contains the conclusions.

2 Analytical model

2.1 Model description

2.1.1 Domain

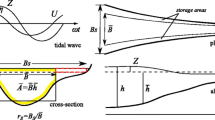
The domain represents an estuary with an exponentially converging width towards the closed landward end (Fig. 1). This estuary has length L _c , maximum depth H _{m a x} and width B at the seaward end. The x-coordinate measures distance along the estuary to the seaward boundary (where x = 0), y is the across-estuary coordinate ( y = 0 is the central axis), and z is measured positive up from the undisturbed water surface (where z = 0). The bottom is located at z = −H, where H is the undisturbed local water depth. The side boundaries of the estuary are located at y = −b and y = b, where b is half the width prescribed by

$$ b=\frac{B}{2}\exp\left(-\frac{x}{L_{b}}\right), $$

(1)

with L _b the width convergence length.

Fig. 1

Sketch of the modelled estuary. As an example, a skewed transverse depth profile is shown. The sketch shows the length of the domain L _c , the width at the seaward end B and the maximum depth H _{m a x} . Also, the direction and origin of the x-, y-, and z-axes (of the Cartesian coordinate system) are shown

The estuary has an arbitrary cross-sectional depth profile, which is the same along the entire estuary, except it is scaled with the local width. Thus, the maximum depth H _{m a x} of the cross-sectional profile along the entire estuary remains the same.

2.1.2 Assumptions with regard to dynamics

The tidal dynamics are assumed to be governed by the three-dimensional shallow water equations. The characteristic amplitude $A_{M_{2}}$ of the tidal sea surface elevations is assumed to be small compared to the typical estuarine depth. As a result, non-linear terms are ignored with respect to linear terms and the level z = η of the free surface is approximated by the undisturbed sea surface z = 0 (see Electronic Supplement A). Also, this imposes a minimum value on the water depth H, as $H\gg A_{M_{2}}$. Locations with depths below a certain minimum H _{m i n} are assumed to belong to the tidal flats, which are not taken into consideration here. It is also assumed that lateral variations in depth are mild, such that topographic variations between the minimum depth H _{m i n} and the maximum depth H _{m a x} occur on length scales that are of the order of B or larger. The estuary is long and narrow, i.e. its length L _c is in the order of $L_{t}=\sqrt {gH_{ref}}\omega ^{-1}$ and B ≪ L _c . Here, L _t is the frictionless tidal wavelength (apart from a factor 2π), H _{r e f} is a reference maximum depth and ω is the angular frequency of the tide. Consequently, lateral tidal velocities v are much smaller than longitudinal velocities u, and lateral variations in sea surface height are small compared to its longitudinal variations.

Horizontal pressure gradient forces in the model result from gradients in sea surface height and from density gradients. The density field is written as

$$ \rho=\rho_{w}+\rho^{*}(x,y,z,t), $$

(2)

where ρ _w is a constant reference density equal to the density of fresh water and the magnitude of density fluctuations ρ ^∗ is much smaller than ρ _w (Boussinesq approximation). The density field is related to the salinity s through the equation of state

$$ \rho^{*}=\rho_{w}\beta_{sc} s, $$

(3)

with β _{s c} ( ∼7.6⋅10⁻⁴ psu ⁻¹) the coefficient of saline contraction. The estuary is assumed to be vertically and laterally well-mixed, which implies that

$$ s=\bar{s}_{0}(x)+s_{1}^{\prime}(x,y,z,t), $$

(4)

with $\bar {s}_{0}$ the tidally and cross-sectionally mean salinity and $s_{1}^{\prime }$ small fluctuations. From Eqs. 3 and 4 it follows that

$$ \rho^{*}=\bar{\rho}_{0}(x)+\rho_{1}^{\prime}(x,y,z,t). $$

(5)

In this model, the mean salinity field is prescribed, following Warner et al (2005), as

$$ \bar{s}_{0}(x)=\frac{s_{sea}}{2}\left\{1-\tanh{\left(\frac{x-x_{c}}{L_{s}}\right)}\right\}, $$

(6)

where s _{s e a} is the reference salinity of sea water, x _c is the position of the maximum salinity gradient, and L _s is the length scale over which salinity varies. Values of the parameters were obtained by fitting mean salinity profiles to Eq. 6.

A simple turbulence closure is adopted, with a vertical eddy viscosity and eddy diffusion coefficient that are independent of the vertical coordinate z and time t, and a partial slip condition is applied at the bed. Horizontal eddy viscosity and effects of wind are not considered.

2.1.3 Equations of motion

The assumptions in Section 2.1.2 lead to the identification of two small parameters, i.e.

$$ \varepsilon=\frac{A_{M_{2}}}{H_{max}},{\kern3pt} \alpha=\frac{B}{L_{t}}. $$

(7)

Making the three-dimensional shallow water equations dimensionless by using appropriate scales for all variables (see Electronic Supplement A) and assuming $\alpha =\mathcal {O}(\varepsilon )$, approximate solutions are constructed as perturbation series in the small parameter ε:

$$ {\Psi}={\Psi}_{0}+{\Psi}_{1}+\mathcal{O}(\varepsilon^{2}), $$

(8)

with [Ψ₁]/[Ψ₀]∼ε, etc. Here, Ψ represents any state variable (e.g., velocity components u, v and w in the x−,y− and z−direction, sea surface elevation η or salinity s), and the first subscript denotes the order of the component. Note that many estuaries are characterised by α ≪ ε. The assumption $\alpha =\mathcal {O}(\varepsilon )$ is nevertheless made to obtain a system of equations that governs tidal dynamics for any value α∼ε or smaller. Retaining only the highest order terms yields the linear equations

$$\begin{array}{@{}rcl@{}} \frac{\partial u_{0}}{\partial t}&=&-g\frac{\partial\eta_{0}}{\partial x}+\frac{\partial}{\partial z}\left(A_{v}\frac{\partial u_{0}}{\partial z}\right), \end{array} $$

(9a)

$$\begin{array}{@{}rcl@{}} \frac{\partial v_{0}}{\partial t}&+&fu_{0}\\ &=&-g\frac{\partial\eta^{\prime}}{\partial y}+\frac{g}{\rho_{w}}{{\int}_{0}^{z}}\frac{\partial\rho_{1}^{\prime}}{\partial y}\ dz^{\prime}+\frac{\partial}{\partial z}\left(A_{v}\frac{\partial v_{0}}{\partial z}\right), \end{array} $$

(9b)

$$\begin{array}{@{}rcl@{}} \frac{\partial u_{0}}{\partial x}&+&\frac{\partial v_{0}}{\partial y}+\frac{\partial w_{0}}{\partial z}=0. \end{array} $$

(9c)

Here, u, v and w are the velocity components in x-, y- and z-direction, η is the free surface elevation, t is time, f is the Coriolis parameter, g is the gravitational acceleration, ∂ ρ ^′/∂ y is the tidally varying lateral density gradient, and A _v is the vertical eddy viscosity.

As is detailed in Electronic Supplement A, the sea surface elevation can be written as

$$ \eta=\eta_{0}(x,t)+\eta^{\prime}(x,y,t), $$

(10)

where η ^′= η ₁ + η ₂ is the higher order sea surface elevation, the first subscript denotes the order of the component and the magnitude of η ^′ is a factor $A_{M_{2}}/H_{max}$ smaller than that of η ₀. As the longitudinal coordinate x scales with L _t and the lateral coordinate y scales with B and B ≪ L _t , the sea surface gradients ∂ η/∂ x and ∂ η/∂ y are of the same order of magnitude.

From the equation of state (Eq. 3), it follows that the tidal lateral density gradient in Eq. 9b is given by

$$ \frac{\partial\rho_{1}^{\prime}}{\partial y}=\rho_{w}\beta_{sc}\frac{\partial s_{1}^{\prime}}{\partial y}, $$

(11)

where the salinity $s_{1}^{\prime }$ is governed by

$$ \frac{\partial s_{1}^{\prime}}{\partial t}+u_{0}\frac{d\bar{s}_{0}}{dx}=\frac{\partial}{\partial z}\left(K_{v}\frac{\partial s^{\prime}_{1}}{\partial z}\right), $$

(12a)

with K _v the vertical eddy diffusion coefficient. This equation describes differential advection of salinity $\bar {s}_{0}$ by the tidal flow u ₀ (Geyer and MacCready 2014). The salinity fluctuations $s_{1}^{\prime }$ and the resulting lateral density gradient $\partial \rho _{1}^{\prime }/\partial y$ are still functions of z. The problem of Eq. 12a is that it yields unstable stratification during part of the tidal cycle. In order to avoid this problem, the lateral density gradient in Eq. 9b is replaced by the lateral gradient of the depth-mean density. The second term on the right-hand side of Eq. 9b thus becomes

$$ \frac{gz}{\rho_{w}}\frac{\partial}{\partial y}\left(\frac{1}{H}{\int}_{-H}^{0}\rho^{\prime}_{1}\ dz^{\prime}\right). $$

(13)

Note that the procedure followed in this study is similar to that of Winant (2007). The crucial differences are that here $\alpha =\mathcal {O}(\varepsilon )$ and that the effect of salinity on density is taken into account with inclusion of differential advection over the width of the estuary. In addition, in this study, width convergence and a partial slip bottom boundary condition are considered.

Regarding the boundary conditions, at the surface the no-stress condition and the kinematic condition are applied:

$$ A_{v}\frac{\partial u_{0}}{\partial z}=A_{v}\frac{\partial v_{0}}{\partial z}=0,\ \ w_{0}=\frac{\partial\eta_{0}}{\partial t}\ \ \text{at}\ \ z=0. $$

(14)

At the bottom ( z = −H), a partial slip condition and impermeability are imposed:

$$\begin{array}{@{}rcl@{}} A_{v}\frac{\partial u_{0}}{\partial z}&=&Su_{0},\ \ A_{v}\frac{\partial v_{0}}{\partial z}=Sv_{0},\\ w_{0}&=&-u_{0}\frac{\partial H}{\partial x}-v_{0}\frac{\partial H}{\partial y}\quad\text{at}\ \ z=-H, \end{array} $$

(15)

where S is the slip parameter. This condition implies a linearisation of the friction (Engelund 1970). As was first applied in a tidal setting by Bowden (1983) and further elaborated on in, i.e. Maas and van Haren (1987) and Chernetsky et al. (2010), the partial slip condition must be evaluated at the top of the constant stress layer instead of at the true bottom.

The side boundaries are impermeable, indicating that the transport perpendicular to the lateral boundaries ( y = ±b) vanishes:

$$ {\int}_{-H}^{0}v_{0}\ dz=\pm\frac{\partial b}{\partial x}{\int}_{-H}^{0}u_{0}\ dz\ \ \text{at}\ \ y=\pm b, $$

(16)

At the seaward boundary ( x = 0), the water motion is forced by a semi-diurnal ( M ₂) sea surface elevation, and at the landward boundary (x = L _c ) the tidal transport is required to vanish at every lateral location y. Hence,

$$ \eta_{0}=A_{M_{2}}\cos{(\omega t)}\quad\quad \text{at}\ \ x=0, $$

(17a)

$$ {\int}_{-H}^{0}u_{0}\ dz=0 \quad\quad\quad {\kern4pt} \text{at}\ \ x=L_{c}, $$

(17b)

where ω is the M ₂ angular tidal frequency and $A_{M_{2}}$ is the amplitude of the M ₂ tidal elevation.

The boundary conditions imposed for salinity involve a vanishing salinity (and density) flux at the bottom and at the surface:

$$ \frac{\partial s_{1}^{\prime}}{\partial z}=0 \quad\text{at}\quad z=0,{\kern4pt} z=-H. $$

(18)

Following Friedrichs and Hamrick (1996), it is assumed that both viscosity and diffusivity increase with H(x, y) because the size of eddies scales with the local water depth, so

$$ \left\{A_{v}(x,y),K_{v}(x,y)\right\}=\left\{A_{v,ref},K_{v,ref}\right\}\frac{H(x,y)}{H_{ref}}, $$

(19)

with A _{v,r e f} and K _{v,r e f} , the values of the vertical eddy viscosity and diffusivity, respectively, at the reference depth H _{r e f} , which is equal to the maximum depth H _{m a x} of the default case. The slip parameter S is also assumed to depend on the local depth, following Schramkowski and de Swart (2002):

$$ S=S_{ref}\frac{H(x,y)}{H_{ref}}, $$

(20)

where S _{r e f} is the value of the slip parameter at the reference depth H _{r e f} . Note that since A _v , K _v and S are all functions of the local depth, the differential influence of friction that occurs for laterally varying bottom profiles is taken into account in a parametric way.

Equations 9a through 20 constitute a closed system. It is, however, convenient, for later use, to derive two additional equations that directly relate sea surface elevation to horizontal velocity components. The first equation is obtained by integrating the continuity equation over the full depth and applying boundary conditions for w at the surface and the bottom (Eqs. 14 and 15). The result is

$$ \frac{\partial\eta_{0}}{\partial t}=-\frac{\partial}{\partial x}{\int}_{-H}^{0}u_{0}\ dz-\frac{\partial}{\partial y}{\int}_{-H}^{0}v_{0} dz. $$

(21)

The second equation is obtained by integration of Eq. 21 over the full width and application of the boundary conditions in Eq. 16. This yields

$$ \frac{\partial\eta_{0}}{\partial t}=-\frac{1}{2b}\frac{\partial}{\partial x}\left({\int}_{-b}^{b}{\int}_{-H}^{0}u_{0}\ dz\ dy\right). $$

(22)

2.2 Analytical solutions

Since the equations of motion (Eqs. 9a through 12a) are linear and the forcing is time-periodic (see Eq. 17a), solutions are of the form

$$\begin{array}{@{}rcl@{}} &&\left(u_{0},\ v_{0},\ w_{0},\ \eta_{0},\ \frac{\partial\eta^{\prime}}{\partial y},s_{1}^{\prime},\frac{\partial\rho_{1}^{\prime}}{\partial y}\right)=\\ &&\quad\text{Re}\left\{\left(\hat{u}_{0},\ \hat{v}_{0},\ \hat{w}_{0},\ \hat{\eta}_{0},\ \frac{\partial\hat{\eta^{\prime}}}{\partial y},\ \hat{s}_{1}^{\prime}, \frac{\partial\hat{\rho}_{1}^{\prime}}{\partial y}\right)e^{-i\omega t}\right\}, \end{array} $$

(23)

with $\hat {u}_{0}$, etc. the complex amplitudes that depend on the spatial coordinates. For example $\eta _{0}=\left |\hat {\eta }_{0}\right |\cos {\left (\omega t-\phi \right )}$, where the phase $\phi =\arg {\left (\hat {\eta }_{0}\right )}$ and arg the argument of a complex number.

The following variable substitution is applied for the lateral coordinate: y ^′=y/b(x), where y ^′ varies between −1 and 1. This variable substitution is convenient when integrating over the width and when prescribing the bottom profile.

The structure of the equations allows for an elegant solution method. First, the longitudinal momentum equation (Eq. 9a) is combined with mass balance (Eq. 22). This yields an ordinary differential equation for sea surface elevation $\hat {\eta }_{0}$, which in fact governs the spatial structure of the wave equation for the M ₂ sea surface elevation. Solutions are

$$\begin{array}{@{}rcl@{}} &&\hat{\eta}_{0}=A_{M_{2}}\exp{\left(\frac{x}{2L_{b}}\right)}\cdot\\ &&\quad\frac{d_{0}\cos{\left(d_{0}[L_{c}-x]\right)}+\frac{1}{2L_{b}}\sin{\left(d_{0}[L_{c}-x]\right)}}{d_{0}\cos{\left(d_{0} L_{c}\right)}+\frac{1}{2L_{b}}\sin{\left(d_{0}L_{c}\right)}}, \end{array} $$

(24)

where

$$ d_{0}=\sqrt{{\kappa_{0}^{2}}-\frac{1}{4{L_{b}^{2}}}}, $$

(25)

with

$$ {\kappa_{0}^{2}}=\frac{2\omega^{2}}{g}\left({\int}_{-1}^{1}{\int}_{-H}^{0}p_{0}\ dz\ dy^{\prime}\right)^{-1}. $$

(26)

Furthermore, p ₀ is given as

$$ p_{0}=1-\frac{\cosh{\left(\gamma z\right)}}{\cosh{\left(\gamma H\right)}+\frac{\gamma}{\delta}\sinh{\left(\gamma H\right)}}, $$

(27a)

with

$$ \gamma=\sqrt{\frac{-i\omega}{A_{v}}}\quad \text{and}\quad \delta=\frac{S}{A_{v}}. $$

(27b)

Here, d ₀ is the complex wavenumber of the tide, which depends on friction (through parameters γ and δ), width convergence (through parameter L _b ) and the shape of the cross-section (through the function p ₀ that depends on H). Note that γ ⁻¹ is the thickness of the Stokes layer (in which friction is important) and δ ⁻¹ is the thickness of the layer in which vertical shear of the horizontal velocity is significant. Thus, Eqs. 23–24 describe a tidal wave that is subject to reflection, friction and width convergence.

The solution for the complex amplitude of the longitudinal tidal flow $\hat {u}_{0}$ follows from substitution of Eq. 23 into the longitudinal momentum balance (Eq. 9a) and by applying boundary conditions (Eqs. 14–15), yielding

$$ \hat{u}_{0}=-\frac{ig}{\omega}\frac{d\hat{\eta}_{0}}{dx}p_{0}. $$

(28)

It shows that longitudinal tidal flow is driven by barotropic pressure gradients and modulated by friction. The complex amplitude of the sea surface gradient $d\hat {\eta }_{0}/dx$ is only a function of x and determines the magnitude of $\hat {u}_{0}$, while the function p ₀ is a function of y ^′ and z and determines how the flow is distributed throughout the cross-section. The magnitude of $\hat {u}_{0}$ decreases towards the bottom and it decreases if the local depth H becomes smaller (Eq. 27a).

The solution for lateral tidal flow follows from the y-momentum equation (Eq. 9b), the continuity equation (Eq. 21), the solution structure (Eq. 23) and the solution for longitudinal tidal flow (Eq. 28) (see Electronic Supplement A). The solution $\hat {v}_{0}$ is written as as the sum of three mechanisms:

$$ \hat{v}_{0}=\underbrace{\hat{v}_{0,f}}_{\text{Coriolis deflection}}+\underbrace{\hat{v}_{0,\rho_{y}}}_{\text{lateral density gradient}}+\underbrace{\hat{v}_{0,c}}_{\text{continuity}}. $$

(29)

Here, $\hat {v}_{0,f}$ is the lateral tidal flow component due to Coriolis deflection of longitudinal flow, $\hat {v}_{0,\rho _{y}}$ is the component due to a tidal lateral density gradient, and $\hat {v}_{0,c}$ is a contribution associated with continuity. The solutions of the individual physical components read

$$\begin{array}{@{}rcl@{}} &&\hat{v}_{0,f}=\frac{fg}{\omega^{2}}\frac{d\hat{\eta}_{0}}{dx}\breve{v}_{0,f}, \end{array} $$

(30)

$$\begin{array}{@{}rcl@{}} &&\hat{v}_{0,\rho_{y}}=\frac{ig}{\omega\rho_{w}}\frac{\partial}{\partial y}\left(\frac{1}{H}{\int}_{-H}^{0}\hat{\rho}^{\prime}_{1}\ dz\right)\breve{v}_{0,\rho_{y}}, \end{array} $$

(31)

$$\begin{array}{@{}rcl@{}} &&\hat{v}_{0,c}\,=\,\frac{igb}{\omega}\left(\frac{\omega^{2}}{g}\hat{\eta}_{0}\breve{v}_{0,c,0}+\frac{1}{L_{b}}\frac{d\hat{\eta}_{0}}{dx}\breve{v}_{0,c,1}+\frac{d^{2}\hat{\eta}_{0}}{dx^{2}}\breve{v}_{0,c,2}\right),\\ \end{array} $$

(32)

where $\breve {v}_{0,f}$, $\breve {v}_{0,\rho _{y}}$, $\breve {v}_{0,c,0}$, $\breve {v}_{0,c,1}$ and $\breve {v}_{0,c,2}$ are dimensionless functions describing the distribution of the different components throughout the cross-section, which depend on y, z and model parameters (for exact definitions see Electronic Supplement A).

The continuity contribution $\hat {v}_{0,c}$ originates from the depth integrated continuity equation (Eq. 21), which contains time variations of the free surface ∂ η ₀/∂ t and longitudinal gradients in the volume transport $\frac {\partial }{\partial x}{\int }_{-H}^{0} u_{0}\ dz$. In the work of, e.g. Huijts et al. (2011), these variations and gradients are not taken into account and the term in Eq. 32 is identically zero. Winant (2007) also incorporates $\hat {v}_{0,c}$, but he employs a different method to compute them, as his scaling is designed for different systems (semi-enclosed seas like the Adriatic Sea or the Gulf of California) than considered here.

The lateral gradient of the depth-mean density in Eq. 31 is calculated using the equation of state (Eq. 11) as

$$ \frac{\partial}{\partial y}\left(\frac{1}{H}{\int}_{-H}^{0}\hat{\rho}_{1}^{\prime}{\kern2pt} dz \right) =\rho_{w}\beta_{sc}\frac{\partial}{\partial y}\left(\frac{1}{H}{\int}_{-H}^{0}\hat{s}_{1}^{\prime}{\kern2pt} dz\right). $$

(33)

The depth mean salinity is found by integrating the salt balance (Eq. 12a) over the full depth and by applying its boundary conditions (Eq. 18) and the solution structure of Eq. 23. The salinity equation then reduces to

$$ -i\omega\frac{1}{H}{\int}_{-H}^{0}\hat{s}_{1}^{\prime}{\kern2pt} dz+\frac{1}{H}{\int}_{-h}^{0}\hat{u}_{0}{\kern2pt} dz\frac{d\bar{s}_{0}}{dx}=0. $$

(34)

Substitution of the solution for $\hat {u}_{0}$ (Eq. 28) yields the solution

$$ \frac{1}{H}{\int}_{-H}^{0}\hat{s}_{1}^{\prime}{\kern2pt} dz=-\frac{g}{\omega^{2}}\frac{d\hat{\eta}_{0}}{dx}\frac{d\bar{s}_{0}}{dx}\frac{1}{H}{\int}_{-H}^{0}p_{0}{\kern2pt} dz, $$

(35)

from which the term in Eq. 33 follows by straightforward means.

3 Experiments

3.1 Default case

As a prototype estuary, the upper Ems estuary has been selected in this study. This estuary is located on the border between The Netherlands and Germany. Its upper part extends from Knock up to the weir at Herbrum and has a length of 64 km. Figure 2 shows a map of this area, on which also the location is indicated of a transect where ADCP depth and velocity data were collected in June 2012. In this study, these data are used for deriving a fitted bottom profile and for model-data comparison. Table 1 shows the default values representative for this estuary during the year 2005. As the maximum depth in the analytical model does not vary with x, the water depths used here represent average depths over the longitudinal direction. In the lateral direction, by default, a Gaussian bottom profile was used. For A _{v, r e f} and S _{r e f} , fitted values obtained by De Jonge et al. (2014) were used.

Fig. 2

Map of the upper Ems estuary from Knock up to the tidal weir in Herbrum. The location of the transect (at around 16 km) where ADCP data were collected is also shown

Table 1 Default parameter values representative for the upper Ems estuary in 2005

Values for the parameters that determine the longitudinal salinity profile ( s _{s e a} , x _c and L _s in Eq. 6) were taken from an analysis by Talke et al. (2009a), assuming an average river discharge of 100 m ³ s ⁻¹. The position of the maximum salinity gradient lies just seaward of the domain considered here (which only incorporates the upper reaches), hence the negative value for x _c .

3.2 Sensitivity experiments

Additional model runs are performed to assess the effect of changing the skewness and the steepness of the cross-sectional bottom profile shape on the tidal elevations and the lateral velocity field. To investigate this, special formulations for the bottom profile shapes were established. In addition, the effect of changing the width convergence length L _b , changing the depth of the main navigation channel and adding sea level rise on the tidal elevation were considered. In each of the sensitivity analyses, only one parameter was varied, while keeping the other parameters at their default values. In the following three subsections, the details of the used cross-sectional bottom profiles, deepening only the main navigation channel and adding sea level rise are discussed.

3.2.1 Varying bottom profile shape

A Gaussian profile was used in the default run. Several other bottom profiles were also designed to investigate the effect of different bottom profile shapes on both sea surface amplitudes and tidal velocities. The total cross-sectional area was kept equal to that of the Gaussian profile for each of these shapes. To study the effect of asymmetry of the cross-sectional bottom profile, a skewed profile was designed. This profile is described by

$$ H=H_{max}\exp\left(-{Y}^{2} C\right), $$

(36a)

where C is the steepness parameter that increases with increasing lateral bottom slope:

$$ C=\log{\left(H_{max}/H_{min}\right)}, $$

(36b)

with H _{m i n} the minimum depth of the Gaussian bottom profile and the profiles with varying skewness and steepness. Furthermore,

$$ Y=\frac{-1+\sqrt{1+a^{2}+2ay^{\prime}}}{a} $$

(36c)

is a mapping of $y^{\prime }$ ( =y/b(x)) which transforms the Gaussian profile using a skewness parameter a, which is allowed to vary from −1 to 1. For a = 0, Eq. 36c has no solution, but when taking the limit $a\rightarrow 0$ and applying L’Hôpital’s rule Y reduces to $y^{\prime }$, reducing the skewed profile to the Gaussian profile. Therefore, Y is replaced by $y^{\prime }$ for a = 0. Figure 3a shows the default Gaussian profile, a left skewed profile (with a = −0.8) and a right skewed profile (with a = 0.8).

Fig. 3

Examples of cross-sectional profiles used to investigate varying the skewness parameter a (a), the steepness parameter C (b) and deepening of the main channel (c)

When varying a for the skewed profiles, the average slope of the cross-sectional bottom profile does not change. To investigate the effect of average cross-sectional bottom slope on tidal elevation and the three-dimensional flow field, profiles were constructed with a varying steepness C. To construct profiles with a different maximum depth H _{m a x} and average lateral bottom slope, but with the same minimum depth H _{m i n} , the following four steps were taken:

• 1. The Gaussian profile ( H = H _G , with H _G given by Eq. 36a with $a\rightarrow 0$) was used and the slope parameter C was varied, resulting in a number of profiles H _{t e m p} .

• 2. The minimum depth was subtracted from the resulting profiles H _{t e m p} .

• 3. The surface area of the remaining profile ( H _{t e m p} −m i n(H _{t e m p} )) was set equal to the surface area of (H _G −H _{m i n} ) by altering the maximum depth H _{m a x} of the remaining profile.

• 4. H _{m i n} was added to the resulting profile.

This was done such that the cross-sectional area was maintained. This resulted in profiles with a different maximum depth H _{m a x} , which was substituted in Eq. 36b to find the new steepness C after step 4. Two examples of profiles constructed using this method are shown in Fig. 3b.

3.2.2 Fitted bottom profile and deepening

In order to facilitate comparison of modelled and measured tidal velocities and to investigate the effect of deepening for navigation, a fit to a profile observed in the upper Ems estuary was also used in this study. This fit was constructed by taking the sum of a constant depth and several Gaussian components. The shape of this fit is similar to that of the depth functions used by Li and Valle-Levinson (1999). The expression for the fitted bottom profile is

$$ H_{fit}=H_{max}\left\{F_{0}+\sum\limits_{j=1}^{J}F_{j}\exp\left(-C_{j}\left(y^{\prime}+D_{j}\right)^{2}\right)\right\}, $$

(37)

where F _j are the magnitudes of the components, C _j are the steepness parameters and D _j are shifts indicating the location of the maximum depth for each component. For the cross-section observed in the Ems around x = 16 km, a fit was made using one flat and two Gaussian components (so J = 2), with values as shown in the first row of Table 2. This profile, hereafter referred to as Fit to observations, is shown by the green curve in Fig. 3c. For this profile, a value for H _{m a x} of 10.0 m was used. This was done to make the tidal amplification at x = L _c approximately equal to that of the default case, so that the modelled cases are comparable before applying changes like deepening or sea level rise.

Table 2 Fitting parameters for the profiles Fit to observations, Prior to deepening and Future deepening

To study the effect of deepening the main channel of an estuary, a bottom profile similar to the Fit to observations profile was constructed with a deeper main channel. To obtain this, the value of F ₂ was increased. The parameters of this profile, called Future deepening, are given in Table 2. The corresponding profile is also shown in Fig. 3c.

3.2.3 Sea level rise

The increase in water depth due to sea level rise is modelled with a spatially uniform sea level rise (hereafter SLR). In this case thus not only the main channel is deepened, but the water depth is increased by the same amount throughout the whole estuary. As a low and high sea level rise scenario in this study, the lower and upper limits of the IPCC low emission scenario (RCP 2.6) were used, which amounts to a rate of 3 mm/year for the low scenario and 6 mm/year for the high scenario (Church et al. 2013). With these rates, the expected rise in sea level SLR in the year 2100 with respect to the default 2005 case is used in the model runs.

Two ways were considered to include the effect of increased sea level on the cross-sectional bottom profile. It is either assumed that the estuary is dyked, or that also flooding of adjacent banks occurs due to the increase in water level. These two scenarios are depicted in Fig. 4. In case of flooding, it is assumed that the minimum water depth at the lateral sides remains equal to H _{m i n} . The width of the banks b _{f l} is obtained by equating H _G + S L R = H _{m i n} at $y^{\prime }=1+b_{f}/b$, with H _G given by Eq. 36a with $a\rightarrow 0$.

Fig. 4

Sea level rise scenarios used in this study. The default mean wetted area with maximum width 2b is shown in blue, sea level rise (SLR) causes an increase of this wetted area, coloured orange. When flooding is included the wetted area extends sideways with b _{f l} on each side and the greenareas are included

4 Results

4.1 Sea surface elevation and longitudinal tidal velocity

4.1.1 Default case

Here, results are discussed for the default model run, which uses the Gaussian profile with a maximum depth H _{m a x} of 10.5 m. Figure 5a, b show the amplitude (blue lines) and phase (green lines) of the tidal elevation η ₀ and the longitudinal tidal velocity u ₀ at the surface in the main channel for the M ₂ tidal wave, respectively. The longitudinal tidal velocity is shown as it is later used as a forcing for the lateral tidal flow (through Coriolis deflection and through continuity). It appears that the amplitude $|\hat {\eta }_{0}|$ of the M ₂ tide increases near the end of the estuary, while its gradient and therefore $|\hat {u}_{0}|$ gradually decreases. The phase of both η ₀ and u ₀ gradually increases towards the landward end of the estuary, while their derivatives decrease with x. The latter indicates that the M ₂ tidal wave is a more travelling wave at the seaward side. The fact that the phase becomes almost constant near the landward side indicates that the tidal wave gains a standing wave character there. Data were available for both the amplitude and the phase of the M ₂ tidal wave in the Ems estuary during 2005, shown as squares and circles in Fig. 5a respectively. Clearly, the behaviour of the tidal wave is reasonably well represented by the model for this case respectively.

Fig. 5

The amplitude $|\hat {\eta }_{0}|$ (blue) and phase $\arg {(\hat {\eta }_{0})}$ (green) of the M ₂ tidal elevation (a), and the amplitude $|\hat {u}_{0}|$ (blue) and phase $\arg {(\hat {u}_{0})}$ (green) of the M ₂ longitudinal tidal velocity at the surface in the middle of the channel (b). The squares (circles) denote amplitudes (phases) measured in the Ems estuary in 2005

4.1.2 Width convergence and bottom profile shape

The width convergence factor μ=L _t /L _b is varied by varying the convergence e-folding length L _b , while using a constant frictionless wavelength $L_{t}=\sqrt {gH_{max}}/\omega$ of the M ₂ tidal wave. In Fig. 6a, b, the effect of varying the width convergence factor μ on the normalised tidal amplitude and on the phase is shown. The normalised tidal amplitude is defined as the ratio of the local tidal amplitude over the amplitude at the seaward side ( x = 0). Red (blue) colours indicate an increase (decrease) of the tidal amplitude with respect to the amplitude at x = 0. Tidal amplification (dampening) is defined as an increase (decrease) of the tidal sea surface amplitude with respect to the default case (denoted by a dashed line in Fig. 6). In the absence of width convergence ( μ=0), the tidal wave is dampened as friction is dominant in that case. For larger values of μ, the tidal wave first amplifies. It turns out that there is a critical μ=μ _{c r i t} =4.3 (corresponding to L _b ≈ 17 km) for which the tidal amplification at x = L _c is maximal (cf. Jay 1991). Beyond μ _{c r i t} , the tidal wave dampens again, indicating that the resonance characteristics are a complex function of μ.

Fig. 6

The normalised amplitude (with respect to the amplitude at the seaward side) and phase of the M ₂ sea surface elevations as a function of the width convergence parameter μ=L _t /L _b (resp. panels a, b) and the steepness parameter C (resp. panels c, d). Dashed lines indicate the default parameter values

An important aspect of the solution for η ₀ is that it also depends on the cross-sectional distribution of flow described in Eq. 27a, which is controlled by the imposed bottom profile $H(y^{\prime })$. Here, considered changes are the skewness of the bottom profile, using the skewness parameter a (see Eq. 36c), and the average slope of the cross-sectional bottom profile, through the steepness parameter C (as determined at the end of the four steps described in Section 3.2.1).

Model results indicate that the amplitude of the tidal sea surface elevation |η ₀| is independent to changes in the skewness parameter a (not shown). This is because both the average depth of the cross-section and the variation around this average depth (or the average slope) remain unchanged when using the bottom profile described in Eq. 36a. In that case, the wave number d ₀ in Eqs. 24 and 25 remains unchanged.

The effect of varying the average bottom slope through the steepness parameter C on the normalised tidal amplitude and the phase is shown in Fig. 6c, d. As can be seen, the M ₂ tidal wave is amplified by about 4 % more at the landward end of the channel if the steepness C increases from 1.66 to 1.83. Amplification thus increases with increasing average lateral bottom slope. The phase towards the landward end of the estuary also decreases slightly with increasing steepness. The increase in tidal propagation due to a deeper main channel thus outweighs the effect of shallower shoals if the steepness C increases. Note that the differential influence of friction, taken into account parametrically in Eq. 19, also plays a role here. As the eddy viscosity A _v varies linearly with the local depth H(x, y), the deeper main channel has a larger friction, while the shallower shoals have a lower friction. This slightly counteracts the effects of the depth changes on the tidal propagation.

4.1.3 Channel deepening and sea level rise

Next, the effect of deepening of the main channel and sea level rise on the amplitude and phase of the sea surface elevation is investigated. The blue and green lines in Fig. 7 show the amplitude and phase of the M ₂ tidal wave, respectively. It is shown that the amplitude increases significantly and more towards the landward end both when deepening the main channel and when applying sea level rise (without flooding). For a clear comparison between the effect of sea level rise and channel deepening, these results were obtained by using the Fit to observations profile for both these experiments. The phase decreases in case of deepening or sea level rise. In addition to having a larger amplitude, the tidal wave will thus also propagate faster through the estuary.

Fig. 7

The amplitudes $|\hat {\eta }_{0}|$ (blue lines) and phases $\arg {(\hat {\eta }_{0})}$ (green lines) of the M ₂ sea surface elevation for the default case with the Fit to observations profile, (a) for deepening of the main channel by 1.5 m (Future deepening profile) and (b) for a sea level rise of 3 and 6 mm/year until 2100 (without flooding)

Figure 8a, b show that for deepening by about 5.0 m and for S L R ≈ 2.8 m (without flooding), a maximum in tidal amplification at x = L _c occurs. Below these critical values, an overall water depth increase due to sea level rise brings the system closer to resonance than deepening only the main channel, as the relative depth change over the shoals is larger in the former case. However, the maximum amplification attained when applying sea level rise is lower compared to that when applying deepening. This is explained by considering that a local increase in depth also increases the local eddy viscosity A _v (Eq. 19) and thereby the friction. In case of sea level rise, the overall increase in friction is larger, as the friction increase over the shoals is relatively large, causing a stronger dampening of the tidal wave.

Fig. 8

The normalised amplitude (with respect to the amplitude at x = 0) of the M ₂ sea surface elevation as a function of deepening (a), sea level rise without flooding (b, c) and sea level rise with flooding of adjacent banks (d). For the top panels, the Fit to observations bottom profile was used, while in the bottom panels the Gaussian profile was used

When including flooding of adjacent banks, the average depth decreases again. However, the width of the estuary also increases by 2b _f (see Fig. 4). The effect on the tidal amplification when including sea level rise without and with flooding when using a Gaussian bottom profile is shown in Fig. 8c, d. The reason for using the Gaussian bottom profile here is that it allowed for a straightforward extrapolation of the bottom profile over the flooded areas. It turns out that the amount of SLR at which the maximum amplification in tidal range occurs reduces from 2.8 to 1.4 m when including flooding. The model results thus suggest that under the influence of sea level rise the system will reach a state of maximum amplification about two times faster when flooding of adjacent banks is taken into account.

4.2 Lateral tidal velocities

4.2.1 Default case

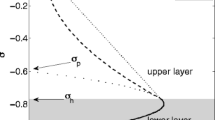
The lateral tidal velocity v ₀ is considered at two different times, namely at maximum flood and slack after flood. Figure 9 shows results for three different longitudinal locations, namely the seaward side x = 0, the middle $x=\frac {1}{2}L_{c}$ and the landward end x = L _c . Positive (negative) lateral velocities indicate a flow towards the right (left) when looking landward. Clearly, both the magnitude and the distribution of v ₀ over the cross-section are quite different at the three longitudinal positions. Near the seaward side, three (two) circulation cells arise during maximum flood (slack after flood). However, during maximum flood at x = 0, the negative lateral velocities of the third cell are suppressed by additional positive velocities on the left side of the cross-section. Towards the middle of the channel, a single circulation cell remains at both maximum flood and slack after flood, while a flow towards the sides (centre) is seen at maximum flood (slack after flood) at the landward side. The plusses (crosses) in Fig. 9a, c, f indicate the weighted centres (in terms of y and z) of areas that are separated by zero contours and contain only positive (negative) lateral velocities. The locations of these weighted centres at maximum flood were determined throughout the estuary for all x. In addition, the average velocity within each of the areas of positive (negative) lateral velocities was determined. In Fig. 10a, the lateral location of the weighted centres corresponding to areas of positive (negative) lateral velocities at maximum flood are shown in red (blue), where the intensity of the colour indicates the average velocity magnitude. It turns out that three circulation cells merge into a single cell around x = 8 km and that the positive and negative velocities of the single cell switch sides (in the lateral direction) around x = 45 km. The differences in both magnitude and cross-sectional structure of the lateral flow at different longitudinal positions is explained by analysing the different physical components of Eq. 29. Figure 10b shows the cross-sectionally averaged amplitude of v ₀ and its components. From this figure, it is clear that the lateral flow due to Coriolis deflection v _0,f and the lateral flow due to lateral density gradients $v_{0,\rho _{y}}$ are the dominant components throughout most of the estuary for the default case. However, their magnitudes decrease with increasing x. The magnitude of v _0,f decreases as the Coriolis deflection scales with the longitudinal velocity u ₀, which obviously decreases towards the landward end because the longitudinal transport must vanish at that location. The magnitude of $v_{0,\rho _{y}}$ decreases more rapidly, as it scales both with u ₀ (which advects the salinity $\bar {s}_{0}$) and with the longitudinal salinity gradient $d\bar {s}_{0}/dx$. As shown in Fig. 11, $d\bar {s}_{0}/dx$ is strongest at the seaward boundary and gradually decreases towards the landward side, since the maximum lies just outside the domain considered by our model. Near x = L _c , both v _0,f and $v_{0,\rho _{y}}$ are negligible and the lateral flow due to continuity v _0,c is the dominant component. However, through most of the estuary, the magnitude of v _0,c is much smaller than that of the other components in this default case. The magnitude of v _0,c shows a dip around x = 45 km (Fig. 10b), which is the location at which the positive and negative lateral velocities switch sides (Fig. 10a). This is attributed to the fact that the continuity component v _0,c , which becomes relatively more important towards the landward end of the estuary, changes sign at this location as well.

Fig. 9

Lateral M ₂ tidal velocities at x = 0 (a, b), $x=\frac {1}{2}L_{c}$ (c, d) and x = L _c (e, f), at maximum flood (a, c, e) and slack after flood (b, d, f) for the default case. Red (blue) colours indicate positive (negative) velocities towards the right (looking landward). The plusses (crosses) in (a, c, f) indicate the centroids of areas that are separated by zero contours and contain only positive (negative) lateral velocities

Fig. 10

Panel a shows the lateral locations of weighted centres of individual areas (separated by zero contours) of positive (red) and negative (blue) lateral velocities at maximum flood, with average velocities within each area as indicated by the colour bar. Panel b shows the cross-sectionally averaged amplitude of the lateral tidal velocity and its components

Fig. 11

The longitudinal salinity $\bar {s}_{0}(x)$ as a function of along-estuary distance x. The longitudinal distance on the x-axis extends 30 km outside of the considered model domain to clearly show the maximum salinity value s _{s e a} =25 psu and the location of the maximum salinity gradient x _c =−4 km

The magnitudes of v _0,f and $v_{0,\rho _{y}}$ are approximately equal around x = 10 km. At this location, the joint action of these components is therefore visible. In Fig. 12, the distribution of v ₀ and its components throughout the default Gaussian cross-section at x = 10 km is shown. It appears that v _0,f is symmetric around the central axis, while $v_{0,\rho _{y}}$ and v _0,c are both antisymmetric. Combined this leads to an asymmetric distribution of the lateral tidal flow, with positive velocities mostly on the right side near the surface and negative velocities on the right side near the bottom for maximum flood. During maximum flood, v _0,f and $v_{0,\rho _{y}}$ are both significant, while during slack after flood $v_{0,\rho _{y}}$ dominates. The latter results in a double circulation cell at slack after flood. When comparing the cross-sectional structure of the different lateral flow components from Fig. 12 with the structure of the lateral flow at different longitudinal locations from Fig. 9, some interesting similarities arise. It can clearly be seen that $v_{0,\rho _{y}}$ with its double circulation structure is dominant at x = 0, while v _0,f with its single circulation cell is clearly represented at $x=\frac {1}{2}L_{c}$. At x = L _c the lateral tidal flow takes on the structure of v _0,c , which is the only non-zero component at that location.

Fig. 12

Lateral M ₂ tidal velocities due all components (a, b), Coriolis deflection (c, d), continuity (e, f) and the lateral density gradient (g, h) at maximum flood (top panels) and slack after flood (bottom panels) for the Gaussian profile at x = 10 km. Red (blue) colours indicate positive (negative) velocities towards the right (looking landward)

4.2.2 Effect of bottom profile asymmetry on lateral tidal velocities

As the tidal wave propagation is not influenced by the asymmetry parameter a (see Section 4.1.2), the cross-sectionally integrated longitudinal M ₂ tidal flow is also not altered when a is varied and the flow is thus only redistributed over the cross-section. The longitudinal flow u ₀ is redistributed such that the velocity distribution has the same skewness as the bottom profile (not shown). As they are determined by the distribution of u ₀, the lateral velocities due to Coriolis deflection v _0,f and the lateral density gradient $v_{0,\rho _{y}}$ are also redistributed over the cross-section in this way.

The lateral locations and magnitudes of the positive and negative lateral velocities as shown in Fig. 10a for the default Gaussian profile are shown in Fig. 13a, d for a left skewed ( a = −0.8) and right skewed ( a = +0.8) asymmetric bottom profile, respectively. Interestingly, the positive (negative) velocities are enhanced for a = −0.8 ( a = +0.8). This is also seen when considering the distribution of v ₀ at maximum flood throughout the cross-section at x = 10 km, as shown in Fig. 13b, e (for a = −0.8 and a = +0.8, respectively), and comparing it with Fig. 12a. It turns out that the lateral tidal flow due to continuity v _0,c , shown in Fig. 13d, f, is responsible for this. Note that v _0,c does not only result from ∂ η ₀/∂ t but also from ∂ u ₀/∂ x. Since u ₀ is redistributed throughout the cross-section as a varies and becomes asymmetric around the central axis, the lateral flow due to continuity also becomes asymmetric. In addition, the magnitude of v _0,c increases from about 0.3 to 0.6 cm/s at x = 10 km for the skewed profiles (with a = +0.8 and a = −0.8), causing it to become 20–25 % of the total lateral flow. For significantly skewed bottom profiles, the cross-sectional average of v _0,c (and therefore of v ₀) is non-zero and at maximum flood its sign is opposite to the sign of a.

Fig. 13

Panels a, d show the lateral locations of weighted centres of individual areas (separated by zero contours) of positive (red) and negative (blue) lateral velocities at maximum flood, with average velocities within each area as indicated by the colour bar, for a = −0.8 and a = +0.8, respectively. Panels b, c, respectively, show the total lateral velocity v ₀ and the lateral velocity due to continuity v _0,c through the cross-section at x = 10 km, at maximum flood for a = −0.8. Panels e, f are similar to b, c, but for a = +0.8

4.2.3 Effect of varying lateral bottom slope on distribution of lateral tidal velocities

The lateral locations and magnitudes of the positive and negative lateral velocities (as shown in Fig. 13a, d for the skewed bottom profiles) are shown in Fig. 14a, d for a steepness C (see Eq. 36b) of 1.54 and 1.83, respectively. For C = 1.54, the magnitudes of the circulation cells are decreased with respect to the default case (which uses C = 1.66), due to the decrease in magnitude of the lateral velocity due to the lateral density gradient $v_{0,\rho _{y}}$ (shown in Fig. 14c, f). As $v_{0,\rho _{y}}$ is small in this case, the lateral flow component due to Coriolis v _0,f dominates and a single circulation cell appears. For C = 1.83, the magnitudes of the circulation cells are increased. When the steepness C increases, the difference between the minimum and the maximum depth is larger, leading to larger differences in longitudinal velocity magnitude and phase between the shoals and the main channel. These larger differences subsequently lead to stronger lateral density gradients, enhancing $v_{0,\rho _{y}}$ with its double circulation structure. This is expected, as this lateral flow component scales quadratically with depth (Huijts et al. 2011).

Fig. 14

Panels a, d show the lateral locations of weighted centres of individual areas (separated by zero contours) of positive (red) and negative (blue) lateral velocities at maximum flood, with average velocities within each area as indicated by the colour bar, for C = 1.54 and C = 1.83, respectively. Panels b, c, respectively, show the total lateral velocity v ₀ and the lateral velocity due to the lateral density gradient $v_{0,\rho _{y}}$ through the cross-section at x = 10 km, at maximum flood for C = 1.54. Panels e, f are similar to b, c, but for C = 1.83

5 Discussion

In this section, first modelled and measured M ₂ sea surface elevations and longitudinal velocities are compared for the Ems estuary. The limitations on the geometry in the model is then discussed shortly. Lastly, the effect of sea level rise on tidal forcing conditions at the seaward boundary is discussed.

5.1 Model-data comparison

The model outcome was compared to measurements from the Ems estuary. Measurements of sea surface elevation in the longitudinal direction from 2005 were obtained from Chernetsky et al. (2010). Figure 5a shows that the qualitative behaviour of the tidal wave is well represented by the model for the 2005 case.

Data obtained with an ADCP by the ICBM in Germany on the 12th of June 2012 allow for comparison of measured and modelled longitudinal tidal velocities through a cross-section around x = 16 km. The ADCP data were subjected to a harmonic analysis to find the M ₂ component of the longitudinal and lateral flow velocities. The lateral velocities obtained from the ADCP measurements were not found suitable to be compared with the model results. This is attributed to the presence of local geometrical characteristics, such as the proximity of a storm surge barrier, the presence of a side channel and a slight local divergence of the estuarine width. These local geometrical properties alter the distribution of the lateral tidal flow such that they cannot be represented by the analytical model. The model runs performed for this comparison use the Fit to observations bottom profile, an eddy viscosity A _{v, r e f} =1.0⋅10⁻² m ² s ⁻¹ and an M ₂ tidal amplitude $A_{M_{2}}=1.40$ m to better represent the 2012 case. Figure 15 shows a model-data comparison for the longitudinal tidal velocities. Clearly, the longitudinal velocities are both qualitatively and quantitatively well represented by the model.

Fig. 15

Modelled (a, b) and observed (c, d) longitudinal M ₂ tidal velocities respectively at maximum flood and slack after flood through a cross-section located at x = 16 km. Positive (negative) values indicate landward (seaward) velocities. The dashed line indicates the part of the cross-section in which measurements were available

5.2 Limitations on the geometry

The present model is designed to gain fundamental insight on tides in estuaries. Consequently, its direct application to natural estuaries is limited. Some geometric properties that are apparent in many estuaries around the world are not accounted for by this model. Examples are longitudinal variations in depth, meandering of the main channel, river bends and tidal flats. Longitudinal changes in depth, frictional properties and convergence can be considered when using a segmented version of the model, as long as proper boundary conditions are applied between the segments. By using a segmented model employing and using formulations of the equations in terms of natural coordinates, meandering and river bends might be taken into account while keeping the model analytical.

5.3 Effect of sea level rise on external forcing

As a result of sea level rise, the amplitudes and phase differences of the tides in oceans in coastal seas will change. If such changes in the coastal sea adjacent to the considered estuary are significant, they should be taken into account in the forcing conditions at the seaward side of this estuary. Changes in tidal characteristics due to sea level rise have been identified in the North Sea and are related to shifts in the amphidromic patterns of the tide. Pickering et al. (2012) showed that the changes in the M ₂ tidal amplitude related to sea level rise near the Ems estuary are negligible. When forcing the estuarine model with an M ₂ tidal amplitude, as is done in this study, these changes can thus be neglected. However, in other parts of the North Sea or in other regions of the world, changes in the tidal amplitude at sea due to sea level rise affect the tidal forcing at the mouth of estuaries. As an example, at Cuxhaven (at the mouth of the Elbe estuary), which is located only 150 km North East from the Ems estuary, Mudersbach et al. (2013) found a significant increase in M ₂ tidal amplitude of 1.76 mm/year due to mean sea level rise in historical data from 1953 to 2008. The results of Pickering et al. (2012) support these findings.

6 Conclusions

In this study, the dependence of the semi-diurnal sea surface elevation on width convergence, the lateral bottom profile shape, channel deepening and sea level rise were investigated. Also the effect of changing both the skewness and the average slope of the bottom profile on the lateral tidal flow was considered. This was done using an analytical model that included width convergence, a partial slip boundary condition and differential advection of salt. This model was applied to a prototype estuary with a geometry that was designed to represent the upper Ems estuary on the border between The Netherlands and Germany.

With respect to a default case, representing the 2005 situation, width convergence was shown to cause the amplitude of the sea surface elevation to first increase with increasing width convergence, but below a critical convergence length the tidal amplitude reduced again. Results pointed out that skewing the lateral bottom profile had no effect on tidal elevations, while increasing the average slope of the cross-sectional bottom profile caused increased amplification of the semi-diurnal sea surface elevation.

Realistic amounts of deepening ( ∼1–2 m) and sea level rise over the coming 50 to 100 years ( ∼30–60 cm) were shown to have a significant amplifying effect on the semi-diurnal tidal sea surface elevation in the Ems estuary. Furthermore, taking into account the effect of flooding of adjacent banks significantly lowers the critical amount of sea level rise after which dampening of the tidal wave occurs (from 2.8 to 1.4 m).

For symmetrical bottom profiles, the dominant lateral tidal components are those due to Coriolis deflection and the lateral density gradient throughout most of the estuary. Seaward of x = 15 km, the lateral density gradient becomes dominant and landward of x = 15 km Coriolis deflection is the determining process. Due to this, the lateral flow distribution shows two or three circulation cells close to the seaward boundary and only one circulation cell in the rest of the estuary. Laterally skewing the lateral bottom profile was shown to amplify the lateral flow due to the contribution from continuity. These velocities show a distribution that is antisymmetric in the lateral direction (around y = 0) when a symmetric bottom shape is used, while their distribution becomes asymmetric for skewed bottom profiles. Increasing the average slope, by varying the steepness parameter, leads to an enhanced lateral component due to the lateral density gradient, increasing the magnitude of the multiple circulation cells found at the seaward side of the estuary.