On the basic structure of oceanic gravity currents

Abstract

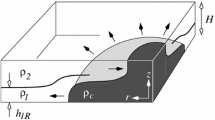
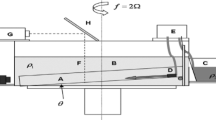
Results from numerical simulations of idealised, 2.5-dimensional Boussinesq, gravity currents on an inclined plane in a rotating frame are used to determine the qualitative and quantitative characteristics of such currents. The current is initially geostrophically adjusted. The Richardson number is varied between different experiments. The results demonstrate that the gravity current has a two-part structure consisting of: (1) the vein, the thick part that is governed by geostrophic dynamics with an Ekman layer at its bottom, and (2) a thin friction layer at the downslope side of the vein, the thin part of the gravity current. Water from the vein detrains into the friction layer via the bottom Ekman layer. A self consistent picture of the dynamics of a gravity current is obtained and some of the large-scale characteristics of a gravity current can be analytically calculated, for small Reynolds number flow, using linear Ekman layer theory. The evolution of the gravity current is shown to be governed by bottom friction. A minimal model for the vein dynamics, based on the heat equation, is derived and compares very well to the solutions of the 2.5-dimensional Boussinesq simulations. The heat equation is linear for a linear (Rayleigh) friction law and non-linear for a quadratic drag law. I demonstrate that the thickness of a gravity current cannot be modelled by a local parameterisation when bottom friction is relevant. The difference between the vein and the gravity current is of paramount importance as simplified (streamtube) models should model the dynamics of the vein rather than the dynamics of the total gravity current. In basin-wide numerical models of the ocean dynamics the friction layer has to be resolved to correctly represent gravity currents and, thus, the ocean dynamics.

Appendix: Force balance in a rotating gravity current

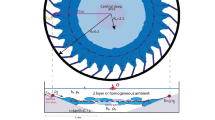
In the x direction (upslope), the dominant force balance is between the Coriolis force and reduced gravity. In the y direction, the reduced gravity vanishes and the dominant force balance is between friction and the Coriolis force (Fig. 7). Using linear Ekman layer theory, I obtain:

$$f H \frac{v}{\cos \theta} \sin \theta - \frac{\nu \sqrt{2} }{\delta} \frac{v}{\cos \theta} \cos (\theta +\pi /4) = 0.$$

(8)

As the angle of descent is small to leading order sinθ ≈ θ and $\cos (\theta +\pi /4)\approx 1/\sqrt{2}$, Eq. 8 then gives:

$$\theta = \frac{\nu}{ H f \delta } = {\sqrt \frac{\nu}{2 f H^2}}= \sqrt{\frac{\rm Ek}{4}} \approx 1.1 \cdot 10^{-2}.$$

(9)

Please note that this result depends only on the Ekman number and is independent of the velocity of the gravity current. The analysis presented here does not apply to the friction layer as the Ekman spiral is not complete and θ is not small in this case, but can be extended to cases with a turbulent Ekman layer using a quadratic drag law.

Fig. 7

Force balance in a gravity current descending at an angle θ to the horizontal at a constant speed u. The Coriolis force is at an angle of 3 π/2 to the direction of propagation and the frictional force at an angle of 5 π/4. In a stationary state, these two forces balance the gravitational force: F _Coriolis + F _friction + F _g = 0. Please note the turned coordinate system