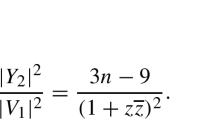Classification of conformal minimal immersions of constant curvature from $S^2$ to $Q_n$

Abstract

In this paper, we investigate geometry of conformal minimal two-spheres immersed in $G(2,n;\mathbb {R})$ and give a classification theorem of linearly full conformal minimal immersions of constant curvature from $S^2$ to $G(2,n;\mathbb {R})$, or equivalently, a complex hyperquadric $Q_{n-2}$ under some conditions.

1 Introduction

The classification of minimal surfaces M with constant curvature in various Riemannian spaces N is an important topic of differential geometry. In fact, these minimal surfaces have been investigated by several authors when the ambient spaces are real space forms and complex space forms (see [3, 4, 6, 15]). When specialized to $M=S^2$ and $N=\mathbb {C}P^{n}$, Bolton et al. [3] proved that any linearly full conformal minimal immersion of constant curvature from $S^2$ to $\mathbb {C}P^n$ belongs to the Veronese sequence, up to a rigid motion. It is well known that, when the ambient space N is general Riemannian symmetric space, for example, complex Grassmannian $G(k,n;\mathbb {C})$, complex hyperquadric $Q_n$ and quaternionic projective space $HP^n$ and so on, Calabi’s rigidity fails for minimal 2-spheres of constant curvature immersed in them. When N is a complex Grassmannian manifold, the study of its harmonic (a generalization of minimal) two-sphere has been the topic of a sequence of papers: for $N=G(2,4;\mathbb {C})$, Chi and Zheng [8] classified all holomorphic curves of the Riemann sphere in $G(2,4;\mathbb {C})$ whose curvature is equal to 2 into two families, up to unitary equivalence, in which none of the curves are congruent; for $N=G(2,5;\mathbb {C})$, Aithal [1]; for $N=G(2,n;\mathbb {C})$, Burstall and Wood [5], Chern and Wolfson [7], Uhlenbeck [17]. When N is a complex hyperquadric $Q_n$ or quaternionic projective space $HP^n$, papers [10, 11, 13, 14, 16, 18] introduced conformal minimal immersions of 2-spheres in N and gave some geometric properties of them. In the two cases $N=Q_3, \ HP^{2}$, papers [10, 16] gave classification theorems of linearly full totally unramified conformal minimal immersions of constant curvature from $S^2$ to $Q_3$ and $HP^2$, respectively. Here, our interest is to investigate minimal 2-spheres with constant curvature in $Q_n$.

As is well known, $G(2,n;\mathbb {R})$ may be identified with complex hyperquadric $Q_{n-2}$ in $\mathbb {C}P^{n-1}$ (for detailed descriptions, see the Preliminaries below). In 1989, Bahy-El-Dien and Wood [2] gave the explicit construction of all harmonic two-spheres in $G(2,n;\mathbb {R})$, which is considered as totally geodesic submanifolds in complex Grassmann manifolds $G(2,n;\mathbb {C})$. They pointed out that any non-isotropic harmonic map $S^2\rightarrow G(2,n;\mathbb {R})$ or $Q_{n-2}$ can be obtained in a unique way from a holomorphic map $f: S^2\rightarrow Q_{n-2}$ by certain flag transforms called forward and backward replacement ([2], Theorem 4.7). Using the method they gave, in this paper, we study classification of conformal minimal immersions of constant curvature from $S^2$ to $G(2,n;\mathbb {R})$ by theory of harmonic maps.

The paper is organized as follows. In Sect. 2, we identify $Q_{n-2}$ and $G(2,n;\mathbb {R})$, state some fundamental results concerning $G(k,n;\mathbb {C})$ from the view of harmonic sequences, and then show some brief descriptions of Veronese sequence and the rigidity theorem in $\mathbb {C}P^n$. In Sect. 3, we characterize reducible harmonic maps of $S^2$ in $G(2,n;\mathbb {R})$ with constant curvature (see Proposition 3.1). In Sect. 4, using Bahy-El-Dien and Wood’s results, we present some properties of the harmonic sequence generated by an irreducible harmonic map from $S^2$ to $G(2,n;\mathbb {R})$ with finite isotropy order $r\ge n-5$, and obtain the explicit characteristics of the corresponding harmonic map in $G(2,n;\mathbb {R})$. Further, we give a classification theorem of linearly full conformal minimal immersions of constant curvature from $S^2$ to $G(2,n;\mathbb {R})$, or equivalently, a complex hyperquadric $Q_{n-2}$ under some conditions (see Theorem 4.6).

2 Preliminaries

• (A) For $0< k < n$, let $G(k,n;\mathbb {R})$ denote the Grassmannian of all real k-dimensional subspaces of $\mathbb {R}^n$ and

  $$\begin{aligned} \sigma : G(k,n;\mathbb {C}) \rightarrow G(k,n;\mathbb {C}) \end{aligned}$$

  denote the complex conjugation of $G(k,n;\mathbb {C})$. It is easy to see that $\sigma$ is an isometry with the standard Riemannian metric of $G(k,n;\mathbb {C})$. Its fixed point set is $G(k,n;\mathbb {R})$; thus, $G(k,n;\mathbb {R})$ lies totally geodesically in $G(k,n;\mathbb {C})$.

  Map

  $$\begin{aligned} Q_{n-2} \rightarrow G(2,n;\mathbb {R}) \end{aligned}$$

  by

  $$\begin{aligned} q \mapsto \frac{\sqrt{-1}}{2} Z \wedge \overline{Z}, \end{aligned}$$

  where $q\in Q_{n-2}$ and Z is a homogeneous coordinate vector of q. It is clear that the map is one-to-one and onto, and it is an isometry. Thus, we can identify $Q_{n-2}$ and $G(2,n;\mathbb {R})$ (for more details, see [19]). Here, suppose that the metric on $G(2,n;\mathbb {R})$ is given by Section 2 of [12], then the metric is twice as much as the standard metric on $Q_{n-2}$ induced by the inclusion $\tau : Q_{n-2} \rightarrow \mathbb {C}P^{n-1}$, where this latter space is endowed with the Fubini-Study metric of constant holomorphic sectional curvature 4.

• (B) In this section we give general expression of some geometric quantities about conformal minimal immersions from $S^2$ to complex Grassmannian manifold $G(k,n;\mathbb {C})$.

Let M be a simply connected domain in the unit sphere $S^2$ and let $(z, \overline{z})$ be complex coordinates on M. We take the metric $ds_M^2=dzd\overline{z}$ on M. Denote

$$\begin{aligned} \partial = \frac{\partial }{\partial z}, \ \overline{\partial } = \frac{\partial }{\partial \overline{z}}. \end{aligned}$$

Consider complex Grassmann manifold $G(k,n;\mathbb {C})$ as the set of Hermitian orthogonal projections from $\mathbb {C}^n$ onto a k-dimensional subspace in $\mathbb {C}^n$. Then a map $\varphi : M\rightarrow G(k,n;\mathbb {C})$ is a Hermitian orthogonal projection onto a k-dimensional subbundle $\underline{\varphi }$ of the trivial bundle $\underline{\mathbb {C}}^n = M \times \mathbb {C}^n$ given by setting fiber $\underline{\varphi }_x = \varphi (x)$ for all $x\in M$. $\underline{\varphi }$ is called (a) harmonic ((sub-) bundle) whenever $\varphi$ is a harmonic map (cf. [2]).

Let $\varphi : S^2 \rightarrow G(k,n;\mathbb {C})$ be a harmonic map. Then from $\varphi$, two harmonic sequences are derived as follows:

$$\begin{aligned} \underline{\varphi }=\underline{\varphi }_{0}\mathop {\longrightarrow }\limits ^{\partial {'}}\underline{\varphi }_1\mathop {\longrightarrow }\limits ^{\partial {'}}\cdots \mathop {\longrightarrow }\limits ^{\partial {'}}\underline{\varphi }_ {i}\mathop {\longrightarrow }\limits ^{\partial {'}}\cdots , \end{aligned}$$

(2.1)

$$\begin{aligned} \underline{\varphi }=\underline{\varphi }_{0}\mathop {\longrightarrow }\limits ^{\partial {''}}\underline{\varphi }_{-1}\mathop {\longrightarrow }\limits ^{\partial {''}}\cdots \mathop {\longrightarrow }\limits ^{\partial {''}} \underline{\varphi }_{-i}\mathop {\longrightarrow }\limits ^{\partial {''}}\cdots , \end{aligned}$$

(2.2)

where $\underline{\varphi }_{i} = \partial ^\prime \underline{\varphi } _{i-1}$ and $\underline{\varphi }_{-i}= \partial ^{ \prime \prime } \underline{\varphi } _{-i+1}$ are Hermitian orthogonal projections from $S^2 \times \mathbb {C} ^n$ onto ${\underline{Im}}\left( \varphi ^{\perp }_ {i-1}\partial \varphi _{i-1} \right)$ and ${\underline{Im}}\left( \varphi ^{\perp }_ {-i+1}\overline{\partial } \varphi _ {-i+1}\right)$, respectively, $i=1,2,\ldots$.

Now recall ([5], §3A) that a harmonic map $\varphi : S^2 \rightarrow G(k,n;\mathbb {C})$ in (2.1) [resp. (2.2)] is said to be $\partial ^{'}$ -irreducible (resp. $\partial ^{''}$ -irreducible) if rank $\underline{\varphi } =$ rank $\underline{\varphi }_1$ (resp. rank $\underline{\varphi } =$ rank $\underline{\varphi }_{-1}$) and $\partial ^{'}$ -reducible (resp. $\partial ^{''}$ -reducible) otherwise. In particular, let $\varphi$ be a harmonic map from $S^2$ to $G(2,n;\mathbb {R})$, then $\varphi$ is $\partial ^{'}$-irreducible (resp. $\partial ^{'}$-reducible) if and only if $\varphi$ is $\partial ^{''}$-irreducible (resp. $\partial ^{''}$-reducible). In this case we simply say that $\varphi$ is irreducible (resp. reducible).

As in [9] call a harmonic map $\varphi : S^2 \rightarrow G(k,n;\mathbb {C})$ (strongly) isotropic if $\varphi _{i} \bot \varphi , \ \forall i\in \mathbb {Z}, \ i \ne 0$.

For an arbitrary harmonic map $\varphi : S^2 \rightarrow G(k,n;\mathbb {C})$, define its isotropy order (cf. [5]) to be the greatest integer r such that $\varphi _{i} \bot \varphi$ for all i with $1\le i \le r$; if $\underline{\varphi }$ is isotropic, set $r= \infty$.

Definition 2.1

Let $\varphi : S^2 \rightarrow G(k,n;\mathbb {C})$ be a map. $\varphi$ is linearly full if $\underline{\varphi }$ cannot be contained in any proper trivial subbundle $S^2 \times \mathbb {C}^m$ of $S^2\times { \mathbb {C}}^n$, ($m< n$).

In this paper, we always assume that $\varphi$ is linearly full.

Suppose that $\varphi : S^2 \rightarrow G(k,n;\mathbb {C})$ is a linearly full harmonic map and it belongs to the following harmonic sequence:

$$\begin{aligned} \underline{\varphi }_0\mathop {\longrightarrow }\limits ^{\partial {'}}\cdots \mathop {\longrightarrow }\limits ^{\partial {'}} \underline{\varphi }= \underline{\varphi }_{i} \mathop {\longrightarrow }\limits ^{\partial {'}} \underline{\varphi }_{i+1}\mathop {\longrightarrow }\limits ^{\partial {'}}\cdots \mathop {\longrightarrow }\limits ^{\partial {'}} \underline{\varphi }_{i_0}\mathop {\longrightarrow }\limits ^{\partial {'}}0 \end{aligned}$$

(2.3)

for some $i = 0, \ldots , i_0$. We choose the local unit orthogonal frame $e^{(i)}_1, e^{(i)}_2, \ldots , e^{(i)}_{k_{i}}$ such that they locally span subbundle $\underline{\varphi }_{i}$ of $S^2 \times \mathbb {C}^n$, where $k_i =$ rank $\underline{\varphi }_{i}$.

Let $W_{i}=\left( e^{(i)}_1, e^{(i)}_2, \ldots , e^{(i)}_{k_{i}}\right)$ be $\left( n\times k_{i}\right)$-matrix. Then we have

$$\begin{aligned} \varphi _{i}=W_{i}W^*_{i}, \end{aligned}$$

$$\begin{aligned} W^*_{i}W_{i} = I_{k_{i}\times k_{i}}, \quad W^*_{i}W_{i+1} =0,\quad W^*_{i} W_{i-1}=0. \end{aligned}$$

(2.4)

By (2.4), a straightforward computation shows that

$$\begin{aligned} \left\{ \begin{array}{l} \partial W_{i} = W_{i+1} \Omega _{i} + W_{i} \Psi _{i}, \\ \overline{\partial }W_{i} =-W_{i-1} \Omega ^*_ {i-1}- W_{i}\Psi ^*_{i}, \end{array}\right. \end{aligned}$$

(2.5)

where $\Omega _{i}$ is a $\left( k_{i+1} \times k_{i}\right)$-matrix and $\Psi _{i}$ is a $\left( k_{i}\times k_{i}\right)$-matrix for $i=0, 1, 2, \ldots , i_0$ and $\Omega _{i_0}=0$. It is very evident that integrability conditions for (2.5) are

$$\begin{aligned} \overline{\partial }\Omega _i= & {} \Psi _{i+1}^{*}\Omega _i-\Omega _i\Psi _{i}^{*},\\ \overline{\partial }\Psi _i+\partial \Psi _{i}^{*}= & {} \Omega _i^*\Omega _i+\Psi _i^*\Psi _i-\Omega _{i-1}\Omega _{i-1}^{*}-\Psi _i\Psi _i^*.\\ \end{aligned}$$

Set $L_{i} =\text {tr} (\Omega _{i} \Omega ^*_{i})$, the metric induced by $\varphi _{i}$ is given in the form

$$\begin{aligned} ds^2_{i} = (L_{i-1}+L_{i})dzd\overline{z}. \end{aligned}$$

(2.6)

From (2.6) and Section 2 of [13], suppose $ds^2 = \lambda ^2 dzd\overline{z}$ is the induced metric by $\varphi$, K and B are its Gauss curvature and second fundamental form, respectively. Then we have

$$\begin{aligned} \left\{ \begin{array}{l} \lambda ^2 = \text {tr} \partial \varphi \overline{\partial }\varphi , \\ K = -\frac{2}{\lambda ^2}\partial \overline{\partial } \log \lambda ^2,\\ \Vert B\Vert ^2 = 4\text {tr}PP^{*}, \end{array}\right. \end{aligned}$$

(2.7)

where $P=\partial \left( \frac{A_z}{\lambda ^2}\right)$ with $A_z=(2\varphi -I)\partial \varphi , \ A_{\overline{z}}=(2\varphi -I)\overline{\partial }\varphi$, and I is the identity matrix, then $P^{*} =- \overline{\partial } \left( \frac{A_{\overline{z}}}{\lambda ^2}\right)$.

In the following, we give a definition of the unramified harmonic map as follows:

Definition 2.2

([12]) If $\det (\Omega _i \Omega ^*_i) dz^{k_{i + 1}} d\overline{z} ^{k_{i+ 1}} \ne 0$ everywhere on $S^2$ in (2.3) for some i, we say that $\varphi _i: S^2 \rightarrow G(k_i,n; \mathbb {C})$ is unramified. If $\det (\Omega _i \Omega ^*_i) dz^{k_{i + 1}} d\overline{z} ^{k_{i+ 1}} \ne 0$ everywhere on $S^2$ in (2.1) [resp. (2.2)] for each $i = 0, 1, 2, \ldots$, we say that the harmonic sequence (2.1) [resp. (2.2)] is totally unramified. If (2.1) and (2.2) are both totally unramified, we say that $\varphi$ is totally unramified.

Set

$$\begin{aligned} \delta _{i} = \frac{1}{2\pi \sqrt{-1} }\int _{S^2}L_{i}d{\overline{z}} \wedge dz. \end{aligned}$$

(2.8)

For some i, if $\varphi _{i}$ is $\partial ^{'}$-irreducible and unramified in (2.3), then $|\det \Omega _{i}|^2dz^{k_{i}} d\overline{z} ^{k_{i}}$ is a well-defined invariant and has no zeros on $S^2$. It can be checked that (cf. [12])

$$\begin{aligned} \frac{1}{2\pi \sqrt{-1} }\int _{S^2}\partial \overline{\partial }\log |\det \Omega _{i}|^2d{\overline{z}} \wedge dz=-2k_i. \end{aligned}$$

(2.9)

• (C) In this section, we review the rigidity theorem of conformal minimal immersions of constant curvature from $S^2$ to $\mathbb {C}P^n$.

Let $\psi :S^2 \rightarrow \mathbb {C}P^n$ be a linearly full conformal minimal immersion, a harmonic sequence is derived as follows

$$\begin{aligned} 0\mathop {\longrightarrow }\limits ^{\partial ^\prime } \underline{\psi } _0 \mathop {\longrightarrow }\limits ^{\partial ^\prime }\cdots \mathop {\longrightarrow }\limits ^{\partial ^\prime } \underline{\psi } =\underline{\psi }_i \mathop {\longrightarrow }\limits ^{\partial ^\prime } \cdots \mathop {\longrightarrow }\limits ^{\partial ^\prime } \underline{\psi } _n \mathop {\longrightarrow }\limits ^{\partial ^\prime } 0, \end{aligned}$$

(2.10)

for some $i =0, 1, \ldots ,n$.

We define a sequence $f_0, \ldots , f_n$ of local sections of $\underline{\psi }_0, \ldots , \underline{\psi }_n$ inductively such that $f_0$ is a nowhere zero local section of $\underline{\psi }_0$ (without loss of generality, assume that $\overline{\partial } f_0 \equiv 0$ ) and $f_{i+1} = \psi ^\perp _{i}( \partial f_{i})$ for $i=0, \ldots ,n-1$. Then we have some formulae as follows:

$$\begin{aligned} \partial f_i= & {} f_{i+1} + \frac{\langle \partial f_i,f_i\rangle }{|f_i|^2}f_i, \ i= 0,\ldots , n, \end{aligned}$$

(2.11)

$$\begin{aligned} \overline{\partial } f_i= & {} - \frac{|f_i|^2}{|f_{i-1}|^2} f_{i-1}, \ i = 1, \ldots , n. \end{aligned}$$

(2.12)

Let $l_i= |f_{i+1}|^2/ |f_i|^2$ and $\delta _i^{(n)} = \frac{1}{2\pi \sqrt{-1}}\int _{S^2}l_i d\overline{z} \wedge dz$, $i =0, \ldots , n-1, \ l_{-1} = l_n =0$. It is easy to check that they are in accordance with $L_i$ and $\delta _i$, respectively, in the case $k=1$. Moreover, if (2.10) is a totally unramified harmonic sequence (i.e., $\psi _i$ is unramified, i=0,..., n), Bolton et al. proved (cf. [3])

$$\begin{aligned} \delta _ i^{(n)} = (i+1)(n-i). \end{aligned}$$

(2.13)

Consider the Veronese sequence

$$\begin{aligned} 0{\longrightarrow }\underline{V}^{(n)}_0\mathop {\longrightarrow }\limits ^{\partial {'}}\underline{V}^{(n)}_1\mathop {\longrightarrow }\limits ^{\partial {'}}\cdots \mathop {\longrightarrow }\limits ^{\partial {'}}\underline{V}^{(n)}_n\mathop {\longrightarrow }\limits ^{\partial {'}}0. \end{aligned}$$

For each $i=0,\ldots , n$, let $V^{(n)}_i: S^2\rightarrow \mathbb {C}P^n$ be given by $V^{(n)}_i = (v_{i,0}, \ldots , v_{i,n})^{T}$, where, for $z\in S^2$ and $j=0,\ldots , n$,

$$\begin{aligned} v_{i,j}(z) = \frac{i!}{(1 + z\overline{z})^i}\sqrt{\left( {\begin{array}{c}n\\ j\end{array}}\right) }z^{j-i}\sum _{k}(-1)^k \left( {\begin{array}{c}j\\ i-k\end{array}}\right) \left( {\begin{array}{c}n-j\\ k\end{array}}\right) (z\overline{z})^k. \end{aligned}$$

(2.14)

Each map $\underline{V}^{(n)}_i$ has induced metric $ds^2_i= \frac{n + 2i(n - i)}{(1+z\overline{z})^2}dzd\overline{z},$ the corresponding constant curvature $K_i$ is given by $K_i= \frac{4}{n + 2i(n-i)}$.

By Calabi’s rigidity theorem, Bolton et al. proved the following rigidity result (cf. [3]).

Lemma 2.3

([3]) Let $\psi : S^2 \rightarrow \mathbb {C}P^n$ be a linearly full conformal minimal immersion of constant curvature. Then, up to a holomorphic isometry of $\mathbb {C}P^n$, the harmonic sequence determined by $\psi$ is the Veronese sequence.

3 Reducible harmonic maps of constant curvature from $S^2$ to $G(2,n;\mathbb {R})$

Recall that an immersion of $S^2$ in $Q_n$ is conformal and minimal if and only if it is harmonic. Thus, we shall analyze harmonic maps from $S^2$ to $G(2,n;\mathbb {R})$ by reducible and irreducible cases, respectively. In this section, we first consider reducible harmonic maps of $S^2$ in $G(2,n;\mathbb {R})$ with constant curvature, and for the irreducible ones, we will discuss in detail in Sect. 4 below.

Let $\varphi : S^2\rightarrow G(2,n;\mathbb {R})$ be a linearly full reducible harmonic map with isotropy order r and constant curvature K. By ([2], Proposition 2.12) we know that, if $\varphi$ has finite isotropy order, then it is a real mixed pair; if $\varphi$ is (strongly) isotropic, then $r=\infty$. To characterize $\varphi$, we only need to consider the (strongly) isotropic ones.

In this case, $\varphi$ has isotropy order $\infty$ and belongs to the following harmonic sequence:

$$\begin{aligned} 0 \mathop {\longleftarrow }\limits ^{\partial {''}}\overline{\underline{\varphi }}_k\mathop {\longleftarrow }\limits ^{\partial {''}} \cdots \mathop {\longleftarrow }\limits ^{\partial {''}} \overline{\underline{\varphi }}_1\mathop {\longleftarrow }\limits ^{\partial {''}} \underline{\varphi } = \underline{\varphi }_0\mathop {\longrightarrow }\limits ^{\partial {'}}\underline{\varphi }_1 \mathop {\longrightarrow }\limits ^{\partial {'}}\cdots \mathop {\longrightarrow }\limits ^{\partial {'}}\underline{\varphi }_k\mathop {\longrightarrow }\limits ^{\partial {'}}0 \end{aligned}$$

(3.1)

for some $k\ge 1$. Here, $\underline{\overline{\varphi }}_1, \ \ldots , \ \underline{\overline{\varphi }}_k, \ \underline{\varphi }_0, \ \underline{\varphi }_1, \ \ldots , \ \underline{\varphi }_k$ are mutually orthogonal, and they are all harmonic maps from $S^2$ to $\mathbb {C}P^{m}\subset \mathbb {C}P^{n-1} (m<n)$ from the fact that $\varphi$ is harmonic and reducible. Let $p=m-k$, choose $f_{p+1}, \ldots , f_{m}$ such that they are local sections of $\underline{\varphi }_1, \ldots , \underline{\varphi }_k$, respectively, and satisfy equations (2.11) and (2.12) (here, the derived $f_0$ is holomorphic). From (3.1), we know that $\underline{f}_p$ and $\overline{\underline{f}}_p$ are both local sections of $\underline{\varphi }$, where $f_p$ is obtained from $f_{p+1}$ by equation (2.12).

Then we prove

Proposition 3.1

Let $\varphi : S^2\rightarrow G(2,n;\mathbb {R})$ be a linearly full reducible harmonic map with Gauss curvature K. Suppose that K is constant. Then $\varphi$ belongs to one of the following cases.

• (a) $\underline{\varphi } = \underline{f}_p \oplus \underline{c}_0$, where $\underline{c}_0$ is a constant vector in $\mathbb {C}^n$, $\ \underline{f}_p = \underline{\overline{f}}_p: S^2\rightarrow \mathbb {C}P^{n-2}$ and $2p=n-2$;

• (b) $\varphi$ is a real mixed pair, i.e., $\underline{\varphi } = \overline{\underline{f}}_0\oplus \underline{f}_0$, where $\underline{f}_0: S^2\rightarrow Q_{n-2}$ is holomorphic. Further, the curvature of $\underline{f}_p$ in (a) and $\underline{f}_0$ in (b) are both constants.

Proof

We first study the easier case $\underline{f}_p = \overline{\underline{f}}_p$. In this case, it is easy to see that $\underline{f}_{p+i} = \overline{\underline{f}}_{p-i}$ for $1\le i\le k$ and $2p=m$. Let $\rho$ be a section of $\underline{\varphi }$ such that $\underline{\varphi }=\underline{f}_p\oplus \underline{\rho }$, then we have $\langle \rho , f_i \rangle =0$ for $0\le i \le m$ since $\varphi$ is (strongly) isotropic. Using the theory of harmonic maps, $\underline{\rho }$ is a constant vector in $\mathbb {C}^n$, this implies that $\varphi$ belongs to case (a), completing the proof in the case $\underline{f}_p = \overline{\underline{f}}_p$.

From now on, we assume that $\underline{f}_p \ne \overline{\underline{f}}_p$. In this case, we claim $p=0$ holds, which implies that $\langle \overline{f}_0, f_0\rangle =0$, i.e., $\varphi$ is a real mixed pair.

Suppose by contrary that $p\ge 1$ holds. Let

$$\begin{aligned} \rho =|f_p|^2\overline{f}_p - \langle \overline{f}_p, f_p\rangle f_p,\end{aligned}$$

(3.2)

thus, we have $\underline{\varphi } = \underline{f}_p \oplus \underline{\rho }$ and $|\rho |^2 = |f_p|^6 - |f_p|^2\langle \overline{f}_p, f_p\rangle \langle f_p, \overline{f}_p\rangle$. Choose local frame

$$\begin{aligned} e_1=\frac{f_p}{|f_p|}, \ e_2=\frac{\rho }{|\rho |}, \ e_3=\frac{f_{p+1}}{|f_{p+1}|}, \ e_4=\frac{\overline{f}_{p+1}}{|{f}_{p+1}|}, \ e_5=\frac{f_{p+2}}{|f_{p+2}|}, \ e_6=\frac{\overline{f}_{p+2}}{|{f}_{p+2}|}. \end{aligned}$$

Set

$$\begin{aligned} W_0=(e_1, e_2), \ W_1=(e_3), \ W_{-1}=(e_4), \ W_2=(e_5), \ W_{-2}=(e_6), \end{aligned}$$

then by (2.5), we obtain

$$\begin{aligned} \Omega _0 = \left( \frac{|f_{p+1}|}{|f_p|}, \ 0\right) , \ \Omega _{-1} = \left( \begin{array}{ccccccc} -\frac{|f_{p+1}|}{|f_p|^3}\langle \overline{f}_p, f_p\rangle \\ -\frac{|f_{p+1}||\rho |}{|f_p|^4}\end{array}\right) .\end{aligned}$$

(3.3)

From (3.3), applying the equation $L_{i} =\text {tr} (\Omega _{i} \Omega ^*_{i})$, a straightforward computation shows $L_0=L_{-1}=\frac{|f_{p+1}|^2}{|f_p|^2}$. Then the metric induced by $\varphi$ is as follows

$$\begin{aligned} ds^2=2l_p dzd\overline{z}. \end{aligned}$$

Under the assumption that $\underline{\varphi }$ is of constant curvature, the curvature of $\underline{f}_p$ is also a constant. By Lemma 2.3, up to a holomorphic isometric of $\mathbb {C}P^{n-1}$, ${f}_p$ is a Veronese surface.

Since $\underline{\overline{\varphi }}_k$ and $\underline{\varphi }_k$ in (3.1) are orthogonal, so $\langle \overline{f}_m, f_m\rangle =0$, which implies that

$$\begin{aligned} \langle \overline{f}_0, f_0\rangle =0. \end{aligned}$$

(3.4)

Using (3.1) and (3.2) we have

$$\begin{aligned} f_{p-i}= & {} \frac{\langle f_{p-i}, \rho \rangle }{|\rho |^2}\rho +\frac{\langle f_{p-i}, \overline{f}_{p+1}\rangle }{|f_{p+1}|^2}\overline{f}_{p+1} +\cdots + \frac{\langle f_{p-i}, \overline{f}_{p+i-1}\rangle }{|f_{p+i-1}|^2}\overline{f}_{p+i-1}\nonumber \\&+\, \frac{\langle f_{p-i}, \overline{f}_{p+i}\rangle }{|f_{p+i}|^2}\overline{f}_{p+i} \end{aligned}$$

(3.5)

for $1\le i\le p$. In particular, take $i=p$, then (3.5) becomes

$$\begin{aligned} f_0=\frac{\langle f_0, \rho \rangle }{|\rho |^2}\rho +\frac{\langle f_0, \overline{f}_{p+1}\rangle }{|f_{p+1}|^2}\overline{f}_{p+1} +\cdots + \frac{\langle f_0, \overline{f}_{2p-1}\rangle }{|f_{2p-1}|^2}\overline{f}_{2p-1} + \frac{\langle f_0, \overline{f}_{2p}\rangle }{|f_{2p}|^2}\overline{f}_{2p}. \end{aligned}$$

(3.6)

Substituting (3.6) into (3.4), using the fact that $\overline{f}_{p+1}, \ldots , \overline{f}_{2p}, \ \rho , \ f_{p+1}, \ldots , f_{2p}$ are mutually orthogonal, we have

$$\begin{aligned} (\langle f_0, \rho \rangle )^2\langle \rho , \overline{\rho }\rangle =0, \end{aligned}$$

which can be rewritten as

$$\begin{aligned} \langle \overline{f}_p, f_p\rangle \langle f_0, \overline{f}_p\rangle =0, \end{aligned}$$

by making use of $\langle f_0, \rho \rangle =|f_p|^2\langle f_0, \overline{f}_p\rangle , \quad \langle \rho , \overline{\rho }\rangle = -\frac{|\rho |^2}{|f_p|^2}\langle \overline{f}_p, f_p\rangle$. We shall divide our discussion into two cases, according as $\langle \overline{f}_p, f_p\rangle =0$ or $\langle f_0, \overline{f}_p\rangle =0$.

If $\langle \overline{f}_p, f_p\rangle =0$, under the assumption that $p\ge 1$, from (3.1) we get $\underline{\overline{f}}_{p-1}=\underline{f}_{p+1}$, which implies that $\overline{\underline{f}}_p=\underline{f}_p$. This contradicts our supposition $\underline{\overline{f}}_p \ne \underline{f}_p$.

Thus, we obtain $\langle f_0, \overline{f}_p\rangle =0$, i.e., $\langle f_0, \rho \rangle =0$ and $\langle \overline{f}_p, f_p\rangle \ne 0$. From (3.5) we have

$$\begin{aligned} \langle f_{p-i}, \overline{f}_{p+i+1}\rangle =0, \end{aligned}$$

which gives

$$\begin{aligned} \langle f_{p-i}, \overline{f}_{p+i}\rangle =(-1)^i\frac{l_pl_{p+1}\ldots l_{p+i-1}}{l_{p-1}l_{p-2}\ldots l_{p-i}}\langle f_p, \overline{f}_p\rangle , 1\le i\le p. \end{aligned}$$

This shows that $\langle f_{p-i}, \overline{f}_{p+i}\rangle \ne 0$ for $0\le i\le p$. Since $p\ge 1$, in the following we write equation (3.5) in the form

$$\begin{aligned} \left\{ \begin{array} {l} f_{p-1}=\frac{\langle f_{p-1}, \rho \rangle }{|\rho |^2}\rho +\frac{\langle f_{p-1}, \overline{f}_{p+1}\rangle }{|f_{p+1}|^2}\overline{f}_{p+1}, \\ f_{p-2}=\frac{\langle f_{p-2}, \rho \rangle }{|\rho |^2}\rho +\frac{\langle f_{p-2}, \overline{f}_{p+1}\rangle }{|f_{p+1}|^2}\overline{f}_{p+1} + \frac{\langle f_{p-2}, \overline{f}_{p+2}\rangle }{|f_{p+2}|^2}\overline{f}_{p+2}, \\ f_{p-3}=\frac{\langle f_{p-3}, \rho \rangle }{|\rho |^2}\rho +\frac{\langle f_{p-3}, \overline{f}_{p+1}\rangle }{|f_{p+1}|^2}\overline{f}_{p+1} + \frac{\langle f_{p-3}, \overline{f}_{p+2}\rangle }{|f_{p+2}|^2}\overline{f}_{p+2}+\frac{\langle f_{p-3}, \overline{f}_{p+3}\rangle }{|f_{p+3}|^2}\overline{f}_{p+3}, \\ \vdots \\ f_1=\frac{\langle f_1, \rho \rangle }{|\rho |^2}\rho +\frac{\langle f_1, \overline{f}_{p+1}\rangle }{|f_{p+1}|^2}\overline{f}_{p+1} +\cdots + \frac{\langle f_1, \overline{f}_{2p-1}\rangle }{|f_{2p-1}|^2}\overline{f}_{2p-1}, \\ f_0=\frac{\langle f_0, \overline{f}_{p+1}\rangle }{|f_{p+1}|^2}\overline{f}_{p+1} +\cdots + \frac{\langle f_0, \overline{f}_{2p-1}\rangle }{|f_{2p-1}|^2}\overline{f}_{2p-1} + \frac{\langle f_0, \overline{f}_{2p}\rangle }{|f_{2p}|^2}\overline{f}_{2p}. \end{array} \right. \end{aligned}$$

(3.7)

Hence, it is possible to have the equations

$$\begin{aligned} \langle f_0, \overline{f}_{p+1}\rangle =0, \ \langle f_0, \overline{f}_{p+2}\rangle =0, \ldots , \langle f_0, \overline{f}_{2p-1}\rangle =0, \end{aligned}$$

by substituting (3.7) into the following equations

$$\begin{aligned} \langle f_{p-1}, f_0\rangle =0, \ \langle f_{p-2}, f_0\rangle =0, \ \langle f_{p-3}, f_0\rangle =0, \ \ldots , \ \langle f_1, f_0\rangle =0. \end{aligned}$$

We can thus arrive at the relation

$$\begin{aligned} \underline{f}_0=\underline{\overline{f}}_{2p}, \ 2p=m. \end{aligned}$$

Moreover, we have $\underline{\overline{f}}_p=\underline{f}_p$, which contradicts the supposition $\underline{\overline{f}}_p \ne \underline{f}_p$. Summarizing the above results, if $\underline{f}_p \ne \overline{\underline{f}}_p$, then we get $p=0$ and $\langle \overline{f}_0, f_0\rangle =0$, i.e., $\varphi$ is a real mixed pair.

Since the curvature K of $\varphi$ is a constant, then the curvature of $\underline{f}_p$ in (a) and $\underline{f}_0$ in (b) are both constants. $\square$

By Proposition 3.1, in the following we discuss case (b) with $\varphi$ of finite isotropy order $r\ge n-4$, and case (a) and case (b) with $\varphi$ of $r=\infty$.

3.1 Reducible harmonic maps from $S^2$ to $G(2,n;\mathbb {R})$ with constant curvature and finite isotropy order $r\ge n-4$

Let $\varphi : S^2 \rightarrow G(2,n;\mathbb {R})$ be a linearly full reducible harmonic map with constant curvature and finite isotropy order $r\ge n-4$. It follows from [2] that r is odd and $\varphi$ can be characterized by harmonic maps from $S^2$ to $\mathbb {C}P^{n-1}$, in fact,

$$\begin{aligned} \underline{\varphi } = \underline{\overline{f}}_0 \oplus \underline{f}_0, \end{aligned}$$

where $f_0: S^2\rightarrow Q_{n-2}$ is holomorphic.

By using $\varphi$, a harmonic sequence is derived as follows

$$\begin{aligned} 0\mathop {\longleftarrow }\limits ^{\partial {''}} \overline{\underline{f}}_m\mathop {\longleftarrow }\limits ^{\partial {''}} \cdots \mathop {\longleftarrow }\limits ^{\partial {''}} \overline{\underline{f}}_1\mathop {\longleftarrow }\limits ^{\partial {''}} \underline{\varphi }\mathop {\longrightarrow }\limits ^{\partial {'}}\underline{f}_1 \mathop {\longrightarrow }\limits ^{\partial {'}}\cdots \mathop {\longrightarrow }\limits ^{\partial {'}}\underline{f}_m \mathop {\longrightarrow }\limits ^{\partial {'}}0, \end{aligned}$$

where $0\mathop {\longrightarrow }\limits ^{\partial {'}} \underline{f}_0\mathop {\longrightarrow }\limits ^{\partial {'}}\underline{f}_1\mathop {\longrightarrow }\limits ^{\partial {'}} \cdots \mathop {\longrightarrow }\limits ^{\partial {'}}\underline{f}_m \mathop {\longrightarrow }\limits ^{\partial {'}}0$ is a linearly full harmonic sequence in $\mathbb {C}P^{m} \subset \mathbb {C}P^{n-1}$ satisfying

$$\begin{aligned} \left\{ \begin{array}{l} \langle \overline{f}_0, f_i \rangle =0 \ (0\le i\le r),\\ \langle \overline{f}_0, f_{r+1} \rangle \ne 0, \end{array}\right. \end{aligned}$$

(3.8)

and $\ {r+1} \le m\le {n-1}$. The induced metric of $\varphi$ is given by

$$\begin{aligned} ds^2 = 2l_0dzd\overline{z}, \end{aligned}$$

(3.9)

where $l_0dzd\overline{z}$ is the induced metric of $f_0$. Since $\underline{\varphi }$ is of constant curvature, using (3.9) we get that the curvature K of $\varphi$ satisfies $K=\frac{2}{m}$. By Lemma 2.3, up to a holomorphic isometry of $\mathbb {C}P^{n-1}$, ${f}_0$ is a Veronese surface. We can choose a complex coordinate z on $\mathbb {C}=S^2\backslash \{pt\}$ so that ${f}_0 = {U}{V}^{(m)}_0$, where $U\in U(n)$ and ${V}^{(m)}_0$ has the standard expression given in part (C) of Sect. 2 (adding zeros to ${V}^{(m)}_0$ such that ${V}^{(m)}_0 \in \mathbb {C}^n$). Then (3.8) becomes

$$\begin{aligned} \left\{ \begin{array} {l} \langle UV^{(m)}_0, \overline{U}\overline{V}^{(m)}_r \rangle = 0, \\ \langle UV^{(m)}_0, \overline{U}\overline{V}^{(m)}_{r+1}\rangle \ne 0, \end{array} \right. \end{aligned}$$

which is equivalent to

$$\begin{aligned} \left\{ \begin{array} {l} \text {tr} WV^{(m)}_0 V^{(m)T}_r= 0, \\ \text {tr} WV^{(m)}_0 V^{(m)T}_{r+1}\ne 0, \end{array} \right. \end{aligned}$$

(3.10)

where $W = U^{T}U$, it satisfies $W\in U(n)$ and $W^{T} = W$.

Define a set

$$\begin{aligned} G_W \triangleq \{U\in U(n)|U^T U = W\}. \end{aligned}$$

(3.11)

For a given W, the following can be easily checked

• (1) $\forall \ U \in G_W, \ A \in SO(n)$, we have $AU \in G_W$;

• (2) $\forall \ U,V \in G_W, \exists \ A \in SO(n), \ s.t.\ U = AV.$

To determine $\varphi$, firstly we need to determine the isotropy order r of it. If n is even, since the isotropy order r of $\varphi$ is greater than or equal to $n-4$ and it is odd, then $r=n-3$. If n is odd, $r=n-2$ or $n-4$.

In the following we discuss W in cases $r=n-3, \ n-2, \ n-4$, respectively.

Case I, $r=n-3$.

In this case, $m=n-2$ or $n-1$ and $\varphi$ belongs to the following two harmonic sequences, respectively:

• (Ia) $\underline{\varphi } \mathop {\longrightarrow }\limits ^{\partial {'}}\underline{f}_1 \mathop {\longrightarrow }\limits ^{\partial {'}}\cdots \mathop {\longrightarrow }\limits ^{\partial {'}}\underline{f}_{n-3}\mathop {\longrightarrow }\limits ^{\partial {'}}\underline{f}_{n-2} \mathop {\longrightarrow }\limits ^{\partial {'}}0$;

• (Ib) $\underline{\varphi }\mathop {\longrightarrow }\limits ^{\partial {'}}\underline{f}_1 \mathop {\longrightarrow }\limits ^{\partial {'}}\cdots \mathop {\longrightarrow }\limits ^{\partial {'}}\underline{f}_{n-3}\mathop {\longrightarrow }\limits ^{\partial {'}}\underline{f}_{n-2} \mathop {\longrightarrow }\limits ^{\partial {'}}\underline{f}_{n-1} \mathop {\longrightarrow }\limits ^{\partial {'}}0$.

  Case II, $r=n-2$.

  In this case, $m=n-1$ and $\varphi$ belongs to the following harmonic sequence:

• (IIa) $\underline{\varphi } \mathop {\longrightarrow }\limits ^{\partial {'}}\underline{f}_1 \mathop {\longrightarrow }\limits ^{\partial {'}}\cdots \mathop {\longrightarrow }\limits ^{\partial {'}}\underline{f}_{n-2} \mathop {\longrightarrow }\limits ^{\partial {'}}\underline{f}_{n-1}\mathop {\longrightarrow }\limits ^{\partial {'}}0$.

  Case III, $r=n-4$.

  In this case, $m=n-3, \ n-2$ or $n-1$, and $\varphi$ belongs to the following three harmonic sequences, respectively:

• (IIIa) $\underline{\varphi } \mathop {\longrightarrow }\limits ^{\partial {'}}\underline{f}_1 \mathop {\longrightarrow }\limits ^{\partial {'}}\cdots \mathop {\longrightarrow }\limits ^{\partial {'}}\underline{f}_{n-4} \mathop {\longrightarrow }\limits ^{\partial {'}}\underline{f}_{n-3}\mathop {\longrightarrow }\limits ^{\partial {'}}0$; (IIIb) $\underline{\varphi } \mathop {\longrightarrow }\limits ^{\partial {'}}\underline{f}_1 \mathop {\longrightarrow }\limits ^{\partial {'}}\cdots \mathop {\longrightarrow }\limits ^{\partial {'}}\underline{f}_{n-4} \mathop {\longrightarrow }\limits ^{\partial {'}}\underline{f}_{n-3}\mathop {\longrightarrow }\limits ^{\partial {'}}\underline{f}_{n-2}\mathop {\longrightarrow }\limits ^{\partial {'}}0$; (IIIc) $\underline{\varphi } \mathop {\longrightarrow }\limits ^{\partial {'}}\underline{f}_1 \mathop {\longrightarrow }\limits ^{\partial {'}}\cdots \mathop {\longrightarrow }\limits ^{\partial {'}}\underline{f}_{n-4} \mathop {\longrightarrow }\limits ^{\partial {'}}\underline{f}_{n-3}\mathop {\longrightarrow }\limits ^{\partial {'}}\underline{f}_{n-2}\mathop {\longrightarrow }\limits ^{\partial {'}}\underline{f}_{n-1}\mathop {\longrightarrow }\limits ^{\partial {'}}0$.

  To determine $\varphi$, we first should consider the type of W or U. From (3.10), the matrices W in cases (Ia), (IIa) and (IIIa) satisfy

  $$\begin{aligned} \text {tr} WV^{(m)}_0 V^{(m)T}_{m-1}= 0, \quad \text {tr} WV^{(m)}_0 V^{(m)T}_{m}\ne 0, \end{aligned}$$

  (3.12)

  where m is even. Similarly, the matrices W in cases (Ib) and

• (IIIb) satisfy

  $$\begin{aligned} \text {tr} WV^{(m)}_0 V^{(m)T}_{m-2}= 0, \quad \text {tr} WV^{(m)}_0 V^{(m)T}_{m-1}\ne 0, \end{aligned}$$

  (3.13)

  where m is odd, and the matrix W in case (IIIc) satisfies

  $$\begin{aligned} \text {tr} WV^{(m)}_0 V^{(m)T}_{m-3}= 0, \quad \text {tr} WV^{(m)}_0 V^{(m)T}_{m-2}\ne 0, \end{aligned}$$

  (3.14)

  where m is even.

  We first consider the type of W in (3.12). The standard expressions of $V^{(m)}_0$ and $V^{(m)}_{m-1}$ show that $V^{(m)}_0 V^{(m)T}_{m-1}$ is a polynomial matrix in z and $\overline{z}$. Assume $W = (a_{ij}), \ 0\le i,j \le n-1$, which is a constant matrix. From (2.14), we have

  $$\begin{aligned} v_{0,j}(z)=\sqrt{\left( {\begin{array}{c}m\\ j\end{array}}\right) }z^j, \quad v_{m-1,j}(z)=\frac{(m-1)!}{(1+z\overline{z})^{m-1}}\sqrt{\left( {\begin{array}{c}m\\ j\end{array}}\right) }(-\overline{z})^{m-j-1}(m-j-jz\overline{z}), \end{aligned}$$

  for $0\le j\le m$, and $v_{0,j}(z)=v_{m-1,j}(z)=0, \ m+1\le j\le n-1$.

  Then equation $\text {tr} WV^{(m)}_0 V^{(m)T}_{m-1}= 0$ can be rewritten in the form

  $$\begin{aligned} \sum _{i,j=0}^{m}a_{ij}\sqrt{\left( {\begin{array}{c}m\\ i\end{array}}\right) \left( {\begin{array}{c}m\\ j\end{array}}\right) }(-1)^{m-j-1}(\overline{z})^{m-i-j-1}[(m-j)(z\overline{z})^i-j(z\overline{z})^{i+1}]=0. \end{aligned}$$

  (3.15)

  For any fixed integer $k\ (0\le k \le 2m)$, the formula (3.15) yields a polynomial equation for $z\overline{z}$ given by

  $$\begin{aligned} \sum _{i+j=k}a_{ij}\sqrt{\left( {\begin{array}{c}m\\ i\end{array}}\right) \left( {\begin{array}{c}m\\ j\end{array}}\right) }(-1)^{j}[(m-j)(z\overline{z})^i-j(z\overline{z})^{i+1}]=0. \end{aligned}$$

  (3.16)

  Using the method of indeterminate coefficients by (3.16), we get

  $$\begin{aligned} \left\{ \begin{array} {l} a_{0k} = 0, \\ (k-i+1)\sqrt{\left( {\begin{array}{c}m\\ i-1\end{array}}\right) \left( {\begin{array}{c}m\\ k-i+1\end{array}}\right) }a_{i-1, k-i+1} + (m-k+i)\sqrt{\left( {\begin{array}{c}m\\ i\end{array}}\right) \left( {\begin{array}{c}m\\ k-i\end{array}}\right) }a_{i, k-i}=0 \end{array} \right. \end{aligned}$$

  (3.17)

  for $0\le k \le m-1, \ 1\le i\le k$;

  $$\begin{aligned} \left\{ \begin{array} {l} a_{m,k-m} = 0, \\ (m-k+i)\sqrt{\left( {\begin{array}{c}m\\ i\end{array}}\right) \left( {\begin{array}{c}m\\ k-i\end{array}}\right) }a_{i, k-i} + (k-i+1)\sqrt{\left( {\begin{array}{c}m\\ i-1\end{array}}\right) \left( {\begin{array}{c}m\\ k-i+1\end{array}}\right) }a_{i-1, k-i+1}=0 \end{array} \right. \end{aligned}$$

  (3.18)

  for $m+1\le k \le 2m, \ m+1\le i\le k$.

  Rearranging (3.16) (3.17) and (3.18), it is easy to see that W in (3.12) satisfies

  $$\begin{aligned} \left\{ \begin{array} {l} a_{ij}=0, \ 0\le i,j\le m, \ i+j\ne m, \\ a_{i-1, m-i+1} + a_{i, m-i}=0, \ 1\le i \le m. \end{array} \right. \end{aligned}$$

  (3.19)

  Similarly, W in (3.13) satisfies

  $$\begin{aligned} \left\{ \begin{array} {l} a_{ij}=0, \ 0\le i,j\le m, \ i+j\ge m+2 \ or\ i+j\le m-2, \\ 3a_{i,i+1} + a_{i-1, i+2}=0, 2i+1=m, \end{array} \right. \end{aligned}$$

  (3.20)

  and W in (3.14) satisfies

  $$\begin{aligned} a_{ij}=0, \ 0\le i,j\le m, \ i+j\ge m+3 \ or\ i+j\le m-3. \end{aligned}$$

  (3.21)

Therefore, we obtain

Proposition 3.2

Let $\varphi : S^2\rightarrow G(2,n;\mathbb {R})$ be a linearly full reducible harmonic map with constant curvature K and finite isotropy order r. Suppose that $r\ge n-4$. Then n must be odd, and up to an isometry of $G(2,n;\mathbb {R})$, $\underline{\varphi } = \overline{\underline{U}}\overline{\underline{V}}^{(n-1)}_0 \oplus \underline{U}\underline{V}^{(n-1)}_0$ with $K = \frac{2}{n-1}$ for some $U\in G \triangleq \{U\in U(n)|U^TU = W_0\}$, where $W_0= antidiag \{1, -1, 1, -1, \ldots , 1\}$, which is an $(n\times n)$-matrix.

Proof

At first, we discuss W in cases $r=n-3, n-2, n-4$, respectively.

• (I) $r=n-3$. In this case, $m=n-2$ or $n-1$. If $m=n-2$, $\varphi$ belongs to (Ia). Using (3.19) and the property of unitary matrix, we get $W = \left( \begin{array}{ccccccc} W_1 &{} 0 \\ 0 &{} a_{m+1, m+1} \end{array}\right)$, where $W_1=antidiag\{a_{0m}, a_{1, m-1}, \cdots , a_{m0}\}$. Obviously, $\varphi$ is not linearly full in this condition. If $m=n-1$, using (3.20) and the property of unitary matrix, we find that there doesn’t exist such W.

• (II) $r=n-2$. In this case, $m=n-1$ and $\underline{\overline{f}}_0=\underline{f}_m$, which is equivalent to

  $$\begin{aligned} \overline{U}\overline{V}^{(m)}_0 = \mu UV^{(m)}_m, \end{aligned}$$

  (3.22)

where $\mu$ is a parameter. Set $W_0 = antidiag\{1, -1, 1, -1, \cdots , 1\}$, which is an $(n\times n)$-matrix. Then condition (3.22) becomes

$$\begin{aligned} \overline{U} = UW_0. \end{aligned}$$

(3.23)

Define a set

$$\begin{aligned} G \triangleq \{U\in U(n)|U^T U = W_0\}. \end{aligned}$$

(3.24)

Then the following can be easily checked

• (1) $\forall \ U \in G, \ A \in SO(n)$, we have $AU \in G$;

• (2) $\forall \ U,V \in G, \exists \ A \in SO(n), \ s.t.\ U = AV.$

• (III) $r=n-4$. In this case, $m=n-3, n-2$ or $n-1$. If $m=n-3$, then $\varphi$ belongs to (IIIa). Using (3.19) and the property of unitary matrix, we get $W = \left( \begin{array}{ccccccc} W_1 &{} 0 \\ 0 &{} W_2 \end{array}\right)$, where $W_1=antidiag\{a_{0m}, a_{1, m-1}, \cdots , a_{m0}\}$ and $W_2 = \left( \begin{array}{ccccccc} a_{m+1, m+1} &{} a_{m+1, m+2} \\ a_{m+1, m+2} &{} a_{m+2, m+2} \end{array}\right)$. Obviously $\varphi$ is not linearly full in this condition. If $m=n-2$ or $m=n-1$, using (3.20) and (3.21), we find that there doesn’t exist such W.

In summary we get the conclusion. $\square$

Remark 3.3

In Proposition 3.2, $G \ne \emptyset$. Since n is odd, let $n=2p+1$.

If p is even, choose

$$\begin{aligned} U_0= & {} \left[ \begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} \frac{1}{\sqrt{2}} &{}\,\, 0 &{}\,\,\ \cdots &{}\,\, 0 &{}\,\, 0 &{}\,\, 0 &{}\,\, \cdots &{}\,\, 0 &{}\,\, \frac{1}{\sqrt{2}} \\ \frac{\sqrt{-1}}{\sqrt{2}} &{}\,\, 0 &{}\,\, \cdots &{}\,\, 0 &{}\,\, 0 &{}\,\, 0 &{}\,\, \cdots &{}\,\, 0 &{}\,\, -\frac{\sqrt{-1}}{\sqrt{2}} \\ 0 &{}\,\, \frac{1}{\sqrt{2}} &{}\,\, \cdots &{} \vdots &{} \vdots &{} \vdots &{} \cdots &{} -\frac{1}{\sqrt{2}} &{}\,\, 0\\ 0 &{}\,\, \frac{\sqrt{-1}}{\sqrt{2}}&{}\,\, \cdots &{} \vdots &{} \vdots &{} \vdots &{} \cdots &{} \frac{\sqrt{-1}}{\sqrt{2}} &{}\,\, 0 \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ 0 &{}\,\, 0 &{}\,\, \cdots &{}\,\, \frac{1}{\sqrt{2}} &{}\,\, 0 &{}\,\, -\frac{1}{\sqrt{2}} &{}\,\, \cdots &{}\,\, 0 &{}\,\, 0 \\ 0 &{}\,\, 0 &{}\,\, \cdots &{}\,\, \frac{\sqrt{-1}}{\sqrt{2}} &{}\,\, 0 &{}\,\, \frac{\sqrt{-1}}{\sqrt{2}} &{}\,\, \cdots &{}\,\, 0 &{}\,\, 0 \\ 0 &{}\,\, 0 &{}\,\, \cdots &{}\,\, 0 &{}\,\, 1 &{}\,\, 0 &{}\,\, \cdots &{}\,\, 0 &{}\,\, 0 \end{array}\right] ;\\ \textit{If p is odd, choose } U_0= & {} \left[ \begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} \frac{1}{\sqrt{2}} &{}\,\, 0 &{}\,\, \cdots &{}\,\, 0 &{}\,\, 0 &{}\,\, 0 &{}\,\, \cdots &{}\,\, 0 &{}\,\, \frac{1}{\sqrt{2}} \\ \frac{\sqrt{-1}}{\sqrt{2}} &{}\,\, 0 &{}\,\, \cdots &{}\,\, 0 &{}\,\, 0 &{}\,\, 0 &{}\,\, \cdots &{}\,\, 0 &{}\,\, -\frac{\sqrt{-1}}{\sqrt{2}} \\ 0 &{}\,\, \frac{1}{\sqrt{2}} &{}\,\, \cdots &{} \vdots &{} \vdots &{} \vdots &{} \cdots &{} -\frac{1}{\sqrt{2}} &{}\,\, 0\\ 0 &{}\,\, \frac{\sqrt{-1}}{\sqrt{2}}&{}\,\, \cdots &{} \vdots &{} \vdots &{} \vdots &{} \cdots &{}\,\, \frac{\sqrt{-1}}{\sqrt{2}} &{}\,\, 0 \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ 0 &{}\,\, 0 &{}\,\, \cdots &{}\,\, \frac{1}{\sqrt{2}} &{}\,\, 0 &{}\,\, \frac{1}{\sqrt{2}} &{}\,\, \cdots &{}\,\, 0 &{}\,\, 0 \\ 0 &{}\,\, 0 &{}\,\, \cdots &{}\,\, \frac{\sqrt{-1}}{\sqrt{2}} &{}\,\, 0 &{}\,\, -\frac{\sqrt{-1}}{\sqrt{2}} &{}\,\, \cdots &{}\,\, 0 &{}\,\, 0 \\ 0 &{}\,\, 0 &{}\,\, \cdots &{}\,\, 0 &{}\,\, \sqrt{-1} &{}\,\, 0 &{}\,\, \cdots &{}\,\, 0 &{}\,\, 0 \end{array}\right] . \end{aligned}$$

Let $C_i$ denote the i -th column of $U_0$. For $1\le i\le p$, all the elements of $C_i$ are zero expect the $(2i-1)$ -th and (2i)-th elements, which are $\frac{1}{\sqrt{2}}$ and $\frac{\sqrt{-1}}{\sqrt{2}}$ respectively. Moreover, the column vectors of $U_0$ satisfy equation $\overline{C}_i+(-1)^iC_{n-i+1}=0, \ 1\le i \le n$. Then we have $U_0\in G$ and $\forall U\in G$ can be obtained from $U_0$ by an SO(n)-motion.

As to the second fundamental form B of $\varphi$, we have the following corollary.

Corollary 3.4

Let $\varphi : S^2\rightarrow G(2,n;\mathbb {R})$ be a linearly full reducible harmonic map with constant curvature K and finite isotropy order r. Suppose that $r\ge n-4$. Then its second fundamental form B satisfies $\Vert B\Vert ^2 = \frac{4(n-2)}{n-1}, \ n\ge 4$.

Proof

Let $n=m+1$, and take $U_0\in U(n)$, which is the one shown in Remark 3.3. For any integer i $\ (0\le i \le m)$, let

$$\begin{aligned} f_i=U_0V^{(m)}_i. \end{aligned}$$

(3.25)

Then $\overline{\underline{f}}_0=\underline{f}_m$, and $\underline{\varphi }$ can be rewritten as $\underline{\varphi }=\overline{\underline{f}}_0\oplus \underline{f}_0$, where $\underline{f}_0$ is of constant curvature. By (2.7), a series of calculations give

$$\begin{aligned} \left\{ \begin{array} {l} \partial \varphi =\frac{1}{|f_0|^2}[\overline{f}_0(\overline{f}_{1})^{*}+f_{1}f_0^{*}], \\ A_z=\frac{1}{|f_0|^2}[\overline{f}_0(\overline{f}_{1})^{*}-f_{1}f_0^{*}], \\ P=\frac{1}{2|f_1|^2}[\overline{f}_0(\overline{f}_{2})^{*}-f_{2}f_0^{*}]. \end{array} \right. \end{aligned}$$

Hence, we get

$$\begin{aligned} \Vert B\Vert ^2=2\left[ \frac{l_1}{l_0}-\frac{|\langle \overline{f}_0, f_2\rangle |^2}{|f_1|^4}\right] . \end{aligned}$$

Since $\underline{f}_0$ is of constant curvature and $m+1=n$, so $\frac{l_1}{l_0}=\frac{\delta ^{(m)}_1}{\delta ^{(m)}_0}=\frac{2(n-2)}{n-1}$, which implies that

$$\begin{aligned} \Vert B\Vert ^2=2\left[ \frac{2(n-2)}{n-1}-\frac{|\langle \overline{f}_0, f_2\rangle |^2}{|f_1|^4}\right] . \end{aligned}$$

(3.26)

From the fact that n is odd, we discuss it as follows:

(1) If $n=3$. Equation $\overline{\underline{f}}_0=\underline{f}_2$ follows immediately from (3.25). Substituting it into (3.26), we obtain $\Vert B\Vert ^2=0$, i.e., $\varphi$ is totally geodesic. In this case, $\varphi$ is a conformal minimal immersion from $S^2$ to $G(2,3;\mathbb {R})$ (or equivalently $Q_1$), which is trivial, we don’t consider it in this paper;

(2) If $n\ge 5$. Since $\overline{\underline{f}}_0=\underline{f}_m$, then we have $\langle \overline{f}_0, f_2 \rangle =0$. Equation (3.26) becomes $\Vert B\Vert ^2=\frac{4(n-2)}{n-1}$. $\square$

3.2 Reducible (strongly) isotropic harmonic maps from $S^2$ to $G(2,n;\mathbb {R})$ with constant curvature

Above we determine all harmonic maps of $S^2$ in $G(2,n;\mathbb {R})$ with constant curvature and finite isotropy order $r\ge n-4$. In the following, using Proposition 3.1, we shall give a classification of reducible (strongly) isotropic harmonic maps from $S^2$ to $G(2,n;\mathbb {R})$ with constant curvature.

Proposition 3.5

Let $\varphi : S^2\rightarrow G(2,n;\mathbb {R})$ be a linearly full reducible harmonic map with constant curvature K and second fundamental form B. Suppose that $\varphi$ is (strongly) isotropic. Then n must be even, and up to an isometry of $G(2,n;\mathbb {R})$, $\varphi$ belongs to one of the following cases.

• (a) $\underline{\varphi } = \underline{U}\underline{V}^{(2p)}_p \oplus \underline{c}_0$ with $K= \frac{8}{n(n-2)}$ and $\Vert B\Vert ^2 = \frac{2(n-4)(n+2)}{n(n-2)}$ for some $U\in U(n-1), \ n\ge 4$, where $\underline{c}_0$ is a constant vector in $\mathbb {C}^n$ and $2p=n-2$;

• (b) $\underline{\varphi }=\overline{\underline{U}}\overline{\underline{V}}^{(m)}_0\oplus \underline{U}\underline{V}^{(m)}_0$ with $K=\frac{4}{n-2}$ and $\Vert B\Vert ^2=\frac{4(n-4)}{n-2}$ for some $U\in U(n)$, $n=2m+2$.

Proof

It follows from Proposition 3.1 that, $\varphi$ belongs to case (a) or case (b). In the following we discuss the two cases of $\varphi$, respectively.

(a) $\underline{\varphi } = \underline{f}_p \oplus \underline{c}_0$, where $\underline{c}_0$ is a constant vector in $\mathbb {C}^n$, $\ \underline{f}_p: S^2\rightarrow \mathbb {C}P^{n-2}$ with constant curvature satisfies $\underline{f}_p = \underline{\overline{f}}_p$ and $2p=n-2$.

In this case, we have $l_{p-1}=l_p$. By (2.7), direct calculations give

$$\begin{aligned} \left\{ \begin{array} {l} \lambda ^2=2l_p, \\ K=\frac{2}{p(p+1)}=\frac{8}{n(n-2)}, \\ \Vert B\Vert ^2=2\frac{l_{p+1}}{l_p}, p\ge 2, \\ \Vert B\Vert ^2=0, p=1. \end{array} \right. \end{aligned}$$

(3.27)

Since $\underline{f}_p$ is of constant curvature, then the map $\underline{f}_p: S^2\rightarrow \mathbb {C}P^{2p}$ is totally unramified. When $p\ge 2$, it follows from (2.13) and (3.27) that

$$\begin{aligned} \Vert B\Vert ^2=2\frac{l_{p+1}}{l_p}=2\frac{\delta ^{(2p)}_{p+1}}{\delta ^{(2p)}_p}=\frac{2(n-4)(n+2)}{n(n-2)}. \end{aligned}$$

Moreover, harmonic sequence $\underline{f}_0, \underline{f}_1, \ldots , \underline{f}_{2p}$ is the Veronese sequence in $\mathbb {C}P^{2p} \subset \mathbb {C}P^{n-2}$, up to $U(n-1)$. Then we can choose a complex coordinate z on $\mathbb {C}=S^2\backslash \{pt\}$ so that $f_i=UV^{(2p)}_i, \ 0\le i\le 2p$, where $U\in U(n-1)$ and $V^{(2p)}_i$ has the standard expression given in part (C) of Sect. 2.

Equation $\underline{\overline{f}}_p=\underline{f}_p$ is equivalent to

$$\begin{aligned} \overline{U}\overline{V}^{(2p)}_p = \mu UV^{(2p)}_p, \end{aligned}$$

(3.28)

where $\mu$ is a parameter. Set $W_0 = antidiag\{1, -1, 1, -1, \cdots , 1\}$, which is an $(2p+1)\times (2p+1)$-matrix. Then condition (3.28) becomes

$$\begin{aligned} \overline{U} = UW_0. \end{aligned}$$

Thus, choose $U=U_0$ as the one shown in Remark 3.3, up to an isometry of $G(2,n;\mathbb {R})$,

$$\begin{aligned} \underline{\varphi } = \underline{U}_0\underline{V}^{(2p)}_p \oplus \underline{c}_0. \end{aligned}$$

(b) $\varphi$ is a real mixed pair.

In this case, $\varphi$ belongs to the following harmonic sequence:

$$\begin{aligned} 0 \mathop {\longleftarrow }\limits ^{\partial {''}}\overline{\underline{f}}_m\mathop {\longleftarrow }\limits ^{\partial {''}} \cdots \mathop {\longleftarrow }\limits ^{\partial {''}} \overline{\underline{f}}_1\mathop {\longleftarrow }\limits ^{\partial {''}} \underline{\varphi } = \underline{\overline{f}}_0\oplus \underline{f}_0\mathop {\longrightarrow }\limits ^{\partial {'}}\underline{f}_1 \mathop {\longrightarrow }\limits ^{\partial {'}}\cdots \mathop {\longrightarrow }\limits ^{\partial {'}}\underline{f}_m\mathop {\longrightarrow }\limits ^{\partial {'}}0, \end{aligned}$$

(3.29)

where $\underline{f}_0, \ldots , \underline{f}_m: S^2\rightarrow \mathbb {C}P^{m}$ is a linearly full harmonic sequence in $\mathbb {C}P^m\subset \mathbb {C}P^{n-1}$. By (2.7) and a series of calculations , we obtain

$$\begin{aligned} \left\{ \begin{array} {l} \lambda ^2=2l_0, \\ K=\frac{2}{m}, \\ \Vert B\Vert ^2=2\frac{l_{1}}{l_0}. \end{array} \right. \end{aligned}$$

(3.30)

Since $\underline{f}_0$ is of constant curvature, by virtue of Lemma 2.3, $\underline{f}_0, \underline{f}_1, \ldots , \underline{f}_m$ is the Veronese sequence in $\mathbb {C}P^m\subset \mathbb {C}P^{n-1}$, up to U(n), and they are all totally unramified. It follows from (2.13) and (3.30) that

$$\begin{aligned} \Vert B\Vert ^2=2\frac{l_{1}}{l_0}=2\frac{\delta ^{(m)}_{1}}{\delta ^{(m)}_0}=\frac{4(m-1)}{m}. \end{aligned}$$

From (3.29), by the assumption that $\underline{\varphi }$ is (strongly) isotropic, we get

$$\begin{aligned} \langle {f}_0, \overline{f}_m\rangle =0, \end{aligned}$$

which is equivalent to

$$\begin{aligned} \text {tr} U^{T}UV^{(m)}_0 V^{(m)T}_{m}= 0, \end{aligned}$$

(3.31)

here, $V^{(m)}_0V^{(m)T}_m$ is a polynomial matrix in z and $\overline{z}$ by the standard expressions of $V^{(m)}_0$ and $V^{(m)}_m$ given in Part (C) of Sect. 2, and $U\in U(n)$ satisfying $UV^{(m)}_0=f_0$ is a constant matrix. Using the method of indeterminate coefficients by (3.31), assume $U^TU=(a_{ij}), \ 0\le i,j \le n-1$, it has the form

Choose

(3.32)

Let $C_i$ denote the i-th column of $U_1$. For $1\le i\le m+1$, all the elements of $C_i$ are zero expect the $(2i-1)$-th and (2i)-th elements, which are $\frac{1}{\sqrt{2}}$ and $\frac{\sqrt{-1}}{\sqrt{2}}$, respectively.

From the above discussion, we have $n=2m+2$, and up to an isometry of $G(2,n;\mathbb {R})$, $\underline{\varphi }=\overline{\underline{U}}_1\overline{\underline{V}}^{(m)}_0\oplus \underline{U}_1\underline{V}^{(m)}_0$. Its curvature K and the second fundamental form B of $\varphi$ are as follows

$$\begin{aligned} K=\frac{4}{n-2}, \quad \Vert B\Vert ^2=\frac{4(n-4)}{n-2}. \end{aligned}$$

This finishes the proof. $\square$

4 Irreducible harmonic maps of constant curvature from $S^2$ to $G(2,n;\mathbb {R})$

In Sect. 3, we consider conformal minimal immersions from $S^2$ to $G(2,n;\mathbb {R})$ with constant curvature under the assumption that they are reducible. To complete the classification of all conformal minimal immersions of $S^2$ in $G(2,n;\mathbb {R})$ with constant curvature, we must discuss the irreducible ones.

For a linearly full irreducible harmonic map $\varphi : S^2\rightarrow G(2,n;\mathbb {R})$ with isotropy order r, in this section we consider the case that $\varphi$ is of finite isotropy order $r\ge n-5$, where $n\ge 5$ (it is easy to check that, if $n=4$ and $\varphi$ is of finite isotropy order, then $\varphi$ must be reducible).

Here, we state one of Bahy-El-Dien and Wood’ results as follows:

Lemma 4.1

(Special case of [2], Theorem 4.7) Let $\varphi : S^2\rightarrow G(2,n;\mathbb {R})$ be an irreducible harmonic map of finite isotropy order r( here $n\ge 5$). Suppose that $r\ge {n-5}$. Then, there is a unique sequence of harmonic maps $\varphi ^i: S^2\rightarrow G(2,n;\mathbb {C}), (i = 0,1,2)$ such that

• (i) $\underline{\varphi }^0$ is a real mixed pair, in fact $\underline{\varphi }^0 = \underline{\overline{f}}_0 \oplus \underline{f}_0$ has finite isotropy order $r+2$ and $f_0$ is a holomorphic map;

• (ii) $\underline{\varphi } = \underline{\varphi }^2$;

• (iii) $\underline{\varphi }^1$ is obtained from $\underline{\varphi }^0$ by forward replacement of $\underline{f}_0$;

• (iv) $\underline{\varphi }^2$ is obtained from $\underline{\varphi }^1$ by backward replacement of $\underline{V}^\bot \cap \underline{\varphi }^1$, where $\underline{V}$ is a holomorphic line subbundle of $\underline{\varphi }^1$ not equal to the image of the first $\partial ^{'}$-return map of $\underline{\varphi }^1$.

Let $\varphi : S^2\rightarrow G(2,n;\mathbb {R})$ be a linearly full irreducible harmonic map of finite isotropy order $r\ge {n-5}$ (here we know that $n\ge 5$). In the following we characterize $\varphi$ explicitly by virtue of Lemma 4.1. First recall ([2], Proposition 2.8 and Lemma 2.15) that the isotropy order r of $\varphi$ is $n-4$ if n is odd and $n-5$ if n is even.

In (i) of Lemma 4.1, $\varphi ^0$ with isotropy order $r+2$ belongs to the harmonic sequence as follows:

$$\begin{aligned} 0\mathop {\longleftarrow }\limits ^{\partial {''}} \overline{\underline{f}}_m\mathop {\longleftarrow }\limits ^{\partial {''}} \cdots \mathop {\longleftarrow }\limits ^{\partial {''}} \overline{\underline{f}}_1\mathop {\longleftarrow }\limits ^{\partial {''}} \underline{\varphi }^0 \mathop {\longrightarrow }\limits ^{\partial {'}}\underline{f}_1 \mathop {\longrightarrow }\limits ^{\partial {'}}\cdots \mathop {\longrightarrow }\limits ^{\partial {'}}\underline{f}_m \mathop {\longrightarrow }\limits ^{\partial {'}}0, \end{aligned}$$

(4.1)

where $\underline{\varphi }^0 = \overline{\underline{f}}_0 \oplus \underline{f}_0$ and $0\mathop {\longrightarrow }\limits ^{\partial {'}}\underline{f}_0\mathop {\longrightarrow }\limits ^{\partial {'}}\underline{f}_1 \mathop {\longrightarrow }\limits ^{\partial {'}}\cdots \mathop {\longrightarrow }\limits ^{\partial {'}} \underline{f}_m\mathop {\longrightarrow }\limits ^{\partial {'}}0$ is a linearly full harmonic sequence in $\mathbb {C}P^{m} \subset \mathbb {C}P^{n-1}$. Here, $m=n-1$ if n is odd, and ${n-2} \le m \le {n-1}$ if n is even.

By (iii) of Lemma 4.1, $\underline{\varphi }^1$ is obtained from $\underline{\varphi }^0$ by forward replacement of $\underline{f}_0$, using (4.1) we have

$$\begin{aligned} \underline{\varphi }^1 = \underline{\overline{f}}_0 \oplus \underline{f}_1. \end{aligned}$$

The isotropy order of $\varphi ^1$ is $r+1$, and a harmonic sequence is derived as follows:

$$\begin{aligned} 0\mathop {\longleftarrow }\limits ^{\partial {''}} \overline{\underline{f}}_m\mathop {\longleftarrow }\limits ^{\partial {''}} \cdots \mathop {\longleftarrow }\limits ^{\partial {''}} \overline{\underline{f}}_2\mathop {\longleftarrow }\limits ^{\partial {''}} \underline{\varphi }^1_{-1}\mathop {\longleftarrow }\limits ^{\partial {''}} \underline{\varphi }^1\mathop {\longrightarrow }\limits ^{\partial {'}}\underline{f}_2\mathop {\longrightarrow }\limits ^{\partial {'}}\cdots \mathop {\longrightarrow }\limits ^{\partial {'}}\underline{f}_m \mathop {\longrightarrow }\limits ^{\partial {'}}0, \end{aligned}$$

(4.2)

where ${\underline{\varphi }}^1_{-1} = \underline{\overline{\varphi }}^1=\underline{\overline{f}}_1\oplus \underline{f}_0$.

From (4.2), the image of the first $\partial ^{'}$-return map of $\underline{\varphi }^1$ is $\overline{\underline{f}}_0$. By (iv) of Lemma 4.1, let $V = f_1 + x_0\overline{f}_0$, where $x_0$ is a smooth function on $S^2$ expect some isolated points. Let $X = -|f_0|^2 \overline{x}_0 f_1+ |f_1|^2\overline{f}_0$, it satisfies $\underline{X} = \underline{V}^{\bot } \cap \underline{\varphi }^1$. Since $\underline{\varphi }^2$ is obtained from $\underline{\varphi }^1$ by backward replacement of $\underline{X}$, so $\underline{\varphi }^2= \underline{V} \oplus \underline{W}$ with $W = \pi _{\varphi ^{1\bot }} (\overline{\partial }X)$, and it belongs to the following harmonic sequence

$$\begin{aligned} 0\mathop {\longleftarrow }\limits ^{\partial {''}} \overline{\underline{f}}_m\mathop {\longleftarrow }\limits ^{\partial {''}}\cdots \mathop {\longleftarrow }\limits ^{\partial {''}} \overline{\underline{f}}_3\mathop {\longleftarrow }\limits ^{\partial {''}} \underline{Y} \oplus \underline{\overline{f}}_2 \mathop {\longleftarrow }\limits ^{\partial {''}} \underline{\varphi }^2\mathop {\longrightarrow }\limits ^{\partial {'}}\underline{\overline{Y}}\oplus \underline{f}_2\mathop {\longrightarrow }\limits ^{\partial {'}}\underline{f}_3\mathop {\longrightarrow }\limits ^{\partial {'}}\cdots \mathop {\longrightarrow }\limits ^{\partial {'}}\underline{f}_m\mathop {\longrightarrow }\limits ^{\partial {'}}0, \end{aligned}$$

(4.3)

where $\underline{Y} = \underline{W}^{\bot } \cap \underline{\varphi }^1_{-1}.$

Applying the equation $W = \pi _{\varphi ^{1\bot }} (\overline{\partial }X)$ we obtain

$$\begin{aligned} W=|f_1|^2\overline{V}, \end{aligned}$$

(4.4)

this implies that

$$\begin{aligned} \underline{W} = \overline{\underline{V}}, \ \underline{Y} = \overline{\underline{X}}. \end{aligned}$$

Obviously, $\underline{\overline{X}},\underline{X},\underline{\overline{V}}$ and $\underline{V}$ are mutually orthogonal. Then $\underline{\varphi }= \underline{\varphi }^2= \underline{V} \oplus \underline{\overline{V}}$, and (4.3) reduces to

$$\begin{aligned} 0\mathop {\longleftarrow }\limits ^{\partial {''}} \overline{\underline{f}}_m\mathop {\longleftarrow }\limits ^{\partial {''}}\cdots \mathop {\longleftarrow }\limits ^{\partial {''}} \overline{\underline{f}}_3\mathop {\longleftarrow }\limits ^{\partial {''}} \underline{\overline{X}} \oplus \underline{\overline{f}}_2 \mathop {\longleftarrow }\limits ^{\partial {''}} \underline{\varphi }\mathop {\longrightarrow }\limits ^{\partial {'}}\underline{X}\oplus \underline{f}_2\mathop {\longrightarrow }\limits ^{\partial {'}}\underline{f}_3\mathop {\longrightarrow }\limits ^{\partial {'}}\cdots \mathop {\longrightarrow }\limits ^{\partial {'}}\underline{f}_m \mathop {\longrightarrow }\limits ^{\partial {'}}0. \end{aligned}$$

Since $\underline{V}$ is a holomorphic line subbundle of $\underline{\varphi }^1$, we get

$$\begin{aligned} \pi _{\varphi ^1}(\overline{\partial } V)\in \underline{V}. \end{aligned}$$

(4.5)

Through a direct computation, condition (4.5) is equivalent to the following equation

$$\begin{aligned} \partial \overline{x}_0 + \overline{x}_0\partial \log |f_0|^2=0, \end{aligned}$$

(4.6)

which can also be obtained from the fact that $\pi _{\varphi _1^{\bot }} (\partial \varphi _1) = \underline{f}_3$, where $\varphi _1=\underline{X}\oplus \underline{f}_2$. Then we have

Proposition 4.2

The map $\varphi : S^2\rightarrow G(2,n;\mathbb {R})$ is a linearly full irreducible harmonic map with finite isotropy order $r\ge {n-5}$ if and only if $\underline{\varphi }= \underline{\overline{V}} \oplus \underline{V}$ with $V = f_1 + x_0\overline{f}_0$, where $f_0$ is a holomorphic map satisfying $\left\{ \begin{array}{l} \langle \overline{f}_0, f_{r+2} \rangle =0\\ \langle \overline{f}_0, f_{r+3} \rangle \ne 0 \end{array}\right.$, and the corresponding coefficient $x_0$ satisfies equation (4.6).

Proof

Through the construction of $\varphi$ as shown above, the necessity is obvious. Since $f_0$ is a holomorphic map satisfying $\left\{ \begin{array}{l} \langle \overline{f}_0, f_{r+2} \rangle =0\\ \langle \overline{f}_0, f_{r+3} \rangle \ne 0 \end{array}\right.$, using (4.6), direct calculation gives $\overline{\partial } A_z = [A_z, A_{\overline{z}}]$, which implies that $\varphi$ is harmonic. Thus, we get the sufficiency. $\square$

Proposition 4.2 gives a characterization of linearly full irreducible harmonic maps from $S^2$ to $G(2,n;\mathbb {R})$ with finite isotropy order $r\ge n-5$. In the following we consider the case of constant curvature.

Let $\varphi :S^2 \rightarrow G(2,n;\mathbb {R})$ be a linearly full irreducible harmonic map of constant curvature K and finite isotropy order r. Suppose that $r \ge n-5$. By Proposition 4.2, we choose local frame

$$\begin{aligned} e_1 = \frac{\overline{V}}{|V|}, \ e_2 = \frac{V}{|V|}, \ e_3 = \frac{X}{|X|}, \ e_4 = \frac{f_2}{|f_2|}, \ e_5 = \frac{\overline{X}}{|X|}, \ e_6 = \frac{\overline{f}_2}{|f_2|}, \ e_7 = \frac{f_3}{|f_3|}, \end{aligned}$$

where $V = f_1 + x_0\overline{f}_0$ and $x_0$ is a smooth function on $S^2$ except some isolate points. Here, the local frame we choose is not unitary frame except $r\ge 3$.

Set $W_0 = (e_1, e_2), \quad W_1 = (e_3, e_4), \quad W_{-1} = (e_5, e_6)$ and $W_2 = (e_7)$, then by (2.5), we obtain

$$\begin{aligned} \Omega _0 = \left( \begin{array}{ccccccc} -\frac{|f_1|}{|f_0|} &{} \frac{\langle \partial V , X\rangle }{|X||V|} \\ 0 &{} \frac{|f_2|}{|V|} \end{array}\right) , \quad \Omega _{-1} = -\left( \begin{array}{ccccccc} \frac{\langle \partial V , X\rangle }{|X||V|} &{} \frac{|f_2|}{|V|} \\ -\frac{|f_1|}{|f_0|} &{} 0 \end{array}\right) , \quad \Omega _1 =\left( 0, \quad \frac{|f_3|}{|f_2|}\right) . \end{aligned}$$

(4.7)

This together with equation $L_{i} =\text {tr} (\Omega _{i} \Omega ^*_{i})$ implies that

$$\begin{aligned} L_0 =L_{-1}= \frac{ \langle \partial V , X\rangle \langle X, \partial V \rangle }{|X|^2|V|^2} + \frac{|f_2|^2}{|V|^2} + l_0, \end{aligned}$$

(4.8)

$$\begin{aligned} L_1 = l_2, \end{aligned}$$

(4.9)

$$\begin{aligned} |\det \Omega _0|^2 dz^2 d{\overline{z}}^2 =l_0^2l_1 \frac{|f_0|^2}{|V|^2}dz^2 d{\overline{z}}^2, \end{aligned}$$

(4.10)

$$\begin{aligned} \det \Omega _1\Omega _1^{*} dz d{\overline{z}} = l_2dz d{\overline{z}}. \end{aligned}$$

(4.11)

Using (4.8) (4.9) and (4.10), direct calculations give

$$\begin{aligned} \partial \overline{\partial } \log |\det \Omega _0|^2 =L_{-1} - 2 L_{0} + L_{1}. \end{aligned}$$

(4.12)

Suppose that $\varphi$ is totally unramified, then $|\det \Omega _0|^2 dz^2 d{\overline{z}}^2 \ne 0$ and $\det \Omega _1\Omega _1^{*} dz d{\overline{z}}\ne 0$ everywhere on $S^2$ and $\underline{f}_i: S^2\rightarrow \mathbb {C}P^m\subset \mathbb {C}P^{n-1} \ (3\le i\le m)$ are all unramified. It follows from (4.11) that $l_2 dzd\overline{z} \ne 0$ everywhere on $S^2$. And, we claim $l_1 dzd\overline{z} \ne 0$ everywhere on $S^2$ holds. Otherwise, if $l_1 dzd\overline{z}=0$ at some point $z=z_0$, since $\frac{|f_2|^2}{|V|^2}=\frac{|f_1|^2}{|V|^2}l_1$ and $\frac{|f_1|^2}{|V|^2}=\frac{|f_1|^2}{|x_0|^2|f_0|^2+|f_1|^2}\le 1 < + \infty$, then $\frac{|f_2|^2}{|V|^2}=0$ at the point $z=z_0$. It follows from $\Omega _0$ in (4.7) that $\varphi$ is degenerate at the point $z=z_0$, which contradicts to the fact that $\varphi$ is non-degenerate. Thus, we have $l_1 dzd\overline{z} \ne 0$ everywhere on $S^2$. Also from the expression of $\Omega _0$ in (4.7), we get $l_0 dzd\overline{z} \ne 0$ everywhere on $S^2$.

From the above discussion, we conclude $l_idz d{\overline{z}}\ne 0 \ (i=0, 1, 2, \ldots , m)$ everywhere on $S^2$, i.e., the harmonic sequence $\underline{f}_0, \ \underline{f}_1, \ \ldots , \underline{f}_m: S^2 \rightarrow \mathbb {C}P^{m} \subset \mathbb {C}P^{n-1}$ is totally unramified.

In this case, we prove

Proposition 4.3

Let $\varphi :S^2 \rightarrow G(2,n;\mathbb {R})$ be a linearly full irreducible totally unramified harmonic map of constant curvature K and finite isotropy order r. Suppose that $r\ge n-5$. Then n must be odd, and up to an isometry of $G(2,n;\mathbb {R})$, $\underline{\varphi } = \overline{\underline{U}}\overline{\underline{V}}^{(n-1)}_1 \oplus \underline{U}\underline{V}^{(n-1)}_1$ with $K = \frac{2}{3n-5}$ for some $U\in G$.

Proof

Since the harmonic sequence $\underline{f}_0, \ldots , \underline{f}_m: S^2\rightarrow \mathbb {C}P^{m}\subset \mathbb {C}P^{n-1}$ is totally unramified, it follows from (2.13), (4.8) and (4.9) that

$$\begin{aligned} \delta _{-1} = \delta _0, \ \delta _1 = \delta ^{(m)}_2 = 3(m-2), \ \delta ^{(m)}_0 = m, \ \delta ^{(m)}_1 = 2(m-1). \end{aligned}$$

(4.13)

On the other hand, by (2.8) (2.9) and (4.12) we have

$$\begin{aligned} \delta _1 - 2\delta _0 + \delta _{-1} = -4, \end{aligned}$$

(4.14)

where $\delta _{i} = \frac{1}{2\pi \sqrt{-1} }\int _{S^2} L_{i}d{\overline{z}} \wedge dz,\quad i =-1, 0, 1$. Hence,

$$\begin{aligned} \delta _0 = 3m-2. \end{aligned}$$

(4.15)

This formula and the fact that $\varphi$ is of constant curvature enable us to set $K=\frac{2}{3m-2}$, and complex coordinate z on $\mathbb {C} =S^2 \backslash \{pt\}$ can be chosen so that the induced metric $ds^2 = 2L_0dz d{\overline{z}}$ of $\varphi$ is given by

$$\begin{aligned} ds^2 = \frac{2(3m-2)}{(1+z\overline{z})^2} dz d{\overline{z}}, \end{aligned}$$

where

$$\begin{aligned} L_0=\frac{3m-2}{(1+z\overline{z})^2}. \end{aligned}$$

(4.16)

Consider local lift of the i-th osculating curve $F_i = f_0 \wedge \ldots \wedge f_i$ ($i=0,\ldots , m$). We choose a nowhere zero holomorphic $\mathbb {C}^n$-valued function $f_0$, then $F_i$ is a nowhere zero holomorphic curve and it is a polynomial function on $\mathbb {C}$ of degree $\delta ^{(m)}_i$ satisfying $\partial \overline{\partial }\log |F_i|^2 = l_i$. So using (4.8) (4.9) (4.10) (4.12) and (4.16), we obtain

$$\begin{aligned} \partial \overline{\partial } \log \frac{ (1 + z\overline{z})^{\delta _0}|f_0|^2}{|F_0|^6|V|^2} =0. \end{aligned}$$

(4.17)

From (4.10), we know that $\frac{|f_0|^2}{|V|^2} l_0$ is a globally defined function without zeros on $S^2$. Then it follows from (4.13) and (4.15) that $\frac{ (1 + z\overline{z})^{\delta _0}|f_0|^2}{|F_0|^6|V|^2}=\frac{(1+z\overline{z})^{\delta _0}}{|F_0|^2|F_1|^2}\cdot \frac{|f_0|^2}{|V|^2}l_0$ is globally defined on $\mathbb {C}$ and has a positive constant limit $\frac{1}{c}$ as $z\rightarrow \infty$. Thus, (4.17) gives us that

$$\begin{aligned} \frac{ (1 + z\overline{z})^{\delta _0}|f_0|^2}{|F_0|^6|V|^2} = \frac{1}{c}, \end{aligned}$$

i.e.,

$$\begin{aligned} |V|^2 = \frac{c(1+z\overline{z})^{\delta _0}}{|f_0|^4}. \end{aligned}$$

(4.18)

Applying the equation $V = f_1 + x_0\overline{f}_0$, equation (4.18) reduces to

$$\begin{aligned} |x_0|^2|f_0|^4 + |F_1|^2 = \frac{c(1+z\overline{z})^{\delta _0}}{|f_0|^2}. \end{aligned}$$

(4.19)

By equation (4.6) we get $\overline{\partial }(x_0|f_0|^2) = 0$. Observing (4.19), from the fact that both $|F_1|^2$ and $\frac{(1+z\overline{z})^{\delta _0}}{|f_0|^2}$ have no singular points except $z=\infty$, we have $x_0|f_0|^2$ is a holomorphic function on $\mathbb {C}$ at most with the pole $z=\infty$. So, it is a polynomial function about z. Without loss of generality, set

$$\begin{aligned} x_0|f_0|^2 = h(z),\end{aligned}$$

(4.20)

the formula (4.19) is rewritten as

$$\begin{aligned} |h|^2+|F_1|^2 = \frac{c(1+z\overline{z}) ^{\delta _0}}{|f_0|^2}. \end{aligned}$$

(4.21)

Since both sides of (4.21) are polynomial functions and $\delta ^{(m)}_0=m$, then we have

$$\begin{aligned} |f_0|^2 = \mu (1+z\overline{z})^m, \end{aligned}$$

(4.22)

where $\mu$ is a real parameter.

If $h\ne 0$, then $1+z\overline{z}$ is a factor of it, which contracts the fact that h is holomorphic. Thus, we have $h=0$, which implies that $x_0=0$. Then

$$\begin{aligned} V = f_1 , \quad \underline{\varphi } = \underline{\overline{f}}_1 \oplus \underline{f}_1. \end{aligned}$$

From (4.22), by Lemma 2.3, up to a holomorphic isometry of $\mathbb {C}P^{n-1}$, ${f}_0$ is a Veronese surface. We can choose a complex coordinate z on $\mathbb {C}=S^2\backslash \{pt\}$ so that ${f}_0 = {U}{V}^{(m)}_0$, where $U\in U(n)$ and ${V}^{(m)}_0$ has the standard expression given in part (C) of Sect. 2 (adding zeros to ${V}^{(m)}_0$ such that ${V}^{(m)}_0 \in \mathbb {C}^n$). Thus, we have $\underline{\varphi }=\underline{\overline{U}}\underline{\overline{V}}^{(m)}_1\oplus \underline{U}\underline{V}^{(m)}_1$. To determine $\varphi$, we just need to determine the matrix U. To do this, consider the reducible map $\underline{\overline{U}}\underline{\overline{V}}^{(m)}_0\oplus \underline{U}\underline{V}^{(m)}_0:S^2\rightarrow G(2,n;\mathbb {R})$, which is of constant curvature and finite isotropy order $r+2$. Thus, Proposition 4.3 immediately follows from Proposition 3.2. $\square$

Remark 4.4

In Proposition 4.3, we have $m=n-1$. Choose the same $U_0$ as the one shown in Remark 3.3, then, up to an isometry of $G(2,n;\mathbb {R})$, $\underline{\varphi } = \overline{\underline{U}}_0\overline{\underline{V}}^{(n-1)}_1 \oplus \underline{U}_0\underline{V}^{(n-1)}_1$ with $K = \frac{2}{3n-5}$.

As to the second fundamental form B of $\varphi$, we have the following corollary.

Corollary 4.5

Let $\varphi :S^2 \rightarrow G(2,n;\mathbb {R})$ be a linearly full irreducible totally unramified harmonic map of constant curvature K and finite isotropy order r. Suppose that $r\ge n-5$. Then the second fundamental form B of $\varphi$ satisfies $\left\{ \begin{array} {l} \Vert B\Vert ^2 = 0, \quad n= 5, \\ \Vert B\Vert ^2 = \frac{12(n-2)(n-3)}{(3n-5)^2}, \quad n\ge 7. \end{array} \right.$

Proof

For any integer i, $\ 0\le i \le m$, let

$$\begin{aligned} f_i=U_0V^{(m)}_i, \end{aligned}$$

(4.23)

$U_0\in U(n)$ is the one shown in Remark 3.3. Up to an isometry of $G(2,n;\mathbb {R})$, $\underline{\varphi }$ can be expressed as $\underline{\varphi }=\overline{\underline{f}}_1\oplus \underline{f}_1$, where $\underline{f}_1$ is of constant curvature. Then by (2.7) and a series of calculations, we obtain

$$\begin{aligned} \left\{ \begin{array} {l} \partial \varphi =\frac{1}{|f_1|^2}[\overline{f}_1(\overline{f}_{2})^{*}+f_{2}f_1^{*}]-\frac{1}{|f_0|^2}[\overline{f}_0(\overline{f}_{1})^{*}+f_{1}f_0^{*}], \\ A_z=\frac{1}{|f_1|^2}[\overline{f}_1(\overline{f}_{2})^{*}-f_{2}f_1^{*}]+\frac{1}{|f_0|^2}[\overline{f}_0(\overline{f}_{1})^{*}-f_{1}f_0^{*}], \\ P=0, \ m=2, \\ P=\frac{|f_0|^2}{2(|f_0|^2|f_2|^2+|f_1|^4)}[\overline{f}_1(\overline{f}_{3})^{*}-f_{3}f_1^{*}], \ m\ge 3. \end{array} \right. \end{aligned}$$

(4.24)

If $m=2$, it is easy to see that $\Vert B\Vert ^2=0$, i.e., $\varphi$ is totally geodesic. Otherwise if $m\ge 3$, we get

$$\begin{aligned} \Vert B\Vert ^2=\frac{2}{(1+\frac{l_0}{l_1})^2}\left[ \frac{l_2}{l_1}-\frac{|\langle \overline{f}_1, f_3\rangle |^2}{|f_2|^4}\right] . \end{aligned}$$

Since $\underline{f}_1$ is of constant curvature and $m+1=n$, we have $\frac{l_0}{l_1}=\frac{\delta ^{(m)}_0}{\delta ^{(m)}_1}=\frac{n-1}{2(n-2)}$ and $\frac{l_2}{l_1}=\frac{\delta ^{(m)}_2}{\delta ^{(m)}_1}=\frac{3(n-3)}{2(n-2)}$, which implies that

$$\begin{aligned} \Vert B\Vert ^2=\frac{8(n-2)^2}{(3n-5)^2}\left[ \frac{3(n-3)}{2(n-2)}-\frac{|\langle \overline{f}_1, f_3\rangle |^2}{|f_2|^4}\right] . \end{aligned}$$

(4.25)

From the fact that n is odd, we discuss it as follows:

• (1) If $n=3$. $\varphi$ is totally geodesic by (4.24). In this case, $\varphi$ is a conformal minimal immersion from $S^2$ to $G(2,3;\mathbb {R})$ (or equivalently $Q_1$), which is trivial, we don’t consider it in this paper;

• (2) If $n=5$. It follows from (4.23) that $\overline{\underline{f}}_1=\underline{f}_3$. Substituting it into (4.25), we obtain $\Vert B\Vert ^2=0$, i.e., $\varphi$ is totally geodesic;

• (3) If $n\ge 7$. It should be remarked that $r\ge n-5$ and r is odd, then we have $r\ge 3$, which implies that $\langle \overline{f}_1, f_3 \rangle =0$. Hence, (4.25) reduces to $\Vert B\Vert ^2=\frac{12(n-2)(n-3)}{(3n-5)^2}$.$\square$

By Proposition 3.2, 3.5, 4.3, we conclude a classification of conformal minimal immersions of constant curvature from $S^2$ to $G(2,n;\mathbb {R})$ as follows:

Theorem 4.6

Let $\varphi :S^2 \rightarrow G(2,n;\mathbb {R})$ be a linearly full conformal minimal immersion with constant curvature K and isotropy order r. Then, up to an isometry of $G(2,n;\mathbb {R})$,

• (i) If $\varphi$ is reducible and (strongly) isotropic, then, $\underline{\varphi } = \underline{U}_0\underline{V}^{(2p)}_p \oplus \underline{c}_0$ with $K= \frac{8}{n(n-2)}$, $2p=n-2$, or $\underline{\varphi }=\overline{\underline{U}}_1\overline{\underline{V}}^{(m)}_0\oplus \underline{U}_1\underline{V}^{(m)}_0$ with $K=\frac{4}{n-2}$, $n=2m+2$;

• (ii) If $\varphi$ is reducible and has finite isotropy order $r\ge n-4$, then, $\underline{\varphi } = \overline{\underline{U}}_0\overline{\underline{V}}^{(n-1)}_0 \oplus \underline{U}_0\underline{V}^{(n-1)}_0$ with $\ K = \frac{2}{n-1}$.

• (iii) If $\varphi$ is totally unramified irreducible and has finite isotropy order $r\ge n-5$, then, $\underline{\varphi } = \overline{\underline{U}}_0\overline{\underline{V}}^{(n-1)}_1 \oplus \underline{U}_0\underline{V}^{(n-1)}_1$ with $\ K = \frac{2}{3n-5}$.

Theorem 4.6 shows that, up to an isometry of $G(2,n;\mathbb {R})$, conformal minimal immersions of constant curvature from $S^2$ to $G(2,n;\mathbb {R})$, or equivalently, a complex hyperquadric $Q_{n-2}$ can be presented by the Veronese surfaces in $\mathbb {C}P^{n-1}$ under three conditions, respectively: the immersion is reducible with finite isotropy order $r\ge n-4$; the immersion is totally unramified irreducible with finite isotropy order $r\ge n-5$; the immersion is reducible and (strongly) isotropic. It is easy to check that these minimal immersions are all homogeneous.

By Theorem 4.6, we obtain classifications of linearly full conformal minimal immersions of constant curvature from $S^2$ to $Q_2$ and $Q_3$, respectively as follows:

Corollary 4.7

Let $\varphi :S^2 \rightarrow G(2,4;\mathbb {R})$ be a linearly full conformal minimal immersion of constant curvature K. Then, $\varphi$ is totally geodesic and up to an isometry of $G(2,4;\mathbb {R})$,

• (1) $\underline{\varphi } = \overline{\underline{f}}_0 \oplus \underline{f}_0$ with  $K= 2$,  $f_0 = [(1, \ \sqrt{-1}, \ z, \ \sqrt{-1}z)^{T}]$;

• (2) $\underline{\varphi } = \underline{f}_1 \oplus \underline{c}_0$ with $K=1$, $c_0 = (0,0,0,1)$, $\underline{f}_1 = [(z-\overline{z}, \ -\sqrt{-1}(z+\overline{z}), \ \sqrt{-1}(1-z\overline{z}))^{T}]$.

Corollary 4.8

([16], Theorem 4.9) Let $\varphi :S^2 \rightarrow G(2,5;\mathbb {R})$ be a linearly full conformal minimal immersion of constant curvature K. Then, up to an isometry of $G(2,5;\mathbb {R})$,

• (1) If $\varphi$ is reducible, then $\underline{\varphi } = \overline{\underline{f}}_0 \oplus \underline{f}_0$ with $K= \frac{1}{2}, \ \Vert B\Vert ^2=3$,

  $$\begin{aligned} f_0 = [(1+z^4, \ \sqrt{-1}(1-z^4), \ 2(z-z^3), \ 2\sqrt{-1}(z+z^3), \ 2\sqrt{3}z^2)^{T}]; \end{aligned}$$

• (2) If $\varphi$ is totally unramified irreducible, then, $\underline{\varphi } = \overline{\underline{f}}_1 \oplus \underline{f}_1$ is totally geodesic with $K =\frac{1}{5}$,

  $$\begin{aligned} \begin{array}{lll} f_1 &{} = &{}[ ((2(z^3-\overline{z}), \ -2\sqrt{-1}(z^3+\overline{z}), \ 1-3z\overline{z}-z^2(3-z\overline{z}), \\ &{} &{} \sqrt{-1}[1-3z\overline{z}+z^2(3-z\overline{z})], \ 2\sqrt{3}z(1-z\overline{z}))^{T}].\end{array} \end{aligned}$$

Irreducible examples. In the following, we give some examples about linearly full irreducible harmonic map $\underline{\varphi }: S^2\rightarrow G(2,n;\mathbb {R})$, which is (strongly) isotropic with constant curvature K and second fundamental form B.

Let $n=2m+2$, and take $U_1\in U(n)$, which is of the same type as (3.32). Then for any integer i $\ (0< i < m)$,

$$\begin{aligned} \underline{\varphi }=\overline{\underline{U}}_1\overline{\underline{V}}^{(m)}_i\oplus \underline{U}_1\underline{V}^{(m)}_i \end{aligned}$$

(4.26)

are all linearly full irreducible (strongly) isotropic harmonic maps from $S^2$ to $G(2,n;\mathbb {R})$. Let $f_i=U_1V^{(m)}_i$, $\underline{\varphi }$ can be rewritten as $\underline{\varphi }=\overline{\underline{f}}_i\oplus \underline{f}_i$, where $\underline{f}_i$ is of constant curvature and $\underline{\overline{f}}_0, \underline{\overline{f}}_1, \ldots , \underline{\overline{f}}_m, \underline{f}_0, \underline{f}_1, \ldots , \underline{f}_m$ are mutually orthogonal. Then by (2.7), a series of calculations give

$$\begin{aligned} \left\{ \begin{array} {l} \partial \varphi =\frac{1}{|f_i|^2}[\overline{f}_i(\overline{f}_{i+1})^{*}+f_{i+1}f_i^{*}]-\frac{1}{|f_{i-1}|^2}[\overline{f}_{i-1}(\overline{f}_i)^{*}+f_if_{i-1}^{*}], \\ A_z=\frac{1}{|f_i|^2}[\overline{f}_i(\overline{f}_{i+1})^{*}-f_{i+1}f_i^{*}]+\frac{1}{|f_{i-1}|^2}[\overline{f}_{i-1}(\overline{f}_i)^{*}-f_if_{i-1}^{*}], \\ P=\frac{1}{2|f_i|^2(l_{i-1}+l_i)}[\overline{f}_i(\overline{f}_{i+2})^{*}-f_{i+2}f_i^{*}]-\frac{1}{2(l_{i-1}+l_i)|f_{i-2}|^2}[\overline{f}_{i-2}(\overline{f}_i)^{*}-f_if_{i-2}^{*}], \ i\ge 2, \\ P=\frac{1}{2|f_1|^2(l_{0}+l_1)}[\overline{f}_1(\overline{f}_{3})^{*}-f_{3}f_1^{*}], \ i=1, \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} \left\{ \begin{array} {l} \lambda ^2=2(l_{i-1}+l_i), \\ K=\frac{2}{m+2i(m-i)}=\frac{4}{n-2+2i(n-2-2i)}, \\ \Vert B\Vert ^2=\frac{2(\delta ^{(m)}_i\delta ^{(m)}_{i+1}+\delta ^{(m)}_{i-1}\delta ^{(m)}_{i-2})}{(\delta ^{(m)}_{i-1}+\delta ^{(m)}_i)^2}. \end{array} \right. \end{aligned}$$

Thus, for any integer i $\ (0< i < m)$, $\underline{\varphi }=\overline{\underline{U}}_1\overline{\underline{V}}^{(m)}_i\oplus \underline{U}_1\underline{V}^{(m)}_i$ is a linearly full irreducible (strongly) isotropic harmonic map from $S^2$ to $G(2,n;\mathbb {R})$ with constant curvature $K=\frac{4}{n-2+2i(n-2-2i)}$ and $\Vert B\Vert ^2=2\frac{\delta ^{(m)}_i\delta ^{(m)}_{i+1}+\delta ^{(m)}_{i-1}\delta ^{(m)}_{i-2}}{(\delta ^{(m)}_{i-1}+\delta ^{(m)}_i)^2}$, where $\delta ^{(m)}_i=(i+1)(m-i)$.

Remark 4.9

Let $\varphi$ be a linearly full conformal minimal immersion of constant curvature from $S^2$ to $G(2,n;\mathbb {R})$, and $f_{\varphi }$ be the corresponding map of $\varphi$ from $S^2$ to $Q_{n-2}$. Summing the maps $\varphi$ given in Sects. 3 and 4, they can be divided into two classes:

• (1) $\underline{\varphi }=\overline{\underline{U}}\overline{\underline{V}}^{(m)}_i\oplus \underline{U}\underline{V}^{(m)}_i$ for any integer i $\ (0\le i \le m <n)$ and some matrix $U\in U(n)$. In this case, the corresponding map of $\varphi$ from $S^2$ to $Q_{n-2}$ is as follows

  $$\begin{aligned} \underline{f}_{\varphi }=[({U}{V}^{(m)}_i)^T]: S^2\rightarrow Q_{n-2}\subset \mathbb {C}P^{n-1}, \end{aligned}$$

  which is also minimal from $S^2$ to $\mathbb {C}P^{n-1}$. In particular, when $\underline{\varphi }=\overline{\underline{U}}_1\overline{\underline{V}}^{(m)}_{i_0}\oplus \underline{U}_1\underline{V}^{(m)}_{i_0}$, where $U_1$ is of the one shown in (3.32) and $4i_0+2=2m+2=n$, the corresponding $\underline{f}_{\varphi }: S^2\rightarrow Q_{n-2}$ is also totally real.

• (2) ${\underline{\varphi }} = {\underline{U}}_0{\underline{V}}^{(n-2)}_p \oplus {\underline{c}}_0$, where $\underline{c}_0$ is a constant vector in $\mathbb {C}^n$ and $2p=n-2$, $U_0$ is of the same type as the matrix shown in Remark 3.3. In this case, the corresponding map of $\varphi$ from $S^2$ to $Q_{n-2}$ is as follows

  $$\begin{aligned} \underline{f}_{\varphi }=[(U_0V^{(n-2)}_p, \ \sqrt{-1}\sqrt{\langle U_0V^{(n-2)}_p, \overline{U}_0\overline{V}^{(n-2)}_p\rangle })^T]: S^2\rightarrow Q_{n-2}\subset \mathbb {C}P^{n-1}. \end{aligned}$$

  By a simple test, we can check that ${f}_{\varphi }$ is a totally real and minimal map from $S^2$ to $Q_{n-2}$, but it is not minimal of $S^2$ in $\mathbb {C}P^{n-1}$.

To completely classify conformal minimal immersions of constant curvature from $S^2$ to $G(2,n;\mathbb {R})$, or equivalently, a complex hyperquadric $Q_{n-2}$, there are many problems deserving further consideration.

• (Q1) When the immersion is of finite isotropy order r, our classification theorem is true under assumptions that the immersion is reducible with $r\ge n-4$ and that the immersion is totally unramified irreducible with $r\ge n-5$. Then whether it is also true after omitting these assumptions.

• (Q2) For the (strongly) isotropic case, we determine all reducible (strongly) isotropic conformal minimal immersions of two-spheres in complex hyperquadric with constant curvature. Then what about the irreducible (strongly) isotropic ones? How to determine them?