Introduction

The research on mathematics teacher competence assumes that teachers’ beliefs are an integral part of their dispositions and have an orienting and action-guiding function when acting in the classroom (Felbrich et al., 2012; Lauermann & ten Hagen, 2021; Schmotz et al., 2010; Schoenfeld, 1998; Thompson, 1992). Corresponding empirical evidence suggests that beliefs affect teachers’ practices and are positively related to instructional quality and students’ learning outcomes (Daumiller et al., 2021; Hettinger et al., 2023; Heyder et al., 2020, 2020; Stipek et al., 2001), favouring student-centred and constructivist beliefs (Dubberke et al., 2008; Kleickmann et al., 2016; Staub & Stern, 2002; Voss et al., 2013). The latter are related to educational approaches and philosophies that emphasise the active role of students in their learning process and place the needs, interests and abilities of students at the core of their learning experience. Constructivist teaching approaches encourage students to ask questions, explore topics and engage in hands-on experiences to construct knowledge and discover answers. Early findings suggest that student-centred mathematics instruction may positively impact student learning outcomes more than teacher-centred pedagogies and respective beliefs (Fennema et al., 1996). However, because student interest and engagement and their specific learning needs might be influenced by teacher beliefs, the affective and conative aspects of student outcomes, such as students’ motivation and enjoyment, are of particular interest as dependent variables, in addition to their mathematical achievement (Radišić, 2023). Furthermore, studies on students’ perceptions of the classroom setting and teachers’ expectations and beliefs show differential effects for girls and boys; for example, boys feel that they can profit more from collaborative work than girls (Samuelsson & Samuelsson, 2016), while girls perceive lower teacher expectations but higher mathematics prestige beliefs from teachers than boys (Lazarides & Watt, 2015). Thus, there might be differential effects of teachers’ beliefs on student motivation and enjoyment concerning students’ gender.

However, although direct links between teachers’ beliefs and diverse student outcomes have been thoroughly studied, our understanding of this relationship is still inconclusive (Lauermann & ten Hagen, 2021; Polly et al., 2013). Moreover, researchers who study teachers’ beliefs have been criticised for lacking research with younger participants (Burr & Hofer, 2002). At the same time, it has been argued that, to improve our understanding of the nature of teachers’ beliefs and their impact, research examining how such beliefs affect other aspects relevant to learning, such as motivation and enjoyment, is greatly needed (Daumiller et al., 2021; Heyder et al., 2020; Muis, 2004; Muis et al., 2006).

In the current study, we examined the relationship between teachers’ beliefs on the nature and learning of mathematics and primary students’ motivation and enjoyment of mathematics across six countries, differentiating the analysis for boys and girls and considering students’ achievement and classroom socioeconomic and behaviour composition. Focusing on primary students, we aim to shed light on a population that is infrequently examined in similar studies (Heyder et al., 2020) while observing different teacher beliefs. A nested data structure across six education systems was considered (Lauermann & Berger, 2021), coupled with students’ mathematics achievement and classroom composition (Yang Hansen et al., 2020; Marsh et al., 2012).

Theoretical background

Motivation and enjoyment of mathematics

Mathematics competence is a vital life skill that supports students’ participation in society today (Heyder et al., 2020; OECD, 2018), yet maintaining productive involvement in mathematics is a systematic challenge (Middleton et al., 2023). Building on Eccles and colleagues’ expectancy-value framework (Eccles & Wigfield, 2020; Wigfield & Eccles, 2020), numerous studies have demonstrated a significant link between students’ expectancies of success (i.e. how well one expects to do on an upcoming task, from now on perceived competence) and task values (e.g. intrinsic value, interest and joy of involvement with the task and utility value, perceived usefulness of the task) to the continuous involvement with mathematics tasks (Wigfield & Eccles, 2020) and later career choices (e.g. Wang, 2012; Watt et al., 2012). Furthermore, relying on the control-value theory (Pekrun, 2017), among the achievement emotions, the enjoyment of mathematics is particularly linked to the intrinsic component (Putwain et al., 2018). Although the latter amplifies the direct positive relationships between perceived control and mathematics achievement, the former promotes this relationship (Putwain et al., 2021). In a similar study, Forsblom et al. (2022) show that students’ perceived competence and values predict subsequent enjoyment when controlled for prior achievement and gender. Chen et al. (2023) provide similar results by observing achievement, enjoyment and perceived competence in mathematics.

Because of the content specificity of motivation and increasing importance of social and emotional learning goals (Radišić, 2023; Putwain et al., 2018), investigating students’ emotions and motivation is crucial for understanding students’ learning of mathematics (Eccles & Wigfield, 2020; Hannula et al., 2019; Schukajlow et al., 2023). Mathematics education research assumes that students’ enjoyment of mathematics is closely related to students’ personal (and often situational) interest and that emotional and motivational constructs can vary in their temporal stability, depending on the object to which they are linked, such as specific mathematical activities or specific tasks that teachers use in the classroom (Schukajlow et al., 2017; Schukajlow & Rakoczy, 2016). For example, in a German study on modelling problems, Schukajlow et al. (2012) show that operative-strategic teaching practices closely related to student-centred approaches led to higher enjoyment among students when compared with traditional directive approaches.Footnote 1

Many studies have also confirmed differences between boys and girls in motivation, particularly related to intrinsic value and perceived competence (Rodríguez et al., 2020; Wigfield & Eccles, 2020), indicating that boys typically exhibit more favourable motivational characteristics in mathematics than girls. Because girls are reported as expressing lower levels of individual interest and perceived competence in mathematics, the impact of intrinsic value on mathematics achievement is even more crucial for girls than boys (Ganley & Lubienski, 2016). Consistent with this, the research on academic emotions in mathematics suggests the existence of more negative feelings and attitudes in girls than boys (Goetz et al., 2013; Hyde et al., 1990) and that positive emotions associated with mathematics (like enjoyment) could have a more pronounced effect on girls’ dedication (Pinxten et al., 2014).

Mathematics teachers’ beliefs

Despite intensive research on teachers’ beliefs, no precise and selective definition of the concept can be discerned so far (Leder, 2019; Törner, 2002). Philipp (2007) defines beliefs as ‘the lenses through which one looks when interpreting the world’ (p. 258). Richardson (1996) proposes a broader, domain-unspecific definition of beliefs as ‘psychologically held understandings, premises or propositions about the world that are felt to be true’ (p. 103). This definition encompasses a teacher’s epistemological stance towards an object, which includes affective attitudes and the readiness to act (cf. Grigutsch et al., 1998) and depends on the degree of individual agreement (Beswick, 2005, 2007). Despite the term’s ambiguity, educational research in mathematics has a broad consensus on differentiating profession-related beliefs (Ernest, 1989). Beliefs are assumed to be domain specific (Törner, 2002) or even situation specific (Kuntze, 2011; Schoenfeld, 2010).

Domain-specific ability beliefs link to the extent to which success in a given domain, like mathematics, is attributed to the innate ability one is not taught in school (Leslie et al., 2015) and can be situated with the broader idea of layperson theories regarding whether the ability is fixed or malleable (Dweck, 2006). Often, mathematics is recognised as a domain in which innate ability is strongly linked to success in the field (Heyder et al., 2020; Leslie et al., 2015). Regarding beliefs about the nature of mathematics, Grigutsch et al. (1998) suggest that static views about the nature of mathematics may emphasise the formal aspect of mathematics (formalism aspect) or an orientation towards procedures and calculation schemes (schema orientation). On the other hand, dynamic views tend to emphasise mathematics’ application aspect and its processual character (Grigutsch et al., 1998).

Beliefs about learning mathematics (Handal, 2003; Kuntze, 2011; Staub & Stern, 2002) represent another significant dimension of beliefs. Transmission-oriented beliefs, which view students as passive recipients of knowledge, are often distinguished from constructivist-influenced beliefs that endorse the principles of constructive learning. The latter emphasises that the teacher’s role is to facilitate students’ knowledge construction while students take a more active role in the learning process (Blömeke & Kaiser, 2014; Staub & Stern, 2002; Thompson, 1992). Later studies recognise that some teachers adopt a mixed view and convey elements of both constructivist and transmissive views (Yang et al., 2020).

Teacher beliefs and their relation to classroom practice and students’ outcomes

Given that the different motivational and emotional characteristics related to mathematics are widely developed within the classroom setting and, thus, shaped by the immediate learning environment (Eccles & Roeser, 2009, 2011; Eccles & Wigfield, 2020; Putwain et al., 2018), it is important to examine how and through which processes teachers’ beliefs in mathematics classrooms can enhance students’ mathematics interest, enjoyment and engagement with mathematics (Hettinger et al., 2023). Even though the impact of teacher beliefs on student learning is still uncertain, most researchers agree that dynamic beliefs about the nature of mathematics and constructivist learning beliefs are more strongly related to an emphasis on processual, iterative mathematics in instructional settings (Reusser et al., 2011). Staub and Stern (2002) show that teachers with constructivist beliefs were associated with greater student achievement gains in mathematical word problems. At the same time, teachers’ ability expectations have been seen as relevant predictors of students’ perceived competence, even with elementary school students (Bohlmann & Weinstein, 2013; Roeser et al., 1993; Wang, 2012). For example, a German study with fourth graders (Heyder et al., 2020) shows the differential effects of teacher beliefs on high- and low-achieving students; the study indicates that the more teachers believed that mathematics requires innate ability, the lower the intrinsic motivation of their low-achieving students was. These results suggest that teachers’ beliefs that success in mathematics depends on innate ability may be an obstacle to creating a classroom atmosphere that fosters student motivation and enjoyment of learning and engagement. At the same time, classroom composition (e.g. the proportion of economically disadvantaged students) can have a differential effect on how teachers decide to promote learning and engagement in their classrooms (Yang Hansen et al., 2020; Marsh et al., 2012).

Teacher beliefs and gender differences

The expectancy-value framework has touched on gender role stereotypes and how these shape socialisers’ beliefs (Eccles et al., 1993; Wigfield & Eccles, 2020), including success expectancies and task values of boys and girls. Early studies by Fennema (1990) and Fennema et al. (1990) have identified gender differences in the teacher expectations of male and female students, resulting in teachers overestimating boys’ mathematical abilities and underestimating girls’ abilities. Teachers tended to attribute boys’ successes to higher effort, competitiveness, independence and enjoyment of mathematics. A later study by Tiedemann (2000) supports these findings, while Dickhauser and Meyer (2006) confirm this pattern, even when girls’ achievements were equal to those of boys. However, when such relationships concerning general teacher ability beliefs have been observed, the differences between boys and girls have not been confirmed (Wentzel et al., 2010). Observing tenth-grade students, Lazarides and Watt (2015) examine the effects of students’ perceived mathematics teachers’ beliefs (i.e. their teachers’ expectations about students’ ability and mathematics prestige), classroom goal orientations (i.e. mastery and performance approach) and their own mathematics motivational beliefs (i.e. perceived competence and task values) on girls’ and boys’ career intentions in mathematical fields. Their results reveal the links between teacher beliefs, learning environments, student motivations and mathematical career intentions, with girls perceiving lower teacher expectations than boys but higher teacher mathematics prestige beliefs. Teachers’ expectations and students’ motivations have been positively related to students’ reported prior mathematics achievement, with the latter being consistent with some earlier studies (e.g. Roeser et al., 1993).

In sum, mathematics is a demanding subject (Heyder et al., 2020), posing challenges to both students and teachers as early as primary school. The research strand focusing on teacher beliefs that is primarily related to ability beliefs and nature of mathematics observes mathematics as a domain in which innate ability is more prevalent (Leslie et al., 2015), thus hindering motivation (Heyder et al., 2020). Significant associations have been confirmed on numerous occasions between students’ perceived competence, task values and their grappling with mathematics, either as a later career choice (Watt et al., 2012; Wang, 2012) or in immediate school surroundings (Chen et al., 2023; Forsblom et al., 2022; Putwain et al., 2018), mostly favouring boys (Rodríguez et al., 2020; Wigfield & Eccles, 2020). This may be because of the evident differences in teachers’ expectations towards boys and girls (e.g. Fennema, 1990; Lazarides & Watt, 2015; Wentzel et al., 2010) and the presence of more negative feelings and attitudes in girls related to mathematics (Goetz et al., 2013; Hyde et al., 1990). However, studies observing such patterns focus primarily on middle school students and older (Burr & Hofer, 2002; Heyder et al., 2020). If we consider that the foundation of successful mathematics learning during secondary school education is grounded on effective mathematics learning during earlier stages of schooling, like primary school (Clements & Samara, 2011; Heyder et al., 2020), then it is essential to explore how teachers’ beliefs shape motivational, emotional and achievement outcomes as early as possible.

Current study and research questions

Focusing on primary school, the current study aims to examine teachers’ beliefs about the nature and learning of mathematics in connection to students’ motivation and enjoyment of mathematics across different settings, here by considering students’ prior mathematics achievement (Lazarides & Watt, 2015; Roeser et al., 1993), gender and classroom composition (Marsh et al., 2012). Rich data from six education systems offer a more robust examination of relevant constructs and participants (Lauermann & Berger, 2021) to shed light on the following research questions:

  1. (1)

    What is the relationship between teachers’ beliefs about the nature and learning of mathematics and students’ motivation, enjoyment and mathematics achievement when controlling for students’ gender and classroom composition (i.e. percentage of students from socioeconomically disadvantaged homes and percentage of students with behavioural problems)?

  2. (2)

    Are there gender differences in students’ motivational dimensions and enjoyment of mathematics, and do these gender gaps vary significantly across different classrooms?

  3. (3)

    Do teachers’ beliefs about the nature and learning of mathematics and classroom contexts predict the variation in the relationship between gender and motivational dimensions and the enjoyment of mathematics?

We expect significant variations in mathematical motivation and enjoyment between boys and girls within and across classrooms (Goetz et al., 2013; Hyde et al., 1990; Rodríguez et al., 2020; Wigfield & Eccles, 2020), where boys display a more favourable motivational pattern concerning intrinsic value, utility value and perceived competence than girls. We also postulate that both teachers’ beliefs (Marsh et al., 2012) and gender differences regarding their task values (i.e. intrinsic and utility values) and expectancy of success (i.e. perceived competence) may be affected by classroom composition. Beliefs connecting mathematics to a set of procedures and rules are expected to dominate classrooms that have a higher percentage of students from socioeconomically disadvantaged families. Moreover, it can be hypothesised that classrooms with a lower number of students with behavioural problems will generally exhibit higher mathematics achievement. In contrast, teachers will exhibit beliefs on the procedural nature of mathematics to a lesser extent, favouring those regarding mathematics as an inquiry process and observing learning closer to constructivist views (Lazarides & Watt, 2015). Finally, the views of the nature of mathematics as an inquiry process and of learning as an active process are assumed to benefit students’ perceived competence and intrinsic value (Bohlmann & Weinstein, 2013; Heyder et al., 2020; Reusser et al., 2011; Wang, 2012).

Methods

Participants

The current study is part of an international longitudinal research focused on the development of mathematics motivation in primary education—Co-constructing Mathematics Motivation in Primary Education–A Longitudinal Study in Six European Countries (MATHMot for short)—funded by the Research Council of Norway (grant number 301033). Data were collected across six European countries (i.e. Norway, Sweden, Portugal, Serbia, Estonia and Finland) (Table 1). A sample in the first year of the MATHMot project consisted of 11,782 students (5700 in grade 3 and 6082 in grade 4) and 686 teachers from 287 schools. In each country, 45 to 52 schools participated in the study, sampling, in most cases, one grade 3 and one grade 4 in each school. All participating schools came from larger metropolitan areas or nearby surroundings (e.g. in Norway, schools in the greater Oslo area; in Serbia, schools in the greater area of Belgrade). School participation (i.e. students and teachers in the project) was voluntary.

Table 1 Participants’ overview by country
Full size table

At the student level, the sample was balanced for sex (50.6% girls), with a mean age of 9.57 (SD = 0.8333). Female teachers are dominant (89.5%) in our sample, reflecting the general gender distribution among the primary school teacher population. The mean age of sampled teachers is 45.34 (SD = 10.679) and with, on average, about 19 years of service as a mathematics or class teacher (M = 18.69, SD = 11.507). Over half (54.2%) hold at least a bachelor’s degree or equivalent.

All data were collected during regular mathematics lessons by trained research assistants, and informed consent was obtained from the students’ parents and teachers.

Variables

A student questionnaire was used to collect sociodemographic information, such as sex, language and socioeconomic background of the family. The Achievement Emotion Questionnaire–Elementary School (AEQ-ES; Lichtenfeld et al., 2012) and a mathematics test were also administered. The Expectancy Value Scale (EVS) captured different aspects of students’ motivation for mathematics (Peixoto et al., 2023).

The EVS (Peixoto et al., 2023) consists of five dimensions, and current analyses include three: intrinsic value (IV), utility value (UV) and perceived competence (PC). Each dimension comprises five items anchored on a 4-point Likert scale (‘never’ to ‘a lot of times’). Reliability across the dimensions was satisfactory (see Table 2 for details on reliability and example items). Metric invariance across grades and countries was established for each dimension (see Appendix Table 5 for more information).

Table 2 Student and teacher measures
Full size table

The AEQ-ES (Lichtenfeld et al., 2012) was used to measure enjoyment. The enjoyment subscale consists of nine items concentrating on the enjoyment of attending mathematics class, doing homework and taking mathematics tests, here anchored on a 5-point Likert scale (‘not at all’ to ‘very much’). Reliability was satisfactory (see Table 2 for details on reliability and example items). Metric invariance across grades and countries was confirmed (see Appendix Table 5 for more information).

Mathematics achievement was measured with a test developed for each grade. The test comprised released items administered in grade 4 of the TIMSS 2011 cycle (Mullis et al., 2012). The test in grade 3 consisted of 12 mathematics problems and 14 in grade 4. Math problems selected for the test were chosen following multiple criteria: item topic (e.g. numbers, geometry, data display), item relative difficulty and curriculum analysis coverage (i.e. provided for each participating country). One point was assigned to each correct answer, resulting in a maximum score of 12 points for grade 3 and 14 for grade 4. The test was timed (i.e. 25 min in grade 3 and 30 min in grade 4). All items in the mathematics test were approved for use by the IEA (Approval IEA-22-022). Next, the test scores for grade 3 and grade 4 students were estimated using the Rasch measurement, here based on all items included in the tests. Because the tests involved seven mathematics problems used in both tests, this enabled us to create a joint mathematics achievement scale. The WLE person parameters were used in the analyses. The overall scale was anchored to an average score of 500 and standard deviation of 100.

Adapted from the Teacher Education and Development Study in Mathematics (TEDS-M) (Laschke & Blömeke, 2014), information on teachers’ beliefs on the nature of mathematics and learning of mathematics was collected by a teacher questionnaire, which was consistent with the theoretical and empirical background (Grigutsch et al., 1998). Teachers’ beliefs on the nature of mathematics comprise two subscales—rules and procedures (RULES) and process of inquiry (INQUIRY)—each comprising six items anchored on a 4-point Likert scale (‘strongly disagree’ to ‘strongly agree’). For the RULES subscale, the model fit had the following parameters: CFI = 0.983, TLI = 0.969, RMSEA = 0.071 and SRMR = 0.029. In the case of the INQUIRY subscale, the parcelling method was conducted (Little et al., 2002), and the model showed the following parameters: CFI = 1.000, TLI = 1.000, RMSEA = 0.000 and SRMR = 0.000. Reliability values are provided in Table 2, together with the example items. The invariance of the subscales was confirmed with the alignment method, showing equal loadings across countries.

Beliefs on the learning of mathematics were examined through the active learning scale (ACTIVE_L), comprising four items anchored on a 4-point Likert scale (‘strongly disagree’ to ‘strongly agree’). The configural model for the ACTIVE_L scale was satisfactory (CFI = 0.993, TLI = 0.978, RMSEA = 0.091, SRMR = 0.015) coupled with scale reliability (see Table 2 for details on reliability and example items). Invariance was confirmed with the alignment method, showing equal loadings across countries.

In addition, teachers provided information about classroom composition, namely, the percentage of students coming from socioeconomically disadvantaged homes (CC_lowSES) and those with behavioural problems (CC_Beh). Please see Table 2 for more details.

Given the international aspect of the project, all instruments followed a two-step translation procedure—from English to one of the project languages, followed by back-translation to English. Concerning TIMSS 2011 items that were embedded in the math test, official translations were used for all countries except Estonia, which did not participate in TIMSS 2011. For Estonia, translation procedures applied to other instruments were utilised.

Analytical procedures

Measurement invariance was tested, and metric invariance (i.e. equal loadings across the countries) was established for all constructs across countries and grades (see Appendix Table 5 for an overview). A two-level (i.e. student level and classroom level) structural equation modelling (TSEM) with random slopes was employed to address our research questions. By estimating a so-called random slope, TSEM allows for the examination of relationships among constructs at the respective level and tests whether the lower-level relationship varies at the higher-level units. In our analysis, for example, the student-level relationship between sex and students’ motivation or enjoyment (i.e. slope) may vary across different classrooms (i.e. random). As in our second research question, this assumption can be tested using a two-level SEM model with random intercepts and slopes. To test this, we allowed the slope to vary and estimated the mean and variance of the individual-level slope. If the estimated variance of the individual-level slope was significant, we could confirm that the individual-level slope was random, implying that the individual-level relationship was significantly different because students belong to diverse classroom contexts. When predicting the variation of the random slopes (i.e. individual-level relationship), as in our research question 3, we introduce a cross-level interaction and regress the random slopes on teacher belief dimensions. A separate analysis was conducted for each of the six educational systems. We refer to the estimated random slopes as Slope_ Enjoy (i.e. SE in Fig. 1), Slope_ Intrinsic, Slope_ PC and Slope_Utility (i.e. SM in Fig. 1). All models were estimated using Mplus 8.8 (Muthén & Muthén, 1998–2017).

Fig. 1
figure 1

The hypothetical mixed effect model. Note. SM and SE include all random slopes between sex, motivational dimensions and enjoyment

Full size image

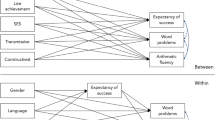
In the next step, we explained the variances of the random slopes by teacher beliefs in terms of cross-level interactions. Cross-level interactions may occur when the lower-level relationship differs depending on the value of the higher-level predictor. In the current analyses, for example, we examined whether the random slope (i.e. the relationship between student sex and their motivation dimensions or enjoyment) can be explained by classroom teachers’ beliefs about the nature and learning of mathematics (i.e. mathematics as a set of rules or as a process of inquiry and active learning), here by taking into account student mathematics achievement and classroom composition. The models also included the regression of classroom mathematics achievement on classroom composition (i.e. percentage of low SES students and percentage of students with behavioural problems). Figure 1 shows the hypothetical mixed effect model to be tested using data from six countries.

As depicted in Fig. 1, the relationship between sex and the conditional enjoyment and motivation dimensions (conditioned by students’ mathematics achievements) are assumed to vary across different classrooms. This means the random slopes of the relationships depicted by the black dots SM and SE. SM and SE are latent variables at the classroom level, and Mplus estimated the means (i.e., the strength of the relationship) and variances (i.e. the difference of the relationship across classrooms) of the random slopes. Teacher beliefs can predict the variation of the random slopes, in turn, by regressing random slope on teacher beliefs about the nature and learning of mathematics. The arrows pointing to the dots SM and SE from teacher beliefs are the cross-level interactions reflecting the impact of the class-level construct on the individual-level relationships. In other words, the model demonstrates that teachers’ beliefs may moderate the relationships between sex and students’ conditional motivation and enjoyment by mathematics achievement and classroom composition.

Results

In this section, we depict the results connected to the research questions guiding the study. We focus on the mechanisms between teachers’ beliefs about the nature and learning of mathematics, mathematics achievement and the differences in students’ conditional motivation and enjoyment between boys and girls by classroom composition. The mechanism is depicted by path diagrams in Figs. 2, 3 and 4 for the respective countries. It should be noted that the TSEM models estimated here are saturated models with a perfect model fit. However, only the significant parameter estimates are included in the path diagrams.

Fig. 2
figure 2

Path diagram for Norway (top) and Finland (down). Note. Only significant paths are shown. Math = mathematics achievement, IV =intrinsic value, UV=utility value, PC=perceived competence, EoM=enjoyment of mathematics, RULES=beliefs on the nature of mathematics—rules and procedures, INQUIRY=beliefs on the nature of mathematics—process of inquiry, ACTIVE_L=beliefs on learning of mathematics—active learning, CC_lowSES=classroom composition as perceived by teachers—students from socioeconomically disadvantaged homes, CC_Beh=  classroom composition as perceived by teachers—students with behavioural problems

Full size image
Fig. 3
figure 3

Path diagram for Sweden (top) and Serbia (down). Note. Only significant paths are shown. Math = mathematics achievement, IV=intrinsic value, UV=utility value, PC=perceived competence, EoM=enjoyment of mathematics, RULES=beliefs on the nature of mathematics—rules and procedures, INQUIRY = beliefs on the nature of mathematics—process of inquiry, ACTIVE_L = beliefs on learning of mathematics—active learning, CC_lowSES = classroom composition as perceived by teachers—students from socioeconomically disadvantaged homes, CC_Beh = classroom composition as perceived by teachers—students with behavioural problems

Full size image
Fig. 4
figure 4

Path diagram for Estonia (top) and Portugal (down). Note. Only significant paths are shown. Math = mathematics achievement, IV = intrinsic value, UV = utility value, PC = perceived competence, EoM = enjoyment of mathematics, RULES = beliefs on the nature of mathematics—rules and procedures, INQUIRY = beliefs on the nature of mathematics—process of inquiry, ACTIVE_L = beliefs on learning of mathematics—active learning, CC_lowSES = classroom composition as perceived by teachers—students from socioeconomically disadvantaged homes, CC_Beh =  classroom composition as perceived by teachers—students with behavioural problems

Full size image

Diverse mechanisms in different countries

Norway

All three dimensions of students’ motivation (i.e. IV, UV and PC) were significantly related to students’ enjoyment. The most substantial relationship was between intrinsic value and enjoyment (0.67). Boys generally perceived higher mathematical competence (0.17) and performed better on the mathematics tests (0.10) than girls. Classrooms’ socioeconomic composition was positively related to teachers’ beliefs in active mathematics learning (0.19).

Finland

Students’ intrinsic value, UV and PC were positively related to their enjoyment of mathematics. Boys performed better in mathematics scores (0.12) and reported higher enjoyment of learning mathematics (0.04) and PC in mathematics (0.14).

Sweden

The relationship between students’ enjoyment of mathematics and their intrinsic value (0.71) was higher than that with the other two motivation dimensions (i.e. UV, 0.08 and PC, 0.11). Moreover, boys were observed to have a higher level of mathematics achievement (0.13), enjoyment of learning mathematics (0.07) and PC in mathematics (0.09). Classroom socioeconomic composition was negatively related to teachers’ inquiry beliefs (−0.23) and active teaching in mathematics (−0.24). A moderate relationship was found between teachers’ beliefs about inquiry and classroom behavioural problems (0.31). In Swedish classrooms, teachers’ beliefs about rules were linked to higher class mathematics achievement (−0.34).

Serbia

Significant relationships were established between the three dimensions of students’ motivation and enjoyment for learning mathematics (i.e. 0.68 for intrinsic value, 0.07 for UV and 0.17 for PC in mathematics). A significant gender difference was also found in favour of boys in mathematics performance (0.12) and PC in mathematics (0.05). Furthermore, a negative relationship was observed between classrooms’ socioeconomic composition and teachers’ beliefs of mathematics being seen as a set of rules and procedures (−0.26).

Estonia

Significant gender differences in favour of boys were observed in the intrinsic value (0.10), PC dimensions (0.15) and mathematics achievement (0.13). The two dimensions of students’ mathematics learning motivation were also positively related to their enjoyment of mathematics, 0.72 and 0.40, respectively. Classroom behavioural problems were negatively associated with average mathematics achievement (−0.23) and teachers’ beliefs about mathematics being a set of rules and procedures (−0.29).

Portugal

Positive relationships between students’ intrinsic value, PC and enjoyment of mathematics were observed. Boys held higher intrinsic value (0.10) and stronger PC (0.15) and achieved higher in mathematics (0.13).

Results across individual countries

Our findings indicate that boys consistently demonstrated significantly higher levels of mathematics achievement and perceived mathematics competence than girls. Additionally, we observed that students’ mathematics achievement mediated the gender difference in perceived mathematics competence. Moreover, mathematics achievement exhibited significant associations with all the motivational dimensions included in our model.

Furthermore, our study revealed a gender difference in intrinsic value in Norway, Estonia and Portugal, which was found to be mediated by mathematics achievement. We observed no associations for between-classroom SES composition, behaviour problems, teacher beliefs dimensions and classroom average mathematics achievement, except for Estonia. These results suggest that other factors, such as teacher classroom practices, may play a crucial role in the missing link between teacher beliefs and mathematics achievement at the classroom level.

Do gender differences in motivation and enjoyment of mathematics vary across classrooms?

The relationships between gender and mathematics motivation and enjoyment were allowed to vary across different classrooms to answer this research question. This meant that a mean and variance were estimated for these parameters, with the mean estimate indicating the individual-level relationship and variance the difference across classrooms for the observed relationship. A significant variance confirmed that the relationship differed over different classrooms (i.e. random slopes). Table 3 presents the estimates of the mean and variance of the relationships in all six countries.

Table 3 Estimates of the mean and variance of the slopes
Full size table

As shown in Table 3, these estimates tended to be minor and, in most cases, nonsignificant. The between-classroom difference in the Sex_Intrinsic relationship was significant in five countries, except Finland. The difference in Sex_Enjoy relationships across classrooms was significant in four countries, except Estonia and Serbia. Norway and Sweden had considerable cross-classroom variance in the relationship between sex and utility. The significant slope variation indicates that gender differences in students’ motivation and enjoyment varied across classrooms. The relationship between sex and PC was positive and significant in all six countries, but only Portugal held a considerable variation in this relationship. This implies that, in all countries, girls perceived themselves to be less competent in mastering mathematics, regardless of their classroom, except in Portugal, where girls’ self-perception differed significantly in different classrooms.

Do teachers’ beliefs and classroom context explain the variation in gender differences in mathematics motivation and enjoyment?

Although significant variances in the countries’ slopes are shown in Table 3, we attempted to account for these variances in more depth in the follow-up analyses. Table 4 presents country-specific patterns of teachers’ beliefs explaining gender differences in motivation and enjoyment of mathematics. The models ascertained the significant explanatory role of teachers’ beliefs in the variation between boys and girls in mathematics motivation and enjoyment in Portugal, Norway and Finland. In Portugal, the negative estimate was from Slope_PC on teachers’ inquiry beliefs, indicating that teachers’ beliefs in inquiry reduced the sex differences in the perceived competence to learn mathematics. In Norway, teachers’ beliefs about active learning positively related to the Sex_Intrinsic and Sex_Utility slopes, implying that the gender differences in intrinsic and UVs can be increased in a classroom where the teacher holds stronger beliefs about active learning.

Table 4 The impact of teachers’ beliefs and classroom contexts on gender differences in motivation and enjoyment of mathematics in six countries
Full size table

In Norway, teachers’ beliefs about active learning were significantly related to the gender difference in the intrinsic value of learning mathematics (0.09) and the UV (0.11). Additionally, the classroom socioeconomic context affected the relationship between gender and UV directly (0.09) and indirectly through teachers’ active learning (0.03). Classroom behavioural problems were found to be related to the gender difference in the intrinsic value of mathematical motivation (−0.18). In Finland, classroom socioeconomic composition reinforced the relationship between gender and enjoyment of learning mathematics (0.08).

Discussion

The major focus of the present study was on examining teachers’ beliefs about the nature and learning of mathematics in connection to students’ intrinsic value, utility value, perceived competence and enjoyment of mathematics. We have studied these patterns across different settings, simultaneously considering students’ mathematics achievement and classroom composition. Against the backdrop of previous research, our findings reveal a differentiated picture of country-specific mechanisms and more general patterns captured across all countries.

Observations from the student-level models indicate that students’ intrinsic value and perceived competence positively related to their enjoyment of mathematics in all six countries. This pattern has been reported elsewhere, and results show it is widespread across different settings (Chen et al., 2023; Forsblom et al., 2022; Putwain et al., 2018). The positive relations between utility value and enjoyment were confirmed in Finland, Norway, Serbia and Sweden, indicating some unique country patterns. In two Nordic countries (i.e. Finland and Sweden), the results showed that boys enjoyed learning mathematics more (Goetz et al., 2013; Hyde et al., 1990). Considering the effect of gender on motivation, boys had higher perceived competence in all six countries but had higher intrinsic value only in Estonia and Portugal (Rodríguez et al., 2020; Wigfield & Eccles, 2020). Future analyses will try to unravel the possible mechanisms of these distinct country patterns, especially because girls are seen as more vulnerable and the impact of interest on mathematics achievement is more critical for them (Ganley & Lubienski, 2016). The latter is coupled with the notion that positive emotions associated with mathematics, such as enjoyment, could have a more pronounced effect on girls’ perseverance (Pinxten et al., 2014). There was no significant relationship between sex and utility value in any of the examined countries. Furthermore, the results for all countries showed that boys had higher mathematics achievement.

Classroom composition had a more pronounced influence on teachers’ beliefs in Sweden, Norway, Estonia and Serbia. Again, the phenomenon was not universal for all countries and might be tied to a distinctive education system organisation (Yang Hansen et al., 2020; Marsh et al., 2012). In Sweden, classrooms with a high percentage of students with behaviour problems had teachers with stronger beliefs about seeing mathematics as a process of inquiry. In classrooms with fewer students from socioeconomically disadvantaged families, teachers held stronger inquiry beliefs on the nature of mathematics and those on active learning. In Norwegian classrooms, teachers’ beliefs about learning mathematics as an active process were significantly firmer when they consisted of more students from disadvantaged socioeconomic families. In Estonia, there was a negative relationship between teachers’ beliefs about mathematics being a set of rules and classrooms comprising students with behavioural problems. That is, weaker beliefs about mathematics as a set of rules were found in classrooms with a higher percentage of students with behavioural problems. With a high proportion of students from advantaged socioeconomic families in the classrooms, the teachers in Serbia did not hold firmer beliefs on the nature of mathematics being a set of rules and procedures one should follow. Compared with other countries, in Estonia and Sweden, classroom mathematics achievement could be explained by other classroom-level predictors. Estonian classrooms with fewer behavioural problems had higher mathematics scores (Marsh et al., 2012). In Swedish classrooms, weaker teachers’ beliefs about rules were associated with higher math scores.

A distinctive element of the present study is that it examines relationships across countries using the same set of variables and relatively similar samples, thus contributing to methodological robustness in the domain (Lauermann & Berger, 2021). Against most studies using single-country samples, this cross-country comparison has allowed us to observe where particular patterns are unique, contradictory or possibly universal. For example, in the Nordic countries (i.e. Finland and Norway), classroom composition is an essential contributing factor to the differential motivation and enjoyment of learning mathematics by boys and girls. In Finland, boys had more enjoyment in classrooms with more students from socioeconomically disadvantaged backgrounds. In Norway, boys were more externally motivated (i.e. higher utility value) to learn mathematics in classrooms composed of students from socioeconomically disadvantaged families. In contrast, girls’ intrinsic value was higher in classrooms with more students with behavioural problems. Described results warrant future investigations of distinctive characteristics pertinent to the education systems included in the analyses. These characteristics could explain possible differences in the presence of certain teacher beliefs against either classrooms with a low (high) percentage of students from socioeconomically disadvantaged homes or those saturated by students with behavioural problems, as well as why these might uniquely affect boys and girls.

Our results indicate that teachers’ beliefs about the nature and learning of mathematics moderate the within-classroom relationship between boys and girls and the motivation and enjoyment of learning mathematics in Portugal and Norway. Although aligned with some previous findings (e.g. Bohlmann & Weinstein, 2013; Heyder et al., 2020; Lauermann & Berger, 2021), again, the phenomenon was not captured across all the countries. In Portugal, the correlation between estimates from the negative significant slope regression was for Slope_PC on inquiry. The results showed that the effect of inquiry on students’ perceived competence was specific to student gender and higher for girls in Portugal. If teachers’ beliefs about the inquiry of mathematics were stronger, girls reported higher perceived competence related to mathematics. In Norway, we found a positive correlation between active learning and Slope_Intrinsic and Slope_Utility. This indicates that boys learn mathematics with higher intrinsic and utility values when teachers hold stronger beliefs about active learning. Nonetheless, this result still confirms the importance of constructivist learning beliefs and their contribution to students’ optimal outcomes (Lazarides & Watt, 2015; Reusser et al., 2011).

Limitations and further research

An ample cross-country sample, accounting for the nested structure of the data and TSEM, certainly contributes to the methodological rigour of the present study. Nonetheless, the current data come from one data point, meaning that no direct causal observations can be claimed. In addition, we relied on self-reported measures alone, despite these being gathered from students and their teachers. In terms of model selection, a random intercept model would not suffice to achieve the outlined study objectives, namely, investigating whether the gender gaps in mathematics motivation and enjoyment vary across different classrooms, and whether teacher beliefs may account for the cross-classroom differences in these gender gaps. Therefore, a random intercept and slope model with cross-level interaction is the most suitable analytical method for gaining insight in our research objectives. The results also posit that country-specific patterns may warrant additional demographic variables about the teachers and their classrooms, which could enable a more nuanced understanding of the patterns we were able to capture. This may include more information on teachers’ prior education, especially regarding their knowledge of mathematics. It should also be noted that the current sample mostly captures teachers whose major may not be mathematics (i.e. subject teaching is not yet the dominant format in primary school). The latter implies that observing how teachers’ beliefs affect their students’ motivational and emotional characteristics may differ in some systems after only one additional year of schooling (e.g. Portugal and Serbia transfer to subject teaching in grade 5).

Conclusion

Against the background of acknowledging the importance of teacher beliefs and their fundamental role in teaching mathematics and students’ learning processes (Daumiller et al., 2021; Hettinger et al., 2023; Heyder et al., 2020; Stipek et al., 2001), as well as distinctive motivational (Rodríguez et al., 2020; Wigfield & Eccles, 2020) and affective (Goetz et al., 2013; Pinxten et al., 2014) patterns between boys and girls related to mathematics, our results confirm that teachers’ beliefs have a certain moderating effect on primary students’ motivation and enjoyment of mathematics and that distinctive cross-level effects on boys and girls can be seen in the importance of classroom characteristics that support feelings of competence and connectedness (Eccles & Wigfield, 2020). At the same time, the observed phenomenon is not equally present in the examined countries, prompting the continuation of our current investigation and emphasising the importance of culture and situated experiences that may be built across observed classrooms and countries (Eccles & Wigfield, 2020). Nonetheless, the results support teachers’ beliefs that favour mathematics as a process of inquiry and those close to constructivist views of learning to be beneficial to students’ intrinsic value, perceived competence and enjoyment of mathematics.