Abstract
Teacher beliefs and practices related to them could provide varying opportunities for students to develop their agency related to learning math. The aim of the current paper is to explore how different math teacher beliefs (concerning the nature of mathematics, constructivist beliefs, and self-efficacy) relate to different dimensions of student agency in primary education. A two-level multilevel model was analyzed to find out to what extent selected teacher beliefs are associated with student math competence and agency dimensions. The study was conducted in Estonia and data from 3rd and 4th grade students (N = 1557) and their teachers (N = 121) was included in the analysis. The results showed that teacher self-efficacy beliefs, constructivist beliefs, and static views on the nature of mathematics were related to students’ agency dimensions. Possible explanations and directions for further studies are discussed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
As highlighted in several policy documents (see, e.g. The Learning Compass 2030 of OECD, OECD, 2019) and in scholarly research, supporting students’ agency is increasingly important in today’s educational context. Similar to other subject areas, opportunities to develop student agency have been explored in the context of mathematics education (see, e.g. Brown, 2020; Hansen, 2022; Nieminen et al., 2022). However, currently, most research on exploring and supporting student agency has been conducted in secondary (e.g. Hansen, 2022; Nieminen et al., 2022) and tertiary levels (e.g. Jääskelä et al., 2021) of education. In this study, we explore student agency in the context of teaching and learning mathematics in primary education.
Broadly understood, agency refers to individuals’ active participation in, and shaping of, realities and is generally recognized as an important condition for learning and participation in different spheres of life (Billett, 2008; Lipponen & Kumpulainen, 2011). Several scholars have theorized how agency emerges and is influenced by environmental conditions (see, e.g. Archer, 2000; Vaughn, 2020). Consequently, it has been shown how, in educational contexts, student agency is influenced both by students’ personal characteristics and by environmental conditions which are significantly influenced by teachers’ beliefs and actions in relation to students (see Erss, 2023; Jääskelä et al., 2021; Lipponen & Kumpulainen, 2011). More specifically, recent research indicates that student agency in secondary and tertiary educational settings is affected by relational, individual, and participatory resources, such as interest, capacity beliefs, self-efficacy, experiences of trust, support from teacher and peers, and opportunities to influence, make choices, and actively participate (see, e.g. Erss, 2023; Hansen, 2022; Nieminen et al., 2022; Jääskelä et al., 2021).
Teachers play an important role in the development of children's competence in mathematics (Hiebert & Grouws, 2007). Effective teaching practices can help to increase student agency and to improve their learning (Niemi et al., 2015; Ruohotie-Lyhty & Moate, 2015). Previous research has also demonstrated that teachers’ beliefs and certain teaching practices can contribute to students’ attitudes towards and competences in mathematics (see, e.g. Muis & Foy, 2010; Seidel & Shavelson, 2007). Drawing on these empirical findings and conceptualizations of agency (Archer, 2000; Priestley et al., 2015), it could be expected that teachers’ beliefs contribute to developing students’ agency in learning mathematics. However, according to our best knowledge, empirical studies that focus on these relations are rare, especially in primary education. The aim of the current paper is to explore how teachers’ beliefs relate to student agency in the context of learning mathematics in primary education.
Theoretical framework
Student agency in a mathematics learning context
An important goal of mathematics education is to develop math competence. Mathematical competence assists individuals in recognizing the role that mathematics plays in the world and to make the well-founded judgments and decisions needed by constructive, engaged, and reflective citizens (Devlin, 2021; OECD, 2018). Therefore, mathematical competence goes beyond just the mathematical processes of reproduction (Johanson et al., 2021; OECD, 2022). Mathematical competence is often treated as the main outcome of early mathematics education, but several authors (e.g. Gutstein, 2007; Nieminen et al., 2022; Norén, 2015) have pointed out that from the long-term perspective, student agency related to mathematics is equally, if not more, important. When students develop agency related to mathematics, they are better prepared for life-long learning, and they will continue to improve their competences long after completing formal education.
Human agency is revealed by commitment, purposiveness, intentionality, and influence, and sometimes also by resisting or transforming existing practices (Archer, 2000; Emirbayer & Mische, 1998; Eteläpelto et al., 2013). In our context, this would mean that students have an active role in shaping mathematics learning experiences. According to the ecological model of agency (Erss, 2023; Leijen et al., 2020; Priestley et al., 2015), this active role manifests itself in the decision-making process. A student has agency if she/he has alternatives for action and can choose between these. This decision-making is influenced by three dimensions that encompass the past-present-future of learning: iterational, projective, and practical-evaluative. Firstly, the iterational dimension indicates that agency is rooted in past experiences. Over time, students develop attitudes and competences related to mathematics, and these will start influencing their future decisions related to learning mathematics (see, e.g. Lange, 2010; Lauermann et al., 2017). The iterational dimension of agency guards for stability in a student’s actions since she/he tends to choose for activities that have proven successful in the past. Secondly, agency is oriented towards the future. The projective dimension reflects a student’s short-term and long-term purposes which guide decision-making towards a student’s plan for the future, thus guarding for potential change in a student’s actions. For example, when a student has clear goals related to learning mathematics and understands the purpose of learning certain content or practising certain skills in light of these goals, then it is more likely that the student chooses to be actively engaged in learning this content or skills (see also Eccles & Wigfield, 2020). In contrast, when a student does not understand the relevance of learning certain content or skills, it is more difficult to engage in learning. Thirdly, the practical-evaluative dimension indicates a student’s capacity to make decisions and navigate learning in specific situations. This decision-making process is, on the one hand, guided by the iterational and projective dimensions and, on the other hand, by the cultural, structural, and material conditions of specific situations such as math classes. These different environmental conditions of math education can be perceived as enablers, constraints, or resources for action which can either hinder or foster a student’s agency in learning mathematics. Learning environments that are sensitive to students’ perspectives, provide alternatives, and support horizontal relations and collaboration between students in making decisions in their learning are recognized as agency supportive, while rigid rules, hierarchical relation, and competition-orientation are recognized as agency suppressive (Nieminen et al., 2022; Priestley et al., 2015). Teachers have a key role in creating supportive environmental conditions for learning in educational settings.
The formation of student agency and its components is therefore influenced by the school context, home learning environment, and also by students’ personal characteristics (see, e.g. Eccles & Wigfield, 2020). Several studies have shown that students’ competency beliefs decline with age (e.g. Eccles et al., 1993; Jacobs et al., 2002; Weidinger et al., 2018), although Anderson et al. (2019) showed the crucial role of personal agency factors on students’ attendance and academic performance. Based on analysis of results from two international student assessment studies (Trends in International Mathematics and Science Study (TIMSS) and Programme for International Student Assessment (PISA)), Else-Quest et al. (2010) concluded that gender differences in math achievements and attitudes exist, but that the size of the gender gap varies across countries. Moreover, numerous studies have shown that math achievement is related to children’s general intellectual abilities (e.g. Filippetti & Richaud, 2017; Józsa et al., 2022). Finally, PISA results have shown that math achievement of Estonian students is related to the language used at home (students speaking Estonian at home have higher results than Russian-speaking students) and the socioeconomic status of students (students with higher status have higher achievements in math) (Täht et al., 2018; Tire, 2021).
Besides these individual student characteristics, students’ math achievement, attitudes, and agency are also affected by the classroom context. Given that more experienced teachers focus more on supporting student learning while less experienced teachers tend to be more concerned with themselves and their own understanding of the content matter (see, e.g. Berliner, 2001; Conway & Clark, 2003), it is expected that teacher experience is positively related to all dimensions of agency. Moreover, class size is also relevant for math learning and achievement, although its effect can vary significantly across education systems (e.g. Li & Konstantopoulos, 2017; Nandrup, 2016).
However, the most important classroom factors are those related to teacher beliefs. In the following section, we will introduce research on teacher beliefs to explore how these contribute to student agency in learning mathematics in primary education.
Teacher beliefs
Research on teachers’ beliefs is rooted in the idea that beliefs structure people’s interactions with the world and consequently influence their perceptions, goals, classroom decisions, and behaviours (Fives & Buehl, 2012; Pajares, 1992; Richardson, 1996). In the school context, Woolfolk Hoy et al. (2006) classified teacher beliefs according to the level of the system to which they apply. At the first level, teachers have certain beliefs about the self. For example, teachers have certain beliefs about their own abilities as a teacher or the role of a teacher. At the next level, teachers hold beliefs about the immediate context of teaching and learning. They are responsible for planning, enacting, and maintaining a complex environment that facilitates and inspires learning. Their beliefs about learning can influence their work and professional development as teachers (Buehl & Beck, 2015) and the way teachers contribute to students’ development (Ashton, 2015).
In particular for mathematics teachers, teachers’ beliefs could be subdivided into beliefs about the nature of mathematics (i.e. epistemological beliefs), beliefs about mathematics teaching and learning (Ernest, 1989; Op’t Eynde et al., 2002), and self-efficacy beliefs related to teaching (Bandura, 1997; Tschannen-Moran and Hoy 2001). Teachers’ epistemological beliefs about the nature of mathematics can lead them to choose specific practices for instruction, thereby influencing student agency (Niemi et al., 2015; Ruohotie-Lyhty & Moate, 2015). Two main views have been shown to be dominant in empirical studies on mathematics teaching: one views mathematics as a static discipline, and the other view emphasizes the dynamic nature of mathematics as a process (Felbrich et al., 2014; Grigutsch et al., 1998; Törner & Grigutsch, 1994; Yang & Leung, 2015). These views of mathematics also correspond closely with teachers’ wider pedagogical beliefs. An understanding of mathematics as a static collection of facts and procedures is closely linked to teachers’ transmissive pedagogical beliefs (i.e. teacher-centred or traditional approach), while the dynamic view corresponds to teachers’ constructivist beliefs (i.e. student-centred or progressive approach) (De Corte, 2010; Voss et al., 2013). According to the transmissive approach, the teacher transmits information and rules to the students who are expected to absorb and reproduce it. From this perspective, mathematical teaching and learning can be seen as a one-way process of information transfer from teacher to students, with an emphasis on reproduction, repetition, automatization, receptive learning from examples, and providing limited support for students’ agency (Voss et al., 2013). With the constructivist approach, students actively engage in mathematical problems and tasks and receive support to explore various methods of reasoning and problem-solving. It enables students to build a deeper conceptual understanding (Collins et al., 2004; Freeman et al., 2014; Wakhata et al., 2023) and construct their own mathematical knowledge through interaction with the environment (Burton, 1993; Ling, 2003; Richards & Gipe, 1994), thus clearly supporting student agency in learning. In this context, the teacher functions as a mediator, whose task is to create learning environments that promote the active and independent engagement with the learning content and to support and scaffold students’ agency and learning processes (Voss et al., 2013).
Teacher self-efficacy beliefs illuminate teachers’ confidence in carrying out particular activities (Bandura, 1997; Tschannen-Moran and Hoy 2001). Overall, higher levels of self-efficacy enable teachers to provide more space to students for their active engagement and to support them to explore learning and therefore support student agency (Lauermann & Berger, 2021). Higher levels of self-efficacy also protect teachers in times of difficulties and support them in successfully staying in the profession (see, e.g. Klassen & Chiu, 2011; Zee & Koomen, 2016). Research has also shown that teacher self-efficacy is related to student outcomes, such as competency beliefs, academic achievement, and motivation to learn mathematics (Chang, 2015; Hettinger et al., 2023; Muis & Foy, 2010; Nurlu, 2015; Perera & John, 2020; Ross, 1992; Thoonen et al., 2011). However, a more recent review by Lauermann and Hagen (2021) synthesized different meta-analyses and concluded that the correlations between teacher self-efficacy and student achievement range from small positive to near-zero. So, although theoretically expected, it has not always been possible to demonstrate this relationship in empirical studies.
Current study
Taking into consideration the fact that teacher beliefs and related practices could enable or inhibit students to develop their agency, the main aim of the current study is to explore the relationship between teachers’ beliefs and student agency. In this paper, we focus on teacher beliefs that are, based on the overview of existing literature, identified as relevant for student agency either as enablers or inhibiters. Moreover, we focus on students attending primary education since there is an overall lack of knowledge about the relevance of teacher beliefs supporting student agency at the beginning of formal education. More specifically, we seek to answer the following research question:
How do different teacher beliefs (concerning the nature of mathematics, constructivist beliefs, and self-efficacy) relate to different dimensions of student agency in primary math education?
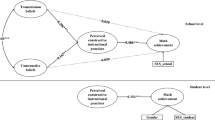
The multilevel model used to answer the research question is presented in Fig. 1.
Multilevel model with explanatory and control variable at the student and teacher level. Note: AG_ST_CS- student agency: iterational dimension (student level); AG_ST_ES- student agency: practical-evaluative dimension (student level); AG_ST_PS- student agency: projective dimension (student level); MATHS – student math achievement; AGE_ST - student age; GENDER_ST - student gender; COG – general cognitive ability of students; LANG_REV - language used at home and school; BOOKS - socioeconomic status of student estimated by number of books at home; AG_ST_CT- average level of iterational dimension of agency for students taught by given teacher (teacher level); AG_ST_ET- average level of practical-evaluative dimension of agency for students taught by given teacher (teacher level); AG_ST_PT- average level of projective dimension of agency for students taught by given teacher (teacher level); MATHT – average level of math achievements of students taught by given teacher (teacher level); TCONF_CA - teacher confidence in cognitive activation of students; TCONF_M - teacher confidence in motivating students; TCONF_P - teacher confidence in goal setting; TNM_STAT - teacher belief about the static nature of mathematics; TNM_DYN - teacher belief about the dynamic nature of mathematics; TCONSTR - teachers’ belief in constructivist learning of mathematics; CLS_NOST - numbers of students in the class; YEARS_EXP - years of experience as a teacher
Based on the conceptual framework, and drawing on the findings of previous research (e.g. Chang, 2015; Freeman et al., 2014; Voss et al., 2013; Wakhata et al., 2023), we expect positive relationships between a dynamic view of the nature of mathematics, a constructivist view of teaching, and teaching self-efficacy and all the dimensions of student agency. We expect negative relationships between a static view of the nature of mathematics and different dimensions of student agency. More specifically, we expect that teachers with higher self-efficacy in terms of cognitive activation of students, motivating students, and setting goals for learning math will create more opportunities for students to make decisions about their learning. They will also support the development of competency beliefs and future perspectives related to mathematics (e.g. Chang, 2015; Muis & Foy, 2010; Perera & John, 2020; Thoonen et al., 2011). Similarly, teachers with a dynamic view of mathematics and teachers practising a constructivist approach in teaching are expected to foster a deeper engagement of students in learning and to develop a higher sense of competence and clearer purposes related to mathematics. Conversely, teachers with a static view would be expected to require students to reproduce concepts and practices more restrictively that would also impact negatively students’ competency beliefs and purposes related to learning mathematics (e.g. Collins et al., 2004; Freeman et al., 2014; Voss et al., 2013; Wakhata et al., 2023).
Since previous studies have shown that certain student (e.g. Eccles et al., 1993; Else-Quest et al., 2010; Filippetti & Richaud, 2017; Józsa et al., 2022; Täht et al., 2018) and teacher characteristics (e.g. Berliner, 2001; Conway & Clark, 2003), as well as class size (Li & Konstantopoulos, 2017; Nandrup, 2016), could affect student agency, it was necessary to include these characteristics in the model to control our findings for their impact. In other words, inclusion of these control variables should enable us to assess the effect of selected teacher beliefs on student agency if teachers have similar years of experience, and if they teach classes of the same size, and students who are similar in terms of their age, gender, and general cognitive abilities.
Methods
Estonian primary education context
In Estonia, compulsory education begins at the age of seven. A particular feature of the Estonian primary school system is that, in the first three or four grades (sometimes up to sixth grade), the same teacher often educates students in the main subjects, such as Estonian language, math, and science. In comparison with some other European countries (e.g. Belgium, Denmark), where a different teacher teaches children every year, in Estonia, this means that an individual teacher might have a greater impact on students’ outcomes than in other countries (Uibu & Kikas, 2014). Therefore, in primary grades, teachers are expected to have good skills for instructing students from the age of 7 to 10/12 years.
The requirements for students’ achievement and demand for study process are set out in the National Curriculum for Basic Schools (Estonian Government, 2011/2014). At the end of each school stage (grades 3, 6, and 9), students must pass national-level math tests (Pedaste et al., 2019a). The syllabus for mathematics contains a variety of pedagogical recommendations for teachers (e.g. perform calculations and use different strategies to solve mathematical problems), but still leaves enough space for teachers to make their own decisions. Most of the tasks primary school students in Estonia have to undertake involve solving mathematical problems and computing (Mädamürk et al., 2018). To solve these tasks, a child must understand the text and the relations between numbers. Each task may require a different combination of skills to solve a math problem. It allows teachers to encourage students to apply learnt strategies in different lessons (Kikas et al., 2022).
Estonian primary school teachers are well educated: their initial teacher education training is at the Master’s degree level and they have broad in-service training possibilities (OECD, 2018). Considerable attention has been given to the quality of teacher training programmes in Estonia. Contemporary primary school teacher education comprises general pedagogical studies, subject studies, and practical training which are developed based on Estonian teacher professional standards (Leijen & Pedaste, 2018; Pedaste et al., 2019b). Based on the national curriculum, primary school teachers are expected to apply practices that will enhance pupils’ age-appropriate cognitive and social development and model real-world situations from the surrounding environment (Estonian Government, 2011/2014). The application of student-centredness and constructivist principles (critical thinking, co-operation skills, etc.) is highlighted in policy documents and in empirical studies (see, e.g. Uibu et al., 2023).
Participants
Data used in this study stem from an international longitudinal study focused on the development of mathematics motivation in primary education—co-constructing mathematics motivation in primary education—a longitudinal study in six European countries (MATHMot for short) funded by the Research Council of Norway (grant number 301033). The current investigation uses data collected in 45 primary schools from different parts of Estonia (the total number of schools providing primary education in Estonia is 468). In total, 1694 students (822 attending grade 3, and 810 attending grade 4) and their mathematics teachers (N = 134) participated. However, 13 teachers were excluded from the analysis either because of key teacher variables data were missing or data for less than five students were available for teachers. Considering multilevel analysis, the students of these teachers were also excluded from the analysis. Finally, 12 students were excluded as they delivered their math test with no answers. Thus, in total, 121 teachers and their students were included in the analysis (N = 1557, 809 attending grade 3, and 748 attending grade 4).
Among the participating teachers, 120 (99%) were female and one (1%) was male. The age ranged from 23 to 68 (7% between 23 and 29, 14% between 30 and 39, 25% between 40 and 49, 41% between 50 and 59, 12% between 60 and 68). Their work experience varied from 1 to 49 years (26% 1–9 years, 10% 10–19, 20% 20–29, 36% 30–39, 7% 40–49).
Out of the 1557 participating students, 807 (52%) were girls, 746 (48%) were boys, and the gender of four (0.3%) students is unknown. Three hundred and fifty-nine (23%) were 9-year-olds, 771 (50%) were 10-year-olds, 402 (26%) were 11-year-olds, 9 (0.6%) were 12-year-olds, and the age of 16 (1%) students is unknown.
Measures
Students’ agency in learning mathematics was measured with a questionnaire based on Leijen et al. (2020) and Leijen et al. (2022). The questionnaire is based on the ecological model of agency and measures, which has three dimensions of student agency: an iterational (students’ competency beliefs), a projective (students short- and long-term goals related to learning mathematics), and a practical-evaluative dimension (environmental conditions in the school supporting agency). Students are asked to rate 18 items using a 5-point Likert-type scale (1, strongly disagree; 5, strongly agree). The iterational dimension of student agency was measured by five items referring to their previous experience in learning mathematics and their self-assurance that they can learn successfully (e.g. I’m good at math). The projective dimension was measured by six items about long- and short-term goals in relation to learning mathematics (e.g. I want to learn math in order to be successful in the future). The practical-evaluative dimension was measured by seven items related to the math learning environment and to what extent it supports students in taking initiative and allows them to make choices while learning mathematics (e.g. The teacher takes my opinion into account). A high score in each agency dimension shows higher student agency and indicates a greater student role in making decisions related to learning mathematics. Confirmatory factor analysis (CFA) showed good fit for the three dimensions model of student agency (RMSEA = 0.046, CFI = 0.96, TLI = 0.953, SRMR = 0.04). Composite reliability for the iteration dimension was 0.924, for the projective dimension 0.901, and for the practical-evaluative dimension 0.754.
Mathematical competence was measured with a math test developed for each grade (i.e. 3 to 4). The test consisted of released items administered in the grade 4 TIMSS 2011 cycle (Mullis et al., 2012). The math test in grade 3 consisted of 12 tasks and 14 tasks in grade 4. Both tests involved seven items that were the same, and it enabled us to make a joint scale of the math competence. The items selected for the test were chosen following multiple criteria related to the topic of the item (e.g. numbers, geometry, data display), their relative difficulty, and curriculum analysis coverage. Scoring was performed by assigning one point for each correct answer, which resulted in a potential score of 12 points for grade 3 and 14 points for grade 4. The test was timed, 25 min in grade 3 and 30 min in grade 4. All items found in the test were approved for use by the IEA (Approval IEA-22–022). Math scores for grade 3 and grade 4 students were estimated by using the Rasch measurement based on all items included in both tests with seven items that served as linking items. Student math scores are estimated at the scale with average score 500 and standard deviation 100. The analysis suggested that reliability of student math scores is 0.73, while reliability of item parameters is 1.00.
Teacher beliefs were investigated with the following scales: teachers’ beliefs on the nature of mathematics, self-efficacy in teaching, and constructivism. All scales were adapted or developed based on the Teacher Education and Development Study in Mathematics (TEDS-M) (Laschke & Blömeke, 2013) for the purposes of the MATHMot project. All items of teacher beliefs were rated on a 4-point Likert-type scale (1, not at all; 2, a minor extent; 3, a moderate extent; 4, a major extent).
Teachers’ self-efficacy was measured using three dimensions: teacher confidence in cognitive activation of students, teacher confidence in motivating students, and teacher confidence in goal setting. Teacher confidence in cognitive activation of students was measured using four items (e.g. Challenging students to engage in critical thinking about mathematics), teacher confidence in motivating students was measured using six items (e.g. Choosing mathematical content to foster student motivation), and teacher confidence in goal setting was measured using five items (e.g. Establishing appropriate learning goals in mathematics for students). CFA analysis showed a good fit of the original three-factor model (χ2 = 123.174, df = 87, χ2/df = 1.484, RMSEA = 0.057, CFI = 0.972, TLI = 0.966, SRMR = 0.066) with the composite reliability of dimensions 0.826, 0.867, and 0.869, respectively.
Teachers’ beliefs on the nature of mathematics were measured using two dimensions—rules and procedures and math as a process of inquiry—which correspond to belief in the static nature of mathematics and belief in the dynamic nature of mathematics, respectively. Teacher beliefs related to rules and procedures was measured using five items (e.g. Mathematics is a collection of rules and procedures that prescribe how to solve a problem), while teacher beliefs related to math as a process of inquiry was measured using four items (e.g. Mathematical problems can be solved correctly in many ways). CFA analysis showed a good fit of the original two-factor model (χ2 = 57.514, df = 26, χ2/df = 2.212, RMSEA = 0.069, CFI = 0.967, TLI = 0.951, SRMR = 0.046) with the composite reliability of 0.759 and 0.859, respectively.
Teachers’ belief in constructivist learning of mathematics was measured using four items developed initially by Peterson et al., (1989) to measure beliefs about learning math through active learning (e.g. Time used to investigate why a solution to a mathematical problem works is time well spent). A principal component analysis showed that these four items measure one dimension with the composite reliability of 0.814.
Control variables
Several background variables that were known to be related to students’ mathematics outcomes and student agency (see, e.g. Gustafsson et al., 2013; Jacobs et al., 2002) were included in the questionnaire. At the student level, we included students’ age, gender, general cognitive ability, home language, and the number of books at home as a proxy indicator of socioeconomic background. Information on students’ age, gender, language used at home, and number of books at home were collected via the student questionnaire, while general cognitive ability was measured using the short version of the Standard Progressive Matrices with 15 items and a reliability of 0.78 (Langener et al., 2022). On average, students solved 10.35 items and the standard deviation was 3.02. Descriptive information on student age and gender is described above, and information on the home language and the number of books at home was collected by the same questions that were used in the TIMSS study. Information on the home language was collected by the question How often do you speak Estonian at home? with four alternatives (never, 2.6%; sometimes, 14.4%; almost always, 19.8%; always, 63.2%), while information on the number of books at home was collected by the question About how many books are there in your home? with five options: none or very few (0–10 books), 9.2%; enough to fill one shelf (11–25 books), 23.9%; enough to fill one bookcase (26–100 books), 40.6%; enough to fill two bookcases (101–200 books), 16.0%; and enough to fill three or more bookcases (more than 200), 10.4%.
At the teacher level, we included the number of students in a class and teachers’ years of experience. Teachers involved in the study worked with classes of different sizes (Min = 1, Max = 26, M = 12.87, SD = 3.90) and had diverse working experience in education (M = 22.23, SD = 12.96).
Data collection and analysis
Ethics committee approval was obtained for the study. The data was collected in spring 2022. Mplus 8.8 was used for the data analysis and it was realized in two phases. First, descriptive analysis of all variables resulted in basic statistics of all variables at the student and teacher level (M, SD, and variance) as well as intercorrelations between these variables. Second, a two-level multilevel model was analyzed to find out to what extent selected teacher beliefs are associated with student math competence and agency dimensions. The multilevel analysis was initiated with a null model with math competence and agency dimensions as criteria variables. The analysis of the null model provided information on within-level variance (“student level”) and between-level variance (“teacher level”). Next, a multilevel model with explanatory and control variables was employed to address the main research question. Since the focus of our study is at the teacher level, we included at this level the following explanatory variables: teacher confidence in cognitive activation of students (TCONF_C), teacher confidence in motivating students (TCONF_M), and teacher confidence in goal setting (TCONF_P), and teacher belief in the static nature of mathematics (TNM_STA), teacher belief in the dynamic nature of mathematics (TNM_DYN), and teachers’ belief in constructivist learning of mathematics (TCONSTR). However, teachers in our sample work with different numbers of students in the class and have different years of experience. Since class size and professional experience might affect both student learning and teacher practices, we included these two variables as control variables at the teacher level. In this way, the model provided an insight into the relationship between teacher beliefs and student learning outcomes (math competence and agency) that is independent of class size and teacher experience. Similarly, teachers in our sample worked with different students, and some student characteristics that are beyond the control of teachers might also affect student math competence and agency, independently of teacher beliefs. In order to estimate the relationship between selected teacher beliefs and student math competence and agency that is independent of the class composition, we included relevant student characteristics mentioned as control variables at the student level of the model: student age (ST_AGE), student gender (GEND_ST) with code 0 for girls and 1 for boys, general cognitive ability of students (COG), use of Estonian language at home (LANG_RE) with four levels (1 (never) to 4 (always)), and socioeconomic status (SES) of students estimated by the number of books at home (BOOKS). Based on such a multilevel model, we were able to identify to what extent different teacher beliefs create opportunities for students to develop math competence and agency independently of class composition and student characteristics.
In all multilevel analysis performed by the Mplus, the MLR estimator was used. As a fit index for the multilevel models, we used the standardized root mean square residual (SRMR) that was reported separately for each level (Hsu et al., 2015).
Results
Table 1 shows the descriptive statistics and correlations between the independent and dependent variables at the student level. A moderate positive correlation (r = 0.38) was found between the mathematics test result and the iterative dimension of agency. A similar positive correlation (r = 0.39) was also found between the mathematics test result and the general cognitive ability test result. Different agency dimensions also had moderate correlations ranging from 0.4 to 0.55.
Table 2 shows the descriptive statistics and correlations between the independent and dependent variables at the teacher level. Moderate positive correlations were found between three confidence sub-scales, ranging from 0.46 to 0.55. Weak positive correlations (r = 0.2) were also found between two confidence sub-scales and the constructivism scale. Interestingly, a weak positive correlation (r = 0.33) was also found between the constructivism scale and the static view of the nature of mathematics. The constructivism scale also had a moderate positive correlation (r = 0.39) with the teachers’ years of working experience.
The results show that nearly 20% of variance of mathematical competence comes from between-teacher variance (see Table 3). Teacher-level variance is lower for student agency. Nearly 13% of variance of students’ sense of environment as agency supportive comes from between-teacher variance. Regarding the two remaining student agency dimensions, the results show that nearly 6% of short- and long-term goals related to learning mathematics and 5% of competency beliefs comes from between-teacher variance.
The multilevel model fits the data well—the SRMR for the student level is 0.038, and for the teacher level 0.034, which is below the value 0.08 that is used as a criterion for a good fit (Table 4). As predicted, several of the student-level characteristics are significant in terms of mathematical competence. For example, one year of age adds nearly 17 points to the mathematics test (the average mathematics test score was 584, see Table 1); boys have nearly 52 points more in the mathematics test than girls; a one-point increase in general cognitive ability test (range 1–15) adds nearly 15 points to mathematics test; a one-step difference of SES (range 1–4) and home language (range 1–4) measures adds nearly 20 and 9 points to the mathematics test, respectively. Several of these characteristics are also important in terms of agency dimensions. Firstly, boys have nearly 0.4 points higher score of competency beliefs (range 1–5) than girls and a one-step difference of SES increases students’ competency beliefs nearly 0.1 points. Secondly, Estonian language spoken at home and at school (range 1–4) increases students’ perception of the learning environment as agency supportive by 0.06 points. Finally, students with a higher SES and better match between home and school language have higher scores of purposes related to mathematics, nearly 0.04 and 0.1, respectively.
The results also showed that none of the teacher-level characteristics was related to mathematical competence. However, several of these characteristics were related to students’ agency scores. First, a step higher estimation of teachers’ confidence related to goal setting added nearly 0.2 points for students’ competency beliefs. Second, a step higher estimation of teachers’ confidence related to goal setting and motivating students added nearly 0.2 points to students’ evaluation of the learning environment being agency supportive. Finally, a step higher estimation on the constructivism scale added 0.2 points to students’ score on purposes related to mathematics, while a step higher estimation on the mathematics as static scale decreased nearly 0.1 points for students’ purposes related to mathematics. These results show clearly that different teacher beliefs have influence on student agency dimensions.
Table 5 reports on the amount of variance at the between level (teacher level) that is explained by variables in our model. The results show that our model explains 65% variance of math competency. Regarding the agency dimensions, the lower amount of variance is shown, namely nearly 23% variance of students’ competency beliefs, 24% variance of students’ perception of environment as agency supporting, and 34% variance of purposes related to mathematics.
Discussion
Contrary to some previous studies (see, e.g. Perera & John, 2020), the results of the current study did not show a relationship between teacher beliefs and students’ mathematical competence. This is in accordance with the findings from the recent review by Lauermann and Hagen (2021) which concluded that although theoretically expected, empirical studies have often not been able to demonstrate the relationship between teacher self-efficacy and student achievement. It seems that the relationship between teacher self-efficacy and math achievements is a complex one since it depends on diverse processes that mediate it. Teacher self-beliefs could be related to student math competence shaping curriculum decisions, influencing teachers to opt for a specific teaching pedagogy and practices over others, providing a particular type of feedback to students, building and maintaining a certain relationship with students and parents, and preferring to guide and support student motivation and learning in a way that is aligned with teacher self-beliefs. Furthermore, the relationship between these characteristics of the teaching and learning process as well as relationships and development of math competence is also mediated by student characteristics. Thus, lack of consistency in findings might be taken as an indication for research studies to focus on processes and dynamics that could mediate the relationship between teacher self-beliefs and student learning achievements in math.
Several of the teacher beliefs were related to student agency dimensions in the current study. First, teachers’ confidence related to goal setting was positively related to the first dimension of agency: students’ competency beliefs. Both of these measures are related to competence beliefs, and previous research has also shown that teachers’ self-efficacy beliefs are positively related to their students’ self-efficacy beliefs in math education (see, e.g. Chang, 2015). An explanation for this specific finding could be that teachers who set up proper goals for students support their sense of competency. More specifically, it is possible that when a teacher sets up realistic goals in the zone of proximal development of students (Vygotsky, 1930–1934/1978), then students will progress better and the teacher would get a confirmation that their approach to goal setting is an appropriate one. Unexpectedly, this relationship was not visible for the other two domains of teachers’ self-efficacy: cognitive activation and motivating students. Further research is needed to understand the possible domain-related differences of these beliefs.
Second, as expected based on previous studies (Hettinger et al., 2023; Nieminen et al., 2022; Priestley et al., 2015; Zee & Koomen, 2016), teachers’ confidence in two areas—goal setting and motivating students—was positively related to the second dimension of agency: students’ evaluation of the learning environment as being agency supportive. This finding suggests that students perceive the learning environment as being most supportive when the learning goals are set up in an appropriate way and when they are motivated to get engaged in learning and meeting the learning goals. However, teachers’ confidence related to cognitive activation was not related to this agency dimension. This could be related to the items used in the current study to measure confidence in cognitive activation. These items were mostly related to supporting students’ critical thinking and challenging them in developing more complex and higher-order thinking skills. It is possible that these beliefs translated to the learning environment could be perceived as more teacher-led rather than student-led.
Third, as expected, teachers’ beliefs related to constructivism were positively related to the third dimension of student agency (students’ purposes related to mathematics), while teachers’ views of mathematics as static were negatively related to the student agency dimension, as also predicted by Voss et al. (2013). These findings suggest that when teachers create opportunities for students to explore math concepts and math items and to construct their knowledge, it seems to enable students to understand what the purpose of math is and how it might empower students in future learning and future life. On the other hand, when teachers require students to adopt knowledge in a way that is formulated by the teacher with no space for their own exploration, re-formulation, and appropriation, the students might engage in surface learning that limits their understanding of the purpose of learning math. Interestingly, teachers’ constructivism beliefs and views of mathematics as static were not related to the other two dimensions of student agency. Moreover, teachers’ views of mathematics as dynamic were not related to any dimensions of student agency. This could be explained by the fact that teachers’ beliefs regarding the nature of mathematics are not always consistent but rather dependent on context and situation (Lerman, 1983). Additionally, teacher beliefs might not automatically lead to the choice of concrete practices, which instead overlap, further confusing the relationship (Beswick, 2012). Thus, the relationship between teachers’ conceptualization of mathematics and their choice of practices, through which they can affect student agency, can be rather ambiguous, as also shown in previous studies (Andrews & Sayers, 2013; Lepik et al., 2012).
These results show that teacher confidence, which illuminates their self-efficacy in teaching, seems to be mostly related to the past and present on student learning, while views related to constructivism and the nature of learning seem to relate more to the future of learning. However, further research is needed to develop a more precise understanding of these dynamics. Teacher beliefs are indirectly related to student outcomes because teachers’ beliefs need to be enacted in practice, and this practice needs to be communicated to students and students need to translate these influences to their competence or agency, so we have a chain effect between teacher beliefs and student outcomes. Further studies are needed to investigate more closely how these beliefs, which we identified in the current study as relevant for developing student agency, are translated to teacher practices and how these practices influence positively or negatively student outcomes such as mathematical competence and agency.
Conclusion and limitations
Our study indicated several relationships between teacher beliefs and student agency. More specifically, we found that teachers’ self-efficacy related to goal setting was positively related to the first dimension of agency (students’ competency beliefs) and that teachers’ self-efficacy related to goal-setting and motivating students was positively related to students’ evaluation of the learning environment as being agency supportive (second dimension of agency). Furthermore, teachers’ beliefs related to constructivism were positively related and teachers’ views on mathematics as static were negatively related to the third dimension of student agency (students’ purposes related to mathematics). These findings contribute to knowledge related to the younger cohorts of students in primary education.
Although the findings of the study are valuable, some limitations need to be pointed out as well. As indicated above, the main limitation concerns the complexity of the relationship between teacher beliefs and students outcomes, such as math competence and student agency. This is related to the fact that teacher beliefs affect student agency in math learning indirectly. Teacher beliefs play an important role in teacher choice of teaching and learning approach. Depending on the way a teacher organizes math learning, students can have less or more space for exploring math concepts and procedures and to make their own decisions throughout learning. Moreover, teacher beliefs also affect the relationship between the teacher and students and between students in a class and also the classroom climate. Our findings indicate that teacher beliefs are a relevant factor for the development of student agency in math learning and, in this way, they indicate that future studies need to shed light on the mediation of this effect. Moreover, focusing on how classroom processes mediate the relationship between teacher beliefs and student outcomes would require a mixed method approach.
References
Anderson, R. C., Graham, M., Kennedy, P., Nelson, N., Stoolmiller, M., Baker, S. K., & Fien, H. (2019). Student agency at the crux: Mitigating disengagement in middle and high school. Contemporary Educational Psychology, 56, 205–217.
Andrews, P., & Sayers, J. (2013). Comparative studies of mathematics teaching: Does the means of analysis determine the outcome? ZDM Mathematics Education, 45(1), 133–144.
Archer, M. S. (2000). Being human: The problem of agency. Cambridge, UK: Cambridge University Press.
Ashton, P. T. (2015). Historical overview and theoretical perspectives of research on teachers’ beliefs. International Handbook of Research on Teachers’ Beliefs, 31, 47.
Bandura, A. (1997). Self-efficacy: The exercise of control. Freeman.
Berliner, D. C. (2001). Learning about and learning from expert teachers. International Journal of Educational Research, 35(5), 463–482.
Beswick, K. (2012). Teachers’ beliefs about school mathematics and mathematicians’ mathematics and their relationship to practice. Educational Studies in Mathematics, 79(1), 127–147.
Billett, S. (2008). Learning throughout working life: A relational interdependence between personal and social agency. British Journal of Educational Studies, 56(1), 39–58.
Brown, R. (2020). Re-conceptualizing the development of agency in the school mathematics classroom. Theory into Practice, 59(2), 139–149.
Buehl, M. M., & Beck, J. S. (2015). The relationship between teachers’ beliefs and teachers’ practices. International Handbook of Research on Teachers’ Beliefs, 1, 66–82.
Burton, L. (1993). The constructivist classroom. Perth: Mathematics, Science & Technology Centre, Edith Cowan University.
Chang, Y. L. (2015). Examining relationships among elementary mathematics teacher efficacy and their students’ mathematics self-efficacy and achievement. Eurasia Journal of Mathematics, Science and Technology Education, 11(6), 1307–1320.
Collins, A. M., Greeno, J. G., & Resnick, L. B. (2004). Educational learning theory. In N. J. Smelser & P. B. Baltes (Eds.), International encyclopedia of the social and behavioral sciences (Vol. 6, pp. 4276–4279). Elsevier.
Conway, P. F., & Clark, C. M. (2003). The journey inward and outward: A re-examination of Fuller’s concerns-based model of teacher development. Teaching and Teacher Education, 19(5), 465–482.
De Corte, E. (2010). Historical developments in the understanding of learning. In H. Dumont, D. Istance, & F. Benavides (Eds.), The Nature of Learning: Using Research to Inspire Practice. OECD Publishing, Paris. https://doi.org/10.1787/9789264086487-4-en
Devlin, K. (2021). Matemaatikat tuleks õpetada kui mõtteviisi, mitte kui arvutamist [Teaching mathematics as a way of thinking – not calculating]. Eesti Haridusteaduste Ajakiri. Estonian Journal of Education, 9(1), 6–32.
Eccles, J. S., & Wigfield, A. (2020). From expectancy-value theory to situated expectancy-value theory: A developmental, social cognitive, and sociocultural perspective on motivation. Contemporary Educational Psychology, 61, 101859.
Eccles, J., Wigfield, A., Harold, R. D., & Blumenfeld, P. (1993). Age and gender differences in children’s self-and task perceptions during elementary school. Child Development, 64(3), 830–847.
Else-Quest, N. M., Hyde, J. S., & Linn, M. C. (2010). Cross-national patterns of gender differences in mathematics: A meta-analysis. Psychological Bulletin, 136(1), 103–127.
Emirbayer, M., & Mische, A. (1998). What is agency? American Journal of Sociology, 103(4), 962–1023.
Ernest, P. (1989). The impact of beliefs on the teaching of mathematics. Mathematics Teaching: The State of the Art, 249, 254.
Erss, M. (2023). Comparing student agency in an ethnically and culturally segregated society: How Estonian and Russian speaking adolescents achieve Agency in School. Pedagogy, Culture & Society, 1–23. https://doi.org/10.1080/14681366.2023.2225529
Estonian Government. (2011/2014). National Curriculum for Basic Schools (Vol. 1). Riigi Teataja I. https://www.riigiteataja.ee/en/eli/524092014014/consolide. Accessed 24 Nov 2023
Eteläpelto, A., Vähäsantanen, K., Hökkä, P., & Paloniemi, S. (2013). What is agency? Conceptualizing professional agency at work. Educational Research Review, 10, 45–65.
Felbrich, A., Kaiser, G., & Schmotz, C. (2014). The cultural dimension of beliefs: An investigation of future primary teachers’ epistemological beliefs concerning the nature of mathematics in 15 countries. In S. Blömeke, F. J. Hsieh, G. Kaiser, & W. Schmidt (Eds.), International Perspectives on Teacher Knowledge, Beliefs and Opportunities to Learn. Advances in Mathematics Education. Springer, Dordrecht. https://doi.org/10.1007/978-94-007-6437-8_10
Filippetti, V. A., & Richaud, M. C. (2017). A structural equation modeling of executive functions, IQ and mathematical skills in primary students: Differential effects on number production, mental calculus and arithmetical problems. Child Neuropsychology, 23(7), 864–888.
Fives, H., & Buehl, M. M. (2012). Spring cleaning for the “messy” construct of teachers’ beliefs: What are they? Which have been examined? What can they tell us? In K. R. Harris, S. Graham, T. Urdan, S. Graham, J. M. Royer, & M. Zeidner (Eds.), APA educational psychology handbook, Vol. 2. Individual differences and cultural and contextual factors (pp. 471–499). American Psychological Association. https://doi.org/10.1037/13274-019
Freeman, S., Eddy, S. L., McDonough, M., Smith, M. K., Okoroafor, N., Jordt, H., & Wenderoth, M. P. (2014). Active learning increases student performance in science, engineering, and mathematics. Proceedings of the National Academy of Sciences, 111(23), 8410–8415.
Grigutsch, S., Raatz, U., & Törner, G. (1998). Einstellungen gegenüber Mathematik bei Mathematiklehrern. Journal Für Mathematik-Didaktik, 19(1), 3–45.
Gustafsson, J., Hansen, Y. K., & Rosen, M. (2013). Effects of home background on student achievement in reading, mathematics, and science at the fourth grade. In M. O. Martin & I. V. S. Mullis (Eds.), TIMSS and PIRLS 2011: Relationships Among Reading, Mathematics, and Science Achievement at the Fourth Grade—Implications for Early Learning (pp. 183–289). Chestnut Hill, MA: TIMSS & PIRLS International Study Center, Boston College.
Gutstein, E. (2007). “And that’s just how it starts”: Teaching mathematics and developing student agency. Teachers College Record, 109(2), 420–448.
Hansen, E. K. S. (2022). Students’ agency, creative reasoning, and collaboration in mathematical problem solving. Mathematics Education Research Journal, 34(4), 813–834.
Hettinger, K., Lazarides, R., & Schiefele, U. (2023). Motivational climate in mathematics classrooms Teacher self-efficacy for student engagement student-and teacher-reported emotional support and student interest. ZDM–Mathematics Education, 55(2), 413–426.
Hiebert, J., & Grouws, D. A. (2007). The effects of classroom mathematics teaching on students’ learning. Second Handbook of Research on Mathematics Teaching and Learning, 1(1), 371–404.
Hsu, H.-Y., Kwok, O., Lin, J. H., & Acosta, S. (2015). detecting misspecified multilevel structural equation models with common fit indices: A Monte Carlo study. Multivariate Behavioral Research, 50(2), 197–215.
Jääskelä, P., Heilala, V., Kärkkäinen, T., & Häkkinen, P. (2021). Student agency analytics: Learning analytics as a tool for analysing student agency in higher education. Behaviour & Information Technology, 40(8), 790–808.
Jacobs, J. E., Lanza, S., Osgood, D. W., Eccles, J. S., & Wigfield, A. (2002). Changes in children’s self-competence and values: Gender and domain differences across grades one through twelve. Child Development, 73(2), 509–527.
Johanson, M., Pedaste, M., Pastak, M., Täht, K., Sõrmus, M., & Jukk, H. (2021). Matemaatikapädevuse hindamine Eesti e-tasemetöödega [Assessment of mathematical competence using the Estonian national e-tests]. Eesti Haridusteaduste Ajakiri. Estonian Journal of Education, 9(2), 100–128.
Józsa, K., Amukune, S., Zentai, G., & Barrett, K. C. (2022). School readiness test and intelligence in preschool as predictors of middle school success: Result of an eight-year longitudinal study. Journal of Intelligence, 10(3), 66.
Kikas, E., Mädamürk, K., Hennok, L., Sigus, H., Talpsep, T., Luptova, O., & Kivi, V. (2022). Evaluating the efficacy of a teacher-guided comprehension-oriented learning strategy intervention among students in Grade 4. European Journal of Psychology of Education, 37, 509–530.
Klassen, R., & Chiu, M. M. (2011). The occupational commitment and intention to quit of practicing and pre-service teachers: Influence of self-efficacy, job stress, and teaching context. Contemporary Educational Psychology, 36, 114–129.
Lange, T. (2010). Tell them that we like to decide for ourselves: Children’s agency in mathematics education. In V. Durand-Guerrier, S. Soury-Lavergne, & F. Arzarello (Eds.), Proceedings of the Sixth congress of the European society for research in mathematics education (pp. 2587–2596). Lyon, France: European Society for Research in Mathematics Education.
Langener, A. M., Kramer, A.-W., van den Bos, W., & Huizenga, H. M. (2022). A shortened version of Raven’s standard progressive matrices for children and adolescents. British Journal of Developmental Psychology, 40(1), 35–45.
Laschke, C., & Blömeke, S. (2013). Teacher education and development study: Learning to teach mathematics (TEDS–M) - Dokumentation der Erhebungsinstrumente. Waxmann.
Lauermann, F., & Berger, J. L. (2021). Linking teacher self-efficacy and responsibility with teachers’ self-reported and student-reported motivating styles and student engagement. Learning and Instruction, 76, 101441.
Lauermann, F., & ten Hagen, I. (2021). Do teachers’ perceived teaching competence and self-efficacy affect students’ academic outcomes? A closer look at student-reported classroom processes and outcomes. Educational Psychologist, 56(4), 265–282.
Lauermann, F., Eccles, J. S., & Pekrun, R. (2017). Why do children worry about their academic achievement? An expectancy-value perspective on elementary students’ worries about their mathematics and reading performance. ZDM Mathematics Education, 49, 339–354.
Leijen, Ä., Pedaste, M., & Lepp, L. (2020). Teacher agency following the ecological model: How it is achieved and how it could be strengthened by different types of reflection. British Journal of Educational Studies, 68(3), 295–310.
Leijen, Ä., & Pedaste, M. (2018). Pedagogical beliefs, instructional practices, and opportunities for professional development of teachers in Estonia. In H. Niemi, A. Toom, A. Kallioniemi, & J. Lavonen (Eds.), The teacher’s role in the changing globalizing world (pp. 33–46). Brill.
Leijen, Ä., Pedaste, M., & Baucal, A. (2022). Assessing student teachers’ agency and using it for predicting commitment to teaching. European Journal of Teacher Education, 45(5), 600–616. https://doi.org/10.1080/02619768.2021.1889507
Lepik, M., Pipere, A., & Hannula, M. S. (2012). Comparing mathematics teachers’ beliefs about good teaching: The cases of Estonia, Latvia and Finland. Nordic Studies in Mathematics Education, 17(3–4), 177–198.
Lerman, S. (1983). Problem-solving or knowledge-centred: The influence of philosophy on mathematics teaching. International Journal of Mathematical Education in Science and Technology, 14(1), 59–66.
Li, W., & Konstantopoulos, S. (2017). Does class-size reduction close the achievement gap? Evidence from TIMSS 2011. School Effectiveness and School Improvement, 28(2), 292–313.
Ling, L. Y. (2003). What makes a good kindergarten teacher? A pilot interview study in Hong Kong.
Lipponen, L., & Kumpulainen, K. (2011). Acting as accountable authors: Creating interactional spaces for agency work in teacher education. Teaching and Teacher Education, 27(5), 812–819.
Mädamürk, K., Kikas, E., & Palu, A. (2018). Calculation and word problem-solving skill profiles: Relationship to previous skills and interest. Educational psychology, 38(10), 1239–1254.
Muis, K. R., & Foy, M. J. (2010). The effects of teachers’ beliefs on elementary students’ beliefs, motivation, and achievement in mathematics. In L. D. Bendixen & F. C. Feucht (Eds.), Personal epistemology in the classroom: Theory, research, and implications for practice (pp. 435–469). Cambridge University Press.
Mullis, I. V., Martin, M. O., Foy, P., & Arora, A. (2012). TIMSS 2011 international results in mathematics. TIMSS & PIRLS International Study Center. Boston College.
Nandrup, A. B. (2016). Do class size effects differ across grades? Education Economics, 24(1), 83–95.
Niemi, R., Kumpulainen, K., Lipponen, L., & Hilppö, J. (2015). Pupils’ perspectives on the lived pedagogy of the classroom. Education 3-13, 43(6), 683–699.
Nieminen, J. H., Chan, M. C. E., & Clarke, D. (2022). What affordances do open-ended real-life tasks offer for sharing student agency in collaborative problem-solving? Educational Studies in Mathematics, 109(1), 115–136.
Norén, E. (2015). Agency and positioning in a multilingual mathematics classroom. Educational Studies in Mathematics, 89, 167–184.
Nurlu, Ö. (2015). Investigation of teachers’ mathematics teaching self-efficacy. International Electronic Journal of Elementary Education, 8(1), 21–40.
OECD. (2018). PISA for development assessment and analytical framework: Reading, mathematics and science. PISA, OECD Publishing, Paris,. https://doi.org/10.1787/9789264305274-en
OECD (2019). Learning Compass 2030. https://www.oecd.org/education/2030-project/teaching-and-learning/learning/learning-compass-2030/. Accessed 24 Nov 2023
OECD (2022). PISA 2022 mathematics framework. https://pisa2022-maths.oecd.org/ca/index.html. Accessed 24 Nov 2023
Op’t Eynde, P., De Corte, E., & Verschaffel, L. (2002). Framing students’ mathematics-related beliefs. In G. C. Leder, E. Pehkonen, & G. Törner (Eds.), Beliefs: A Hidden Variable in Mathematics Education?. Mathematics Education Library, vol 31. Springer, Dordrecht, pp. 13–37. https://doi.org/10.1007/0-306-47958-3_2
Pajares, M. F. (1992). Teachers’ beliefs and educational research: Cleaning up a messy construct. Review of Educational Research, 62(3), 307–332.
Pedaste, M., Uibu, K., Rannikmäe, M., & Tagamets, E. (2019). Kuidas toetada tasemetöödega aineõppes üldiste oskuste kujunemist. [How to support the general competencies in subject teaching with national-level tests.]. Riigikogu Toimetised, 40, 125134.
Pedaste, M., Leijen, Ä., Poom-Valickis, K., & Eisenschmidt, E. (2019b). Teacher professional standards to support teacher quality and learning in Estonia. European Journal of Education, 54(3), 389–399.
Perera, H. N., & John, J. E. (2020). Teachers’ self-efficacy beliefs for teaching math: Relations with teacher and student outcomes. Contemporary Educational Psychology, 61, 101842.
Peterson, P. L., Fennema, E., Carpenter, T. P., & Loef, M. (1989). Teacher’s pedagogical content beliefs in mathematics. Cognition and instruction, 6(1), 1–40.
Priestley, M., Biesta, G. J. J., & Robinson, S. (2015). Teacher agency: An ecological approach. Bloomsbury Academic.
Richards, J. C., & Gipe, J. P. (1994). Metaphor analysis: An alternative approach for identifying preservice teachers’ orientations. Research in the Schools, 1(2), 53–60.
Richardson, V. (1996). The role of attitudes and beliefs in learning to teach. Handbook of Research on Teacher Education, 2(102–119), 273–290.
Ross, J. A. (1992). Teacher efficacy and the effects of coaching on student achievement. Canadian Journal of Education/Revue canadienne de l’education, 17(1), 51–65.
Ruohotie-Lyhty, M., & Moate, J. (2015). Proactive and reactive dimensions of life-course agency: Mapping student teachers’ language learning experiences. Language and Education, 29(1), 46–61.
Seidel, T., & Shavelson, R. J. (2007). Teaching effectiveness research in the past decade: The role of theory and research design in disentangling meta-analysis results. Review of Educational Research, 77(4), 454–499.
Täht, K., Konstabel, K., Kask, K., Rannikmäe, M., Rozgonjuk, D., Schults, A., Soobard, R., Tõugu, P. & Vaino, K. (2018). Eesti Ja Vene Õppekeelega Koolide 15-Aastaste Õpilaste Teadmiste Ja Oskuste Erinevuse Põhjuste analüüs. Tartu Ülikool. [Analysis of the Reasons for the Gap in the Knowledge and Skills of 15-Year Old Students in Estonian and Russophone Schools. University of Tartu]. https://www.hm.ee/sites/default/files/uuringud/pisa_ev_raport_0507_006.pdf. Accessed 24 Nov 2023
Tatto, M. T., & Smith, W. M. (2018). Introduction: Exploring different dimensions of teacher education programs in the TEDS-M study. In M. Tatto, M. Rodriguez, W. Smith, M. Reckase, & K. Bankov (Eds.), Exploring the Mathematical Education of Teachers Using TEDS-M Data. Cham: Springer.
Thoonen, E. E., Sleegers, P. J., Peetsma, T. T., & Oort, F. J. (2011). Can teachers motivate students to learn? Educational Studies, 37(3), 345–360.
Tire, G. (2021). Estonia: A positive PISA experience. In N. Crato (Ed.), Improving a Country’s Education: PISA 2018 Results in 10 Countries (pp. 101–120). Springer.
Törner, G., & Grigutsch, S. (1994). Mathematische Weltbilder” bei Studienanfängern—eine Erhebung. Journal Für Mathematik-Didaktik, 15, 211–251.
Tschannen-Moran, M., & Hoy, A. W. (2001). Teacher efficacy: Capturing an elusive construct. Teaching and Teacher Education, 17(7), 783–805.
Uibu, K., & Kikas, E. (2014). Authoritative and authoritarian-inconsistent teachers’ preferences for teaching methods and instructional goals. Education 3–13: International Journal of Primary, Elementary and Early Years Education, 42(1), 5–22.
Uibu, K., Salo, A., Ugaste, A., & Rasku-Puttonen, H. (2023). Observed teaching practices interpreted from the perspective of school-based teacher educators. European Journal of Teacher Education, 46(2), 203–221.
Vaughn, M. (2020). What is student agency and why is it needed now more than ever? Theory into Practice, 59(2), 109–118.
Voss, T., Kleickmann, T., Kunter, M., & Hachfeld, A. (2013). Mathematics teachers’ beliefs. In M. Kunter, J. Baumert, W. Blum, U. Klusmann, S. Krauss, & M. Neubrand (Eds.), Cognitive activation in the mathematics classroom and professional competence of teachers – results from the COACTIV project (pp. 249–271). Springer, New York.
Vygotsky, L. S. (1978). Mind in society: Development of Higher Psychological Processes. In M. Cole, V. Jolm-Steiner, S. Scribner, & E. Souberman (Eds.). Harvard University Press. https://doi.org/10.2307/j.ctvjf9vz4
Wakhata, R., Mutarutinya, V., & Balimuttajjo, S. (2023). Relationship between active learning heuristic problem-solving approach and students’ attitude towards mathematics. Eurasia Journal of Mathematics, Science and Technology Education, 19(2), em2231.
Weidinger, A. F., Steinmayr, R., & Spinath, B. (2018). Changes in the relation between competence beliefs and achievement in math across elementary school years. Child Development, 89(2), 138–156.
Woolfolk Hoy, A., Davis, H., & Pape, S. J. (2006). Teacher knowledge and beliefs. In P. H. Winne & P. A. Alexander (Eds.), Handbook of educational psychology (pp. 715–737). Lawrence Erlbaum Associates Publishers.
Yang, X., & Leung, F. K. (2015). The relationships among pre-service mathematics teachers’ beliefs about mathematics, mathematics teaching, and use of technology in China. Eurasia Journal of Mathematics, Science and Technology Education, 11(6), 1363–1378.
Zee, M., & Koomen, H. M. Y. (2016). Teacher self-efficacy and its effects on classroom processes, student academic adjustment, and teacher well-being: A synthesis of 40 years of research. Review of Educational Research, 86(4), 981–1015.
Funding
This study was part of the project co-constructing mathematics motivation in primary education—a longitudinal study in six European countries (MATHMot) that has received funding from the Research Council of Norway within FINNUT Programme for Research and Innovation in the Educational Sector (grant number 301033).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Ä. Leijen.
Current Themes of Research: Teacher education, teacher support to student learning, inclusive education, self-regulated learning.
Relevant Publications:.
Leijen, Ä., Malva, L., Pedaste, M., & Mikser, R. (2022). What constitutes teachers’ general pedagogical knowledge and how it can be assessed: A literature review. Teachers and Teaching, 28(2), 206-225.
Leijen, A., Arcidiacono, F. & Baucal, A. (2021). The dilemma of inclusive education: ‘inclusion for some’ or ‘inclusion for all’". Frontiers in Psychology, 12: 633066.
Edisherashvili, N., Saks, K., Pedaste, M., & Leijen, Ä. (2022). Supporting self-regulated learning in distance learning contexts at higher education level: systematic literature review. Frontiers in Psychology, 12, 6132.
A. Baucal:.
Current Themes of Research: Student learning and achievements, teacher support to student learning, inclusive education.
Relevant Publications:.
Zittoun, T. & Baucal, A. (2021). The relevance of a sociocultural perspective for understanding learning and development in older age. Learning, Culture and Social Interaction, 28.
Pedaste, M., Baucal, A. & Reisenbuk, E. (2021). Towards a science inquiry test in primary education: development of items and scales. International Journal of STEM Education 8.
Radišić, J., Selleri, P., Carugati, F. & Baucal, A. (2021). Are students in Italy really disinterested in science? A person‐centered approach using the PISA 2015 data. Science Education, 105(2), 438-468.
K. Pikk.
Current Themes of Research: Teacher education, teacher support to student learning, student learning and achievements .
Relevant Publications: No previous publications.
K. Uibu.
Current Themes of Research: Teacher education, effect of teaching strategies on student learning, student text comprehension.
Relevant Publications: .
Uibu, K., Salo, A., Ugaste, A., & Rasku-Puttonen, H. (2021). Observed teaching practices interpreted from the perspective of school-based teacher educators. European Journal of Teacher Education, 1-19.
Kärbla, T., Uibu, K., & Männamaa, M. (2021). Teaching strategies to improve students’ vocabulary and text comprehension. European Journal of Psychology of Education, 36, 553-572.
Käsper, M., Uibu, K., & Mikk, J. (2020). The effects of teaching strategies on primary school students' reading outcomes and interest in reading. L1-Educational Studies in Language and Literature, 20, 1-24.
L. Pajula.
Current Themes of Research: sustainability education, teacher education, sustainability in higher education.
Relevant Publications: No previous publications.
M. Sõrmus.
Current Themes of Research: motivation to learn mathematics in primary school, mathematics education.
Relevant Publication:.
Peixoto, F., Radišić, J., Krstic, K., Hansen, K., Laine, A., Baucal, A., Sõrmus, M., & Mata, L. (2022). Contribution to the Validation of the Expectancy-Value Scale for Primary School Students. Journal of Psychoeducational Assessment.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Leijen, Ä., Baucal, A., Pikk, K. et al. Opportunities to develop student’s math-related agency in primary education: the role of teacher beliefs. Eur J Psychol Educ 39, 1637–1659 (2024). https://doi.org/10.1007/s10212-023-00771-9
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10212-023-00771-9