Abstract
This paper discusses the delay dynamics of monopoly with discrete timescales. It is assumed that a monopoly has delayed and limited information on demand. It is also assumed that the firm wants to react to an average of past data instead of reacting to sudden market changes and this average is used to determine the marginal profit. In the case of one-step delay, the output of the previous time period is selected. In the cases of two and three delays where data at one, two, and three previous time periods are available, it is shown that the steady state undergoes to complex dynamics through either a period-doubling or a Neimark–Sacker bifurcation, depending on the specified values of the parameters. Numerical examples illustrate the theoretical results. Finally, the case of geometric delay is also analyzed to show the birth of the period-doubling bifurcation.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
Notes
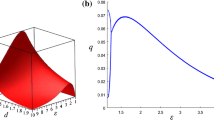
Using a variable change, \(x(t)=q(t)/\bar{q}\) with \(\bar{q}=(1+a\alpha )/[2\alpha (b+c)],\) we can transform Eq. (3) to the logistic map \( x(t+1)=(1+a\alpha )x(t)[1-x(t)]\) where \(x(t)\ge 0\) for any \(x(0)\ge 0\) if \(1+a\alpha \le 4\) or \(a\alpha \le 3\).
Although the existence of an Neimark–Sacker bifurcation in two-dimensional system is proved, a generalization to \(n\)-dimensional system does not exist \( (n\ge 3)\) (see Lorenz 1993). In spite of this, we call the locus of \( \varphi (\omega _{0}, \omega _{1}, a\alpha )=0\) a NS boundary even in three-dimensional system since numerical examinations yield the occurence of such a bifurcation on the boundary.
By definition of \(a\alpha _{(+)},\)
$$\begin{aligned} 2-a\alpha _{(+)}=\frac{1}{2A}\left\{ 4A-\sqrt{D}+(1-\omega _{0})\right\} . \end{aligned}$$By (16) and (19), we have \(4A=D-(1-\omega _{0})^{2}\) which is substituted into the expression in the parentheses to obtain
$$\begin{aligned} \left\{ \sqrt{D}-(1-\omega _{0})\right\} \left\{ \sqrt{D}-\omega _{0}\right\} >0 \end{aligned}$$where the inequality is due to \(\sqrt{D}>(1-\omega _{0})\) and \(1-\omega _{0}>\omega _{0}\) if \(\omega _{0}<1/2.\)
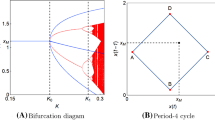
\(a\alpha _{M}\) is not depicted in Fig. 4 as it is larger than the upper bound of the figure.
Fig. 5 
Dynamics for \(0<\omega _{1}\le 1/4\)
To make Fig. 6a simpler, we do not label \(\omega _{0}^{(-)}\) and \( \omega _{0}^{(+)}\) on the horizontal line. These are the abscissas of the red points while \(\omega _{0}^{a}\) and \(\omega _{0}^{b}\) are the abscissas of the blue points.
Fig. 6 
Dynamics for \(1/4<\omega _{1}\le 1/3\)
Even in the case of \(\omega _{1}<5/16,\) the partition curve has essentially the same shape.
References
Agiza, H.N., Hegazi, A.S., Elsadany, A.A.: The dynamics of Bowley’s model with bounded rationality. Chaos Solitons Fractals 12, 1705–1717 (2001)
Bellman, R., Cooke, K.L.: Differential-Difference Equations. Academic Press, New York (1956)
Bischi, G.-I., Chiarella, C., Kopel, M., Szidarovszky, F.: Nonlinear Oligopolies: Stability and Bifurcations. Springer, Berlin (2010)
Cushing, J.: Integro-differential Equations and Delay Models in Population Dynamics. Springer, Berlin (1977)
Farebother, R.W.: Simplified Samuelson condition for cubic and quartic equations. Manchester School 41, 396–400 (1973)
Lorenz, H.-W.: Nonlinear Dynamical Economics and Chaotic Motion, Second, Revised and Enlarged Edition. Springer, Berlin/HeidelBerg/New York (1993)
Martelli, M.: Introduction to Discrete Dynamical Systems and Chaos. Wiley-Interscience, New York (1999)
Matsumoto, A., Szidarovszky, F.: Nonlinear delay monopoly with bounded rationality. Chaos Solitions Fractals 45, 507–519 (2012a)
Matsumoto, A., Szidarovszky, F.: Boundedly Rational Monopoly with Continuously Distributed Single Time Delays. IERCU discussion paper #180. http://www.chuo-u.ac.jp/chuo-u/ins_economics/pdf/f06_03_03_04/discussno180.pdf (2012b)
Okuguchi, K., Irie, K.: The Schur and Samuelson conditions for a cubic equation. Manch. Sch. 58, 414–418 (1990)
Okuguchi, K., Szidarovszky, F.: The Theory of Oligopoly with Multi-Product Firms. Springer, Berlin (1990)
Sun, Z.: Effect of delay on stability of monopoly system with delayed bounded rationality. Chin. J. Phys. 49, 1060–1070 (2011)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Matsumoto, A., Szidarovszky, F. Discrete-time delay dynamics of boundedly rational monopoly. Decisions Econ Finan 37, 53–79 (2014). https://doi.org/10.1007/s10203-013-0141-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10203-013-0141-2
Keywords
- Bounded rationality
- Delay with discrete timescales
- Gradient dynamics
- Hopf bifurcation
- Neimark–Sacker bifurcation