Analysis of the Cochlear Amplifier Fluid Pump Hypothesis

Abstract

We use analysis of a realistic three-dimensional finite-element model of the tunnel of Corti (ToC) in the middle turn of the gerbil cochlea tuned to the characteristic frequency (CF) of 4 kHz to show that the anatomical structure of the organ of Corti (OC) is consistent with the hypothesis that the cochlear amplifier functions as a fluid pump. The experimental evidence for the fluid pump is that outer hair cell (OHC) contraction and expansion induce oscillatory flow in the ToC. We show that this oscillatory flow can produce a fluid wave traveling in the ToC and that the outer pillar cells (OPC) do not present a significant barrier to fluid flow into the ToC. The wavelength of the resulting fluid wave launched into the tunnel at the CF is 1.5 mm, which is somewhat longer than the wavelength estimated for the classical traveling wave. This fluid wave propagates at least one wavelength before being significantly attenuated. We also investigated the effect of OPC spacing on fluid flow into the ToC and found that, for physiologically relevant spacing between the OPCs, the impedance estimate is similar to that of the underlying basilar membrane. We conclude that the row of OPCs does not significantly impede fluid exchange between ToC and the space between the row of OPC and the first row of OHC–Dieter’s cells complex, and hence does not lead to excessive power loss. The BM displacement resulting from the fluid pumped into the ToC is significant for motion amplification. Our results support the hypothesis that there is an additional source of longitudinal coupling, provided by the ToC, as required in many non-classical models of the cochlear amplifier.

Introduction

There is evidence that the cochlear traveling wave discovered by von Békésy (1949) in his experimental work on cadaver cochleae is amplified as it propagates to its resonant point in the living cochleae. Calculations based on data from sensitive cochleae suggest that the traveling wave-induced basilar membrane (BM) vibrations are indeed biologically amplified (Brass and Kemp 1993; Diependaal et al. 1987). This amplification process is termed the cochlear amplifier (CA), which is believed to enhance hearing for low sound levels. The cellular basis of the CA is believed to be found in outer hair cell (OHC) somatic electromotility, the electrically induced longitudinal deformation of the OHC (Brownell 1985). Despite efforts to explain how the CA works, it is still not well understood.

Some cochlear models have attempted to account for the CA by means of longitudinal coupling mechanisms. In classical cochlear models, the only means of longitudinal coupling is via the scalae fluids. These classical models can replicate some of the experimental data but do not capture all the unique features of the cochlear response. Several non-classical models have been introduced that include multiple modes of longitudinal coupling. In one approach, it is hypothesized that a longitudinal tilt of the OHCs provides additional longitudinal coupling. When this coupling is incorporated into cochlear models, enhanced amplification takes place (Geisler and Sang 1995; Steele 1999).

Hubbard (1993), in his traveling wave amplifier model, showed that two wave modes can add their energies to create amplification such as that desired in the CA. The tunnel of Corti (ToC) was later used to represent the second wave mode for the proposed traveling wave amplifier model, and was incorporated in a multicompartmental hydromechanical model of the cochlea, which successfully replicated BM motion (Hubbard et al. 2000). This result led to the hypothesis that the CA can function as a fluid pump (Hubbard et al. 2003). However, this hypothesis must comply with the anatomical structure of the organ of Corti (OC). Indeed, the fluid must pass between the outer pillar cells (OPCs) before reaching the ToC, and the ToC fluid and the underlying basilar membrane arcuate zone (BM-AZ) must constitute an appropriate waveguide.

Here, a finite-element (FE) model of the ToC is developed to investigate these questions: whether the ToC can support traveling wave in response to fluid pumped into the ToC by the active OHC and whether the spaces between the OPCs will cause excessive power loss when fluid is forced into the ToC by the OHCs. The region along the cochlea tuned to the characteristic frequency (CF) of 4 kHz is modeled, and the simulation frequency f is chosen to be equal to the CF.

Methods

A simple model of the OC: the ToC

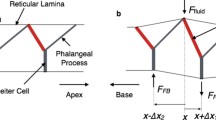
In order to characterize the ToC response to the OHC electromotility, the fluid around the OHCs is assumed to be forced between the OPCs and into the ToC. Therefore, a small region of the OC (see Fig. 1) comprising the ToC and the first row of OHC–Dieter’s cells complex (OPC–OHC1 space) is studied in this simplified FE model, and the scalae tympani (ST) is not included in the model unless otherwise specified. The method for specifying the geometry, the material properties, and the input of the model is described below.

Fig. 1

An actual gerbil cochlea cross-section obtained from histological sectioning showing the modeled region of the OC, the delimited trapezoidal region. The arrows point to the OHC1, to the OPC, and to BM-AZ, respectively. The OPC row separates the ToC and the OPC–OHC1 space.

Tunnel structure dimensions

The dimensions of the cellular structures in the OC were measured from stacks of digital images obtained from experiments on excised cochleae (Karavitaki and Mountain 2007b). The measurements relied on a priori known diameter of the gerbil OHC. The diameter is estimated to be 8 μm (Edge et al. 1998; Karavitaki 2002). Using the available free software ImageJ to visualize and measure distances gave an OHC measurement of ~35 pixels in diameter. Thus, the resolution used for all subsequent image measurements was 231 nm/pixel.

The height (H _ToC) and width (W _ToC) of the ToC in the middle turn of the cochlea, more precisely at the location corresponding to CF = 4 kHz, are approximately 64 and 50 μm, respectively. The angle between the long axis of the OHC and the reticular lamina (RL) as measured in Karavitaki and Mountain (2007b) is θ _r = 71^o. Based on these available dimensions, the remaining dimensions of the arch of Corti are determined as follows. In the middle turn the RL is almost parallel to the BM, therefore θ _r is also the angle between the long axis of an OHC and the BM. Assuming that the OPCs are parallel to the OHCs, if the arch of Corti is considered as an isosceles triangle, its base angle is given by

$$ \alpha = {\tan^{{ - 1}}}\left\{ {\frac{{2{H_{\text{ToC}}}}}{{{W_{\text{ToC}}}}}} \right\} \approx 69^\circ {.} $$

This value of α is almost equal to the measured value of θ _r and shows that the arch of Corti is indeed an isosceles triangle under the reasonable assumptions on the angles of the BM and the OPCs. The ToC is thus modeled as an isosceles triangle with base angle α ≈ 69^o.

The model dimensions associated with this location characterized by CF = 4 kHz are summarized in Table 1.

TABLE 1 Dimensions of the isosceles ToC model (base angle α = 69^o)

Model simplifications and assumptions

The model assumptions are based on experimental observations and some common simplifications made in cochlea models. The dimensions were obtained as explained in the previous paragraph, and the simplified ToC geometry is shown in Figure 2.

FIG. 2

Portion of the ToC Model showing the tunnel, a number of OPCs, the OPC–OHC1 space and the underlying BM. The input wall represents the OHC1. The complex formed by the phalangeal cells, the row of IPCs and the row of IHCs and the heads of the pillar cells are modeled as fixed walls.

• The OPCs are modeled as a row of regularly spaced rigid cylinders parallel to the side of the ToC and to the OHCs.

• In this model of the ToC, the deformation of the OHCs is not of direct interest; therefore, the OHCs are not physically represented. Only the first row of OHCs (OHC1) was modeled to represent the effect of OHC motility. OHC1 was represented as a rigid wall moving fluid in and out of the tunnel as inferred from the observed motions in the hemicochlea experiment (Karavitaki and Mountain 2007b). This experiment consisted in electrically exciting the OHCs through the cochlear fluids and measuring their motion. In response to the electrical current, each OHC in the first row appeared to be tightly constrained by its neighbors. The OHC1 thus formed an impervious wall, which was observed to move in phase in and out in the radial direction while oscillatory fluid movements could be seen in the ToC. In the modeled region of the cochlea, the OHC1 is assumed to respond in direct proportion to the magnitude of the local current density, and its measured displacement is used to drive the model.

• A straight ToC with a uniform triangular cross-section is modeled assuming that the wavelength is small compared to the radius of curvature of the spiraled cochlea, and also small compared to the longitudinal distance over which geometrical variations are significant. This is a valid assumption for more basal locations on the cochlea, which however breaks down toward the apex where the radius of curvature is on the order of the wavelength. Manoussaki et al. (2006), in their study of the effect of the coiling of the cochlea, have indeed found that the tectorial membrane (TM)–RL shear gain from BM deflection is higher than the uncoiled cochlea and also that the wave gets tilted toward the cochlear wall in the apical region.

• On the inner hair cell side of the ToC, the phalangeal supporting cells, the inner pillar cells and the IHCs are assumed to be bound together such that no flow through the complex would occur. Furthermore, due to the presence of the rigid IPCs, the complex is modeled as a rigid wall. The heads of the pillar cells form a rigid surface modeled as a fixed wall.

• Both ends of the tunnel model are open as was the case in the in vitro excised cochlea middle turn experiment that is being simulated.

• The underlying BM-AZ, supporting the ToC, is modeled as an isotropic elastic layer clamped along its long edges. The BM is known to be orthotropic due to the radial arrangement of collagen fibers in the membrane. This property is however less pronounced in the middle and apical turns than in the basal turn of the gerbil cochlea. It is even less pronounced in the BM-AZ where, in addition to the decrease in fibers density, the radially grouped bundle structure seen in the BM pectinate zone (BM-PZ) is lost. It is therefore reasonable to treat the BM-AZ as an isotropic elastic layer.

Solution method

The fluid surrounding the OHCs, when pushed between the pillars, interacts with the BM-AZ to produce fluid flow along the tunnel. The resulting fluid–structure interaction problem is governed by the equations below.

The fluid in the ToC satisfies the viscous incompressible fluid equations:

$$ \rho _{f} {\mathop {\text{v}}\limits^ \cdot } = \nabla \cdot \underline{\underline \sigma } ^{f} $$

(1)

Where ∇ is the gradient operator, ρ _f the fluid density, $\dot{v}$ the time derivative of the fluid velocity v, and the relation between the fluid stress and the strain rate tensors ${\underline{\underline \sigma }^f}\left( {{{\underline{\underline {\text{e}}} }^f}} \right)$ defined as

$$ {\underline{\underline \sigma }^f} = - P\underline{\underline {\text{\bf{I}}}} + 2{\mu_f}{\underline{\underline {\text{e}}}^f};\quad {\underline{\underline {\text{e}}}^f} = \frac{1}{2}\left( {\nabla {{\text{v}}^T} + \nabla {\text{v}}} \right). $$

(2)

In Eq. 2, P is the pressure in the fluid, μ _f the dynamic viscosity coefficient, and $\underline{\underline {\text{\bf{I}}}}$ the identity tensor.

The BM-AZ, modeled as an isotropic linear elastic solid, satisfies the equation:

$$ {\rho_s}\ddot{\bf{u}} = \nabla \cdot {\underline{\underline \sigma }^s} $$

(3)

Where ρ _s is the solid density, and ${\underline{\underline \sigma }^s} = {\underline{\underline \sigma }^s}\left( {{{\underline{\underline {\text{\bf{e}}}} }^s}} \right)$ is the stress–strain relation defined as:

$$ {\underline{\underline \sigma }^s} = \lambda \left( {\nabla \cdot {\text{\bf{u}}}} \right)\underline{\underline {\text{\bf{I}}}} + 2\mu {\underline{\underline {\text{\bf{e}}}}^s};\quad {\underline{\underline {\text{\bf{e}}}}^s} = \frac{1}{2}\left( {\nabla {{\text{\bf{u}}}^T} + \nabla {\text{\bf{u}}}} \right). $$

(4)

Here λ and μ are the Lamé constants, which are related to the Young’s modulus E and the Poisson’s ratio ν of the isotropic solid, and u is the displacement vector in the solid.

The boundary conditions are as follows.

• The kinematic and dynamic conditions at the fluid–solid interface are:

  $$ \begin{array}{*{20}l} {{{\text{v}} = {\mathop {\text{u}}\limits^ \cdot }} \hfill} \\ {{\underline{\underline \sigma } ^{s} \cdot {\text{n}} = \underline{\underline \sigma } ^{f} \cdot {\text{n}}} \hfill} \\ \end{array} $$

  (5)

  where n is the unit vector normal to the fluid–solid interface.

• The no-slip condition at the fluid walls is

  $$ {\bf{v}} = 0. $$

  (6)

• The boundary condition along the clamped edges of the elastic solid is

  $$ {\mathbf{\bf{u}}} = 0. $$

  (7)

• The open tunnel end condition is

  $$ P = 0. $$

  (8)

• At the input wall (shown in Figs. 1 and 2), the OHC1 velocity distribution, obtained from the OHC displacement measurements (D) and described in the appendix, is specified:

  $$\bf v = {\mathbf{\dot{D}}}{.} $$

  (9)

The OPCs impedance ($Z$) to flow can be expressed as:

$$ \frac{{{P_2} - {P_1}}}{{{V_n}}} = Z, $$

(10)

where P ₁ is the input pressure at the OHCs (first row); P ₂, the pressure in the ToC (past the OPCs) and V _n the fluid velocity normal to the OPCs.

The solution was obtained numerically with Automated Dynamical Incremental Nonlinear Analysis (ADINA), a commercial package (Bathe 2003), run on a shared memory computer node with eight 3 GHz Intel processors on a Linux cluster. ADINA provides strong capabilities and flexibility in structural, flow and fluid–structure interaction analysis based on the FE method. Using ADINA, the OPCs were modeled as rigid cylinders as mentioned in the model simplifications, and the no-slip condition was applied on the cylinders surfaces. In a typical simulation model, the FE model was ~0.7 mm long, representing 150 OPCs. The fluid region was discretized using approximately 500,000 tetrahedral finite elements of various sizes throughout the fluid. The BM-AZ was modeled with elastic solid elements. At least 12 solid elements were used across the thickness of the BM-AZ. The fluid and the structure elements were fully coupled. The BM-AZ mass density was assumed to be the same as that of the perilymphatic fluid on both sides of the BM-AZ, i.e., ρ _s = ρ _f = ρ. The latter fluid is assumed to have the same properties as water with ρ = 1,000 kg/m³ and μ _f  = 1.2 × 10⁻³ Pa s, respectively.

Estimating BM elastic properties

The material properties of the internal structures of the OC are difficult to determine because the inside of the OC is not easily accessible. However, relatively easy access to the RL and BM is possible. Point stiffness measurements on the BM were performed by Naidu and Mountain (1996) for the gerbil cochlea. In their experiment, the BM was deflected in 1 μm increments up to a maximal deflection of 15 μm using a force probe with a 10-μm-tip diameter. The deflection and the measured applied force were used to calculate stiffness as a function of deflection. The curve exhibited two plateaus followed by a quadratic increase in stiffness; the highest plateau was taken as the physiologically relevant stiffness. The experiment was carried out at multiple locations in the OC radial and longitudinal directions and revealed multiple stiffness gradients across the OC. Fitted to an exponential function, the point stiffness data are summarized as:

$$ k_p^{\text{Naidu}}(x) = {k_0}{e^{{cx}}} $$

(11)

where x is the location in mm from the base along the gerbil cochlea, c is a negative real number representing a stiffness gradient factor and k ₀ is a constant with units of newtons per meter. Both c and k ₀ depend on the radial position across the OC. For the position modeled, c = −0.23 mm⁻¹.

These experimental data are used here with the FE model of the BM-AZ to determine the Young’s modulus of the BM-AZ model at the location of interest.

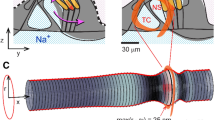
Naidu’s experiment is reproduced by performing a linear static deflection of the elastic solid model of fixed dimensions matching the arcuate zone at the location of interest. The FE experiment is shown in Figure 3a. For a fixed Poisson’s ratio, ν = 0.3, an initial value of Young’s modulus E ₁ is set. A localized uniform pressure over an area of the elastic solid, exactly the same as that of the experimental probe tip, is applied. The ratio of the applied force to the maximum deflection corresponds to the point stiffness k _p1. The Young’s modulus is then adjusted to the value

$$ {E_2} = {E_1} \times \frac{{k_p^{\text{Naidu}}}}{{{k_{{p1}}}}} $$

(12)

that yields the same value as Naidu’s point stiffness, $k_p^{\text{Naidu}} = 0.62\;{\text{N/m}}$ at CF = 4 kHz. The Young’s modulus value found is E ₂ = 1.0 MPa. The Young’s modulus value found is certainly not representative of that of the collagen fibers, which is on the order of a gigapascal (GPa). It reflects more that of the ground substance, whose E is a fraction of a megapascal (MPa).

Fig. 3

A 3D FE model simulating the point stiffness measurement experiment. A linear static deflection of the BM-AZ model to determine elastic properties; an equivalent probe force is applied to a quarter plate model of the BM-AZ using symmetric boundary conditions (force shown as downward pointing arrows). B Deflection u_z of the BM-AZ as function of the position x. The space constant is estimated at 20.8 μm, corresponding to the ordinate at 37% of the maximum deflection (shown by the square symbol).

As seen in Figure 3, the deformation at a point affects the surrounding region, exhibiting a non-locally reactive surface behavior that is characterized by a space constant λ _c defined as the spread of the deformation from its center. The space constant in the longitudinal direction was also checked against the experimental results while matching the elastic properties of the model to the experimental point stiffness data. The space constant determines the distance along the cochlea over which the displacement falls from the maximum to 37% of the maximum value. The FE estimate is λ _cn = 20.8 μm, as shown in Figure 3b. The experimental value of the space constant at any location along the cochlear is given in Naidu and Mountain (2001) by the following equation:

$$ {\lambda_c} = 8.5 + 1.8x\quad \left( {{\text{BM}}\;{\text{alone}}} \right) $$

(13)

where λ _c is in micrometers while x is in millimeters. x _CF = 6.44 mm for the CF location of 4 kHz according to Muller’s frequency-place map (Muller 1996). The corresponding value of the space constant given by Eq. 13 is λ _c = 20.1 μm which is very similar to the FE estimate.

Results

OPC impedance to fluid flow into the ToC

OHC motility generates fluid flow inside the ToC. This flow, however, must pass between the rigid pillars of the arch of Corti. Here, we estimate the permeability of the OPC array to flow into the ToC. We use two approaches: an analytical approach for closely spaced cylinders, and a numerical approach valid for wide spacing.

The analytical approach is based on a low Reynolds number assumption. At low frequencies, where OHC motions are the largest, the OHC motion is at most a few micrometers. For the CF, f equal to 4 kHz, the largest experimentally observed radial displacement of the OHCs is less than X = 150 nm. The flow Reynolds number based on the diameter of the OPCs is given by:

$$ {\text{Re}} = \frac{{2{\text{R}}_{d} \omega {\text{X}}}} {{v_{{\text{f}}} }} $$

(14)

where ω = 2πf, R _d corresponds to the OPC radius and ν _f = μ _f/ρ is the kinematic viscosity of the perilymphatic fluid of the ToC. Based on the value for R _d = 2.54 μm, this yields a value of Re less than 0.017. Therefore, the flow around the pillars is laminar and the inertial contribution may be neglected. Moreover, in the worst case analysis of the pillar cell impedance based on the optical image measurement, the spacing between the pillars of the ToC is quite small (a = 1.85 μm), i.e., $r = \frac{{{R_d}}}{{{R_d} + \frac{a}{2}}} \approx 0.73$ (a value r = 1 indicates no space between the pillars). In this case, the pillars are closely spaced and the resistance to flow is concentrated in the narrow gap between the OPCs. Under these conditions, the resistance per unit length of pillar can be estimated by Keller’s formula (Keller 1964) for a closely spaced array of cylinders perpendicular to a slow, viscous two-dimensional flow:

$$ \frac{{\Delta P}}{Q} = \frac{{9\pi \rho {ν_{\rm f}}\sqrt {{R_d}} }}{{2{a^{{5/2}}}}} $$

(15)

where ∆P is the pressure drop across the array, Q, the volume velocity of the fluid and ρ corresponds to the density of the perilymphatic fluid. This gives an estimated resistance value of $\frac{{\Delta P}}{Q} = 5.4 \times {10^9}\;{\text{Pa}}\;{\text{s/}}{{\text{m}}^2} = Rea{e_{{eal}}}(Z)$, the real part of the impedance $Z$ as defined below.

A second estimate of the flow impedance presented by a row of pillar cells was evaluated numerically with a = 1.85 μm. A planar z-section of an FE model such as the one shown in Figure 4a was used to numerically compute the impedance of the OPCs. A two-dimensional numerical computation was performed. Figure 4b shows a detailed view of the gap between two OPCs and the gap nomenclature used. The impedance was computed as the ratio of the temporal Fourier transform of the pressure drop through the gap in the y-direction to the Fourier transform of volume velocity through the gap. The real and imaginary parts of the impedance obtained for multiple gap location along the ToC are plotted in Figure 5.

Fig. 4

A ToC z-plane section showing a cut through the row of outer OPCs and meshing around them. B Detailed view of the gap between two consecutive OPCs with OPC gap nomenclature used (figure not drawn to scale).

Fig. 5

OPCs impedance to flow into the ToC due to the motion of the OHC1 as a function of the gap location along the ToC in percent distance from the maximum input location at x = 0.

We note that the imaginary part is negligible compared with the real part and can be associated with a relatively small acoustic inertance. The real part, which represents the resistive part of the impedance, is slightly greater than that obtained using Keller’s formula. This is reasonable since the later formula is an asymptotic formula that is valid only for very closely spaced cylinders, i.e. r = 1 The average value of the real impedance was used to characterize an OPC, yielding a value of (6.85 ± 0.04) × 10⁹ Pa s/m² for the OPC resistance per unit length of OPC for this limiting case of gap size studied.

It is worthwhile considering the impedance to flow presented by the OPCs relative to the impedance presented by the BM-AZ. For the BM-AZ model shown in Figure 3a, we estimate the volume stiffness of the BM-AZ to be $K = 24 \times {10^{{12}}}\;{\text{Pa/}}{{\text{m}}^2}$. An analytical derivation based on a plate model (Steele 1986) gives similar result, $K = 27 \times {10^{{12}}}\;{\text{Pa/}}{{\text{m}}^2}$. In order to estimate the relative significance of the impedance imposed by the row of OPCs to the overall cochlea function, we form the nondimensional ratio ${α_{\text z}} = \left( {2\pi {f_0}} \right)Z/K$, where $Z$ is the impedance to flow presented by the row of OPCs, and f₀ is a characteristic frequency chosen here to be the CF for the cross-section under consideration. We found α _z = 7. Thus, for this worst case analysis of the OPCs spacing studied, the BM-AZ impedance is on the same order of magnitude as the OPCs row impedance. This comparison indicates that the OPCs do not present a significant barrier to flow relative to other anatomical structures.

Influence of the OPCs spacing on the power loss

The gap size between the OPCs determines the impedance and therefore the power delivered to the ToC wave. Since the spacing between the OPCs is difficult to estimate from the imaging stacks from which the dimensions were taken, the effect of the gap size was assessed by calculating the power loss through the OPC array as a function of the OPC spacing. In fact, the edges were not clearly delimited in the images and the gap size was also seen to vary along the length of the OC. There were locations where it appeared that a whole pillar could easily fit in a gap. For these reasons, in addition to the experiment where the gap size was r = 0.73, with the nondimensional spacing r defined as previously, i.e., $r = \frac{{{R_d}}}{{{R_d} + \frac{a}{2}}}$, larger gap sizes were also considered. The spacing between the OPCs is increased gradually with r decreased from 0.73 to 0.3 by increasing the gap size a for a constant value of the OPC radius R _d. In effect, Formula 15 shows that the impedance tends to be more sensitive to the OPC spacing a than to change in the OPC radius R _d. Thus, r was varied with respect to a.

The average power loss in the gap between the OPCs is defined as:

$$ {\left\langle {p_{{loss}} } \right\rangle } = \frac{1} {2}R_{{eal}} {\left( {\widehat{{Q_{0} }}\Delta \widehat{P}^{ * } } \right)} $$

(16)

where ${\hat{Q}_0}$ is volume velocity through the gap; $\Delta \widehat{P}^{ * }$ is the complex conjugate of the pressure difference across the gap; ${R_{{eal}}}$ designates the real part of the complex quantity in parentheses. In terms of the impedance $Z = \frac{{\Delta \hat{P}}}{{{{\hat{Q}}_0}}}$, we have:

$$ \left\langle {{P_{\text{loss}}}} \right\rangle = \frac{{\left| {\Delta \hat{P}} \right|}}{2}{R_{{eal}}}\left( {\frac{1}{Z}} \right) = \frac{{{{\left| {{{\hat{Q}}_0}} \right|}^2}}}{2}{R_{{eal}}}(Z) $$

(17)

The OHC input power is calculated using Formula 16, with $\Delta \hat{P}$ taken as the pressure at the input wall representing the OHC and Q the velocity at the wall times the OHC diameter. As illustrated in Figure 6a, as the gap size is increased the power loss decreases. For a fixed gap size, the power loss through the gaps decreases along the length of the tunnel. The OHCs power input computed as explained above, normalized with respect to the OHC power input for the finest spacing, is also shown in Figure 6b. As the gap size is increased, a smaller fraction of the OHCs power is required to push fluid into the OPC gap. As r is decreased, the maximum power input location along the tunnel drifts longitudinally towards the apex, away from the maximum velocity input location. For r < 0.5, the maximum OHC input power asymptotes to ~0.3. We also note that for this sort of spacing, less than ~35% of the input power from the OHC closest to the gap is lost pushing fluid through OPCs. This is shown in Figure 7 where the ratio of the power loss to the OHC input power is plotted. This limiting spacing r = 0.5 corresponds to the case where a whole OPC fits exactly into the gap between two adjacent OPCs, i.e., a = 2R _d. For the finest OPC gap (r = 0.73), at least 35% of the OHC input power is lost pushing fluid through the gap.

Fig. 6

Power varies with OPC spacing. A Power loss through OPC. B Power input by OHC. Five OPC gap sizes are studied. They are designated by symbols as follows: open circle r = 0.73 (smallest gap); ex symbol r = 0.54; open square r = 0.42; asterisk r = 0.35; open diamond r = 0.3(widest gap), where r is the dimensionless gap size. Power is normalized with respect to the maximum power across all gap sizes.

Fig. 7

For physiologically relevant gap sizes, less than 35% of the OHC power input is lost through the OPC gap. Five OPC gap sizes are studied by increasing the dimensionless gap size, r. They are designated by symbols as follows: open circle r = 0.73 (smallest gap); ex symbol r = 0.54; open square r = 0.42; asterisk r = 0.35; open diamond r = 0.3 (widest gap). For each gap size, fixed along the row of OPCs, the ratio of power lost to OPC gap to OHC input power is plotted as a function of the gap location along the ToC model. The 35% mark is shown by the horizontal line.

Power loss drops considerably for gap sizes larger or comparable to the OPC diameter as does the input power for fixed input velocity.

Wave constant estimate of the fluid wave launched into the ToC

The compliant architecture of the BM suggests that traveling waves will propagate along the ToC. For a simulation frequency equal to the CF, we predicted the wavelength and the attenuation factor of the fluid wave launched by a small group of OHCs located in the middle turn region around the CF of 4 kHz and compared the result to theoretical derivations.

FE model estimates

We used a time domain solution to estimate the ToC wave properties. Two ToC models were built in order to consider the effects of wave reflections at the tunnel’s opened end. A short tunnel (0.7 mm long) which included the OPCs and also incorporated the spatial spread in the input, as described in the appendix, was first modeled. Then, a longer tunnel (6.24 mm long) was modeled as follows. Since the spacing between the OPCs is much smaller than the wavelength calculated from the short model, the periodicity of the OPCs does not affect the wave properties. However, the presence of the OPCs in the model increases the number of degrees of freedom, hence the computational time. Therefore, the OPC row was omitted and replaced with a fluid mesh in the longer tunnel model and the longitudinal spatial resolution was preserved. This model was approximately nine times longer, and the number of cycles of simulation was doubled. A localized OHC input at one end of the model was used to excite the model. Both models comprised a single compartment, the ToC duct, and are equivalent to a drained ST. The computational time taken was ~7 min per time step for the short model and ~45 min per time step for the long model. The solutions are analyzed as follows.

The time response of a fluid line inside the ToC (see Figs. 8a and 9a) is Fourier-transformed in time. The fluid line is defined as collections of nodal points in the longitudinal direction. We track the spatial phase variation along the ToC from the FFT phase to compute the wavelength. The wavelength at the CF corresponding to the modeled region of the ToC is estimated from the phase-position function ϕ = (x) as:

$$ \lambda = \frac{{2\pi }}{k};\quad k = \left| {\frac{{d\phi }}{{dx}}} \right|. $$

(18)

k is given by the slope of the regression line fit to the phase data away from the edges of the ToC as shown on the phase-position plot of Figures 8c or 9c.

Fig. 8

A Sample waveforms along the ToC centerline for the longitudinal fluid velocity (x-velocity) within two cycles of running time. B Scaled magnitude of FFT of x-velocity. C Phase variation along the tunnel; the straight line is the linear regression fit to the phase data away from the ToC ends. The slope of the line yields the wavenumber $k = \left| {\frac{{d\phi }}{{dx}}} \right| = 7.0\;{\text{m}}{{\text{m}}^{{ - 1}}}$.

Fig. 9

A Sample waveforms along the ToC centerline for the longitudinal fluid velocity (x-velocity) within 5 cycles of running time. B Scaled magnitude of FFT of x-velocity. C Phase variation along the tunnel; The straight line is the linear regression fit to the phase data. The slope of the line is $k = \left| {\frac{{d\phi }}{{dx}}} \right| = 3.9\;{\text{m}}{{\text{m}}^{{ - 1}}}$.

For the short model, the numerical values are k = 7.0 mm⁻¹ and λ = 0.9 mm. In the magnitude response of the FFT shown in Figure 8b, we see that the wave is rapidly attenuated over a distance of 0.5 mm. The longer tunnel wavelength is estimated to be 1.6 mm (see Fig. 9c), and the wave propagates a little more than 0.5 mm before its magnitude drops to 37% of its maximum as shown in Figure 9b. We see from these results that the tunnel’s end reflections influenced the short model’s results. The experimental wavelength estimate at CF = 4 kHz is 0.5 mm (Karavitaki and Mountain 2007a; Naidu and Mountain 2001). This is about one third of the simple model prediction for the OC wave.

To assess the effect of the ST fluid, the short single duct model was extended by adding a bottom fluid compartment matching the size of the actual ST at the site of interest. We observed that the flow in the ST is concentrated near the BM and is characterized by a very small penetration depth. There was no noticeable change in the wavelength estimate when the ST was added. In fact, the cross-section area of the ToC is about 2 orders of magnitude smaller than that of the ST. The conservation of mass shows that the longitudinal gradient of the ST fluid velocity is negligible. The wavelength is a by-product of the longitudinal fluid impedance and the BM impedance. The fluid impedance depends on the effective area of the scalae A ^eff = (A _st × A _ToC)/(A _st + A _ToC) as defined in Dallos (1973) and Zwislocki (1965). Here, A ^eff ≈ A _ToC. Therefore, the wavelength is determined by the ToC alone.

In this model, at the location’s best frequency of 4 kHz, the thickness of the fluid boundary layer formed near the BM-AZ is estimated as δ = 2(v _f /ω)^1/2 (Lighthill 1978), yielding δ = 20 μm. This is about one third of the ToC height. There were approximately four elements in the boundary layer for the model. The fluid viscosity will not only contribute in damping the wave but will also affect the wavelength estimate slightly. Using the 3D FE model an estimate of the effect of viscosity was performed by reducing the viscosity 3 orders of magnitude with respect to the viscosity of water. A localized (spatial delta-Dirac with respect to longitudinal x-direction) impulse was used as the input to compute the wave characteristics at CF. The result of the decreasing viscosity was that the wave amplitude was increased, and the wave speed was increased from 3.80 to 3.95 m/s (∼ 4% increase) as calculated from the linear fits in Figure 10. This corresponds to a wavelength increase of 37.5 μm at 4 kHz.

Fig. 10

Dispersion curve from localized impulse response in middle turn (CF = 4 kHz) shows that fluid viscosity decreases wavelength by ~4%. Open circle nearly inviscid (μ _water/1,000), wave speed estimate: 3.95 m/s; closed circle viscous (μ _water), wave speed estimate: 3.80 m/s. The wave speeds are estimated from the linear fits shown as solid lines.

Theoretical prediction of the wavelength

The numerical estimate of the wavelength indicates that the long-wave theory may apply to this problem since kW _ToC = 0.2 < 1 and kH _ToC = 0.3 < 1. In the so called long-wave approximation, which we adapt to the modeled ToC, the fluid velocity in the vertical direction (z-direction) is assumed to be a linear function of z and a section of the BM is considered as an independent oscillator, a rigid piston loaded uniformly with fluid. This implies that the fluid viscous effects are not important and that the wavelength is long enough that the pressure is uniform over the cochlea cross-section. In this case and for a single-channel cochlea, the pressure near the BM satisfies the Helmholtz equation, and the wave number k is derived from the long-wave discussion in de Boer (1996) as:

$$ {k^2} = \frac{{ - i\omega \rho }}{{HZ}}, $$

(19)

where H designates the height of the channel and $Z$ the acoustic impedance of the underlying BM. For a compliance-dominated BM, the wave velocity at a given location along the BM, is given by:

$$ {v_{\phi }} = \sqrt {{\frac{H}{{\rho C}}}}, $$

(20)

where $C$ is the volume compliance per unit area of the BM and ρ is the fluid density. The compliance, $C$ is obtained from the FE calculation of the BM stiffness $K$ as:

$$ C = {\left\{ {K\,{W_{\text{ToC}}}} \right\}^{{ - 1}}}{,} $$

(21)

With H taken as the equivalent height of the ToC defined as the area of the ToC divided by its width, Eq. 20 yields v _ϕ  = 6.2 m/s. The corresponding wavelength at CF is 1.5 mm, which is similar to the prediction from the 3D model.

An identical result is found using a 2D model, which also neglects the fluid viscosity and the damping in the BM, and which assumes only that kW _ToC ≪ 1. The wavelength is obtained from the dispersion relation below, for which a full derivation can be found in Steele and Taber (1979), for the excitation frequency of 4 kHz:

$$ \rho {\omega^2}\left( {\frac{1}{{k\tanh \left( {kH} \right)}} + h} \right) - \frac{1}{C} = 0, $$

(22)

where h is the thickness of the BM-AZ.

Relationship of the ToC wave to the classical BM traveling wave

It is difficult to predict the relative phase between the tunnel wave and the main BM macro-mechanical wave. However, since an effective amplification can occur only if the waves are in phase, we will assume a phase match at the location of interest in order to relate the amplitude of the two waves. The magnitude of the cochlear partition displacement in response to low sound pressure can be compared to the arcuate zone displacement amplitude in the current model. The ratio of the displacement magnitudes determines how much boost the ToC wave can provide.

For the smallest OPC spacing, the ToC waveguide model predicts that a 4 kHz wave (f = CF = 4 kHz) propagating on the BM-AZ in response to radial OHC displacements (lengthwise average displacement) of Ū _OHC = 4.5 nm generates a peak displacement of Ū _BM-AZ ~ 0.4 nm. A similar BM-AZ displacement is obtained when the ST is added to the model. This displacement is consistent with the electrical stimulation experiments results reported in Chan and Hudspeth (2005), Nuttall et al. (1999), Xue et al. (1993). In these experiments, BM displacement was found to be relatively small ~0.1–1.5 nm.

The power gain G of the BM partition as the result of OHC fluid pumped in ToC in term of the displacement gain G _u is defined as:

$$ G = \frac{{{{\left\{ {K \cdot {W^2} \cdot {{\overline U }^2}} \right\}}_{{{\text{BM - AZ}}}}}}}{{{{\left\{ {K \cdot {W^2} \cdot {{\overline U}^2} } \right\}}_{\text{Partition}}}}} = \frac{{{{\left\{ {K \cdot {W^2}} \right\}}_{{{\text{BM - AZ}}}}}}}{{{{\left\{ {K \cdot {W^2}} \right\}}_{\text{Partition}}}}} \cdot G_u^2, $$

(23)

where G _u = Ū _BM-AZ/Ū _Partition, $K$ is the stiffness, W is the width, and U denotes an average displacement. The values of $K$ are estimated numerically from the current BM-AZ model and from a detailed BM + OC model, giving respectively, ${K_{{{\text{BM - AZ}}}}} = 24 \times {10^{{12}}}{\text{Pa/}}{{\text{m}}^2}$ and ${K_{\text{Partition}}} = 4 \times {10^{{11}}}{\text{Pa/}}{{\text{m}}^2}$. Thus, we find $G = 2.2G_u^2$, or G = 3.4 + G _u in decibels.

For a typical partition’s displacement gain G _u = 1,000 corresponding to 60 dB amplification, the predicted average partition displacement is Ū _Partition = 0.4 × 10⁻³ nm. This would represent the passive BM displacement to low sound pressure level (e.g., <30 dB SPL). What then is the in vivo partition displacement magnitude around CF = 4 kHz (for f = CF) to very low sound level in the absence of amplification? Experimental studies in the middle turn are scarce, and no data exist for this CF location. However, we can expect the passive partition displacement to be very small such that the total in vivo BM displacement at low sound level is mainly the result of the CA.

The OHC pump model operates linearly; hence a BM-AZ displacement of 1 nm is produced by an OHC displacement of ~13 nm. Nanoscale displacements of the BM-AZ can be reached since the maximum OHC displacement at 4 kHz, as estimated from the low frequency measurements (see Appendix), is about 12 nm. Moreover, in vivo BM displacements measured in guinea pigs at CF = 13 kHz, are only a fraction of a nanometer below 30 dB SPL (Russell and Nilsen 1997); In particular, at ~10 dB SPL, the displacement is ~0.3 nm. Therefore BM displacements on the order found in the ToC model could well be significant for motion amplification.

Discussion

Several factors will affect the accuracy of the wavelength estimate at the peak response of the region of the OC considered. The material properties of the underlying basilar membrane must be accurately incorporated in the model, and properties such as the edge support conditions, the overall flexibility and the defining components of the OC must be reliably represented.

In our model, BM-AZ was treated as an isotropic elastic material. We used the analytical solution of the BM volume stiffness provided in Steele (1986) to estimate the error on the wavelength when BM is treated as isotropic rather than an orthotropic material. The relative increase in the stiffness value resulting from isotropic property modeling was less than 1%, and so was the error on the wavelength estimate. It has also been shown that the degree of orthotropy does not affect the peak location, but could sharpen the BM response at the peak location (Steele and Zais 1983). This contribution would come mainly from the BM-PZ.

In the simplified ToC model, wave reflection was a concern since the length of the model was limited. Simultaneously resolving the OPC gap and the wavelength proved to be costly in computation time. Thus, in order to calculate the wavelength, the OPCs were omitted and the model was lengthened to avoid wave reflection at the opened ToC end. The wavelength found with the long model was 1.6 mm while the shorter model yielded a shorter wavelength estimate of 0.9 mm. Wave reflection effects were thus evident in the short model which was only half a wavelength long. The FE estimate of the ToC wavelength was similar to the theoretical predictions by the 1D or 2D models.

The actual cochlea is naturally impedance-matched at each longitudinal location, excluding perhaps the helicotrema. In the absence of the active process, wave reflections along the cochlea are usually negligible compared with the incident wave generated at the stapes (Siebert 1974). Similarly, the wave generated in the ToC may propagate in both directions along the cochlea with negligible local reflections. And if the phases are matched, this wave can interfere constructively with the main cochlear wave to create motion amplification.

The ToC model prediction of the wavelength at the best frequency place of 4 kHz is longer than the estimates from auditory nerve recordings of 0.5 mm. However, the model estimate of the wavelength might be shorter in reality than currently estimated. In fact, by assuming rigid inner pillar and phalangeal cells, and by not considering a pivoting arch of Corti about the Primary Spiral Lamina bony shelf may make the resultant ToC model stiffer than it is in reality. Therefore a longer wave length estimate might be expected. It is also possible that multiple wave modes exist where the arcuate zone would propagate wave with a different velocity from the mode that stimulates the inner hair cells. In response to an input incorporating a spatial spread, this fluid wave propagates over approximately one wavelength (with respect to the experimental wavelength estimate of 0.5 mm) before it gets attenuated to 18% of its peak value. For a localized velocity input without a spatial spread, the wave propagates a little longer before it gets attenuated to 37% of the peak value. In both cases, the distance over which the wave propagates is shorter than that found using a one dimensional hydromechanical model (Karavitaki and Mountain 2007a) but long enough to be of physiological importance. Thus, the wave in the tunnel of Corti provides an additional longitudinal coupling component within the cochlea which may be critical for CA as hypothesized in non-classical models of the cochlea mechanics (Hubbard 1993). More recently, another source of longitudinal coupling was revealed in Ghaffari et al. (2007) which showed that the TM can support a shearing traveling wave, which acts directly on the connected OHC cilia. The CA could then be the result of complex interactions between multiple wave propagation modes.

While the structural periodicity may not play an important role in determining the wavelength, the permeability of the OPC region must play a determinant role in an OC that functions as fluid pump.

As the gap size between adjacent OPCs is increased the power loss decreases. This implies that more power is injected into the tunnel wave. Also, only a smaller fraction of the OHCs input is lost to the gap. This would suggest the existence of an optimal OPC gap size for which a minimal OHC input power is required to feed the tunnel wave. The maximum power input location moves away from the maximum input velocity location towards the apex. For spacing greater than the limiting spacing where a whole OPC fits exactly into the gap, the maximum OHC input power asymptotes to 30% of the input power corresponding to the smallest gap size. Also, for this sort of spacing, less than 35% of the OHC power is lost pushing fluid through the OPCs.

For the smallest gap size, we estimate the impedance of the BM-AZ to be of the same order of magnitude as the impedance of OPCs row. This comparison indicates that the OPCs do not present a significant barrier to flow relative to other anatomical structures.

Modeling OHC1 as a rigid wall may affect the OHC input power calculation but would have no effect on the wavelength and the OPC impedance estimates. In order to account for the mass of the OHC1 and fluid behind it, we designed two simple experiments. In the first experiment, the OHC was modeled as an elastic solid pushing fluid into the ToC with the same stimulation conditions as used previously. We found that the power estimate with this model was the same as that of the OHC wall model. OHC inertial effect was thus negligible. We, thus, verify that the ToC model with OHC represented as a moving wall describes the situation where the OHC cell body is present. In a second numerical experiment, the fluid effect in the model was assessed by adding fluid behind the elastic OHC model. The OHC power calculated with this model is the same as when no fluid is added. This would suggest that the fluid surrounding the OHC does not affect the OHC input impedance. The OHC region can therefore be modeled as a moving wall without substantially modifying the input impedance or power estimate. The Hensens cells are very compliant and we expect their presence to lead to the same conclusion.

Although the inner side of the tunnel was modeled as a rigid wall, in reality this is a moderately compliant wall, composed of the inner pillar and the phalangeal cells complex, which connects directly to the cochlear input receptors: the inner hair cells. Therefore, the tunnel wave motion could affect directly the bulk of the inner hair cell through this phalangeal wall. A more detailed model of the OC is necessary to unravel the relative motion between the OC components, and to help infer the functional dependencies between these components. A modal analysis of the detailed OC is a starting point for achieving this goal.

We have shown that the tunnel can support a traveling wave and that if the spacing between OPCs is sufficient, the power loss due to viscous fluid moving in and out of the tunnel through the spaces between the OPCs will not be excessive. The limiting OPC spacing found, above which the power loss pushing fluid through the OPC row falls below 35%, is of the order of the OPC diameter. This kind of spacing is quite reasonable and has been seen along the OPC row and at various levels of our image stacks. The peak BM-AZ displacement found in the ToC model, as the result of the fluid pushed into the ToC by the motile OHC, is significant for motion amplification at low sound pressure levels. Therefore, we conclude that our results support the hypothesis that the amplifier can function as a fluid pump.

APPENDIX

The OHC electromotile input to the ToC waveguide model

The model input represents the effect of OHC motility. The input was determined from the observation of the motion of the first row of OHCs in response to electrical stimulation (Karavitaki and Mountain 2007b). The sketch in Figure 11 shows the experiment imaging plane (I _p) oriented at an angle γ _r with respect to the OHC axis. The radial direction, denoted by the subscript r, is chosen to be in the I _p plane and is indicated by the unit vector n in the figure. The radial component of the OHC displacement sketched in the figure, thus, has one component in the y- and z-directions, respectively. Based on this figure, the OHCs displacement (D) measured in I _p is given in the Cartesian coordinates in Eq. 24 for a given stimulus frequency ω. The OHC velocity is deduced from the displacement vector and is used as the input to the FE model. The measured displacement magnitude (D _lm, D _rm) and phase (ϕ _l, ϕ _r), which are functions of the depth (d) of the imaging level, are interpolated along the depth to match the nodes in the FE model. An exponential decay factor was added to simulate the longitudinal variation in the input, as the OHCs are not excited equally. Indeed, as mentioned in Karavitaki and Mountain (2007b), the electrically evoked OHC motion showed a gradient due to the spread of current away from the location of the electrode which is where maximal excitation occurred. This effect is incorporated as an input spread factor δ in the model with x _p denoting the location of maximal excitation. The model input parameter values are x _p = 0 μm, δ = 0.12 × L _ToC. For the experiment simulated, the viewing axis is aligned with the OHC axis such that γ _r = 90^o.

Fig. 11

Sketch of the model cross-section showing the imaging plane (I _p) orientation and the model input. n is a unit vector in the radial direction and vector d indicates the depth within the OC. d is assumed orthogonal to n. In our simulation the viewing axis is the OHC1 axis, i.e., γ _r = 90^o. For this case, the radial OHC displacement D _rm(d) is sketched for the positive phase (towards the spiral lamina) of the model’s input. The in-plane longitudinal component (D _lm) is measured along the x-axis.

$$ D = e^{{{\left( {\frac{{ - {\left| {x - xp} \right|}}} {\delta }} \right)}}} \left\{ {\begin{array}{*{20}l} {{D_{{lm}} {\left( d \right)}\sin {\left( {\omega t + \phi _{l} {\left( d \right)}} \right)}} \hfill} \\ {{ - D_{{rm}} {\left( d \right)}\cos {\left( {\gamma _{r} - a} \right)}\sin {\left( {\omega t + \phi _{r} {\left( d \right)}} \right)}} \hfill} \\ {{D_{{rm}} {\left( d \right)}\cos {\left( {\gamma _{r} - a} \right)}\sin {\left( {\omega t + \phi _{r} {\left( d \right)}} \right)}} \hfill} \\ \end{array} } \right. $$

(24)

The simulation frequency was chosen to be the CF of the location of interest (CF = 4 kHz). The in-plane radial and longitudinal input displacement magnitude and phase are inferred from measurement at a lower frequency of 60 Hz as expressed in Eq. 25 and explained below.

$$ \begin{array}{*{20}l} {{D_{{{\text{rm}}}} {\left( {f = 4{\text{kHz}}} \right)} \approx D_{{rm}} {\left( {f = 60{\text{Hz}}} \right)}/12;} \hfill} \\ {{\phi _{{\text{r}}} {\left( {f = 4{\text{kHz}}} \right)} \approx \phi _{r} {\left( {f = 60{\text{Hz}}} \right)} + \pi /2 = 3\pi /2} \hfill} \\ {{D_{{{\text{lm}}}} {\left( {f = 4{\text{kHz}}} \right)} \approx D_{{lm}} {\left( {f = 60{\text{Hz}}} \right)}/12;} \hfill} \\ {{\phi _{{\text{l}}} {\left( {f = 4{\text{kHz}}} \right)} \approx \phi _{l} {\left( {f = 60{\text{Hz}}} \right)} + \pi /2 = \pi /2} \hfill} \\ \end{array} $$

(25)

The experimental in-plane input magnitude D _lm, D _rm as a function of the depth within the OC are obtained at 60 Hz (Karavitaki and Mountain 2007b). The corresponding phases along the cell’s length ϕ _l, ϕ _r were constant at ~0^o and ~180^o, respectively. The 4 kHz radial and longitudinal displacement amplitude and phase functions, with respect to the depth, of the first row of hair cell were assumed to be similar to those at 60 Hz as reported in Karavitaki (2002). The relative displacement magnitude and phase are determined from additional experimental data. Experimental results were also available for a sweep of frequencies between 10–10,000 Hz, and showed a low pass characteristic: past a frequency of ~1,000–2,000 Hz, the displacement decreased to the noise level of 60 nm (see Karavitaki and Mountain 2007b, Fig. 3b and c). The ratio of the response magnitude at the low frequency of 60 Hz to that at the higher frequencies past 4 kHz was estimated to be 12, and there was about a quarter of a cycle phase roll-off. From these observations, the model OHC1 multilevel displacement profile for 4 kHz was derived from the 60 Hz data as shown in Eq. (25).