Skip to main content
SpringerLink
Log in

A robustification approach in unconstrained quadratic optimization

  • Full Length Paper
  • Series A
  • Published:
Mathematical Programming Submit manuscript

Abstract

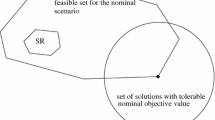
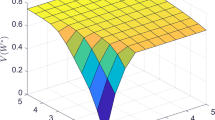
Unconstrained convex quadratic optimization problems subject to parameter perturbations are considered. A robustification approach is proposed and analyzed which reduces the sensitivity of the optimal function value with respect to the parameter. Since reducing the sensitivity and maintaining a small objective value are competing goals, strategies for balancing these two objectives are discussed. Numerical examples illustrate the approach.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Ben-Tal A., Nemirovski A.: Robust optimization-methodology and applications. Math. Program. 92(3, Ser. B), 453–480 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  2. Boyd S., Vandenberghe L.: Convex Optimization. Cambridge University Press, Cambridge (2004)

    MATH  Google Scholar 

  3. Calafiore G., Dabbene F.: Near optimal solutions to least-squares problems with stochastic uncertainty. Syst. Control Lett. 54, 1219–1232 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  4. Diehl M., Bock H.G., Kostina E.: An approximation technique for robust nonlinear optimization. Math. Program. 107(1–2, Ser. B), 213–230 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  5. Fiacco A.: Introduction to Sensitivity and Stability Analysis in Nonlinear Programming. Academic Press, New York (1983)

    MATH  Google Scholar 

  6. Griewank A.: Evaluating Derivatives. SIAM, Philadelphia (2000)

    MATH  Google Scholar 

  7. Kanellakopoulos, I.: Robustification tools for nonlinear control design. In: Proceedings of the 33rd conference on decision and control, vol.4, pp. 3464–3468. IEEE (1994)

  8. Quevedo, D.E., Salgado, M.E.: Robustification of model predictive control. In: Proceedings of the 39th conference on decision and control, vol. 1, pp. 178–180. IEEE (2000)

  9. Rodriguez P., Dumur D.: Generalized predictive control robustification under frequency and time-domain constraints. IEEE Trans. Control. Syst. Technol. 13(4), 577–587 (2005)

    Article  Google Scholar 

  10. Rump, S.: INTLAB-INTerval LABoratory. In: Csendes, T. (ed.) Developments in Reliable Computing, pp. 77–104. Kluwer Academic Publishers, Dordrecht (1999). http://www.ti3.tu-harburg.de/rump/

Download references

Author information

Authors and Affiliations

  1. Faculty of Mathematics, Chemnitz University of Technology, 09107, Chemnitz, Germany

    Martin K. Bernauer & Roland Griesse

Authors
  1. Martin K. Bernauer
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Roland Griesse
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Martin K. Bernauer.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Bernauer, M.K., Griesse, R. A robustification approach in unconstrained quadratic optimization. Math. Program. 128, 231–252 (2011). https://doi.org/10.1007/s10107-009-0302-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10107-009-0302-9

Keywords

Mathematics Subject Classification (2000)

Search

Navigation