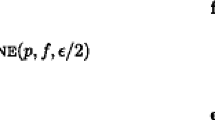Skip to main content
SpringerLink
Log in

Maximum network flows with concave gains

  • Published:
Mathematical Programming Submit manuscript

Abstract

This paper deals with a generalized maximum flow problem with concave gains, which is a nonlinear network optimization problem. Optimality conditions and an algorithm for this problem are presented. The optimality conditions are extended from the corresponding results for the linear gain case. The algorithm is based on the scaled piecewise linear approximation and on the fat path algorithm described by Goldberg, Plotkin and Tardos for linear gain cases. The proposed algorithm solves a problem with piecewise linear concave gains faster than the naive solution by adding parallel arcs.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Ahlfeld, D.P., Mulvey, J.M., Dembo, R.S., Zeniosm, S.A.: Nonlinear programming on generalized networks. ACM Trans. Math. Softw., 13, 350–367 (1987)

    Article  MathSciNet  Google Scholar 

  2. Eguchi, A., Fujishige, S., Takabatake, T.: A polynomial-time algorithm for the generalized independent-flow problem. J. Oper. Res. Soc. Japan, 47, 1–17 (2004)

    MATH  MathSciNet  Google Scholar 

  3. Goldberg, A.V., Plotkin, S.A., Tardos, É.: Combinatorial algorithms for the generalized circulation problem. Math. Oper. Res., 16, 351–381 (1991)

    MATH  MathSciNet  Google Scholar 

  4. Goldberg, A.V., Tarjan, R.E.: Finding mimimum-cost circulations by canceling negative cycles. J. ACM, 36, 388–397 (1989)

    Article  Google Scholar 

  5. Goldfarb, D., Jin, Z., Orlin, J.B.: Polynomial-Time Highest-Gain Augmenting Path Algorithms for the Generalized Circulation Problem. Math. Oper. Res., 22, 793–802 (1997)

    MATH  MathSciNet  Google Scholar 

  6. Gondran, M., Minoux, M.: Graphs and algorithms. J. Wiley & Sons, New York, 1984

  7. Hochbaum, D.S., Shanthikumar, J.G.: Convex separable optimization is not much harder than linear optimization. J. ACM, 37, 843–862 (1990)

    Article  MATH  MathSciNet  Google Scholar 

  8. Karzanov, A.V., McCormick, S.T.: Polynomial methods for separable convex optimization in unimodular linear spaces with applications. SIAM J. Comput., 26, 1245–1275 (1997)

    Article  MATH  MathSciNet  Google Scholar 

  9. Merchant, D. K., Nemhauser, G. L.: A model and an algorithm for the dynamic traffic assignment problems. Transp. Sci., 12, 183–199 (1978)

    Google Scholar 

  10. Minoux, M.: Solving integer minimum cost flows with separable convex cost objective polynomially. Math. Program. Study, 26, 237–239 (1986)

    MATH  MathSciNet  Google Scholar 

  11. Nakayama, A., Su, S.F.: Two efficient algorithms for the generalized maximum balanced flow problem. J. Oper. Res. Soc. Japan, 45, 162–173 (2002)

    MATH  MathSciNet  Google Scholar 

  12. Onaga, K.: Dynamic programming of optimum flows in lossy communication nets. IEEE Trans. Circuit Theory, 13, 308–327 (1966)

    Google Scholar 

  13. Radzik, T.: Faster algorithms for the generalized network flow problem. Math. Oper. Res., 23, 69–100 (1998)

    Article  MATH  MathSciNet  Google Scholar 

  14. Radzik, T.: Contracting the network during maximum generalized network flow computation. Technical Report TR-01-08, King's College, 2001

  15. Radzik, T., Yang, S.: Experimental evaluation of algorithmic solutions for the maximum generalised network flow problem. Technical Report TR-01-09, King's College, 2001

  16. Tseng, P., Bertsekas, D.: An ɛ-relaxation method for separable convex cost generalized network flow problems. Math. Program., 88, 85–104 (2000)

    Article  MATH  MathSciNet  Google Scholar 

  17. Wayne, K.D.: Generalized maximum flow algorithms. Ph.D. thesis, Cornell University, 1999

Download references

Author information

Authors and Affiliations

  1. Graduate School of System and Information Engineering, University of Tsukuba, Tsukuba, Ibaraki, 305-8573, Japan

    Maiko Shigeno

Authors
  1. Maiko Shigeno
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Maiko Shigeno.

Additional information

Supported by a Grant-in-Aid for Scientific Research (No. 13780351 and No.14380188) from The Ministry of Education, Culture, Sports, Science and Technology of Japan.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Shigeno, M. Maximum network flows with concave gains. Math. Program. 107, 439–459 (2006). https://doi.org/10.1007/s10107-005-0608-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10107-005-0608-1

Keywords

Search

Navigation