1 Introduction

Transportation operations, of people and goods, are well known to be responsible for a large share of the air pollutants. Technological developments are modifying in different directions the way we move and transport goods. One of these directions aims at reducing the number of kilometers traveled by road vehicles and/or at increasing the used capacity of a vehicle. Examples of initiatives in this direction that concern the transportation of people are ride-sharing, car sharing, mobility-as-a-service (MAAS) (see Mourad et al. 2019) for a comprehensive survey on optimization models for shared mobility). The expressions Demand-Responsive Transport and Flexible Transport Services are often used to collectively indicate this class of services (see Vansteenwegen et al. 2022; Nelson and Wright 2021). While the potential of collaboration initiatives to reduce the number of vehicles on the road is recognized by many, there are also several obstacles that are known to limit the number of successful collaborations (see, for example, Basso et al. 2019).

It is well-known that collaboration initiatives may fail because larger companies benefit more than smaller companies from the collaboration and smaller companies may loose customers or even be pushed out of the market (see Cruijssen et al. 2007) for the results of a large survey). In fact, the unconstrained optimization of the exchange of customers, that has as objective the minimization of the total alliance costs, could tend to benefit larger companies and to be detrimental for smaller companies. One of the challenges in the design of successful collaboration schemes is to find mechanisms that make the collaboration beneficial to all the companies involved (see Gansterer and Hartl 2018; Gansterer et al. 2020). We will say that a collaboration scheme is fair when it contains such mechanisms. The literature on horizontal collaboration in the transportation area is wide. We refer to Aloui et al. (2021) for a literature review on collaborative sustainable transportation.

Some contributions have appeared that constrain the optimization to be fair towards all companies. In Fernández et al. (2016) this goal is modeled by means of a lower bound on the profit of each company. In Gansterer and Hartl (2021) lower bounds are set on the profit and also on the number of customers served by each company. In Angelelli et al. (2022) the workload exchange is controlled by means of constraints on the number of served customers and on the time traveled by each company. In these papers, the customers exchange is optimized on a daily basis, that is, it is assumed that each day, given the customers of all companies, a constrained optimization model is run and the solution implemented. We observe that controlling the exchanges on a daily basis may fail to exploit opportunities when the planning horizon contains more than one day, as the illustrative example provided later shows. In this context, a multi-day optimization model offers more flexibility, potential for savings and, at the same time, can guarantee fairness in the long run.

In this paper, we consider an extension of the problem approached in Angelelli et al. (2022). According to the literature (see for example Gansterer and Hartl 2018) and Fernández et al. (2016)), we use the term ‘coalition’ to indicate a set of companies involved in a collaboration initiative. A set of companies involved in a shared taxi service have agreed to form a coalition and to exchange customers over a multi-day horizon. On each day of the planning horizon a company may concede the service of some of its customers to other companies and may acquire customers from other companies.

According to the idea that every company would consider fair to keep a customer exchange that does not modify the workload, different unfairness measures could be considered:

  • The daily customer balance of a company in a day of the time horizon: the percentage difference between the number of acquired and conceded customers on that day w.r.t. the original number of customers in that day;

  • The cumulated customer balance of a company up to a day of the time horizon: the percentage difference between the number of acquired and conceded customers w.r.t. the original number of customers up to that day;

  • The daily time balance of a company in a day of the time horizon: the percentage difference between the acquired and conceded travel time on that day w.r.t. the original travel time in that day;

  • The cumulated time balance of a company up to a day of the time horizon: the percentage difference between the acquired and conceded travel time w.r.t. the original travel time up to that day.

The nature of the problem is multi-objective. On one side, we want to minimize the overall cost for the alliance in the time horizon. On the other side, we want to reduce the unfairness for each company as much as possible. We approach the problem through an optimization model that assigns customers to companies and identifies the route for each vehicle so that the total routing cost over the time horizon is minimized while unfairness measures for the coalition are bounded (namely, maximum daily customer balance registered by any company on any day of the time horizon, maximum cumulated customer balance registered by any company on the last day, maximum daily time balance for any company on any day of the time horizon, maximum cumulated time balance on last day).

The model we present is able to coordinate decisions among days in the time horizon and obtains better results with respect to the application of a single-day model to each day of the horizon.

A heuristic that follows the Adaptive Large Neighborhood Search (ALNS) algorithmic approach is presented for the solution of the optimization model.

1.1 Motivation and assumptions

Demand-responsive transportation services are usually divided in two streams: services for which the booking is mandatory and has to be done in advance (e.g., dial-a-ride services, transit to hospitals, school services, etc.) and services that can be requested at any time (e.g., taxi services). Our context is the former, where bookings can be booked days in advance. The proposed scheme could be applied to working periods that span from few days to weeks, depending on the nature of services involved.

While the topic of profit distribution among the companies involved in a collaboration initiative is very important, we will not treat this aspect in this paper, as it can be seen as a further a posteriori mechanism of the collaboration scheme.

1.2 An illustrative example

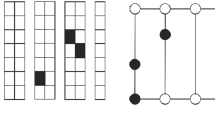
To illustrate the benefits of horizontal collaboration over a multi-day horizon, a 2-day example of two companies is presented where the depot and customer locations of the two companies (5 customers each for the red and blue companies) are depicted in Figs. 1, 2, 3 and 4. For each customer c, the pick-up location is denoted by \(O_c\) while the delivery location is denoted by \(D_c\). For the sake of simplicity, in this small example, customers and depots are the same in both days and we take into account only daily and cumulated customer balance.

We consider the following collaboration schemes:

  • the Non-Collaboration (NC) scheme: each company serves its own customers; no exchange is allowed at any time (optimal plan in Fig. 1);

  • the 1-Day Collaboration scheme: the daily customer balance, in absolute value, is bounded to be lower than 20% on each day for each company (optimal plan in Fig. 2);

  • the 2-Day Collaboration scheme: the cumulated customer balance on the last day, in absolute value, is bounded to be lower than 20% for each company, while no bound is applied on single days (optimal plan in Fig. 3);

  • the Unconstrained Collaboration (UC) scheme: each company could serve any customer without any bound on daily or cumulated customer balance (optimal plan in Fig. 4).

Fig. 1
figure 1

NC scheme plan in day 1 (left) and day 2 (right)

Full size image
Fig. 2
figure 2

1-Day Collaboration scheme plan in day 1 (left) and day 2 (right)

Full size image
Fig. 3
figure 3

2-Day Collaboration scheme plan in day 1 (left) and day 2 (right)

Full size image
Fig. 4
figure 4

UC scheme plan in day 1 (left) and day 2 (right)

Full size image

In Table 1, we summarize the main features of the plans produced by the three collaboration schemes with respect to the non-collaboration scheme NC (shown as percentages). Savings are computed, for each company and for the entire coalition (column All), as the percentage reduction of the cost with respect to the non-collaboration cost. More details on these plans are reported in Appendix A.

Table 1 Savings, daily and cumulated customer balance for each company (%)
Full size table

All collaboration schemes realize savings for the coalition with respect to the NC scheme and, as expected, the UC realizes the maximum savings (+ 22.7%) while the 1-Day scheme ranks last (+ 4.5%). Interestingly enough, not only does the 2-Day scheme produce an overall saving quite close to the UC (+20.5%), but also a positive saving for both companies (+ 28% for blue company and + 10.5% for the red company).

In Fig. 5, a general overview of the results is proposed. Three performance indicators have been considered for each scheme: the savings, the maximum daily customer balance registered by companies on the 2 days, and the maximum cumulated customer balance registered by companies on the second day. The savings are located on the x axis, while the maximum daily customer balance is located on the y axis of the left panel, and the maximum cumulated customer balance is located on the y axis of the right panel. While the UC allows the maximum savings, it also provides the highest unfairness (40% for both daily and cumulated customer balance).

A compromise solution is represented by the 1-Day scheme, for which the maximum daily and cumulated customer balance is halved with respect to the UC, i.e. 20%. However, this comes with a poor performance in terms of saving as the total cost is more similar to NC scheme than to the UC.

The 2-Day scheme outperforms the other ones as it produces savings that are just slightly less than those produced by the UC, and a final maximum cumulated customer balance equal to zero which definitely dominates the 1-Day scheme. This result comes at the cost of a higher value of the maximum daily customer balance for both the companies that is averaged out through the days of the horizon.

Fig. 5
figure 5

Savings (x-axis) versus maximum daily and maximum cumulated customer balance (y-axis) for different collaboration schemes

Full size image

1.3 Contribution of the paper

The main contribution of the paper is the introduction of a flexible optimization model able to model a number of different approaches (collaboration schemes) to the multi-day horizon context. On one side, the model we propose can be used to implement a day-by-day approach where, in line with Angelelli et al. (2022), independent optimizations are executed for every day in the time horizon. On the other side the model can be used to implement a global optimization on the whole time horizon where only the cumulated exchange operations up to the last day are taken into account and bounded. A number of midway schemes can be implemented where both day-by-day and final cumulated exchanges are bounded. An effective ALNS algorithm has been developed for this general model. The model is then used to assess the impact of bounding unfairness in the long-run (multiple days) versus different levels of short-run (daily) unfairness bounding. We provide insights to the management in order to cope with the trade-off between cost and unfairness.

1.4 Structure of the paper

The remainder of the paper is organized as follows. In Sect. 2 the problem studied is presented together with the optimization model. In Sect. 3 the ALNS heuristic is described. Section 4 is devoted to the computational experiments and the results. Finally, in Sect. 5, some concluding remarks are provided.

2 Problem definition and modelization

The problem we deal with can be defined as follows. A set of companies agree to form a coalition offering a shared taxi service where customers book in advance the transportation on a given day of a fixed multi-day time horizon. We call request the booking, made at a specific company, of a transportation service for a number of customers on a specific day of the time horizon. The request must be accomplished within given time windows on the pickup and delivery time at origin and destination, respectively. A maximum allowed on-board time (including pick-up and drop-off service time) is known for each request. Each company has a fleet of vehicles of given capacity that have to accomplish their daily routes in a fixed amount of time. On each day of the planning horizon, a company may concede the service of some of its requests to other companies and may acquire requests from other companies. The management has several objectives: minimizing the overall cost of planned routes and minimizing the daily and the cumulated customer and time balance for each company on each day. We model the problem as an optimization problem where the objective is the minimization of the overall routing cost, and bounds are applied to the absolute values of:

  • maximum daily customer balance and daily time balance realized by any company over the time horizon;

  • maximum cumulated customer balance and cumulated time balance realized by any company on the last day of the time horizon.

Next, we formalize the notation and model the problem as a MILP.

For the sake of simplicity, in the following we describe the set of constraints for a single day f in the horizon \(F=\{1, \ldots , |F|\}\) and omit the index f from the notation. Later, we will introduce the index f only for those quantities that have a time-dependent role in the multi-day problem (i.e cost, and time and customer balance).

A set of requests \(C_m\) is associated with each company \(m\in M\), and \(C = \bigcup _{m \in M} C_m\) is the set of all requests. Each request \(c \in C\) has the following attributes: an origin \(o_c\) (pick-up point), a destination \(d_c\) (drop-off point), a demand \(p_c\) (number of customers that travel from \(o_c\) to \(d_c\)), a minimum travel time \(t_c\) (direct transfer from \(o_c\) to \(d_c\)), a service time \(s_c'\) and \(s_c''\) at origin and destination, a time window \([e_c',l_c']\) and \([e_c'',l_c'']\) at origin and destination, respectively, and a maximum time allowed on-board \(T_c\) (obviously, \(T_c \ge t_c\)).

From now on, the term ’travel time’ for a request is intended as the minimum traveling time \(t_c\) from origin to destination of customer c. We denote as \(O=\{o_c\ | c \in C\}\) and \(D=\{d_c\ | c \in C\}\) the set of all origins and destinations, respectively.

Each company \(m \in M\) has the following attributes: an origin depot \(h_m'\) and a destination depot \(h_m''\), which we denote together as \(H_m=\left\{ h_m',h_m''\right\}\), and a set of vehicles \(K_m\). We denote as \(H = \bigcup _{m \in M} H_m\) the set of all depots and as \(K = \bigcup _{m \in M} K_m\) the overall coalition fleet, where each vehicle \(k\in K\) has capacity \(Q^k\) and maximum route duration \(T^k\).

We consider a complete directed graph \(G =(V,A)\) where \(V = H \bigcup O \bigcup D\). Each node \(i \in V\) represents either a depot or an origin or a destination, while arc \((i,j) \in A\) represents a direct transfer from node i to node j with an associated traveling time \(t_{ij}\) and cost \(c_{ij}\). Each node \(i\in V\) representing an origin for a request c, i.e. \(i=o_c\) for some \(c\in C\), inherits service time \(s_i=s_c'\), time window \([e_i,l_i]=[e_c',l_c']\), and has an associated flow quantity \(q_i = p_c\). Similarly, each node \(i\in V\) representing a destination for a request c, i.e. \(i=d_c\) for some \(c\in C\), inherits service time \(s_i=s_c''\), time window \([e_i,l_i]=[e_c'',l_c'']\), and has an associated flow quantity \(q_i = -p_c\). Finally, each node \(i\in V\) representing a depot for a company m, i.e. \(i=h_m'\) or \(i=h_m''\) for some \(m\in M\), has service time \(s_i=0\), time window \([e_i,l_i]=[0,\infty ]\), and a flow quantity \(q_i = 0\).

The decision variables are:

  • binary variables \(y_c^k\): a variable takes value 1 if request \(c\in C\) is served by vehicle \(k\in K\), and 0 otherwise;

  • binary variables \(x_{ij}^{k}\): a variable takes value 1 if arc \((i,j)\in A\) is traversed by vehicle \(k\in K\), and 0 otherwise;

  • integer variables \(w_{i}^k\): a variable represents the number of on-board customers when vehicle \(k\in K\) leaves node \(i\in V\);

  • continuous variables \(u_{i}^k\): a variable represents the arrival time of vehicle k at node \(i\in V\);

  • continuous variables \(r_{c}^k\): a variable represents the time spent by request \(c\in C\) on-board vehicle k (excluding service time);

  • continuous variable \(\textit{Cost}\) represents the routing cost.

The notation for the constraints, that have to be satisfied for each day \(f \in F\), is summarized in Table 2.

$$\begin{aligned}&\textit{Cost} = \sum _{m \in M} \sum _{i \in V} \sum _{j \in V} \sum _{k \in K_m} c_{ij}x_{ij}^k&\end{aligned}$$
(1)
$$\begin{aligned}&\sum _{j \in V} x_{h_m',j}^{k} = \sum _{i \in V} x_{i,h_m''}^{k} = 1&m \in M \quad k \in K_m \end{aligned}$$
(2)
$$\begin{aligned}&\sum _{i \in V} x_{i,l}^{k} - \sum _{j \in V} x_{l,j}^{k} = 0&l \in V \quad k \in K \end{aligned}$$
(3)
$$\begin{aligned}&\sum _{k \in K} y_c^k = 1&c \in C\end{aligned}$$
(4)
$$\begin{aligned}&\sum _{j \in V} x_{o_c,j}^{k}=y_c^k&c \in C \quad k \in K \end{aligned}$$
(5)
$$\begin{aligned}&\sum _{j \in V} x_{o_c,j}^{k} - \sum _{i \in V} x_{i,d_c}^{k} = 0&c \in C \quad k \in K \end{aligned}$$
(6)
$$\begin{aligned}&u_j^k \ge u_i^k + s_i + t_{ij}-U_{ij}(1-x_{ij}^k)&i,j \in V \quad k \in K\end{aligned}$$
(7)
$$\begin{aligned}&r_c^k = u_{d_c}^{k} - (u_{o_c}^{k} + s_{o_c})&c \in C \quad k \in K \end{aligned}$$
(8)
$$\begin{aligned}&u_{h_m''}^{k} - u_{h_m'}^{k} \le T^k&m \in M \quad k \in K_m\end{aligned}$$
(9)
$$\begin{aligned}&e_{i} \le u_{i}^{k} \le l_{i}&i \in V \quad k \in K \end{aligned}$$
(10)
$$\begin{aligned}&t_{o_c,d_c} \le r_{c}^k&c \in C \quad k \in K \end{aligned}$$
(11)
$$\begin{aligned}&r_{c}^k \le T_c&c \in C \quad k \in K \end{aligned}$$
(12)
$$\begin{aligned}&w_j^k \ge w_i^k + q_i-W^k_{i}(1-x_{ij}^k)&i,j \in V \quad k \in K \end{aligned}$$
(13)
$$\begin{aligned}&\max \{0 , q_i \} \le w_{i}^{k} \le \min \{ Q^k,Q^k+q_i\}&i \in V \quad k \in K \end{aligned}$$
(14)
$$\begin{aligned}&w_{h_m'}^{k} = 0&m \in M \quad k \in K_m \end{aligned}$$
(15)
$$\begin{aligned}&y_{c}^k \in \{0,1\}&k \in K \quad c \in C \end{aligned}$$
(16)
$$\begin{aligned}&x_{ij}^k \in \{0,1\}&k \in K \quad i \in V \quad j \in V \end{aligned}$$
(17)
$$\begin{aligned}&w_{i}^k \in \mathbb {N}&k \in K \quad i \in V \end{aligned}$$
(18)
$$\begin{aligned}&u_{i}^k \ge 0&k \in K \quad i \in V. \end{aligned}$$
(19)

Equation (1) defines the daily cost of operations. Constraints (2)–(6) define the routing constraints of the model. Constraints (2) guarantee that each vehicle \(k\in K_m\) traverses exactly one arc exiting from the origin depot \(h_m'\) and exactly one arc entering the destination depot \(h_m''\) allowing only one trip per day to each vehicle. Constraints (3) guarantee flow conservation through nodes. Constraints (4) guarantee that each request \(c\in C\) is served by exactly one vehicle of the coalition. Constraints (5) guarantee that vehicle k exits origin node \(o_c\) if and only if it serves request \(c\in C\). Constraints (6) guarantee that vehicle k visits origin node \(o_c\) if and only if it also visits destination node \(d_c\). Subtour elimination constraints are implied by constraints on traveling times (7)–(12). In particular, constraints (7) ensure the consistency of the arrival time at node j visited by vehicle k after node i, provided that the constant \(U_{ij}\) is such that \(U_{ij} \ge \max \{0,l_i+s_i+t_{ij}-e_j\}\). Constraints (8) evaluate the on-board time \(r_c^k\) for each request \(c\in C\) as the difference between the arrival time of vehicle \(k \in K\) at destination node \(d_c\) and the departure time (arrival time plus service time) from origin node \(o_c\). Constraints (9) bound with \(T^k\) the route duration for each vehicle k. Constraints (10) implement the time window constraints for the visited nodes. Constraints (11), together with constraints (8), enforce precedence constraints between origin and destination of each request as, by imposing \(r_c^k\) non-negative, we enforce \(u_{d_c}^k\) in being larger than \(u_{o_c}^k\). Furthermore, according to Cordeau (2006), bounding \(r_c^k\) to be greater than \(t_{o_c,d_c}\) gives a stronger formulation. Constraints (12) bound with \(T_c\) the on-board time of each request \(c\in C\). Capacity constraints are implemented in (13)–(15). In particular, constraints (13) ensure the consistency of vehicle load at nodes visited by vehicle k provided that constant \(W^k_{i}\) are such that \(W^k_{i} \ge \min \{Q^k,Q^k+q_i\}\). Constraints (14) ensure the respect of vehicle capacity. Constraints (15) set the initial load of each vehicle k. Finally, constraints (16)–(19) define the variables domains.

Table 2 Notation—Part I
Full size table

In the following, we move from the single-day horizon to the multi-day horizon context. We formally introduce the daily and multi-day fairness constraints and present the complete multi-day optimization model. To this aim, we index quantities and variables that depend on the day of the horizon with the superscript \(f\in F\). For example, \(C_m^f\) is the set of requests of company \(m\in M\) in day f and \(Cost^f\) is the total cost in day f. To avoid a cumbersome notation, we do not make a detailed list of the quantities and variables that depend on the day f. Constraints (1)–(19) will be imposed on each day f, for all \(f \in F\). The objective function, to be minimized, is the total cost, that is the sum, over the time horizon, of the daily costs \(\sum _{f\in F}Cost^f\), where \(Cost^f\) is defined in (1). In Table 3 we summarize only the notation dependent on the day f that we will explicitly use. The level of unfairness in terms of customers and time exchange is measured through the daily and the cumulated customers and time balances, whose absolute values will be constrained by upper bounds to reduce unfairness among companies.

According to definition, the daily customer balance for company \(m\in M\) on day \(f\in F\) is computed as

$$\begin{aligned} \textit{B}_m^f = \frac{\sum _{k \in K_m} \sum _{c \in C^f\setminus C_m^f} p_c y_c^k-\sum _{k \in K\setminus K_m} \sum _{c \in C_m^f} p_c y_c^k}{\sum _{c \in C_m^f} p_c}, \end{aligned}$$

and the daily time balance for company \(m\in M\) on day \(f\in F\) is computed as

$$\begin{aligned} \textit{S}_m^f = \frac{\sum _{k \in K_m} \sum _{c \in C^f\setminus C_m^f} t_c y_c^k-\sum _{k \in K\setminus K_m} \sum _{c \in C_m^f} t_c y_c^k}{{\sum _{c \in C_m^f} t_c}}. \end{aligned}$$

In order to measure balances in the long-run and according to the definition we gave in the introduction, the cumulated customer balance for company \(m\in M\) until day \(f\in F\) is computed as

$$\begin{aligned} \textit{cumB}_m^f = \frac{\sum _{j\le f}(\sum _{k \in K_m} \sum _{c \in C^f\setminus C_m^f} p_c y_c^k-\sum _{k \in K\setminus K_m} \sum _{c \in C_m^f} p_c y_c^k)}{\sum _{j\le f}\sum _{c \in C_m^j} p_c}, \end{aligned}$$

and the cumulated time balance for company \(m\in M\) until day \(f\in F\) is computed as

$$\begin{aligned} \textit{cumS}_m^f = \frac{\sum _{j\le f}(\sum _{k \in K_m} \sum _{c \in C^f\setminus C_m^f} t_c y_c^k-\sum _{k \in K\setminus K_m} \sum _{c \in C_m^f} t_c y_c^k)}{\sum _{j\le f}\sum _{c \in C_m^j} t_c}. \end{aligned}$$

We recall that \(\textit{cumB}_m^{|F|}\) and \(\textit{cumS}_m^{|F|}\) refer respectively to the cumulated customer balance and to the cumulated time balance for company \(m\in M\) at the end of the time horizon.

The complete model is then formulated as follows:

$$\begin{aligned}&\min z= \quad \sum _{f \in F} Cost^f\end{aligned}$$
(20)
$$\begin{aligned} \nonumber&\text {+ constraints (1)--(19)}&f\in F\nonumber&\end{aligned}$$
$$\begin{aligned} \underset{m\in M,f\in F}{\max }|\textit{B}_m^f|\le \alpha ^{DC} \end{aligned}$$
(21)
$$\begin{aligned}&\underset{m\in M,f\in F}{\max }|\textit{S}_m^f|\le \alpha ^{DT}\end{aligned}$$
(22)
$$\begin{aligned}&\underset{m\in M}{\max }|\textit{cumB}_m^{|F|}|\le \alpha ^{WC}\end{aligned}$$
(23)
$$\begin{aligned}&\underset{m\in M}{\max }|\textit{cumS}_m^{|F|}|\le \alpha ^{WT} \end{aligned}$$
(24)

Observe that constraints (2)–(19) are replicated for each day of the time horizon \(f\in F\).

To control unfairness on a daily basis, Constraint (21) bounds the maximum, among all companies \(m\in M\) and all days \(f\in F\), of the absolute value of the daily customers balance to be not greater than a fixed value \(\alpha ^{DC}\)Ċonstraint (22) is its daily time balance counterpart.

To control unfairness on the long-run, Constraint (23) bounds the maximum, among all companies \(m\in M\), of the absolute value of the cumulated customers balance on the last day of the time horizon \(f=|F|\) to be not greater than the fixed value \(\alpha ^{WC}\)Ċonstraint (24) is its cumulated time balance counterpart.

Constraints (21) can be easily linearized with the matrix of constraints

$$\begin{aligned} -\alpha ^{DC}\le \textit{B}_m^f\le \alpha ^{DC}\qquad m\in M, f\in F. \end{aligned}$$

Constraints (22)–(24) can be linearized in the same way.

Table 3 Notation—Part II
Full size table

3 The algorithm

The Adaptive Large Neighborhood Search (ALNS) algorithmic approach has been widely used in the literature, especially for routing and scheduling problems (see Muller 2009; Pisinger and Ropke 2010 and references therein). The ALNS scheme, first proposed in Ropke and Pisinger (2006), is an extension of the Variable Neighbourhood Search (VNS, see Mladenović and Hansen 1997 for details) in which a number of destroy and repair operators are iteratively and pseudo-randomly applied in order to improve the current solution. The underlying metaheuristic scheme adopted is the simulated annealing (as in Ropke and Pisinger 2006) and the random choice of destroy and repair operators is guided by the success frequency they had in previous iterations.

The general ALNS heuristic is outlined in Algorithm 1. To start, the ALNS algorithm needs a feasible solution \(x_0\), which is used to initialize the current solution x and the incumbent solution \(x^*\), along with a pool of destroy and a pool of repair operators. In our case, the initial solution is the non collaborative solution, i.e. each company serves its own customers. Since the ALNS uses the simulated annealing as underlying metaheuristic, two parameters are needed: \(T_{max}\), representing the starting temperature, and \(\gamma\), representing the cooling rate at each iteration. At each iteration, in order to improve the current solution x, a destroy operator and a repair operator are randomly drawn from their respective pools. Each operator has a probability to be chosen which depends on how many times the operator has been effective, in past iterations, in finding improving solutions. The drawn destroy operator removes q requests from the current solution x and, then, the selected repair operator reconstructs a feasible, possibly improved, solution \(x'\) from the destroyed one. The repaired solution might replace the current solution depending on a probability defined according to the simulated annealing paradigm. Every R iterations in which a new incumbent solution is found, the probability to be chosen for each operation is reset to default values, i.e. equal probability to be selected.

figure a

In the ALNS heuristic we propose six destroy and three repair operators have been used. The destroy operators are the random removal, the worst removal, the related removal, the proximity removal, the closeness removal, and the interchangeability removal. The former three destroy operators resemble the original ones proposed in the seminal work of Ropke and Pisinger (2006), the fourth operator is inspired by the one introduced by Molenbruch et al. (2017) and the fifth and sixth destroy operators are inspired by the ones proposed in Angelelli et al. (2022). On the other hand, the selected repair operators are the best insertion, the k-regret insertion (with \(k=2,3\) and 4) and the closeness insertion. The former two repair operators follow the original ones suggested as performing operators for routing problems in the seminal work of Ropke and Pisinger (2006). The third repair operator is derived by the one proposed in Angelelli et al. (2022). In the following, we describe how these operators have been adapted to the multy-day horizon scenario.

Destroy operators. Each destroy operator takes in input the current solution along with the degree of destruction q. Each destroy operator removes the first of the q requests according to the operator rule and, then, removes the remaining requests among same-day requests. Removing same-day customers fosters the customers exchange among companies as they are allowed to be exchanged, if beneficial. On the contrary, removing a (usually small) number of requests to be served in different days could prevent requests to be easily exchanged as each request cannot be postponed or anticipated.

Repair operators. Given a destroyed solution, in which \(|C|-q\) requests are feasibly served and q requests have been removed, repair operators try to feasibly insert excluded requests to routes. A selection probability, according to the operator rules, will be assigned to each destroyed request and, when one is selected to be repaired, the insertion procedure is guided towards feasibility. Once a request has been selected to be inserted in the destroyed solution, a list of eligible companies \(M_{Eligible}\) is searched for such that:

  • the assignment of the request to the company does not violate the upper bound on the cumulated and/or daily constraints on customers and time,

  • after the assignment, the requests still to be assigned are able to cover the possible total violation of the lower bound of cumulated and/or daily constraints on customers and time.

Among the eligible companies \(m \in M_{Eligible}\), we search for companies with violated lower bounds on the cumulated and/or daily constraints on customers and time, creating set \(M_{Likely}\). For feasible insertion of a request in the solution, we mean the one proposed in Molenbruch et al. (2017), assessing the feasibility with respect to the maximum trip time of each request and of the involved vehicles. If \(M_{Likely}\) is not empty, then the request is feasibly assigned at the minimum cost among these companies. If \(M_{Likely}\) is empty or there exists no feasible insertion in such companies, the request is feasibly assigned at minimum cost among companies \(m \in M_{Eligible}\). In case no feasible insertion in \(M_{Eligible}\) can be found, then the solution we had before destruction is restored. Otherwise, we iterate by selecting a new request to be inserted until all removed requests have been reinserted.

4 Computational analysis

In this section, a computational study is presented to assess the effectiveness of the proposed model and the impact of parameters used to control the level of fairness of the collaboration. In Sect. 4.1, we describe the benchmark instances used. The different tested settings and the collected statistics are presented in Sects. 4.2 and 4.3, respectively. In 4.4 the computational results are provided.

The results were obtained on a Windows 64-bit computer with Intel Xeon processor E5-1650, 3.50 GHz, and 16 GB RAM. The ALNS parameters have been tuned and fixed at \(T_{max}=10^7\), \(\gamma = 0.001\) and \(q = 2\). The tuning of parameters has been done by testing a small set of instances with increasing values of \(T_{max}\), \(\gamma\) and q, following the scheme provided in Angelelli et al. (2022). We observed that greater values of \(T_{max}\) and smaller values of \(\gamma\) considerably affect computational time without significant improvements in the objective function. We also observed that enlarging the destroy radius q reduces the possibility to find improving feasible solutions in the repair phase.

4.1 The benchmark instances

To generate the instances for the computational experiments, we used the benchmark instances of groups C and D introduced in Angelelli et al. (2022). The instances have 4 companies and 48 customers for Group C and 10 companies and 100 customers for Group D on a daily basis. Each group contains instances based on 4 big European metropolitan areas (Paris, Berlin, London and Rome). For each metropolitan area, 7 demand scenarios have been generated and grouped in a 7-day (week) instance for the multi-day context. Thus, we obtained, from Group C, 4 instances with 4 companies and 48 customers per day and, from Group D, 4 instances with 10 companies and 100 customers per day. All instances are available at http://or-brescia.unibs.it/instances.

Instances have been generated by randomly choosing origin and destination addresses in the city network area and choosing a random position for the companies’ depot within the same area. Although these positions could affect the final results, in Angelelli et al. (2022), a thorough study of the impact of depot positioning has been conducted. It was found out that, when the number of customers is sufficiently large and customers origin and destination points are randomly located, as for the instances we used in this study, depots position does not impact on the effectiveness of the collaboration. In fact, depot position is just one of the many factors that influence the final results of horizontal collaboration optimization such as customers composition, the time windows distribution over customers, heterogeneity of companies in terms of number of customers.

4.2 Settings and collaboration schemes

We call setting the values we assign to parameters \(\alpha ^{DC}\), \(\alpha ^{DT}\), \(\alpha ^{WC}\)and \(\alpha ^{WT}\). Values may be assigned according to some dependency rule in order to implement a particular operational logic, which we call collaboration scheme (or just scheme for short). In this paper, we consider the following collaboration schemes:

  1. 1.

    Independent daily collaboration (Daily). The collaboration is managed every day independently of each other. The same percentage is applied to bound daily customer and time balance. No bound is applied on weekly customer and time balance. The scheme implies

    $$\begin{aligned} \alpha ^{WC}=\alpha ^{WT}=\infty . \end{aligned}$$

    We tested the following settings

\(\alpha ^{DC}\)

\(\alpha ^{DT}\)

\(\alpha ^{WC}\)

\(\alpha ^{WT}\)

0.1

0.1

\(\infty\)

\(\infty\)

0.2

0.2

\(\infty\)

\(\infty\)

0.4

0.4

\(\infty\)

\(\infty\)

The choice of values is meant to give enough margin to the model to achieve significant savings compared to the non-collaborative scheme on one side, and to maintain an acceptable level of fairness on the other side. Since a single value is enough to characterize this scheme, we may shortly represent the implemented settings as \(\textit{Daily}(\alpha )\) with \(\alpha =\alpha ^{DC}=\alpha ^{DT}\). Observe that the percentage applied every day to bound the balance implies that the same bound will be respected also for the cumulated balance at the end of the week.

  1. 2.

    Weekly collaboration with daily bounds (Weekly-DB). The collaboration is managed every day like in Daily, but a percentage is applied to bound weekly the customer and time balance and the daily bound is relaxed by doubling this percentage. The scheme implies the following relationship on the four parameters

    $$\begin{aligned} \alpha ^{DC}=\alpha ^{DT}=2\cdot \alpha ^{WC}=2\cdot \alpha ^{WT}. \end{aligned}$$

    We tested the following settings

\(\alpha ^{DC}\)

\(\alpha ^{DT}\)

\(\alpha ^{WC}\)

\(\alpha ^{WT}\)

0.2

0.2

0.1

0.1

0.4

0.4

0.2

0.2

The choice of values is meant to allow an easy and direct comparison to the Daily scheme. For example, \(\textit{Weekly-DB}(0.1)\) applies the same bound as \(\textit{Daily}(0.1)\) on the cumulated balance at the end of the week. Daily bounds in \(\textit{Weekly-DB}(0.1)\) have been doubled with respect to \(\textit{Daily}(0.1)\) in order to allow much more margin to the model on single days and to better exploit the benefits of the collaboration. Since a single value is enough to characterize this scheme, we may shortly represent the implemented settings as \(\textit{Weekly-DB}(\alpha )\) with \(\alpha =\alpha ^{WC}=\alpha ^{WT}\) and \(\alpha ^{DC}=\alpha ^{DT}=2\alpha\).

  1. 3.

    Weekly collaboration (Weekly). Two distinct percentages \(\alpha ^{WC}\) and \(\alpha ^{WT}\) are applied to bound the overall customer and time balance at the end of the week. No bound is applied on the daily customer and time balance. The scheme implies

    $$\begin{aligned} \alpha ^{DC}=\alpha ^{DT}=\infty . \end{aligned}$$

    We tested the following settings

\(\alpha ^{DC}\)

\(\alpha ^{DT}\)

\(\alpha ^{WC}\)

\(\alpha ^{WT}\)

\(\infty\)

\(\infty\)

0

0.05

\(\infty\)

\(\infty\)

0

\(\infty\)

\(\infty\)

\(\infty\)

0.05

0.05

\(\infty\)

\(\infty\)

0.05

\(\infty\)

\(\infty\)

\(\infty\)

0.1

0.05

\(\infty\)

\(\infty\)

0.1

\(\infty\)

where a set of ‘small’ bounds on the weekly cumulated customer balance are tested versus on/off bound for the time (\(\alpha ^{WT}\in \{0,\infty \}\)). Actually, as perfect null balance on times is very hard to satisfy, we used 0.05 in place of 0. This scheme is characterized by the two values of \(\alpha ^{WC}\) and \(\alpha ^{WT}\). Thus, we may shortly denote the implemented settings as \(\textit{Weekly}(\alpha ^{WC},\alpha ^{WT})\). The most interesting assignment for the parameters is \(\textit{Weekly}(0.05,0.05)\) meaning that we want the daily balance to be practically ruled out by the end of the week. We will see in the computational experiments that this collaboration scheme is very effective at almost reaching the objective of minimizing coalition costs and attaining the fairness among companies.

  1. 4.

    Unconstrained collaboration (UC). No bound is applied, neither on the daily balances nor on the weekly balance. This scheme provides a lower bound on overall cost for all other collaboration schemes. We have only one setting with

    $$\begin{aligned} \alpha ^{DC}=\alpha ^{DT}=\alpha ^{WC}=\alpha ^{WT}=\infty . \end{aligned}$$

Observe that, according to their description, \(\textit{Daily}(2\alpha )\) is a relaxation of \(\textit{Weekly-DB}(\alpha )\) which in turn is a relaxation of \(\textit{Daily}(\alpha )\).

4.3 Statistics

Comparing the collaborative models with the non-collaborative one, we consider the following measures.

  • \(\textit{Savings}:\) percentage cost savings obtained by collaborative setting with respect to the non-collaborative one;

  • \(\textit{maxB}= \max _{m,f}(|\textit{B}_m^f|)\): maximum absolute value of daily customer balance paid by any company on any day;

  • \(\textit{maxS}= \max _{m,f}(|\textit{S}_m^f|)\): maximum absolute value of daily time balance paid by any company on any day;

  • \(\textit{maxFinB}= \max _{m}(|\textit{cumB}_m^{|F|}|)\): maximum absolute value of cumulated customer balance paid by any company on last day of the time horizon;

  • \(\textit{maxFinS}= \max _{m}(|\textit{cumS}_m^{|F|}|)\): maximum absolute value of cumulated time balance paid by any company on last day of the time horizon.

We observe that statistics maxB, maxS, maxFinB and maxFinS are explicitly considered in constraints (21)–(24).

4.4 Computational results

For the sake of completeness, the 4 parameters \(\alpha ^{DC}\), \(\alpha ^{DT}\), \(\alpha ^{WC}\) and \(\alpha ^{WT}\) are reported in the tables that follow. Reported results are calculated on 4 instances (4 cities \(\{\textit{Berlin}, \textit{London}, \textit{Paris}, \textit{Rome}\}\)) for each of the two coalition sizes (i.e. a4c48, a10c100).

4.4.1 Average savings

In Table 4 we report the average Savings obtained by the tested settings with respect to the non-collaborative scheme. We observe that Savings obtained for the Weekly collaboration are comparable with those of the UC when \(\alpha ^{WC}\ge 5\%\). Only when \(\alpha ^{WC}=0\%\) we have a strong reduction in performance, which cannot be recovered even by allowing an unlimited balance of time workload (\(\alpha ^{WT}=\infty\)). However, the performance of these schemes remain comparable with that of other schemes in which a weekly bound on customer and time balance greater than \(5\%\) is allowed. As expected, the performances of Weekly-DB and Daily are, in terms of Savings, such that \(\textit{Daily}(0.1)<\textit{Weekly-DB}(0.1)<\textit{Daily}(0.2)<\textit{Weekly-DB}(0.2)<\textit{Daily}(0.4)\).

Table 4 Savings averaged on 4 instances for two coalition sizes
Full size table

4.4.2 Balances

In Tables 5 and 6 we analyze how imbalanced the most imbalanced company during the week is. The maximum of daily percentage balance realized by companies in the tested schemes is reported for customers (maxB) and times (maxS), respectively. In particular, for each instance we consider the maximum percentage balance realized by the companies during the week (maximum out of \(7\times 4\) values for coalition size a4c48, and out of \(7\times 10\) values for coalition size a10c100). We, thus, obtain 4 values for each coalition size (one for each city). We report the averages in columns Avg. maxB (customers) and Avg. maxS(times), and the maximums in columns Max. maxB and Max. maxS for each coalition size. In columns Avg. maxB and Avg. maxS we can see that for all Weekly-DB and Daily schemes values are as close as possible to the daily bounds \(\alpha ^{DC}\) and \(\alpha ^{DT}\) (observe that in coalition size a4c48 every single customer weighs \(8.33\%\) in the balance), proving that on all instances the bound is tight. A fortiori, also columns Max. maxB and Max. maxS, where the maximum is reported in place of the average, are close to the bound. Indeed, the UC scheme, which does not apply any bound on the balances, reports for maximum values always above \(50\%\). Thus, the daily bound must become active in Weekly-DB and Daily schemes, where the applied daily bound is always below \(40\%\). However, in the Weekly scheme, we observe that both maximum and average values are higher than those produced by the UC scheme when \(\alpha ^{WC}>0\). This phenomenon can be explained by the fact that, having to close the accounts at the end of the week, some balances are even more stretched during the week. When \(\alpha ^{WC}=0\), the exchanges remain a little smaller, but as we have seen, at the expense of cost performance.

Table 5 Average and Maximum of maximum customer daily exchange (maxB) on 4 instances for 2 coalition sizes
Full size table
Table 6 Average and Maximum of maximum time daily exchange (maxS) on 4 instances for 2 coalition sizes
Full size table

In Tables 7 and 8 we analyze how imbalanced the most imbalanced company at the end of the week is, taking into account all the exchanges incurred in that period. The maximum of the cumulated percentage balance, realized on the last day of the week by companies in the tested schemes, is reported for customers (maxFinB) and times (maxFinS), respectively. In particular, for each company, we consider the maximum percentage of the cumulated balance realized at the end of the week with respect to the workload of the whole week, for each coalition size (e.g. a4c48 and a10c100). We, thus, obtain 4 values for each coalition size (one for each city). We report the averages in columns Avg. maxFinB (customers) and Avg. maxFinS(times), and the maximums in columns Max. maxFinB and Max. maxFinS for each coalition size.

Furthermore, we immediately observe that, in general, these values are much smaller than the corresponding maximum values reported in Tables 5 and 6. This indicates that during the week each company realizes both positive and negative balances which, to some extent, compensate each other in the long run.

From the obtained results, we can also observe some significant difference in the values produced by the tested schemes. In particular, as expected, the UC scheme produces maximum values that are similar between customers and times and significantly high: around \(12\%\) and \(20\%\) for coalition sizes a4c48 and a10c100, respectively. This suggests that, in the case of unconstrained collaboration, some company may be systematically overloaded (or devoid) and a certain imbalance is generated in exchanges from or towards one or more companies.

In terms of maximum and average cumulated exchange balance, the schemes Weekly-DB and Daily appear to be not well-performing with respect to the UC  as for \(\alpha ^{WC}\ge 0.2\) they produce a similar average and maximum values of cumulated balance for both customers and times while they do not reach the savings of UC scheme. When \(\alpha ^{WC}=0.1\) the exchanges improve a lot, but the Savings definitely deteriorate.

The scheme Weekly seems to perform better versus the UC scheme producing values almost always largely smaller; on the other side the Savings are comparable.

Table 7 Average and Maximum customer cumulative exchange balance (maxFinB) on day 7
Full size table
Table 8 Average and Maximum time cumulative exchange balance (maxFinS) on day 7
Full size table

In Tables 9 and 10 we investigate how imbalanced the companies during the week are, both on single days and with respect to the cumulated balance up to any intermediate day of the week. In the previous tables, we investigated the maximum level of dissatisfaction; here we address the global satisfaction. In particular, for each coalition size, we consider the daily and cumulated balance on each day of the week for each company. As we have 4 instances, we end up with a sample of \(4\times 7\times 10=280\) daily (and cumulated) balance values for the coalitions of size a10c100 and with \(4\times 7\times 4=112\) daily (and cumulated) balance values for the coalitions of size a4c48. We average the samples both for customer and time balance.

Table 9 Average over daily (B) and cumulative (cumB) customer exchange balance
Full size table
Table 10 Average over daily (S) and cumulative (cumS) time exchange balance
Full size table

Given that every situation has its own peculiarities, many of the proposed schemes ensure a good trade-off in terms of Savings and balance. On the tested instances, the Weekly scheme performs similarly to the UC one and controls very well the balance over the time horizon. In fact, if no daily bounds are required, the Weekly produces the best trade-off results in terms of fairness and efficiency.

4.4.3 Average savings versus balances

We depict, in Figs. 6 and 7, some results already reported numerically in Tables 4-8. In Fig. 6 we consider the average values obtained by a sample of collaboration schemes on all cities for the coalition size a4c48. In the top row, we plot the average Savings versus the average of maxB and maxS (Customers and Times) reporting column Savings of Table 4 vs. columns Avg.maxB and Avg.maxS of Tables 5 and 6, respectively. In the bottom row, we plot the average Savings versus the average of maxFinB and maxFinS (Customers and Times) reporting column Savings of Table 4 vs. columns Avg.maxFinB and Avg.maxFinS of Tables 7 and 8, respectively. Analogous results are reported in Fig. 7 for coalition size a10c100.

Fig. 6
figure 6

Average Savings versus maxB (up-left), maxS (up-right), maxFinB (bottom-left) and maxFinS (bottom-right)

Full size image
Fig. 7
figure 7

Average Savings versus maxB (up-left), maxS (up-right), maxFinB (bottom-left) and maxFinS (bottom-right)

Full size image

We observe that, while scheme \(\textit{Weekly}(0.05,0.05)\) attains the Savings closest to UC scheme, in general it provides the worst (highest) values of maxB and maxS, but definitely excellent values of maxFinB and maxFinS. Thus, it is an excellent candidate for an actual implementation of collaboration.

The same pattern is followed in Figs. 8 and 9, where the case of a single instance (Berlin) is presented for coalition size a4c48 and coalition size a10c100.

All Figs. 6, 7, 8 and 9 should be read in terms of a multi-objective problem where we want the points on the graphs to be as far to the right, as the more right the point is the higher the saving is, and as low as possible, as the lower the point is the lower the balance is.

With respect to the cumulated balances at the end of the week (bottom rows of the figures) we observe that the point representing \(\textit{Weekly}(0.05,0.05)\) is efficient with respect to the point representing the UC scheme: a slightly smaller savings, but a smaller unfairness as well. Moreover, \(\textit{Weekly}\,\,(0.05,0.05)\) produces the second best saving after UC while having the least cumulated balances at the end of the week. The same can not be said of UC, which is more unfair than several other collaboration schemes.

On the contrary, with respect to the maximum daily balance over the week, the Weekly scheme seems to perform often worse than other schemes. However, collaboration schemes able to perform much better the Weekly in this regard, have a very poor performance in terms of savings.

Thus, from a managerial viewpoint, the collaboration initiative can be exploited to obtain great savings with a very small level of cumulated unfairness at the end of the period, or to obtain smaller savings with a day-by-day high level of unfairness.

Fig. 8
figure 8

Average Savings versus maxB (up-left), maxS (up-right), maxFinB (bottom-left) and maxFinS (bottom-right)

Full size image
Fig. 9
figure 9

Average Savings versus maxB (up-left), maxS (up-right), maxFinB (bottom-left) and maxFinS (bottom-right)

Full size image

4.4.4 Day-by-day balances

In Fig. 10 we provide detailed results obtained by the \(\textit{Weekly}(0.05,0.05)\) scheme, on each day of the horizon \(F=\{1,2,...,7\}\) for each company on instance Berlin in coalition size a4c48.

Fig. 10
figure 10

Daily and cumulated customer and time balance for the given scheme

Full size image

In particular, we show the percentage cumulated customer balance (top row) and percentage cumulated time balance (bottom row) as determined by the collaboration scheme. The bar charts report day-by-day the percentage balance, while in the line charts we see the cumulated percentage balance. We can observe that all companies are involved in the exchange almost every day and with alternating signs. As expected, exchanges present a peak (on day 5), but are quite limited for the rest of the week. Not surprisingly, the cumulated percentage balance tends to be smoother as time goes on in the week. At the end of the week, \(\textit{Weekly}(0.05,0.05)\) manages to keep the most imbalanced company at the end of the week quite under control, as required by the model. In Appendix B we report the same kind of figures concerning all other schemes we reported in Fig. 6 (see Figs. 11, 12, 13, 14, 15 and 16).

5 Conclusions

In this paper, we have presented an optimization model that controls the level of fairness in the assignment of customers to shared taxi companies engaged in a collaboration initiative. The model assigns the customers with the objective of minimizing the total routing cost while bounding the number of customers and the traveled time of each company over a pre-defined time horizon and/or in a single day. Different approaches to control the fairness are compared on a set of benchmark instances. The computational results show the flexibility of the multi-day approach and its potential to further reduce the operational costs compared with the single-day optimization and, at the same time, to be fair to all companies, and, thus, to make the collaboration sustainable.

Further research should be devoted to the application of the approach to companies engaged in different transportation services and to experiments on real data. Other approaches may be designed that have the same goal, that is to guarantee to each company involved in a collaboration that it will always gain from the collaboration (daily certainly or over a period of time). Only with this guarantee the collaboration initiative can be sustainable and exploit its potential to reduce the environmental impact of transportation services.