Interactions between the individual and the group level in organizations: The case of learning and group turnover

Abstract

Previous research on organizations often focuses on either the individual, team, or organizational level. There is a lack of multidimensional research on emergent phenomena and interactions between the mechanisms at different levels. This paper takes a multifaceted perspective on individual learning and autonomous group formation. To analyze interactions between the two levels, we introduce an agent-based model that captures an organization with a population of heterogeneous agents who learn and are limited in their rationality. To solve a task, agents form a group which experiences turnover from time to time, i.e., its composition changes periodically. We explore organizations that promote learning and changes in group composition either simultaneously or sequentially and analyze the interactions between the activities and the effects on performance. We observe underproportional interactions when tasks are interdependent and show that pushing learning and group turnover too far might backfire and decrease performance significantly.

1 Introduction

Learning in organizational contexts and issues related to dynamic capabilities are usually researched at different (and often isolated) levels. First, at the level of the individual, research mainly addresses the enablers of learning and causes of group turnover–i.e., periodical changes in group composition–, contingencies, and the effects of learning and group turnover for the individual (Jyothibabu et al. 2010; Murray and Moses 2005). Second, at the organizational level, research is often concerned with developing and maintaining learning systems, institutionalizing learning in terms of embedding it into the processes, structures and strategies effective in the organization, promoting learning, and issues related to how organizational capabilities emerge (Fiol and Lyles 1985; Teece et al. 1997). Third, at the intermediate level, the importance of groups to link the individual and the organizational level is usually emphasized. It is addressed how individually learned information can be integrated, shared and adjusted (Murray and Moses 2005). Research on learning at the intermediate level is, for example, concerned with how to compose groups ideally, how to use individual knowledge optimally, and how to take advantage of synergies (Bell and Outland 2017; LiCalzi and Surucu 2012). Nevertheless, since the capabilities at the individual level might be dynamic because of learning, the composition of groups at the intermediate level may have to be dynamic too. Thus, the layers are apparently interrelated.

Previous studies often take an unidimensional perspective and focus on one level only. This lack of integration across levels reflects the micro–macro divide that is predominant, for example, in the field of managerial science (Aguinis et al. 2011; Molloy et al. 2011). The focus on only one of the interrelated levels can, to some extent, be explained by disciplinary borders (Bargiela-Chiappini and Nickerson 2002). Research in psychology, for example, tends to focus on issues related to learning at the individual level. In contrast, research on organizational design is likely to be more interested in matters concerning the collective level. To overcome the gap between micro- and macro-level research, Hitt et al. (2007) recommend (1) applying a multi-level design to existing models, (2) considering the consequences of micro-level activities for macro-level performance, (3) pushing disciplinary boundaries, and (4) addressing problems of practical relevance.

Our research follows the suggestions provided by Hitt et al. (2007). We apply a multi-level approach that connects the individual and group level. In particular, we investigate whether individual learning and adaptive group composition mutually reinforce or attenuate each other concerning their effects on performance. We aim at answering the following research questions: (1) How will individual learning and changes in group composition interact and affect task performance if they are promoted simultaneously? (2) When individual learning and changes in group composition are promoted sequentially, what are the effects on performance in the sequential stages? (3) Are there any moderating effects of task decomposability, i.e., the fact that the tasks assigned to different agents are interdependent or not?

To answer these questions, we propose an agent-based model with a population of heterogeneous agents who are limited in their rationality (Simon 1957). In our model, the limitations imposed on agents are two-fold: First, the agents’ abilities to solve tasks are restricted to a particular area of expertise. In an organizational context, we consider agents who are experts in fields such as accounting, marketing, or production management. Second, agents have limited information within their area of expertise and limited cognitive capabilities. Consequently, they cannot oversee the entire solution space immediately but explore it only sequentially. This means that agents learn new ways to perform their tasks over time (Leitner and Wall 2020). The population of agents autonomously forms a group employing an auction-based mechanism, and agents can re-organize their groups from time to time.

We base our model on the well-known $N\!K$-framework that allows placing the agents in task environments of different complexity (Levinthal 1997; Wall and Leitner 2021). A related model is employed in Blanco-Fernández et al. (2021) and Blanco-Fernández et al. (2022). Nevertheless, while they mainly analyse the dependence of the macro-level outcome of selected model parameters, we follow a multi-level approach and particularly focus on the analysis of interdependencies between the individual and the group level in organizations. We deem our multi-level approach to analyze interactions between individual learning and group turnover a relevant contribution to bridging the gap between the micro- and macro-level in managerial science. Our results are also of relevance for decision making in organizations since such multi-level approaches appear to be particularly interesting for corporate practice (Aguinis et al. 2011).

The remainder of this paper is structured as follows: We discuss the related literature on dynamic capabilities and multi-level considerations, individual learning and bounded rationality, and group formation and turnover in Sect. 2. The simulation model is introduced in Sect. 3. The results of the simulation experiments are presented in Sect. 4 and discussed in Sect. 5. Finally, Sect. 6 concludes the paper.

2 Related research

2.1 Dynamic capabilities and multi-level considerations

An organization’s dynamic capabilities are usually regarded as some sort of higher-order capability that affects how tasks are solved (Winter 2003). Dynamic capabilities are manifold, making it particularly difficult to find a coherent and tangible definition (Spanuth et al. 2020). We follow the conceptualization provided in Zollo and Winter (2002), according to which dynamic capabilities are the stable and learned patterns of activity within an organization, through which an organization modifies its routines. In the dynamic capabilities framework, the learning of the routines needs to take place at both the individual and organizational level and is driven by a steady demand for adaptation to the task environment. Naturally, having learned the appropriate patterns of activity substantially increases task performance (Eisenhardt and Martin 2000; Teece et al. 1997). This means that individuals and organizations need to reconfigure their capabilities (e.g., knowledge, skills, abilities) to meet the requirements for solving the tasks they face efficiently and successfully.

Bendig et al. (2018) argue that there are two parallel developments in this research context: The first stream of research focuses on the micro-foundations of how capabilities evolve and aims to understand how learning by individual employees aggregates to an organization’s capability (see, e.g., also Abell et al. 2008). The second stream of research exclusively focuses on the macro-level and analyzes how managerial decisions at the top level affect an organization’s performance (Helfat and Martin 2015).

Accordingly, prior research attempts to bridge these micro- and macro-level features by studying the interrelations between dynamic capabilities at the individual and collective level. Barkoczi and Galesic (2016) and Lazer and Friedman (2007), for instance, study how the adoption of social learning strategies moderates the effect of network structures on task performance. Piezunka et al. (2022) find that organizations should balance information aggregation at the collective level with promoting individual learning, while Fang et al. (2010) examine the relationship between organizational learning and the degree of interaction between subgroups. Finally, Estévez-Mujica et al. (2018) show that individual learning interacts with group composition, specifically, with the degree of homophilic interactions between group members and with diversity in individual knowledge.

These prior studies reflect how research related to the emergence of dynamic capabilities is tightly connected to the literature on learning in organizational contexts. The latter distinguishes between three levels of learning, i.e., (1) individual learning, (2) team learning, and (3) organizational learning (see, e.g., Edmondson et al. 2001; Kirkman and Rosen 2000; Murray and Moses 2005; Senaratne and Malewana 2011). By doing so, the literature on learning adds an intermediate layer to the two levels already considered in the context of dynamic capabilities, i.e., a group level between the individual and the organizational level. Murray and Moses (2005) emphasize the role of the intermediate layer and particularly underline the role of learning at the level of teams as a link between individual and organizational learning. Also, it is widely agreed in previous research that individual learning is the foundation for learning at higher levels and that the learning outcomes at the collective level are more than the accumulation of individual learning (Casey 2005; Dodgson 1993; Garratt 1987; Hedberg 1981; Miller 1996; Popper and Lipschitz 2000).¹ As Vriend (2000) argue, individual- and collective-level learning are interrelated processes which differ in their functioning and effects on task performance.

Within this three-layer framework, our focus follows an argument put forward by Simon (1991). He claims that learning in organizations may occur in two ways: First, the individual members of an organization may learn. Second, the organization may ingest new members who have new knowledge that was not available to the organization before. In line with this argumentation, we focus on understanding the effects of a variation in two organizational design parameters, namely (1) individual learning and (2) periodical changes in group composition. For this purpose, we consider the probability of learning at the individual level and groups of different lifetimes. Our research analyzes how efficiently agents use the information they have previously learned and how promoting learning and changes in group composition affects the performance of organizations.

2.2 Individual learning and bounded rationality

In the literature on learning in organizations, there are two main streams of research. The first stream focuses on the enablers of learning, the second on the results of learning in organizations (Jyothibabu et al. 2010). Research focusing on the enablers of learning explores and discusses ways and means to promote individual learning. Such ways and means comprise, for example, the methods of mentoring (Lankau and Scandura 2007), learning by doing or exploration (Arrow 1971; Beugelsdijk 2008), fostering a creative working environment (Annosi et al. 2020; Oldham 2003), employee training (Salas et al. 1999; Tharenou et al. 2007), and the design of information flows (Cohen 1991). In this paper we are not concerned with the efficiency of the different ways and means to promote learning but rather consider them as given. We locate our research in the second stream. Hence, we particularly emphasize the effects of promoting individual learning on performance, its interplay with promoting changes in group composition, and the results for an organization. Thereby, we contribute to closing the gap between (changes in) micro-level behavior, i.e., the behavior of individual agents, and the organization’s macro-level outcome (Aguinis et al. 2011).

Following the concept of dynamic capabilities, individual learning allows for adapting to the requirements posed on the organization by dynamic environments, which, in turn, is key to organizational competitiveness and survival (Teece et al. 1997). As soon as we break down the problem of adaptation to smaller entities within the organization—such as groups or individual decision-makers – and consider decentralized decision-making authority, a similar but extended argumentation applies: From the perspective of the individual, it is not just important to adapt to the organizational environment by learning, but the individual agent is also well-advised to adapt to their individual environment when making decisions. This individual environment captures, for example, the decisions made by fellow agents within a group. This is particularly relevant if the tasks assigned to different decision-makers are interdependent (Rivkin and Siggelkow 2007).

Learning at the individual level is affected by characteristics such as cognitive capability, learning styles, and interpretative ability (Crossan et al. 1999; Murray and Moses 2005; Neisser 2014). Research often considers limitations in these characteristics and addresses, amongst others, decision-makers who over-weight information in favor of prior beliefs (Darley and Gross 1983), slant information towards a preferred state (Kunda 1990), and over- or under-react to information (Leitner et al. 2017). More generally speaking, research often assumes that individual agents suffer from the limitations of bounded rationality in the sense of Simon (1957), to which Hendry (2002) refers as ‘incompetence’. In particular, he argues that humans might have limited knowledge and foresight and face limitations of rational understanding and communication that may arise from language, culture, and cognition (see also Martin 1993). Of course, this directly translates into consequences for individual learning. First, suppose humans suffer from limited foresight. In this case, they might have problems in correctly predicting the outcomes of their future actions, or they might not be able to form beliefs about the actions of others (Enke and Zimmermann 2019). Second, if the cognitive capabilities are limited, decision-makers might not be able to understand and oversee their entire solution space. In practical terms, one might not be aware of all feasible ways to carry out a specific task at a time but rather sequentially explore this space (Leitner and Wall 2020). Third, the extent to which learning is successful might be affected, amongst others, by the individuals’ cultural backgrounds (Kim and McLean 2014) or their technical literacy (Qureshi et al. 2009).

There is a long tradition of studying (individual) learning in organizational contexts. March (1991), for example, relates decision-making to a process by which agents balance learning new solutions to a particular task (i.e., exploration) and building on the solutions they already know (i.e., exploitation). By choosing a specific mix of both strategies, agents adapt more or less successfully to the organizational and individual environments. Previous research suggests that an appropriate balance of exploration and exploitation is the key to improving task performance (Levinthal 1997; March 1991; Rivkin and Siggelkow 2003). In particular, it has been found that exploration is important for increasing task performance in the early stages of task-solving, but exploitation becomes more relevant in later periods (Leitner and Wall 2021; Levinthal 1997; Yang et al. 2007).

2.3 Group formation and turnover

In Sect. 2.1 we addressed the intermediate level of the group that plays a pivotal role in organizational learning since it links the individual and the organizational level. One fundamental question in this context is how groups should be ideally composed (Higgs et al. 2005). Mello and Ruckes (2006) argue that heterogeneous groups perform better than homogeneous groups since heterogeneity assures access to various information. The argument that heterogeneity might increase the performance is in line with the findings presented in LiCalzi and Surucu (2012), who analyze the power of heterogeneous agents joining forces in a group to solve tasks over a large solution space. They find, for example, that larger groups can solve problems that individual agents cannot solve alone. They also claim that positively correlated abilities of agents require larger groups to solve tasks efficiently. Nevertheless, they also show that teaming up does not necessarily guarantee success in all cases. Further empirical evidence corroborates this finding by relating the poor performance of heterogeneous groups to differences in the agents’ abilities and characteristics and to heterogeneous preferences, which cause different behaviors and objectives (Ancona and Caldwell 1992; Bertrand and Schoar 2003).

The characteristics that make a group heterogeneous are manifold. Previous research argues that heterogeneity might result from differences in the social background, age, gender, education, national culture, and professional development, amongst others (Bell 2007; Bell and Outland 2017; Hoffman and Maier 1961; Hofstede et al. 1991; Mello and Ruckes 2006). Krech et al. (1962) provide a systematic analysis of the variables that might affect the performance of groups and clusters them into four categories: (1) structural variables (characters, talent, size, etc.), (2) situative environmental variables (e.g., functional position), (3) task-related variables (type of task, restrictions in, e.g., time, etc.), and (4) intervening variables (personal relations, level of interaction, etc.). Following the categorization provided in Krech et al. (1962), we focus on the role of the (1) structural variables in group heterogeneity. Also in line with the arguments brought forward in Mello and Ruckes (2006), we consider the professional background by explicitly modeling agents that are experts in specific fields, such as accounting, marketing, or production management. We do not take into account the (2) situative and (4) intervening variables. Our research, however, actively controls for the (3) task-related variables by modeling tasks of different degrees of decomposability and complexity.

We follow the argument raised by Simon (1991) and use the intermediate group level to endow the group with knowledge that was not available earlier. We do so by ensuring that only those agents who are best prepared for the task join forces in a group. Groups can be formed either by a top-down or a bottom-up approach. The top-down approach corresponds to the idea of classical organizational design and considers that managers conceptually develop a group’s composition before implementation (Romme 2003). The bottom-up approach, on the contrary, follows an evolutionary perspective and regards a group’s composition as an emergent property (Tsoukas 1993). This corresponds to the ideas of plastic control (Popper 1978) and guided self-organization (Prokopenko 2009). In our paper, we follow the bottom-up approach to group formation and implement a corresponding mechanism based on a second-price auction. The design of this mechanism is inspired by previous research in the fields of robotics and transportation research, which also employs auction-based mechanisms for bottom-up task allocation and collaboration (Dai and Chen 2011; Ng et al. 2020; Rizk et al. 2019).

Since we consider agents with dynamic capabilities, a group composition yielding the best possible results at one particular point in time is not necessarily the optimal composition at another point in time. This argumentation is in line with research on the interface between dynamic capabilities and temporary organizations. Spanuth et al. (2020), for example, claim that temporary structures enhance an organization’s innovative capacity and strategic flexibility, finally resulting in better performance. We account for this relationship by controlling for a group’s lifetime and analyzing the effects of different lifetimes on performance. Examples of autonomously formed (temporal) groups can, amongst others, be found in the context of agricultural cooperatives (Hannachi et al. 2020), consulting firms (Creplet et al. 2001), and professional services partnerships (Gershkov et al. 2009).

3 The model

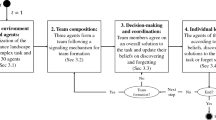
We set up an agent-based model of an organization formed by a population of $P=30$ agents. This organization aims at solving a particular task. We endow the agents with (heterogeneous) capabilities related to specific areas of expertise.² The agents are limited in their cognitive capacities. For example, they might have limited cognitive resources and they suffer from restrictions in information processing. As a consequence, they cannot handle the task alone but have to collaborate with other agents. That is why a subset of the agent population autonomously forms a group of M members who jointly solve the task. The group formation mechanism follows the idea of a second-price auction. Depending on the studied scenario, we allow for individual learning (see Sect. 3.2) and changing the group’s composition from time to time (see Sect. 3.3). We run simulations and observe the agents’ behavior and the task performance achieved by the group over $t=\{1,\dots ,T\} \subset \mathcal {N}$ periods. In the following subsections, we introduce the model’s three main building blocks: (1) the task environment in Sect. 3.1, (2) agents and individual decision-making in Sect. 3.2, and (3) the group formation mechanism in Sect. 3.3. Section 3.4 discusses the key parameters and the sequencing during simulation runs. Finally, in Sect. 3.5, we introduce the performance measures.

3.1 Task environment

Task and performance contributions—We represent the task environment by a performance landscape based on the $N\!K$ framework with an N-dimensional decision-making task and K interdependencies among decisions. We denote the task by the binary vector

$$\begin{aligned} \textbf{d}=\left( d_1, \dots , d_N \right) ~, \end{aligned}$$

(1)

consisting of N individual decisions $d_n$, where $n=\{1,\dots ,N\}$ and $d_n \in \{0,1\}$. For this paper, we set $N=12$. Thus, there are $2^{12}$ feasible solutions to $\textbf{d}$ that all take the form of a 12-digit binary string.³

There are K interdependencies among the individual decisions that determine task complexity and decomposability (i.e., the extent to which tasks are decomposable). Higher values of K stand for more interdependencies and, thus, higher task complexity. In our framework, the interdependencies indicate that the outcome of a single task is not only affected by the decision associated with this task but also by K other decisions (Levinthal 1997). The decomposability is affected by the patterns of interdependencies. We denote the performance contribution of an individual decision $d_n$ by the pay-off function

$$\begin{aligned} c_n=f(d_n, d_{i_1}, \dots , d_{i_K})~, \end{aligned}$$

(2)

where $\{i_1, \dots , i_K \} \subseteq \{1, \dots , n-1, n+1, \dots , N \}$. Following the $N\!K$ framework, we draw the performance contributions of individual decisions independently from a uniform distribution so that $c_n \sim U(0,1)$ (Weinberger and Kauffman 1989).

In line with the $N\!K$ framework, we compute the overall task performance as the mean of all individual performance contributions, such that

$$\begin{aligned} C \left( \textbf{d} \right) = \frac{1}{N} \sum ^{N}_{n=1} c_{n}~, \end{aligned}$$

(3)

Subtasks Recall that the population of agents forms a group of M members who jointly perform the task. We symmetrically divide the N-dimensional task into M subtasks of size $S=N/M$, and we sequentially assign agents a subtask.⁴ Thus, within the group, all agents $m=\{1,\dots ,M\}$ are assigned their subtasks, such that

$$\begin{aligned} \textbf{d}_m = \left( d_{S\cdot (m-1)+1},\dots , d_{S\cdot m} \right) ~, \end{aligned}$$

(4)

where $S\cdot (m-1)+1$ to $S\cdot m$ indicate the decisions of each subtask. For instance, with a task consisting of $N=12$ decisions and a group of $M=3$ agents, each subtask is formed by $S=N/M$= 4 decisions. This means that agent $m=1$ is responsible for individual decisions 1 to 4, agent $m=2$ is in charge of decisions 5–8, and decisions 9–12 are assigned to agent $m=3$. The subtasks can be related to specific areas of expertise that reflect the need for different skills required to solve tasks (Hsu et al. 2016). During the phase of model initialization, we randomly place every agent in the population in one area of expertise. Agent 1 might, for example, be an expert in accounting, while agents 2 and 3 could be experts in, e.g., marketing and production management, respectively. Once placed in an area of expertise, the agents’ respective capabilities are limited to performing tasks that are within this area (Giannoccaro et al. 2019; Hsu et al. 2016; Rivkin and Siggelkow 2003).

Task decomposability—Since our aim is to understand the moderating role of task decomposability, we explicitly control for the patterns of interdependencies. We consider the following two cases:

• In the case of a decomposable task, every decision affects the contributions of three other decisions ($K=3$) of one subtask. Figure 1A (Decomposed tasks) illustrates this case. The solid lines and ‘x’ indicate the subtasks and interdependencies, respectively. There is complete interdependence within subtasks but no cross-interdependencies with other agents’ subtasks. Thus, one agent’s individual decisions do not affect the performance contributions associated with decisions assigned to other agents.

• In the case of an interdependent task, each decision affects the contributions of five other decisions ($K=5$). Interdependent tasks are characterized by cross-interdependencies between the agents’ respective subtasks. This structure implies that an agent’s decisions also affect the performance contributions associated with decisions assigned to other agents (see Fig. 1B, Interdependent tasks).

Fig. 1

Interdependence matrices

Performance landscape—The number of decisions N, the task complexity K, and the performance contributions jointly determine a particular performance landscape. We use the pay-off function introduced in function Eq. (2) to map the $2^N$ feasible solutions to their performances, resulting in the performance landscape. If there are no interdependencies between individual decisions ($K=0$), the resulting performance landscape will have a single peak. Increasing K to its maximum of $K=N-1$, results in maximally complex performance landscapes since altering one single decision would affect the outcomes associated with all tasks. Consequently, as K increases, the performance landscape gets more rugged with numerous local maxima in the extreme case (Altenberg 1994; Rivkin and Siggelkow 2007). By making decisions, the group moves in the performance landscape and follows the objective to increase its performance step-wise. The following section introduces the agents’ characteristics and their decision rules.

3.2 Agents and individual decision-making

Agents’ characteristics—Recall that we model a population of $P=30$ heterogeneous agents. Bounded rationality imposes limits on them in two respects (Simon 1957). First, agents are limited in their cognitive capacity and can only perceive a subtask but not the entire decision problem. In consequence, agents are experts in one area such as accounting, marketing, or production management. Also, agents do not monitor the history of solutions to the decision problem, which results in myopic agents who only optimize their immediate utility and refrain from making forecasts based on the history of solutions (Artinger et al. 2021; Leitner and Wall 2020). Second, the limitation in the cognitive capacity also affects the agents’ search behavior and memory. Our model considers agents who, when making their decisions, cannot oversee the entire solution space but only possess the cognitive capabilities to evaluate some solutions at a time. We endow agents with the ability to explore feasible solutions to their subtasks sequentially and forget already explored solutions because of their limited memory.

Individual learning—To overcome the limitations at the level of the performance components, agents explore the solution space over time, i.e., they learn.⁵ Recall, Eq. (4) denotes agent m’s subtasks by $\textbf{d}_m$. Since we model binary decisions, the set of feasible solutions to subtask $\textbf{d}_m$ includes $2^{S}$ solutions, which we refer to as solution space. Above, we argue that agents cannot oversee the entire solution space at a time. Let us refer to the solutions that agent m is aware of in period t by

$$\begin{aligned} {\textbf{S}}_{mt} =\{\hat{\textbf{d}}_{m1},\dots ,\hat{\textbf{d}}_{mI}\}~, \end{aligned}$$

(5)

where $\hat{\textbf{d}}_{mi}$ are bitstrings that represent feasible solutions to subtask $\textbf{d}_m$, $i=\{1,\dots ,I\}$ and $1 \le I \le 2^{S}$. If agent m is, for example, an expert in production management, ${\textbf{S}}_{mt}$ would represent all possible ways to organize the production process she is aware of in period t. Consequently, the symbol I is a proxy for agent m’s cognitive capacity. The higher (lower) value of I, the more (fewer) solutions the agent knows to the subtask. The known solutions are dynamic, so I changes over time. At every period, agents might learn new solutions that differ in one bit from any of their already known solutions, or they forget solutions that are not utility-maximizing in the current period.

Our characterization of individual learning follows Miller and Martignoni (2016) and reflects the limited cognitive capacities of the agents. Specifically, this characterization of individual learning is built on the observation that human knowledge deteriorates over time. This has several implications for exploration in groups. Specifically, as Miller and Martignoni (2016) show, forgetting causes agents to learn constantly, as they might forget some solutions over time. This, in turn, increases creativity, i.e., the diversity of solutions employed by a group of agents. To account for this characterization, we define learning and forgetting as two independent processes that occur with a fixed probability $\mathbb {P}$. By setting equal probabilities for learning and forgetting, we ensure that agents do not know all possible solutions at the same time (LiCalzi and Surucu 2012; Miller and Martignoni 2016). We consider the following three scenarios:

• In the case of zero individual learning, agents neither learn nor forget any solution they already know, so we set $\mathbb {P}=0$.

• In the case of moderate individual learning, we set $\mathbb {P}=0.25$.

• In the case of high individual learning, we set $\mathbb {P}=0.5$.

Initially, agents are aware of one solution to their subtask. Depending on the value of $\mathbb {P}$, the agents’ known solution spaces are more or less dynamic. Increases in the value of $\mathbb {P}$ could indicate that organizations support employees in learning, e.g., by providing learning resources, training, or incentives for the creation of new products, procedures, and methods (Creplet et al. 2001). We refer to the actions taken by the organization to increase the probability of learning (i.e., to increase $\mathbb {P}$) as promoting individual learning.

Individual decision-making rule—In every period, every agent m who is part of the group can decide which solution in her solution space ${\textbf{S}}_{mt}$ she wants to implement. We denote the solution to agent m’s subtask implemented in period t by $\textbf{d}_{mt}$. We formalize the corresponding decision rule in Eq. (9).

Agent m’s utility in period t results from the performance contributions generated by the implemented solution to her subtask (i.e., her own performance) and the performance generated by the solutions implemented by the remaining agents $r=\{1,\dots ,M\}$, where $r\ne m$. We define agent m’s performance as the mean of the performance contributions coming from the decisions of their assigned subtask. We denote it by $C(\textbf{d}_{mt})$ and compute it by:

$$\begin{aligned} C(\textbf{d}_{mt})= \frac{1}{S} \sum ^{S} c_{S\cdot (m-1)+1}~, \end{aligned}$$

(6)

where $c_{S\cdot (m-1)+1}$ is the contribution of its associated decision $d_{S\cdot (m-1)+1}$ to performance (see Eq. 4). The performance of the remaining agents is the residual performance. We denote the other agents’ solutions by

$$\begin{aligned} \textbf{D}_{mt} = \left( \textbf{d}_{1t}, \dots , \textbf{d}_{\{m-1\}t}, \textbf{d}_{\{m+1\}t},\dots , \textbf{d}_{Mt} \right) ~. \end{aligned}$$

(7)

It follows that the performance of the residual decisions $C(\textbf{d}_{rt})$ is calculated following Eq. (6) for $r \ne m$ Then, agent m’s utility follows the linear function

$$\begin{aligned} U \left( \textbf{d}_{mt}, \textbf{D}_{mt} \right) = \alpha \cdot C(\textbf{d}_{mt}) + \beta \cdot \frac{1}{M-1} \sum _{\begin{array}{c} {r=1}\\ {r\ne m} \end{array}}^{M} C(\textbf{d}_{rt}) ~. \end{aligned}$$

(8)

We compute the performance in line with Eq. (3). The agent’s utility is affected by a linear incentive scheme that is parameterized by $\alpha \in \mathbb {R}$ and $\beta \in \mathbb {R}$ to weight agent m’s own and residual performances, respectively, and $\alpha + \beta = 1$. These parameters also reflect indirect interactions between agents. For instance, if $\beta >0$, the agents have some degree of collectivist incentives, and will redirect their decisions towards improving task performance (Leitner 2021). Thus, there are two ways agents interact indirectly. First, by making decisions which are interdependent with other agents’ contributions (see Sect. 3.1) and second, by affecting the remaining agents’ utility via their residual performance.

Every agent’s objective is to maximize their utility, which is only possible by participating in the group.⁶ We omit the coordination of decisions between agents and allow them to act autonomously. Consequently, agent m is not aware of the solutions that the other $r \ne m$ group members intend to implement in a period. Agents, however, can observe the solutions implemented in the previous period, $\textbf{D}_{m\{t-1\}}$. Agents use this information and base their decisions in t on the estimated utility, for which it is assumed that the residual decisions do not change from the previous period. Consequently, agent m’s decision rule takes the form of

$$\begin{aligned} \textbf{d}_{mt} := \mathop {{{\,\mathrm{arg\,max}\,}}}_{d^\prime \subset \textbf{S}_{mt}} ~ U\left( d^\prime , \textbf{D}_{m\{t-1\}} \right) ~. \end{aligned}$$

(9)

The function ‘arg max’ returns the argument that maximizes the utility function.

Group solution—Once all agents have made their decisions, we compute the entire solution to the task in period t by

$$\begin{aligned} \textbf{d}_{t} := \textbf{d}_{1t}^{} {}^\frown \dots {}^\frown \textbf{d}_{Mt} ~, \end{aligned}$$

(10)

where $^\frown$ indicates the concatenation of the solutions individually implemented by the agents. Once the entire solution $\textbf{d}_t$ is implemented, all agents in the population can observe it.

3.3 Group formation mechanism

The model considers that the population of agents autonomously forms one group consisting of M agents. In a group, there is one agent per area of expertise. Thus, if the task at hand requires experts from accounting, marketing, and production management, a group formation mechanism makes sure that one experts per area will join the group.

Recall, we consider an organization formed by $P=30$ agents, and we split the overall task into M subtasks. We symmetrically allocate the agent population to areas of expertise. $P_m=P/M$ potential candidates could solve a particular subtask and, consequently, be a group member.⁷ Thus, with a population of 30 agents and three subtasks, there would be ten experts that could solve a particular subtask. Let us denote the agents who possess the capabilities to solve the subtask $\textbf{d}_m$ by $p_{m}^{j}$, where $j=\{1,\dots ,P_m\}$. The challenge is to identify those agents in the areas of expertise who are best prepared to solve the task in a group. To do so, agents employ a mechanism that follows the concept of a second-price auction (see also Fig. 2). Every time an auction is held, the agents use the following procedure to form a group (Rizk et al. 2019):

• 1. Agents are informed about the auction, and they can place bids to join the group. Since agents can only experience utility by joining the group, every agent has the incentive to participate in the auction. Auctions are anonymous, and agents have no information about the other agents’ bids. The bids are independent, and the ‘price’ of joining the group is determined by the bids only.

• 2. Agents compute their bids by drawing on the information available to them in the following way: In line with Eq. (5), let us denote agent $p_{m}^j$’s known solution space in period t by $\textbf{S}_{mt}^j$. Then, agents compute their bid, which is the maximum estimated utility they can attain given the known solution space in the current period, according to

  $$\begin{aligned} b_{mt}^j =\max _{d^\prime \in \textbf{S}_{{m}t}^j} U\left( d^\prime , \textbf{D}_{m\{t-1\}} \right) ~. \end{aligned}$$

  (11)

  In line with Eq. (7), $\textbf{D}_{m\{t-1\}}$ indicates the solutions implemented outside of agent $p_{m}^j$’s subtask in the last period, which agents can infer from $\textbf{d}_{t-1}$.⁸

• 3. Since every agent has the incentive to participate in the auction, $P_m$ bids are submitted by the agents capable of solving the associated subtask for each slot in the group.

• 4. The agent who submitted the highest bid for task $\textbf{d}_m$ wins the auction, joins the group at slot m, and gets charged the second-highest bid.⁹ Consequently, the group in that particular period is composed of M agents (one per subtask) who know the solutions that lead to the best (estimated) performance.

Fig. 2

Group formation process within the organization

Figure 2 summarizes the group formation process. By recurrently holding such auctions, the group adapts its composition so that it best fits the task. Throughout T periods, auctions occur every $\tau$ time steps. Lower (higher) values of $\tau$ indicate a larger (smaller) interval between two auctions and can be interpreted in terms of a long-term (short-term) group composition. An auction always occurs in the first time step, irrespective of the value of $\tau$. We consider three different scenarios:

• In the case of long-term group composition, the group is formed once in the first period. Only one auction is held. For practical purposes, we refer to this case as $\tau =\infty$.

• In the case of medium-term group composition, we set auctions taking place every $\tau =10$ time steps.

• To model a short-term group composition, we set $\tau =1$, so that auctions occur at every time step.

From an organization’s perspective, $\tau$ is a design parameter since by changing the value of $\tau$, organizations can control the lifetime of groups. For example, when $\tau$ is very low (high), an organization gives a group the opportunity of autonomously changing its composition in short (long) intervals. We refer to the actions taken by the organization to reduce the time between auctions (i.e., to decrease $\tau$) as promoting changes in group composition.

3.4 Scheduling and parameters for simulation experiments

We summarize the sequence of events during a simulation run in Fig. 3. In the previous sections, we have introduced the following independent variables considered in the model: (1) The probability of individual learning $\mathbb {P}$, (2) the number of auctions $\tau$ during the observation period, and (3) the task complexity K.

Fig. 3

Sequence of events during simulation runs

Since organizations can control the learning probability $\mathbb {P}$ and the number of auctions $\tau$ in a real-world setting, we regard those two variables as design parameters. The task complexity K and the structure of interdependencies, on the contrary, are usually given and cannot be controlled by an organization. All relevant parameters included in the model are summarized in Table 1. The parameter settings result in a total number of $3 \cdot 2 \cdot 3 = 18$ different scenarios. We set the observation period to $T=200$ and fix the number of subtasks included in the task to $M=3$. We perform $R=1500$ simulations for every scenario and observe the performance at the group level as the dependent variable.¹⁰ The computation of the group’s solution and the corresponding performance is formalized in Eqs. 3 and 10, respectively.

3.5 Performance measures

Normalized performance—To assure that the results are comparable across all simulation runs, we normalize the performance of the group solution by the maximum achievable performance in every landscape. We compute the average normalized performance in period t according to

$$\begin{aligned} \bar{C}_t = \frac{1}{R} \sum _{r=1}^{R} \frac{C\left( \textbf{d}_{tr}\right) }{C^{*}_r}~, \end{aligned}$$

(12)

where $C^{*}_r$ indicates the maximum performance in simulation run r, $\textbf{d}_{tr}$ stands for the group solution implemented in simulation run r and period t. The performance $C\left( \textbf{d}_{tr}\right)$ is computed according to Eq. (3).

Mean performance—To give a condensed performance measure, we also report the mean performance over the entire observation period,

$$\begin{aligned} \bar{\bar{C}} = \frac{1}{T} \sum _{t=1}^{T} \bar{C}_t~. \end{aligned}$$

(13)

Please note that the mean performance includes information about the attainable performance and the speed at which this performance level is reached in a specific scenario. Thus, the mean performance is also a proxy for the convergence speed.

Interaction effect—In addition to the two measures of performance introduced above, we aim to analyze the interaction between individual learning and changes in group composition when they are promoted simultaneously. To do so, we compute the interaction coefficient based on the final and the mean performance. The analysis starts at a baseline scenario in which neither learning nor changes in group composition are promoted. We refer to the parameter set for this case by $\delta _0 = \{\mathbb {P}=0, \tau =\infty \}$. To analyze the isolated effects of promoting the design parameters, we start from the baseline scenario and promote either learning or changes in group composition, so that the parameters are $\delta _{\mathbb {P}} = \{\mathbb {P}>0, \tau =\infty \}$ or $\delta _{\tau } = \{\mathbb {P}=0, \tau >0\}$, respectively. Finally, we analyze the case when learning and changes in group composition are promoted simultaneously with the corresponding parameters $\delta _{\mathbb {P}\tau } = \{\mathbb {P}>0, \tau >0\}$.¹¹ We denote the normalized performance in the final period $t=200$ given a specific parameter setting by $\bar{C}^{\delta }$, where $\delta \in \{\delta _0, \delta _{\mathbb {P}},\delta _{\tau },\delta _{\mathbb {P}\tau }\}$ (see also Eqs. 12 and 13). We suppress the subscript $t=200$ for readability.

Table 1 Parameter setting

Next, we compute the differences in the achieved final performances. We denote the difference between the final performance achieved in the baseline scenario and the final performance when either individual learning or changes in group composition are promoted by $\bar{\Delta }_0^{{\mathbb {P}}} = \bar{C}^{\delta _{\mathbb {P}}} - \bar{C}^{\delta _0}$ and $\bar{\Delta }_0^{{\tau }} = \bar{C}^{\delta _{\tau }} - \bar{C}^{\delta _0}$, respectively. The increase in the final performance when individual learning and changes in group composition are promoted simultaneously is denoted by $\bar{\Delta }_0^{{\mathbb {P}\tau }} = \bar{C}^{\delta _{\mathbb {P}\tau }} - \bar{C}^{\delta _0}$. Finally, we compute the interaction coefficient by

(14)

The effect of simultaneously promoting individual learning and changes in group composition on the mean performance is computed correspondingly. Consequently, an interaction coefficient $I\!E>1$ and $I\!E<1$ indicates over- and underproportional interactions, respectively (Leitner 2014). An overproportional (underproportional) interaction effect means that the joint effect on task performance of simultaneously promoting learning and changes in group composition is higher (smaller) than the sum of their isolated effects. Isolated effects refer to the effects on mean and final performance of solely promoting individual learning or changes in group composition. This coefficient indicates whether individual learning and group turnover reinforce or mitigate each other’s effect on task performance.

Offsetting effect—In addition to the interaction between individual learning and group turnover, we are interested in the potential offsetting effects when the design parameters are changed sequentially. To do so, we analyze the relative difference in the performance of promoting individual learning (changes in group composition) after changes in group composition (individual learning) has been promoted. When individual learning is promoted after promoting changes in group composition, we compute the difference in the final performance by $\bar{\Delta }_{\tau }^{{\mathbb {P}\tau }}= \bar{C}^{\delta _{\mathbb {P}\tau }} - \bar{C}^{\delta _{\tau }}$. Consequently, the relative difference in the final performance follows:

(15)

For the case of promoting individual learning first and changes in group composition second, we compute the absolute differences in the final performance by $\bar{\Delta }_{\mathbb {P}}^{{\mathbb {P}\tau }}= \bar{C}^{\delta _{\mathbb {P}\tau }} - \bar{C}^{\delta _{\mathbb {P}}}$ and the relative difference in the final performance by

(16)

The relative differences in the mean performances are computed correspondingly. A negative coefficient, i.e., either $O\!E_{\tau }<0$ or $O\!E_{\mathbb {P}}<0$, indicates an offsetting effect. This offsetting effect means that promoting individual learning (changes in group composition) on the second stage reduces the positive effects of promoting changes in group composition (individual learning) on the first stage, i.e., that promoting only changes in group composition (individual learning) has a higher positive effect on task performance than promoting both individual learning and changes in group composition.

4 Results

We analyze the effects of an adaptation at two levels–via individual learning and changing group composition–on task performance and report the final and mean performances for decomposed and interdependent tasks in Table 2. We organize the results in three subsections: In Sect. 4.1, we analyze the interaction effects between individual learning and group turnover and study how a simultaneous variation in both design parameters affects task performance. In Sect. 4.2 and 4.3, we focus on a sequential promotion of individual learning and changes in group composition. In particular, Sect. 4.2 analyzes the effects of promoting individual learning after promoting changes in group composition. Hence, a group’s lifetime is fixed before there is any promotion of individual learning. We plot the effects of a subsequent variation in individual learning on task performance in Figs. 5 and 6. Table 6 includes information about whether or not subsequently promoting learning has significant effects on the mean and final performances. In Sect. 4.3, we explore the effects of promoting changes in group composition after learning has been promoted. Figures 7 and 8 and Table 7 show whether and how a variation in the lifetime of a group after promoting learning affects task performance.

Table 2 Mean and final performances

Our analysis also considers whether different configurations of the incentive systems (i.e., $\alpha$ and $\beta$) and different structures of interdependencies (i.e., Fig. 1) affect the results. In both cases, there are slight differences in the overall performances achieved, but the findings presented in Sects. 4.1 to 4.3 hold true for different configurations of the incentive system. Also, when tasks are interdependent, we observe the same patterns in the performances for different structures of interdependencies. The details are provided in the Appendix.

4.1 Interactions between promoting individual learning and changes in group composition

Interaction effects—Following Eq. (14), we consider a baseline scenario in which neither individual learning nor changes in group composition are promoted (i.e., zero individual learning and long-term group composition). Starting from there, we change both design parameters simultaneously by promoting learning (moderate or high) and changes in group composition (medium- or short-term composition). The logic of the interaction coefficient is illustrated in Fig. 4, where we refer to one scenario included in Table 2: In the baseline scenario for an interdependent task with no learning and long-term group composition, a final performance of 0.7529 can be achieved. Promoting a short-term group composition (individual learning towards a high probability) increases this performance by 0.0391 (0.1812). When both design parameters are changed simultaneously, however, the performance increases by 0.1179; see the first path indicated by the solid line in Fig. 4. The resulting interaction coefficient is $I\!E=0.54$, which suggests that the joint effect is smaller than the sum of their isolated effects. Thus, the effects of promoting individual learning and changes in group composition simultaneously interact underproportionally in this case.

Fig. 4

Interaction effect and potential offsetting effects (numbers are for the final performance and interdependent tasks)

The interaction coefficients for decomposed and interdependent tasks are presented in Table 3. When tasks are decomposed, the effects of promoting individual learning and changes in group composition interact more or less linearly. This means that, generally, the joint effect on task performance of simultaneously promoting individual learning and changes in group composition is more or less equivalent to the sum of their isolated effects. We observe a slight overproportional effect on the mean performance only if the probability of individual learning increases to 0.25 with a simultaneous promotion of changes in group composition in the medium- or short-term. By contrast, when tasks are interdependent, the results indicate underproportional interactions in all cases. This means that the joint effect on task performance of simultaneously promoting individual learning and changes in group composition is smaller than the sum of the isolated effects.

Table 3 Interaction coefficients

Potential offsetting effects—These underproportional interactions in interdependent tasks imply that either promoting individual learning reduces the positive effects on task performance of promoting changes in group composition or vice versa.¹² To study this relationship, we consider two-stage paths that promote individual learning and changes in group composition sequentially in a different order and compute the relative changes in performance in the second stage (see Eqs. 15 and 16). The logic behind our analysis is illustrated in Fig. 4. Again, we start at the baseline scenario with a performance of 0.7529. The first path, indicated by a solid line, captures the interaction effect as described above. The second path, indicated by dashed lines, considers promoting changes in group composition first, resulting in a performance of 0.7920, and individual learning second. In the second stage, the performance increases by $9.95\%$ to 0.8708 (see Tables 2 and 4). Thus, promoting individual learning after promoting changes in group composition does not offset any positive effects in this scenario. The third path, indicated by dotted lines in Fig. 4, considers promoting individual learning first, resulting in a performance of 0.9341, and changes in group composition second. In the second stage, the performance decreases by $6.78\%$ to 0.8708 (see Tables 2 and 5). This decrease on performance indicates that promoting changes in group composition at the second stage reduces the benefits of promoting individual learning at the first stage. Promoting only individual learning, thus, is more beneficial for task performance than promoting both individual learning and changes in group composition.

Table 4 Relative performance changes caused by promoting individual learning (interdependent tasks)

Table 4 shows the relative changes for promoting individual learning in the second stage when tasks are interdependent. There are no offsetting effects, which indicates that promoting individual learning in the second stage always increases task performance. This observation is most pronounced if groups do not change at all (i.e., $24.37\%$ and $24.07\%$) and least pronounced if groups change their composition in the short-term (i.e., $12.79\%$ and $9.95\%$). Additionally, these results also show that, in the second stage, promoting moderate individual learning is better in terms of final performance than promoting high individual learning. For instance, promoting learning from zero to moderate results in an increase of $24.37\%$ for a long-term composition, $18.49\%$ for a medium-term composition, and $12.79\%$ for a short-term composition. Conversely, promoting learning from zero to high leads to an increase of $24.07\%$ for a long-term composition, $17.64\%$ for a medium-term composition, and $9.95\%$ for a short-term composition.

Table 5 Relative performance changes caused by promoting changes in group composition (interdependent tasks)

Table 5 shows the relative changes for promoting changes in group composition in the second stage when tasks are interdependent. The performance slightly increases only if there is no individual learning. In particular, changing a group’s composition in the medium-term and in the short-term increases task performance almost equally (i.e., $5.49\%$ and $5.20\%$, respectively).

At higher levels of individual learning, promoting a medium-term group composition in the second stage only improves mean performance slightly (i.e., $1.60\%$) in scenarios of moderate learning. Conversely, promoting a medium-term group composition in the second stage does not significantly affect final performance for moderate learning (i.e., $0.51\%$) and mean (i.e., $0.12\%$) and final (i.e., $0.03\%$) performances for high learning. Additionally, promoting a short-term group composition decreases both mean and final performances for moderate (i.e., $-2.33\%$ and $-4.60\%$, respectively) and high (i.e., $-5.55\%$ and $-6.78\%$, respectively) learning. These results suggest that a promoting short-term group composition offsets the preceding positive effects of promoting individual learning. Consequently, promoting moderate and high individual learning with a long-term group composition increases task performance more than promoting both individual learning and a short-term group composition.

4.2 Promoting individual learning after promoting changes in group composition

The results presented in Table 2 suggest that the performance always increases as agents start to learn at the second stage, i.e., when the learning probability increases from $\mathbb {P}=0$ to $\mathbb {P}=0.25$. This finding follows intuition and can be observed for decomposed and interdependent tasks. Since learning enables agents to find new and perhaps better-performing solutions to their subtasks, performance may steadily increase. After a certain number of periods, however, the performance cannot be further improved and settles at a specific level, which we refer to as the limit performance (i.e., the maximum performance that agents can achieve on average, given the conditions considered in the scenario). The limit performance increases significantly with the learning probability. While both the final and mean performances increase when agents only start to learn, further increases in the learning probability lead to more differentiated effects that require taking into account the lifetimes of groups.

Long-term group composition In the case of promoting a long-term group composition at the first stage, task performance will grow faster if the learning probability increases from moderate ($\mathbb {P}=0.25$) to high ($\mathbb {P}=0.5$). Nevertheless, an increase in the learning probability to values above 0.25 has no significant effect on the final performance. The results included in Tables 4 and 6 confirm this finding, and Fig. 5 shows the same pattern for decomposed and interdependent tasks.¹³

Table 6 Significance test for the effects of promoting individual learning at the second stage

Fig. 5

Effects of promoting individual learning in the case of a long-term group composition

Medium-term and short-term group composition For the case of promoting a medium-term group composition at the first stage, there are no moderating effects of task decomposability and no significant effects of increasing the learning probability to 0.5 on the final and the mean performances (see Table 6). This corresponds to the results presented in Sect. 4.1 and in particular in Table 4. There are marginal effects of an increase in the learning probability on the speed of performance improvement only in very early periods (see Fig. 6A).

For the case of promoting a short-term group composition at the first stage, the results included in Fig. 6 and Table 6 indicate that the effects of promoting learning in the second stage are moderated by task decomposability. There is a significant decrease in the final and mean performance when tasks are interdependent. This result is in line with the decrease in the relative performance changes presented in Table 4 (e.g., $12.79\%$ to $9.95\%$ for the final performance in the case of a short-term group composition). Further, there are no significant effects of promoting learning on performances when tasks are decomposed, reflecting the linear interactions presented in Table 3.

Fig. 6

Effects of promoting individual learning in the case of a medium-term and short-term group composition

4.3 Promoting changes in group composition after promoting individual learning

While promoting individual learning at the second stage has significant consequences for the performance in most cases, promoting changes in group composition after promoting individual learning has less pronounced effects.

No individual learning—In the case of not promoting individual learning at the first stage, the results included in Fig. 7B and Tables 2 and 7 show that groups of a short-term or medium-term composition achieve significantly higher performances than groups that do not change at all. Still, this effect can only be observed when tasks are interdependent. Thus, there is a moderating effect of task decomposability. The observation that promoting changes in group composition increases performance follows intuition: When individuals do not learn and a group has the opportunity to change its composition in the short- or medium term, new group members may know better-performing solutions to the task at hand and, consequently, performance may increase. Since groups that do not change at all cannot acquire knowledge by attracting new members, the increase in task performance comes to a standstill at a low level early in the observation period. The effects on performance, however, are relatively small. Promoting a short-term instead of a medium-term composition has no significant effect on the final performance, when agents do not learn at the individual level. Yet, the level of the final performance is achieved slightly faster (see Fig. 7B). This is also reflected in the results presented in Sect. 4.1 and in particular in Table 5.

Table 7 Significance test for the effects of promoting changes in group composition at the second stage

Moderate individual learning—When moderate individual learning is promoted at the first stage, groups of a medium-term composition improve their performance significantly faster than groups that do not change at all. There are, however, no significant differences in the achieved final performances (see Table 7). While the same result can be observed for both interdependent and decomposed tasks, task decomposability appears to have a moderating effect on the performance growth and the final performance when changes in group composition are further promoted towards a short-term composition. For interdependent tasks, the results presented in Fig. 7B indicate that groups that are of a short-term composition achieve a significantly lower performance than groups that change less frequently, i.e., are of a medium-term composition (see Table 2). That means, excessive group turnover might unfold adverse effects on performance (see also the negative values reported in Table 5 in Sect. 4.1).

Fig. 7

Effects of increasing group turnover in the case of no and moderate individual learning

High individual learning—If high individual learning is promoted at the first stage, the effects of promoting changes in group composition will be similar to those identified for moderate individual learning. Nevertheless we can highlight some relevant results. First, results depicted in Fig. 8 suggest that the higher the value of the learning probability, the faster performance grows for groups with a long-term composition. Additionally, there are moderating effects of task decomposability on the performance of groups with a short-term composition. For decomposed tasks, the mean performances achieved by groups of a short-, medium- and long-term composition become even more similar than in the case of moderate learning (see Table 2). Thus, the benefits of promoting a relatively short-term group composition decrease. Additionally, if tasks are interdependent, groups of a short-term composition will perform significantly worse than groups of a long- or medium-term composition (see Tables 2 and 7). In contrast, the performances achieved by groups of a long-term and a medium-term composition are almost equal (see Fig. 8B). Our results suggest that promoting a short-term group composition is not necessarily advantageous if individual learning is already high and that it might even decrease performance for interdependent tasks.

Fig. 8

Effects of promoting changes in group composition in the case of high individual learning

5 Discussion

Our research aims to gain insights into the interaction effects of variations in two design parameters, namely (1) individual learning and (2) changes in group composition. In particular, we aim to understand how the simultaneous and sequential promotion of individual learning and changes in group composition affects task performance and how task decomposability moderates any effects. To do so, we have extended the NK-framework by a learning mechanism and a group formation mechanism to account for adaptation at the level of the individual agent and the group of agents, respectively. We provide a summary of the model’s results in Table 8. In the following subsection, we discuss the main theoretical contributions and practical implications of our research.

Table 8 Summary of results

5.1 Results related to interaction effects

The results presented in this paper can be related to the exploration-exploitation dilemma, which is concerned with the trade-off between obtaining new knowledge and using the available knowledge to improve performance (Berger-Tal et al. 2014). Previous research points out that the key to improving performance is a proper balance between exploration and exploitation (Berger-Tal et al. 2014; Levinthal 1997; Yen et al. 2002). Further factors, such as the managerial initiative (Podolny 2018), feedback (Giannoccaro et al. 2019; Håkonsson et al. 2016), information about the organizational environment (Leitner and Wall 2020), task complexity (Uotila 2017), and organizational policies (Staber and Sydow 2002) need to be taken into account.

The previous literature on the topic often employs a unidimensional perspective, in which exploration and exploitation occur either at the individual (Giannoccaro et al. 2019; Håkonsson et al. 2016; Leitner and Wall 2020; Podolny 2018) or group level (Staber and Sydow 2002; Uotila 2017). Please note that, from the perspective of the organization, promoting individual learning and promoting changes in group composition are key design parameters to control whether groups lean more towards exploration or exploitation. Naturally, promoting high learning motivates agents to obtain new knowledge and, thereby, exploration is fostered at the individual level. The group formation mechanism implemented in our model makes sure that the agents who have the best knowledge to solve the task join forces in a group. Thus, promoting changes in group composition can be interpreted as a mechanism to foster exploration from a group’s perspective. The shorter (longer) the group’s lifetime, the more (less) often this mechanism is carried out, and, consequently, the more exploration (exploitation) is promoted. We contribute to this stream of literature by analyzing the interactions between individual learning and group turnover and quantifying them in terms of the interaction coefficient.

In Sect. 4.1, we have shown that there are not just linear but also non-linear interactions when individual learning and changes in group composition are promoted simultaneously. While these interactions are close to linear in all cases for decomposed tasks, we find (highly) underproportional interactions in interdependent tasks. Previous research has addressed the interaction between the effects of promoting learning and changes in group composition, too. Savelsbergh et al. (2015), for example, found a positive relationship between a long-term group composition and team learning. We show that a similar relation also holds true for individual learning. Moreover, Bartsch et al. (2013), Edmondson (2003), and Sergeeva and Roehrich (2018) claim that the promotion of more frequent changes in group composition might reduce the positive effects of individual learning. This finding is in line with our observations, and we contribute to this stream of research by showing that this decrease in performance indeed occurs, but just when tasks are interdependent.

Moreover, previous research suggests that interactions across subtasks require a broader exploration to develop well-performing solutions to tasks, mainly when landscapes are characterized by a relatively high number of peaks (Rivkin and Siggelkow 2007). This is in line with our findings, as they suggest that promoting solely individual learning or changes in group composition increases performance, specially for interdependent tasks. Nevertheless, we also show that overpromoting exploration–e.g., by promoting individual learning with a short term group composition–might reduce task performance. Thus, we regard it highly important, particularly for corporate practice, not to overpromote learning and changes in group composition. Billinger et al. (2014), for example, find that human decision-makers are indeed prone to overexploration. We show that cheering this tendency might unfold unwanted behavioral dynamics and might result in a decreasing performance.

5.2 Results related to promoting individual learning

In Sect. 4.2, we find that starting to learn at the second stage, i.e., increasing the learning probability such that $\mathbb {P}>0$, increases performance in all cases. The effects of promoting high learning, however, depend on a group’s lifetime and are moderated by task decomposability. These results relate to previous research on the relationship between means to promote individual learning and organizational performance measures, such as productivity and financial and innovative performance. These means include mentoring (Lankau and Scandura 2007), allowing for ‘learning by doing’ (Arrow 1971) and exploratory learning (Beugelsdijk 2008), determining the flow of information that surrounds learning (Cohen 1991), and, more generally, creating work environments that stimulate creativity and learning (Annosi et al. 2020; Oldham 2003; Sung and Choi 2014). In addition, Stinchcombe (1990), Cohen (1991), Salas et al. (1999), and Tharenou et al. (2007) highlight the importance of employee training to promote individual learning since the agents’ skills are the foundation of organizational capabilities and, hence, employee training contributes substantially to organizational competitiveness. In this regard, it is important to note that providing training to promote individual learning is widely employed in corporate practice. This can – not least – be seen in the enormous amounts of money spent on it (Haccoun and Saks 1998).

Previous research on promoting learning through training mainly focuses on the individual-level outcomes in terms of what was learned by the agent, while the consequences of training for the organizational level is seldom in focus and, consequently, still needs to be explored (Glaveli and Karassavidou 2011; Kozlowski et al. 2000). The first large-scale studies concerned with the link between training and performance are those carried out by Holzer et al. (1993) and Bartel (1994). They found evidence for a direct positive relationship between learning and productivity, which is in line with our finding that performance increases when agents start to learn.

Becker (1975) distinguishes between general and specific training. Specific training exclusively increases the performance of a particular organization, makes new employees familiar with the organization, and helps gain new knowledge in monopolistic environments, where no other organizations exist for which the knowledge would be useful. By contrast, in the case of general training, the knowledge gained might be useful also for competitors (see also Barrett and O’Connell 2001). Becker (1975) claims that most training is neither purely general nor completely specific. We argue that the learning included in our model is of a general nature since it is concerned with how to carry out a task that similar organizations could face. In our model, specific knowledge could be the agents’ knowledge about the functioning of the auction mechanism for group formation. We assume specific knowledge to be given and, hence, do not focus on it.

The emphasis on general training allows us to connect our results to the literature on gift-exchange: As soon as agents realize that the knowledge gained from promoting learning might be useful in other employments as well, they might regard it as a ‘gift’ (Akerlof 1982; Barrett and O’Connell 2001). Following gift-exchange models (Duffy and Puzzello 2014), employees would eventually repay the gift in one or the other form. In an organizational setting, this repay could take the form of putting more effort into solving the task at hand, which might result in higher performance (Cropanzano and Greenberg 1997; Falk and Fischbacher 2006). Thus, for the positive relationship between learning and performance observed in our model, the theory of gift-exchange explains a similar pattern. Our agents, however, act utility maximizing under bounded rationality, which apparently leads to the same patterns at the macro-level. Moreover, it is well known that increasing the ‘gift’ does not necessarily lead to agents making more effort since the marginal effect decreases. For the context of monetary incentives, this observation has been explained by a crowding-out effect of rewards or individual earnings targets that pose an upper limit on effort (Camerer et al. 1997; Frey and Oberholzer-Gee 1997). We observe that performance does not increase but perhaps even decreases if learning is promoted too intensely. In these cases, the agents’ behavior can, thus, be described by a decreasing marginal ‘gift’-effort relation. It is, however, not a crowding-out effect or a compensation target that drives our observation, but the maximum attainable performance. If agents learn with a high probability, they will achieve this performance faster. Nevertheless, any further promotion of learning does not pay off because there is no more room for further improvement.

Glaveli and Karassavidou (2011) argue that, in particular, the factors that mediate the outcomes of promoting learning by training have not yet been substantively explored. We contribute in this respect by showing that promoting learning for untrained individuals yields positive effects in all cases. This finding contrasts that by Barrett and O’Connell (2001), who found that the positive effects of general training are robust against corporate restructuring. In the context of our model, corporate restructuring can be translated to the design parameter of changes in group composition. We contribute to this line of research by showing that task interdependence and promoting changes in group composition impair the positive effects of training on performance as soon as agents learn with a higher probability; in the worst cases, learning can even yield negative effects for performance.

5.3 Results related to promoting changes in group composition

Previous research asks to take into account temporal aspects of a group’s composition. Mathieu et al. (2014), for example, argue that including the aspect of time into group composition research allows, amongst others, to model how teams move through a lifecycle from birth to death, temporal norms, and the future orientation of the organizational culture (Mohammed et al. 2008). This is also particularly relevant for organizational research, as Tannenbaum et al. (2012) and Bell and Outland (2017) claim, because organizations more frequently keep relying on team-based structures. This means that groups are formed for a predetermined time to solve a specific number of tasks (Lundin and Söderholm 1995). In our research, we account for the lifetime of groups by promoting a long-term, medium-term, or short-term group composition. Our approach differs from previous research which argues that organizations might strategically use a limited lifetime of groups to redeploy their human capital (Bell and Outland 2017). Instead, we follow an (evolutionary) bottom-up approach of group formation (Tsoukas 1993) that is driven by a second-price auction (see, e.g., Leitner 2021) to assure that the best-prepared agents join forces in a group. Previous research, in contrast, sometimes appears to stick to the concept of more classical top-down approaches to group composition (Romme 2003).

Furthermore, it has already been argued that promoting changes in group composition might have different consequences. It either increases the performance because it stimulates creativity within a group (Choi and Thompson 2005) or it decreases performance because newly formed groups require some time to develop efficient modes of collaboration (Lewis et al. 2007). We contribute to this line of research by shedding light on the interactions between the effects of promoting individual learning and changes in group composition and by exploring the moderating role of task decomposability. In addition, we show that only the speed of performance growth might increase in the case of decomposed tasks, but not the final performance. These results support the argument brought forward in Choi and Thompson (2005). On the contrary, we indeed observe decreases in the final performance when groups change their composition too frequently for interdependent tasks. This insight supports the claim by Lewis et al. (2007). We, however, add that it is not only the initial phase of coalescing that might decrease the performance, but also that over-promoting exploration might lead to significant decreases in performance.

6 Conclusion

In this paper, we analyze and discuss how learning and adaptation at multiple levels in an organization affect task performance. We contribute to previous research by extending the traditionally unidimensional perspective on either the individual or the group level and exploring the effects when individual learning and group turnover occur simultaneously and sequentially, respectively. Our results indicate that, in general, organizations are well-advised to promote learning and changes in group composition to increase task performance. We, however, also show that individual learning and group turnover should not be pushed too far because there are interaction effects between the two levels. Whether or not interactions are close to linear is moderated by task decomposability.

In particular, if the group members are very much engaged in learning at the individual level, changing the group composition may backfire and even decrease performance, at least when tasks are interdependent. When individuals only learn to a rather minor extent, changing the composition of a group from time to time is beneficial to task performance. Still, very short intervals between group turnover do not pay off. Nevertheless, if organizations allow groups to change their composition in the short term, learning at the individual level will be in general beneficial; although the marginal effects of pushing learning beyond a moderate level are negligible. Our results shed new light on the consequences of simultaneously or sequentially promoting individual learning and changes in group composition for performance. By revealing the effects of micro-level activities on macro-level performance we contribute to closing the still predominant gap between micro- and macro-level research in managerial science.

Our research, of course, is not without its limitations. First, we assume that the agents are heterogeneous concerning their capabilities and limited in their rationality. We do not consider the effects of any other individual characteristics – such as social background, age, gender, education, or national culture – on performance. Further research may want to elaborate on this. Second, we omit communication and coordination between agents, and we exclusively focus on one group within an organization. Further research could extend our approach by adding communication channels between agents and analyzing the co-evolution of multiple (potentially interdependent) groups. Third, we do not take into account the potential costs of individual learning and group turnover. Finally, we fix the probability of individuals learning and the intervals at which groups may change their composition exogenously. Future research could consider some self-control and self-generated initiative by individuals and groups and investigate how endogenous decisions on the learning probability and the lifetime of groups affect the results.

Appendices

Appendix A: Alternative structure of interdependencies

Figure 9 illustrates the interdependencies and subtasks for an alternative structure of interdependencies, e.g., a roll structure. The interdependencies are partly located outside the subtasks, irrespective of the level of task complexity K.

Fig. 9

Interdependence matrices for a roll structure

Table 9 shows the mean and final performances for the roll structure. As compared to Table 2, the mean performances are lower for the case of a roll structure.

Table 9 Mean and final performances for a roll structure

Table 10 shows whether and how a variation in individual learning after promoting changes in group composition affects the mean and final performances under the condition of a roll structure. Similarly, Table 11 shows whether promoting changes in group composition after promoting individual learning has significant effects on the mean and final performances. The general patterns described in Sects. 4 hold for true the roll structure.

Table 10 Significance test for the effects of promoting individual learning for a roll structure

Table 11 Significance test for the effects of promoting changes in group composition for a roll structure

Appendix B: Alternative incentive schemes

Table 12 Mean and final performances for an incentive scheme that favors individualism

Table 13 Mean and final performances for an incentive scheme that favors collectivism

Tables 12 and 13 show the mean and final performances for an incentive scheme that favors individualism (i.e., $\alpha =0.75$ and $\beta =0.25$) and collectivism (i.e., $\alpha =0.25$ and $\beta =0.75$), respectively. For decomposed tasks, the performances are very similar to those reported in Table 2. For interdependent tasks, an incentive scheme that favors individualism decreases group performance. By contrast, an incentive scheme that favors collectivism is associated with higher performances.

Table 14 Significance test for the effects of promoting individual learning for an incentive scheme that favors individualism

Table 15 Significance test for the effects of promoting changes in group composition for an incentive scheme that favors individualism

Table 16 Significance test for the effects of promoting individual learning for an incentive scheme that favors collectivism

Table 17 Significance test for the effects of promoting changes in group composition for an incentive scheme that favors collectivism

Tables 14 and 16 show whether promoting individual learning after promoting changes in group composition has significant effects on the mean and final performances, if the incentive scheme favors individualism and collectivism, respectively. Similarly, Tables 15 and 17 show whether promoting changes in group composition after promoting individual learning significantly affects task performance, if the incentive scheme favors individualism and collectivism, respectively. The results suggest that the general patterns described in Sects. 4.2 and 4.3 hold true for alternative configurations of the incentive scheme.