1 Introduction

Sustainable development can be defined simply as improving the quality of life without affecting the environment. Sustainability is a holistic and complex multi-dimensional concept comprising economic, social and environmental issues (United Nations 1992; Rio Declaration 1992). An extensive overview of sustainability performance evaluation, including literature review and future directions, was provided by Büyüközkan and Karabulut (2018). They suggested that “sustainability performance evaluation models shall be more balanced, suitable criteria and their interrelations shall be well defined and subjectivity of qualitative criteria inherent to sustainability indicators shall be considered”.

The sustainability decision context, requires the decision maker to take a position on a concept of “sustainability”. There are two different levels of sustainability: weak and strong (Ayres et al. 2001; Cabeza-Gutes 1996; Dietz and Neumayer 2007; Ekins et al. 2003; Neumayer 2003; Munda 2005a). Weak sustainability states that “human capital” can substitute “natural capital”. Weak sustainability is the idea where the natural capital could be used as long as it is converted into manufactured capital of equal value. In contrary, strong sustainability states that “human capital” and “natural capital” are complementary, but not interchangeable.

The United Nations Conference on Sustainable Development (Rio+20) resulted in creating a document with clear and practical measures for implementing sustainable development (The future we want 2012). In Transforming Our World—the 2030 Agenda for Sustainable Development targets and topics related to the SDG are defined (United Nations 2015). The EU SDGs indicator set, which constituted the basis for assessing the level of sustainability implementation, is collected in Eurostat.

Many studies on sustainability implementation are conducted by using the multi-criteria techniques (Munda 2005a, b, 2008; Azapagic and Perdan 2005a, b; Singh et al. 2009, among others). In this work we propose a new methodological framework based on TOPSIS (Technique for Order Preference by Similarity to an Ideal Solution) (Hwang and Yoon 1981) procedure. In our proposal, the extended TOPSIS takes into consideration EU targets and/or national targets in building PIS and NIS. This algorithm allows compensatory and non-compensatory approach in integrated sustainability assessment from targets’ perspective.

Our framework has been applied to measure sustainable development in the field of education. In recent years, there have been many new aspects and ideas in the area of education, which due to their “global-character”, are reflected in educational policy, in the practice of education development and education for sustainable development. Numerous reforms in the field of education, requiring a clear knowledge of accountability, efficiency and measurement, have brought the need for deeper research in this area. In this context, a synthesis of the literature pertaining Development Education (DE), Education for Sustainable Development (ESD), and Global Citizenship Education (GCE), considered from the perspective of policy and practice, was presented by O’Flaherty and Liddy (2017). Obtained results confirm a strong need for further studies in the area of education. Also, designing and employing appropriate and adequate research methods to address the complexity and multiplicity of learning arising from DE/ESD/GCE, requires investigation and innovation.

The Europe 2020 strategy (European Commission 2010) is the EU’s agenda adopted for growth and jobs which emphasizes smart, sustainable and inclusive growth. Smart growth denotes a developing economy based on knowledge and innovation. Sustainable growth promotes a more resource efficient, greener and more competitive economy. Inclusive growth fosters a high-employment economy delivering social and territorial cohesion. Taking into consideration key priorities, the EU defined eight targets which belong to five thematic areas: employment, education, poverty and social exclusion, climate change and energy, R&D and innovation. One of the most important areas, which is associated with smart growth, is education. Two main EU targets for education in Europe 2020 strategy are the following (European Commission 2010):

  • rates of early school leavers below 10%;

  • at least 40% of people aged 30–34 having completed higher education.

The EU targets have been also modified into national targets, so that each EU country can check its own progress towards each goal. The Eurostat collected the EU SDGs indicator set which constituted the basis for assessing the level of implementation of the Europe 2020 strategy, the main EU targets identified in this strategy and national targets accepted by the Member States. The Europe 2020 strategy also plays an important role in addressing the internationally adopted 2030 Agenda for Sustainable Development, which have given a new direction for achieving sustainable development (United Nations 2015). This agenda contains 17 goals including global education (SDG 4) which ensures inclusive and equitable quality education and promotes lifelong learning opportunities for everyone. SDG 4 “seeks to ensure people have access to equitable and quality education through all stages of life, from early childhood education and care, through primary and secondary schooling, to technical, vocational training and tertiary education” (Eurostat 2017a). To monitor the progress towards SDG 4 on ensuring inclusive and quality education for everyony—the indicators from the subset SDG 4 are used.

The Strategic Framework for Education and Training 2020 (ET 2020) is a program providing common strategic objectives for Member States with a view to respond to the challenges that are important in creating a knowledge-based Europe and which make lifelong learning reality for everyone. In order to measure progress achieved on these objectives, they are also accompanied by indicators SDG 4 and European benchmarks.

In a complex process of assessment of the level of sustainability in the education area, multi-criteria analysis can be a useful tool. In this context, a methodological approach based on Multi-criteria Decision Analysis (MCDA), in order to monitor sustainability in education area, was presented. Our research was carried out basing on the TOPSIS method, which enabled the construction of a synthetic measure of sustainable development. The modified TOPSIS technique was used to rank EU countries in order to understand the specifics of education necessary to develop sustainable growth. Specifically, the following research questions are addressed:

  • Q1 How to evaluate and compare 28 EU countries in implementing EU’s strategic goals in the area of education?

  • Q2 How to evaluate and compare 28 EU countries in implementing EU’s strategic goals in the area of education taking into consideration EU targets?

  • Q3 How to evaluate and compare 28 EU countries in implementing EU’s strategic goals in the area of education taking into consideration national targets?

In the paper we also try to answer the following questions:

  • Q4 Are there any significant disparities in the level of implementation of the strategic goals in the area of education within the EU regions in 2015?

  • Q5 How do countries manage to implement the EU goals in the area of education taking into account EU targets/national targets? Which countries are the best and the worst in implementing these objectives?

To handle the problems mentioned in questions Q1–Q3 the extended TOPSIS technique was proposed. The main idea of TOPSIS is to evaluate the alternatives by simultaneously measuring their distances to PIS and to NIS. The classical TOPSIS method assumes that PIS is an alternative which maximizes the benefit criteria and minimizes the cost ones, whereas NIS maximizes the cost criteria and minimizes the benefit ones. The proposed extended TOPSIS procedure used EU targets and/or national targets in building PIS and NIS. Using this technique, we analyzed the level of realizing the SDG 4 in 28 EU countries in 2015 answering questions Q4 and Q5.

This way we contributed to the sustainable development analysis by proposing the extended TOPSIS method for evaluating and comparing 28 EU countries in implementing EU’s strategic goals, which is an integral part of the EU Sustainable Development Strategy. The proposed approach may be applicable for measuring and monitoring progress towards sustainable development in different areas using SG indicators from the national or EU targets’ perspective. Our paper also contributes to the sustainable education area, showing disparities among EU countries in the level of implementation of the strategic goals in the education area in 2015.

The rest of the paper is organized as follows. Section 2 presents a literature review on measuring the assessment of sustainability based on multi-criteria analysis. In Sect. 3 the classical and extended TOPSIS methods are presented. Section 4 describes the goals in education and empirical data in use. Section 5 presents the research findings on the rank-ordering of EU countries obtained by different TOPSIS techniques followed by the assessment of the achievement of the strategic goals. The concluding section summarizes the paper.

2 Measuring sustainable development using multi-criteria methods: a literature review

The assessment of sustainability can be regarded as a decision-making problem and because it looks for compromise solutions among conflicting criteria and indicators, it could be handled by multi-criteria decision-aid methods (Munda 2005a). Decision Analysis is a discipline, dealing with decision making with multiple and conflicting criteria and objectives, particularly in terms of choice, ranking or sorting of options (Figueira et al. 2005). According to Slowinski et al. (2002) we can distinguish three main approaches used in multi-criteria methods: utility function, outranking relation and sets of decision rules. The utility-based theory includes methods of synthesizing the information in a unique parameter (Keeney and Raiffa 1976). The most popular methods based on the synthesizing criterion, which enable rank-ordering alternatives using appropriate predefined scale, are SMART (The Simple Multi Attribute Rating Technique) (Edwards 1971), SAW (Simple Additive Weighting) (Churchman and Ackoff 1954), TOPSIS (Hwang and Yoon 1981), MACBETH (Measuring Attractiveness by a Categorical Based Evaluation Technique) (Bana e Costa and Vansnick 1999), AHP (Analytic Hierarchy Process) (Saaty 2008). The outranking relation theory involves methods based on comparisons between pairs of options to verify whether “alternative a is at least as good as alternative b” (Roy 1991). The main methods using a synthesizing preference relational system, which compare alternatives with each other to establish preference relations between them, are ELECTRE (Elimination and Choice Expressing Reality) (Roy and Bouyssou 1993), PROMETHEE (Preference Ranking Organization Method for Enrichment Evaluations) (Brans 1982). The decision rule theory allows one to derive a preference model through the use of classification or comparison of decision examples (Greco et al. 2001). The thorough overview of multi-criteria methods can be found in Figueira et al. (2005).

We divided multi-criteria techniques into compensatory and non-compensatory ones. General definition of compensation and non-compensation in multi-criteria decision making within the framework of Multiattribute Preference Structures was presented by Bouyssou (1986). According to him “compensation refers to the existence of ‘tradeoffs’, i.e. the possibility of offsetting a ‘disadvantage’ on some attribute by a sufficiently large ‘advantage’ on another attribute whereas smaller ‘advantages’ would not do the same”. Similarly, Munda (2005b) said that “compensability refers to the existence of trade-offs, i.e. the possibility of offsetting a disadvantage on some criteria by a sufficiently large advantage on another criterion, whereas smaller advantages would not do the same”. In general, the aggregating techniques (e.g. SMART, SAW, TOPSIS, AHP) are compensatory, while the outranking methods (e.g. ELECTRE, PROMETHEE) and rules-based methods are non-compensatory (Jeffreys 2004; Rowley et al. 2012).

MCDA has been used extensively to evaluate sustainability in different areas. The good review of environmental applications of MCDA summarizing over 300 papers from the Web of Science database published between 2000 and 2009 was given by Huang et al. (2011). The papers were classified by their application area, decision or intervention type and by the MCDA methods used in the analysis (analytic hierarchy process, multi-attribute utility theory, and outranking). Diaz-Balterio et al. (2017) studied a set of papers appearing in the Web of Science database showing that multi-criteria techniques have been applied to a great variety of problems related to sustainability. Those techniques have been grouped in five large clusters: Distance Functions, Outranking Methods, Hierarchic Methods, Ranking Methods, and One Way/Optimizing Averages. A structured overview of sustainability performance evaluation related to publications about the current state of literature was provied by Büyüközkan and Karabulut (2018). In particular, they collected and categorized the articles beetwen 2007 and 2018 taking into account applied MCDM techniques (Büyüközkan and Karabulut 2018, p. 261).

Munda (2005b) discussed the use of multi-criteria framework for sustainability measuring. He suggested avoiding complete compensability, i.e. the “possibility that a good score on one indicator can always compensate a very bad score on another indicator”. He argued (2005b) that “complete compensability implies that an excellent performance on one economic dimension can justify any type of very bad performance on the other dimension, which is exactly what the concept of sustainability tries to avoid”. Munda pointed out (2005a, b) that compensatory aggregation method can be used from the weak sustainability perspective, but in implementing strong sustainability context, a non-compensatory method must be used. Rowley et al. (2012) compared the methodological requirements of the main MCDA approaches and clarified the theoretical implications of choice of multi-criteria techniques to be more appropriate in given problem context. He also noticed that performance aggregation-based MCDA methods (AHP, SMART, TOPSIS) can be used only to enforce a weak sustainability concept, because they assume complete compensation among the criteria. On the contrary, preference aggregation-based methods (i.e. ELECTRE, PROMETHEE) “allow the use of a strong concept of sustainability by limiting or abolishing the compensation among sustainability spheres”.

Some methodological problems concerning steps of sustainable analysis in the context of MCDM techniques were discussed by Azapagic and Perdan (2005a, b), Singh et al. (2009) and Cinelli et al. (2014). Azapagic and Perdan in two papers (2005a, b) proposed an integrated multi-criteria decision support framework for sustainability assessment based on three steps: problem structuring, problem analysis and problem resolution. The multi-criteria techniques such as multi-objective optimisation, goal programming, value-based and outranking approaches were discussed and guidance on the choice of the most appropriate MCDA method was also proposed. Singh et al. (2009) gave an overview of various sustainability indices used in policy practice. They measured sustainable development taking into consideration scaling, normalization, weighting and aggregation methodology, etc. Cinelli et al. (2014), in the review paper, reported and discussed the results of a comparative analysis of five MCDA methods (MAUT, AHP, PROMETHEE, ELECTRE and DRSA) with specific reference to ten important criteria aimed at sustainability-related evaluations. The use of qualitative and quantitative data, life cycle, weights typology, thresholds values, compensation degree, uncertainty treatment/sensitivity analysis, uncertainty, robustness, software support and graphical representation, ease of use, were used for comparisons of the selected MCDA methods.

Some practical application of multi-criteria methods to monitor sustainability in different domains can be found in (Boggia and Cortina 2010; Bolcárová and Kološta 2015). Boggia and Cortina (2010) in their work confirmed usefulness of MCDA methods in a complex process such as the assessment of the level of sustainability of a certain area. They showed that results, obtained in this way, are easy to understand and the evaluation path is clear and transparent. Bolcárová and Kološta (2015) built an aggregated index of the sustainable development from EU set of SDIs for each of 27 EU countries based on the PCA (Principal Component Analysis) which allows one to rank each EU country and its development in terms of the sustainability over time.

The usefulness of MCDM methods as evaluation tools, in ranking areas, are also applied by other researchers. Ture et al. (2019) proposed the VICOR and the TOPSIS methods as the effective and easily practicable measures for ranking and monitor 27 EU countries in terms of each EU 2020 Strategy. The same two methods are taken up by Piwowarski et al. (2018). They analyzed 14 indicators selected out of 14 SDG goals in order to study the level of sustainable development of the EU countries. Zinatizadeh et al. (2017) evaluated urban sustainability in areas of the Kermanshah city of Iran by using three MCDM methods: SAW, ELECTRE and TOPSIS. Roszkowska and Filipowicz-Chomko (2016) used TOPSIS method with a common pattern and anti-pattern of development to study the level of the institutional development of Polish voivodeships in 2010-2014. Dos Santos et al. (2019) identified fourtheen application areas of AHP to support sustainable development. They highlighted that manufacturing and urban-related sustainable decisions most often use AHP.

In our paper we used extended TOPSIS procedure to build the composite indicators integrating individual indicators which let us handle the problems mentioned in introduction. Hsu-Shih et al. (2007) noticed four main advantages of TOPSIS: “(i) a sound logic that represents the rationale of human choice; (ii) a scalar value that accounts for both the best and worst alternatives simultaneously; (iii) a simple computation process that can be easily programmed into a spreadsheet; and (iv) the performance measures of all alternatives on attributes can be visualized on a polyhedron, at least for any two dimensions”. They also pointed out that: “these advantages make TOPSIS a major MADM technique as compared with other related techniques such as analytical hierarchical process (AHP) and ELECTRE”. This was the motivation of our study. In addition to the listed advantages of TOPSIS such as simplicity, rationality, comprehensibility, one should pay attention to the possibility of taking into account EU targets and/or national targets. In the proposed extension TOPSIS, the distances to both: PIS and NIS, are based on individual targets simultaneously and a preference order is ranked according to their relative closeness, and a combination of these two distance measures. The major weakness of TOPSIS is in not providing for weight elicitation (Hsu-Shih et al. 2007). The different weighting schemes in TOPSIS models can be found in Olson (2004). Several authors suggested AHP to obtain the weights in TOPSIS (Shih 2007), rank ordering methods may also be useful (Roszkowska 2013).

The SMART or SAW methods are also simple and easy for computing but they cannot handle individual targets in evaluation countries. The AHP method uses pairwise comparison among criteria/option, therefore it is useful for quantitative criteria rather than qualitative indicators. However, it is also worth noting that AHP method can be easy applied to weights determination, in a situation where different weights can be considered. Similarly, the outranking methods such as ELECTRE or PROMETHE are based on alternative comparison so they cannot be used to handle the problem mentioned before.

3 The TOPSIS procedure

3.1 Classical TOPSIS approach

In the MCDM ranking problem, the decision maker has to rank m alternatives A1,…Am described by n criteria C1,…Cn. We assume that each alternative is defined as Ai = [xi, …xin] where \( x_{ij} \in {\mathcal{R} } \) is the resolution level of the alternative Ai (i = 1,…, m) with respect to the criterion Cj (j = 1,…, n). Let \( A = \left\{ {A_{1} , \ldots , A_{m} } \right\} \) be the set of \( m \) alternatives described by \( n \) criteria from the set \( C = \{ C_{1} , \ldots , C_{n} \} \). We have \( I \cup J = C, I \cap J = \emptyset , {\text{were }} I \) is a set of benefit criteria (the greater value the better) and \( J \)—set of cost criteria (the lower value the better). Finally, let \( w = \left[ {w_{1} , \ldots ,w_{n} } \right] \) be a weight vector, where \( w_{j} \in {\mathcal{R} }\left( {j = 1, \ldots ,n} \right) \) is the weight of criterion \( C_{j} \).

The TOPSIS (Hwang and Yoon 1981) is a multi-criteria technique based on two reference points: the ideal and the anti-ideal one. The preference order is then built according to the relative closeness of the alternatives to the ideal, which is a scalar criterion that combines two distance measures to the ideal and the anti-ideal. This method proposes the minimization of the distance with respect to the ideal and, simultaneously, the maximization of the distance with respect to the anti-ideal. The classical TOPSIS procedure consists of the following steps:

Step 1:

Defining the alternatives form the set A.

The alternative \( A_{i} \) is denoted as \( A_{i} \) = [\( x_{i1} , \ldots .,x_{in} ] \) where \( x_{ij} \) is the evaluation of \( i \)-th option with respect to \( j \)-th criterion.

Step 2:

Defining the vector of weights

$$ w = \left[ {w_{1} , \ldots ,w_{n} } \right],\;{\text{where}}\;w_{j} > 0,\mathop \sum \limits_{i = 1}^{n} w_{j} = 1 $$
(1)

where \( w_{j} \) is a weight of \( j \)-th criterion.

Step 3:

Building the ideal \( I = \left[ {x_{1}^{ + } , \ldots ,x_{n}^{ + } } \right] \) and the anti-ideal \( AI = \left[ {x_{1}^{ - } , \ldots ,x_{n}^{ - } } \right] \). vectors for alternatives is as follows:

$$ x_{j}^{ + } = \left\{ {\begin{array}{*{20}c} {\mathop {\hbox{max} }\nolimits_{i} x_{ij}\quad if\,x_{ij} \in I} \\ {\mathop {\hbox{min} }\nolimits_{i} x_{ij}\quad if\,x_{ij} \in J } \\ \end{array} } \right. $$
(2)
$$ x_{j}^{ - } = \left\{ {\begin{array}{*{20}c} {\mathop {\hbox{max} }\nolimits_{i} x_{ij}\quad if\,x_{ij} \in J} \\ {\mathop {\hbox{min} }\nolimits_{i} x_{ij}\quad if\,x_{ij} \in I } \\ \end{array} } \right. $$
(3)

where \( x_{ij} \) is the evaluation of \( i \)-th option with respect to \( j \)-th criterion, I is the set of benefit criteria, J is the set of cost criteria.

Step 4:

Building the normalized i-th alternative \( \overline{A}_{i} \) = [\( \overline{x}_{i1} , \ldots .,\overline{x}_{in} ] \) is as follows:

$$ \overline{x}_{ij} = \frac{{x_{ij} - x_{j}^{ - } }}{{x_{j}^{ + } - x_{j}^{ - } }} $$
(4)

where: \( x_{ij} \) is the evaluation of \( i \)-th option with respect to \( j \)-th criterion.

Step 5:

Building the weighted normalized i-th alternative \( \widetilde{A}_{i} \) = [\( \widetilde{x}_{i1} , \ldots .,\widetilde{x}_{in} ] \) is as follows:

$$ \widetilde{x}_{ij} = w_{j} \bar{x}_{ij} $$
(5)

where \( \overline{x}_{ij} \) is the normalized values of \( i \)-th option with respect to \( j \)-th criterion, \( w_{j} \) is a weight of \( j \)-th criterion.

Step 6:

Building the alternatives \( PIS \) and \( NIS \) as normalized and weighed alternatives \( I \) and \( AI \), respectively.

Let us observe that:

$$ PIS = \left[ {w_{1} , \ldots ,w_{n} } \right], NIS = \left[ {0, \ldots , 0} \right]. $$
(6)
Step 7:

Calculating the distances of each weighted normalized i-th alternative from PIS (\( d_{i}^{ + } \)) and NIS \( \left( {d_{i}^{ - } } \right) \), respectively.

We use the classical Euclidean distance measure:

$$ d_{i}^{ + } = \sqrt {\mathop \sum \limits_{j = 1}^{n} \left( {\widetilde{x}_{ij} - w_{j} } \right)^{2} } $$
(7)
$$ d_{i}^{ - } = \sqrt {\mathop \sum \limits_{j = 1}^{n} \left( {\widetilde{x}_{ij} } \right)^{2} } $$
(8)

where \( \widetilde{x}_{ij} \)—is the weighted normalized values of \( i \)-th option with respect to \( j \)-th criterion, \( w_{j} \) is a weight of \( j \)-th criterion.

Step 8:

Calculating the relative closeness to the PIS.

For each alternative the closeness coefficient \( T_{i} \) is determined, which aggregates the values of \( d_{i}^{ + } \) and \( d_{i}^{ - } \) into a scalar criterion. For the i-th alternative we compute:

$$ T_{i} = \frac{{d_{i}^{ - } }}{{d_{i}^{ - } + d_{i}^{ + } ,}} $$
(9)

where \( 0 \le T_{i} \le 1 \), i = 1, 2,…, m.

The relative closeness formula (9) is an aggregation formula which was originally proposed by Hwang and Yoon (1981) for the classical TOPSIS algorithm.

Step 9:

Ranking of all alternatives according to descending \( T_{i} \), i = 1, 2,…,m.

3.2 Extended TOPSIS approach

In the context of further analysis, \( A \)—is the set of EU countries\( , C \)—is the set of variables (SD indicators), \( x_{ij} \) is the value of \( j \)-th SD indicator for \( i \)-th country, \( I \) the set of benefits (stimulants) and \( J \) the set of costs (destimulants). The problem considered here is related to the notion of the ideal and the anti-ideal vectors and the distances’ measures. In the classical TOPSIS procedure the coordinates of the ideal and the anti-ideal vectors are represented by the maximum and minimum values of options for all the criteria. To take into consideration EU targets and Member States’ individual targets, we introduced the notion of ideal and ani-ideal vector for i-th country as reference values with target values as coordinates.

We assume that the decision maker defines the ideal and the anti-ideal vector for each alternative (country) by comparing coordinates of those vectors with the extremes defined as reference points by target points (benchmarks). Next, the target points were used for the normalization procedure (4). Hence some steps in TOPSIS procedure can be realized on other methodological assumptions. We adopt here the concept of non-compensatory and compensatory fuzzy TOPSIS approach (Roszkowska and Wachowicz 2015) and TOPSIS for real values (Roszkowska and Wachowicz 2016).

Let us denote by \( x_{ij}^{ - } ,\varvec{ }x_{ij}^{ + } \varvec{ } \) reference values (i.e. target values) for \( i \)-th alternative and \( j \)-th criterion. Then \( I_{i} = \left[ {x_{i1}^{ + } , \ldots ,x_{in}^{ + } \varvec{ }} \right] \) is the ideal vector and \( AI_{i} = \left[ {x_{i1}^{ - } , \ldots ,x_{in}^{ - } \varvec{ }} \right] \) the anti-ideal vector for \( i \)-th alternative.

If for every \( i,k {\text{holds}} \) \( I_{i} = I_{k} \), we get the common ideal vector, which we denote by I \( = \left[ {x_{1}^{ + } , \ldots ,x_{n}^{ + } } \right]. \) Consequently, if for every \( i,k \,{\text{holds}} \) \( AI_{i} = AI_{k} \), then we get the common anti-ideal vector, which we denote by AI \( = \left[ {x_{1}^{ - } , \ldots ,x_{n}^{ - } } \right]. \) If moreover, we define:

$$ x_{ij}^{ + } = x_{j}^{ + } \quad \left( {{\text{see}}\;{\text{formula}}\;2} \right) $$
(10)
$$ x_{ij}^{ - } = x_{j}^{ - } \quad \left( {{\text{see}}\;{\text{formula}}\; 3} \right) $$
(11)

then the classical TOPSIS procedure holds. In general, target values \( x_{ij}^{ + } \) or \( x_{ij}^{ - } \) are different from \( \mathop {\hbox{max} }\nolimits_{i} x_{ij} \) or \( \mathop {\hbox{min} }\nolimits_{i} x_{ij} \), where \( x_{ij} \) is the value of \( j \)-th SD indicator for \( i \)-th country.

If all alternatives are not worse than the anti-ideal AI and not better than the ideal I,

$$ x_{ij}^{ - } \le x_{ij } \le x_{ij}^{ + } \quad {\text{for}}\;{\text{every}}\;i, j $$
(12)

the classical Euclidean distance measure is sufficient, we use the formula (7)-(8) and consequently the aggregation formula (9).

Now we have to take into consideration two situations:

  1. (a)

    the value \( x_{ij } \) is over good, i.e.

    $$ x_{ij } > x_{ij}^{ + } \; {\text{or}}\;{\text{equivalently}}\;\widetilde{x}_{ij} > w_{j} $$
    (13)
  2. (b)

    the value \( x_{ij } \) is under bad, i.e.

    $$ x_{ij } < x_{ij}^{ - } \varvec{ }\; {\text{or}}\;{\text{equivalently}}\; \widetilde{x}_{ij} < 0 $$
    (14)

    where \( x_{ij} \) is the value of \( j \)-th SD indicator for \( i \)-th country;\( x_{ij}^{ - } ,\varvec{ }x_{ij}^{ + } \)—reference values (target values) for \( i \)-th country and \( j \)-th SD indicator, \( \widetilde{x}_{ij} \)-is the weighted normalized values of \( j \)-th SD indicator for \( i \)-th country (see formula 5), \( w_{j} \) is a weight of \( j \)-th criterion.

To deal with both situations we proposed two approaches: non-compensatory and compensatory.

The non-compensatory approach (see also Roszkowska and Wachowicz 2015, 2016): In the non-compensatory approach we ignore the fact, that value \( x_{ij } \) is outside the interval [\( x_{ij,}^{ - } x_{ij}^{ + } ] \). Then the potential surplus value of such \( x_{ij } \) over \( x_{ij}^{ + } \varvec{ } \) or shortages in relation to \( x_{ij,}^{{ - \varvec{ }}} \) will not be compensated in any way with the option values of other criteria. Formally, the evaluation of the alternative \( A_{i} \) under the non-compensatory approach will be carried out taking into account the non-compensatory normalized weighted values \( \left( {\widetilde{x}_{ij} } \right)_{nc} \) for this alternative, i.e.:

$$ \left( {\widetilde{x}_{ij} } \right)_{nc} = \left\{ {\begin{array}{*{20}c} {w_{j} } &\quad {{\text{if}} \, \widetilde{x}_{ij} > w_{j} } \\ 0 &\quad {{\text{if }}\widetilde{x}_{ij} < 0 } \\ {\widetilde{x}_{ij} } &\quad {\text{otherwise}} \\ \end{array} } \right. . $$
(15)

where \( \widetilde{x}_{ij} \)—is the weighted normalized values of \( j \)-th SD indicator for \( i \)-th country (see formula 5), \( w_{j} \) is a weight of \( j \)-th criterion.

The Euclidean distance measures \( \left( {d_{i}^{ + } } \right)_{nc} \) i \( \left( {d_{i}^{ - } } \right)_{nc} \) of each non-compensatory normalized weighted i-th alternative from PIS and NIS are used next:

$$ \left( {d_{i}^{ + } } \right)_{nc} = \sqrt {\mathop \sum \limits_{j = 1}^{n} \left( {\left( {\widetilde{x}_{ij} } \right)_{nc} - w_{j} } \right)^{2} } , $$
(16)
$$ \left( {d_{i}^{ - } } \right)_{nc} = \sqrt {\mathop \sum \limits_{j = 1}^{n} \left( {\left( {\widetilde{x}_{ij} } \right)_{nc} } \right)^{2} } . $$
(17)

where \( \left( {\widetilde{x}_{ij} } \right)_{nc} \) is non-compensatory normalized weighted values of \( j \)-th SD indicator for \( i \)-th country (see formula 15), \( w_{j} \) is a weight of \( j \)-th criterion.

Step 8a:

Calculating the relative closeness \( \left( {T_{i} } \right)_{nc} \) to the PIS.

For the i-th alternative we compute:

$$ \left( {T_{i} } \right)_{nc} = \frac{{\left( {d_{i}^{ - } } \right)_{nc} }}{{\left( {d_{i}^{ - } } \right)_{nc} + \left( {d_{i}^{ + } } \right)_{nc} }} $$
(18)

where \( 0 \le \left( {T_{i} } \right)_{nc} \le 1, i = 1, \ldots , m \).

Step 9a:

Ranking of all alternatives according to descending \( \left( {T_{i} } \right)_{nc} \).

Let us observe that the non-compensatory TOPSIS approach is related to strong sustainability perspective, were we assumed that the targets for individual indicators are complementary, but not interchangeable.

The compensatory approach (see also Roszkowska and Wachowicz 2015, 2016): The estimated alternatives may fully compensate for by options that go beyond the values from the interval [\( x_{ij}^{ - } ,x_{ij}^{ + } ] \). However, it is necessary in this case to give up the idea of distance measurement. Therefore, the distance concept will be replaced by a deviation concept that will allow to distinguish the aggregated positive and negative deviations. The deflection measures the remoteness of a given alternative from the PIS but distinguishes whether the remoteness is favorable (the option of the alternative exceeds the PIS) or unfavorable (the option of the alternative is worse than the PIS) from the point of view of the decision maker. In the first case, we can say about a positive deviation, in the second—about a negative one. The deviations from NIS are defined analogically. The aggregated deviations from PIS (\( \left( {d_{i}^{ + } } \right)_{com} ) \) and NIS (\( \left( {d_{i}^{ - } } \right)_{com} ) \) for the i-th evaluated alternatives are determined by the formulas:

$$ \left( {d_{i}^{ + } } \right)_{com} = q_{i}^{ + } \sqrt {\left| {\mathop \sum \nolimits_{j = 1}^{n} q_{ij}^{ + } \left( {\widetilde{x}_{ij} - w_{j} } \right)^{2} } \right|} , $$
(19)
$$ \left( {d_{i}^{ - } } \right)_{com} = q_{i}^{ - } \sqrt {\left| {\mathop \sum \nolimits_{j = 1}^{n} q_{ij}^{ - } \left( {\widetilde{x}_{ij} } \right)^{2} } \right|} , $$
(20)

where \( q_{ij}^{ + } \) (\( q_{ij}^{ - } \)) is an indicator of the direction of a single-criterion deviation from PIS (NIS) formulated by:

$$ q_{ij}^{ + } = \left\{ {\begin{array}{*{20}c} { 1} &\quad {{\text{if }} w_{j} > \widetilde{x}_{ij} } \\ { - 1} &\quad {{\text{if }} w_{j} \le \widetilde{x}_{ij} } \\ \end{array} } \right., $$
(21)
$$ q_{ij}^{ - } = \left\{ {\begin{array}{*{20}c} { 1} &\quad {{\text{if }}\widetilde{x}_{ij} > 0} \\ { - 1} &\quad {{\text{if }}\widetilde{x}_{ij} < 0} \\ \end{array} } \right., $$
(22)

and \( q_{i}^{ + } \) (\( q_{i}^{ - } ) \)-an indicator of the direction of the deviation aggregated from PIS (NIS):

$$ q_{i}^{ + } = \left\{ {\begin{array}{*{20}c} 1 &\quad {{\text{if }}\mathop \sum \nolimits_{j = 1}^{n} q_{ij}^{ + } \left( {\widetilde{x}_{ij} - w_{j} } \right)^{2} > 0} \\ { - 1} & {\text{otherwise }} \\ \end{array} } \right., $$
(23)
$$ q_{i}^{ - } = \left\{ {\begin{array}{*{20}c} { 1} &\quad {{\text{if }}\mathop \sum \nolimits_{j = 1}^{n} q_{ij}^{ - } \left( {\widetilde{x}_{ij} } \right)^{2} > 0} \\ { - 1} & {\text{otherwise}} \\ \end{array} } \right. $$
(24)

where \( \widetilde{x}_{ij} \)—is the weighted normalized values of \( j \)-th SD indicator for \( i \)-th country (see formula 5), \( w_{j} \) is a weight of \( j \)-th criterion.

Step 8b:

Calculating the relative closeness \( \left( {T_{i} } \right)_{com} \) to the PIS.

For the i-th alternative we compute:

$$ \left( {T_{i} } \right)_{com} = \frac{{\left( {d_{i}^{ - } } \right)_{com} }}{{\left( {d_{i}^{ - } } \right)_{com} + \left( {d_{i}^{ + } } \right)_{com} }} $$
(25)

where \( 0 \le \left( {T_{i} } \right)_{com} \le 1 \), \( i = 1, \ldots ,m \).

Step 9b:

Ranking of all alternatives according to descending \( \left( {T_{i} } \right)_{com} \).

Let us note, that the compensatory TOPSIS approach is related to weak sustainability perspective, where we assumed that the targets for individual indicators can be substituted.

4 Material and data

The Europe 2020 strategy is the EU’s agenda which emphasizes smart, sustainable and inclusive growth to overcome the structural weaknesses in Europe’s economy, improve its competitiveness and productivity and develop sustainable social market economy. The educaon and training are “the heart of the Europe 2020 strategy” and important policy components whic“are seen as key drivers for growth and jobs” (Eurostat 2017b). Taking into consideration the “smart growth” priority the objectives were adopted to address the phenomenon of early school leaving and raise the level of higher education. As mentioned before, the Europe 2020 strategy sets out two targets: reducing the share of early leavers of education and training to less than 10% and increasing the share of the population aged 30–34 having completed tertiary or equivalent education to at least 40% by 2020 (European Commission 2014). Taking into account national circumstances, the overall EU education targets have been translated into national targets by EU Member States (Eurostat 2017c).

Upper secondary education is considered as the minimum desirable educational attainment level for EU citizens. People who finished their education early more often undertake unstable or low-paid jobs, social welfare benefits, are less likely to be “active citizens” or engage in adult education. Higher education gives opportunity for better paid and stable employment, which in turn reduces the risk of poverty or social exclusion. Tertiary education combined with research and innovation, provides highly qualified human capital. The lack of these skills is a barrier to economic growth and employment in condition of fast technological progress and global competition (Eurostat 2017b).

The two Europe 2020 education targets also feature as EU benchmarks under the Strategic Framework for ET 2020. In addition, there are other five quantitative benchmarks to fulfill by 2020:

  • at least 95% of children between the age of four and the age for starting compulsory primary education should participate in early childhood education

  • the share of low-achieving 15-year olds in reading, mathematics and science should be less than 15%

  • the share of graduates (20–34-year olds) having left education and training in the past one to 3 years who are employed and not in any further education and training should be at least 82%

  • an average of at least 15% of adults should participate in learning

  • an EU average of at least 20% of higher education graduates and of at least 6% of 18–34 year olds with an initial vocational qualification should have spent some time studying or training abroad.

The Europe 2020 educational targets are monitored with the two headline indicators: early leavers from education and training [sdg_04_10] and tertiary education [sdg_04_20] (Eurostat database). Other SDG indicators are also used to monitor progress towards additional benchmarks set under ET 2020. These indicators include participation in early childhood education [sdg_04_30], underachievement in reading, maths, science [sdg_04_40], employment rates of recent graduates [sdg_04_50] and adult participation in learning [sdg_04_60] (Eurostat database). The set of all SDG 4 indicators allows for looking at educational attainment in general and its impacts on the labour market. We start with early school leaving and next followed by the typical educational pathway, starting with early childhood education, followed by the acquisition of basic skills (reading, maths and science) leading to tertiary education and adult participation in learning (Eurostat 2018).

It is worth noting that the EU’s educational targets are also interlinked with the other Europe 2020 goals as higher educational attainment improves employability, which in turn reduces poverty. In particular, the tertiary educational target is interrelated with research and development (R&D) and innovation target as investment in the R&D sector (see, e.g. Knight 2005; De Wit et al. 2015; Albareda-Tiana et al. 2018).

The list of indicators with EU targets used in analysis is presented in Table 1, definition of indicators can be found (Eurostat 2018).

Table 1 The list of SDG4 indicators and EU targets.
Full size table

5 Results

The empirical study is to evaluate the implementation of the Europe 2020 strategic goals in the education area in the EU member states in 2015. Using SDG 4 indicator data, we created some composite indexes of sustainability related to education, based on extended TOPSIS procedure. The main function of those indexes is checking the ability to synthetically express the level of implementation of SDG 4 goals. This objective is pursued using extended TOPSIS techniques, from the perspective of rank-ordering countries, taking into consideration the idea of evaluation ofeducational goals, realizing EU educational targets, realizing national educational targets, respectively. We assumed that national and EU targets can not be interchangeable, so only non-compensatory TOPSIS procedure is used.

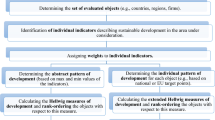
Three different TOPSIS models, suitable for evaluating the education domain from three perspectives of ideal and anti-ideal understanding, i.e. classical approach based on the maximum and minimum values of SDG 4 indicators, based on EU targets and national targets are proposed (see Fig. 1). Our multi-dimensional approach enabled comparisons across EU countries.

Fig. 1
figure 1

TOPSIS models, suitable for evaluating the education domain

Full size image

T1, T2 and T3 are the proposed methods of evaluation of EU countries in implementing EU goals in the area of education addressing questions Q1–Q3 from the introduction

The educational goals defined in the Strategy 2020 are measurable and comparable. Therefore, a set of the Europe 2020 indicators SDG 4, from Table 1, adequately describe the phenomenon of education by introducing appropriate load of information into the analysis and sufficiently differentiate the classified objects. However, we found strong correlation between underachievement in reading, maths and science we used all indicators from Table 1 for constructing composite indexes. Final set of data for 28 EU countries in 2015 consisting of eight indicators, marked by symbols from C1 to C8, together with national targets for C1 and C2, are presented in Table 2. National targets for early leavers from education and training, range from 4% for Croatia to 16% for Italy and for tertiary education from 26% for Italy to 66% for Luxembourg in 2015. Table 2 also shows that in 2015 eleven countries had already achieved their national targets for early leavers from education and training and thirteen countries for tertiary education. Table 2 also consists of main statistic parameters. Let us note that the EU countries are the most differentiable with respect to adult participation in learning (C8), and the least in participation in early childhood education (C3).

Table 2 The data of 28 EU countries and national targets in 2015.
Full size table

Assigning weights of indicators is an important part of sustainability analysis. Gana et al. (2017) categorized the methods for weighting indicators into three groups: (1) equal weighting, which means that all the indicators have the same weights, (2) statistic-based weighting obtained from the statistical characteristics of the data (OECD 2012) and (3) public/expert opinion-based weighting. Gana et al. (2017) analyzed the characteristics, strengths and weaknesses of nine most commonly used weighting methods, showing that among the 96 reviewed papers—46,88% adopted equal weighting method. Also, Maggino and Ruviglioni (2009) noticed that equal weighting was used in most of the applications. They said that “this happens mainly when (i) the theoretical structure attributes to each indicator the same adequacy in defining the variable to be measured, (ii) the theoretical structure does not allow hypotheses to be consistently derived on differential weightings, (iii) the statistical and empirical knowledge is not adequate for defining weights, (iv) the correct adoption and application of alternative procedures do not find any agreement”. According to (i), in this paper, the same weights for all indicators were adopted.

Table 3 summarizes the rankings of the EU countries obtained by using classical TOPSIS procedure based on the maximum and minimum values of SDG 4 indicators (T1), non-compensatory TOPSIS procedure based on UE targets (T2) and national targets (T3), all with equal weights.

Table 3 The values and rank-ordering EU countries obtained by TOPSIS measures.
Full size table

Additionally, taking into account the values of synthetic measure T, grouping of EU countries was made. The following division allowed to distinguish the countries according to different level of education development with respect to TOPSIS procedures:

  • Group 1: \( T \in \left[ { \overline{T} + S_{T} ,\hbox{max} \left\{ {T_{i} } \right\}} \right] \) represents a very high level of education development,

  • Group 2: \( T \in \left[ { \overline{T} ,\overline{T} + S_{T} } \right) \) represents a medium–high level of education development,

  • Group 3: \( \overline{T} \in \left[ {\overline{T} - S_{T} ,\overline{T} } \right) \) represents a medium–low level of education development,

  • Group 4: \( T \in \left[ {\hbox{min} \left\{ {T_{i} } \right\}, \overline{T} - S_{T} } \right) \) represents a very low level of education development,

    where \( T \in \left\{ {T1, T2, T3} \right\} \), \( \overline{T} \) and \( S_{T} \) are the average value and the standard deviation of synthetic measures.

The classification of countries with respect to the measures T1–T3 is presented in Table 4.

Table 4 Classification of countries with respect to the measures T1–T3.
Full size table

Answering question Q4, we can observe that the results demonstrate significant disparities in the level of implementation of the Strategy 2020 in education area across EU countries. Moreover, the following analysis also provides the answer to the question Q5.

We have found that according to composite index T1, the countries characterized by a very high level of implementation of educational goals in 2015 were: Denmark—with a value of 0.804, Sweden—0.756 and the Netherlands—0.734. The largest group, consisting of 13 countries was composed of countries with medium–low levels of sustainable development. Eleven countries included in the group 1 and 2 are the countries of the so-called „old EU”, five (Estonia, Slovenia, Poland, Lithuania, Latvia) are the countries that joined the Union in 2004. The regions characterized by the lowest level of implementation of educational goals (Group 4) were: Bulgaria (0.290), Romania (0.229), Greece (0.336) and Slovakia (0.379).

During the next stage of the research, we built the rankings based on extended TOPSIS method with EU targets (T2) and national targets (T3). We observed a greater spread between the highest and the lowest values in these rankings. Both of them, once again, highlighted Denmark (0.988) as the region with the highest level of realization of education goals from the perspective of EU or/and national targets. The next three positions were taken by the Netherlands (0.936), the United Kingdom (0.899) and Sweden (0.884). These four mentioned countries are characterized by high (from 4 to 6) numbers of realized EU education targets. As a consequence, they were placed in the Group 1. In the case of T3 method, Estonia (which also reached 4 EU targets) can be found in the group represented by a very high level of education development. The last two places in rankings were allocated to the same states as in the first ranking (T1): Bulgaria (0.425 for T3 and 0.401 for T2), Romania (0.298 for T3 and 0.285 for T2). Both countries are characterized by a zero number of realized EU educational targets. With the exception of these two countries and Portugal, the other EU countries have realized at least one EU goal. In the case of classification by means of T2 and T3 methods besides Slovakia, Greece, Bulgaria and Romania, also Cyprus, Malta and Croatia were placed in the group of countries with a very low level of education development. Except Greece, all of them are the countries of so-called “new EU”.

It is worth mentioning, that the national targets are considered only for two (C1 and C2) among eight studied indicators. It caused rather small differences between the rankings obtained by means of T2 and T3 methods. The range of assumed national targets was from 4 (Croatia) to 16 (Italy) for the indicator C1 (when the EU target is below 10) and from 26 (Italy) to 66 (Luxemburg) for the indicator C2 (while the EU target is at least 40). Lower assumed national targets were a reason of a higher position of the country in the ranking used by T3 in comparison with the ranking based on T2. It concerned Latvia and Czech Republic. In the classification with respect to the measure T3, Czech Republic was in the group of the countries with a medium–high level of education development. On the other hand, the ambitiously assumed national targets can influence lower position in the ranking. It happened in case of Luxembourg, Poland and Belgium.

While analyzing positions of EU countries, in the overall classification obtained by different TOPSIS procedures, it has to be emphasized that some EU countries improved, while others worsened their position in the ranking. Comparing values of T2 and T1, three countries improved their values the most: Austria (0.221), the United Kingdom (0.210) and the Netherlands (0.203) which resulted in an increase of the position in the ranking: Austria (4 positions), the United Kingdom (3 positions), the Netherlands (1 position). The smallest increase in the value of the indicator was recorded for Malta (0.038) (decrease by 2 positions) and Romania (0.055), which takes the last position in all rankings. The largest drop (from 5th position to 10th position) was recorded for Ireland with a small increase by the 0.107 index value.

Comparing values of T3 and T1, the same three countries improved their values the most: Austria (0.225), the United Kingdom (0.210) and the Netherlands (0.202). These changes of the values were translated into the same increase of position in the ranking: Austria (4 positions), the United Kingdom (3 positions), the Netherlands (1 position). However, the largest increase in the ranking was observed for Latvia (5 positions), with a moderate change in the value of the indicator (0.176). The smallest increase in the value of the indicator was recorded for Malta and for Romania. The largest drop in the position was recorded also for Ireland with a small increase by the 0.09 index value.

Figure 2 presents graphical representation and comparison of the results obtained by TOPSIS procedures and confirms diversity among the countries.

Fig. 2
figure 2

Comparison of rankings obtained by means of methods T1–T3

Full size image

The spread in case of three applied methods is as follows: 0.575 (for T1), 0.690 (for T2), 0.694 (for T3). The Pearson’s correlation coefficients between the used methods is as follows: r(T1,T2) = 0.978, r(T1,T3) = 0.970, r(T2,T3) = 0.996 and all are statistically significant (p < 0.05).

The analysis allowed to answer all questions stated in the introduction. Obtained results show vast differences between EU countries as far as education is concerned. The results show educational leaders among EU countries but also reveal that some of them still have much to do in this area.

6 Conclusion

This article describes how two main scientific goals are achieved through our research. The first goal of this study is to propose a new methodological framework based on extended TOPSIS, which integrates assessment of sustainability goals taking into consideration target levels. The classical TOPSIS formula aggregates all criteria in a unique value which implies full compensation among them (bad performance in some criteria can be made up by good performance in the others). Two extensions of TOPSIS procedure, in the form of distinction between “weak sustainability” (compensatory TOPSIS) and “strong sustainability” (non-compensatory TOPSIS) were presented. As far as we are aware, there are no other studies which have proposed a multi-criteria methodology that can be applied to measure sustainable development allowing an integrated sustainability assessment and taking into account both compensatory and non-compensatory approach in the context of target points. For completeness in this paper, theoretical concept of compensatory and non-compensatory sustainability approach is explained. However, we only used the concept of non-compensatory approach in our case study. From the methodological point of view, both approaches can lead to interesting results and they are worth further analyses. Moreover, the extended TOPSIS procedures are easy to understand and the evaluation is clear and transparent. The proposed extensions of TOPSIS algorithm allow us to conduct a complex evaluation of EU countries. Our results show that TOPSIS technique is the right approach to sustainability assessment.

The second goal of this paper is the multiple-criteria analysis of the level of implementation of the Europe 2020 strategy recommendations and the spatial diversity of EU countries in the area of education in 2015. The obtained results have certain practical implications. In 2015, the European Union has reached the halfway point in the implementation of the Europe 2020 strategy. The extended TOPSIS procedures allow for the analysis of the disparities of EU countries in the field of education. The study also resulted in a number of findings related to the method of measuring the level of implementation of Strategy 2020 in education area. The multi-criteria model for evaluation of education has been developed with respect to the sustainable development educational goals of EU or national targets. In the literature on the subject there are no clear indications as to the level of impact of individual indicators SDG 4 on the implementation of Strategy 2020. For this reason, all indicators were treated with the same importance and the same weight was assumed. However, the problem of different weights is interesting (see also Gana et el 2017; Maggino and Ruviglioni 2009) and should be taken into consideration in the future research. The study confirmed the strong disparities between EU Member States. The results of the study can be used by the European Commission as well as the appropriate institutions of the countries to evaluate the progress made in education domain.

This paper suggests new directions for further studies where we will be able to monitor the impact on the development of the country taking into consideration the national or EU targets and measuring sustainable development in other areas based on SGD set of indicators. Further studies will be dedicated to the analysis of regional characteristics that will allow to explain the value of the synthetic measure.