Skip to main content
SpringerLink
Log in

Positive blending Hermite rational cubic spline fractal interpolation surfaces

  • Published:
Calcolo Aims and scope Submit manuscript

Abstract

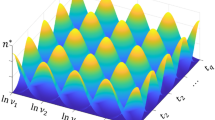
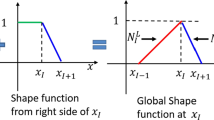
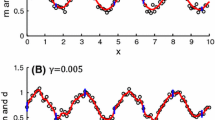
Fractal interpolation provides an efficient way to describe data that have smooth and non-smooth structures. Based on the theory of fractal interpolation functions (FIFs), the Hermite rational cubic spline FIFs (fractal boundary curves) are constructed to approximate an original function along the grid lines of interpolation domain. Then the blending Hermite rational cubic spline fractal interpolation surface (FIS) is generated by using the blending functions with these fractal boundary curves. The convergence of the Hermite rational cubic spline FIS towards an original function is studied. The scaling factors and shape parameters involved in fractal boundary curves are constrained suitably such that these fractal boundary curves are positive whenever the given interpolation data along the grid lines are positive. Our Hermite blending rational cubic spline FIS is positive whenever the corresponding fractal boundary curves are positive. Various collections of fractal boundary curves can be adapted with suitable modifications in the associated scaling parameters or/and shape parameters, and consequently our construction allows interactive alteration in the shape of rational FIS.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

References

  1. Barnsley, M.F.: Fractal functions and interpolation. Constr. Approx. 2, 303–329 (1986)

    Article  MATH  MathSciNet  Google Scholar 

  2. Barnsley, M.F., Harrington, A.N.: The calculus of fractal interpolation functions. J. Approx. Theory. 57(1), 14–34 (1989)

    Article  MATH  MathSciNet  Google Scholar 

  3. Bouboulis, P., Dalla L., Drakopoulos, V.: Image compression using recurrent bivariate fractal interpolation surfaces. J. Bifur. Chaos. 16(7), 2063–2071 (2006)

    Google Scholar 

  4. Bouboulis, P., Dalla, L.: Closed fractal interpolation surfaces. J. Math. Anal. Appl. 327, 116–126 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  5. Bouboulis, P., Dalla, L.: Fractal interpolation surfaces derived from fractal interpolation functions. J. Math. Anal. Appl. 336, 919G936 (2007)

    Article  MathSciNet  Google Scholar 

  6. Brodlie, K., Mashwama, P., Butt, S.: Visualization of surface data to preserve positivity and other simple constraints. Comput. Graph. 19(4), 585–594 (1995)

    Article  Google Scholar 

  7. Cambell, B.A., Shepard, M.K.: Shadows on a planetary surface and implications for photometric roughness. ICARUS. 134, 279–291 (1998)

    Article  Google Scholar 

  8. Casciola, G., Romani, L. : Rational interpolants with tension parameters. In: Cohen A., Merrien J.L., Schumaker L.L. (eds.) Curve and surface design, pp. 41–50. Brentwood (TN), Nashboro (2003)

  9. Chand, A.K.B., Kapoor, G.P.: Hidden variable bivariate fractal interpolation surfaces. Fractals. 11(3), 277–288 (2003)

    Article  MATH  MathSciNet  Google Scholar 

  10. Chand, A.K.B., Kapoor, G.P.: Generalized cubic spline fractal interpolation functions. SIAM J. Numer. Anal. 44(2), 655–676 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  11. Chand, A.K.B.: Natural cubic spline coalescence hidden variable fractal interpolation surfaces. Fractals. 20(2), 117–131 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  12. Chand, A.K.B., Navascués, M.A.: Natural bicubic spline fractal interpolation. J. Nonlinear Anal. 69, 3679–3691 (2008)

    Article  MATH  Google Scholar 

  13. Chand, A.K.B., Navascués, M.A.: Generalized Hermite fractal interpolation. Rev. Real Acad. Cienc. Zaragoza. 64, 107–120 (2009)

    MATH  Google Scholar 

  14. Chand, A.K.B., Vijender N.: Monotonicity preserving rational quadratic fractal interpolation functions. Adv. Num. Anal. 2014, Art ID 504825, 1–17 (2014)

  15. Chand, A. K. B., Vijender, N., Navascués, M. A.: Shape preservation of scientific data through rational fractal splines, Calcolo. doi:10.1007/s10092-013-0088-2

  16. Chand, A.K.B., Viswanathan, P.: Cubic Hermite and cubic spline fractal interpolation functions. AIP Conf. Proc. 1479, 1467–1470 (2012)

    Article  Google Scholar 

  17. Chand, A.K.B., Viswanathan, P.: A constructive approach to cubic Hermite fractal interpolation function and its constrained aspects. BIT Numer. Math. 53(4), 841–865 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  18. Dalla, L.: Bivariate fractal interpolation functions on grids. Fractals. 10(1), 53–58 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  19. Duan, Q., Djidjeli, K., Price, W.G., Twizell, E.H.: The approximation properties of some rational cubic splines. J. Comput. Math. 72, 155–166 (1999)

    MATH  MathSciNet  Google Scholar 

  20. Feng, Z., Feng, Y., Yuan, Z.: Fractal interpolation surfaces with function vertical scaling factors. Appl. Math. Lett. 25(11), 1896–1900 (2012)

    Google Scholar 

  21. Geronimo, J.S., Hardin, D.P.: Fractal interpolation functions from \(\mathbb{R}^n \rightarrow \mathbb{R}^m\) and their projections. Z. Anal. Anwend. 12, 535–548 (1993)

    Google Scholar 

  22. Kapoor, G.P., Prasad, S.A.: Smoothness of coalescence hidden-variable fractal interpolation surfaces. Int. J. Bifur. Chaos Appl. Sci. Eng. 19(7), 2321–2333 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  23. Mulansky, B., Schmidt, J.W.: Nonnegative interpolation by biquadratic splines on refined rectangular grids, In: Laurent, P.J., Le Mehaute, A., Schumaker, L.L. (eds.) Wavelets, images, and surface fitting, pp. 379–386. A K Peters, Wellesley (1994)

  24. Malysz, R.: The Minkowski dimension of the bivariate fractal interpolation surfaces. Chaos Solitons Fractals. 27(5), 1147–1156 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  25. Navascués, M.A.: Fractal polynomial interpolation. Z. Anal. Anwend 25(2), 401–418 (2005)

    Article  Google Scholar 

  26. Navascués, M.A., Sebastián, M.V.: Smooth fractal interpolation, J. Inequal Appl. 2006, Art ID 78734, 1–20 (2006)

  27. Sarfraz, M., Hussain, M.Z.: Data visualization using rational spline interpolation. J. Comp. Appl. Math. 189, 513–525 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  28. Schmidt, J.W., Heß, W.: Positivity of cubic polynomial on intervals and positive spline interpolation. BIT. 28, 340–352 (1988)

    Article  MATH  MathSciNet  Google Scholar 

  29. Xie, H., Sun, H.: The study of bivariate fractal interpolation functions and creation of fractal interpolated surfaces. Fractals. 5(4), 625–634 (1997)

    Article  MATH  MathSciNet  Google Scholar 

  30. Zhao, N.: Construction and application of fractal interpolation surfaces. Vis. Comput. 12, 132–146 (1996)

    Article  Google Scholar 

Download references

Acknowledgments

The first author is thankful to the Science and Engineering Research Council, Department of Science and Technology India (Project No. SR/S4/MS: 694/10). The authors are thankful to the anonymous referee for valuable suggestions.

Author information

Authors and Affiliations

  1. Department of Mathematics, Indian Institute of Technology Madras, Chennai,  600036, India

    A. K. B. Chand & N. Vijender

Authors
  1. A. K. B. Chand
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. N. Vijender
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. K. B. Chand.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Chand, A.K.B., Vijender, N. Positive blending Hermite rational cubic spline fractal interpolation surfaces. Calcolo 52, 1–24 (2015). https://doi.org/10.1007/s10092-013-0105-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10092-013-0105-5

Keywords

Mathematics Subject Classification (2000)

Search

Navigation