Introduction

In the last decades, due to global warming, the frequency of extreme events, such as rapid and severe rainstorms, glacier melting and permafrost degradation, has rapidly increased. These aspects may contribute to triggering many different types of gravitational movement, such as rockslides, debris avalanches and debris flows, which are decisive in the morphological evolution of mountainous areas, which are often extensively urbanized and therefore characterized by a high hazard potential (Fioraso 2000).

Due to their unpredictability, extreme-rapid mobilization and large volume, debris flows are among the most devastating landslide processes on Earth. In urbanized areas, these phenomena cause enormous economic damages and loss of human life, reminding us once again of society’s vulnerability to natural disasters (Zimmermann and Haeberli 1992; Jakob and Hungr 2005).

Since the stabilization of source areas is not always a viable solution (Hungr 1995), a detailed risk analysis is required, including prediction of possible event scenarios both for safer land-use planning and hazard mapping and for designing mitigation measures accordingly.

Mitigation strategies must focus on the preliminary identification of basin geologic and morphometric characteristics and classifying them according to their dominant hydrogeomorphic processes (Crosta and Frattini 2004; Vagnon et al. 2015, 2020; Vagnon 2020; Wei et al 2017). Detailed field-work analyses, by applying methods based on hazard indicators or stratigraphic evidence, are fundamental for defining potentially erodible zones inside the basin and estimating the debris flow volume. However, analyses at basin scale require significant resources and time and may not be practicable in inaccessible mountainous areas. Geographic information systems (GIS) and digital terrain models (DTMs) are two tools that assist in overcoming or supplementing the need for field analyses. DTMs have enabled new perspectives (Ferrero et al. 2016) for geomorphological interpretation (e.g. lineament extraction, slope gradient evaluation, etc.) and for accurate modelling of debris flow dynamics (Savage and Hutter 1989; Hungr 1995; Iverson 1997; Pastor et al. 2002; Pirulli 2005; Vagnon et al. 2017; Wei et al. 2018; Bonetto et al. 2021). Many geomorphological and analytical–numerical models, implemented in GIS, allow for analysis, reconstruction and prediction of different debris flow scenarios and directly mapping debris flow hazards (Grelle et al. 2019).

Forecasting and modelling debris flow dynamics can be divided into empirical approaches, based on correlation among historical data (Cannon 1993; Corominas 1996; Rickenmann 1999), and numerical models (Savage and Hutter 1989; Hungr 1995; Iverson and Denlinger 2001; McDougall and Hungr 2005; Pirulli 2005; Pastor et al. 2002; Zhang et al. 2022). These methods support the evaluation of debris flow propagation velocity, deposition thickness and entrainment of material along the run-out path, on complex topography. The continuum-based depth-averaged models (DAM) have been widely used since the 1990s. From their first appearance in 1989 (Savage and Hutter 1989), many improvements were proposed: for instance, Gray et al. (1999) performed DAM analyses over complex basal topography. Iverson and Denlinger (2001) developed a model in which the fluid continuum was treated as a mixture of a solid matrix and a liquid fraction.

DAMs have the main advantage of requiring little computational time, even if the geometry, or the boundary conditions, are complex, making them particularly recommended for a first screening of the possible areas subjected to debris flow runout or for planning mitigation strategies.

RASH3D (Pirulli 2005) is one of the most recent single-phase codes developed within DAMs. It has proven its reliability in reproducing flow-like landslides paths over complex topography (Pasqua et al. 2021; Pirulli 2005; Pirulli et al. 2015, 2017; Vagnon et al. 2018, 2019). Compared to other codes, it allows the analysis of entrainment effects on runout analysis results, by implementing the well-established erosion law proposed by McDougall and Hungr (2005), which is a good compromise between simplicity and accuracy.

In this paper, a multidisciplinary approach, combining detailed geomorphological analyses and modern technologies, was used to study debris flow events occurred in the Torrent Rochefort (Aosta Valley—north-western Italy). In particular, the event that occurred on 17th September 2015 was studied and back analysed because it is the largest event recorded to date, with an estimated mobilized volume of about 100,000 m3 and that caused extensive damage to local infrastructures. Two DTMs were used for performing numerical analyses and hazard mapping. A pre-event DTM was provided by the regional authorities and a post-event DTM was generated from an unmanned aerial vehicle (UAV) photogrammetric point cloud. Moreover, the availability of the two DTMs allowed for the estimation of erosion processes along the Rochefort basin: numerical results carried out with RASH3D code were validated by comparing post-event information, geomorphological evidence and erosion/deposition areas detected along Torrent Rochefort.

Description of study area

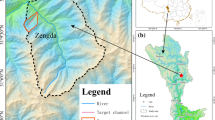
This research focused on the mountainous watershed of Rochefort Torrent (Aosta Valley—north-western Italy). The basin belongs to the Ferret Valley, located in the south-eastern part of the Italian side of Mont Blanc massif (Fig. 1). It is a glacial valley with a NE-SW trend and stretches from the top of Col Ferret (2490 m a.s.l) and the Entrèves municipality. The Dora Ferret and the Dora Veny streams are in the upper part of the Dora Baltea basin, which continues southbound and perpendicular to the Mont Blanc massif. The geological context of Ferret Valley, its tectonic structure, age of the relief, climatic conditions and Quaternary glaciation have given rise to a complex geodynamic framework that is expressed through frequent and various types of flow-like landslides, such as debris flows, glacial and fluvial floods, and rock–ice avalanches. In particular, the Rochefort Torrent basin, a tributary sub-glacial stream of the Dora Ferret, is uniquely susceptible to glacial floods that, due to its geological and geomorphological setting, may evolve into debris flow events. Rochefort Torrent originates from the Rochefort glacier at 2580 m a.s.l and flows for 2.77 km. Despite its modest basin extension of about 2.13 km2, many events have been recorded that caused extensive damage to local infrastructures (the Regional Road La Palud and its bridge on Rochefort Torrent, Fig. 1b).

Fig. 1
figure 1

a Location of the Rochefort watershed (red dashed line) and Rochefort Torrent, Mayen Torrent, Dora Veny, Dora Ferret and Dora Baltea rivers (blue lines). b Local infrastructures affected in the past by debris flow events originating from Rochefort watershed

Full size image

Geological and geomorphological settings

The study area lies between the Graian and the Pennine (western) Alps in the Mont Blanc Massif, formed following the convergence (Cretaceous) and collision (Eocene) of the European and Adriatic (Apulian) plates. The Alpine chain is composed of four structural domains. The study site belongs to the Helvetic–Dauphinois structural domain in the upper flanks and to the Ultrahelvetic domain in the valley floor (Fig. 2a).

Fig. 2
figure 2

a Geological–structural framework of the Western Alps (from Balestro et al. 2015). In the red circle the study area. b Geomorphological sketch. 1—arete; 2—cirque scarp; 3—ice; 4—ice buried by stones; 5—lateral moraine; 6—erosional scarp; 7—debris fan; 8—debris material; 9—gully erosion area; 10—2015 accumulation body; 11—erosional area; 12—road

Full size image

The Helvetic–Dauphinois domain consists of a 10-km-thick sheet of Mont Blanc crystalline basement rocks with little Alpine deformation. The Ultrahelvetic domain is composed of a succession of Triassic limestone, black schists and Jurassic-age calceschists.

The most important macrostructure present in the region is the Pennidic front, which marks the boundary between the Pennidic domain (material formed from both the former European and Adriatic Plates) and the Helvetic domain (from the European Plate). Uplift of the Mont Blanc massif occurred along the Mont Blanc Back Thrust (MBbt), a steep North dipping fault bounding the southern flank of the range (Leloup et al. 2005).

The MBbt separation of granites overlying Mesozoic roofing units is an important lithological transition. It establishes a critical change of slope where the mechanical resistance is lowered resulting in erosion of the calceschists.

Torrent Rochefort lithology includes outcrops of thin sheets of clayey calceschist, occasionally containing cubes of pyrite and dark limestone nodules, dark grey marble layers with white carbonate veins parallelized with schistosity and silver or black schists. Geomorphologically, the Val Ferret is closely linked to glacial episodes from 25,000–11,500 years B.P., resulting in the typical U-shaped morphology of alpine valleys (Perello et al. 2001) and both depositional and erosional landforms. Alluvial fans are a dominant landform in the valley. Meteorological events in the watershed may be short and localized or prolonged and heavy (as much as 600 mm in two days), leading to debris flows and gravitational phenomena (Giardino et al. 2013). According to the interpretative model of Carraro and Giardino (2004), geomorphologic processes were carried out simultaneously with a marked deepening of the glacial bed. A highly erosive environment was created by the size and the thickness of the individual glacial masses, the lithology and structure of the bedrock, and by tectonic activity. This correlation is also presumed by Giardino et al. (2013) to explain, in the context of the Val Veny, the close correlation between structure, climatic conditions, evolution of the glaciers and the highly geodynamic region. Sharp peaks, steep rock slopes and the high gravitational activity are indicative of a “young” relief, mainly due to glacial activity, and strong tectonic activity. The Rochefort stream is inscribed in a large catchment area that collects and conveys the melting waters of the Rochefort Glacier (Fig. 2b). The river basin covers an area of about 2.13 km2, with a length of 2.77 km (2.57 km if you exclude the conoid).

Torrent Rochefort and Torrent Mayen are not easily distinguishable (see Fig. 1) due to continuous movements of the glacier that reshapes the topography of the upper sector of the basin, changing the stream source point and, sometimes, causing the merging of the two streams.

The alteration of the flow networks and the great availability of water easily mobilizes the loose deposits of the glacier moraine. About 20% of the upper basin is covered with glaciers and about 60% is composed of recent glacial deposits and rocky outcrops up to the apex of the fan. Lower altitudes are mainly debris, bare ground and young, low vegetation. A rare forest of larches and fir trees exists at about 1500 m a.s.l.

Figure 3 shows the slope map of the study area and two sections, one along the main course of Torrent Rochefort (AA’) and one perpendicular (BB’). From upstream to the valley, six main sectors (a to f in Fig. 3) can be identified. The first sector (a) represents the crown of the basin, characterized by a steep slope of granite, 50° on average. Sector (b) begins at about 3000 m a.s.l, where a huge drop in elevation highlights the bergschrund of the glacier. Currently, the glacier reaches the 2750 m a.s.l. where it has reshaped granite sheepback rocks (sector (c)). The MBbt, located at 2000 m a.s.l., marks a clear separation between the sector (d), characterized by loose deposit of debris with average slope of 30°, and the sector (e) where the Rochefort stream path becomes defined and well recognizable. As stated above, MBbt marks a change in lithology, from granite to calceschist: this also reflects a variation in mechanical characteristics of the material. In particular, the lower part of sector (e) and all sector (f) are extremely erodible, and deeply incised: the channel assumes the characteristic trapezoidal shape, as represented in BB’ section of Fig. 3. Both sectors (e) and (f) are common to Torrent Mayen and Torrent Rochefort (Fig. 4): the riverbeds are laterally confined and covered by heterogeneous deposits of granite and calceschist rocks. These mobilized deposits were generated by the combined action of water, glacier movements and gravitational phenomena, such as rock fall and debris flow along the stream path. Occasionally debris flow events are related to ice mass movements. In other cases, ephemeral lakes breach the cirque perimeter of ice on the valley side and generate sudden floods and debris flows. For these reasons, a direct relationship cannot be made between precipitation and debris flows of the past.

Fig. 3
figure 3

Slope map of the study area elaborated using DTM with spatial resolution of 2 m and topographical longitudinal profiles and transverse of the watershed of Torrent Rochefort, highlighting the six main sectors of the basin (a to f)

Full size image
Fig. 4
figure 4

Frontal view of the Torrent Rochefort and Torrent Mayen, few meters below the MBbt

Full size image

Description of the 2015 Torrent Rochefort event

From 1991 to today, four debris flows were recorded in Torrent Rochefort as listed in Table 1. All these events were debris flows that occurred mainly in late spring and summer, triggered by intense rainfall and/or because of glacial flooding. In particular, the 2003 event was triggered by high temperatures that rapidly melted the glacier, mobilizing debris along the torrent and causing much damage along the main road. A glacial flood generated by high temperature was also the cause of the most destructive event, which occurred in 1991, where about 100,000 m3 flowed to the valley, causing extensive damage to the infrastructures. Although smaller than the 1991 event, the debris flows of 2003, 2004 and 2015 all resulted in inundation and blockage of the bridge (Fig. 1b) and road (Fig. 5).

Table 1 List of events in the Rochefort basin from 1991 to today (μ is the mean value and σ is the standard deviation)
Full size table
Fig. 5
figure 5

Photograph of the 2015 Torrent Rochefort debris flow deposition at the bridge on the main road

Full size image

In this paper, the authors analysed the 2015 event that occurred after a short but intense rainfall (cumulative rainfall higher than 40 mm/3 days, with peak of about 9 mm/h the day of the event). No indications of its magnitude were given by the local administration in its event report; however, about 6000 m3 of deposition, with a maximum thickness of about 1.5 m, were removed at the bridge and from the road (Fig. 5). The mobilized volume was undoubtedly larger, considering the runout distance covered in a few minutes from the glacier to the Dora Ferret River. In the following section, using two available DTMs, analyses were performed for estimating the magnitude of the 2015 event.

The continuum mechanics approach

The September 2015 Rochefort debris flow was numerically simulated using RASH3D code (Pirulli 2005; Pirulli and Scavia 2007). The theoretical basis of RASH3D code relies on the depth-averaged system of mass and momentum conservation equations, as follows:

$$\left\{\begin{array}{c}\frac{\partial h}{\partial t}+\frac{\partial \left(\overline{{v }_{x}}h\right)}{\partial x}+\frac{\partial \left(\overline{{v }_{y}}h\right)}{\partial y}=\frac{\partial z}{\partial t}\\ \rho \left(\frac{\partial \left(\overline{{v }_{x}}h\right)}{\partial t}+\frac{\partial \left(\overline{{v }_{x}^{2}}h\right)}{\partial x}+\frac{\partial \left(\overline{{v }_{x}{v}_{y}}h\right)}{\partial y}+\frac{\partial \left(\frac{{\mathrm{g}}_{\mathrm{z}}{h}^{2}}{2}\right)}{\partial x}\right)={T}_{{x}_{\left(z=b\right)}}+\rho {g}_{x}h-\overline{{v }_{x}}\frac{\partial z}{\partial t}\\ \rho \left(\frac{\partial \left(\overline{{v }_{y}}h\right)}{\partial t}+\frac{\partial \left(\overline{{v }_{y}{v}_{x}}h\right)}{\partial x}+\frac{\partial \left(\overline{{v }_{y}^{2}}h\right)}{\partial y}+\frac{\partial \left(\frac{{\mathrm{g}}_{\mathrm{z}}{h}^{2}}{2}\right)}{\partial y}\right)={T}_{{y}_{(z=b)}}+\rho {g}_{y}h-\overline{{v }_{y}}\frac{\partial z}{\partial t}\end{array}\right.$$
(1)

where h is the flow depth, \(\overline{v }=(\overline{{v }_{x}}, \overline{{v }_{y}})\) denotes the depth-averaged flow velocity in a (x, y, z) reference system, \(\frac{\partial z}{\partial t}={E}_{t}\) is the erosion rate, ρ is the mass density, \(T=({T}_{x}, {T}_{y})\) is the traction vector, and g = (gx, gy) is the gravity vector.

The assumptions used to derive the system of Eq. (1) are:

  • The material is considered as a single-phase incompressible and homogeneous material (Savage and Hutter 1989; Hungr 1995; Iverson and Denlinger 2001).

  • The moving mass, which may in reality be heterogeneous and complex, is replaced by an equivalent fluid whose bulk properties will approximate the behaviour of the real mass.

  • During the flowing process, the characteristic length in the flowing direction L is generally much larger than the vertical one, e.g. the mass thickness H. Such characteristic allows the depth averaging of the balance equations (Savage and Hutter 1989).

  • A kinematic boundary condition is imposed on free and bed surfaces according to which mass neither enters nor leaves at these two surfaces unless an erosion law is introduced.

  • The flow surface is stress free, while the velocity vector is tangent to the bottom of the flowing mass (i.e. v⋅n = 0)

  • The debris rheology is included in a single term, T, which describes the basal shear stress.

The RASH3D code

The RASH3D code was developed by Pirulli (2005), upgrading a pre-existing numerical code (SHWCIN) developed by Audusse et al. (2000). Running a numerical analysis with RASH3D requires i) knowledge of position and magnitude of the source area, ii) availability of a pre-event DTM, iii) choice and calibration of a proper rheological law, iv) erosion rate evaluation and v) identification of erodible sectors along the runout path. RASH3D is based on the classical finite volume approach for solving hyperbolic systems using the concept of cell centred conservative quantities.

The balance Eq. (1) are discretized on general triangular grids with a finite element data structure using a particular control volume which is the median dual cell (Mangeney-Castelnau et al. 2003; Pirulli 2005). For each vertex of the mesh, the code returns the values of thickness and velocity (in x and y directions) in time and the maximum values reached during the process up to final deposition of the mass.

A proper calculation of the projection of the term of gravity in the system of Eq. (1) is obtained by computing the line of maximum dip of each cell, projecting it on the plane tangent to the topography and re-projecting the obtained direction on the x and y axes of the reference system (Pirulli 2005).

Solving the system of Eq. (1) requires introducing a rheological law. As stated above, T represents the tangential stress generated at the interface between the flowing mass and the topographical surface: it opposes the debris motion and, being v⋅n = 0, has an opposite sign compared to v.

RASH3D allows the use of different rheological laws (Pirulli 2005; Pirulli and Scavia 2007): in this paper, the Voellmy rheology was used to perform numerical analyses. With this rheology, it is possible to better simulate debris flow spreading and distribution compared to other rheological laws (e.g. Hungr and Evans 1996; Rickenmann and Koch 1997; Revellino et al. 2004; Pirulli 2009; Vagnon et al. 2019). In Voellmy rheology, T is given as:

$${T}_{i}=-\rho g\left(h\mu +\frac{{\overline{{v }_{i}}}^{2}}{\xi }\right)\frac{\overline{{v }_{i}}}{\Vert \overline{v}\Vert } i=(x,y)$$
(2)

where μ is the frictional coefficient, equal to the tangent of the bulk friction angle, ξ is the turbulent coefficient, and \(\Vert \overline{v }\Vert\) is the norm of depth-averaged velocity.

Many benchmarks and back analyses have been published for validating the RASH3D numerical results proving its reliability in reproducing both laboratory tests and real events (e.g. Pirulli and Scavia 2007; Manzella et al. 2008; Pirulli 2009, 2016; Pirulli and Marco 2010; Pirulli and Pastor 2012; Pirulli et al. 2017; Vagnon et al. 2019).

RASH3D code provides a good compromise between reliability of results and number of input parameters. The results carried out are useful for hazard mapping, for the verification of adequacy drainage channels or bridges and for a preliminary design of mitigation measures. However, averaging velocity and pressure along the flow depth leads to losing key information regarding, for instance, the interaction with structures in terms of exerted forces and pressures.

Erosion rate formula

All numerical codes have an empirical nature since they cannot simulate the complex internal and basal behaviour of a flowing mass. Moreover, this aspect is emphasized when entrainment processes are taken into account in numerical simulations. In this study, the simple erosion law based on theory developed by McDougall and Hungr (2005) has been selected to reproduce erosion/deposition along Torrent Rochefort:

$$\frac{\partial z}{\partial t}={E}_{t}={E}_{s}h\overline{v }$$
(3)

where Es is the average growth rate that can preliminary be evaluated as follows:

$${E}_{s}=\frac{\mathrm{ln}\left(\frac{{V}_{f}}{{V}_{i}}\right)}{l}$$
(4)

where Vf is the debris final volume, Vi is the debris initial volume, and l is the length of an erosion sector. This erosion law implies an exponential growth of the erosion process as a function of the displacement (McDougall and Hungr 2005).

Numerical back analysis of the 2015 Torrent Rochefort event

The first step to numerically back analyse flow-like landslides is the estimation of the event magnitude and its location on a pre-event topography. The pre-event topography was determined using a high resolution 2008 LIDAR DTM (hereafter referred to as DTM_2008) with 2-m grid spacing obtained from the Aosta Valley Region website. There were no recorded debris flow events since 2008 (see “Description of the 2015 Torrent Rochefort event”), and consequently, no significant changes along the torrent path were expected; therefore, it can be assumed that the DTM_2008 closely reflects the pre-event topography. Considering this assumption, the mobilized volume was estimated as the difference between a DTM generated in 2018 (DTM_2018) and the DTM_2008. The DTM_2018 was created utilizing a “DJI Spark” UAV. A quadricopter of ultra-compact dimensions (170 mm) weighing 300 g. The drone is equipped with GPS and GLONASS technology, and mounts a two-axis gimbal, a 12 MP camera, rear and front shock sensors (http://www.djitop.com/it/droni-dji/dji-spark-detail). The point cloud and resulting DTM were produced using Agisoft Photoscan.

Volume estimation from DTM comparison

The geomorphological and geological analyses have highlighted that the upper sector of Torrent Rochefort is susceptible to a large amount of debris discharge and the lower sector is prone to erosional processes. Thus, it is likely that the 6000 m3 removed from the valley bottom in the last event did not represent the total mobilized volume.

The 7 cm DTM_2018 was constructed along the lower sector of Torrent Rochefort path using UAV technology and resized to a grid spacing of 2 m to reduce code running time. To avoid errors and verify the reliability of the resized DTM, elevations of known points (e.g. elevation of the bridge and mountain peaks surrounding the basin) were compared. The identified differences were acceptable and within a few centimetres.

Comparison of the DTM_2008 and DTM_2018 provided an estimation of the volume of material mobilized along Torrent Rochefort, as in the following:

$${V}_{mobilised}=\sum_{i}^{n}{\left({{z}_{DT{M}_{post-event}}-z}_{DT{M}_{pre-event}}\right)}_{i}\cdot\Delta x\cdot\Delta y$$
(5)

where zDTMpost-event and zDTMpre-event are the terrain elevations evaluated using, respectively, DTM_2018 and DTM_2008 and Δx and Δy are the DTM grid spacings, both equal to 2 m. The total mobilized volume was estimated to be equal to about 100,000 m3. Analysing the historical series “Description of the 2015 Torrent Rochefort event”, an event of this magnitude has occurred in this basin in the past, showing the high debris availability along the path and its potential to cause destructive events. Figure 6 compares the results of the DTM elevation analysis with field evidence: positive variations (blue areas) correspond to depositional areas and negative variations (red areas) correspond to erosional areas. The aforementioned results are confirmed by field observations: where in the upper part, the right bank of the stream (up to “The continuum mechanics approach” in Fig. 6), granite and calceschist rocks outcrop, and consequently, only deposition is observed (Fig. 6b). On the contrary, the left bank is strongly affected by erosional processes, where erosion is the dominant feature in the middle part of the basin (cfr. Figs. 2 and 4) where the Rochefort Torrent flow nears the Mayen Torrent. The lower part of the stream, in proximity to the bridge and the main road, is not intensely affected by erosional processes (Fig. 6c) due to the significant flattening of the terrain. Moreover, during field surveys of the upper sector, evidence of material availability in the range of 1000 to 10,000 m3 was seen and is attributed to its proximity to the glacier. In fact, the varying position of the Rochefort glacier increases or decreases the amount of deposited debris along the steep slopes and consequently influences the magnitude of potential debris flows.

Fig. 6
figure 6

a Quantification of erosional and depositional areas by using DTM_2018 (red lines) and DTM_2008 (black lines) and comparison with field evidences of the upper (b) and lower (c) sectors of the stream

Full size image

Definition of numerical simulation parameter values

Based on geomorphological and geological analyses previously described, three different estimated volumes (1000, 5000 and 10,000 m3) were used for performing numerical simulations. The source area was located at the mouth of Rochefort Glacier at 2000 m a.s.l. (Fig. 7). Unstable volumes were estimated thereby changing the initial thickness of the source area. Consequently, from Eq. 4, three different erosion growth rate values were calculated, respectively, equal to 0.0023, 0.0015 and 0.0012 m−1. These values were obtained considering a final volume of 100,000 m3 and the length of the erodible sector of 2000 m. Moreover, pre- and post-event DTM analyses and on-site evidences defined the erodible area (Fig. 7) and a maximum erosion depth of 5 m. Using the previous input data, three different scenarios (S1, S2 and S3) were considered (Table 2).

Fig. 7
figure 7

Identification of the Rochefort basin source and erodible areas used in numerical simulations

Full size image
Table 2 Different scenarios used for performing numerical simulations
Full size table

With regard to rheological parameter values, since no previous studies were conducted in the basin and no indications on rheological features of the material were available, three values of frictional coefficient, μ, (0.1, 0.15 and 0.2) and turbulence, ξ, (200, 500 and 1000 m/s2) were chosen. These values are in agreement with already published values used in similar geological and geomorphological environments (Hungr and Evans 1996; Pirulli and Pastor 2012; Pastor et al. 2015; Vagnon et al. 2019). By combining all variables, the back analysis of the 2015 Torrent Rochefort debris flow was performed and discussed.

Results of dynamic analysis of the Rochefort debris flow

Figures 8 and 9 show the results of the numerical simulations performed in S1, in terms of depositional height (Fig. 8) and maximum velocity values reached along the debris flow path (Fig. 9). Even if no direct measurements of thickness and velocity were performed immediately after the 2015 event, some information about depositional height and spatial distribution were derived: i) by analysing Fig. 5, especially around the bridge and the surrounding areas; ii) from internal reports of technicians of municipality, in which a depositional height of about 3 m around the bridge was reported; iii) through testimonies of some inhabitants which quantify in 5/6 min the travel time of the flowing mass from glacier to the bridge. These observations were fundamental for the choice of the best-fit rheological parameters of performed numerical simulations.

Fig. 8
figure 8

S1 depositional height distribution

Full size image
Fig. 9
figure 9

S1 velocity distribution obtained considering an initial volume of 1000 m3 and Es equal to 0.0023 m.−1

Full size image

Moreover, by following the verification procedure suggested by Zhou et al. (2022), the accuracy of the simulated fan was compared with the available information on the event fan. In particular, the procedure requires the definition of: i) the observed debris fan, X (see deposit of the 17/09/2015 event in Figs. 2 and 6); ii) the missing accuracy area, Y, which occurs when the simulated fan is greater than the observed one (excessive later spreading); iii) the negative accuracy area, Z, which occurs when the simulated fan is not capable to reproduce the observed one (simulated deposit is smaller than the observed one).

The results for each numerical simulation performed within the S1 are listed in Table 3.

Table 3 Comparison of the simulation accuracy for each rheological parameter combination of S1
Full size table

In detail, after an initial examination, all simulations using μ = 0.2 can be neglected since, regardless of the value of ξ, the mass does not reach the bridge, in contrast with the runout travel indications provided by the local authorities and testimonies of some inhabitants (cfr. “Description of the 2015 Torrent Rochefort event”). For the same reasons, the runout analysis obtained with μ = 0.15 and ξ = 200 m/s2 can be rejected. Moreover, the simulations with μ = 0.1 and ξ = 500 m/s2 and ξ = 1000 m/s2 show an excessive lateral spreading around the bridge, as highlighted by the highest values of Y in Table 3 (respectively, 57% and 74%). Even if no direct measurements were performed, runout analysis with μ = 0.1 and ξ = 200 m/s2 has high velocity values in the deposition zone (up to 9 m/s), where the basin slope becomes gentle (see Fig. 3), incompatible with the duration of the event. Furthermore, the simulation was not capable to reproduce the observed event fan as mirrored by the high value of Z (Table 3). Lastly, the shape of the depositional area was well reproduced by μ = 0.15 and ξ = 1000 m/s2 (see low values of Y and Z in Table 3). Even if, this combination overestimated the depositional heights up to 20% (Fig. 8 and Table 3) around the bridge and at the confluence with the Dora Ferret River, compared to those observed during 2015 event (Fig. 5).

The previous analyses were not able to reproduce the dynamics of the analysed event in a satisfactory way in terms of deposited material volume or erosion depth. In fact, considering the best simulation obtained with μ = 0.15 and ξ = 500 m/s2, the deposited volume around the bridge was about 2800 m3, less than the half of that removed after the 2015 event. This is also in agreement with the results listed in Table 3, where the simulation has the highest capability to reproduce observed depositional thickness but it reproduced a smaller debris fan (Z value in Table 3). Furthermore, the final mobilized volume, numerically computed equal to 28,184 m3, underestimates the 100,000 m3 of the analysed debris flow (Table 4). Further differences can be observed comparing the DTM analysis (Fig. 10a) and the numerically simulated erosion depth (Fig. 10b): even if, the shape of the erodible area is well reproduced, there are large differences between the values of erosion depth/depositional height.

Table 4 Comparison between expected and simulated results for the three scenarios
Full size table
Fig. 10
figure 10

Comparison between erosional and depositional areas obtained by using a geomorphological and DTM information and b from numerical analyses

Full size image

The previous observations suggest that the hypothesis of an initial volume of 1000 m3 was incorrect. Consequently, two more simulations were run increasing the initial debris magnitude to find the best fit between depositional volume, erosion depth along the debris path and deposition shape. Figure 11 shows the comparison in terms of deposit thickness distribution among S1 (Fig. 11a), S2 (Fig. 11b) and S3 (Fig. 11c), carried out using the best-fit rheological parameters of previous analyses (μ = 0.15 and ξ = 500 m/s2).

Fig. 11
figure 11

Comparison between depositional thickness for S1 (a), S2 (b) and S3 (c), using the best-fit rheological parameters (μ = 0.15 and ξ = 500 m/s.2)

Full size image

Based on geomorphological evidence analysed in the previous sections, S2 closely reproduced the 2015 event scenario both qualitatively and quantitatively (Fig. 11b). The deposited volume around the bridge and the roads was estimated at 5900 m3, in agreement with the material removed immediately after the event. Furthermore, the total mobilized volume was calculated roughly equal to 124,000 m3. The best fit between S2 simulation and the 2015 event was also confirmed quantifying and comparing the erosional and depositional areas numerically calculated with that derived using the DTM comparison (Fig. 12). Locations of the maximum values were consistent.

Fig. 12
figure 12

Comparison between erosional and depositional areas obtained by using a geomorphological and DTM information and from S2 b and S3 c

Full size image

In S3 (Fig. 11c), a large lateral spreading can be observed both in depositional area and along the torrent path. Depositional thicknesses are overestimated with respect to the observation made after the 2015 event: consequently, the total mobilized volume was estimated to be greater than 150,000 m3. This is also confirmed by analysing the distribution of the erosional and depositional areas along the runout path (Fig. 12c).

Results from numerical simulations of the three scenarios are resumed in Table 4.

In the central sector of the basin, both numerical S2 and S3 show diffuse lateral spreading in the flat terrain between Torrent Rochefort and Torrent Mayen (cfr. Figs. 3 and 4). Even if the hypothesis of Vi = 10,000 m3 does not correlate with the back analysis of 2015 Rochefort debris flow, it is a relevant parameter for mapping potential future hazards in this area. Geomorphological evidences in the upper sector of the Torrent Rochefort have highlighted the possibility of mobilizing large volumes of debris and water in relation to the general stability conditions of the glacier.

The presented analyses and results clearly highlight the complexity of a numerical simulation of the phenomenon. Nowadays more complex numerical models (compared to RASH 3D) based on multi-phase materials (Pastor et al. 2018; Pudasaini 2012; Pudasaini and Mergili 2019; Rosatti and Begnudelli, 2013) or full 3D models (Leonardi et al. 2014) have been developed. However, such as in this real case, where the uncertainties related to the definition of the mobilizing volume and rheological input parameters cannot be neglected, their use could add no more suitable information to dynamic simulations. Consequently, RASH3D or other mono-phase DAMs can be used for a preliminary hazard mapping where a qualitatively forecasting is an essential prerequisite. Furthermore, the numerical entrainment results obtained with RASH3D are in good agreement with on-site geomorphological observations and with DTM analyses, proving the effectiveness of RASH3D in simulating these phenomena.

As for the choice of a numerical code and the interchangeability of calibrated values of rheological parameters, the authors have recently demonstrated that there is a dependence with the numerical scheme adopted for solving depth-averaged equations (Vagnon et al. 2018, 2019). In particular, Eulerian- (such as RASH3D) and Lagrangian-based codes can differ up to 10% in estimated runout characteristics (Vagnon et al. 2019), with relevant consequences both for hazard mapping and for planning preliminary countermeasures.

Lastly, numerical velocity distribution provides useful information about real dynamic behaviour of 2015 event. Coupling velocity with thickness distribution, it is fundamental for the choice and the design of future mitigation measures to protect the local infrastructures from event of such magnitude.

Conclusions

This paper presents a description and analysis of the debris flow that occurred along the Rochefort Torrent (Aosta Valley—Italy) in September 2015. The analysis combined techniques from the fields of earth sciences and engineering.

A detailed geological and geomorphological study was performed for recognizing potential source areas and depositional and erosional zones along the stream path. In particular, the lithological and topographical characteristics of the basin affect the degree of entrainment of material during the event. A quantitative estimation of the total mobilized volume was performed by comparing a pre-event DTM with a post-event DTM made using UAV techniques.

The RASH3D code was used for dynamic numerical simulations since its capability and reliability are widely demonstrated. Voellmy rheology was selected for its simplicity and reduced number of parameters to calibrate and for its proven reliability in debris flow simulations.

Uncertainties related to volume estimation of the source area, required modelling at a range of magnitudes (from 1000 to 10,000 m3). However, the best-fit simulation was obtained with an initial volume of 5000 m3, frictional and turbulent coefficients of 0.15 and 500 m/s2, respectively, and erosion rate values of 0.0015 m−1 (S2).

This multidisciplinary approach allowed for the reconstruction of debris flow dynamics and calibration of rheological parameters, useful for the prediction of future events. In particular, the 10,000 m3 initial volume simulation highlighted a likely scenario with large effects on the morphological condition of the Rochefort basin for potential debris flows resulting in damage to local infrastructures. Mitigation measures at the bridge and road area should be designed to account for these potential hazards.

Due to climate change and the associated variation in glacier stability, an increase in frequency and magnitude of debris flow events in Rochefort Torrent is plausible. Consequently, studies such as the here presented should be performed to simulate potential runout paths and associated potential mobilizing debris volumes.