Equilibrium design in an n-player quadratic game

Abstract

As in public good provisions, in a public bad situation such as abatement, the non-cooperative interplay of the participants typically results in low levels of quantities (provision or abatement). In a simple class of n-person quadratic games, we show how Coarse correlated equilibria, using simple mediation devices, can significantly outperform Nash equilibrium outcomes in terms of a stated policy objective.

1 Introduction

In non-cooperative games, mediated communication is a true and tested way to achieve incentive-compatible coordinated outcomes, using randomisation, commonly known as, correlation devices. Solution concepts such as correlated equilibrium (CE), as proposed by (Aumann 1974, 1987) and coarse correlated equilibrium (CCE) (Moulin and Vial 1978),¹ coarsen the set of Nash equilibria and thus may improve upon the Nash outcome(s). Such correlation devices do have a natural interpretation in a number of real-life economic situations (Arce 1995, 1997) and thus may provide a stylised representation of the mediating role of government agencies, international bodies or trade associations like European Union, World Trade Organisation (WTO), United Nations Framework Convention on Climate Change (UNFCCC), etc. Unsurprisingly therefore, in the recent past, there have been quite a few applications in the literature of correlation in non-cooperative games to analyse relevant economic situations.

Randomisation devices are used and interpreted in different ways in two concepts of correlation, namely, CE and CCE. The most effective way of explaining correlation in non-cooperative games is via a mediator who could help the players to play a given game; however, the mediator, is not a part of the game, in any respect. A (direct) correlation device is simply a probability distribution over all the outcomes for a given game. In Aumann’s CE, the mediator first uses the device to choose an outcome; once chosen, each component of the outcome is conveyed to the corresponding player (privately and separately) as recommendations for them and having received such private messages, players then play the game. The device is an equilibrium (CE) if all such recommendations are followed (played in the game) by all the players. In contrast, the mediator implementing a CCE first reveals publicly the lottery over the outcomes it recommends, then offers to each player the option to commit to that lottery: any player i who chooses this option, lets the device choose her strategy $q_i$ according to the lottery in question; if on the contrary she refuses this “help” offered by the device, she simply picks her own strategy (possibly mixing pure strategies) of the original game, without any further input from the mediator. A CCE is a lottery such that all the players committing to this lottery is self-enforcing; that is, for each player, knowing that every other player is committed, she has no incentive to refuse to commit to the device. The device can still operate (out of equilibrium), by selecting a strategy only for those players who agreed to commit, but then the self-enforcement property may be lost.

Admittedly, between CE and CCE, CE is more popular in the applied literature, perhaps because, the step from Nash equilibrium to correlated equilibrium can be justified by appealing to concepts of rationalizability (Aumann 1987), while the step from Nash or correlated equilibrium to coarse correlated equilibrium might be a bit harder to visualise and interpret. Still, the CCE structure has been successfully used in the literature for quite a few games of economic significance, like expending effort (Fleckinger 2012; Deb et al. 2016), gathering information ( Gromb and Martimort 2007), Cournot duopoly (Gerard-Varet and Moulin 1978; Ray and SenGupta 2013, public good provision (Moulin et al. 2014), etc. CCE in one-shot games are shown to approximate Nash equilibria in repeated games (Awaya and Krishna 2019, 2020 ). A number of studies relate CCE to no-regret learners (Forgo et al. 2005; Roughgarden 2009). CCEs have also received widespread attention in recent and growing literature within algorithmic game theory, as no-regret dynamics converge to approximate CCEs. There are important findings in implementing CCE, based on experiments (Reischmann and Oechssler 2018; Georgalos et al. 2020).

The main motivation and purpose, at least initially in the literature, for using correlation devices in many economic situations has simply been that it may be important to improve upon Nash outcomes (in terms of equilibrium payoffs achieved by the players). The sets of CEs and CCEs are often fairly large and thus one may hope to construct an efficient (in the sense of Pareto optimality) equilibrium using correlation schemes for many games. A typical instance is Ray (1996). However, for some (classes of) games, such as potential games (that include standard oligopoly models), CE cannot not help (Neyman 1997), whereas CCE does, as it’s now well-known; efficient CCEs can also be characterised and derived for some important economic models (Moulin et al. 2014).

We in this paper consider another well-known economic situation, also a potential game, namely, the n-person symmetric abatement game (Barrett 1994) as our testing ground for CCE, as CE cannot improve upon Nash. We believe a (direct) correlation device can be easily interpreted as a commitment mechanism, and if players can be organised to follow the rules (i.e., if and when they choose to accept the device), CCE can implement many outcomes. In real life, our abstract mediator (correlation device) embodies in spirit the kind of commitment shown in the 1992 UNFCCC that several authors have analysed (see for example, Slechten 2020). In the context of climate change negotiation, an independent agency (e.g., the European commission for EU Emissions Trading Scheme) can choose an outcome (with the ultimate goal of global emission reduction) and recommend the signatories the abatement levels to be achieved by each of them (see also, Forgo et al. 2005; Forgo 2010, 2011).

Our agenda however certainly is not to mimic the previously known results in this exercise (for an abatement game). There are many situations in economics, where one may find “desirable” outcomes not just in terms of utility of players, but also in other aspects; one may be interested in improving exogenous social variables, such as, aggregate effort or aggregate physical output or quantity levels in some contexts (eg., see Bramoullé and Kranton 2007; Chadha and Kulkarni 2020). Two such situations provide the motivation for our work: (i) public good provision game, with constant marginal cost of contribution and with the benefit from the public good being concave, quadratic in total contributions, and (ii) emission abatement game (Barrett 1994), where each agent’s benefit function is a function of the total abatement level chosen by all agents, and the cost function of each agent is a convex quadratic function of its own abatement level. In situations like above, a mediator (a public authority or an environmental agency) may want to reach incentive compatible outcomes which extract better quantity levels (total contributions or abatement levels) than do the standard non-cooperative Nash outcomes. Correlation schemes may provide a tool to find equilibrium outcomes performing better in terms of a criterion other than utility-maximisation. For example, a mediator might prefer to choose a correlation device which, at equilibrium, maximises total abatement levels. This is the kind of “equilibrium design” problem that we address here, and to which the literature has not paid much attention till date.

To test this approach we take a simple version of one-shot abatement game; we use a quadratic cost function for tractability and in line with many other models and papers in the literature (See, Bosetti et al. 2009; Finus et al. 2005; Klepper and Peterson 2006, amongst others). The version of the abatement game we use here can also be viewed as a public good game with quadratic costs, hence, with a concave potential function. Following, Moulin et al. (2014), who explicitly computed utility-maximising CCEs in a 2-player quadratic game, one may just compute CCEs that obtain better overall utility than Nash equilibria for the players in this game; however, we use CCEs to address the issue of “equilibrium design” based on both abatement and utility. Our simple game does serve the purpose for a more general analysis.

Barrett (1994) seminal paper became extremely popular in the relevant environmental literature mainly because it provides a simple and transparent model for countries to participate in an IEAs (International Environmental Agreements) to sign a binding contract that specifies abatement targets for the coalition members. International and transnational environmental agreements have been the subject of many research papers in last two decades. Following Barrett’s work on the feasibility of creating stable international environmental agreements (IEAs), a number of cooperative and non-cooperative game theoretic approaches have been explored including coalition formation and applications of coalitional form games, (see Finus 2008; Tulkens 1998; Barrett 2004; McGinty 2007; Finus and Caparros 2015; Hovi et al. 2015; Marrouch and Chaudhuri 2015, and the references therein).

Our agenda here is to provide a different approach. Our version of “equilibrium design” involving CCEs does not allow players to sign a binding climate contract. Instead, it focuses (in its main application) on a non-cooperative abatement game in a static context (but with the twist that players can commit to accept a randomisation device, as pointed out above). The question that can be answered by our approach is how much an externally given randomisation device lead to an outcome that somehow dominates the usual Nash equilibrium outcome in terms of payoffs or in terms of abatement quantities. We however do not provide a comparison between use of correlation devices and IEAs in abatement games as it is not the purpose of this paper. A more recent literature (Karp and Sakamoto 2020; Kovac and Schmidt 2021) on dynamic coalition formation applied to IEAs uses some form of external randomisation device to solve inherent coordination problems. However, CE and CCE have not been explored in our context. Our results provide theoretical underpinnings to the belief that mediation is instrumental in such discussions.

It should be noted that in the context of CCE, the only decision the signatories (simultaneously and independently) have to make is whether to ‘commit’ to the mediating agency or not. Once this decision is made, the ‘committed’ signatories act according to the recommendation of the agency. This is however different to the literature (Barrett 1994) which involves a participation stage before the coalition formation where the countries have to first decide whether or not to participate in a climate coalition, and hence the sequential nature of the games. At a more micro-level, a regulating agency for a group industrial plants, or a leader of cartel (chosen by the members of the cartel), can play the role of the mediator. The concept of CCE requires stronger commitment of the signatories to a treaty, in the sense that the signatories have to decide (simultaneously) whether to abide by the recommendations of the agency or act on their own.

To illustrate our main contribution, consider a baseline 2-player abatement game in which the utility of country i is given by the function $q-2q^{2}-q_{i}^{2}$, where $q_{i}$ is the choice of abatement level by country i and thus q ($=q_{1}+q_{2}$) is the total abatement level. For this specific game, it can be shown that the CCE which maximises total utility improves the abatement level over the Nash equilibrium level by only $5.7\%$. However, if one’s agenda is to achieve the highest abatement level, then the best possible abatement-maximising CCE improves the Nash abatement level of abatement by $53\%$; unfortunately, at this CCE, the corresponding utility falls about $35\%$ below the Nash utility level. One may then ask what if we wish to achieve at least the Nash utility while maximising the abatement level;² the answer to this question for this particular game is that we can have a maximum of $11.5\%$ improvement in the abatement maintaining such a constraint.

Our paper develops the above discussion and the 2-player example. In an n -person abatement game, we show that optimising utility and quantity levels are two conflicting design goals, and illustrate the severity of the trade-off between the CCE maximising players’ utility and the CCE maximising aggregate abatement.

We formally characterise CCEs in our n-person abatement game and prove that the improvement in abatement over the Nash level depends on the ratio between the cost (c) and the benefit (b) parameters of the utility functions; more precisely, it increases as $r(=\frac{c}{b})$ decreases. We also show how CCEs obtain abatement levels higher than the Nash level, even with the constraint of utility being at least Nash utility. However, this (relative) improvement diminishes with the number of players, n; that is, the “mediation value” is higher with fewer players, in other words, mediation becomes harder with more players involved. We illustrate these features by plotting the maximum abatement gain by CCE over Nash, with respect to r, for different values of n, see Fig. 1. Finally, as a by-product of our analysis, we generalise the result presented in Moulin et al. (2014) to the n-player case by finding an analytical algorithm to compute the optimal quantity-maximising CCE for such an n-person game.

Fig. 1

$\frac{q^{CCE}}{q^{N}}$ vs r for $n=3$ (blue), $n=10$ (green) and $n=50$ (red) (color figure online)

2 Model

We present below a class of symmetric n-player games with quadratic payoffs (1) that include games of economic significance (Cournot oligopoly, Bertrand oligopoly, public good games, abatement games, among others), where CEs do not offer anything more than the NE (Neyman 1997). For this class of games, we provide a CCE-characterising condition and the precise values for the parameters which supports existence of the CCE lottery. The results from this section are valid for any quadratic game, and will be explicitly used in Sect. 3 for our working example of abatement game. All proofs in this and the following sections are in the Appendix A.

2.1 Coarse correlated equilibrium (CCE)

Consider an n-person normal form game, $G=[Q_{1},Q_{2},\ldots ,Q_{n};u_{1},u_{2},\ldots ,u_{n}]$, with the strategy sets, $Q_{i}= {\mathbb {R}}_{+}$, for all i, with ${\mathbb {Q}}=\prod _{i}Q_{i}$, with generic elements $\hbox {q}_{{i}}$ and q respectively, and where the payoff functions $u_{i}:$ ${\mathbb {Q}}\rightarrow {\mathbb {R}}$, $i=1,\ldots ,n$ , are continuous. We write ${\mathbb {C}}({\mathbb {Q}})$ for the set of such continuous functions and similarly, ${\mathbb {C}}(Q_{i})$ for the set of continuous functions on $Q_{i}$.

Let ${\mathcal {L}}({\mathbb {Q}})$ with generic element L and ${\mathcal {L}} (Q_{i})$ with generic element $\ell _{i}$ denote the sets of probability measures on ${\mathbb {Q}}$ respectively. Let the expectation of $u_{i}$ with respect to L be denoted by $u_{i}(L)$.

The deterministic distribution at z is denoted by $\delta _{z}$, and for product distributions such as $\delta _{q_{1}}\otimes \ell _{2}\otimes \cdots \otimes \ell _{n}$ we write $u_{1}(\delta _{x_{1}}\otimes \ell _{2}\otimes \cdots \otimes \ell _{n})$ simply as $u_{1}(q_{1},\ell _{2},\ldots ,\ell _{n})$, and for short $u_{1}(q_{1},\ell _{-1})$ or more generally for any player i we write $u_{i}(q_{i},\ell _{-i})$. Given $L\in {\mathcal {L}}( {\mathbb {Q}} )$, we write $L^{i}$ for the marginal distribution of L on $Q_{i}$, defined as follows: $\forall f\in {\mathbb {C}}(Q_{i})$, $f(L^{i})=f^{*}(L)$ , where $f^{*}(q )=f(x_{1})$ for all $q\in {\mathbb {Q}}$.

Definition 1

A coarse correlated equilibrium (CCE) of the game G is a lottery $L\in {\mathcal {L}}( {\mathbb {Q}} )$ such that $u_{i}(L)\ge u_{i}(q_{i},L^{-i})$ for all $q\in {\mathbb {Q}}$.

Note that, in contrast to Definition 1, for a lottery $L \in {\mathcal {L}}({\mathbb {Q}})$ to be a correlated equilibrium (CE) a la Aumann, we need $u_i(L) \ge u_i(q_i, L|q_i))$, for all i and $q_i$, where $(L|q_i)$ is the lottery on ${\mathbb {Q}}_{-i}$ conditional on the choice of $q_i$. The usual interpretation of CE holds: the mediator reveals to player i the coordinate $q_i$ of the outcome of L and then player i has no incentive to choose another strategy.

2.2 Quadratic games and its CCEs

We consider the following symmetric n-player game that we call a quadratic game; in this game the payoffs are of the following general (quadratic) form:

$$\begin{aligned} u_{i}(q)=\sum _{i=1}^{n}dq_{i}+\sum _{i=1}^{n} \sum _{j=1}^{n}eq_{i}q_{j}+fq_{i}^{2}\text {,} \end{aligned}$$

(1)

where d, e, f are positive constants.

We now describe the set of CCEs for the above game. If L is the distribution of a symmetric random variable $Z=(Z_{1},\ldots ,Z_{n})$, consider respectively the expected values of $Z_{i}$, $Z_{i}^{2}$, and $Z_{i}\cdot Z_{j\ne i}$ and denote them as below; for $i=1,\ldots ,n$:

$$\begin{aligned} \alpha&=E_{L}[Z_{i}]\text {,} \\ \beta&=E_{L}[Z_{i}^{2}]\text { and} \\ \gamma&=E_{L}[Z_{i}\cdot Z_{j}]\,\text {for any }\,j\ne i\text {, }j=1,\ldots ,n\text {.} \end{aligned}$$

We first show that the CCE equilibrium constraint (as in Definition 1) for the n-player quadratic game can be completely expressed in terms of these three moments of a lottery L from the set of symmetric lotteries $\mathcal { L}^{sy}({\mathbb {Q}})\subset {\mathcal {L}}({\mathbb {Q}})$.

Lemma 1

Any symmetric lottery $L\in {\mathcal {L}}^{sy}(\mathbb { Q})$ is a CCE of the quadratic game (1) if and only if

$$\begin{aligned} {max_{z\ge 0}\left\{ (d+e(n-1)\alpha )z+fz^{2}\right\} \le d\alpha +e(n-1)\gamma +f\beta \text {;}} \end{aligned}$$

Lemma 1 shows that a CCE, in the symmetric n-player quadratic game, can be characterised by the expected quantities of the individual players, by their variances and by the co-variances between the quantities of any pairs of players, hence, by symmetry with only three parameters, $\alpha , \beta$ and $\gamma$. Proof of Lemma 1 is a straightforward application of Definition 1 above for our n -person quadratic game, and hence is omitted here. We now identify the range of the vector $(\alpha , \beta , \gamma )$ when $L\in {\mathcal {L}}^{sy}({\mathbb {R}}^n_+)$ in the following lemma.

Lemma 2

• 1. For any $L\in {\mathcal {L}}^{sy}({\mathbb {R}}_{+}^{n})$ and the corresponding n dimensional random variable $Z=(Z_{i})$, we have

  $$\begin{aligned} \alpha ,\gamma \ge 0\text {; }\beta \ge \gamma \text {; }\beta +(n-1)\gamma \ge n\alpha ^{2}\text {.} \end{aligned}$$

  (2)

• 2. Moreover, if $\alpha$, $\beta$ and $\gamma$ meet the system (2), there exists a symmetric lottery L with precisely these parameters.

3 Abatement game

3.1 Preliminaries

The following model of emission-abatement game played by n countries, is due to Barrett (1994). The payoff function of a country $i=1,2,...,n$ is a function of the abatement levels $(q_{i})$ chosen by the countries, with the total abatement as $Q=\sum _{i=1}^{n}q_{i}$. For simplicity we rewrite the payoff function (from Barrett (1994))³ in the following form:

$$\begin{aligned} u_{i}\left( q_{i},q_{-i}\right) =a\left( \sum _{i=1}^{n}q_{i}\right) -b\left( \sum _{i=1}^{n}q_{i}\right) ^{2}-cq_{i}^{2}\text {;} \end{aligned}$$

(3)

where a, b and c are all positive. We call the above game an abatement game. The (symmetric) Nash equilibrium level of abatement $(q_{i}^{Neq})$ and the corresponding payoff $\pi _{i}^{Neq}$ are given by

$$\begin{aligned} q_{i}^{Neq}=\frac{a}{2(nb+c)}\text {; }\pi _{i}^{Neq}=\frac{ a^{2}[n^{2}b+(2n-1)c]}{4(nb+c)^{2}}\text {.} \end{aligned}$$

The abatement game is clearly a potential game with the potential function⁴

$$\begin{aligned} P(q)=a\left( \sum _{i=1}^{n}q_{i}\right) -b\left( \sum _{i=1}^{n}\sum _{j=1}^{n}q_{i}q_{j}\right) -(b+c)\sum _{i=1}^{n}q_{i}^{2}, \end{aligned}$$

which is smooth and concave. Therefore, the only CE is the Nash equilibrium $q^{Neq}$ (Neyman 1997). Using Lemma 1, the following Proposition characterises the CCE of this game.

Proposition 1

A symmetric lottery $L\in {\mathcal {L}} ^{sy}( {\mathbb {R}} _{+}^{n})$ is a CCE of the abatement game if and only if

$$\begin{aligned} \max _{z\ge 0}\left\{ [a-2(n-1)b\alpha ]z-(b+c)z^{2}\right\} \le a\alpha -(b+c)\beta -2b(n-1)\gamma \end{aligned}$$

(4)

and the corresponding utility (for country i) is

$$\begin{aligned} u_{i}(L)=na\alpha -(nb+c)\beta -n(n-1)b\gamma \text {.} \end{aligned}$$

Furthermore, the lottery $L(\alpha ,\beta ,\gamma )$ is a CCE of the abatement game if and only if

$$\begin{aligned} \text {either, }\alpha >\frac{a}{2b(n-1)}&\text { and }a\alpha \ge (b+c)\beta +2(n-1)b\gamma \text {,} \end{aligned}$$

(5)

$$\begin{aligned} \text {or, }\alpha \le \frac{a}{2b(n-1)}\text { and }&a\alpha \ge (b+c)\beta +2(n-1)b\gamma +\frac{[a-2(n-1)b\alpha )]^{2}}{4(b+c)}\text {.} \end{aligned}$$

(6)

We now present two further important observations out of the above characterisation (proofs of which are in the Appendix).

Claim 1

When $n=2$, the case $\alpha >\frac{a}{2b(n-1)}$ is impossible.

Claim 1 shows that an abatement game with three or more players requires separate analysis as there are more CCEs possible resulting in different outcomes of the game.

Our next observation relates to the benefit and cost parameters of the game. Let us denote $r=\frac{c}{b}$.

Claim 2

When $r=\frac{c}{b}>1$, the only CCE of the abatement game coincides with the Nash equilibrium of the game.

Henceforth, we will only consider the case when $r=\frac{c}{b}<1$.

3.2 Abatement maximisation

Below, we provide the precise characterisation of the CCE for the abatement game that maximises the total abatement level, $Q=\sum _{i=1}^{n}q_{i}$ and compare it with the Nash equilibrium abatement level.

Proposition 2

For a fixed $r=\frac{c}{b}<1$,

• 1. when $(1-r)\ge \frac{2}{n}$, the optimal values of the three moments of the abatement-maximising CCE for the abatement game are $\alpha =\frac{a}{ n(b+c)}$, $\beta =n\alpha ^{2}$ and $\gamma =0$,

• 2. when $(1-r)<\frac{2}{n}$, the optimal values of the three moments of the abatement-maximising CCE for the abatement game are $\alpha =\frac{a}{ 2b[(n+r)-\sqrt{(n-1)(1-r^{2})}]}$, $\beta =n\alpha ^{2}$ and $\gamma =0$.

As one may observe, in both the cases listed under Proposition 2, the abatement-maximising CCE for this game involves $\gamma =E_L(Zi\cdot Zj )= 0$, regardless of the values of parameters (r and n) of the model. From $\gamma = 0$, it follows that $Z_i$ and $Z_j$ are never simultaneously positive. As this is true for all pairs, only one coordinate can be positive at any draw of the lottery; by symmetry this player is selected with uniform probability. So the structure of L is simple: pick uniformly a player and choose his random level of abatement with mean and variance following from $\alpha$ and $\beta$.

We also note that both $\alpha$ and $\beta$ decrease with the number of players, n; for sufficiently large n, the first statement applies in which case, $\alpha = \frac{a}{n(b+c)}$ and $\beta = n \alpha ^2 = \frac{a^2}{n(b+c)^2}$ that decrease at the same rate as $\frac{1}{n}$. This implies, both the mean and the variance of the level of abatement chosen by the abatement-maximising lottery are low when n is high. It is however not easy to identify the actual structure of the abatement-maximising lottery for this game for any $n>2$.

Using Proposition 2, we can immediately measure the relative improvement in the abatement level from the abatement-maximising CCE over that of the Nash equilibrium abatement level, given by $\frac{q^{CCE}}{q^{N}}$.

Corollary 1

For a fixed $r=\frac{c}{b}<1$,

• 1. when $(1-r)\ge \frac{2}{n}$, $\frac{q^{CCE}}{q^{N}} = \frac{2(n+r)}{ n(1+r)}$,

• 2. when $(1-r)<\frac{2}{n}$, $\frac{q^{CCE}}{q^{N}} = \frac{n+r}{(n+r)- \sqrt{(n-1)(1-r^2)}}$.

Corollary 1 requires no detailed proof. Figure 1 gives an illustration of Corollary 1. We note that the total abatement from the abatement-maximising CCE over the Nash abatement increases as r decreases. Also, notice that for larger n, the condition $(1-r)\ge \frac{2}{n}$ is more likely to be satisfied. The coloured vertical lines in Fig. 1 provide the cutoffs in Corollary 1; case 1 lies to the left of the corresponding line (blue for $n=3$, green for $n=10$ and red for $n=50$) while case 2 lies to the right.

3.3 Utility maximisation

We can also compare the Nash equilibrium with the utility-maximising CCE. The expressions (of $\alpha$, $\beta$ and $\gamma$) for a general n are messy and are difficult to interpret. Instead, here we present the simpler case of a 2-player abatement game.

Proposition 3

If $r=\frac{c}{b}<1$, the optimal values of the three moments of the utility-maximising L in a 2-player abatement game are given by $({\widetilde{\alpha }},{\widetilde{\beta }},{\widetilde{\gamma }})$:

$$\begin{aligned} {\widetilde{\alpha }}= & {} \frac{a}{b}\frac{2+2r-r^{2}}{2(4+5r)}\text {,}\\ {\widetilde{\beta }}= & {} \frac{a^{2}}{b^{2}}\frac{4+8r+r^{2}-4r^{3}}{4(4+5r)^{2}} \text { and }{\widetilde{\gamma }}=\frac{a^{2}}{b^{2}}\frac{ 4+8r-r^{2}-4r^{3}+2r^{4}}{4(4+5r)^{2}}\text {;} \end{aligned}$$

while the optimal CCE is ${\widetilde{L}}=\frac{1}{2}\delta _{(z,z^{\prime })}+ \frac{1}{2}\delta _{(z^{\prime },z)}$, with

$$\begin{aligned} z,z^{\prime }=\frac{a}{b}\frac{2+2r-r^{2}\pm r\sqrt{1-r^{2}}}{2(4+5r)}\text {. } \end{aligned}$$

Recall from Claim 1 that the CCE in the 2-player case can be very different from that of the n-player game.

We can illustrate our results in Proposition 3 by considering the baseline example introduced in the Introduction, where $a = 1$, $b = 2$ and $c = 1$ ; hence, $r = \frac{1}{2} < 1$. From Proposition 3, the utility maximising CCE corresponds to the optimal values of ${\widetilde{\alpha }} = \frac{11}{104},{\widetilde{\beta }} = \frac{31}{2704},{\widetilde{\gamma }} = \frac{59}{5408}$ and the optimal CCE ${\widetilde{L}}$ chooses the two outcomes $(\frac{11+\sqrt{3}}{104},\frac{11- \sqrt{3}}{104})$ and $(\frac{11-\sqrt{3}}{104},\frac{11+\sqrt{3}}{104})$ each with probability $\frac{1}{2}$. The optimal CCE (total) payoff is $\frac{23}{104}$, which implies an improvement of $5.7\%$ over the Nash abatement levels and an improvement of $0.5\%$ over the Nash utility $(= \frac{11}{50})$, which may seem small in percentage terms, however, can very well be a significant figure if one considers real-life magnitudes.

It turns out that, for our baseline example, the optimal Abatement maximising CCE (Proposition 2) has the associated values $\alpha = 0.153$, $\beta = 0.049$ and $\gamma = 0$, with the optimal (total) payoff of 0.1438, which is $35\%$ lower than the Nash payoff, but the corresponding improvement of $53\%$ over the Nash abatement levels.

3.4 Abatement and utility

We observe that in the 2-player abatement game, the utility at the abatement-maximising CCE is always lower than the Nash utility level. One can thus naturally ask how much improvement in the abatement level can be achieved, keeping the utility level at least that of Nash. The analytical answer to this question can be found for the 2-player case; the maximum improvement in the abatement level over Nash, keeping the utility level held at least at the Nash outcome, is at most $25\%$ (Proposition 4 in the working paper by Dokka et al. 2019). In fact, for our baseline example, the values of $\alpha = 0.1115$, $\beta = 0.0135$ and $\gamma = 0.01136$, correspond to the (constrained) optimal CCE which results in an improvement of $11.5\%$ over the Nash abatement levels and $0.05\%$ over Nash utility levels.

We perform a simulation for this analysis with $n>2$ and observe that even after imposing the utility constraint, we still achieve improvement over the Nash abatement level, however this diminishes with n. In Table 1, we illustrate our simulation results for different value of n ($n=3,4,5,10,50,100$) for the parameter values $a=b=1$ and $c=0.78$.

Table 1 Abatement level at the optimal CCE with utility constraint

The simulation results presented in Table 1⁵ clearly show that CCEs (maintaining the same utility as in Nash equilibrium) do obtain higher abatement levels than the Nash levels; however, this improvement decreases with n.

4 Remarks

Our main objective behind this project has been to investigate whether CCEs may prove to be analytically interesting in a public bad situation, such as an abatement game. Our results in this paper suggest this is indeed the case, even if just as a theoretical concept. As an example of n-person symmetric quadratic games, we have characterised the abatement-maximising CCE for a simple n-person abatement game. Such a computation using CCEs is new (certainly, for the abatement game) and, this is why we regard this exercise as a successful first step towards more sophisticated computations to understand mediation in general for such games.

We realise that one actually may analyse CCEs to find the quantity-maximising outcome for any n-person symmetric quadratic games, as described in subsection 2.2 in this paper. Given the set of lotteries ${\mathcal {L}}^{sy}({\mathbb {R}}_{+}^{n})$, it is however difficult to obtain any further explicit characterisation (of such lotteries); so, we provide a computational result of L for given parameters that satisfy (2).

Using symmetry, the quantity-maximising CCE can be computed by solving the following convex quadratic programme:

$$\begin{aligned} \max _{\alpha ,\beta ,\gamma }\quad&\alpha \end{aligned}$$

(7)

$$\begin{aligned} \text {such that }\beta&\ge \gamma \end{aligned}$$

(8)

$$\begin{aligned} \beta +(n-1)\gamma&\ge n\alpha ^{2} \end{aligned}$$

(9)

$$\begin{aligned} (n-1)b\gamma +c\beta&\ge max_{z\ge 0}\left\{ (a+(n-1)b\alpha )z+cz^{2}\right\} -a\alpha \end{aligned}$$

(10)

$$\begin{aligned} \alpha ,\gamma&\ge 0; \end{aligned}$$

(11)

We claim that the quantity-maximising CCE can be obtained (up to a given tolerance level, call it, tol, say) by solving finitely many linear programs simply by checking feasibility of the system above using the steps of the algorithm below:

Algorithm 1

Algorithm Quantity-CCE:

• 1. Fix $\alpha$ and tol.

• 2. Find a feasible point in the polytope (8)–(11). If there exists such a point go to step 3; else, go to step 4.

• 3. Set $\alpha =\alpha +\epsilon$ and go to step 2.

• 4. Set $\epsilon =\frac{\epsilon }{2}$. If $\epsilon >tol$ go to step 3 else stop and output $\alpha$.

The above claim can be proved easily, using Lemmata 1 and 2 in this paper. Since the objective of (7)–(11) is independent of $\beta$ and $\gamma$, it is enough to find the largest value of $\alpha$ such that there exists at least one feasible solution to (8)–(11). Algorithm Quantity-CCE imitates binary search to find this maximum $\alpha$, which proves our claim.

One may then wish to compare the maximised quantity levels from the optimal CCE found by Algorithm 1 with that from the Nash equilibrium of any quadratic game, although this would be computationally challenging. Our analysis on abatement game provides such comparisons only in a subclass of such games.

Our main contribution in this paper is abatement maximisation, maintaining the utility level at the Nash outcome for any n-person abatement game. We should emphasise here that CCEs have recently received widespread attention in the growing literature within algorithmic game theory, mainly because no-regret dynamics converge to approximate CCEs. Our result suggests a form of no-regret play may be seen as an indirect way of implementation of abatement-maximising CCE. Unfortunately, however, our current paper does not suggest a way to “implement” it. We believe this is out of scope of this paper and requires further investigation. The question naturally thus arises if there exists a no-regret play which converges to a specific CCE. To the best of our knowledge, this is indeed an interesting open question and it deserves to be one of the future directions of research. A thorough simulation providing a possible answer to this question will change the scope of the current work.

The contribution of this paper is therefore two-fold. First, we characterise the benefit from coarse correlation in a particular, yet very popular, class of games. Second, as the importance of enforcing agreements is an important theme in the environmental literature, our characterisation for the abatement game suggests why and how a mediator (an independent agency) could be used in practice for enforcing stable agreements and commitments in this and in other similar games.

Recent literature in the algorithmic game theory introduces a couple of popular ratios, known as the price of anarchy (PoA) and price of stability (PoS). While computing both the PoA and the PoS for CCEs with respect to a measure (say, utility) could be attempted in this situation, the questions we consider are different as we link the performance of the equilibria with respect to two measures (players’ utility and the abatement level).

There are clear limitations to our results. We use a quadratic payoff function, and not a general differentiable concave function. Quadratic approximation to payoffs is routinely used in the literature, for instance, in the models by Bosetti et al. (2009); Finus et al. (2005); Klepper and Peterson (2006). We considered only symmetric equilibria of our symmetric games. These choices are also common in the literature, such as, the RICE model in Nordhaus and Boyer (2000) that tries to set up abatement cost functions fitting real data.

A natural extension of our work could be to the version of our abatement game with asymmetric quadratic costs; alternatively, asymmetry could arise in player-specific benefit functions. Simple closed form expressions for the equilibrium parameters in these cases would be hard to obtain. An alternative payoff function in the literature on IEAs, which has been frequently used, is the linear benefit and quadratic cost function for which it is known that the stable coalition comprises 3 countries. It would be interesting to derive results for CCE for this payoff function, and we postpone this for future research.

Appendix: Proofs

Proof of Lemma 2

Part 1    For L to be feasible, it should be true that the variance-covariance matrix $M_{L}(Z)$ is positive semi-definite (PSD). Omitting the subscript L for ease of notation, let $Y_{i}=Z_{i}-\alpha$ for all i:

$$\begin{aligned} Var(Z_{i})=E[Y_{i}^{2}]&=\beta -\alpha ^{2}=\beta ^{*}\text {,} \\ Cov(Z_{i},Z_{j})=E[Y_{i}Y_{j}]&=\gamma -\alpha ^{2}=\gamma ^{*}\text {.} \end{aligned}$$

So, we need to express a matrix with $\beta ^{*}$ on the diagonal and $\gamma ^{*}$ on the off-diagonal is PSD. This means that we have for all $x\in {\mathbb {R}}^{n}$

$$\begin{aligned} \beta ^{*}\left( \sum _{1}^{n}x_{i}^{2}\right) +2\gamma ^{*}\left( \sum _{1\le i\le j\le n}x_{i}x_{j}\right) \ge 0\text {.} \end{aligned}$$

(12)

Standard techniques show that this holds if and only if

$$\begin{aligned} \beta ^{*}\ge \gamma ^{*}\text { and }\beta ^{*}+(n-1)\gamma ^{*}\ge 0\text {,} \end{aligned}$$

(13)

where $\beta ^{*}\ge 0$ but $\gamma ^{*}$ can be positive or negative. Note that $\beta ^{*}$ is necessary, and if $\beta ^{*}=0$ then we need $\gamma ^{*}=0$ as well. Assume now $\beta ^{*}>0$.

• Case 1 $\gamma ^{*}\ge 0$. In this case, we can write (12) as

  $$\begin{aligned} \left( 1-\frac{\gamma ^{*}}{\beta ^{*}}\right) \left( \sum _{1}^{n}x_{i}^{2}\right) +\frac{ \gamma ^{*}}{\beta ^{*}}\left( \sum _{1}^{n}x_{i}\right) ^{2}\ge 0\text {,} \end{aligned}$$

  (14)

  which holds if and only if $\beta ^{*}\ge \gamma ^{*}$.

• Case 2 $\gamma ^{*}<0$. In this case, (12) is

  $$\begin{aligned} \left( 1-\frac{-\gamma ^{*}}{\beta ^{*}}\right) \left( \sum _{1}^{n}x_{i}^{2}\right) \ge \frac{ -\gamma ^{*}}{\beta ^{*}}\left( \sum _{1}^{n}x_{i}\right) ^{2}\text {.} \end{aligned}$$

  (15)

If we fix the sum $\sum _{1}^{n}x_{i}$, the minimum of the LHS above is achieved when all $x_{i}$ are equal, so that the inequality holds for all x if and only if it holds for x on the diagonal, i.e.,

$$\begin{aligned} 1+\frac{-\gamma ^{*}}{\beta ^{*}}\ge n\frac{-\gamma ^{*}}{\beta ^{*}}\Longleftrightarrow \beta ^{*}+(n-1)\gamma ^{*}\ge 0\text {. } \end{aligned}$$

Combining both cases and switching back to $\beta$ and $\gamma$, we get the result.

Part 2    Note that, given $\alpha$, $\beta$ and $\gamma$ satisfying (2), it should be true that for some $\frac{k_{1}}{k_{2}}=\xi >1$,

$$\begin{aligned} \beta&=(k_{1}+1)\alpha ^{2} \end{aligned}$$

(16)

$$\begin{aligned} \gamma&=\frac{n-1-k_{2}}{n-1}\alpha ^{2} \end{aligned}$$

(17)

Now observe that there exist distributions of the symmetric random variable $(Q_{1},\ldots ,Q_{n})$ with the mean vector $({\mathbb {E}}(Q_{1})={\mathbb {E}} (Q_{n})=\alpha )$ and co-variance matrix:

$$\begin{aligned} \sum =k_{1}\alpha ^{2} \begin{bmatrix} 1 &{}\quad \rho &{}\quad \cdots &{}\quad \rho \\ \rho &{}\quad &{}\quad &{}\quad \rho \\ \vdots &{}\quad &{}\quad \ddots &{}\quad \\ \rho &{}\quad \rho &{}\quad &{}\quad 1 \end{bmatrix} \text {,} \end{aligned}$$

where $\rho =-\frac{1}{\xi (n-1)}$.. $\square$

Proof of Proposition 1

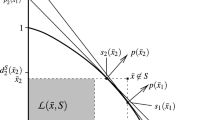
First note that the expected utility (for a country) from any lottery $L\in {\mathcal {L}}^{sy}({\mathbb {R}} _{+}^{n})$ can be written as

$$\begin{aligned} u_{i}(L)=a\sum _{j=1}^{n}E_{L}[Z_{j}]-b\sum _{j=1}^{n}E_{L}[Z_{j}^{2}]-2b \sum _{j=1}^{n}\sum _{j\ne k=1}^{n}E_{L}[Z_{j}\cdot (Z_{k})]-cE_{L}\left[ Z_{i}^{2}\right] \text {,} \end{aligned}$$

which is, by symmetry, for $i\ne j$,

$$\begin{aligned} u_{i}(L)= & {} naE_{L}[Z_{i}]-(nb+c)E_{L}[Z_{i}^{2}]-n(n-1)bE_{L}[Z_{i}\cdot Z_{j}] \\= & {} na\alpha -(nb+c)\beta -n(n-1)b\gamma \text {.} \end{aligned}$$

We write the expected payoff when country i plays a pure strategy z and country $j\ne i$ commit to L, as

$$\begin{aligned} u_{i}(z,L^{2})&=az+a\sum _{i\ne j}^{n}E_{L}[Z_{j}] \\&\quad -bz^{2}-b\sum _{i\ne j=1}^{n}E_{L}[Z_{j}^{2}] \\&\quad -2bz\sum _{i\ne j}^{n}E_{L}(Z_{j})-\frac{(n-1)(n-2)}{2}2b\left( \sum _{i\ne j}^{n}\sum _{k=j+1}^{n}E_{L}(Z_{j}.Z_{k})\right) -cz^{2} \\&=[a-2(n-1)b\alpha ]z-(b+c)z^{2}\\&\quad +a(n-1)\alpha -b(n-1)[\beta +(n-2)\gamma ] \text {.} \end{aligned}$$

Hence, L is a CCE if and only if

$$\begin{aligned}&\max _{z\ge 0}\left\{ \left[ a-2(n-1)b\alpha \right] z-(b+c)z^{2}\right\} +a(n-1)\alpha -b(n-1)\left[ \beta +(n-2)\gamma \right] \\&\quad \le na\alpha -(nb+c)\beta -n(n-1)b\gamma \text {,} \end{aligned}$$

which after rearranging, gives us the condition in the statement. $\square$

Proof of Claim 1

Fix $\alpha$ and consider the system of conditions on the vector $(\beta ,\gamma )$. The line $(b+c)\beta +2(n-1)b\gamma =a\alpha$ is flatter than the line $\beta +\gamma =2\alpha ^{2}$; therefore, the two corresponding half spaces intersect in the positive orthant if and only if $\frac{a\alpha }{b+c}\ge 2\alpha ^{2}$. But the latter contradicts $\alpha >\frac{a}{2b}$. $\square$

Proof of Claim 2

Consider the following polytope for a fixed $\Psi =\{(\beta ,\gamma )|\beta \ge \gamma ,\beta +(n-1)\gamma \ge n\alpha ^{2}\}$ under the additional constraint 6. Note that $\Psi$ is unbounded from above and bounded from below by the interval [P, Q], where $P=(\alpha ^{2},\alpha ^{2})$ and $Q=(n\alpha ^{2},0)$. The minimum in $\Psi$ of $(b+c)\beta +2(n-1)b\gamma$ is achieved at P. Therefore, if P meets 6 it is our optimal pair of $(\beta (\alpha ), \gamma (\alpha ))$; if not there is no CCE. P meets 6 if and only if $((2n-1)b+c)\alpha ^2 \le - \frac{b^2 \alpha ^2 - a(nb+c)\alpha +\frac{a^2}{4}}{b+c}$, which is $(a - 2(nb+c)\alpha )^2 \le 0$. This is only possible when $\alpha = \frac{a}{ 2(nb+c)}$ which is nothing but Nash outcome. $\square$

Proof of Proposition 2 (First part)

Increasing the value of $\alpha$ shrinks the feasible region of the polytope

$$\begin{aligned} \left\{ (\beta ,\gamma )|\beta \ge \gamma ;\beta +(n-1)\gamma \ge n\alpha ^{2};(b+c)\beta +2b(n-1)\gamma \le a\alpha \right\} \end{aligned}$$

eventually to a single point which is the intersection of the half-lines $(b+c)\beta +2b(n-1)\gamma =a\alpha$ and $\beta +(n-1)\gamma =n\alpha ^{2}$ on the $\beta$-axis. This point gives $\alpha =\frac{a}{n(b+c)}$. However, this is only valid when resulting $\alpha \ge \frac{a}{2b(n-1)}$, that is, we must have $(1-r)>\frac{2}{n}$. $\square$

Proof of Proposition 2 (Second part)

For the second case, the intersection point of $\beta =n\alpha ^{2}$ and $(b+c)\beta +2b(n-1)\gamma =a\alpha -\frac{(a-2b(n-1)\alpha )^{2}}{4(b+c)}$ is the positive root of the following quadratic equation:

$$\begin{aligned} \left[ (n-1)^{2}+(1+r)^{2}n\right] \alpha ^{\prime 2}-(n+r)\alpha ^{\prime }+\frac{ 1}{4}=0\text {,} \end{aligned}$$

where $\alpha =\frac{a}{b}\alpha ^{\prime }$. $\square$

Proof of Proposition 3

First consider the equilibrium condition in Proposition. Note that if $a-2b\alpha <0\Longleftrightarrow \alpha >\frac{a}{2b}$, the LHS. of that inequality (the maximum over $z\ge 0$) is 0; therefore, the equilibrium condition in Proposition becomes

$$\begin{aligned} a\alpha \ge (b+c)\beta +2b\gamma =b(\beta +\gamma )+c\beta +b\gamma >b(\beta +\gamma )\ge 2b\alpha ^{2}\text {,} \end{aligned}$$

which is a contradiction. So, we must have $\alpha \le \frac{a}{2b}$; then, the LHS. of the equilibrium condition is $\frac{(a-2b\alpha )^{2}}{4(b+c)}$ and the condition is now

$$\begin{aligned} (b+c)\beta +2b\gamma \le a\alpha -\frac{(a-2b\alpha )^{2}}{4(b+c)}=-\frac{ b^{2}\alpha ^{2}-a(2b+c)\alpha +\frac{a^{2}}{4}}{b+c}\text {.} \end{aligned}$$

(18)

We now fix $\alpha$ and solve step 1 in Lemma 3: we must minimise $(2b+c)\beta +2b\gamma$ in the polytope $\Psi =\{(\beta ,\gamma )|\beta \ge \gamma ,\beta +\gamma \ge 2\alpha ^{2}\}$ under the additional constraint (18). Note that $\Psi$ is unbounded from above and bounded from below by the interval [P, Q], where $P=(\alpha ^{2},\alpha ^{2})$ and $Q=(2\alpha ^{2},0)$. We distinguish two cases here.

Here, the minimum of $(b+c)\beta +2b\gamma$ in $\Psi$ is achieved at Q; so, if Q fails to meet the constraint (18), this constraint does not satisfy anywhere in $\Psi$. Thus, we must choose $\alpha$ such that

$$\begin{aligned} 2(b+c)\alpha ^{2}\le & {} -\frac{b^{2}\alpha ^{2}-a(2b+c)\alpha +\frac{a^{2}}{ 4}}{b+c} \end{aligned}$$

(19)

$$\begin{aligned}\Longleftrightarrow & {} \Lambda (\alpha )=(3b^{2}+4bc+2c^{2})\alpha ^{2}-a(2b+c)\alpha +\frac{a^{2}}{4}\le 0\quad \end{aligned}$$

(20)

The discriminant of the right-hand polynomial $\Lambda (\alpha )$ is $a^{2}(b^{2}-c^{2})$; therefore, (19) restricts $\alpha$ to an interval $[\alpha _{-},\alpha _{+}]$, between the two positive roots of $\Lambda (\alpha )$. For such a choice of $\alpha$, the constraint (18) cuts a subinterval [R, Q] of [P, Q], where R meets (18) with an equality. Note that $R=P$ only if $\alpha =q_{i}^{N}$ (from Case 1 and the fact that $\Lambda (q_{i}^{N})<0$); otherwise $R\ne P$. Clearly, R is our optimal choice for $(\beta (\alpha ),\gamma (\alpha ))$ and it solves the system

$$\begin{aligned} \beta +\gamma =2\alpha ^{2}\text {; }(b+c)\beta +2b\gamma =-\frac{b^{2}\alpha ^{2}-a(2b+c)\alpha +\frac{a^{2}}{4}}{b+c}\text {.} \end{aligned}$$

Therefore,

$$\begin{aligned} \beta (\alpha )= & {} \frac{1}{b^{2}-c^{2}}\left[ b(5b+4c)\alpha ^{2}-a(2b+c)\alpha +\frac{a^{2}}{4}\right] \text { and}\\ \gamma (\alpha )= & {} \frac{1}{b^{2}-c^{2}}\left[ { -}(3b^{2}+4bc+2c^{2}) \alpha ^{2}+a(2b+c)\alpha -\frac{a^{2}}{4}\right] \text {.} \end{aligned}$$

Now in step 2 of Lemma 3, we must maximise $2a\alpha -(2b+c)\beta (\alpha )-2b\gamma (\alpha )$ under the constraints $\alpha \ge 0$ and $\Lambda (\alpha )\le 0$. Developing this objective function yields the programme

$$\begin{aligned} \frac{1}{b^{2}-c^{2}}\max _{\alpha }\left\{ -b^{2}(4b+5c)\alpha ^{2}+a\left( 2b^{2}+2bc-c^{2}\right) \alpha -\frac{a^{2}c}{4}\right\} \end{aligned}$$

(21)

under the constraints

$$\begin{aligned} \alpha \ge 0\text { and }\Lambda (\alpha )=\left( 3b^{2}+4bc+2c^{2}\right) \alpha ^{2}-a(2b+c)\alpha +\frac{a^{2}}{4}\le 0\text {.} \end{aligned}$$

The unconstrained maximum of the objective function is achieved at ${\widetilde{\alpha }}=\frac{a(2b^{2}+2bc-c^{2})}{2b^{2}(4b+5c)}$.

We now show that $\Lambda ({\widetilde{\alpha }})\le 0$. With the change of variable $r=\frac{c}{b}$, this amounts to

$$\begin{aligned}&\frac{\left( 3+4r+2r^{2}\right) \left( 2+2r-r^{2}\right) ^{2}}{4(4+5r)^{2}}-\frac{(2+r)\left( 2+2r-r^{2}\right) }{ 2(4+5r)}+\frac{1}{4}\le 0\\&\quad \Longleftrightarrow 4+8r-5r^{2}-12r^{3}+3r^{4}+4r^{5}-2r^{6}\ge 0\text {.} \end{aligned}$$

The above polynomial is 0 at $r=1$; it is also easy to check, numerically, that it is non-negative on [0, 1]. The proof is now complete if we express ${\widetilde{\alpha }}$, ${\widetilde{\beta }}$ and ${\widetilde{\gamma }}$ in terms of r. This is indeed easy for ${\widetilde{\alpha }}$. One may also verify, using the expression for ${\widetilde{\alpha }}$ that

$$\begin{aligned} {\widetilde{\beta }}= & {} \beta ({\widetilde{\alpha }})=\frac{1}{b^{2}-c^{2}}\left[ b(5b+4c){\widetilde{\alpha }}^{2}-a(2b+c){\widetilde{\alpha }}+\frac{a^{2}}{4} \right] \\= & {} \frac{a^{2}}{b^{2}}\frac{4+8r+r^{2}-4r^{3}}{4(4+5r)^{2}}\text { and}\\ {\widetilde{\gamma }}= & {} \gamma ({\widetilde{\alpha }})=\frac{1}{b^{2}-c^{2}} \left[ {-}\left( 3b^{2}+4bc+2c^{2}\right) {\widetilde{\alpha }}^{2}+a(2b+c) {\widetilde{\alpha }}-\frac{a^{2}}{4}\right] \\= & {} \frac{a^{2}}{b^{2}}\frac{4+8r-r^{2}-4r^{3}+2r^{4}}{4(4+5r)^{2}}\text {.} \end{aligned}$$

Finally, we construct the optimal CCE ${\widetilde{L}}$. For $n=2$, our Lemma 2 implies ${\widetilde{\beta }}+{\widetilde{\gamma }}=2{\widetilde{\alpha }}^{2}$ ; moreover, from Lemma 2iii) in Moulin et al. (2014), we see that ${\widetilde{L}}$ is an anti-diagonal lottery of the form ${\widetilde{L}}=\frac{1 }{2}\delta _{(z,z^{\prime })}+\frac{1}{2}\delta _{(z^{\prime },z)}$, where z and $z^{\prime }$ are non-negative numbers such that $z+z^{\prime }=2 {\widetilde{\alpha }}$ and $z^{2}+z^{\prime 2}=2{\widetilde{\beta }}$. This implies $2zz^{\prime }=(2{\widetilde{\alpha }})^{2}-(2{\widetilde{\beta }})=2 {\widetilde{\gamma }}$; hence, $z,z^{\prime }$ solve $Z^{2}-2\widetilde{\alpha }Z+{\widetilde{\gamma }}=0$. The discriminant is ${\widetilde{\alpha }}^{2}- {\widetilde{\gamma }}={\widetilde{\beta }}-{\widetilde{\alpha }}^{2}=\frac{a^{2}}{ b^{2}}\frac{r^{2}(1-r^{2})}{4(4+5r)^{2}}$; thus, the expressions for z and $z^{\prime }$ follow. $\square$