1 Introduction

In the last decades, the mechanical behavior of granular materials has been the subject of several experimental and theoretical research [1]. Extensive knowledge of the mechanical behavior of granular materials has been obtained from the various laboratory testing methods on homogeneous specimens subjected to uniform stress and strains, such as the triaxial test [2, 3], hollow cylinder test [4], plane strain biaxial test [5]. Typical experimental investigations, however, usually provide the macroscopic response of granular materials only, without offering any particle-scale information due to the challenges associated with microscopic measurements [6]. Nonetheless, it is widely accepted that the macroscopic behavior of granular materials is governed by the microscopic mechanisms that occur at the particle level [7]. Moreover, such particle-level mechanisms are significantly affected by the characteristics of individual particles, such as size and shape [8]. While particle shape distributions can be partially controlled in experiments [9], a detailed systematic experimental campaign to grasp the effect of particle shape on particle-level mechanisms remains exceptionally challenging.

The discrete element method (DEM) introduced by Cundall [10] is one of the most popular numerical methods to investigate the behavior of discrete materials. If used correctly and calibrated rigorously, it has proven its ability to simulate granular behavior effectively [11, 12]. The main advantage of DEM is that particle arrangements interacting thanks to simple and physical contact laws are modeled explicitly, making it suitable for studying the mechanical behavior of granular materials from a microscopic point of view [1]. Unlike conventional laboratory tests, particle characteristics can be controlled efficiently in DEM simulations, and particle-level information can be observed and analyzed [13]. The DEM allows users to consider a wide range of shapes ranging from perfect spheres to sharp corner angular particles and simultaneously provide particle scale kinematics [14].

Roundness/angularity is an important mesoscale shape descriptor that describes the curvature and sharpness of a particle’s corners. It reflects the transportation process of particles in the geological cycle, especially transportation distance [15]. The effect of particle roundness on the mechanical response of granular materials has been studied extensively in the past [9, 16,17,18]. Robinson et al. [19] investigated the effect of particle shape on avalanching of granular media by using three different shape materials showing a strong relationship between particle shape and slope angle. As expected, less-spherical particles have highly stable slope angles. Interestingly, the effect of particle size distribution on slope angle and the avalanching mode was found to be more significant with increasing angularity. Ashmawy et al. [20] numerically studied particle roundness's effect on liquefaction behavior, and Wei et al. [21] investigated the same effect through experiments with natural sands. They both concluded that angular particles are more resistant to liquefaction. Storti et al. [22] studied the particle shape evolution during the fracturing of rock and found that fracturing a big round particle produces multiple small angular particles. The same phenomenon can be imagined happening continuously in crushable soils and seems to be confirmed by the numerical studies of Zhu et al. [23]. Nie et al. [24] studied particle shape evolution due to erosion phenomena and its effect on the shear behavior of granular material using DEM. They found that particles become more rounded as erosion progresses, and the shear strength generally decreases.

Although particle roundness is recognized as a key in the behavior of granular systems, a systematic experimental study on its effects on the macro and microscopic behavior of granular materials still needs to be included. This is due to the difficulties associated with controlling the material’s shape and performing microscale measurements. The usual laboratory investigations reported in the literature (e.g., [25]) involve comparing the test results of round and angular sands. For example, to investigate the effect of increasing overall angularity [26, 27] tried mixing round and angular sands by gradually increasing the proportion of angular sand. Comparing two specific natural materials is always associated with some limitations. In such investigations, it is difficult to control particle shape, and it may evolve during loading, such as by particle crushing. Furthermore, two materials may have different geological histories, resulting in different particle crushing potentials and other particle characteristics such as sphericity and surface smoothness. Ahmed et al. [28] conducted bender element tests on 3D-printed sand mixtures to investigate the effect of particle shape on the shear wave velocity and shear modulus. The 3D-printed grains in each mixture had complex shape features, including roundness and sphericity, that closely resembled those of actual sands. The results indicated that particles with high roundness and sphericity exhibited greater shear wave velocity and shear modulus. Nonetheless, studying the individual effect of particle roundness/angularity on natural or 3D-printed granular materials remains challenging.

In this study, biaxial shearing tests are conducted on dual-size aluminum rods of circular and hexagonal cross-sections. A novel image analysis technique is used to estimate particle kinematics. A parametric study using DEM to simulate the biaxial shearing of angular particles is performed to study a broader range of particle roundness systematically. The experimental biaxial test results on circular and hexagonal aluminum rods are first used to calibrate and validate the DEM model by comparing macroscopic stress–strain data, and particle rotations at the microscale. The validated DEM model is then used to investigate the effect of particle roundness on biaxial shearing.

2 Description of the biaxial experimental setup

2.1 Biaxial apparatus

Figure 1 shows the schematic plan of the biaxial test apparatus. It consists of a square sample box with rigid boundaries made of aluminum. The box dimensions are 350 mm × 350 mm, and the walls’ thickness is 50 mm. The top and side walls are only allowed to move normally while the bottom wall is fixed. The front and back sides of the sample box are open, and deformations of the sample can be visualized during the test. Loading can be applied using pneumatic cylinders (load-controlled loading) or by rotating the pulleys at a fixed strain rate (displacement-controlled loading). The samples were first subjected to isotropic compression by applying load-controlled loading until a desired confining pressure was reached. Then, the samples were sheared under displacement-controlled loading applied in the axial direction by assigning a specific strain rate (slow enough to ensure quasi-static shearing) to the load piston through the pulley.

Fig. 1
figure 1

A schematic plan of the biaxial test apparatus

Full size image

To experimentally investigate the mechanical behavior of granular materials under plane strain conditions, aluminum rods are commonly used [29]. This work uses 50 mm long dual-sized aluminum circular rods of 10 mm and 6 mm diameters and hexagonal rods of 10 mm and 6 mm inscribed diameters. Samples comprising rounded and angular particles with a mixing ratio of 2:3 of large to small particles by weight were prepared and arranged manually in layers inside a biaxial box. The thickness of each layer ranged from approximately 20 mm to 30 mm, resulting in a final configuration consisting of about 2700 circular and 2400 hexagonal particles, respectively. The walls of the biaxial box were made of aluminum, ensuring that the friction coefficient between particle–wall and particle–particle was identical. The friction coefficient was determined by performing simple shear tests with two aluminum disks, which resulted in a value of approximately 0.2. Experiments were performed under three different confining pressures (19.6, 39.2 and 58.8 kPa). The repeatability of the experiments was confirmed by performing multiple tests under identical testing conditions. The findings demonstrated that specimens comprised of hexagonal particles exhibit greater shear strengths and dilations.

2.2 Particle kinematics measurement

To evaluate particle kinematics, an innovative 2D image analysis is implemented, which involves attaching circular black stickers on the silver cross-section of aluminum rods to obtain high-quality images during the test and facilitate the detection and tracking of particles. Moreover, two red and green colored dots are added to each black sticker to monitor geometric movement through the digital correlation of two consecutive images captured during the test. Particles are detected with the aid of the ‘imfindcircles’ function in MATLAB, and their translations are tracked using the algorithm proposed by Crocker and Grier [30]. Applying the algorithm introduced by Chen et al. [31] to the trajectories of red and green dots in each particle, the particle rotations are determined. The rotation of stickered particles during the biaxial test is assessed by correlating two consecutive images. Additional information on biaxial testing and image analysis for particle motion assessment can be found in Ali et al. [32]. The analysis of the images demonstrated that particles in circular specimens have higher rotation rates, while hexagonal particles are more rotation-resistant due to their superior interlocking properties, resulting in higher strengths.

3 Description of discrete element model

3.1 Contact model and input parameters

In this study, the simulations are conducted with commercial software PFC2D 7.0 [33]. The Hertz contact model based on the theory of Mindlin and Deresiewicz (1953) is used for the particle–particle and particle–wall interactions. It can produce both normal and shear forces based on the theoretical analysis of the deformation of smooth elastic spheres in frictional contact. This model uses a spring-dashpot response to normal contact between particles and a coulomb friction coefficient (µ) for shear interaction. The elastic response of the simplified Hertz–Mindlin contact model is governed by effective shear modulus G and poison’s ratio \(\nu\). The material parameters used in the numerical simulation are those of aluminum, as summarized in Table 1. To achieve a quantitative agreement between the simulation results and laboratory tests, it is crucial to replicate the laboratory test boundary conditions [34]. Consequently, the material parameters for the walls are selected to be identical to those of the particles, ensuring that the laboratory test boundary conditions are replicated. Furthermore, a local damping coefficient was implemented with a value of 0.2 to dissipate the unwanted energy along with sliding.

Table 1 DEM model contact parameters used in the numerical simulations
Full size table

3.2 Generation of granular sample

The numerical samples are generated using the radius expansion method. ITASCA polygon particles were used to create non-circular shapes. The rigid wall boundaries were servo controlled until an equilibrated sample at the desired porosity was obtained. A 1:1 scale numerical model of the experimental biaxial shearing apparatus is created by filling a 350 mm-sided square with DEM particles. All samples were generated at almost the same initial void ratio (i.e., around e = 0.2).

3.3 Particle shape quantification

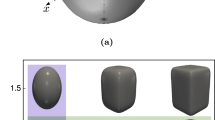
To solely investigate the effect of roundness/angularity, eight non-elongated convex polygonal shape samples with 5, 6, 7, 11, 13, 15, 20, and ∞ corners (Nc), as shown in Fig. 2a, are considered. All other shape descriptors, such as sphericity and surface roughness, are kept constant. In literature, multiple definitions of roundness (R) have been proposed [35,36,37]. Among these, the well-known and widely used Wadell’s [35] definition is used in this work. Using the two-dimensional projection of particles, R is defined as the ratio of the average radius of curvature of the corners to the radius of the maximum inscribed circle. R is computed for each polygon using 2D binary images (600 dpi image resolution) and algorithms based on Wadell’s definition [38]. Its relationship with the number of corners of regular polygons is shown in Fig. 2b. Increasing the Nc increases R as it decreases the corner’s sharpness suggesting that the Nc is a good roundness descriptor for a single shape regular polygon. Similar to the experiments, the same dual-size samples with a big to small mixing ratio of 2:3 by weight are used in the simulations.

Fig. 2
figure 2

a Particle shapes used in the simulation and roundness estimation process [35], b relationship between the number of corners of regular polygon and roundness

Full size image

3.4 Simulation of biaxial shearing tests

As for the experiments, the simulations are performed in two parts: an isotropic compression phase followed by a shearing. First, isotropic compression is conducted by fixing the bottom and left walls and increasing vertical and horizontal load simultaneously on the top and right walls until the desired confining pressure is reached. Next, the shearing phase is performed using a servo control that maintains the confining pressure constant while the top wall is moved normally downward at an axial strain rate of 0.0005. The shearing phase is performed for all the numerical samples at three different confining pressures (σ3 = 19.6, 39.2, and 58.8 kPa). Table 2 summarizes the complete set of numerical simulations performed.

Table 2 Summary of simulations performed
Full size table

4 Calibration and validation of DEM contact parameters

Figure 3 illustrates the initial states of the DEM model of bi-disperse circular and hexagonal particles. To calibrate the parameters for the DEM contact model, the behavior of the circular particles (Nc = ∞) was simulated. The particle sizes, size distribution, and initial void ratio were kept the same as those of the experiment. The coefficient of friction, µ, was determined through direct shear tests using two aluminum disks. To precisely calibrate the value of G, the stress–strain relationships and rotational response of circular particles predicted by the numerical simulation were matched with the corresponding observation in the experiments. After calibrating the DEM contact model parameters using circular particles, the response of the hexagonal particles (Nc = 6) is simulated to assess the contact model’s ability to incorporate the effect of particle shape. Finally, as the validation proved successful, the six remaining particle shapes considered are used as numerical samples to investigate particle R's effect systematically. The following sections discuss the comparison of numerical and experimental macro and microscopic responses in detail.

Fig. 3
figure 3

Biaxial shearing simulation model a circular assembly (for calibration), b hexagon assembly (for validation)

Full size image

4.1 Macroscopic response

In the following, the mean stress and the deviatoric stress are expressed as p = (σ1 + σ3)/2 and q = σ1 – σ3, where σ1 and σ3 are principal stresses in the y and x directions, respectively. ε1 and ε3 are the major and minor principal strains exhibited in the y and x directions, respectively. Volumetric strain (εn) is the sum of major and minor principal strains (ε1 + ε3) and deviatoric strain (εs) is their difference (ε1 − ε3). Figure 4 presents the stress–strain relationship and volumetric deformations of circular and hexagonal samples obtained from the experiment and simulations under confining stress of 39.2 kPa. The simulation results reasonably capture the effect of particle shape on critical state (CS) strength, although they do not fully reflect the stiffness observed in the initial shear stage as seen in experiments. The hexagonal samples show higher critical strengths and volumetric dilations, and a similar trend is observed in the simulations. The circular sample exhibits an average CS stress ratio (q/p) of 0.61 and 0.57 for the experiments and simulations, respectively. The hexagonal sample, on the other hand, has an average CS q/p of 0.87 and 0.89 for the experiments and simulations, respectively. The comparison of numerical and simulation results is mostly consistent, regardless of the magnitude of the confining stress.

Fig. 4
figure 4

Comparison of stress–strain and volumetric behavior in the experiment and simulation (σ3 = 39.2 kPa)

Full size image

4.2 Microscopic response

Rotational behavior observed in the biaxial experiment showed that circular particles are more susceptible to rotations while angular particles are resistant to rotations due to interlocking characteristics. To quantitatively evaluate the effect of R on the rotational behavior of particles during shearing, the cumulative mean absolute rotation (rm) is determined based on the following formula:

$$\begin{array}{*{20}c} {r_{m} = \frac{{\mathop \sum \nolimits_{i = 1}^{N} \left| {\theta_{i} } \right|}}{N}} \\ \end{array}$$
(1)

where θi is the cumulative rotation of an individual particle i, and N is the total number of particles in the sample. Figure 5a presents the relationship between rm and ɛs observed in the biaxial experiment. At an εs of 20%, the rm values for circular and hexagonal samples are 18.6° and 9.7°, respectively, indicating that a circular particle rotates approximately twice as much as a hexagon particle, on average. In Fig. 5b, the corresponding relationship between rm and ɛs is shown for the simulation. At the same εs value of 20%, the rm values for circular and hexagonal samples are 21.6° and 10.0°, respectively, also indicating the circular particles rotate, on average, about twice as much as the hexagonal particles. It is worth noting that the calibration was performed on circular samples, and the hexagonal sample’s response serves as a validation of the model. This confirms that the DEM can identify the changes in the behavior of granular samples due to particle shape, both qualitatively and quantitatively.

Fig. 5
figure 5

Comparison of rotational behavior of circle and hexagon for σ3 = 39.2 kPa a experiment, b DEM

Full size image

5 Effect of particle roundness on shearing response

5.1 Macroscopic effects

Figure 6 shows the stress–strain relationships and volumetric deformations for all the shapes used in the simulation. As the initial void ratio of all assemblies is the same (e = 0.2) the effect of initial packing density should not be affecting the results. The assemblies of more angular particles (lower number of corners) exhibit a higher critical state stress ratio, with the sample of pentagons (R = 0.152) showing the highest strength. As R increases, the CS strength decreases gradually and tends to approach the strength of circular particles. In terms of volumetric response, all samples dilate after an initial compression stage. Dilation is higher in angular assemblies. Figure 7 displays the CS strength of all eight particle shapes simulated under three different confining pressures (19.6, 39.2 and 58.8 kPa). Each marker on the graph represents a simulation result for a specific shape and confining pressure. We plotted straight dotted lines for each shape assembly obtained through simple linear regression analysis passing through the origin, which fits well with the CS lines for each shape assembly in the q-p plane. The CS is found to be significantly influenced by particle R. The highest position in the q-p plane is reached by pentagon samples and as the R increases, the CS gradually shifts downward, approaching the CS of circular particles. This shift of CS is exclusively due to a change in R, as all other particle parameters are the same in all simulations. Therefore, the slope of the CS line in the p-q plane, denoted as Mcs, was determined for each particle shape. The relationship between R and Mcs is shown in Fig. 8. Mcs is an important strength parameter that does not depend on the initial packing. We found that Mcs is a function of R, and we used a power regression to describe this relationship, as shown in Fig. 8a. In Fig. 8b, we present a 3d plot of Mcs as a function of p, q, and R.

Fig. 6
figure 6

Stress–strain and volumetric behavior observed in DEM for various shape assemblies (σ3 = 39.2 kPa)

Full size image
Fig. 7
figure 7

Variation of average deviatoric stress (q) with average mean stress (p) during the critical state for different R values observed in simulations

Full size image
Fig. 8
figure 8

a relationship between roundness R and critical state stress ratio Mcs, b representation of the critical state strength (Mcs) surface defined by mean stress and roundness in the space of R, p, and q

Full size image

5.2 Microscopic response

5.2.1 Particle rotations

Figure 9 shows the cumulative rotation magnitude of individual particles in all the assemblies at the same strain level (i.e., εs = 30%). Generally, rounded particles exhibit high rotations, and rotations decrease as the R decreases (particles become more angular). The highest rotations can be seen in samples of circular particles, while the lowest are in pentagon particles. In rounded assemblies, any rotation in either direction is accompanied by the neighboring particle's opposite rotation of the same magnitude. As observed by Kuhn [39], in some cases, a group of particles (cluster) exhibit rotations in the same direction. Here it was also observed that clusters rotating in any direction are accompanied by an opposite rotating group in the neighboring region. The phenomenon is more visible in angular assemblies due to the strong interlocking characteristics of angular particles forming interlocked clusters. Furthermore, rotations are seen to concentrate along the diagonals of the box, forming two X shape high rotation zones in each sample. Generally, the first high rotation zone starting from top-left to bottom-right usually contains clockwise rotating particles (indicated in blue), and the second high rotation zone starting from top-right to bottom-left contains counterclockwise rotating particles (in brown). As shearing progresses, the horizontal rigid walls expand laterally, and particles in the first zone will prefer clockwise rotations. In contrast, the particles in the second zone prefer counterclockwise rotations to allow sample deformation.

Fig. 9
figure 9

Spatial distribution of particle rotations at the end of shearing (εs = 30%) under σ3 = 39.2 kPa

Full size image

Figure 10a shows the relationship between rm and εs. Circular particles exhibit the highest rotations, and rotation magnitude decreases gradually with R. The most angular shape exhibits the lowest rotation magnitude. Figure 10b shows the relationship between rm and R at different strain levels εs = 7.5%, 15%, 22.5%, and 30%. Generally, the rm exhibited by any shaped particle depends on the magnitude of shearing. But at the same strain, rm increases with the increase in R, indicating that angular particles are more resistant to rotations during shearing. The rolling resistance of an individual particle increases with the decrease in R, resulting in the inhibition of the rotation of angular particles [40]. Figure 11 shows the histograms of the density distribution of particle rotations at the end of the shearing, i.e., εs = 30%. In all assemblies, rotations are found to be normally distributed in both directions (clockwise and counterclockwise) around an average value of almost zero. Angular particles show higher concentrations at the mean value, indicating that more angular particles prefer not to rotate. As R increases, the density distribution becomes flatter and broader, indicating that more particles rotate.

Fig. 10
figure 10

a relationship between rm and εs, b relationship between rm and R at multiple same strain levels (σ3 = 39.2 kPa)

Full size image
Fig. 11
figure 11

Density distribution of particle rotation for simulations conducted under σ3 = 39.2 kPa

Full size image

5.2.2 Coordination numbers

The mechanical coordination number for a collection of particles is defined as [41]:

$$\begin{array}{*{20}c} {z^{m} = \frac{{2N_{C} - N_{1} }}{{N_{P} - N_{0} - N_{1} }}} \\ \end{array}$$
(2)

where Nc and Np are the numbers of contacts and particles in the specimen, respectively, and N1 and N0 are the numbers of particles with 1 and 0 contacts, respectively.

Figure 12 shows the evolution of the Zm with εs for all samples sheared. Generally, it can be seen that Zm decreases as the εs increases until a steady state for all samples is achieved. Zm at the CS is nearly the same for all samples, indicating no apparent effect of R. A similar observation has been reported for inter-particle contacts by [11, 42]. The mean coordination number is an indicator of the structural features of a granular sample, reflecting the arrangement of its constituent particles [2]. During shearing, regular hexagonal particles exhibited an anomalous mean coordination number, deviating from the trend. This is due to the fact that, among various shapes investigated, only regular hexagons have the ability to tessellate the 2D plane. The use of two different sizes of regular hexagons reduces the overall tessellation effect. However local tessellation, such as between a group of identically-sized hexagons, can still occur, leading to a stable local structure and increased interlocking.

Fig. 12
figure 12

Relationship between Zm and εs for simulations conducted under σ3 = 39.2 kPa

Full size image

5.2.3 Particle size effect on rotation

Interlocking refers to a kind of resistance caused by the particle arrangement of granular materials. In geotechnical engineering, it is considered one of the important sources of shear strength [43]. In the literature, interlocking is quantified using various macro and micro features, such as the ratio between vertical strain to lateral strain [44], shear strength [45], particle rotations [46, 47], and particle shape [43, 48]. For example, Zhao et al. [49] investigated the effect of particle angularity on shear strength. They concluded that the angular particles exhibit higher shear strengths and dilations because of interlocking effects. In comparison, rounded particles show lower strengths because of the impossibility of the interlocking of the perfect round edges. In this study, we used dual-size samples. Hence the effect of particle size on rotational behavior is quantified to discuss the interlocking for binary granular mixtures and how it is affected by R. For this, the rotation ratio, which is the ratio between the average rotation of small particle to big particles, is used:

$$\begin{array}{*{20}c} {{\text{Rotation ratio}} = \frac{{\left( {\mathop \sum \nolimits_{i = 1}^{{n^{S} }} \left| {\theta_{i}^{s} } \right|} \right)/n^{S} }}{{\left( {\mathop \sum \nolimits_{i = 1}^{{n^{B} }} \left| {\theta_{i}^{B} } \right|} \right)/n^{B} }}} \\ \end{array}$$
(3)

where n refers to the total number of particles, θi represents the rotation of i-th particle, and superscripts S and B correspond to small and big particles, respectively. If a significant difference in absolute cumulative average rotation of small and big particles is observed, then both size particles can rotate independently, indicating no or weak interlocking. On the other hand, if no significant difference between the absolute cumulative average rotation of small and big particles is observed, then strong and relatively stable connections with neighboring particles are expected to prevent particles from rotating independently (strong interlocking). The magnitude of the difference between small and big particle rotation can give a simple estimate of the amount of interlocking, e.g., a high value of rotation ratio corresponds to weak interlocking. In contrast, a small value corresponds to strong interlocking. Figure 13 shows the relationship between the rotation ratio and εs. Generally, at the start of shearing, interlocking between particles is weak, so the rotation ratio is higher (small particle rotation dominant behavior). As the mean stress increases, the samples tend to compress, achieving a dense packing; interlocking becomes strong, indicated by the fall of the rotation ratio curves, and eventually reaches a steady state. The attained steady state depends on R. Rounded particles exhibit weak interlocking indicated by rotation ratio curves close to the rotation ratio value 2. This suggests that in round samples, smaller particles tend to rotate almost twice as big particles. In comparison, angular sample curves are close to rotation ratio 1, indicating relatively strong interlocking between big and small particles. This agrees with previous researchers' findings of [43, 49].

Fig. 13
figure 13

Evolution of rotation ratio with an increase in deviatoric strain (εs) for simulations conducted under σ3 = 39.2 kPa

Full size image

Figure 14 shows the mean Zm during the CS for big and small particles. Bigger particles tend to maintain a higher Zm. Generally, a high coordination number restricts the rotational freedom of particles [37]; hence bigger particles were expected to rotate significantly lesser than small particles. However, the results revealed that the difference in rotation magnitude of big and small particles decreases with R. This emphasizes that the effect of particle size on rotational response is induced mainly due to different roundness.

Fig. 14
figure 14

Relationship between mean Zm during the critical state with R for big and small particles

Full size image

5.2.4 Force chains

Contact forces among individual particles have been regarded as a significant factor affecting the mechanical behavior of granular assemblies [49]. Therefore, it is crucial to investigate the effect of particle roundness on the normal contact force distribution (i.e., the normal contact force chain) during shearing. Figure 15 shows the force chains for all the samples at the end of shearing (i.e., when εs = 30%) for the simulations conducted under σ3 = 39.2 kPa. The thickness of force lines is directly proportional to the magnitude. The normal contact forces are divided into two groups indicated by red and blue colors to compare the force chains of different samples. In round samples, the forces are relatively uniformly distributed, and contact forces always pass through the center of connected particles. The contacts between angular particles are more complex; hence the normal contact force does not pass through the center of touching particles in most cases. Consequently, the contact forces in angular samples can be visualized as non-uniformly distributed. Some contacts experience very high forces indicated by the red color. Kuhn et al. [50] conducted a numerical investigation into structured deformation in rounded material, and their findings suggest that high particle rotations can relieve sliding between most particles while transferring the sliding to a few contacts where frictional slipping is intense. Therefore, high rotations in round samples ease sliding between most of the contacts; hence the possibility of generating very high contact force is low (indicated by a few red color forces in round samples). However, as the R decreases, inhibitions to free rotations increase; hence intense sliding becomes relatively apparent. As a result, some contacts will experience very high forces, which can be visualized by increasing red color contact forces with a decrease in R. Furthermore, the force concentration in angular samples also indicates the microstructure is relatively stable than round samples due to inhibition to free rotations and strong interlocking; hence they exhibit higher strengths.

Fig. 15
figure 15

Normal contact force distribution for simulation conducted under σ3 = 39.2 kPa (εs = 30%)

Full size image

5.2.5 Shear band identification

In shear bands, the void ratio increases, and the coordination number decreases. Therefore, microstructural constraints on particle kinematics inside the shear band are very different [25]. Consequently, it is vital to identify the particles inside the shear band. For this, a nominal deviatoric strain is assigned to each particle using a procedure developed for DEM post-processing [51]. In this procedure, a Voronoi cell hosting each particle is created using a regular Delaunay triangulation having as vertices the mass centers of the labeled grains [52]. The particle positions at two arbitrary instants towards the end of the shearing (e.g., when deviatoric strain is 24% and 30%) were extracted. Displacements of neighboring grains were then used to compute a nominal displacement gradient tensor for the triangles whose vertices are the centers of each particle. Finally, a nominal averaged deviatoric strain was projected back to each grain, and a threshold strain value was used to assign grains to the shear band. The shear band identification procedure results are shown in Fig. 16, in which the black particles are identified inside the shear band. The threshold value is set at 0.05. In each particle shape assembly, two shear bands of X shape are observed, which closely correspond to the high rotation zones shown in Fig. 9. Boundary conditions used in the simulation are rigid, restricting non-uniform displacements on the sides of the sample. Due to this, the shear band forms along the diagonals of the biaxial box. Figure 16 shows that the thickness of shear bands is not uniform for a given shape. However, it is generally observed that the shear band is relatively clear for circular particles, and as the R decreases, it becomes less distinct.

Fig. 16
figure 16

Shear band identified for simulations conducted under σ3 = 39.2 kPa

Full size image

5.2.6 Particle-scale behavior inside the shear band

Figure 17 shows the rm and Zm evolution inside and outside the shear band for circular particles for the simulation conducted under σ3 = 39.2 kPa. As shown in Fig. 17a, the rm growth inside the shear band is significantly higher, i.e., rotation concentration in intensely deformed zones. The same observation was reported by several researchers [7, 25, 39, 53,54,55]. Outside the shear band, particles rotate significantly at the start of shearing and gradually achieve a steady state towards the end of shearing, indicated by the slope of the rotation curve. However, the particles inside the shear band continue to exhibit significant rotations even at the end of shearing. The void ratio inside the shear band is higher than other parts of the sample, corresponding to fewer contacts per particle inside the shear band. Thus, higher rotations inside the shear band are associated with low coordination numbers [2], as shown in Fig. 17b. The overall tendency of the behavior inside and outside the shear band is qualitatively similar regardless of the shape of the particles. Thus for all samples, rotations tend to concentrate inside the shear band and are associated with low particle connectivity as shown in Fig. 18.

Fig. 17
figure 17

Particle-scale behavior of circular particles (for σ3 = 39.2 kPa) (a) rm evolution (b) Zm evolution

Full size image
Fig. 18
figure 18

Relationship between a mean Zm during CS and R, b rm and R for simulations conducted under σ3 = 39.2 kPa

Full size image

5.2.7 Competition between coordination number and particle shape

Previous studies have investigated the shear response of granular samples containing irregularly shaped concave particles and have reported that particle shape affects the coordination number in such a way that irregularly-shaped particles have higher coordination numbers to obstruct their rotations [13, 42]. However, the complex shape features of the irregularly-shaped concave particles make it difficult to systematically control one specific shape descriptor, such as roundness. Therefore, we focused solely on the effect of particle roundness on coordination number and rotational response. Figure 18 presents the relationship between mean Zm during CS, rm at εs = 30%, and R. The solid lines represent linear fitting lines. The results indicated that mean Zm does not vary much with R for the overall sample average (R2 = 0.104) and the inside shear band average (R2 = 0.066), as shown in Fig. 18a. On the other hand, a strong linear relationship between rm at a specific strain level and R is observed for the overall sample average (R2 = 0.951) and inside shear band average (R2 = 0.970). The rm increases with R, as shown in Fig. 18b.

Despite having almost, the same Zm at the CS, the rotational behavior is significantly different, indicating the rotational behavior to be dominantly controlled by particle geometry. Particle shape influences the ability of rotation. For example, angular particles have substantially higher resistance to rotation than rounded particles [40]. Alternatively, in granular systems, the ability of angular particles to rotate is relatively lesser than round particles under the same conditions. This highlights that rotational behavior is mainly a function of particle shape. A recent popular approach to mimic angular shape particles in DEM simulations is to artificially assign a rolling resistance to circular or spherical particles to reduce their ability to rotate [55,56,57,58,59]. With this approach, using identical shape particles with different rotation abilities, researchers also pointed out that the particle’s ability to rotate is one of the main phenomena affected by its shape.

5.2.8 Effect of roundness/angularity in periodic space

In all simulation results discussed above, rigid frictional boundaries are used to keep the simulation conditions consistent with the biaxial experiment used for calibration and validation. In addition, the same simulations were performed with periodic boundaries to investigate the effect of boundary conditions. Figure 19 shows the effect of roundness/angularity on the CS stress ratio, cumulative mean absolute rotation (rm), and the mean mechanical coordination number (Zm) with rigid and periodic boundaries. Generally, it was observed that the effect of particle roundness/angularity on micro–macro mechanical response is similar regardless of the boundary conditions. However, a rigid boundary provides slightly larger confinement; the samples macroscopically exhibit slightly higher shear strength (as shown in Fig. 19a). At the same time, higher dilation with a rigid boundary causes the mean coordination number to decrease; hence the rotations become relatively easy. Therefore, it can be seen in Fig. 19b and c that slightly higher rotation of particles is associated with lower mean mechanical coordination numbers when rigid boundaries are applied.

Fig. 19
figure 19

Effect of roundness with rigid and periodic boundaries, a relationship between Mcs and R (identical to Fig. 8a), b relationship between mean Z.m during critical state and R (identical to Fig. 18a), c relationship between rm at 30% deviatoric strain and R (identical to Fig. 18b)

Full size image

6 Conclusions

In this study, we conducted the biaxial shearing test on dual-size circular and hexagonal aluminum rods. A novel image analysis technique also assesses particle kinematics along with macroscopic stress–strain characteristics. Since it is very challenging to consider a wide range of particle shapes in the experiment therefore, to conduct a systematic study on the effect of particle roundness, a DEM model of the biaxial shearing test is developed. A complete set of experimental data, including macroscopic response and particle-level motion, is used to calibrate and validate the DEM model. After validation, particles with different roundness values are considered to investigate the effect of roundness/angularity systematically.

Macroscopically, shear strength and volumetric deformations of granular materials are observed to increase with the decrease in particle roundness. In angular samples, higher shear strengths and volumetric dilations are associated with lesser rotations and strong interlocking between particles. On the other hand, assemblies with rounded particles exhibit higher rotations, and the net effect of high particle rotation is the reduction of strengths, as also reported by Kuhn [39]. The critical state stress ratio, which is an important macroscopic strength indicator, is observed to be a function of particle roundness and is related to the particle’s rotational behavior during shearing. The deformation patterns of granular material are significantly affected by particle roundness. For instance, assemblies of circular particles exhibit a distinct shear band with relatively uniform thickness, whereas the shear band becomes less defined as particle roundness decreases. Commonly, the particles inside the shear band tend to rotate more than outside particles and are associated with low coordination numbers. Particle roundness has an insignificant effect on the mean mechanical coordination number at the critical state however, the rotational behavior varies much with particle roundness, indicating that the effect of particle roundness on rotational behavior is more dominant than the coordination number.