1 Introduction

The macroscopic response of granular materials is influenced by microstructural characteristics of particles, their contacts and interstitial pores (or voids) [22]. The shape and size distribution of discrete particles forming the granular assembly can affect packing structure and strength properties [34, 35]. Interparticle contacts form a complex network and the associated anisotropy of this contact network provides insights into the nature of stress transmission and the development of shear strength [7, 26, 32]. Particles and their associated contact networks have been extensively studied and this is aided by the fact that both can be regarded as discrete objects.

In contrast, the effect of pores (or more generally, pore space characteristics) on mechanical response of the medium has received relatively limited attention. This may be attributed to the complexity associated with the description of continuous, entirely interconnected pore space in granular materials. Prior studies have focused on how pore space characteristics affect fluid flow and transport properties, such as conductivity [3, 33], water retention [4, 8] and filtration [24, 30].

However, features of the pore space can also provide insights into deformation characteristics in sheared granular assemblies. Oda et al. [23] observed the formation of elongated pores in bi-axial compression tests on photoelastic disks and quantified this pore anisotropy using a scan-line technique. Ghedia and O’Sullivan [6] extended this method to analyse digital images, while Muhunthan et al. [21] and Muhunthan and Chameau [20] employed a similar technique in exploring the concept of yielding and an ultimate state boundary surface.

An alternate approach is to tessellate the pore space, or identify individual pores forming the granular assembly. Common approaches include the classical Delaunay and Voronoi tessellations, which typically rely on the centroidal coordinates of particles. Other tessellation methods such as the approach proposed in Li and Li [16] explicitly consider the interparticle contact points. Space tessellation techniques have also been considered in the formulation of a micromechanical strain tensor for a granular assembly [2, 14, 15, 27]. Li and Dafalias [18] explicitly considered a pore fabric measure in their model of anisotropic critical state based on the length of void vectors obtained from a slight modification of the space tessellation proposed by Li and Li [16]. They proposed that limiting states of pore space fabric would be attained at critical state conditions (in addition to the usual constraints of critical state soil mechanics). These examples suggests that the use of space tessellation is a useful means to gain fundamental understanding of deformation characteristics.

This study investigates how pore space characteristics affect the deformation response of sheared granular assemblies by employing the space tessellation method. Pore-scale data for sheared granular assemblies are extracted from numerical simulations employing the discrete element method, and individual pores are identified using the modified Delaunay tessellation [1]. While it is acknowledged that there is no unique way to tessellate the pore space, several studies [10, 25, 31] have suggested that the modified Delaunay tessellation provides a physically representative delineation of the pore space. Two particular properties of the pore space are investigated in detail: (i) pore orientation and the associated anisotropy of pores, and (ii) pore shape as an indicator for macroscopic density. The influence of pore size is also considered indirectly, while some elements of the contact networks are briefly discussed.

2 Pore characterisation from numerical simulations of sheared granular assemblies

2.1 Discrete element simulations

Numerical simulations were performed using the discrete element method (DEM) on the open-source software LIGGGHTS [12]. Four cases are considered in this study corresponding to common geotechnical elemental shear tests [32]:

  1. 1.

    CP-L: axisymmetric test with constant radial pressure (mimicking a drained triaxial test) for a loose sample \(\left( e_{0}=0.68\right) \).

  2. 2.

    CP-D: axisymmetric test with constant radial pressure for a dense sample \(\left( e_{0}=0.56\right) \).

  3. 3.

    CV-D: axisymmetric test with constant volume condition (mimicking an undrained triaxial test) for a dense sample \(\left( e_{0}=0.59\right) \).

  4. 4.

    SS-D: simple shear test with constant volume condition for a dense sample \(\left( e_{0}=0.59\right) \).

Note that loose constant volume (CV) and simple shear (SS) samples were metastable and exhibited collapse mechanisms, where the samples were unable to sustain any shear stress. These metastable samples are not considered further in this study. Samples are generated by randomly inserting particles within a cuboidal domain with no interparticle contacts and subsequently isotropically compressed to 200kPa. In the CP-L and CP-D simulations, the particles were bound by rigid frictionless walls, while periodic boundary conditions were imposed for the CV-D and SS-D simulations. The effects of gravity were not considered. All samples comprised monodisperse assemblies of particles with diameter \(d_{s}=1 \, \hbox {mm}\) with contacts characterised by the Hertz-history model (available in LIGGGHTS), with particle elastic modulus and Poisson ratio of \(E=70 \, \hbox {GPa}\) and \(\nu =0.25\). The local packing density in subsets of the particle assemblies were monitored to check if the packing density exceeded the random close packing limit. These checks found that there was no significant crystallisation in the simulations. Samples of varying density were generated by adjusting the interparticle friction angle during the sample generation process. The interparticle friction angle was set at \(\mu =0.25\) for all samples during shearing. Each case simulated two-way cyclic shear test comprising initial loading, unloading and reloading phases in order to explore the influence of shearing direction (i.e. compression or extension), sudden load reversals and history effects on the evolving pore space features. All samples were sheared in a quasi-static manner. Further details on these numerical simulations are available in Sufian et al. [32]. The macroscopic response for all samples are reproduced in Figs. 1 and 2, which shows that the results agree well with typical, measured behaviour of granular materials.

These simulations encompass a broad range of stress and volumetric conditions. The axisymmetric simulations include two different packing densities (i.e. loose and dense) and two different loading paths (i.e. drained and undrained). The direction of principal stress axes are fixed in the axisymmetric simulations, while rotation of principal axes is explored in the simple shear simulation. Further, the CP-L and CP-D simulations experience macroscopic volume change, while CV-D and SS-D maintain a constant volume constraint. Very few studies explore pore space characteristics in sheared granular assemblies for the broad range of stress and volumetric conditions considered here.

Fig. 1
figure 1

Numerical stress and volumetric response for the CP-L and CP-D simulations. Note that the colour scheme for loading, unloading and reloading is maintained for the remainder of this paper, unless stated otherwise [32]

Full size image

2.2 Pore space tessellation

The pore space is tessellated using the modified Delaunay tessellation proposed by Al-Raoush et al. [1]. This method initially considers the classical Delaunay tessellation, which produces a space-filling set of tetrahedral cells, where the vertices of the tetrahedron are the centres of the four particles forming the tetrahedron. The classical Delaunay tessellation over-segments the pore space, and thereby does not capture the wide variation in pore sizes (that is, the existence of small and large pores) and the variable connectivity of the pores (as tetrahedrons have exactly four four faces). Merging of these tetrahedral Delaunay cells using the modified Delaunay tessellation addresses both these concerns to produce a more physically representative tessellation of the pore space.

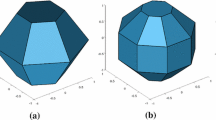
Each Delaunay cell has an inscribed sphere contained entirely within the pore space. Part of the inscribed sphere may be located outside the Delaunay tetrahedron and intersect neighbouring inscribed spheres. Individual Delaunay cells are then merged with adjacent cells if their respective inscribed spheres overlap. This results in a space-filling set of polyhedral pore units which are representative of individual pores. Figure 3 provides several examples of pores identified using the modified Delaunay tessellation, and further details can be found in Sufian et al. [31].

This modified Delaunay tessellation is used to track pore units for each of the granular assemblies through the two-way cycle of shearing described above. Pore unit properties are obtained at specified strain increments, with \(\delta \varepsilon _{a}=0.083\%\) for CP-L and CP-D, \(\delta \varepsilon _{a}=0.016\%\) for CV-D and \(\delta \gamma =0.042\%\) for SS-D, allowing for a detailed investigation of pore space characteristics.

Fig. 2
figure 2

Numerical stress-strain and stress path response for the CV-D and SS-D simulations [32]

Full size image
Fig. 3
figure 3

a Tetrahedral Delaunay cell, or pore unit with no merging (termed unmerged in this paper); b pore unit formed by merging two Delaunay cells; c pore unit formed by merging four Delaunay cells [33]

Full size image

2.3 Properties of individual pores

For each individual pore, there are several geometric properties of interest in this study: (i) pore volume, (ii) pore orientation, and (iii) pore shape.

Pore volume, \(V_{p}\), is calculated by subtracting the solid volumes from the total volume of the unit cells, and can be determined analytically with the assumption of non-overlapping particles (which is reasonable for the numerical simulations considered in this study).

The orientation of individual pores can be determined using the pore orientation tensor introduced by Sufian et al. [31]:

$$\begin{aligned} P_{ij}=\frac{1}{N_{f}}\sum _{\alpha =1}^{N_{f}}a^{\alpha }n_{i}^{\alpha } n_{j}^{\alpha } \end{aligned}$$
(1)

where, \({\mathbf {n}}^{\alpha }\) and \(a^{\alpha }\) are the unit normal vector and corresponding area of the face of the unit cell, and the summation is over all \(N_{f}\) faces forming the pore unit. The major principal orientation of the pore, \({\mathbf {p}}\), is determined from an eigen-decomposition, where \({\mathbf {p}}\) is the eigenvector corresponding to the minimum eigenvalue of \(P_{ij}\). The eigen-decomposition of \(P_{ij}\) has a physical basis, where the eigenvalues are the projected areas in the principal directions specified by the eigenvectors, as detailed in Sufian et al. [31].

The pore orientation tensor in Eq. 1 is of a similar form to the Minkowski interface tensor \({\mathbf {W}}_{1}^{0,2} = \oint _{S}{\mathbf {n}}\otimes {\mathbf {n}}\text {d}S\) [29] and has been considered by Schröder-Turk et al. [28] and Kraynik et al. [13] to explore cell shape anisotropy. In particular, Schröder-Turk et al. [28] considered the ratio \(\frac{\xi _{min}}{\xi _{max}}\), where \(\xi _{min}\) and \(\xi _{max}\) are the minimum and maximum eigenvalues of the interface tensor, to quantify shape anisotropy of Voronoi cells in disordered sphere packing. In a similar manner, this study employs the shape factor:

$$\begin{aligned} \beta =1-\frac{\xi _{min}}{\xi _{max}} \end{aligned}$$
(2)

where \(\xi _{min}\) and \(\xi _{max}\) are obtained from the eigenvalues of the pore orientation tensor (Eq. 1). The shape factor \(\beta \in \left[ 0,1\right] \), where \(\beta =0\) represents a pore with regular geometry (e.g. cube, regular tetrahedron or sphere), while \(\beta =1\) implies that the pore is a line or plane (depending on the intermediate eigenvalue). The slight difference in the definition of the shape factor ensures consistency with the following pore anisotropy analysis, where a value of zero implies isotropy, and a non-zero value reflects some degree of anisotropy.

3 Pore orientation and induced anisotropy of the pore space

The directional distribution of a collection of pores at any instance during shearing can be quantified by the probability density function of pore orientation, \(E^{k}\left( {\mathbf {p}}\right) \), given by the following second-order polynomial expression:

$$\begin{aligned} E^{k}\left( {\mathbf {p}}\right) =\frac{1}{4\pi }\left( 1+D_{ij}^{k}p_{i}p_{j} \right) \end{aligned}$$
(3)

where \(D_{ij}^{k}\) is termed the deviatoric directional probability density tensor [17]. While this formulation is typically used to describe the directional distribution of contact normal vectors, it can also be applied to describing the distribution of individual pores.

In Eq. 3, the superscript k refers to a particular subset of pores. This concept of partitioned subsets was previously applied to the interparticle contact network [32], where dominant contributors to shear strength were identified. Sufian et al. [32] found a unique linear relation between the mobilised internal friction and the anisotropy of a partitioned subnetwork. The current paper considers whether a partitioned subset of pores can be identified as the dominant contributors to pore space anisotropy. In addition to considering the complete collection of pore units, this study will also investigate subsets of unmerged and merged pores, as delineated by the modified Delaunay tessellation and denoted \(k\in \left\{ u,\,m\right\} \), respectively. An absence of any value for k implies a quantity calculated for the complete collection of pores. Note that unmerged pores are representative of smaller pores in the assembly, while merged pores represent larger pores. Hence, the \(\left\{ u,\,m\right\} \) partition also explores the influence of pore size on the anisotropy of the pore space.

Following Kanatani [9], \(D_{ij}^{k}\) in Eq. 3 is given by:

$$\begin{aligned} D_{ij}^{k}=\frac{15}{2}\left[ N_{ij}^{k}-\frac{N_{kk}^{k}}{3} \delta _{ij}\right] \end{aligned}$$
(4)

where

$$\begin{aligned} N_{ij}^{k}=\frac{1}{N_{p}^{k}}\sum _{\alpha =1}^{N_{p}^{k}}p_{i}^{\alpha } p_{j}^{\alpha } \end{aligned}$$
(5)

is the moment tensor of pore orientation or alternatively a pore space fabric tensor. \(N_{p}^{k}\) is the number of pores within the \(k^{\text {th}}\) subset. A scalar measure of the degree of anisotropy can be defined by the second invariant of \(D_{ij}^{k}\):

$$\begin{aligned} a_{p}^{k}=\sqrt{\frac{3}{2}D_{ij}^{k}D_{ij}^{k}} \end{aligned}$$
(6)

3.1 Orthogonal preferential alignment of unmerged and merged pores

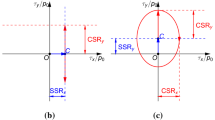
Figure 4a–d show the evolution of the pore anisotropy for the four sheared granular assemblies comparing i) all pore units, \(a_{p}\); ii) merged Delaunay cells, \(a_{p}^{m}\); and iii) unmerged cells, \(a_{p}^{u}\). Note that a signed measure of anisotropy is presented, where for axisymmetric simulations (Fig. 4a–c), positive values imply preferential alignment in the vertical direction, while negative values imply preferential orientation in the horizontal direction (Fig. 5a). For the simple shear simulation (Fig. 4d), negative values imply preferential orientation of pores tilted to the right (Fig. 5b), while positive values imply preferential orientation of pores tilted to the left (when observing the x–z plane).

Fig. 4
figure 4

Evolution of the pore anisotropy parameter, \(a_{p}^{k}\), for the complete collection of pores and the \(\left\{ u,\,m\right\} \) partition. a CP-L, b CP-D, c and CV-D d SS-D

Full size image

When considering the complete collection of pores, there is a preferential alignment in the direction of expansion. This implies that in the axisymmetric simulations, pores are orientated horizontally in the loading phase, before becoming vertical in the unloading phase and returning to a horizontal preference in the reloading phase. This is consistent with the observations in the simple shear simulation, where pores align to the right in the loading phase (which is the direction of tilt and the macroscopic direction of expansion), while they are orientated to the left in the unloading phase and align to the right in the reloading phase.

A more detailed perspective is provided by considering the anisotropy in the \(\left\{ u,\,m\right\} \) partition. Unmerged pores are the dominant contributor to pore space anisotropy, with \(a_{p}^{u}>a_{p}^{m}\) and this is particularly noticeable in the CP-L (Fig. 4a) and CP-D (Fig. 4b) simulations. In contrast, the magnitude of pore anisotropy is significantly smaller in the constant volume shear simulations (CV-D in Fig. 4c and SS-D in Fig. 4d). These cases show a near linear trend in pore anisotropy due to the (relatively) small strain range considered in these simulations. Similar linear response in pore anisotropy was found in the CP-L and CP-D samples for shearing to \(\left| \varepsilon _{a}\right| =2\%\) (not presented here).

In all simulations, unmerged pores exhibit strong preferential orientation in the expansion direction (perpendicular to the compression loading direction), while merged pores have a slight orientational preference parallel to the compression direction. This is schematically shown in Fig. 5 and was also observed in numerical simulations of bi-axial compression tests and direct shear tests [10, 11].

This orthogonal preferential orientation of merged and unmerged pores can be explained by considering the interparticle contacts along the edges of a pore unit. Recall that a pore unit formed by the modified Delaunay tessellation has polyhedral geometry (Fig. 3). Some edges of the polyhedral unit cell may contain interparticle contacts, while other edges will have a separation distance between non-interacting particles. Suppose \(\kappa _{c}=\frac{N_{c}}{N_{e}}\) is the ratio of active contacts, where \(N_{c}\) is the number of contacting edges and \(N_{e}\) is the number of edges of the pore unit. Also of importance is the ratio of sliding contacts, \(\kappa _{s}=\frac{N_{s}}{N_{c}}\), where \(N_{s}\) is the number of contacts which are sliding (i.e., at the Coulomb friction limit). Consider also the magnitude of the interparticle normal force, \(f_{n}\) of the active contacts. The average force magnitude of contacts forming a pore unit is defined as \(\kappa _{f}=\left\langle f_{n}/\overline{f_{n}}\right\rangle \), where the force is normalised by the mean normal force, \(\overline{f_{n}}\), and the average is taken only over active contacts. The parameters \(\kappa _{c}\), \(\kappa _{s}\) and \(\kappa _{f}\) effectively capture the influence of the contact network on individual pores.

Figure 6a shows that the ratio of active contacts \(\left( \kappa _{c}\right) \) and sliding contacts \(\left( \kappa _{s}\right) \) fluctuate around a constant value for pores of all size, but the average interparticle normal force increases with pore volume (Fig. 6b). Note that an approximate delineation between unmerged and merged pores is shown in Fig. 6. Even though merged pores contain the same proportion of active and sliding contacts as unmerged pores, it is clear that merged pores can only be sustained by interparticle contacts with large normal force (Fig. 6b). This is an intuitive result, as large pores would collapse if the surrounding interparticle contacts had relatively small normal force. It is well-known that contacts with relatively large normal force magnitudes tend to align parallel to the loading direction. Hence, if merged pores predominantly comprise strong contacts, then it would be anticipated that these pore units would also exhibit a preferential orientation in the direction of compressive loading, as indicated in Fig. 4. Based on bi-axial compression tests on photoelastic disks, Oda et al. [23] had previously indicated that elongated pores were formed parallel to the major principal stress direction due to arching structures of strong force chains. This study suggests that the observation by Oda et al. [23] is only applicable for merged pores.

Fig. 5
figure 5

Schematic diagram showing the sign convention (shown by plus and minus symbols) used for the determination of pore space anisotropy in axisymmetric and simple shear simulations. The diagram illustrates the orthogonal preferential orientation smaller unmerged and larger merged pores, with unmerged pores aligning the expansion direction (as discussed in Sect. 3.1). It also illustrates that smaller unmerged pores are more rounded in shape compared to the elongated larger pores (as discussed in Sect. 4)

Full size image
Fig. 6
figure 6

a Average percentage of active and sliding contacts for individual pores as a function of normalised free pore volume, where \(V_{p}\) is the pore volume, \(V_{p,min}\) is the minimum pore volume assuming no particle overlaps and \(d_{s}\) is the particle diameter. This normalisation enables comparison between samples of different densities and particle diameter. Note that the averaging is conducted over all data in the initial loading phase for all simulations. b Average interparticle normal force as a function of pore volume. In both figures, the green line represents the approximate delineation between unmerged and merged pores

Full size image

3.2 Steady state conditions and lag in the response of pore anisotropy

Figure 7 shows that steady state pore anisotropy is attained at large strains (and hence only observed in the CP-L and CP-D simulations). This steady state pore anisotropy is attained even though the sample is macroscopically undergoing volume change, suggesting that there are additional factors contributing to the deformation response. Comparisons of pore anisotropy in the loose and dense assemblies suggests the attainment of a “critical state” for the \(a_{p}\) parameter (i.e. for the complete collection of pores), although shearing to higher strains is required to confirm this observation. Additional analysis are required to establish uniqueness of this pore space parameter for shearing to large strain critical state conditions. This critical state characteristic is not found for the subsets of unmerged or merged pores (Fig. 4a, b). Li and Dafalias [18] proposed that there is a unique pore fabric parameter that characterises critical state conditions, along with the usual constraints of stress state and void ratio. This suggests that the current pore anisotropy parameter, \(a_{p},\) may be incorporated into such an approach, provided it is expressed in a thermodynamically consistent manner as per the suggestion of Li and Dafalias [19].

Fig. 7
figure 7

Pore anisotropy, \(a_{p}\), plotted on the same strain scale for all numerical simulations. Note that loading, unloading and reloading branches are distinguished in the CP-L and CP-D simulations only (using the same colour scheme as previous figures)

Full size image

Figure 7 also indicates that the steady state pore anisotropy mobilised in the unloading phase (i.e. triaxial extension) is not equal and opposite to that observed in the loading and reloading phase (i.e. triaxial compression). The steady state value in compression is \(\left( a_{p}\right) _{ss,\,comp}\approx -\, 0.27\), while in extension it is \(\left( a_{p}\right) _{ss,\,ext}\approx 0.46\). Note that there is a natural asymmetry in the maximum attainable pore anisotropy in the radial and axial direction, due to the fact that alignment in the axial direction allows for only perfectly vertical pores, while alignment in the radial direction can have an infinite number of orientations in the horizontal plane. This asymmetry is also evident in the stress-strain response in Fig. 1 during triaxial shear, as there is one major principal axis in the axial direction during compression, but two major principal axes in the radial direction during extension. However, this significant asymmetry was not noted for the contact network anisotropy parameters [32]. For example, Fig. 8 shows that the steady state contact anisotropy is \(\left( a_{c}\right) _{ss,\,comp}=0.74\) in compression and \(\left( a_{c}\right) _{ss,\,ext}=-\,0.76\) in extension for the CP-D simulation. Contact anisotropy, \(a_{c}\), is also obtained by using the contact normal vectors in Eqs. 3–6 in place of the pore orientation vectors, thus enabling comparison with the pore anisotropy parameter, \(a_{p}\). This asymmetry in pore anisotropy, and the lack of it in the particle contacts, makes it difficult to correlate these two properties. Fu and Dafalias [5] used numerical simulations of (2D) bi-axial compression tests to suggest that pore space and contact network fabrics can be related (noting that they employ different definitions of pore and contact fabric). However, a direct correlation between \(a_{c}\) and \(a_{p}\) has not been found in this study.

Fig. 8
figure 8

Comparison of stress ratio, \(\frac{q}{p}\), contact network anisotropy, \(a_{c}\), for the complete contact network, and pore anisotropy, \(a_{p}\), for the complete collection of pores in the CP-D simulation. Note that the x-axis for two-way shearing has been unfolded into a single linear strain axis, and that a negative value of pore anisotropy is shown to allow for ease of comparison with the other parameters

Full size image

In addition to this asymmetry, comparison of the pore and contact anisotropy indicates that pore space anisotropy is substantially smaller than observed for the contact network with \(\left| a_{p}\right| <0.5\), while \(\left| a_{c}\right| <1.0\) (similar trends are noted for the partitioned subsets of pores and contacts). This was also noted in Oda et al. [23] (albeit with different measures of contact and pore space anisotropy) and reflects the fact that a highly anisotropic pore space (e.g. all pores aligned in a particular direction) would not form a mechanically stable assembly when subject to shear.

Figure 8 also shows that the stress ratio response has a slight asymmetry (\(\frac{q}{p}=0.71,\;0.59\) for critical state compression and extension conditions, respectively). However, a direct correlation with the stress ratio is hindered by the fact that pore space anisotropy \(\left( a_{p}\right) \) evolves at a much slower rate than the contact network anisotropy \(\left( a_{c}\right) \) and the macroscopic stress response. This is most evident by considering the unloading and reloading phases in Fig. 8. In the unloading phase, the strain required to change loading direction (or anisotropy direction) is \(\left| \delta \varepsilon _{a}\right| =0.8\%\) for the stress ratio, while it is \(\left| \delta \varepsilon _{a}\right| =2.5\%\) for contact anisotropy and \(\left| \delta \varepsilon _{a}\right| =4.1\%\) for pore anisotropy. In the reloading phase, sign reversal requires \(\left| \delta \varepsilon _{a}\right| =2.0,\;7.1,\;14.3\%\) for stress ratio, contact anisotropy and pore anisotropy, respectively. This apparent lag in the response of the pore space reflects the fact that re-alignment of pores requires a substantial displacement of particles, which in a “dense” or slow-flowing granular assembly (with low inertia number) takes substantial amount of time. In contrast, the stress state can switch directions quickly by adjusting the magnitude of contact forces initially and then allowing the contacts to re-align as observed by Sufian et al. [32].

3.3 Isotropic directional distribution of pore volume in sheared assemblies

The observations in Sect. 3.1 for pore anisotropy suggests that parallel to the loading direction there are larger pores but fewer of them, while perpendicular to the loading direction, there are smaller pores but in greater number. This is schematically illustrated in Fig. 5. This raises an interesting hypothesis as to whether these two competing effects cancel each other out and result in an isotropic distribution of pore volume. To further investigate this hypothesis, consider the following distribution function:

$$\begin{aligned} V\left( {\mathbf {p}}\right) =V_{0}\left( 1+T_{ij}p_{i}p_{j}\right) \end{aligned}$$
(7)

which represents the average pore volume in a given direction. This analysis is only conducted for the complete collection of pores and hence, the superscript k denoting partitioned subsets is omitted. \(T_{ij}\) is given by:

$$\begin{aligned} T_{ij}=\frac{15}{2V_{0}}\left[ M_{ij}-\frac{M_{kk}}{3}\delta _{ij}\right] \end{aligned}$$
(8)

where

$$\begin{aligned} M_{ij}=\frac{1}{N_{p}}\sum _{\alpha =1}^{N_{p}}\left( V_{p}^{\alpha }-V_{p,min} \right) p_{i}^{\alpha }p_{j}^{\alpha } \end{aligned}$$
(9)

is a moment tensor and also of the same form as the global orientation tensor introduced in Sufian et al. [31].

Fig. 9
figure 9

a Evolution of \(a_{t}\) throughout the two-way cyclic loading shown in colour for the CP-L, CP-D, CV-D and SS-D simulations. The parameter \(a_{p}\) (solid black line) for the CP-D simulation is also shown, as a reference to indicate that \(a_{t}\approx 0\) for all simulations. Inset: \(a_{t}\) in the CP-D simulation showing slight deviation away from perfect isotropy. b Comparison of the diagonal elements of the global orientation tensor, \(M_{ij}\), against the mean free pore volume, \(\frac{\left\langle V_{p}\right\rangle -V_{p,min}}{3}\), shown in grey for the CP-L, CP-D, CV-D, SS-D simulations), along with results for static assemblies in Sufian et al. [31], where error bars have been shown to indicate deviation from isotropy in the static assemblies. The dashed black line indicates perfect correspondence, and hence, perfect isotropy of the global orientation tensor. Inset: Detailed view of \(M_{33}\) (i.e. the axial direction) for the CP-D simulation showing slight deviations from perfect isotropy. Note that loading, unloading and reloading branches are distinguished in the inset figure

Full size image

Note that \(M_{ij}\) incorporates both competing effects of distribution by number and distribution by volume, and hence, differs from the representative value analysis presented in Li and Yu [17] which is typically used to explore directional distribution of normal and tangential force magnitude independent of any contact normal anisotropy [32]. Within the context of this paper, it is desirable to explore pore distribution by number and volume together.

It can be shown that \(V_{0}=M_{kk}=\left\langle V_{p}\right\rangle -V_{p,min}\), that is, the mean free pore volume, and in a similar manner to above, a scalar measure of anisotropy can be defined by:

$$\begin{aligned} a_{t}=\sqrt{\frac{3}{2}T_{ij}T_{ij}} \end{aligned}$$
(10)

If the distribution in Eq. 7 is isotropic, then \(a_{t}=0\) and the global orientation tensor \(M_{ij}\) must be an isotropic tensor with diagonal elements given by \(\frac{\left\langle V_{p}\right\rangle -V_{p,min}}{3}\). Sufian et al. [31] showed that the global orientation tensor was isotropic for a collection of static granular assemblies obtained experimentally and numerically.

Figure 9a shows that the anisotropy parameter \(a_{t}\approx 0\) in sheared granular assemblies, with some slight deviations away from perfect isotropy (as shown in the inset to Fig. 9a), but this deviation is two orders of magnitude less than the observed values for \(a_{p}\). Fig. 9b shows that the global orientation tensor is approximately isotropic with diagonal elements defined by the mean free pore volume. Note that this is not observed when considering the unmerged or merged pores separately. Therefore, deforming granular assemblies maintain isotropic pore volume distribution for all the simulations considered in this study. This suggest that when subject to external mechanical loading, particles adjust in a manner to maintain isotropic volume distribution, despite the induced anisotropy in pore orientation.

4 Pore shape as an indicator for the macroscopic density

Further insights into deformation characteristics can be gained by exploring pore shape properties. Figure 4a, b show that CP-L and CP-D specimens show similar pore anisotropy in loading, although the loose specimen undergoes contraction during shearing and the dense dilates (Fig. 1b). This difference in their volumetric behaviour can be captured by exploring pore shape.

Pore shape is defined using the shape factor, \(\beta \), in Eq. 2. Figure 10 plots the average shape factor throughout the two-way loading cycle. Both the complete collection of pores, and the \(\left\{ u,\,m\right\} \) partition are considered.

Fig. 10
figure 10

Average pore shape factor, \(\left\langle \beta ^{k}\right\rangle \), for the complete collection of pores and the \(\left\{ u,\,m\right\} \) partition in the CP-L and CP-D simulations. a Complete collection of pores b Unmerged and merged pores

Full size image

When comparing the CP simulations, Fig. 10a shows that the loose sample (CP-L) initially comprises more elongated pores (i.e. higher \(\left\langle \beta \right\rangle \)), while the dense sample (CP-D) contains more rounded pores (i.e. lower \(\left\langle \beta \right\rangle \)), when averaging over the complete collection of pores. This was noted in Schröder-Turk et al. [28] with regards to Voronoi cell shape in static assemblies of spheres, where it was suggested that elongated Voronoi cells contain more free volume and hence, represents a loose assembly. In the \(\left\{ u,\,m\right\} \) partition, Fig. 10b shows that smaller unmerged pores have more regular geometry, while larger merged pores are elongated. The observation of large elongated pores is also in good agreement with experimental observations by Oda et al. [23] on photoelastic disks.

Fig. 11
figure 11

Average pore shape factor, \(\left\langle \beta ^{k}\right\rangle \), for the complete collection of pores and the \(\left\{ u,\,m\right\} \) partition in constant volume shear tests (CV-D, SS-D)

Full size image

Moreover, Fig. 10 shows that \(\left\langle \beta \right\rangle \) (i.e. for the complete collection of pores) closely correlates with the void ratio response for the CP-L and CP-D simulation (Fig. 1b), suggesting that it is a good indicator of macroscopic density. This is confirmed in the results for the CV-D and SS-D simulations in Fig. 11, where \(\beta \) maintains a constant value, reflecting the constant volume constraint in these simulations. The constant shape factor is also observed in the \(\left\{ u,\,m\right\} \) partition for the CV-D and SS-D simulations. This strong correlation between shape factor and void ratio is illustrated in Fig. 12 and suggests that (averaged) pore shape characteristics represent a micro-scale indicator of the tendency of the assembly to contract or dilate. Nevertheless, it is important to recognise that at the scale of individual pores, there is a distribution in pore shape as shown in the inset to Fig. 12.

Fig. 12
figure 12

Relationship between average shape factor, \(\left\langle \beta \right\rangle \), and the macroscopic void ratio for all simulations. Note that a similarly strong correlation is noted for unmerged pores, \(\left\langle \beta ^{u}\right\rangle \), indicating the dominant contribution of unmerged pores. Inset: Distribution of pore shape factors in the CP-D simulation at \(\epsilon _{a}=5\%\) in the initial loading phase for the complete collection of pores (solid line), unmerged pores (dashed line) and merged pores (dotted line)

Full size image
Fig. 13
figure 13

Average shape factor of pores within certain ranges in elevation angle, \(\theta \), as measured from the horizontal. a CP-D and b CV-D

Full size image

The average shape factor \(\left\langle \beta \right\rangle \) can be viewed as a measure of shape anisotropy, while \(a_{p}\) provided a measure of orientational anisotropy of the granular assembly. Note that these two forms of anisotropy have opposing trends. The loose assembly (CP-L) exhibits a lower degree of orientational anisotropy (Fig. 4) but a higher degree of shape anisotropy compared to the dense assembly (CP-D). This suggests that deformation characteristics may be represented as a competition between shape and orientational anisotropy.

There is an interesting interplay between shape and orientation of pores when combining the results of the orientational analysis in Sect. 3 and the above shape analysis. Smaller unmerged pores are more rounded and align in the expansion direction, while larger merged pores are more elongated and align in the compression direction (schematically shown in Fig. 5). This is reflected in the directional averaged \(\beta \) in Fig. 13.

In the initial loading phase for the CP-D simulation (Fig. 13a), sub-horizontal pores (\(\theta =0^{\circ }-30^{\circ }\), perpendicular to the loading direction) are more rounded, while sub-vertical pores (\(\theta =60^{\circ }-90^{\circ }\)) are more elongated, and pores with \(\theta =30^{\circ }-60^{\circ }\) fall in between. As the loading direction is changed in the unloading phase, sub-horizontal pores become more elongated (as they are now aligned parallel to the loading direction), while sub-vertical pores become more rounded (and so on for the reloading phase). This demonstrates that pore shape properties are closely tied to the orientational anisotropy of the pore space, which is confirmed in the CV-D simulation (Fig. 13b). Although the average shape factor was constant in the CV-D simulation, there is a clear directional dependence, and in fact the trends noted for the CP-D simulation are equally applicable for the CV-D simulation.

5 Conclusion

This paper provides insights into the deformation characteristics in sheared granular assemblies from consideration of the orientation and shape properties of the pore space. This was explored using discrete element simulations for common geotechnical elemental shear tests including drained and undrained axisymmetric and simple shear modes. Individual pores were identified using the modified Delaunay tessellation [1], which provides a physically intuitive representation of the pore space. The modified Delaunay tessellation was applied at small strain increments throughout each two-way loading cycle. Properties of individual pores including their size, orientation and shape could be readily determined. The key insights into the deformation response in shearing granular assemblies are:

  1. 1.

    Average shape factor was a micro-scale indicator of macroscopic void ratio. The loose assembly comprised more elongated pores, while the dense assembly consisted of more rounded pores.

  2. 2.

    Local shear induced deformation anisotropy, where large pores are aligned in the direction of compression, while smaller pores are aligned perpendicular to the larger pores and in the direction of extension. This orthogonal preferential orientation of small and large pores can be related to the interparticle contacts along the edges of a pore.

  3. 3.

    There exists an interplay between pore shape, size and orientation, with smaller rounded pores aligning in the expansion direction, while larger elongated pores aligned in the compression direction. This suggests that the deformation response in sheared granular assemblies may be represented by a competition between shape and orientational anisotropy.

  4. 4.

    Macroscopic deformation response has a time lag, as demonstrated by larger levels of macroscopic shear strain required to mobilise pore anisotropy. This lag in the anisotropy response was also observed in DEM simulations reported by Zhao and Guo [36], where anisotropy in particle orientation (for non-spherical particles) evolved at a slower rate than the contact anisotropy. This highlights the importance of considering pore space anisotropy, in conjunction with contact network and particle orientation anisotropy, when describing the macroscopic response of granular materials.

  5. 5.

    Conventional definitions of critical state conditions (based on void ratio and stress state) can be complemented with pore space fabric measures. The pore anisotropy parameter in this study showed evidence of critical state characteristics and can be implemented into continuum-based models, such as Li and Dafalias [18]. However, further studies (including different particle size distribution and stress states) are required to confirm the uniqueness of this critical state.

  6. 6.

    The directional distribution of pore volume remained isotropic. This implied that in the compression direction, there were fewer larger pores, while in the expansion direction there were many smaller pores, and this effectively balanced to provide a net isotropic distribution of pore volume. This suggests that there is a constraint on the overall deformation, that is, particles rearrange to ensure isotropic volume distribution, but further studies are required to confirm this hypothesis.

These results demonstrate the importance of considering pore space characteristics, in particular the orientation and shape of pores, in understanding the deformation behaviour of granular materials. Ongoing research is exploring the incremental response of these characteristics within a single strain increment, in order to develop predictive capabilities or relating macroscopic properties such as dilatancy to micro-scale features of the pore space and interparticle contact network. Although the current study of evolving pore space characteristics has focused on shearing of monodisperse particle assemblies, the methods developed in this paper are directly applicable to polydisperse systems. Future studies should consider how particle size distribution affects the role of the pore space on deformation properties.