Quasi-static collapse of two-dimensional granular columns: insight from continuum modelling

Abstract

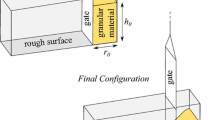
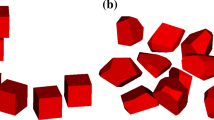
We investigate numerically the mechanism governing the quasi-static collapse of two-dimensional granular columns using a recently proposed continuum approach, the particle finite element method (PFEM), which inherits both the solid mathematical foundation of the traditional finite element method and the flexibility of particle methods in simulating ultra-large deformation problems. The typical collapse patterns of granular columns are reproduced in the PFEM simulation and the physical mechanism behind the collapse phenomenon is provided. The collapse processes obtained from the PFEM simulation are compared to experimental observations and discrete element modeling, where a satisfactory agreement is achieved. The effects of the macro density and friction angle of the granular matter, as well as the roughness of the wall surfaces on the quasi-static collapse, are also investigated in this paper. Furthermore, our simulations reveal new quasi-static collapse patterns, as supplements to the ones already observed in the experimental tests, due to the change of the roughness of the basal surface.

Appendix

1.1 Time discretisation

The momentum conservation equations (1) can be discretised using $\theta$-method [50] as:

$$\begin{aligned}&{\varvec{\nabla }}^\textsf {{\tiny T}}[ \theta _1{\varvec{\sigma }}_{n+1} + (1-\theta _1){\varvec{\sigma }}_n] + {\varvec{b}} = \rho \displaystyle \frac{{\varvec{v}}_{n+1}-{\varvec{v}}_n}{\varDelta t}, \end{aligned}$$

(10)

$$\begin{aligned}&\theta _2{\varvec{v}}_{n+1} + (1-\theta _2){{\varvec{v}}_n} = \displaystyle \frac{{\varvec{u}}_{n+1}-{\varvec{u}}_n}{\varDelta t}, \end{aligned}$$

(11)

where ${\varvec{v}}$ are velocities, subscripts n and $n+1$ refer to the known and new, unknown states, and $\varDelta t=t_{n+1}-t_n$ is the time step. Rearranging the above equations leads to

$$\begin{aligned}&{\varvec{\nabla }}^\textsf {{\tiny T}}{\varvec{\sigma }}_{n+1} + \tilde{\varvec{b}} = \tilde{\rho }\frac{\varDelta {\varvec{u}}}{\varDelta t^2}, \end{aligned}$$

(12)

$$\begin{aligned}&{\varvec{v}}_{n+1} = \displaystyle \frac{1}{\theta _2}\left[ \frac{\varDelta {\varvec{u}}}{\varDelta t} - (1-\theta _2){\varvec{v}}_n\right] , \end{aligned}$$

(13)

where $\varDelta {\varvec{u}} = {\varvec{u}}_{n+1}-{\varvec{u}}_n$ and

$$\begin{aligned} \tilde{\rho }= & {} \displaystyle \frac{\rho }{\theta _1\theta _2}, \end{aligned}$$

(14)

$$\begin{aligned} \tilde{\varvec{b}}= & {} \displaystyle \frac{1}{\theta _1}{\varvec{b}} + \tilde{\rho }\displaystyle \frac{{\varvec{v}}_n}{\varDelta t} + \displaystyle \frac{1-\theta _1}{\theta _1}{\varvec{\nabla }}^\textsf {{\tiny T}}\varvec{\sigma }_n, \end{aligned}$$

(15)

The natural boundary conditions (6) are approximated in an analogous manner leading to

$$\begin{aligned} \varvec{N}^\textsf {{\tiny T}}{\varvec{\sigma }}_{n+1} = \tilde{\varvec{t}},\,\text {on}\,S, \end{aligned}$$

(16)

where

$$\begin{aligned} \tilde{\varvec{t}} = \frac{1}{\theta _1}{\varvec{t}} - \frac{1-\theta _1}{\theta _1}{\varvec{N}}^\textsf {{\tiny T}} {\varvec{\sigma }}_n. \end{aligned}$$

(17)

Following [26], the above problem can be stated in terms of a min-max problem:

$$\begin{aligned} \begin{array}{lcl} \underset{\varDelta \varvec{u}}{\text {min}}~~\underset{(\varvec{\sigma },\varvec{r})_{n+1}}{\text {max~~}} &{}~&{} \langle \varvec{\sigma }_{n+1},\varvec{\nabla }(\varDelta \varvec{u})\rangle _V - \langle \tilde{\varvec{b}},\varDelta {\varvec{u}} \rangle _V - \langle \tilde{\varvec{t}},\varDelta {\varvec{u}}\rangle _S \\ &{}~&{} -\frac{1}{2}\varDelta t^2\langle {\varvec{r}}_{n+1},{\tilde{\rho }}{}^{-1}{\varvec{r}}_{n+1}\rangle _V + \langle {\varvec{r}}_{n+1},\varDelta {\varvec{u}}\rangle _V \\ \text {subject to} &{}~&{}F({\varvec{\sigma }}_{n+1}) \le 0 \end{array} \end{aligned}$$

(18)

on the basis of the Hellinger-Reissner variational principle. In above, ${\varvec{r}}_{n+1}$ are a set of variables interpreted as dynamic forces [26], and the notation

$$\begin{aligned} \langle {\varvec{x}},{\varvec{y}}\rangle _A = \int _A{\varvec{x}}^\textsf {{\tiny T}}\varvec{y}\,\text {d} A \end{aligned}$$

(19)

is utilised. The equivalence between the optimisation problem (18) and the governing equations at hand is established by demonstrating that the Euler-Lagrange equations associated with (18) indeed reproduce the governing equations [26].

1.2 Spatial discretisation

Using the standard finite element notation, the following approximations

$$\begin{aligned}&{\varvec{\sigma }}(\varvec{x}) \approx {\varvec{N}}_\sigma \hat{\varvec{\sigma }}, \end{aligned}$$

(20)

$$\begin{aligned}&{\varvec{r}}({\varvec{x}}) \approx \varvec{N}_r\hat{\varvec{r}}, \end{aligned}$$

(21)

$$\begin{aligned}&{\varvec{u}}({\varvec{x}}) \approx \varvec{N}_u\hat{\varvec{u}}, \end{aligned}$$

(22)

$$\begin{aligned}&{\varvec{\nabla }} {\varvec{u}} \approx \varvec{ B}_u\hat{\varvec{u}}, \end{aligned}$$

(23)

are introduced for the state variables, where $\hat{\varvec{\sigma }}$, $\hat{\varvec{r}}$ and $\hat{\varvec{u}}$ are the nodal variables, $\varvec{N}$ matrices contain the shape functions, and $\varvec{B}_u = \varvec{\nabla } \varvec{N}_u$. Substituting the above approximations into the variational principle (18) results in the following discrete principle:

$$\begin{aligned} \begin{array}{lcl} \underset{\varDelta \hat{\varvec{u}}}{\text {min}}~~\underset{(\hat{\varvec{\sigma }},\hat{\varvec{r}})_{n+1}}{\text {max~~}} &{}~&{} \hat{\varvec{\sigma }}_{n+1}^\textsf {{\tiny T}}\varvec{B}\varDelta \hat{\varvec{u}} - {\varvec{f}}^\textsf {{\tiny T}}\varDelta \hat{\varvec{u}}\\ &{}~&{}-\frac{1}{2}\varDelta t^2\hat{\varvec{r}}_{n+1}^\textsf {{\tiny T}}\varvec{D}\hat{\varvec{r}}_{n+1}+ \hat{\varvec{r}}_{n+1}^\textsf {{\tiny T}}\varvec{A}\varDelta \hat{\varvec{u}} \\ \text {subject to} &{}~&{} F(\hat{\varvec{\sigma }}_{n+1}^j) \le 0,~~j=1,\ldots ,n_\sigma \end{array} \end{aligned}$$

(24)

where $n_\sigma$ is the number of Gauss integration points, and

$$\begin{aligned}&{\varvec{B}} = \int _V \varvec{N}_\sigma ^\textsf {{\tiny T}}{\varvec{B}_u}\,\text {d} V, \end{aligned}$$

(25)

$$\begin{aligned}&{\varvec{f}} = \int _V \varvec{N}_u^\textsf {{\tiny T}}\tilde{\varvec{b}}\,\text {d} V + \int _S \varvec{N}_u^\textsf {{\tiny T}}\tilde{\varvec{t}}\,\text {d} S, \end{aligned}$$

(26)

$$\begin{aligned}&{\varvec{D}} = \int _V \varvec{N}_r^\textsf {{\tiny T}}\tilde{\rho }{}^{-1}\varvec{N}_\sigma \,\text {d} V, \end{aligned}$$

(27)

$$\begin{aligned}&{\varvec{A}} = \int _V \varvec{N}_u^\textsf {{\tiny T}} {\varvec{N}_r}\,\text {d} V. \end{aligned}$$

(28)

Then, solving the minimisation part of (24) gives a maximisation problem as:

$$\begin{aligned} \begin{array}{lcl} \underset{(\hat{\varvec{\sigma }},\hat{\varvec{r}})_{n+1}}{\text {maximise}} &{}~&{} -\frac{1}{2}\varDelta t^2\hat{\varvec{r}}_{n+1}^\textsf {{\tiny T}}\varvec{D}\hat{\varvec{r}}_{n+1} \\ \text {subject to} &{}~&{}\varvec{B}^\textsf {{\tiny T}}\hat{\varvec{\sigma }}_{n+1} + \varvec{A}^\textsf {{\tiny T}}\hat{\varvec{r}}_{n+1} = \varvec{f}\\ &{}~&{} F(\hat{\varvec{\sigma }}_{n+1}^j) \le 0,~~j=1,\ldots ,n_\sigma \end{array} \end{aligned}$$

(29)

At this stage, the contact constrains (4) are imposed on all potential contact nodes (i.e. mesh nodes located on the boundaries), which leads to a final problem of the type:

$$\begin{aligned} \begin{array}{lcl} \underset{(\hat{\varvec{\sigma }},\hat{\varvec{r}},p_j)_{n+1}}{\text {maximize}} &{}~&{} -\frac{1}{2}\varDelta t^2\hat{\varvec{r}}_{n+1}^\textsf {{\tiny T}}\varvec{D}\hat{\varvec{r}}_{n+1}-\sum _{j=1}^{n_c}{ g_{0j} p_j} \\ \text {subject to} &{}~&{}\varvec{B}^\textsf {{\tiny T}}\hat{\varvec{\sigma }}_{n+1} + \varvec{A}^\textsf {{\tiny T}}\hat{\varvec{r}}_{n+1} + {\varvec{E}}^\textsf {{\tiny T}}\varvec{\rho } = \varvec{f}\\ &{}~&{} F(\hat{\varvec{\sigma }}_{n+1}^i) \le 0,~~i=1,\ldots ,n_\sigma \\ &{}~~&{} p_j = -\varvec{n}^\textsf {{\tiny T}}\varvec{\rho }_j,~~~j=1,\ldots , n_c \\ &{}~~&{} q_j = -\hat{\varvec{n}}^\textsf {{\tiny T}}\varvec{\rho }_j \\ &{}~&{} |q_j| - \mu p_j \le 0 \end{array} \end{aligned}$$

(30)

where $\varvec{\rho } = (\rho _1,\rho _2)^\textsf {{\tiny T}}$ are the nodal forces, $\varvec{n}=(n_1,n_2)^\textsf {{\tiny T}}$ and $\hat{\varvec{n}} = (-n_2,n_1)^\textsf {{\tiny T}}$ are the normal and the tangential of the rigid boundary, $\varvec{E}$ is an index matrix of zeros and ones, and $n_c$ is the number of potential contacts.

The above problem can be transformed into a standard form of the second-order cone program (SOCP) and then solved using the high performance optimization solver MOSEK [38]. The transformation of (30) into SOCP standard form is straightforward and has been documented in [40]. In the course of solving the problem, the kinematic variables (displacement increments and plastic multipliers) are recovered as the dual variables, or Lagrange multipliers, associated with the discrete equilibrium constraints.