Skip to main content
SpringerLink
Log in

Deconvolution of a Cumulative Distribution Function with Some Non-standard Noise Densities

  • Published:
Vietnam Journal of Mathematics Aims and scope Submit manuscript

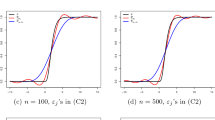
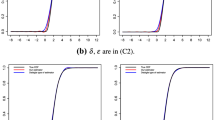
Abstract

Let X be a continuous random variable having an unknown cumulative distribution function F. We study the problem of estimating F based on i.i.d. observations of a continuous random variable Y from the model Y = X + Z. Here, Z is a random noise distributed with known density g and is independent of X. We focus on some cases of g in which its Fourier transform can vanish on a countable subset of ℝ. We propose an estimator \(\hat F\) for F and then investigate upper bounds on convergence rate of \(\hat F\) under the root mean squared error. Some numerical experiments are also provided.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Butucea, C., Comte, F.: Adaptive estimation of linear functionals in the convolution model and applications. Bernoulli 15, 69–98 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  2. Cordy, C.B., Thomas, D.R.: Deconvolution of a distribution function. J. Am. Stat. Assoc. 92, 1459–1465 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  3. Comte, F., Lacour, C.: Data-driven density estimation in the presence of additive noise with unknown distribution. J. R. Stat. Soc. Ser. B 73, 601–627 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  4. Devroye, L.: Consistent deconvolution in density estimation. Can. J. Stat. 17, 235–239 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  5. Diggle, P.J., Hall, P.: A Fourier approach to nonparametric deconvolution of a density estimate. J. R. Stat. Soc. Ser. B 55, 523–531 (1993)

    MathSciNet  MATH  Google Scholar 

  6. Delaigle, A., Meister, A.: Nonparametric function estimation under Fourier-oscillating noise. Stat. Sin. 21, 1065–1092 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  7. Dattner, I., Goldenshluger, A., Juditsky, A.: On deconvolution of distribution functions. Ann. Stat. 39, 2477–2501 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  8. Dattner, I., Reiser, B.: Estimation of distribution functions in measurement error models. J. Stat. Plan. Inference 143, 479–493 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  9. Dattner, I.: Deconvolution of P(X < Y ) with supersmooth error distributions. Stat. Probab. Lett. 83, 1880–1887 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  10. Fan, J.: On the optimal rates of convergence for nonparametric deconvolution problems. Ann. Stat. 19, 1257–1272 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  11. Gil-Pelaez, J.: Note on the inversion theorem. Biometrika 38, 481–482 (1951)

    Article  MathSciNet  MATH  Google Scholar 

  12. Gaffey, W.R.: A consistent estimator of a component of a convolution. Ann. Math. Stat. 30, 198–205 (1959)

    Article  MathSciNet  MATH  Google Scholar 

  13. Hall, P., Meister, A.: A ridge-parameter approach to deconvolution. Ann. Stat. 35, 1535–1558 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  14. Kawata, T.: Fourier Analysis in Probability Theory. Academic Press, New York (1972)

    MATH  Google Scholar 

  15. Kappus, J., Mabon, G.: Adaptive density estimation in deconvolution problems with unknown error distribution. Electron. J. Stat. 8, 2879–2904 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  16. Levin, B.: Lectures on Entire Functions. Translations of Mathematical Monographs, vol. 150. American Mathematical Society, Providence (1996)

    Google Scholar 

  17. Meister, A.: Deconvolving compactly supported densities. Math. Methods Stat. 16, 63–76 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  18. Meister, A.: Deconvolution from Fourier-oscillating error densities under decay and smoothness restrictions. Inverse Probl. 24, 015003 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  19. Neumann, M.H., Hössjer, O.: On the effect of estimating the error density in nonparametric deconvolution. J. Nonparametr. Stat. 7, 307–330 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  20. Pensky, M.: Minimax theory of estimation of linear functionals of the deconvolution density with or without sparsity. Ann. Stat. 45, 1516–1541 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  21. Trong, D.D., Phuong, C.X., Tuyen, T.T., Thanh, D.N.: Tikhonov’s regularization to the deconvolution problem. Commun. Stat. Theory Methods 43, 4384–4400 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  22. Trong, D.D., Phuong, C.X.: Ridge-parameter regularization to deconvolution problem with unknown error distribution. Vietnam. J. Math. 43, 239–256 (2015)

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

We would like to thank the reviewers for their kind and careful reading of the paper and for helpful comments and suggestions which led to this improved version.

Funding

This research is funded by the Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number 101.02-2016.26.

Author information

Authors and Affiliations

  1. Faculty of Mathematics and Computer Science, University of Science, Vietnam National University Ho Chi Minh City, No. 227 Nguyen Van Cu Street, Ward 4, District 5, Ho Chi Minh City, Vietnam

    Dang Duc Trong

  2. Faculty of Mathematics and Statistics, Ton Duc Thang University, No. 19 Nguyen Huu Tho Street, Tan Phong Ward, District 7, Ho Chi Minh City, Vietnam

    Cao Xuan Phuong

Authors
  1. Dang Duc Trong
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Cao Xuan Phuong
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Cao Xuan Phuong.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Trong, D.D., Phuong, C.X. Deconvolution of a Cumulative Distribution Function with Some Non-standard Noise Densities. Vietnam J. Math. 47, 327–353 (2019). https://doi.org/10.1007/s10013-018-0308-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10013-018-0308-9

Keywords

Mathematics Subject Classification (2010)

Search

Navigation