Weight-scheduling for linear time-variant model predictive wind turbine control toward field testing

Abstract

Modern multi-megawatt wind turbines require powerful control algorithms which consider several control objectives at the same time and respect process constraints. Model predictive control (MPC) is a promising control method and has been a research topic for years. So far, very few studies evaluated MPC algorithms in field tests. This work aims to prepare a real-time MPC system for a full-scale field test in a 3 MW wind turbine. To this end, we introduce a weight-scheduling scheme for a linear time-variant MPC in order to ensure control operation over the entire operating range from the partial to the full load range. We use a rapid control prototyping process, in particular with comprehensive software-in-the-loop (SiL) tests, in order to design and validate the MPC system for the field test.

In this contribution, we present the implementation of the linear time-variant MPC with weight-scheduling to be tested in the field test. With the weight-scheduling for the optimization problem inside the MPC, we achieved good performance over the entire operating range of the wind turbine. In the SiL tests, the proposed MPC algorithm achieved loads, comparable to the baseline controller of the wind turbine and improved the reference tracking of the power output and the rotational speed. The proposed linear time-variant MPC with weight-scheduling is fully validated in the presented software-in-the-loop tests and is ready for full-scale field test in the 3 MW wind turbine. We present the experimental field test results of the introduced MPC system in a separated contribution.

1 Introduction

In the last decades, wind turbines (WTs) have been steadily growing in size. This results in more flexible components that are increasingly sensitive to loads. Active load reduction already became a major control objective in WT controllers [1]. With larger wind turbines, also the complexity of the dynamic behavior increases, leading also to a more difficult control behavior [1,2,3]. Therefore, multi objective control methods, like model predictive wind turbine control, have been studied throughout the past to further improve the control performance for new WT prototypes. Up to now, the focus of studies about MPC for WTs was rather on simulation studies than on experimental tests [1]. In contrast to previously conducted research, this paper will show the design of a real-time implementation of an MPC which has been tested in the field on a 3 MW WT in July 2020. The structural and functional integration of the control strategy into the wind turbine’s automation system is shown in [4] and the associated results of the full-scale field test are presented in our companion paper [5].

1.1 Research context and objectives

To meet the challenge of larger WTs and their increasing complexity of control objectives, many modern control methodologies were investigated. Due to its ability to intrinsically handle multi objective control tasks and constraints, MPC has been investigated [1]. For linear MPC, the operation in partial load region (region II) and full load region (region III), and especially the transition between partial and full load region is challenging [1]. In various simulation studies up to wind tunnel tests [6], the advantage of MPC over state of the art control (SC) concepts was demonstrated [1]. To the author’s knowledge only [7] describes a full-scale field test of trailing edge flaps on a Vestas V27 WT with a frequency weighted MPC. However, the rated power of this WT with 225 kW is much lower than the multi-MW dimensions of most state of the art WTs.

One major issue in field tests is the performance of the control method in all operating points. Besides the full load region, the control algorithm has to work properly below rated wind speed in the partial load region as well as in the transition range between the partial and full load region. For linear MPC for WTs there has to be taken some effort to operate not only on above rated wind speeds only [1]. Because wind conditions in (onshore) sites are barely found exclusively in this range, the controller must operate the WT with high performance, also when the wind speed drops below rated.

Based upon the authors’ studies, one major issue that significantly affects MPC operation over the entire operating range is that the dynamical behavior and the sensitivity of the control actions significantly change when transitioning from the partial to the full load region.

Nonlinear MPC (NMPC) can face this problem by means of nonlinear models and constraints, which allow the controller to be aware of the varying behavior [1,2,3]. However, the computational burden of these control algorithms can vary between control steps and guaranteeing convexity of the optimization problem is challanging [2, 8], which is an obstacle performing these algorithms on programmable logic controllers (PLC). To circumvent these obstacles, we investigate how a linear time-variant (LTV) MPC [4] can be extended, to be suitable in all operational conditions.

1.2 Research questions

When operating a WT with linear MPC, the prediction model is adapted to the operating point [9]. With this adaption, the sensitivities of the control objectives to the control actions vary. The wider the operating range of the controller is the greater this variation becomes. Usually, these sensitivities vary too much so that an adaption of the prediction model is required for robust performance. This leads to the first research question:

• 1 How can an LTV-MPC operate in both partial and full load wind conditions with high performance?

Compared to the so-called baseline controller (BC), a SC, which usually operated the WT, no additional mechanical loads should be induced during field tests in order to prevent any structural damage. Therefore, its performance related to the load mitigation of the WT should be comparable to the BC currently used in the WT. In this case, the BC is a state of the art single-input single-output PID controller that the operator of the WT, W2E Wind to Energy GmbH ² currently uses [10]. The second research question therefore is:

• 2 Which different mechanical loads does an LTV-MPC induce compared to a state of the art industrial WT controller?

To answer the first research question, we propose a weight-scheduling scheme within the MPC algorithm to cope with the varying sensitivities of the control objectives to the control actions and analyze the loads occuring in the wind conditions in the partial and full load range. The aim of this publication is to show that the proposed weight-scheduling approach ensures an MPC operation in the entire operating range and enables field testing of the MPC in the real WT.

The paper is organized as follows. Sect. 2 introduces the proposed MPC structure with its reduced order prediction model, the optimization problem and the weight-scheduling approach. In Sect. 3, we describe the WT used in the field tests and the simulation setup for the presented results. In Sects. 4 and 5, we describe and discuss the simulation results. Sect. 6 concludes the paper and explains potential future research questions.

2 Model predictive control with weight-scheduling

In modern WT control during power production, there are two operational regions [8] with different major control objectives. In the partial load region, the objective is to produce as much energy as can be extracted from the wind. In the full load region, when the nominal rotational speed is reached and the nominal power can be extracted from the wind, the objective is to keep the rotational speed and the power output constant at their rated values. During the transition between the regions, the nominal rotational speed is reached, but the nominal power is not. In SC, there are different controller parametrizations for these regions present. Also the control of the pitch usually is not used in the partial load regions.

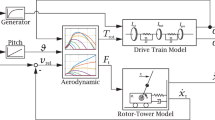
The MPC formulation proposed here gives a formulation for the complete operational range by scheduling the weights (so-called weight-scheduling) depending on the operating point. The MPC uses a reduced order dynamical model to predict the WT’s behavior and to optimize the control variables with regard to the control goals. The structure of the closed loop with the MPC system consisting of MPC and an Extended Kalman Filter (EKF) is shown in Fig. 1a. To predict the WT’s behavior, the MPC needs the WT’s state vector, which cannot be measured. Therefore, we use an EKF in order to estimate these states.

Fig. 1

Structure of the closed loop with MPC, EKF and wind turbine, and overview of the reduced-order model with its components and in- and outputs. a Controller structure. b Structure of the reduced-order model [11]

This section introduces the MPC formulation, starting with the employed reduced-order WT model and its discretization. Afterwards, the general formulation of the optimization problem is given, which solves the MPC. Finally, we specify the formulation for the scheduled weights, to ensure an MPC operation for all wind speeds. For detailed information about the EKF, we refer to [9].

2.1 Reduced order prediction model

MPC needs a dynamic prediction model of the controlled process. The process on how to choose the model is explained in [9] and [11] in detail. The applied structure of the prediction model with its components, in- and outputs is shown in Fig. 1b. The submodels are the linear models of the drive train and the fore-aft dynamic, static maps of aerodynamic coefficients and the linear actor dynamics. The state space formulations for the drive train (1) and fore-aft dynamics (2) are given as follows

$$\dot{\boldsymbol{x}}_{\mathrm{dt}}=A_{\mathrm{dt}}\boldsymbol{x}_{\mathrm{dt}}+B_{\mathrm{dt}}\boldsymbol{u}_{\mathrm{dt}},$$

(1)

$$\dot{\boldsymbol{x}}_{\mathrm{fa}}=A_{\mathrm{fa}}\boldsymbol{x}_{\mathrm{fa}}+B_{\mathrm{fa}}F_{t}.$$

(2)

The state vectors are given by $\boldsymbol{x}_{\mathrm{dt}}=\left(\begin{array}{ccccc} \omega _{\mathrm{rot}} & \omega _{\mathrm{hub}} & \omega _{\mathrm{gen}} & \Updelta \varphi _{\mathrm{rh}} & \Updelta \varphi _{\mathrm{rh}} \end{array}\right)^{T}$ and $\boldsymbol{x}_{\mathrm{fa}}=\left(\begin{array}{cccc} x_{t} & \dot{x}_{t} & \varphi _{b} & \dot{\varphi }_{b} \end{array}\right)^{T}$. The drive train inputs are given as $\boldsymbol{u}_{\mathrm{dt}}=\left(\begin{array}{cc} T_{\mathrm{rot}} & T_{\mathrm{gen}} \end{array}\right)^{T}$—with the aerodynamic torque $T_{\mathrm{rot}}$ and the generator torque $T_{\mathrm{gen}}$, which act on the rotor and the generator and accelerate the drive train, respectively. The inertias ($I_{\mathrm{rot}}$, $I_{\mathrm{hub}}$ and $I_{\mathrm{gen}}$; compare Fig. 1b) of the rotor, hub and generator rotate with the speeds $\omega _{i}$. The twists between the inertias are given by $\Updelta \varphi _{\mathrm{rh}}$ and $\Updelta \varphi _{\mathrm{hg}}$. The thrust force $F_{\mathrm{t}}$ acts onto the rotor blades and deflects them by the angle $\varphi _{b}$, and the tower by $x_{t}$. Details how to derive the state matrices $A_{i}$ and $B_{i}$ are given in [9]. With this formulation, the deviations from an operating point are given; the names of the absolute value are given in Table 1. The absolute values of the state variables are denoted by capital letters. Their deviations from an operating point $\boldsymbol{X}_{0}$ are defined by $\boldsymbol{x}=\boldsymbol{X}-\boldsymbol{X}_{0}$.

Table 1 Overview of systems states and corresponding symbols [9]

The aerodynamic torque $T_{\mathrm{rot}}$ and the thrust force $F_{t}$ are derived by (3) and (4) and are calculated using the air density $\rho$ and the rotor diameter $R_{\mathrm{rot}}$. The aerodynamic power and thrust coefficients, $c_{P}$ and $c_{T}$, are given by static maps and depend on the pitch angle $\theta$, the rotor speed $\Omega _{\mathrm{rot}}$ and the relative wind speed to the rotor $v_{\mathrm{rel}}$.

$$T_{\mathrm{rot}}=0.5\pi \rho R_{\mathrm{rot}}^{2}v_{\mathrm{rel}}^{3}\,\Omega _{\mathrm{rot}}^{-1}c_{\mathrm{P}}\left(\uptheta ,\Omega _{\mathrm{rot}},v_{\mathrm{rel}}\right)$$

(3)

$$F_{\mathrm{t}}=0.5\pi \rho R_{\mathrm{rot}}^{2}v_{\mathrm{rel}}^{2}\,c_{\mathrm{T}}\left(\uptheta ,\Omega _{\mathrm{rot}},v_{\mathrm{rel}}\right).$$

(4)

Due to nonlinear static maps $c_{P}$ and $c_{T}$, exemplarily given for $c_{\mathrm{P}}$ in Fig. 2, the dynamic model is nonlinear. The lines of the zero gradients $\partial c_{\mathrm{P}}/\partial \theta$ over the pitch angle and $\partial c_{\mathrm{P}}/\partial \lambda$ over the tip speed ratio $\lambda$ with $\begin{array}{c} \uplambda =\left(\Omega _{\mathrm{rot}}R_{\mathrm{rot}}\right)/v_{\mathrm{rel}} \end{array}$ show that these gradients particularly change their signs depending on the operating point. The controller should avoid the stall region with small tip speed ratios and pitch angles. Here, the sensitivity of the power and hence the rotor torque $T_{\mathrm{rot}}$ to the pitch angle $\theta$ differs significantly from the desired operating region.

Fig. 2

Map of $c_{\mathrm{P}}$ and lines of zero gradients

To further use this model in an LTV-MPC, the dynamic description is set up in state space with the absolute state vector $\boldsymbol{X}$ given in Table 1, and the inputs $\boldsymbol{U}$. The input values are the manipulated variables, the generator torque $T_{\mathrm{gen}}$ and the pitch angle rate $\dot{\theta }$.

2.2 Linear time-variant prediction model

For setting up the prediction model, we linearize and discretize the system model introduced in Sect. 2.1. Therefore, the nonlinear parts of the model are linearized using the first order Taylor approximation:

$$F_{\mathrm{t}}\cong F_{\mathrm{t}0}+\left.\frac{\partial F_{\mathrm{t}}}{\partial \Omega _{\mathrm{rot}}}\right| _{0}\dot{\varphi }_{\mathrm{rot}}+\left.\frac{\partial F_{\mathrm{t}}}{\partial \theta }\right| _{0}\vartheta +\left.\frac{\partial F_{\mathrm{t}}}{\partial v_{\mathrm{rel}}}\right| _{0}v_{\mathrm{rel}}$$

(5)

$$T_{\mathrm{rot}}\cong T_{\mathrm{rot},0}+\left.\frac{\partial T_{\mathrm{rot}}}{\partial \Omega _{\mathrm{rot}}}\right| _{0}\dot{\varphi }_{\mathrm{rot}}+\left.\frac{\partial T_{\mathrm{rot}}}{\partial \theta }\right| _{0}\vartheta +\left.\frac{\partial T_{\mathrm{rot}}}{\partial v_{\mathrm{rel}}}\right| _{0}v_{\mathrm{rel}}.$$

(6)

The WT controller only operates for positive values of wind speed $V$, and rotational speed $\Upomega$. Especially for the power coefficient $c_{P}$, there are states where its partial derivative $\partial c_{P}/\partial \theta$ can either be positive or negative or even be zero. Particularly in the partial load region, the control objective is to maximize the power output, which corresponds to $c_{P}=c_{P,\max }$, and thus its derivatives become zero.

Afterwards, the discrete-time formulation can be derived in the form of:

$$\boldsymbol{x}_{k+1}=\boldsymbol{A}_{k}\boldsymbol{x}_{k}+\boldsymbol{B}_{k}\boldsymbol{u}_{k}+\dot{\boldsymbol{X}}_{k,\mathrm{OP}}$$

(7)

$$\boldsymbol{y}_{k}=\boldsymbol{C}_{k}\boldsymbol{x}_{k}+\boldsymbol{D}_{k}\boldsymbol{u}_{k},$$

(8)

with:

$$\boldsymbol{y}=\left(\begin{array}{cccc} \omega _{\mathrm{gen}} & p_{\mathrm{el}} & \ddot{x}_{t} & \vartheta \end{array}\right)^{T};\boldsymbol{u}=\left(\begin{array}{cc} \dot{\vartheta } & \tau _{\mathrm{gen}} \end{array}\right)^{T}.$$

(9)

The values of $\boldsymbol{x}_{k}$, $\boldsymbol{u}_{k}$ and $\boldsymbol{y}_{k}$ have very different magnitudes. To simplify the selection of the weights, the system matrices $\boldsymbol{A}_{k}$, $\boldsymbol{B}_{k}$, $\boldsymbol{C}_{k}$ and $\boldsymbol{D}_{k}$ also include scaling factors introduced in [9]. This enshures that the states, inputs and outputs have values of the same magnitude. The inputs of the system $\boldsymbol{u}_{k}$ are the command values for the actuators which are the pitch angle rate $\dot{\vartheta }$ and the generator torque $\tau _{\mathrm{gen}}$. The output values $\boldsymbol{y}_{k}$ (9) are the controlled variables, in detail the generator speed $\omega _{\mathrm{gen}}$, the produced electrical power output $p_{\mathrm{el}}$ and the tower top acceleration $\ddot{x}_{t}$ are the primary control objectives. Furthermore, additional control objectives become relevant in partial load operation, so we add the pitch angle $\vartheta$ also as controlled variable.

2.3 Cost function and optimization problem

The MPC determines its optimal manipulated variables by minimizing a cost function in which the control objectives are weighted against each other.

$$J=\left\| \boldsymbol{y}\left(\cdot |k\right)-y_{\mathrm{ref}}\left(\cdot |k\right)\right\| _{Q\left(\boldsymbol{y}\left(k\right)\right)}^{2}+\lambda \left(\left\| \Updelta \boldsymbol{u}\left(\cdot |k\right)\right\| _{R_{\Updelta u}\left(y\left(\boldsymbol{k}\right)\right)}^{2}+\left\| \boldsymbol{u}\left(\cdot |k\right)\right\| _{R_{u}\left(y\left(\boldsymbol{k}\right)\right)}^{2}\right)$$

(10)

with:

$$\boldsymbol{u}\left(k+i+1|k\right)=\boldsymbol{u}\left(k+i|k\right)+\Updelta \boldsymbol{u}\left(k+i|k\right)$$

(11)

We formulate a reference tracking MPC with the cost function $J$ (10), which consists of two parts. The first part of the cost function $J$ is described by the deviations of the output values $\boldsymbol{y}$ from the references $\boldsymbol{y}_{\mathrm{ref}}$. Additionally, adjusting the actuators result in energy consumption and thereby produce costs. This is considered in the second part of the cost function which penalize the changing command values $\Updelta \boldsymbol{u}$ and the actual command values $\boldsymbol{u}$ (11). So optimally, the MPC tracks the reference and needs a minimum amount of command energy.

The different control objectives and command values are weighted against each other by means of the weighting matrices $\boldsymbol{Q}$ and $R_{i}$ (12)–(13), where both matrices are diagonal with entries $q_{i}$ and $r_{i}$ (10), respectively. Additionally, these matrices depend on the plant’s actual output $\boldsymbol{y}$ as shown in Sect. 2.2. The weighting parameter $\lambda$ determines how much the control effort is weighted compared to the control objectives.

$$\boldsymbol{Q}\left(\boldsymbol{y}\left(k\right)\right)=\text{diag}\left(\begin{array}{ccc} q_{1}\left(\boldsymbol{y}\left(k\right)\right) & \cdots & q_{n}\left(\boldsymbol{y}\left(k\right)\right) \end{array}\right)$$

(12)

$$\boldsymbol{R}_{i}\left(\boldsymbol{y}\left(k\right)\right)=\text{diag}\left(\begin{array}{ccc} r_{i,1}\left(\boldsymbol{y}\left(k\right)\right) & \cdots & r_{i,m}\left(\boldsymbol{y}\left(k\right)\right) \end{array}\right)$$

(13)

With these definitions made, the MPC optimizes the trajectory of control actions. Therefore, the system’s output trajectory $\boldsymbol{y}\left(\cdot |k\right)$ is predicted based on the actual state at time step $k$ and the trajectory of controlled variables $\Updelta \boldsymbol{u}(\cdot |k)$ are optimized to minimize the cost function $J$ with respect to linear constraints

$$\Updelta \boldsymbol{u}_{\mathrm{opt}}\left(\cdot |k\right)=\underset{\Updelta \boldsymbol{u}\left(\cdot |k\right)}{\text{argmin}}J\left(\Updelta \boldsymbol{u}\left(\cdot |k\right)\right)$$

(14)

$$\boldsymbol{u}_{\min }\leq \boldsymbol{u}\leq \boldsymbol{u}_{\max }$$

(15)

$$\Updelta \boldsymbol{u}_{\min }\leq \Updelta \boldsymbol{u}\leq \Updelta \boldsymbol{u}_{\max }$$

(16)

$$\boldsymbol{A}_{n}\Updelta \boldsymbol{u}\left(\cdot |k\right)-\boldsymbol{b}_{n}\leq 0.$$

(17)

As there are constraints regarding the inputs and states, the optimization is subject to Eqs. 15–17 with the constraint matrices $\boldsymbol{A}_{n}$ and $\boldsymbol{b}_{n}$. Different quadratic program solvers such as qpOASES can solve the optimization problem [13].

2.4 Weight-scheduling

As shown in Sect. 2.2 for the linearization, the WT dynamics vary during operation. Especially in the partial load region, when operating near the optimal $c_{P}=c_{P,\max }$, the sensitivity of the system to pitch actions is small. In this term, to gain even a small effect onto the rotor torque, the pitch angle has to be actuated strongly. In MPC with fixed weights, this would finally lead to small pitch actions due to less additional cost. In full load region, the sensitivity of the WT to the pitch angle has smaller variations.

Also, the linear MPC only predicts the system’s behavior with a linearized model and is thus not aware of the sensitivities vary over the outputs $y_{i}$. When using an LTV-MPC for wind turbine control, it may be advantageous to adjust the weights depending on the operating point. To tackle these problems, we suggest varying the values for the weights $q_{i}$ depending on the actual values of the controlled variables $y_{j}$, whose sensitivity is strongly affected by the operating point. Therefore, for each varying weight a pair of limits is chosen

$$q_{i}\left(\boldsymbol{y}\left(k\right)\right)=q_{i,0}+\left(\frac{y_{j}-y_{j,0}}{y_{j,1}-y_{j,0}}\right)^{2}\left(q_{i,1}-q_{i,0}\right).$$

(18)

An exemplary curve of a scheduled weight is given in Fig. 3. The weights are scheduled within the range defined by the minimum $q_{0}$ and the maximum $q_{1}$. Both correspond to controlled variables $y_{0}$ and $y_{1}$. The quadratic form allows weights of control objectives, which are only active in certiain operation regions to smoothly increase. This is especially useful when operating points near the stall region are reached.

Fig. 3

Curve of weight-scheduling

Compared to an LTV-MPC tuned for above rated wind speed, all scheduled weights have new tuning parameters. The region of weight-scheduling between the values $(y_{0},y_{1})$, can be chosen as the region, where the sensitivities of the model start varying significantly. The first weight $q_{o}$ is taken from the existing MPC [9] formulation, and the second weight $q_{1}$ is tuned for the MPC to perform in the critical operational regions as well.

An example: The control objectives are tracking the electrical power and the rated WT speed. Both respond to the generator torque, but in opposite directions. In regions near the optimal power coefficient, the sensitivity of the power to a variation in the rotor speed is small. This sensitivity changes when the rotor speed is changed, but as the prediction model is linear the MPC cannot consider this. Here, the sensitivity varies with the operating point. To avoid that the MPC increases the generator torque to track the power reference and decelerates the WT, the weight of the rotor speed $q_{\omega }$ is increased or the weight of the power $q_{p}$ is decreased. As this effect is minor in full load region, we suggest adapting this weight depending on the wind speed.

2.5 Avoiding stall region

As shown in Sect. 2.2, the sensitivity of the aerodynamic torque $T_{\mathrm{rot}}$ to the pitch angle $\theta$ varies over the operation range. When a gust effects the WT, the stall region can be reached and even the directions of action of the speed and pitch angle to the power coefficient reverse. This can result in an MPC action with the opposite direction of which is needed to leave the stall region. In the full load region, this is not as critical as in the partial load region, because the operating points usually are far from the stall region. In the partial load region, the WT operates near the optimal $c_{P}$ and this effect becomes critical.

To avoid that the MPC maneuvers into the stall region, we suggest to use an additional control objective. This can ensure that the MPC maneuvers out of the stall region, after the wind conditions lead into it. Therefore, we added the pitch angle $\theta$ as additional controlled variable to the output vector $\boldsymbol{y}$ (see (9)).

For the pitch angle $\theta$, there is a critical value $\theta _{\text{Crit}}\left(\Omega _{\mathrm{rot}},v_{\mathrm{rel}}\right)$, where $\partial c_{\mathrm{P}}/\partial \theta \leq 0$ holds. This critical pitch angle depends on the actual rotor and wind speed. Thus, we choose the reference $\theta _{\mathrm{ref}}>\theta _{\text{Crit}}$ for the pitch angle. This control objective should only be active if $\theta >\theta _{\mathrm{ref}}\left(\Omega _{\mathrm{rot}},v_{\mathrm{rel}}\right)$ holds for the pitch angle. Therefore, the weight of this control objective $q_{{\theta _{\text{Crit}}}}$ is scheduled between $\theta _{\mathrm{ref}}\left(\Omega _{\mathrm{rot}},v_{\mathrm{rel}}\right)$ and $\theta _{\min }$ and the weight value should be chosen so that its impact onto the cost function is greater than the impact of the pitch angle onto the power.

3 Wind turbine model and simulation setup

The WT considered in this study is based on the 3 MW WT “W2E-120/3.0fc”, designed by W2E Wind to Energy GmbH², described in [12]. The prototype of this WT has been built in Kankel, Mecklenburg-Western Pommerania (Germany) in 2013. It is a variable speed WT generator with medium speed converter system with collective pitch control and a rated wind speed of 12.5 m/s.

The MPC system consists of the EKF described in [9] and the proposed MPC. The sample rate of the EKF is set to 100 Hz, while the MPC is executed on a slower 10 Hz task. The prediction horizons are set to 50 steps for the prediction of the outputs and the control horizon is set to 10 steps. The solver of the optimization problem is the online active set solver qpOASES [13].

As discibed in [4], the design of the controller is developed in MATLAB/Simulink. During the design process, the controller is validated by means of a reduced order model. Afterwards it is tested in a system simulation using a multibody model in alaska/Wind, as described in [12]. The design of the WT is tested in the simulation environment of FLEX5, conforming to the standards of the GL2010 [14]. As the used version of FLEX5 offers no interface to MATLAB or Simulink, we generate a DLL-file of the controller model, which we than include into a software-in-the-loop (SiL) simulation with FLEX5 as described in [4].

4 Simulation results

There are two steps of simulations. First, we exemplarily show how the weight-scheduling effects the MPC with results from the system simulation with the reduced order model and synthetic wind conditions. Afterwards, we show the operational regions and some loads of the chosen parameter set from the SiL simulation.

4.1 Variation of weight-scheduling

Fig. 4 shows different variations of the weight-scheduling parametrization under synthetically wind conditions. For synthetic wind conditions, different steps in the wind speed are chosen for the WT to maneuver through the different operating points fast. Without weight-scheduling (orange), only above rated wind speeds are considered, because the MPC would maneuver the WT into the stall region and could not reach the operation region, above the curves of zero gradients again. For partial and full weight-scheduling, the same ranges ($y_{0},y_{1}$) are chosen and the scheduled weights differ from each other.

Fig. 4

Different controller performance for different weight-scheduling

In the time series, the MPC shows different dynamic behavior. For increasing weight-scheduling, the overshoot and the time until the reference is tracked again decrease. In the pitch angle, the characteristic of the overshoot strongly differs for the different wind speeds. This difference is further reduced for the full weight-scheduling.

The operational range in the $c_{P}$-map shows that the unscheduled MPC stays above the curve of $\partial c_{\mathrm{P}}/\partial \theta =0$. But here, the wind speed was chosen, to achieve this. Regarding the weight-scheduling, the MPC is able to leave the stall region, after the wind speed pushed the WT into this region. With the partial weight-scheduling, the operational range in the $c_{P}$-map is greater than for full weight-scheduling.

For stronger weight-scheduling, than the here presented case, the pitch angle starts oscillating, and the performance decreases again. The parametrization therefore enables the MPC to operate in both partial and full load region.

4.2 Operational regions and loads

To analyze the proposed MPC’s capability regarding field operation, we compare the MPC with a BC, which usually operates the WT and has been tuned with great effort over the recent years. Therefore, the WT is simulated in different turbulent wind conditions, which are used in the standardized design and validation process of WT manufacturers.

The operational region ranges from wind speeds of 3 m/s (cut-in) up to 25 m/s (cut-out). Therefore, the controller behavior is simulated in 10 min simulations each to fill the turbulent wind condition bins. The mean wind speed is varied in 1 m/s steps. Analyzing different turbulence intensities is necessary, because those vary in the field, too. Therefore, we used turbulence intensities of 10%, 15% and 20%, as defined in IEC 61400‑1.

As the proposed controller is designed to prove the concept of MPC in the field, it is necessary, that the MPC operates in similar ranges as the BC. To analyze if the MPC satisfies requirements of a field test, its performance and stability capabilities must be shown in simulations first. Furthermore, the operating loads need to maintain inside the boundaries for the whole operation range. Therefore, we statistically analyze the differences between both controllers by comparing characteristic values.

Therefore, we analyze the power and the rotor speed, as they are controlled variables of the BC. To achieve the control objectives, the controller consumes a certain control effort, which is here shown for the pitch angle (see Fig. 5). The second command value has a direct impact on the power, so that the analysis of the power is sufficient. As stated before, the loads are an important issue in WT control. One of the main drivers of the WT’s loads is the thrust force, thus we use this quantity to show the differences in the loads between the two controllers.

Fig. 5

Statistical values of power $P_{\mathrm{el}}$, pitch angle $\theta$, thrust force $F_{\mathrm{t}}$, and rotor speed $\Omega _{\mathrm{rot}}$ from simulations of wind speeds with a turbulence intensity of 15%. For MPC (blue) and BC (yellow), the mean values (‑), with their standard deviations (‑-) and the maximum/minimum values (⋯) are given

We use two analysis methods to compare both controllers. Firstly, statistical values (mean values, standard deviations and maximum/minimum values) give an overview over the operational range of the controllers. Secondly, we compare fatigue loads determined in simulations with damage equivalent loads (DEL) in order to analyze how much critical parts of the WT would be stressed by the field test. The DELs are defined as follows

$$\mathrm{DEL}=\sum _{i}\frac{M_{i}^{m}n_{i}}{n_{eq}},$$

(19)

with the results of the loads rainflow counting $M_{i}(n_{i})$ from the time series. The equivalent number of load cycles $n_{eq}$ is set to frequency of 1 Hz and the Wöhler coefficient is $m=5$. For the comparison of the DELs, we chose values, which represent loads of different relevant parts of the WT. These are the generator torque representing the fatigue loads of the drive train, the pitch load representing the loads of the pitch actors and the thrust force on the yaw bearing represents the fore-aft loads on the WT.

Fig. 5 shows the statistical values of the power, the rotor speed, the pitch angle and the thrust force onto the yaw bearing exemplarily for 15% turbulence intensity. As the results for the other turbulence intensities are similar, here we only discuss the results for 15% turbulence intensity. The mean values (the solid lines) show, that the power and the thrust force in the transition region between wind speeds from 7 to 12 m/s are slightly increased for the MPC, whereas the rotor speed and the pitch angle slightly differ in both directions between the controllers. The standard deviation (the dashed lines) show that the deviation of the power and especially the rotor speed is lower for the MPC compared to the BC. For the pitch and the thrust force, the differences of the standard deviations are negligible.

The extremum values of the rotor speed and the minimum values of the power are closer to the mean values for the MPC than for the BC. For the pitch angle and the thrust force, these values are remarkably similar for both controllers but are slightly increased for the MPC. This shows the operational range for the MPC is smaller or comparable to the BC.

The fatigue loads, represented by the DEL of the considered values, are given for the three different turbulence intensities in Fig. 6. For rising turbulence intensity, the DELs increase. The MPC reduces the DEL for the generator torque, for higher wind speeds by up to the half, compared to the BC. For wind speeds below 12 m/s, the MPC slightly increases the torque DEL compared to the BC and this difference increases for rising turbulence intensities.

Fig. 6

Damage equivalent loads of MPC (blue) and BC (orange) for turbulence intensities of 10% (‑), 15% (‑-) and 20% (⋯), 1 Hz equivalent loads

The DEL of the pitch actors, represented by the pitch angle rate, is increased for all wind speeds by using the MPC approximately doubling the values. For wind speeds under 8 m/s, the DEL induced by the BC is nearly zero, as the BC does not use the pitch actors in this region.

The DEL of thrust forces only slightly differ for both controllers. The difference is less the 5% between both controllers.

5 Discussion

With the previously given results, we now discuss the research questions. With the first research question we want to address is how the LTV-MPC can operate in the entire operating range from the partial to the full load range. The results show that by adding scheduled weights, the MPC shows good performance for all wind conditions. For all simulations, the MPC’s performance can compete with the BC as no operating limits were exceeded and the differences in the DEL’s are not critical to the WT. This proves that weight-scheduling allows LTV-MPC to operate in all wind conditions. Until now, results with comparable performance could be achieved mainly by using more complex algorithms like NMPC.

To answer the second research question, we will have to analyze the mechanical loads induced by the controllers. The operating regions concerning power and rotor speed are smaller for the proposed MPC compared to the BC, which also reduces the DEL’s in the full load region. The proposed MPC includes hard limits because the optimization problem is subject to constraints. The BC achieves this by choosing more defensive gains to prevent violating constraints. This results in a more conservative controller parametrization and thus in wider operational regions (see Fig. 5). Comparing the limitations of the loads representing thrust force, both control concepts result in remarkably similar extremum loads. As mainly the wind conditions and the maximum actor dynamics influence those extremum loads, this was expected.

Regarding the DEL in Fig. 6, the fatigue resulting from the thrust force (right) are very similar for both controllers. Therefore, regardless of turbulence intensity or wind speed, the fore-aft loads do not differ significantly.

For the generator torque (Fig. 6a), we can clearly observe a different characteristic. Especially for above rated wind speed over 12 m/s, the MPC reduces the DEL up to 50%, compared to the BC. For below rated wind speeds, the DEL of the generator torque is increased by the MPC—the higher the turbulence intensity rises. This increased DEL reaches up to 20% for a wind speed of 9 m/s, where the loads are already high. Above rated wind speeds, the reduction of the loads result from the control algorithm’s underlying optimization, which is designed to reduce especially the loads in this region However, the increased loads found in the simulation are not considered critical for the short time of the field test. As the present parameters for the partial load region are the result of a short tuning period, compared to the BC, the MPC still provides opportunities of parameter optimization.

The reduction of the DEL above rated wind speed is achieved by an increased pitch activity (Fig. 6b), which can be seen in the higher DEL of the pitch angle. Especially for high wind speeds, where the DELs are already high, the MPC increases them. For the MPC, the pitch is active even for small wind speeds, which is a major difference between both control concepts. Whereas the BC keeps the pitch constant for small wind speeds, the optimization in the MPC results in unsteady pitch angles, when the wind speed changes fast to reach the optimal rotor speed earlier. In the BC, this is not considered and thus the pitch angle is kept constant here. The differences thereby can be found in the rotational load, which are slightly increased in the partial load region and reduced in the full load region, was well as in the increased pitch activity.

6 Conclusion

Toward the aim of preparing the control algorithm to be applied in the field with a full-scale WT of the 3‑MW class, we showed in detail that the weight-scheduled MPC successfully performs in the entire operational range and that the occurring loads found in the simulation are not considered critical for field tests. The proposed weight-scheduling algorithm enables an LTV-MPC to operate a state of the art WT in the full wind speed range, even though the tuning took a much shorter time, than BC usually does. This MPC also provides the opportunity to use well-known QP-solvers to calculate the solution in real-time.

The chosen parametrization results in reduced loads of the drive train modules for above rated wind speed with the cost of increased loads in the pitch actors. As this is the purpose of the MPC and the loads inside the design region of the WT, it is not critical for the field tests. Especially the differences in the fore-aft loads between the BC and the MPC can be neglected. The increased torsional loads only appear for high turbulence intensities, which only seldom occur. From comprehensive simulation studies, we can conclude that this weight-scheduled LTV-MPC helps to reach the major milestone for applying model predictive controllers to commercial state of the art WTs in field tests.

Results of an already conducted full-scale field test and deviations in the behavior of the MPC between the field and the simulation is shown in the companion paper [5]. In future studies, we investigate the robustification of the MPC algorithm. With increasing computational power of the PLCs, we will also include field testing of NMPC algorithms. This will allow the controller to predict the WT dynamics more accurately. Furthermore, we will investigate the parametrization of the weight-scheduling in more detail to also reduce loads below rated wind speed.